Multi-objective Optimization of the Distributed Permutation Flow Shop Scheduling Problem with Transportation and Eligibility Constraints

Abstract

In this paper, we consider the distributed permutation flow shop scheduling problem (DPFSSP) with transportation and eligibility constrains. Three objectives are taken into account, i.e., makespan, maximum lateness and total costs (transportation costs and setup costs). To the best of our knowledge, there is no published work on multi-objective optimization of the DPFSSP with transportation and eligibility constraints. First, we present the mathematics model and constructive heuristics for single objective; then, we propose an improved The Nondominated Sorting Genetic Algorithm II (NSGA-II) for the multi-objective DPFSSP to find Pareto optimal solutions, in which a novel solution representation, a new population re-/initialization, effective crossover and mutation operators, as well as local search methods are developed. Based on extensive computational and statistical experiments, the proposed algorithm performs better than the well-known NSGA-II and the Strength Pareto Evolutionary Algorithm 2 (SPEA2).

1 Introduction

Scheduling is a decision-making process that plays important roles in both manufacturing and service industries [1]. The flow shop scheduling problem (FSSP) is one of the most common manufacture layouts in practice where all productions have the same processing sequence. The permutation FSSP (PFSSP) is a special case of the FSSP, which satisfies every job to be processed on all machines is in the same order. This results in a set of n! different candidate solutions, where n is the number of jobs to be processed. The PFSSP is proved to be strongly NP-hard when there are more than three machines [2]. A few heuristics have been proposed with aim to obtain high-quality solutions, such as shortest processing time (SPT), largest processing time (LPT), Johnsons’ rule [3], the index heuristics of Palmer [4], Campbell-Dudek-Simth (CDS) method of Campbell, Dudek and Smith [5] and so on. Among these algorithms, the Nawaz-Enscore-Ham (NEH) heuristics developed by Nawaz et al. [6] is believed to be the most effective one.

In the PFSSP, there is only one production place or factory, which means that all jobs must be assigned to the same factory. However, to meet the demand of making factories closer to customers, the managers usually locate their factories in different geographic locations. Scheduling in distributed systems is more difficult than the classical non-distributed scheduling, as we need to make two decisions: which factory to produce each job and in which order each job to be produced in its assigned factory. Compared with considerable literatures on single factory scheduling, few literatures addressed distributed scheduling. The distributed job shop scheduling problem is probably the first field to be studied in distributed scheduling by Jia et al. [7], and genetic algorithm was employed to solve the problem. Later, researchers proposed several GA-based algorithms to solve the distributed job shop scheduling problem [8,9,10,11,12]. In recent years, different types of the distributed flow shop scheduling problem with assembly lines have been studied by many researchers, such as Deng et al. [13] and Wang et al. [14]. Naderi and Ruiz [15] first studied the DPFSSP with objective makespan. In their study, six different mixed integer linear programming models for the DPFSSP and 12 heuristic algorithms were presented. The results demonstrated that the NEH method [6] with the second job to factory assignment rule (NEH2) has the best performance among the 12 heuristic algorithms. Liu and Gao [16] presented a complex electromagnetism meta-heuristic (EM) for the DPFSSP, and they extended Variable Neighborhood Descent (VND) local search which is proposed by [15] to a more powerful variable neighborhoods such as insertion within the critical factory, swap in the critical factory and general insertion and swap. Gao and Chen [17] proposed a GA with local search, in which NEH2 and VND (a) were employed for initialization. Gao et al. presented an improved NEH2 heuristics in [18] and a knowledge-based GA in [19] that performs better than $\hbox {GA}\backslash$LS. Recently, Gao et al. [20] proposed a tabu search method which outperforms the hybrid GA (HGA) of Gao and Chen [17]. Lin et al. [21] presented an iterated greedy (IG) algorithm. Wang et al. [22] proposed an estimation of distribution algorithm (EDA) which outperforms VND (a). Xu et al. [23] proposed a hybrid immune algorithm (HIA) for solving the DPFSSP, and the effectiveness of the HIA was demonstrated by comparing with some heuristics and the variable neighborhood descent methods. Naderi and Ruiz [24] present a scatter search (SS) method for the DPFSSP to optimize makespan. Compared with 10 existing algorithms, the results showed that the proposed SS has better performance than existing algorithms by a significant margin. Recently, a hybrid discrete cuckoo search algorithm was proposed by Wang et al. [25] for the DPFSSP and a fuzzy logic-based hybrid estimation of distribution algorithm was proposed by Wang et al. [26] for the DPFSSP under machine breakdown.

Practical scheduling is usually faces multi-objective decisions. The multi-objective optimization problems are originally conceived with finding Pareto optimal solutions, i.e., efficient solutions [27]. Such solutions are non-dominated, i.e., no other solutions are superior to them when all objectives are taken into account. A significant number of researches studied the flow shop scheduling problem with more than two objectives, e.g., [28,29,30,31]. The objectives include makespan, maximum lateness, maximum tardiness, total flow time, total costs and so on. Yagmahan et al. [32] presented an ant colony algorithm to solve the multi-objective flow shop scheduling problem with three objectives makespan, total flow time and total machine idle time. To minimize the sum of weighted flow time and weighted tardiness of jobs for the m-machine flow shop scheduling problem, Gelders and Sambandam [33] developed four simple heuristics to obtain approximate Pareto solutions. Ponnambalam et al. [34] proposed a GA based on the traveling salesman algorithm for the m-machine flow shop scheduling problem with three scheduling objectives, i.e., the weighted combination of makespan, mean flow time and machine idle time. This hybrid GA employed randomly generated weights to sum the objectives as a scalar fitness function. Although rich papers have been published for solving multi-objective of flow shop scheduling [35], however, seldom literatures are dedicated for solving the multi-objective DPFSSP. Till now, only Deng et al. [36] solved the bi-objective DPFSSP with respect to the minimization of makespan and total tardiness by competitive memetic algorithm (CMA). Compared with the random algorithm and the well-known NSGA-II, the CMA performed better.

As complexity of the multi-objective scheduling problem, researchers developed heuristic and meta-heuristic algorithms to solve this kind of problem. Among the meta-heuristics, the SPEA2 (Zitzler et al. [37]) and NSGA-II (Deb et al. [38]) are considered to be the most well known algorithm for providing better results. Bandyopadhyay et al. [39] presented a modified NSGA-II to solve the parallel machine scheduling problem with three objectives (total cost due tardiness, the deterioration cost and makespan) and compared the results with the SPEA2 and NSGA-II. Bolanos et al. [40] used the NSGA-II for solving the multiple traveling salesman problems. For task scheduling in grid computing, Sahu et al. [41] applied the NSGA-II to optimize the problem with two objectives: maximizing availability and minimizing makespan. In order to solve practical scheduling with release times in steel plants, Long et al. [42] proposed a new algorithm based on the NSGA-II. Autuori et al. [43] considered the flexible job shop problem with two objectives: makespan and to producing jobs just in time. The authors compared the space exploration between the NSGA-II and SPEA2.

In most manufacturing and distribution systems, the unfinished jobs (raw materials) are transferred from supplies to manufacturing factories by transporters and the finished jobs are delivered to clients or warehouses by vehicles [44]. As transportation is one of the most important parts of logistics, it has great effects on the performance of competitiveness of modern enterprises [45]. Considerable research efforts have been put on minimizing transportation costs since 1960 ([46, 47]). Specifically, in flow shop scheduling, researches usually considered the transportation time from one machine to the next machine, such as [48,49,50,51].

The constraints of factory eligibility in the DPFSSP could be considered as the extension of conventional machine eligibility constraints in FSSP. Factory eligibility puts limitation on the assignment of jobs to factory, which means that a job cannot be assigned to a factory if this job cannot be processed on at least one machine of this factory. Machine eligibility has been concentrated on parallel machines or hybrid flow shop scheduling such as [52, 53], while it has seldom been considered in the DFPSP.

Based on the above literature analysis, it could be concluded that there is no published work on multi-objective optimization of the DPFSSP with transportation and eligibility constraints. The objective of this investigation is explicitly set out to fulfill this role. In this paper, three stages are considered. In stage 1, each job needs to be transported from suppliers to one of its available factories. In stage 2, each job is produced in its assigned factory. After production, each job will be transported to the clients 1, 2 ${\cdots }$ S in stage 3. Each factory transports the productions to fixed clients or warehouses (only related to factories) in the third or last stage. The production times of job j on machine i are related to its assigned factory. For each job, it must be assigned to one of its available factories. At any factory, each assigned job goes through processing over m machines in the flow shop mode. We focus on permutation flow shop such that all the jobs are processed in the same order on the m machines. We can denote the problem by the notation of $\alpha /\beta /\gamma$ in [1]: ${\text {DPFSSP}}/{\text {Transportation}},M_j ,d_j /C_{\max } ,L_{\max } ,\mathrm{TC}$, where the factory eligibility $M_j$ and due date $d_j$ of job j are known; $C_{\max } ,L_{\max }, \mathrm{TC}$ are three scheduling objectives, i.e., makespan, maximum lateness and total costs, respectively. The overall process is depicted in Fig. 1. However, even though the problem we considered has three stages, it can be transformed into two stages by combining the first stage and the last stage into one stage, as jobs assigned the same factory have the same transportation time to the final client or warehouse. Then the problem can be cast as: in stage 1, each job needs to be transported from suppliers to one of its available factories (the transportation time (cost) of each job is the sum of transportation times (costs) from suppliers to factories and from factories to the final client or warehouse); in stage 2, jobs are processed sequentially in the distributed factories. Once the assignment is determined for each factory, it can be seen as PFSSP with releasing time.

The remaining paper is arranged as follows. In Sect. 2, we give the mixed integer mathematic programming model of the DPFSSP with transportation and eligibility constraints. In Sect. 3, several simple constructive heuristic algorithms for minimizing makespan and maximum lateness and a greedy algorithm for minimizing total costs are described. In Sect. 4, an improved NSGA-II is introduced; and in Sect. 5, computational results and comparisons with the NSGA-II and SPEA2 are provided. Finally, we conclude the paper and present the future research in Sect. 6.

Fig. 1

Framework of procedure from the suppliers to the final clients

2 Mathematic Model

This section contains three parts: the assumptions, the notations and formulation of the problem.

2.1 Assumptions

Here are all the assumptions for the problem:

• 1. Each job can be processed in at least one factory;

• 2. Each job can only be assigned to one of its available factories;

• 3. Each factory can be seen as a permutation flow shop;

• 4. Each machine of any factory can process only one job at a time; each job can only be processed by one machine of a factory at a time;

• 5. There may be different transportation times (costs) when transporting a job to different factories;

• 6. The setup cost of each factory is a fixed value when we assign at least one job to it; otherwise, its setup cost is 0;

• 7. There is a due date for each job.

2.2 Notations

Variables are as follows:

$X_{k,j,f}$::

1 if job $J_{j}$ is processed in factory f, immediately after job $J_{k}$, 0 otherwise.

$Y_{j,f}$::

1 if job $J_{j}$ is processed in factory f, 0 otherwise.

I(x)::

1 if x is positive and 0 otherwise.

$C_{j,i}$::

Continuous variable for the complete time of job $J_{j}$ on machine i.

$C_{\max }$::

Continuous variable for the complete time of all the jobs.

$L_{\max }$::

Continuous variable for the maximum lateness of all the jobs.

Parameters and indices are as follows:

F::

Number of factories.

n::

Number of jobs.

m::

Number of machines in each factory.

j, k::

Index of job $J_{j}, J_{k}$.

f::

Index of factory, $f=1,2\cdots F$.

$p_{j,i}^{f}$::

Processing time of job j on machine i in factory f.

$M_{j,f}$::

1 if job j can be processed in factory f; 0 otherwise.

$D_{j}$::

The due date of job j.

S::

A sufficiently large positive number.

$T_{j,f}$::

Transportation time of job j when transporting it to factory f.

$c_{j,f}$::

Transportation cost of job j when transporting it to factory f.

$c_{f}^{g}$::

The fixed setup cost of factory f.

2.3 Formulation of the Proposed Problem

We introduce a dummy job 0 which precedes the first job in the sequence. Three objectives can be formulated as:

$$\begin{aligned} \min \qquad&C_{\max },\end{aligned}$$

(2.1)

$$\begin{aligned}&L_{\max }, \end{aligned}$$

(2.2)

$$\begin{aligned}&\mathrm{TC}=\sum _{f=1}^{F} {\sum _{j=1}^{n} {c_{j,f}}} Y_{j,f}+\sum _{f=1}^{F} {I\left( \sum _{j=1}^{n} {Y_{j,f}}\right) } c_{f}^{g}, \end{aligned}$$

(2.3)

where makespan $(C_{\max })$ represents the maximum complete time of all jobs, maximum lateness $(L_{\max })$ means the maximum of lateness of all jobs, total costs (TC) include the transportation costs of all jobs and setup costs of all factories which process at least one job.

Subject to the constraints:

$$\begin{aligned}&\sum _{k=0,k\ne j}^n {\sum _{f=1}^F {X_{k,j,f} } } =1,\quad \forall 1\leqslant j\leqslant n, \end{aligned}$$

(2.4)

$$\begin{aligned}&\sum _{f=1}^F {Y_{j,f} } =1,\quad \forall 1\leqslant j\leqslant n, \end{aligned}$$

(2.5)

$$\begin{aligned}&\sum _{k=1,k\ne j}^n {\left( X_{k,j,f} +X_{j,k,f}\right) } \leqslant 2Y_{j,f} ,\quad \forall 1\leqslant j\leqslant n,1\leqslant f\leqslant F, \end{aligned}$$

(2.6)

$$\begin{aligned}&\sum _{j=1,j\ne k}^n {\sum _{f=1}^F {X_{k,j,f} } \leqslant 1,\quad \forall 0\leqslant k\leqslant n}, \end{aligned}$$

(2.7)

$$\begin{aligned}&\sum _{f=1}^{F} \left( X_{k,j,f}+X_{j,k,f}\right) \leqslant 1,\quad \forall 1\leqslant k\leqslant n-1,j>k, \end{aligned}$$

(2.8)

$$\begin{aligned}&Y_{j,f} \leqslant M_{j,f},\quad \forall 1\leqslant j\leqslant n,1\leqslant f\leqslant F, \end{aligned}$$

(2.9)

$$\begin{aligned}&C_{j,i} \geqslant C_{j,i-1} +P_{j,i}^f -S\left( 1-Y_{j,f}\right) ,\nonumber \\&\forall 1 \leqslant j \leqslant n,2 \leqslant i \leqslant m,1 \leqslant f \leqslant F, \end{aligned}$$

(2.10)

$$\begin{aligned}&C_{j,i} \geqslant C_{k,i} {+}P_{j,i}^f {-}S\left( 1{-}X_{k,j,f}\right) ,\nonumber \\&\forall 1 \leqslant j,k \leqslant n,j{\ne } k,1 \leqslant i \leqslant m,1 \leqslant f \leqslant F,\end{aligned}$$

(2.11)

$$\begin{aligned}&C_{\max } \geqslant C_{j,m}, \quad \forall 1\leqslant j\leqslant n, \end{aligned}$$

(2.12)

$$\begin{aligned}&L_{\max } \geqslant C_{j,m} -D_j ,\quad \forall 1\leqslant j\leqslant n, \end{aligned}$$

(2.13)

$$\begin{aligned}&C_{j,1} \geqslant T_{j,f} +P_{j,1}^f -S\left( 1-Y_{j,f}\right) ,\quad \forall 1\leqslant j\leqslant n,1\leqslant f\leqslant F, \end{aligned}$$

(2.14)

$$\begin{aligned}&X_{j,k,f} ,Y_{j,f} \in \left\{ 0,1\right\} ,\quad \forall 1\leqslant j,k\leqslant n,j\ne k,1\leqslant f\leqslant F, \end{aligned}$$

(2.15)

where constraint (2.4) controls every job has exactly at one position and only at one factory; constraint (2.5) ensures every job must be exactly assigned to one factory; constraint (2.6) represents every job can be at most one successor of a job and one predecessor of another job; constraint (2.7) assures every job has no more than one successor; constraint (2.8) avoids cross-precedence of any two jobs, which means that a job cannot be both a predecessor and a successor of another job; constraint (2.9) avoids assigning a job to an unavailable factory; constraint (2.10) represents every job is processed at most on one machine at a time while constraint (2.11) guarantees a machine can only process one job at a time; constraints (2.12–2.13) define the makespan and maximum lateness; constraint (2.14) makes sure every job cannot be processed until it arrives the assigned factory.

3 Heuristics for the DPFSSP with Single Objective

3.1 Heuristics for Makespan or Maximum Lateness

In this subsection, we propose two rules for assigning jobs to factories and eight heuristics for generating a permutation of jobs. The heuristics for generating a permutation are SPT, LPT, Johnson [3], Palmer [4], earliest releasing time (ERT), earliest due date (EDD), NEH [6] and a new heuristic NEH adaptive (NEHA) proposed in this paper based on least flexible job (LFJ) and NEH (by Taillard method [54]), respectively.

Here the new algorithm NEHA is proposed to solve the PFSSP with releasing time based on Taillard method. The procedure is described as follows.

• Step 1 Sequence the n jobs (n is the total number of jobs) by LFJ method. If two jobs have the same number of available factories, the job with a smaller total processing time in these factories will have a forward position;

• Step 2 Take the first two jobs and schedule them in order to minimize the partial makespan (or maximum lateness);

• Step 3 For $k=3$ to n do:

• Step 4 Insert job k at the place, among the k possible ones, which approximately minimize the partial makespan (or maximum lateness).

The time complexity of step 1 is $O(\log n)$ and that of step 2 is O(m). For every $3\leqslant k\leqslant n$ in step 4, it needs O(km) operations to calculate one partial makespan. Here we give an approximate algorithm to calculate the k makespan (or maximum lateness) in O(km) time:

Determining $\mathrm{CM}_{j}$, the makespan after insertion of job k at the jth position and the maximum lateness time $\mathrm{LM}_j$, $r_s$ is the releasing time of job s, $t_{j,i}$ is the processing time of thejth job on machine i.

• 1. Compute the earliest completion time $e_{j,i}$ of the jth job on the ith machine; the starting time of the first job on the first machine is its releasing time;

  $$\begin{aligned} e_{1,1}= & {} r_1 +t_{1,1},\\ e_{1,i}= & {} e_{1,i-1} +t_{1,i},\\ e_{j,1}= & {} \max \left( r_j ,e_{j-1,1}\right) +t_{j,1},\\ e_{j,i}= & {} \max \left( e_{j,i-1} ,e_{j-1,i}\right) +t_{j,i},\\&j=2,\cdots ,k-1, \ i=2,\cdots ,m. \end{aligned}$$

• 2. Compute the tail $q_{j,i}$, i.e., the real duration between the starting time of the jth job on the ith machine and the end of the operations before inserting job k;

  $$\begin{aligned} q_{j,i}= & {} e_{k-1,m} -e_{j,i} +t_{j,i},\\&j=k-1,\cdots ,1,\;i=m,\cdots ,1. \end{aligned}$$

• 3. Compute the earliest completion time $f_{j,i}$ on the ith machine of job k inserted at the jth position;

  $$\begin{aligned} f_{1,1}= & {} r_k ,f_{1,i} =f_{1,i-1} +t_{k,1},\\ f_{j,1}= & {} \max \left( e_{j-1,1} ,r_k\right) +t_{k,1},\\ f_{j,i}= & {} \max \left( f_{j,i-1} ,e_{j-1,i}\right) +t_{j,i},\\&i=2,\cdots ,m, \ j=2,\cdots ,k. \end{aligned}$$

• 4. The value of the partial makespan $\mathrm{CM}_j$ and maximum lateness $\mathrm{LM}_{j}$ when adding job k at the jth position is

  $$\begin{aligned} \mathrm{CM}_j= & {} \mathop {\max }\limits _{1\leqslant i\leqslant m} \left( f_{j,i} +q_{j,i}\right) ,\\ \mathrm{LM}_j= & {} \max \big (f_{j,m} -D_k, \mathop {\max }\limits _{j^{\prime }\geqslant j} \left( e_{j^{\prime },m} -D_{j^{\prime }} +\mathrm{CM}_j -e_{k-1,m}\right) ,\\&i=1,\cdots ,m, \ j=1,\cdots ,k. \end{aligned}$$

All these computations (2.1–2.4) can be calculated in time O(km). Considering step (4) of the NEHA algorithm which has O(km) time complexity, we conclude the NEHA algorithm runs in time $O(n^{2}m)$.

The processing (releasing) time of each job is calculated by the average of all processing (transportation) times in its available factories. Then the 8 heuristic algorithms can be used as before.

According to Naderi and Ruiz [15], two rules for assignment are proposed (1) assign a given job j to its available factory with the lowest current makespan, not including job j; and (2) assign job j to its available factory which completes it at the earliest time, i.e., the available factory resulting in the lowest makespan after assigning job j. We should make two decisions: (1) assign each job to one of its available factories (2) the permutation of each factory. Then we can obtain 16 heuristic algorithms for the combination of job assignment and job priority. Latter we will give the results of these 16 heuristic algorithms with 400 examples (150 small-sized instances and 250 large-sized instances) in Table 1 with objectives makespan and maximum lateness. The relative percentage deviation (RPD) is regarded as the results of algorithm:

$$\begin{aligned} {\mathrm{RPD}}_{g,h}=\left| \frac{V_{g,h} -V_{g,\min }}{V_{g,\min }}\right| , \end{aligned}$$

(3.1)

where $V_{g,h}$ is the objective value makespan or maximum lateness of the gth instance using algorithm $h, V_{g,\min }$ is the minimum objective value of the gth instance among all algorithms. It can be seen from Table 1 that the second rule of assignment is better compared with the first one and the new heuristic algorithm has better performance with objective makespan than the other algorithms except NEH1 and NEH2. When the objective is maximum lateness time, the permutation of EDD is better and the performance of EDD2 is almost the same as NEH2. This is partly because any two jobs may have different due date in our instances, as the due-date time of each job is different in our instances and the rule of EDD makes sure that the job with smaller due date can be completed earlier. It can be seen that EDD is an effective rule for scheduling jobs with different due dates for objective maximum lateness.

Table 1 Average RPD of the heuristic algorithm

3.2 A Greedy Algorithm for Objective Total Costs

In Sect. 3.2, we proposed a greedy algorithm for objective total costs. As the costs are not relevant to the schedule of each factory, the greedy algorithm only deals with the assignment of jobs.

The greedy algorithm can be easily described as follows:

• 1. For each job j from 1 to n,

• 2. Assign job j to factory f which has the smallest transportation cost $c_{j,f}$.

The complexity of this greed algorithm is O(nF). Even though the number of all available assignments is $\left| M_{1}\right| \left| M_{2}\right| \cdots \left| M_{n}\right|$ ($M_{j}$ is the set of available factories of job j), there has an exact algorithm which has the complexity of $O(nF2^{F})$ based on the greedy algorithm.

The exact algorithm is based on greedy algorithm:

For each subset of $\{1,2,\cdots ,F\}$,

If every job has at least one available factory, use the above greed algorithm.

There are $2^{F}$ subsets of $\{1,2,\cdots ,F\}$ and the complexity of step 2 for each subset is O(nF), so the complexity of this algorithm is $O(nF2^{F})$. Because the minimum total costs must be one of the conditions, this algorithm can be easily proved to be an exact algorithm.

4 An Improved NSGA-II Algorithm

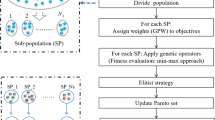
In this section, an improved NSGA-II (Non-dominated Sorting Genetic Algorithm) is proposed to solve multi-objective optimization of the DPFSSP with transportation and eligibility constraints. NSGA-II could be characterized by population based on GA and non-domination sorting which assigns rank and crowding distance to each individual (chromosome) in the population. Besides, NSGA-II is the most widely applied multi-objective evolutionary algorithm (MOEA) as observed in the existing literature, especially in scheduling. Both crossover and mutation operators based on the type of problem have been embedded in the proposed modified NSGA-II. After crossover and mutation, local search is used to find the better neighborhoods of individuals. Figure 3 shows the procedure for the improved NSGA-II. The algorithm continues to execute till the maximum experiment time. The main components of the algorithm are summarized below.

4.1 The Representation of Individuals

For each individual (an available schedule), we have to make two decisions for every job: which factory it is assigned to and which position in its assigned factory. The first decision is called job assignment, and second decision is called job priority. We encode each individual in $2\times n$ matrix if the total number of jobs is n. Here we give a theorem to explain the rationality of this encoding.

Theorem 4.1

Each individual can be encoded in a $(2\times n)$ matrix A, which represents job priority (a permutation from 1 to n) in the first row and job assignment in the second row, respectively, when the number of jobs is $n$ $;$ each $2\times n$ matrix A, which consists of a permutation from 1 to n in the first row and integers between 1 and F in the second row, respectively, when there are n jobs and F factories, is an available schedule when $A_{2,j} \in M_{A_{1,j}}$.

Proof

For any available schedule, each job must be assigned to a position of its available factory. If factory $f\;(1\leqslant f\leqslant F)$ has the production sequence (the number of jobs assigned to factory f is $N_{f}$) $f_1 ,f_2 ,\cdots ,f_{N_f}$, then the job priority can be written as $1_1 ,\cdots ,1_{N_1 } ,\cdots ,F_{N_F}$; job assignment recodes the factories where jobs are processed and if the mapping between the jobs and the factories is $\varphi :\{1,2,\cdots n\}\rightarrow \{1,2,\cdots ,F\}$. Here we have $\varphi (f_{i})=f$. Just let A be

$$\begin{aligned} \left( {\begin{array}{llllllll} 1_{1} &{}\,1_{2} &{}\,\cdots &{}\,1_{N_1}&{}\,\cdots &{}\,F_1 &{}\,\cdots &{}\,F_{N_F}\\ 1&{}\,1&{}\,\cdots &{}\,1&{}\,\cdots &{}\,F&{}\,\cdots &{}\,F \\ \end{array}}\right) . \end{aligned}$$

If a matrix A is given, we get the job priority in the first row and job assignment in the second rule. Every job will be processed in the fixed factory according to the job assignment and jobs assigned to the same factory are processed sequentially by job priority, i.e., a job with higher priority will be processed before a job with lower priority. If every job is assigned to its available factory, the matrix A represents an available schedule.

The standard encoding scheme satisfies the second row of A is non-reduced. The individuals in our proposed algorithm are encoded as a standard coding almost all the time.

4.2 Initialization

In order to obtain a population with better performance for the three objectives, the initial population are initialized by three parts with the three scheduling objectives, respectively. After obtaining $P_{{\mathrm{size}}}$ individuals as an initial population, we copy them to the archives.

• Part 1 The assignment of each job to factory is generated by using the greedy algorithm with objective TC if each job can be processed in one of the selected r (generated randomly) factories; else, continue adding factory until we get a set of factories which satisfies that each job can be processed in one of the selected factories. The sequence of each factory is generated by applying NEHA for objective makespan and EDD for objective maximum lateness.

• Part 2 First an individual is obtained by using EDD2 with objective maximum lateness. The job priority of each of the remaining individuals is randomly generated. Then, the remaining individuals are obtained by applying NEHA2 with objective maximum lateness.

• Part 3 Each individual is obtained by using the NEHA2 heuristic algorithm with objective makespan, and its job priority is randomly generated. Then we can get different solutions when using different job priorities.

Fig. 2

Procedure of crossover operator

4.3 Crossover

As there are factory eligibility constraints in the considered problem, a two-point crossover operator is applied in the algorithm based on the structure of individuals. By the following method, two generated children will be available schedules after crossover. The crossover operator is as follows (the procedure of crossover is shown in Fig. 2):

• Step 1 Generate two points randomly: first get one integer point $r_{1}$ randomly in [1, n], and then get next integer point $r_2$ randomly in $[1,n-1]$. If $r_{2}\geqslant r_1$, let $r_2 =r_2 +1$.

• Step 2 For two parents $P_{1}$ and $P_{2}$, the assignments of jobs are $A_1 (A_2 )$ for $P_1 (P_2)$.

• Step 3 Crossover $A_1$ and $A_2$ between the $r_1$th position and the $r_{2}$th position.

4.4 Mutation

According to the characteristics of the DPFSSP with eligibility constraints, two mutation operators are designed to modify the factory with largest completion time or the job with maximum lateness time in the schedule. For a given schedule, one job j is chosen by one of two methods with the same probability 1/2:

• Method 1 The job with maximum lateness time (denoted by j);

• Method 2 A job which is selected randomly from the jobs which are assigned to the factory with the latest completion time.

Then the total processing time of job j in its available factories is calculated. Suppose that the available factory of job j is $f_{1},f_2 ,\cdots ,f_{a_j}$. For $f_{i}$, the total processing time of job j in factory $f_{i}$ is $t_{j,i}=\sum \nolimits _{k=1}^{m} {p_{j,k}^{f_i}}$. Without lose of generality, the original assignment of job j is $f_{1}$, we get the probability of assignment to factory $f_{i}$ of job j

$$\begin{aligned} p_{i}=\frac{1/t_{j,i}}{\sum \nolimits _{k=2}^{a_{j}} {1/t_{j,k}}},\quad i=2,3,\cdots ,a_{j}. \end{aligned}$$

The mutation is very similar with the method of roulette wheel selection, and the implementation is the same.

4.5 Non-dominated Sorting and Crowding Distance

In this paper, we use the method of NSGA-II to get a permutation of a group of individuals (a population). The individuals (chromosomes) in the population will be assigned a rank based on non-domination sorting: All non-dominated individuals are classified into one category (its rank is denoted by 1). Deleting the individuals with rank 1, the non-dominated individuals among the remaining jobs belong to a new category with rank 2 and so on. The fast sort algorithm is used in our paper.

Once the non-dominated sort is completed, the crowding distance is assigned. The crowding distance is calculated and the larger distance is chosen to keep a diverse front by making sure that each member stays a crowding distance apart. This keeps the population diverse and helps the algorithm to explore the fitness landscape. Since the individuals are selected based on rank and crowding distance, all individuals in the population should be assigned a crowding distance value. The crowing distance is calculated as below.

For each front $F_{i}$ (the individuals set with rank i), let $n_{i}$ be the number of individuals. Initialize the distance to be zero for all the individuals, i.e., $d_h (F_i (j))=0$, where j is corresponding to the jth individual in front $F_i$ and h is corresponding to the hth scheduling objective.

• Step 1 For each objective function h, sort the individuals in front $F_{i}$ based on objective h, i.e., $I_{h}={\mathrm{sort}}(d_{h} (F_{i}))$, here $I_{h}$ represents a permutation (1 to $n_{i}$) of individuals in front $F_{i}$.

• Step 2 Assign infinite distance to boundary values for each individual in $F_i$, i.e., $d_h (F_i (I_h (1)))=\infty$ and $d_h (F_i (I_h (n_i )))=\infty$.

• Step 3 For $k=2$ to $n_i -1$.

  $$\begin{aligned} d_h \left( F_i (I_h (k))\right) =\frac{f^{h}\left( F_i \left( I_h (k+1)\right) \right) -f^{h}\left( F_i (I_h (k-1))\right) }{f_{\max }^{h} -f_{\min }^{h}}. \end{aligned}$$

  Here $f_{\max }^{h} (f_{\min }^{h})$ is the maximum (minimum) hth objective value of all individuals, $f^{h}(j)$ is the hth objective value of individuals j.

• Step 4 As we have three objectives, i.e., $h=1,2,3$,

  $$\begin{aligned} d_j =\sqrt{\left( d_1 (j)\right) ^{2}+\left( d_2 (j)\right) ^{2} +\left( d_3 (j)\right) ^{2}}. \end{aligned}$$

  Here $d_{j}$ is the crowding distance for individual (chromosome) j.

The basic idea behind the crowing distance is to obtain the Euclidian distance based on three objectives in the three-dimensional hyper space. The individuals in the boundary are always selected since they have infinite distance assignment.

When there are two individuals which have the same objectives, it may be the case that they are the same individual and one of them should be eliminated. But the above algorithm keeps both of them when they have boundary objective values. Here we give an eliminating algorithm after getting the rank and crowding distance of each individual.

Suppose the maximum rank is $r, n_{i}$ is the number of individuals in rank i and n is the number of jobs.

Non-dominated sorting is performed after local search operators are completed in the proposed algorithm and $P_{{\mathrm{size}}}$ individuals are selected into the next generation. The population individuals will be compared with the archive individuals by using non-dominated sorting and the best N individuals are selected into the archives.

4.6 Local Search

It is widely accepted that local search operators are efficient in improving the quality of solutions when using meta-heuristic algorithm. In this paper, two kinds of local search operators are designed based on the scheduling objectives makespan and maximum lateness.

• 1. Operators for the makespan criterion

Since the makespan of a solution can be reduced by modifying the schedule in the factory (denote as $f_\mathrm{c}$) with the latest completion time, four operators are proposed as follows:

• Job-swap randomly select two jobs in factory $f_\mathrm{c}$ and swap the positions of two jobs.

• Job-insert randomly select two jobs in factory $f_\mathrm{c}$ and move the latter job immediately before the former one.

• Job-inverse randomly select two jobs in the factory $f_\mathrm{c}$ and inverse the jobs between the selected two jobs.

• Factory-insert randomly select a job in factory $f_\mathrm{c}$ and insert it to a randomly selected position in one of its available factories.

• 2. Operators for the maximum lateness criterion

Since the maximum lateness of a solution can be reduced by modifying the job (denote as $J_{l}$ in factory $f_{l}$) with the maximum lateness time, four operators are proposed as follows:

• Job-swap randomly select a job which has the front position compared with $J_{l}$ in factory $f_{l}$ and swap the positions of these two jobs.

• Job-insert randomly select a job which has the front position compared with $J_{l}$ in factory $f_\mathrm{c}$ and insert $J_{l}$ to the front one.

• Job-inverse randomly select a job which has the front position compared with $J_{l}$ in the factory $f_\mathrm{c}$ and inverse the jobs between the selected two jobs.

• Factory-insert delete job $J_\mathrm{c}$ in factory $f_\mathrm{c}$ and insert it to a randomly selected position in each available factory of the other $F-1$ factories.

4.7 Selection

For every generation, after crossover and mutation, individuals of the population are selected from both parents and children, and then local search is carried out. After local search, we have to update the next population. The principle of our selection is based on the rank and crowding distance of each individual. After the update of generation, we put the original archives and the new population together. Then, the archives are updated by choosing the lower rank and the larger crowding distance.

4.8 Re-/initialization

If the objectives of the archives are not improved several times, two kinds of re-/initialization have been used:

• Case 1 If the total times reach $n_{1}$, we update half of the population by half of the randomly selected archives.

• Case 2 If the total times reach $n_2\,(n_2 >n_1)$, we update half of the population by new individuals which are generated by the following method: The job priority is obtained by random and all jobs are randomly assigned to available factories for getting P / 2 individuals.

Fig. 3

Framework of the proposed algorithm procedure

4.9 Procedure of the Improved NSGA-II

With the above design, the procedure of this algorithm for solving the considered multi-objective problem is illustrated in Fig. 3.

• Step 1 Initialize the population by the method of Sect. 4.2 and then copy the individuals to archives. Calculate the objectives of population (archives).

• Step 2 Apply crossover and mutation operators to each population without selection.

• Step 3 Select P individuals from the parents and children according to non-dominated sorting in Sect. 4.5.

• Step 4 Apply one kind of local search operators to P individuals.

• Step 5 Update the population from the generated individuals from Step 4 and the original P individuals.

• Step 6 Update the archives from the original archives and new population.

• Step 7 If stopping condition is satisfied, end with the results of new archives; else do the re-initialization operator.

• Step 8 Update the sequence of population into a substitution of the original sequence randomly and go to Step 2.

It can be seen that when the population go to the steps of crossover and mutation, we do not select parts of individuals to crossover and mutation as they are usually non-dominated solutions. All individuals will be parents, and they all have children. Of course, before the individuals of population go to the step of crossover, the sequence of individuals in population will be updated into a substitution of the original sequence randomly.

4.10 Computational Complexity Analysis

In our proposed algorithm, the initial solutions are generated based on the three proposed heuristic algorithms. According to Sect. 4.2, there are three parts of individuals and the time complexity of them are $O(P_{{\mathrm{size}}} F+P_{{\mathrm{size}}}^{2} m), O(P_{{\mathrm{size}}}^2 m)$ and $O(P_{{\mathrm{size}}}^{2} m)$, respectively, so the total time complexity for initialization is $O(P_{{\mathrm{size}}} F+P_{{\mathrm{size}}}^{2} m)$.

At each generation of the population excluding initialization, the computational complexity can be analyzed as follows.

First, we need the crossover and mutation operators for each parent when updating, so the time complexity is $O(P_{{\mathrm{size}}} \log P_{{\mathrm{size}}})$. The time complexity for non-dominated sorting and crowding distance is $O(P_{{\mathrm{size}}}^{2})$ and $O(P_{{\mathrm{size}}} \log P_{{\mathrm{size}}})$. When doing local search operators, all the eight methods have at most $O(P_{{\mathrm{size}}}\log P_{{\mathrm{size}}} +P_{{\mathrm{size}}} F)$ time complexity. The selection and Re/-initialization both have $O(P_{{\mathrm{size}}})$ time complexity. The time complexity for updating the archives is $O(P_{{\mathrm{size}}}^{2})$.

From the above analysis, we can conclude that the computational complexity is not large. The time complexity of the proposed algorithm is almost the same as both the original NSGA-II and SPEA2 (time complexity $O(P_{{\mathrm{size}}}^{2})$).

5 Experiment of the Proposed NSGA-II Method

In order to test the performance of the new algorithm, lots of instances are carried out based on two sets of benchmarks (Naderi and Ruize [15]). The first set includes 150 small-sized instances, and the other one includes 250 larger-sized instances. We will test the improved NSGA-II with two algorithms, NSGA-II and SPEA2, which are the most efficient multi-objective algorithms. The experiments have been conducted in a PC with 2.8 GHz processor and 1 GB memory. MATLAB 2014a has been used to program the proposed algorithm, the original NSGA-II and SPEA2.

5.1 The Evaluation of Results of the Experiments

The proposed algorithm is a meta-heuristic algorithm, and we expect to find the approximate optimal solution (Pareto frontier). Therefore, we give four measures to evaluate the performance of results, and there are ten runs for each instance and each algorithm. The first measure is the minimum and average values of three objectives among the final results of an algorithm ([39]). The second measure was the average number of non-dominated solutions obtained after ten runs of each instance ([55]). Next one is a quality indicator that creates a Pareto frontier composed of the non-dominated solutions from all three algorithms and calculates the percentage of solutions in each algorithm ([56]). The last measure is expressed by the equation below, which is called spacing, that reflects the uniformity of the spread of solutions in ten runs (the total number of results of ten runs is Q = 10 $\times$ 40 = 400).

$$\begin{aligned} S=\sqrt{\frac{1}{Q}\sum _{i=1}^Q {\left( d_{i} -{\overline{d}}\right) ^{2}}}, \end{aligned}$$

(5.1)

where $d_{i}$ and ${\overline{d}}$ is calculated by the following Eqs. (5.2) and (5.3)

$$\begin{aligned} d_{i}= & {} \mathop {\min }\limits _{k\ne i} \left\{ \sum _{h=1}^{3}{\left| f_{h}^{k}-f_{h}^{i}\right| }\right\} , \end{aligned}$$

(5.2)

$$\begin{aligned} {\overline{d}}= & {} \frac{1}{Q}\sum _{i=1}^{Q} {d_i}. \end{aligned}$$

(5.3)

Here $f_{h}^{k}$ represents the hth objective of the kth result (three objectives).

5.2 Parameters Setting

The proposed algorithm contains several key parameters:

$P_{{\mathrm{size}}}$ (population size), ${\overline{P}}_{{\mathrm{size}}}$ (archive size), $P_\mathrm{c}$ (crossover probability), $P_\mathrm{m}$ (mutation probability), $E_\mathrm{t}$ (experimentation time of algorithm).

In order to get high-quality solutions of the considered problem, we need to give an appropriate value to each parameter. As it is difficult to find the best results of each instance, we set the experiment time (seconds) $E_\mathrm{t} =120$ according to [55]. Here we implement an experiment by using a moderate-sized instance $(n{=}14, m{=}5, F{=}4)$.

For each parameter combination, we run 10 times of our proposed algorithm and use the volume of three objective deviations (deviation i is calculated by $\left( {\bar{f}}^{i}-f_{\min }^{i}\right) /\left( f_{\max }-f_{\min }\right)$, where ${\bar{f}}^{i}$ represents the average ith objective value) as the evaluation value (EV). Here we set $P_{{\mathrm{size}}}={\bar{P}}_{{\mathrm{size}}}$.

As $\{P_\mathrm{c}, P_\mathrm{m}\}$ (put $P_\mathrm{c}$ and $P_\mathrm{m}$ together as $P_\mathrm{c} +P_\mathrm{m} =1$) and $P_{{\mathrm{size}}}$ are independent parameters, according to the data of Table 2, we choose the value of $P_{{\mathrm{size}}} ={\overline{P}}_{{\mathrm{size}}} =40, P_\mathrm{c} =0.5, P_\mathrm{m} =0.5, E_\mathrm{t}=120$.

Table 2 Parameter setting

5.3 Comparison with NSGA-II and SPEA 2 in Small-Sized Instances

The set of small-sized instances which are randomly generated are as follows:

$n=4,6,8,12,14,16, m=2,3,4,5, F=2,3,4$ and M is a 0-1 matrix generated randomly which make sure that the sum of each line is at least one. We randomly selected 30 combinations of $n\times m\times F$ and for each combination, 5 different M are generated, so the total number of small-sized instances is 150. The transportation times and costs are generated by the following expressions $T_{i,f} =U([1,50\,m])+10\,{m}$ and $c_{i,f} =U([1,10])$. The setup cost of each factory is $c_f^g =U([1,10\,\mathrm{F}])+10$. Due date of each job is calculated by the expression $D_j =U([1,50\,{nm})+100\,{m}$. Here U([a, b]) is the uniform distribution of integers between a and b. The processing times are uniformly distributed over the range (1, 99) as usual in the scheduling literature. The results of the experiments are presented in Tables 3 and 4.

Table 3 Minimum and average values of objectives for small-sized instances (problem 1–150)

Table 4 Results of 2–4 measures for small-sized instances (problem 1–150)

Table 3 shows the minimum and average values of objectives among the three algorithms. The minimum and average results of each algorithm are calculated by the following equations:

$$\begin{aligned} {\mathrm{ARD}}_{j,m,i,k}= & {} \left| {V_{j,m,i,k}/\min \nolimits _{1\leqslant i\leqslant 3} V_{j,m,i,k} -1} \right| , \end{aligned}$$

(5.4)

$$\begin{aligned} {\mathrm{ARD}}_{j,a,i,k}= & {} \left| {V_{j,a,i,k} /\min \nolimits _{1\leqslant i\leqslant 3} V_{j,a,i,k} -1}\right| . \end{aligned}$$

(5.5)

Here $V_{j,m,i,k} (V_{j,a,i,k})$ represents the minimum (average) objective k of algorithm i of instance $j, {\mathrm{ARD}}_{j,m,i,k}\,({\mathrm{ARD}}_{j,a,i,k})$ represents the deviation compared with the best results of three algorithms. Table 3 shows that the proposed algorithm obtained the best results with respect to the minimum and average objective values.

Table 4 shows the number of Pareto optimal solutions of the three algorithms, the percentage of Pareto optimal solutions when putting solutions together and the last measure value (spacing), respectively. It shows that the proposed algorithm has the best results comparing the second and third measures with other two algorithms. For the last measure spacing, smaller values usually represent better solutions. Our algorithm outperforms SPEA2 for all problems in average. The original NSGA-II has a smaller spacing than the proposed algorithm with problem 1-100 on average, which may partly because the results are distributed more concentrated.

It can be concluded that the improved NSGA-II performs better than the original NSGA-II and SPEA2 in the small-sized instances although the fourth measurement is not perfect based on all obtained results (SPEA2 performs better than the original NSGA-II, which may because that the NSGA-II cannot eliminate the repeated boundary solutions).

5.4 Comparison with NSGA-II and SPEA2 in Large-Sized Instances

The set of large-sized instances which are randomly generated as follows:

$n=20,50,100,200,500, m=5,10,20, F=2,3,4,5,6,7$ and M is a 0–1 matrix generated randomly which make sure that the sum of each line is at least one. We randomly selected 50 combinations of $n\times m\times F$ and for each combination, 5 different M are generated, so the total number of large-sized instances is 250. The remaining data of each instance have the same generating method as the small-sized instances. The results of experiments are presented in Tables 5 and 6.

Table 5 Minimum and average values of objectives for large-sized instances (problem 151–400)

Table 6 Results of 2–4 measures for large-sized instances (problem 151–400)

Table 5 includes the minimum and average values of objectives among three algorithms, and it is the same with Table 3. It shows that the proposed algorithm obtains the best results with respect to the minimum and average objective values, which has the same analysis with the small-sized instances, and the proposed algorithm has the best results compared with the original NSGA-II and SPEA2.

Table 6 shows the number of Pareto optimal solutions of the three algorithms, the percentage of Pareto optimal solutions when putting solutions together and the last measure value (spacing), respectively, which is the same with Table 4.

It can be primarily ascertained that the improved NSGA-II performs better than the original NSGA-II and SPEA2 for both small-sized instances and large-sized instances (SPEA 2 also has a better performance than the original NSGA-II).

5.5 Statistical Analysis

To show the statistical significance of the experiment results among the three algorithms, we conduct two nonparametric pairwise comparisons (Sign test and Wilcoxon test, Zhang et al. [57]) on the results achieved by 4 measures of 400 instances (Table 7).

Table 7 Results of sign test

5.5.1 Sign Test

As the first measure is the minimum and average values of three objectives, every algorithm has $400\times 3\times 2=$ 2 400 data after putting these values together. Every other measure has 400 results for each algorithm. The average performance of the proposed algorithm is compared separately with the other two algorithms. Wins (Loses) count the times when the proposed algorithm performs superior (inferior) to its counterpart algorithm. The detected difference indicates that the improved NSGA-II outperforms the original NSGA-II and SPEA 2 with a significance level of 0.05 when using the first, the third and the last measures. The detected differences of Sign test cannot support the proposed algorithm which has better performance compared with SPEA2 when using the second measure.

5.5.2 Wilcoxon Test

Compared with Sign test, a more powerful pairwise test tool, Wilcoxon test (Derrac et al. [58]) is utilized which could take into consideration the degree of difference among searching performances. Specifically, the difference between two algorithms will be ranked according to its absolute value among all test instances. The sum of ranks that the proposed algorithm is superior (inferior) to the other algorithms is indicated by $R^{+}(R^{-})$ in Table 8. As observed from Table 8, the p values show that the improved NSGA-II performs better than the original NSGA-II and SPEA2 are at significance level of 0.05 in the first and third measure, and better than SPEA2 and the original NSGA-II at significance 0.1 in the second measure. For the fourth measure, the original NSGA-II outperforms the improved NSGA-II and the improved NSGA-II outperforms SPEA2 both at significance 0.05.

Table 8 Results of Wilcoxon test

6 Conclusions and Future Research

In this paper, we proposed a more general DPFSSP (the processing time of jobs in different factory can be different and not all factories can process each job) with transportation conditions. Three objectives are considered (makespan, maximum lateness, total costs). The mixed integer linear programming model has been formulated based on the sequence of jobs in each factory. For each objective, we proposed a new heuristic algorithm. With objective makespan or maximum lateness, the heuristics is proposed based on Taillard method. The greedy algorithm is used to solve the problem with objective total cost. An effective MOEA known as NSGA-II has been modified in order to improve the results of the considered problem in this paper. The proposed algorithm employs heuristics for each objective as an initialization. A total of 400 instances, consisting of 150 small-sized instances and 250 large-sized instances, are designed to compare the results with the original NSGA-II and SPEA 2. Running results and statistical analysis show that the proposed algorithm has better performance than both the original NSGA-II and SPEA 2. To the best of our knowledge, there is no published work on multi-objective optimization of the DPFSSP with transportation and eligibility constraints.

As for the future work, there is some room for improvement in both the model and the algorithm. Firstly, the considered problem in this paper assumes the transportation time or cost of job i to any factory which is fixed which is a strong assumption that can be generalized to limited transportation tools or quantity discounts. Secondly, more elaborated meta-heuristics can be designed to obtain better solutions and more complex local search methods can be used to search better neighborhoods.