FormalPara Key Points for Decision Makers

Cost-effectiveness analyses are often based on single-cohort models.

Use of a cohort-based approach that does not adjust for heterogeneity underestimates benefits when there is heterogeneity in efficacy and overestimates benefits when there is heterogeneity in the rates of a slow-progressing disease.

Depending on the type of heterogeneity being considered, estimates of cohort-based models failing to address heterogeneity may lead to the wrong recommendation regarding the use of a technology.

1 Introduction

Heterogeneity, defined as variation in outcomes between persons, is common in health and medicine, and arises from various sources [1, 2]. Some forms of heterogeneity can be related to baseline demographic characteristics of patients, such as age, sex and race. For example, differences in patients’ ages lead to variability in survival (i.e. greater life expectancy among younger patients). Various sources of patient heterogeneity can impact input parameters used in a cost-effectiveness analysis. Examples include impacts on treatment effects (e.g. patients’ weight affecting efficacy), disease factors (e.g. higher incidence among a given ethnic group), costs (e.g. resource use varying by disease severity), utilities (e.g. varying by age), and baseline risk (e.g. changing by observable or unknown genetic factors at the time of the decision) [1, 3, 4].

Cohort-based, state-transition (also known as Markov) models are routinely used in cost-effectiveness analysis (CEA) [5]. Numerous applications of these models make the assumption that the cohort is homogeneous with respect to baseline risk and determine the cost effectiveness of an intervention on the basis of a single set of average parameter inputs. Some CEAs incorporate heterogeneity through use of a subgroup analysis and quantify the potential health gains from restricting the use of a given intervention to subgroups of patients in whom the intervention is cost effective [1, 6, 7]. Others have extended the concept of subgroup analysis further by assessing the value of individualized treatment decisions and have shown that this value can be far greater than the value of improved decision making at the subgroup level [8]. Recently, individual-based simulation models have been increasingly employed, among other things, to incorporate heterogeneity in patient characteristics [9].

However, it is not always possible to address heterogeneity through these approaches. Sometimes, the analyst is faced with the task of using a cohort analysis to predict outcomes and make decisions for a heterogeneous cohort. There are several situations that represent this decision context. Examples include situations where (1) heterogeneity should not be considered, because of potential ethical and equity constraints (e.g. equality considerations may prohibit the use of age as a source of heterogeneity in decisions) [7]; (2) heterogeneity is related to factors unknown at the time of the decision either because it is costly or because it may not be feasible to obtain information on these factors (e.g. genetic mutations associated with a particular cancer) [3]; (3) heterogeneity is represented by a continuous variable for which only broad categories are available; and (4) there are limited skills or time to build a detailed individual-based model.

Because of the non-linear relationship between some model inputs and outcomes, the choice of the modelling technique (cohort versus individual-based simulation) can influence the outcomes of interest in the presence of heterogeneity [10]. The literature provides little guidance on how to investigate the impact of heterogeneity on CEA results. Previous research using numerical methods has shown that the choice of the modelling technique—cohort versus individual—can result in significant bias in model outcomes [11, 12]. However, the direction of the bias is not known a priori. In reviewing the small literature that has compared the two approaches, Briggs et al. [13] observed that the comparison was limited by differing model structures and inputs, and they concluded that more research of this type is needed.

In this paper, we studied the impact of ignoring heterogeneity in patient characteristics on model outcomes, using a standard disease prevention model. Our purpose was to compare health outcomes predicted by a single-cohort model (which does not capture baseline heterogeneity) with outcomes from an individual-based model (which does capture baseline heterogeneity) and to derive analytically (i.e. mathematically) the conditions that lead to upward or downward heterogeneity bias.

2 Methods

We used a standard three-state (Well, Disease and Dead) transition model to estimate the clinical benefits and cost effectiveness of a hypothetical intervention to prevent disease progression [14, 15]. Briefly, the model can be described as follows (Fig. 1). In the absence of interventions, the disease progresses at rate p per year, which results in disease-specific death at rate d per year, costs $c per year and degrades the quality of life of a sick person by q. We assumed that the hypothetical intervention has efficacy h and costs $I. All-cause mortality is given by the constant m per year. We used the continuous-time version of the model and assumed all transition rates are constant over time [16]. We assumed all parameters are positive and imposed the following additional restrictions on q and h: 0 < q < 1 and 0 ≤ h ≤ 1. The last two restrictions imply that the disease results in a proportionate reduction in the quality of life of a healthy person and that the efficacy ranges from the intervention working in all persons to it working in none of them, respectively.

Fig. 1
figure 1

Transition diagram and ordinary differential equations of the continuous-time, state-transition model of disease progression—Well (W), Disease (S) and Dead (D). d transition rate to the Dead state due to the disease, h probability of intervention halting disease progression, m all-cause death rate, p transition rate to the Disease state, QoL quality of life

Full size image

We represented the model by a system of ordinary differential equations (see the “Appendix”). We solved the model analytically to determine the number of persons in each health state over time, and we derived expressions for life expectancy, discounted (at rate r per year) quality-adjusted life years (QALYs), discounted (at rate r per year) lifetime disease costs, the incremental cost-effectiveness ratio (ICER) and incremental net monetary benefits (INMB) [17].

Next, we assumed that there is heterogeneity in all-cause mortality (i.e. m), disease progression (i.e. p), disease-specific death (i.e. d), efficacy (i.e. h), costs (i.e. c) and utilities (i.e. q). We investigated analytically the impact of heterogeneity on outcomes by varying one parameter at a time (e.g. p) while keeping all others constant (e.g. h, m, d, q and c). An outcome was calculated using the mean of the input under the cohort-based approach and the whole input distribution for all persons under the individual-based approach.

To determine whether a cohort model under- or overestimated a heath outcome, we used Jensen’s inequality, which relates the value of a concave or convex function evaluated at the mean to the expected value of the function [18, 19]. Suppose f(.) is a real-valued concave function relating an outcome function f(X) to an input parameter X. We assumed that both X and f(X) have finite expectations. Jensen’s inequality states that f(E[X]) ≥ E[f(X)], where E denotes the expected value operator (or expectation operator). Thus, if an outcome f is concave in a heterogeneity parameter X, then a single-cohort-based model, which uses the mean value E(X) to calculate f(E[X]), overestimates the outcome compared with an individual-based model, which computes E[f(X)]. In this case, by ignoring heterogeneity in X, a cohort-based model results in an upward heterogeneity bias in the estimates of outcome f(X). Jensen’s inequality is reversed for a convex function (Fig. 2), in which case ignoring heterogeneity could result in a downward bias in the estimates of outcomes.

Fig. 2
figure 2

Geometric illustration of Jensen’s inequality. The grey curve along each horizontal axis is an arbitrary discrete distribution of X. a The solid black curve shows a function f(X) that is concave in X. The two values X 1 and X 2 correspond to the values f(X 1) and f(X 2). Halfway between X 1 and X 2 is their average, E[X]. The average, E[f(X)], is halfway between f(X 1) and f(X 2): \( E\left[ {f\left( X \right)} \right] = \left[ {f(X_{1} } \right) + f\left( {X_{2} } \right)]/2 \). Thus, f(E[X]) > E[f(X)]. b The solid black curve shows a function g(X) that is convex in X. The two values X 1 and X 2, corresponding to g(X 1) and g(X 2), have an average of E[X]. The average of g(X 1) and g(X 2) is \( E\left[ {g\left( X \right)} \right] = \left[ {g(X_{1} } \right) + g\left( {X_{2} } \right)]/2 \). Thus, g(E[X]) < E[g(X)]

Full size image

To apply Jensen’s inequality, we evaluated the curvature of each outcome function with respect to each heterogeneity parameter. Because all outcome functions in this example are twice differentiable, we took the second derivative of each outcome function with respect to the heterogeneity variable and evaluated its sign (positive or negative). A positive sign of the second derivative indicates that the function is convex, signifying a downward heterogeneity bias. All mathematical expressions were derived by hand and validated using Mathematica® 9.0 (Wolfram Research, Champaign, IL, USA).

3 Results

The model solution and the derivations are shown in the “Appendix”. Lifetime outcomes as functions of parameters are presented in Table 1. We present the solution and cumulative outcomes in terms of mathematical expressions relating model outcomes (e.g. life expectancy) to model inputs (e.g. progression rate). Such analytic solutions describe relationships between inputs and outputs under different conditions, which otherwise cannot be easily obtained from numerical results. Table 2 shows the curvature of lifetime outcomes as functions of heterogeneity variables and the direction of bias when using a cohort model that ignores heterogeneity in this parameter. The derivations are given in the Electronic Supplementary Material.

Table 1 Formula of lifetime outcomes as functions of parameters
Full size table
Table 2 Curvature of lifetime outcomes as functions of parameters and direction of bias
Full size table

3.1 Heterogeneity in Disease Progression

As a function of the disease progression rate, discounted QALYs is convex, whereas discounted cost is concave. This implies that a single-cohort model that fails to incorporate heterogeneity in disease progression will result in a downward bias (i.e. underestimation) in QALYs and an upward bias (i.e. overestimation) in cost (Table 2). Because persons exiting the Well state and entering the Disease state experience higher mortality over time, we would expect QALYs to decrease at an increasing rate when the disease progression rate increases. A single-cohort analysis uses the average progression rate to calculate QALYs, which would be less than the weighted average values of QALYs computed using the corresponding individual values of the progression rate.

For low (high) values of the disease progression rate, the incremental cost function is convex (concave), whereas both the incremental QALYs and INMB functions are concave (convex). Therefore, use of a single-cohort model results in an upward heterogeneity bias (i.e. overestimation) in INMB for slow-progressing diseases and a downward heterogeneity bias (i.e. underestimation) in INMB for fast-progressing diseases.

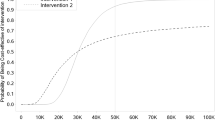
Using specific parameter values (λ = 100,000, c = 500, d = 0.05, h = 0.4, I = 10,000, m = 0.10, q = 0.05, r = 0.03, and p follows a beta distribution with a mean of p and variance of 0.04), Fig. 3 depicts INMB using individual- and cohort-based models as a function of the mean progression rate, p. It shows the direction and magnitude of bias for slow- and fast-progressing diseases. The magnitude of the heterogeneity bias (defined as the difference between the INMB obtained with the cohort-based models and that under the individual-based model) is positive and high for slow-progressing diseases and is negative and small for fast-progressing diseases (see Fig. A5 in the Electronic Supplementary Material).

Fig. 3
figure 3

Differences in incremental net monetary benefits (INMB) using individual- and cohort-based models as a function of the mean progression rate. Parameter values: λ = 100,000, c = 500, d = 0.05, h = 0.4, I = 10,000, m = 0.10, q = 0.05, r = 0.03. c cost of disease per year, d transition rate (per year) to the Dead state due to the disease, h probability of intervention halting disease progression, I one-time cost of the intervention, m all-cause death rate per year, p rate of disease progression per year, q quality of life decrement due to disease, r discount rate per year. INMB of the individual-based model was computed assuming that heterogeneity in the rate of disease progression follows a beta distribution with a mean of p and variance of 0.04

Full size image

Figure 3 also illustrates the case where the results of a cohort model suggest that intervention is cost effective over the entire range of progression rates, as evidenced by the positive INMB. However, the individual-based model clearly indicates that the intervention is not cost effective when the mean progression rate is less than 10 % per year. It should be noted that although the parameter values used in this example are realistic, they are chosen for illustration only and may not be generalizable to all situations.

3.2 Heterogeneity in Treatment Effects

Both the cost and incremental cost functions are concave with respect to efficacy. However, the relationship between efficacy and QALYs, incremental QALYs and INMB is given by a convex function. Therefore, use of a single-cohort model when treatment effects vary between persons results in an upward heterogeneity bias in the estimates of cost and incremental cost, and a downward heterogeneity bias (i.e. underestimation) in QALYs, incremental QALYs and INMB (Table 2).

3.3 Heterogeneity in All-Cause Mortality

The relationship between all-cause mortality and QALYs, cost and incremental QALYs is given by a convex function (Table 2). Thus, by failing to account for heterogeneity in all-cause mortality, use of a single-cohort model results in a downward heterogeneity bias in the estimates of cost, QALYs and incremental QALYs. The curvature of incremental cost and INMB with respect to all-cause mortality cannot be determined for all cases. For the special cases where disease-specific mortality is low (i.e. d approaches 0) or efficacy is high (i.e. h approaches 1), the incremental cost function is concave and the INMB function is convex in the all-cause mortality rate. Therefore, a single-cohort model that ignores heterogeneity in all-cause mortality results in an upward heterogeneity bias (i.e. overestimation) in incremental cost and a downward heterogeneity bias (i.e. underestimation) in INMB when disease-specific mortality is low or efficacy is high.

3.4 Heterogeneity in Disease-Specific Mortality

The relationship between disease-specific mortality and QALYs and cost is given by a convex function (Table 2). Both incremental QALYs and incremental cost functions are concave in the disease-specific mortality rate. For low (or high) values of the maximum willingness to pay (WTP) for a QALY gained, the INMB function is convex (or concave). Thus, failure to incorporate heterogeneity in disease-specific mortality results in downward bias (i.e. underestimation) in INMB when WTP is low (i.e. below a specific threshold value) and positive bias when WTP is high.

3.5 Heterogeneity in Cost and Utilities

The relationship between outcomes and quality of life decrement q and disease cost c is either linear or does not exist (Table 2). Thus, there will be no heterogeneity bias in measures of cost and effectiveness when there is heterogeneity only in disease costs or health state utilities.

4 Discussion

A single-cohort model, by using average measures of cost and effectiveness, can mask important sources of heterogeneity. In this paper, we derived mathematically the conditions under which a single-cohort model (which does not capture baseline heterogeneity) will result in an upward (i.e. overestimated) or downward (i.e. underestimated) heterogeneity bias in the estimates of health outcomes. To our knowledge, this is the first study that shows, using a simple model, that it is feasible to determine a priori (i.e. before building and solving a model) the direction of heterogeneity bias in cohort-based models. Earlier studies only established the bias by numerically comparing the outcomes of cohort and individual-level models.

We found that when there is heterogeneity in rates of disease progression, use of a single-cohort model leads to overestimation in INMB of slow-progressing diseases and underestimation in INMB of fast-progressing diseases. Therefore, reliance on single-cohort models may increase the likelihood of erroneously devoting more resources to slow-progressing diseases and denying funding to fast-progressing diseases.

Our results suggest that a single-cohort model that does not incorporate heterogeneous treatment effects overestimates cost and incremental cost, and underestimates QALYs, incremental QALYs and INMB. The implication of this finding is that by failing to incorporate heterogeneity in treatment effects, single-cohort models undervalue the benefits of the interventions and may lead to erroneous rejection of interventions that are cost effective. We also found that failure to incorporate heterogeneity in disease-specific mortality results in underestimation of INMB when WTP is low and overestimation of INMB when WTP is high, thereby raising the likelihood of rejection of worthwhile interventions or acceptance of worthless interventions.

In addition to being analytical, rather than numerical, our method for characterizing bias is general and does not require specification of the distribution function of the underlying heterogeneity parameter. The heterogeneity can be represented by any appropriate discrete distribution (e.g. binomial) or continuous distribution (e.g. gamma). All that is required of the distribution function is for it to have a finite expected value. This follows directly from the application of Jensen’s inequality [18, 19].

It is worth mentioning that our definition of an individual-level analysis is different from the regular use of the term where a large number of patients are evaluated stochastically using first-order Monte Carlo simulation. The analytical solution and results from our individual-based analysis (which is akin to conducting a deterministic analysis) would be similar to the results of an individual-level simulation with a very large number of patients.

We made several simplifying assumptions to obtain analytical results. First, we did not allow transition rates to vary by time. This may not be realistic in several situations. For example, all-cause mortality changes according to the age of the person. Second, we used only a three-state model and assumed that the disease is progressive without the possibility of recovery. Preliminary tests showed that our results are generalizable to alternative model structures that (1) allow recovery from disease; (2) include age-dependent all-cause mortality, using a Gompertz model; or (3) analyse a progressive disease model with any arbitrary number of stages. However, our results may not be generalizable to other state-transition models with different structures. Considering a more flexible model structure that allows recovery from disease and additional health states may be one of the logical extensions of this framework and is left for future research.

Finally, we investigated the impact of heterogeneity on outcomes by varying one parameter at a time while keeping all others constant. For some decision problems, heterogeneity may manifest itself in more than one parameter and may necessitate consideration of heterogeneity in all parameters simultaneously. To the extent that an outcome function has the same curvature with respect to all heterogeneity parameters, the results of our study hold. However, if the curvature of the outcome function varies by parameter (e.g. convex in some parameters and concave in others), it will not be possible to determine the direction of the heterogeneity bias without a numerical analysis.

5 Conclusion

Use of a cohort-based approach that does not adjust for heterogeneity with this three-state Markov chain structure (1) underestimates life expectancy and QALYs; (2) underestimates INMB when there is only heterogeneity in efficacy; (3) yields the same outcomes when there is only heterogeneity in disease management cost or health state utilities; (4) overestimates total costs and QALYs gained, underestimates incremental costs and overestimates INMB when there is heterogeneity in rates of a slow-progressing disease; (5) overestimates incremental cost and underestimates INMB of diseases with low fatality rates or high-efficacy intervention when there is heterogeneity in all-cause mortality; and (6) underestimates (or overestimates) INMB when WTP is low (or high) in the presence of heterogeneity in disease-specific mortality. Our results imply that estimates of cohort-based models failing to address heterogeneity may overstate or understate the potential benefits of interventions, depending on the type of heterogeneity considered.