1 Introduction

Analytical fatigue strength of welded components can be estimated using the so-called effective notch stress approach as described in the IIW recommendations [1] and related literature (see, e.g., [2,3,4]). The method requires input of a stress concentration factor either referring to maximum principal stress or von Mises equivalent stress calculated using linear elastic material.

By increasing the real notch radius in a weld root or weld toe by using a substituted and fictitious radius r in the model to calculate the stress concentration factor Kt, this value obtained can be intrinsically interpreted as an effective fatigue notch factor Kf. The effective notch stress concept as embedded in the IIW recommendations [5] was developed by Seeger and co-workers at Darmstadt University in the 1980s [5]. This concept was motivated by early work of Radaj [6] who derived a fictitious rounding of a notch stress model of welds based on the idea of Neuber’s microstructural support effect [7] assuming worst-case conditions of the real notch radius in toes and roots. Seeger’s concept is based on a modeling guideline for unified modeling of welds using a fixed radius for toes and roots to standardize the analytical stress calculation. The scatter of fatigue strength of the welds, e.g., influence of weld geometry details and material data, was fully combined in the SN curve to be applied to the stress values obtained by this standardized modeling. Those SN data have been obtained by back calculation from experimental fatigue testing of different weld joints using the same rules for modeling. Therefore, the concepts of Radaj and Seeger seem to be identical but both are based on different ideas and have been derived independently and using different assumptions. Fortunately, both methods merge into a similar modeling and have proven good quality of prognosis in many cases.

In today’s computer-driven design, those stress concentration factors obviously might be obtained by numerical simulations, e.g., finite element analysis. This process requires the creation of a suitable computer model, performing a numerical analysis and performing convergence studies to obtain a result of reliable and sufficient numerical quality. This effort deters many practitioners to perform such estimations which in turn is a reason why the effective notch stress concept often is second choice for proving the integrity of welded structures. For product safety and reliability, this method gives an alternative and diverse method to evaluate structural integrity of welded structures. The method also covers some size effect since the same notch radius for thicker welds results in higher stress concentration factors. Also, analysis of the influence of flank angles is possible which increases the applicability of this method compared to the nominal or structural stress concepts.

As an alternative to performing time-consuming numerical simulations, different authors have developed a number of empirical formulae obtained by regression analysis of existing solutions since decades. In the first days, those empirical formulae have been the only economic way to supply the factors. With increasing capabilities in finite element simulation, these methods have taken a back seat though. Reliable empirical formulae—because of their efficiency—are worth thousands of simulations. If those equations supply results of high quality with respect to the exact or reference solutions, their application will save a lot of time, effort, and cost. Therefore, those methods are still valuable to be applied for using the effective notch stress approach efficiently.

2 Numerical simulation of welded cruciform joints

Welded cruciform joints were considered in this study. The sheets might be welded by simple double fillet welds, K-butt welds with double fillet welds, or double-sided Y-butt welds, both with full or partial penetration. No axial or angular misalignment is considered. If misalignment is present in the structure, it needs to be contained in the stress analysis as secondary effect or by reducing allowable stresses. Since the raw data from tests at Darmstadt University is based on fatigue testing of T-joints under primary bending, secondary stresses occurring from angular or axial misalignment are not contained in the SN data as for example included to some extent for the nominal stress approach.

2.1 Parameterization

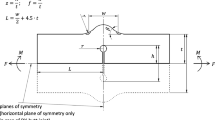
At first, a finite element model of the cruciform joint with parametric geometry was modeled using ANSYS Mechanical™ 18.1Footnote 1 (see Fig. 1 and Table 1) [25]. This model enables numerical assessment of stress concentration factors at the weld toe and the weld root, respectively, for loading in pure tension as well as pure bending for a large parametric design space. Full as well as partial penetration welds are considered.

Fig. 1
figure 1

Parameterized geometry of the cruciform joint with symmetric fillet welds and weld root faces

Full size image
Table 1 Parameter ranges of numerical model
Full size table

The following assumptions are used:

  • Symmetric geometry

  • No axial or angular misalignment

  • No nonlinear contact in the root face

  • Equal reference radii of weld toe and weld root, modeled as fillet radii

  • Plain strain condition

  • Constant parameters for linear elastic material:

    • Module of elasticity E = 210 GPa

    • Poisson ratio ν = 0.3

  • Uniform tension or bending nominal stress of St = Sb = 1 MPa applied along the sheet end faces t1 (see Fig. 1)

  • Evaluation of maximum principal stress σ1

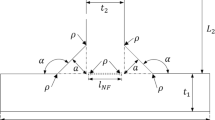
The use of the effective notch stress approach requires a reference radius depending on the sheet thicknesses t1 and t2. For this model, extended recommendations for the radius selection according to Merkblatt DVS 0905 [3] have been used. Those recommendations represent an extension to the IIW recommendations for thin- and thick-walled welded structures [1]. The range of the sheet thickness was divided into six subranges where an adequate reference radius can be assigned (see Table 2). For weld joints with root face, the minimum sheet thicknesses t1 and t2 are at least 10 times the reference radii to prevent the top and bottom root fillets of the idealized root face geometry from overlapping. In order to analyze a wide range of leg lengths without creating unrealistic geometries, the range of leg length l1 is also between 0.5 … 2 t1 (see Table 1). The ranges according to Table 1 exceed the allowable values for almost all of the existing empirical rules to calculate the notch stresses. It was a main goal of this project to increase the design space of new empirical rules towards more general applicability and versatility.

Table 2 Parameter ranges for space-filling Latin hypercube samplings
Full size table

2.2 Discretization

To enable tension as well as bending loading, half of the joint was modeled and symmetric boundary conditions were applied (see Fig. 2) using the symmetric geometry of the cruciform joint.

Fig. 2
figure 2

Finite element model for effective notch stress analysis including boundary conditions. Left side: notch areas with mapped mesh of hex element with mesh size 0.05r. Right side: evaluation of the first principle stress at the weld toe and root face

Full size image

In order to analyze the notch stresses correctly, the generally coarse global mesh is refined at the weld toe and the weld root. A preliminary convergence study showed convergent notch stresses using a mapped mesh of quadratic PLANE183 elements [27] with element lengths of 0.05r in the notch until a depth of 0.4r (see Fig. 2).

2.3 Applicability of 2D modeling vs. 3D structures

As mentioned above, a 2D modeling approach with plain strain condition was used for finite-element calculation of the first principle stresses in the weld toe and root. Nevertheless, the differences between the plain strain and plain stress condition in simulation must be taken into account. A minimum total width of the sample has to be met to establish a plain strain condition in the middle of the sample.

2.4 Sampling

To analyze the accuracy of existing approaches, the stress concentration factor is determined for different geometric designs using the finite element model as shown in Fig. 2. The system was split into six subsystems in dependency of wall thicknesses and their corresponding reference radii as well as existent or nonexistent weld root faces (see Table 2), according to the recommendations for the ratio of wall thickness to reference radius given in [3]. For each subsystem, a space-filling Latin hypercube sampling was created with optiSLang® 6.1.0Footnote 2 [26]. The number of samples was determined to be 1000. In summary, 5973 samples were generated automatically; the finite element simulation of the remaining 27 samples failed due to modeling failure in the batch run because of extreme parameter combinations. The corresponding stress concentration factors were evaluated with an additional number of 2238 samples, as far as no restrictions by the evaluation methods were given. These additional samples were generated to cover all restrictions given by all methods, even the ones outside the application ranges of the new methods.

Figure 3 shows the sampling results by two representative anthill plots. Homogenous dispersion of the samplings within the allowable ranges of the selected parameters can be seen.

Fig. 3
figure 3

Exemplary schematic representation of the space-filling Latin hypercube sampling for two parameter combinations—analogous for all other parameter combinations

Full size image

2.5 Resulting stress concentration factors

A relationship between the notch radius and the stress concentration factors resulting from the simulations is not apparent on the first glance (see Table 3, which lists the simulated radii and the corresponding stress concentration factor ranges).

Table 3 Simulated radii and corresponding stress concentration factor ranges
Full size table

Due to the ranges for application of the different notch radii, the stress concentration factors are within about the same ranges for each radius. This is due to the size recommendations for each radius. Table 3 demonstrates that the suggested ranges for application of the different notch radii with respect to weld size as summarized in Table 2 is reasonably chosen. Please note that also stress concentration factors below 1000 are possible in the case of concurring notches if a notch is in the stress shadow.

3 Known methods of notch factor estimation of cruciform welded joints

Equations to support efficient estimations of stress concentration factors applying the effective notch stress approach have been derived by different authors for many decades already. Early notch factor determination methods were based either on experimental data or on photoelastic methods [2]. Procedures that are more recent are mainly based on numerical finite element simulation, but also these procedures lack precision because of limited computing capacity in the end of the last decade. Nevertheless, a variety of methods for notch factor determination have been proposed as listed by [2].

To mention are the methods by Yung and Lawrence [8, 9], Rainer [10,11,12], Radaj et al. [13,14,15], Anthes et al. [16, 17], and Ushirokawa et al. [18] and Tsuji [19]. A selection of these procedures for cruciform joints is described in this section.

All of the following equations as well as the new methods in the following chapters of this paper are based on maximum principal stress σ1.

3.1 Method by Yung and Lawrence

On the basis of Lawrence’ procedure [8] based on finite element simulations, Yung and Lawrence described a refined method in 1985, including a variety of data from other publications [9].

Their approximation formulae are valid for cruciform joints with and without root face under tension and bending loading, limited by the ranges as given in Table 4.

Table 4 Restrictions of Yung and Lawrence’s method
Full size table

Yung and Lawrence are using the weld toe angle α, the plate thickness t1, the notch radius r, the ratio of root face to sheet thickness z, and the leg length l1 for their approximation formulae given in Table 5. The factor y · sin α represents the ratio between the weld thickness and wall thickness, converted to parameters y and α used in this paper.

Table 5 Method by Yung and Lawrence
Full size table

3.2 Method by Rainer

Rainer conducted an excessive study on notch factors of welded components in 1985 [10, 11]. The results of his study are summarized in Haibach’s “Betriebsfestigkeit” [12]. His stress concentration factors are derived from finite element simulations with relatively high accuracy, using high-order elements and fine meshing.

He is offering approximation formulae for cruciform joints with and without root face under tension and bending loading, valid for parameter combination ranges given in Table 6.

Table 6 Restrictions of Rainer’s method
Full size table

Rainer is using the leg length l1, the notch radius r, the wall thickness t1, and the ratio of root face to sheet thickness z in his formulation. His formulae are given in Table 7.

Table 7 Method by Rainer
Full size table

3.3 Method by Radaj

Radaj also published stress concentration factors for a large variety of welded joints [13,14,15]. His investigations are generally based on a boundary element simulation of nine different parameter combinations and a worst-case consideration of the results with a 1-mm replacement radius in the weld toe and root.

Therefore, Radaj’s formulae are restricted to cruciform joints with root face and a constant weld angle of 45°. Further restrictions by Radaj are given in Table 8. His formulae are only valid for tension loading.

Table 8 Restrictions of Radaj’s method
Full size table

He uses the parameters leg length l1, wall thicknesses t1 and t2, and notch radius r. Radaj’s formulae are given in Table 9.

Table 9 Method by Radaj
Full size table

3.4 Method by Anthes et al.

The method by Anthes et al. [16, 17] is based on boundary element simulation results, being valid for tension and bending loading.

Anthes et al. restrict their method to certain parameter combination ranges (see Table 10).

Table 10 Restrictions of Anthes’ method
Full size table

Their method uses the parameters leg length l1, wall thickness t1, notch radius r, weld angle α, and ratio of root face length to wall thickness z. Table 11 gives Anthes’ formulae.

Table 11 Method by Anthes et al.
Full size table

4 New methods of notch factor determination

Metamodeling is an umbrella term for modern regression methods. Among those methods, one can find linear models as well as nonlinear ones like response surface methods, vector machines, kriging, random forests, neural networks, and Gaussian processes. Usually, it is not possible to know which method performs best for a specific problem.

From those, polynomial regressions involving coupling terms to generate response surfaces and neural networks have been selected for this study. The selection of polynomial regression is a reasonable approach because the resulting formulae can easily be applied with a pocket calculator only. Neural networks have been chosen because some promising results, e.g., in estimation of material properties, have been recently made (see e.g. [20]). The results are presented in the following.

4.1 Polynomial regression with coupling terms (PRC method)

In optiSLang® 6.1.0, polynomial regression functions with quadratic order and coupling terms are fitted using the numerically calculated stress concentration factors from finite element analysis [21]. The calculation is carried out according to Eq. (17). The factors according to Table 14, Table 15, and Table 16 can be chosen according to Table 13.

$$ {K}_{t,\mathrm{PRC}}=\sum \limits_{k=1}^{15}{c}_k\cdotp {f}_k\left(\alpha, {t}_1,y,z\right) $$
(17)

Since four parameters (α, t1, y, z), their squares, each combination of two parameters, and an additional constant term are used, a total number of 15 terms is used in the regression formulas. In order to simplify the regression model, an automatic variable reduction is done during regression. Only variables which meet the conditions of the significance and importance filter are considered in the regression function [22]. The standard filter setting of optiSLang is used. Therefore, an easier applicability while maintaining almost the same predictive quality is achieved. In total, 18 regression formulas have been developed, one for each combination of stress location (weld root or weld toe), loading (tension or bending), and reference radius (see Table 13).

Also, the PRC method has to be restricted to certain geometry parameters according to the simulated parameter combinations which were used for regression (see Table 12).

Table 12 Restrictions of the PRC method
Full size table
Table 13 Stress concentration factor for maximum principal stress formulae according to the new method
Full size table
Table 14 Regression formulae for the PRC method for fully penetrated welds
Full size table
Table 15 Regression formulae for the PRC method for partially penetrated welds at weld toe
Full size table
Table 16 Regression formulae for the PRC method for partially penetrated welds at root face
Full size table
Table 17 Restrictions of the ANN method
Full size table
Table 18 Formulae of the ANN method
Full size table
Table 19 Neural network data for full penetration joints
Full size table
Table 20 Neural network data for partial penetration joints
Full size table
Table 21 Overview of all restrictions given by the authors
Full size table
Table 22 Statistical data of all evaluated parameter combination, sorted by evaluation method, quantiles counted, and percentage of samples used for the respective method
Full size table

4.2 Application of artificial neural networks (ANN method)

Data fitting of the calculated finite element results was done with Matlab’s Neural Network Toolbox. The classical feed-forward neural network used consists of three hidden layers. Each hidden layer consists of six neurons in accordance with the number of input variables (t1, t2, l1, α, z, r). The output layer consists of four neurons for each output variable in the case of partial penetration (kt = (Kt, ANN, root, b, Kt, ANN, root, t, Kt, ANN, toe, b, Kt, ANN, toe, t)), respectively, two neurons for each output variable in the case of full penetration (kt = (Kt, ANN, toe, b, Kt, ANN, toe, t)) (see Fig. 4).

Fig. 4
figure 4

Schematic structure of the artificial network

Full size image

After normalization of the input variables to avoid overestimation or underestimation of the inputs influence, each layer multiplies its inputs with a weight matrix Wi and shifts it by a bias bi, which results in the layers potential ϕi. The potential is then put into a hyperbolic tangent sigmoid transfer function in the case of the three hidden layers or a linear transfer function in the case of the output layer, which finally gives a vector of outputs in terms of stress concentration factors after renormalization.

One of the most important benefits of this method is that the neural network is able to handle all load cases at once and to give all results at once, making it only necessary to choose between the neural network for fully penetrated welds or partially penetrated welds. Nevertheless, restrictions in terms of parameter ranges according to Table 17 have to be given, defined by the parameter ranges of the training data.

For more information on the mathematics of neural networks, see for example Hagan et al. [23]. The multilayer approach with a low number of neurons in each hidden layer resulted in better estimation of stress concentration factors than a single-layer approach with a high number of neurons in the layer. Additionally, benefits in training and evaluation time could be accomplished.

The mathematical expressions for the used network can be found in Table 18;Footnote 3 the corresponding normalization vectors, weighting matrices, and bias vectors can be found in Table 19 and Table 20.

4.3 Comparison of notch factor determination and quality

All aforementioned existing and new methods have been applied to the data taken from the finite element simulation and compared with its results. Keep in mind that limitations to the methods were given:

  • All authors give limitations to their methods, summarized in Table 21. Some of them are significantly restricting the allowable design space compared to the new approaches as presented in this paper.

  • As a further restriction, the method by Yung and Lawrence was not used for calculation of stress concentration factors at the root face in the case of bending loading. This is because resulting stress concentration factors obtained by this method and compared with the finite element simulations have gained results differing by a factor 3 and higher.

  • Stress concentration factors below unity were neglected. Please be advised that the ratio of notch stress to structural stress Kw = σe/σw has to meet a lower limit Kw, min for the corresponding stress concentration factor to be permissible for use in the notch stress concep; see Rother and Fricke [24]:

    • Kw, min = 1.6 for r = 1 mm

    • Kw, min = 2.13 for r = 0.3 mm

    • Kw, min = 3.56 for r = 0.05 mm

These ratios have been exceeded by 58.1% for the bending load case and 79.3% for the tension load case of the data with structural stresses derived by quadratic extrapolation according to [1]. Nevertheless, samples not exceeding these ratios were used in regression as well, since these ratios always have to be checked by the user himself, depending on parameter combination and loading.

Additionally, linear extrapolation with two support points and the determination methods in a distance of 1 mm and 2 mm from the weld toe for structural stress identification were considered. It was found that the quadratic extrapolation method leads to the lowest structural stresses and therefore to the most nonconservative results for Kw, min.

Due to the given limitations, summarized in Table 21 and shown in Fig. 5, some of the results have to be neglected. The graphical overview shows the minimum and maximum allowed value of each parameter or parameter ratio on the x-axis (0–100%) and each limited parameter range true to scale. If a method does not give restrictions for the parameter or parameter ratio, it is not shown for these parameters. The method by Radaj restricts the value for z in a way that also constructively impossible parameter combinations (z > 1) can occur.

Fig. 5
figure 5

Graphical overview of the methods’ restrictions—overlapping, joint areas marked in red

Full size image

Figure 6 shows boxplots for those restrictions with simulation data fulfilling all restrictions given by the different authors simultaneously as shown by the red boxes in Fig. 5. In Fig. 7, the boxplots are generated with data fulfilling the restrictions the authors have given individually for each method. Additionally, Table 22 shows the percentage of data that had to be neglected in comparison to the total data available for evaluation. Remarkable are the low error values for the PRC and ANN methods that demonstrate the much larger range of application of those metamodels.

Fig. 6
figure 6

Boxplot and probability plot of the relative errors for normal distribution—generated with data fulfilling all restrictions simultaneously

Full size image
Fig. 7
figure 7

Boxplot and probability plot of the relative errors for normal distribution—generated with data fulfilling the individual restrictions given for each method

Full size image

Both figures show the resulting relative errors for all investigated methods as boxplots on the left side. The red line in the central blue boxes indicates the median relative error which should ideally be zero. The blue box around it shows 50% of the data points with their upper and lower boundaries indicating the 25% and 75% quantiles. The black lines, so-called whiskers, embed 98% of the data from the 1% to the 99% quantile. Finally, the red crossed data outside of the whiskers indicate data points being below the 1% or above the 99% quantile. On the right side, both figures show probability plots of each method for normally distributed data. Perfect normal distributed data would adapt to the linear regression line.

For the following, the relative error is calculated by

$$ {\mathrm{err}}_{\mathrm{rel}}=\frac{K_{t,\mathrm{EST}}-{K}_{t,\mathrm{FEM}}}{K_{t,\mathrm{FEM}}} $$
(23)

In Fig. 6 showing the simultaneous fulfillment of all restrictions, the method by Anthes et al. as well as the two new methods cluster the estimated stress concentration factors around the correct values from finite element simulation. The method by Yung and Lawrence is clearly shifted to the unsafe side, mainly underestimating the correct stress concentration factors. Rainer’s and Radaj’s methods are generally shifted to the safe side. The linear regression line for the method of Yung and Lawrence on the right hand side show that most of the data is clustered in the area from − 25 to − 12% relative error, resulting in the linear regression going mainly through that area.

In terms of scattering, the new ANN method shows the lowest scattering comparing to 25% and 75% quantiles, followed by the PRC method and the method by Anthes et al. The methods by Yung and Lawrence as well as Radaj and Rainer clearly show higher spacing between these two quantiles. Comparing the 1% and 99% quantiles, the ANN method and the method by Anthes et al. show the lowest scattering, with 98% of the data only deviating about −12% to the unsafe side and 10% to the safe side, followed by the PRC method as well as the methods by Rainer and Radaj. Yung’s and Lawrence’s method shows the highest deviations from the mean.

When looking at the evaluation in Fig. 7 which only shows samples fulfilling the individual restrictions for each method, the general behavior is very similar. The ANN and PRC method as well as the method by Anthes et al. while clustering around a median of 0% relative error show the lowest scattering for 50% and even for 98% of the data. Please be aware that the red crosses outside of the whiskers always show only 2% of all simulated samples. Since The PRC and ANN methods can evaluate almost all or all parameter combinations while all other methods have to neglect at least 78.54% of the data (see also Table 22), the presentation of the new methods contains at least about five times more data than the presentation of the known methods. This holds true also for the number of outliers shown in the presentations. In total numbers, 2% outliers of the evaluated data means 18 data points for Radaj’s method, 80 − 100 data points for all other known methods, and over 400 data points for the new PRC and ANN methods, for only the latter using almost 100% of all samples generated for this study.

Additional investigations for a fixed flank angle of 45° did not show significant reduction in scattering.

These outliers could be evaluated in extreme parameter combinations being less relevant in practice. These are very small sheet thicknesses less than 1 mm in combination with small leg lengths or radii.

The new methods using PCR and ANN have been programmed and made available to the community by http://rother.userweb.mwn.de/scf-predictor.html [28]. With this application, user-friendly and quick computations of stress concentration factors using Eqs. (17) till (22) can be performed.

5 Conclusion

To investigate the quality of selected existing analytical estimation methods for stress concentration factors for cruciform welded joints with full and partial penetration (with and without root face) under tension and bending loading, numerical simulation using many samples and a broad range of parameter variations were conducted. The resulting stress concentration factors with respect to maximum principal effective notch stress were used as reference solutions for comparison of the estimated factors.

Selected methods for the estimation of stress concentration factors by empirical formulae have been investigated and presented in summary, also considering their respective ranges for application as given by the authors for the geometrical parameters. Additionally, two new methods for metamodeling were introduced and suggested for future use: one analytical method based on polynomial regression involving mixed terms and one method using artificial neural networks. In both cases, the ranges of application cover a significantly improved versatility by allowing very large ranges of the different parameters involved. Using the two proposed methods, thin-, medium-, and thick-walled welded cruciform joints are covered as well as three different notch radii and a varying flank angle. Both methods yield stress concentration factors of similar quality and low scatter with respect to error from numerical reference values.

It can clearly be shown that using the new methods can give a significant improvement on both the mean estimation of stress concentration factors and on reducing the scatter in estimated results by simultaneously increasing the range of applicability significantly compared to existing approximate methods. The methods suggested in this paper provide a reliable basis for an efficient, quick, and reliable estimation of assessing relevant stress concentration factors for different notch radii used in the effective notch stress concept according to IIW and related guidelines. Thus, time-consuming creation and analysis of numerical models can be avoided without significant lack of accuracy. The new methods presented might also be included in higher-level applications for design and efficient optimization of welded structures involving cruciform joints. The stress concentration values obtained by the new methods are valid for plane strain conditions and maximum principal stress.