1 Introduction

Resistance spot welding (RSW) is a widely used welding process to weld sheet steels. It is so widely used that there are 3,000–7,000 spot welds [1] in a typical automobile. Because of the importance of RSW, there has been much effort to model the welding process. These models typically focus on correlating welding parameters to weld geometry and are solved using finite element analysis (FEA) [2, 3]. Although these models are able to predict welding size directly from base material properties and welding parameters, they cannot easily be used to predict the change in properties across the weldment.

Generally, the prediction of weld properties is not an issue in conventional strength steels such as high strength low alloy (HSLA) steels, where the hardness across the weldment is only a function of cooling rate and weld strength can be easily related to nugget size [4]. However, in advanced high strength steels (AHSS) such as dual-phase (DP), transformation induced plasticity (TRIP) and martensitic steels where the base material contains metastable phases such as martensite and retained austenite, the sub-critical heat-affected zone (HAZ) tempers so its hardness is reduced from its base material hardness. When HAZ softening occurs, failure may occur in the softened region at lower than expected joint strengths. This was seen by tests showing that the joint strengths of dissimilar DP600–DP780 welds were equivalent to DP600-HSLA welds because the strength of the softened HAZ of the DP780 was equivalent to that of the HSLA base material [4]. Some researchers have used complex modelling techniques such as neural networks to predict complex changes in weld properties when areas of the weldment are tempered [5]. However, this technique requires much computing power and data to teach the model, making it an inaccessible technique for industry as well as researchers having limited resources. Therefore, a simpler technique is needed that can use existing geometrical weld data, generated either by direct measurement or accessible FEA models to predict weld properties.

This study puts forward a simple technique to predict the hardness profile across RSW in martensitic steels. This will be done by first separating the two issues of determining temperature history and determining how material chemistry affects metallurgical transformations within the material. Temperature history determines the cooling rates, peak temperatures and tempering time along the weld. Material chemistry determines both the hardenability of the steel in the super-critical HAZ, where the peak temperature during welding exceeded the Ac 1 temperature, and the resistance to tempering in the sub-critical HAZ, where the peak temperature during welding remained below the Ac 1 temperature. Once the thermal history is calculated at each point along the weld and the effect of material chemistry on the reactions that occur during welding is known, the thermal history may be used to determine the local transformations and the whole hardness profile may be constructed.

2 Predicting thermal history of a resistance spot weld

2.1 Calculating the instantaneous temperature throughout the weld

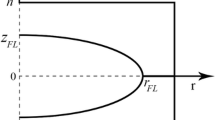
In this work, the temperature field was determined using the two-dimensional Rosenthal equation, which describes the conduction heat transfer of a stationary temperature field heated by a line energy source (see Fig. 1). Although it is acknowledged that the heat transfer in RSW violates the line heat source and two-dimensional heat transfer assumptions that this is based on, and Rosenthal cannot accurately predict the temperature field in the molten pool, this technique has been successfully used to model the temperature fields in previous work [6–8]. It is believed that in high heat input RSW, when the thickness of the nugget approaches that of the material stackup, heat flow in the material will be two dimensional. The heat loss to the electrodes and the width of the energy source will be addressed by an efficiency term that will be calibrated to the weld geometry.

Fig. 1
figure 1

Representation of the heat input in LBW and RSW used in the Rosenthal equation

Full size image

The specific form of the Rosenthal equation for spot welding is shown below [9]:

$$ T-{T}_0=\frac{\eta {u}_{\mathrm{RMS}}{i}_{\mathrm{RMS}} \cos \left(\varphi \right){t}_{\mathrm{RSW}}}{ d\rho c4\pi at}{e}^{\raisebox{1ex}{$-{r}^2$}\!\left/ \!\raisebox{-1ex}{$4 at$}\right.} $$
(1)

where T and T 0 are the instantaneous and initial temperatures, η is the thermal, u RMS is the root mean squared (RMS) welding voltage, i RMS is the RMS welding current, cos(ϕ) is the power factor, t RSW is the welding time, d is the thickness of the joint stackup, ρ is the density of steel (7,860 kg m−3), c is the specific heat capacity of steel (680 J kg−1 K−1), λ is the thermal conductivity (30 W m−1 K−1), a is the thermal diffusivity (λ/ρc), t is time after the welding pulse and r is the distance from the centre of the nugget. The values of λ, ρ and c are supposed to be invariant with steel grades and temperature. The term u RMS i RMScos(ϕ)t RSW represents the heat input due to the joule effect. To determine u RMS, the voltage curve during welding of different steels of various sheet thicknesses and coatings was carried out on three different 50 Hz AC spot welding machines. The average value of u RMS ranged from 0.9 V to 1.2 V. It was then determined that the value of u RMS changes with no obvious link to steel, machine, thickness or coating, so a value of 1 V was chosen for this study.

The only unknown parameter needed to calculate the temperature profile of the weld is the thermal efficiency, η. The thermal efficiency was fit to measurements taken from the cross sections from actual welds by comparing the actual and predicted distance between the weld centreline and the point on the weld where the peak temperature during welding reached the material Ac 1 temperature (T Ac1). This was noted as r Ac1 (see Fig. 2).

Fig. 2
figure 2

Cross section of a RSW showing r Ac1

Full size image

2.2 Determining thermal efficiency, η

The product u RMS i RMScos(ϕ)t RSW is the energy that the resistance spot welding machine imparts to the material; however, as energy is lost from the joint, a thermal efficiency must be applied to the calculated energy value to determine the real heat input absorbed by the material. The application of an efficiency term to the energy value means that the real energy responsible for the temperature rise in the stackup is ηu RMS i RMScos(ϕ)t RSW.

η was determined experimentally by correlating r Ac1 in the welds studied to r Ac1 predicted by the Rosenthal equation. η may be calculated using one of two methods. The first is by comparing the r Ac1 predicted by Rosenthal to either measurement from an actual weld or calculated value from a validated RSW simulation package. The second method to calculate η is by using a relation that empirically fits the welding parameter used to η.

To calculate η using a known weld geometry, the peak temperature throughout the weld zone must be known. This may be solved using the Rosenthal equation. By differentiating the Rosenthal equation with respect to time and equating the result to 0, the time taken for a particular point away from the weld to reach its maximum temperature may be calculated. This is equal to

$$ {t}_{\mathrm{pk}}=\frac{r^2}{4a} $$
(2)

where t pk is the time necessary to reach the peak temperature at a general distance from the weld centreline. If t pk is substituted back into Eq. 1 and T is equated to the Ac 1 temperature, then r Ac1 may be solved as follows:

$$ {r}_{Ac1}=\sqrt{\frac{\eta {u}_{\mathrm{RMS}}{i}_{\mathrm{RMS}} \cos \left(\varphi \right){t}_{\mathrm{RSW}}}{ d\rho c\pi e\left({T}_{Ac1}-{T}_0\right)}} $$
(3)

By comparing Eq. 3 to actual or simulated weld geometries, η may be calculated.

Alternatively, η may also be calculated using an empirically derived relation based on thermal heat balance correlating η to welding parameters and electrode size. This correlation was based on welding results carried out on various press hardened, DP, TRIP and martensitic steels with AlSi, galvanized, galvanneal and no coating [10]. The correlation is as follows:

$$ \eta ={\left\{1+\frac{2{r_{\mathrm{e}}}^2{d}_{\mathrm{HAZ}}}{{\left( AI+B\right)}^2\left(d-2{d}_{\mathrm{HAZ}}\right)}\right\}}^{-1} $$
(4)

where r e is the electrode diameter, d HAZ is the distance between the weld nugget and the outside edge of the stackup (typically this is about 0.1 mm) and A and B are fitting constants, which are equal to 5 × 10−8 m/A and 8 × 10−5 m, respectively. d, d HAZ and r e are represented on Fig. 1. The validity range of this thermal history is r e from 3 to 4 mm, i RMS from 6.1 to 12.2 kA, t RSW from 0.26 to 1.1 s and d from 1.6 to 8 mm.

2.3 Comparison of predicted and measured HAZ thermal history

The ability of the Rosenthal equation to predict temperature history was verified by comparing its predicted results against those generated using Sorpas (ver. 8.2, SWANTEC Software and Engineering ApS, Lyngby, Denmark), a commercial modelling package designed to model RSW. To do this, the Rosenthal prediction and the Sorpas calculations were compared both in terms of local temperature history in a weld and the predicted distance between the weld centreline and the area where an arbitrary peak temperature was achieved during welding, r Temp. When the Rosenthal and Sorpas temperature predictions were overlaid, they agreed with each other well (see Fig. 3). Although the temperature profiles from the Rosenthal equation did not agree with those from Sorpas very early in the welding cycle, it is not believed to affect the accuracy of the weld hardness profile predicted using this procedure. The two areas where it is critical that the temperature history is accurate are near the peak temperature, where the bulk of the tempering occurs [6] and when cooling through the 800–500 °C temperature range, which predicts the phases formed on cooling [11]. Near the peak temperature, the Rosenthal equation well matched the results calculated by Sorpas, so it is believed that both temperature profiles will result in similar amounts of tempering. However, the cooling time between 800 and 500 °C did not match as well. In the case of the profile with the 900 °C peak temperature, a cooling time of 300 ms was predicted by the Rosenthal equation, whereas Sorpas calculated that the material would cool in 513 ms. Although Sorpas calculated almost twice the cooling time of Rosenthal, it is not expected to affect the hardness prediction as this cooling time represents a cooling rate of about 580 °C/s which is much faster than the cooling rate required to form a fully martensitic microstructure. The prediction of the cooling rates may be easily improved by taking into account the dependence of λ, ρ and c with steel chemistry and temperature. When the r Temp values from Sorpas and the Rosenthal equation were compared for TRIP 800 and DP600 steel, it was also seen that Rosenthal agreed with the Sorpas calculations (see Fig. 4). Based on the agreement between the r Temp measurements calculated using the Rosenthal equation and Sorpas, it is believed that the Rosenthal equation may be used to model the hardness profile across the weld.

Fig. 3
figure 3

Comparison between the Rosenthal and Sorpas predicted temperatures in the HAZ of a weld in 1.2-mm TRIP steel welded with 8 kA for 0.42 s

Full size image
Fig. 4
figure 4

Distance between the weld centreline and the point on the weld where an arbitrary peak temperature was reached predicted by Rosenthal and calculated using Sorpas

Full size image

3 Predicting the hardness at a general point along the weld profile

With the knowledge of the thermal history throughout the weld and HAZ, the post-welding hardness may be predicted anywhere within the weld zone. However, to do this, first the weld must be split into two sections: the super-critical areas of the weld and the sub-critical areas of the weld. These regions must be separated as the hardness in the super-critical zone is driven by phase transformation, whereas the mechanism controlling the final hardness of the sub-critical zone is tempering. How to handle each of these cases will be dealt with separately, starting with the super-critical HAZ, as it is better known.

3.1 Post-welded hardness in the super-critical HAZ

The post-welded hardness of the super-critical HAZ is a function of the phases that form when the weld cools. Predicting which phases form in the HAZ of gas metal arc welds was studied by Yurioka et al. [11] who related the hardness of a fully martensitic structure (H M) and the hardness of a fully bainitic structure (H B) to material chemistry. The study then predicted how the two phases interacted to develop the hardness of a mixed structure including both phases (H V). To predict the structure that forms on cooling, they compared the time for the material to cool from 800 °C to 500 °C (t 8/5) to the maximum t 8/5 time that would result in a fully martensitic structure (t M) and minimum t 8/5 time that would form a structure containing no martensite (t B), both of which they were also able to relate to material chemistry. All the relations needed to predict the hardness of the cooled microstructure are given below:

$$ {H}_{\mathrm{V}}=\frac{H_{\mathrm{M}}+{H}_{\mathrm{B}}}{2}-\frac{H_{\mathrm{M}}-{H}_{\mathrm{B}}}{2.20} \arctan \left[4\frac{ \log \left(\frac{t_{8/5}}{t_{\mathrm{M}}}\right)}{ \log \left(\frac{t_{\mathrm{B}}}{t_{\mathrm{M}}}\right)}-2\right] $$
(5)
$$ {H}_{\mathrm{M}}=884\mathrm{C}\left(1-0.3{\mathrm{C}}^2\right)+294 $$
(6)
$$ {H}_{\mathrm{B}}=145+130 \tanh \left(2.65{\mathrm{CE}}_{\mathrm{HB}}-0.69\right) $$
(7)
$$ {\mathrm{CE}}_{\mathrm{HB}}=\mathrm{C}+\frac{\mathrm{Si}}{24}+\frac{\mathrm{Mn}}{5}+\frac{\mathrm{Cu}}{10}+\frac{\mathrm{Ni}}{18}+\frac{\mathrm{Cr}}{5}+\frac{\mathrm{Mo}}{2.5}+\frac{\mathrm{V}}{5}+\frac{\mathrm{Nb}}{3} $$
(8)
$$ {t}_{\mathrm{M}}= \exp \left(10.6{\mathrm{CE}}_{\mathrm{tm}}-4.8\right) $$
(9)
$$ {\mathrm{CE}}_{\mathrm{tm}}={C}_{\mathrm{p}}+\frac{\mathrm{Si}}{24}+\frac{\mathrm{Mn}}{6}+\frac{\mathrm{Cu}}{15}+\frac{\mathrm{Ni}}{12}+\frac{\mathrm{Cr}\left(1-0.16\sqrt{\mathrm{Cr}}\right)}{8}+\frac{\mathrm{Mo}}{4}+{f}_{\mathrm{B}}\frac{\left(0.02-N\right)}{0.02} $$
(10)
$$ {t}_{\mathrm{B}}= \exp \left(6.2{\mathrm{CE}}_{\mathrm{tb}}+0.74\right) $$
(11)
$$ {\mathrm{CE}}_{\mathrm{tb}}={C}_{\mathrm{p}}+\frac{\mathrm{Mn}}{3.6}+\frac{\mathrm{Cu}}{20}+\frac{\mathrm{Ni}}{9}+\frac{\mathrm{Cr}}{5}+\frac{\mathrm{Mo}}{4} $$
(12)

where all of the chemical compositions are given in wt%. There are two chemistry-related terms that are non-linearly related to chemistry: f B and C P. f B relates the B and N interaction to hardenability, where it is equal to 0 if B ≤ 1 ppm, 0.03 if B = 2 ppm, 0.06 if B = 3 ppm and 0.09 when B ≥ 4 ppm. C P is a factor that accounts for the change in the observed relation between the cooling time to achieve a 50 % martensitic structure and C content that occurs at a C content of 0.3 wt%. When the C content is less than 0.3 %, C P = C, and when it is greater than 0.3 %, C P = C/6 + 0.25 [11].

Although the hardness model developed by Yurioka et al. was developed for arc welding, it has been shown to effectively determine fusion zone hardness in RSW [12]. As this model relates the post-welded hardness to t 8/5, it may be easily applied to the temperature results generated by the Rosenthal equation.

3.2 Post-welded hardness in the sub-critical HAZ

Calculating the post-welded hardness of the sub-critical HAZ is more difficult than the technique used above for the super-critical weld area. The hardness of the sub-critical HAZ is determined by the initial hardness of the martensite, the amount tempering that the local microstructure undergoes and the equilibrium hardness of the fully tempered structure. Predicting the final hardness is further complicated as the heat treatment that the HAZ is subjected to during RSW is non-isothermal, so the softening rate is a function of both temperature and time for each discrete time increment during the welding cycle. These issues will be addressed by applying an appropriate material model to describe the tempering reaction. The tempering that material undergoes will be summed throughout the welding cycle. Then, with the calculated tempering prediction, the initial martensite hardness and the theoretical minimum tempered hardness of the tempered structure, the local hardness may be calculated.

3.2.1 Modelling the progression of martensite tempering

The literature cites two main techniques to sum the tempering damage in non-isothermal tempering cycles. Both techniques involve defining a temperature depending damage parameter and integrating it over the welding cycle [13–15]. However, where they differ is that some of the techniques use a convenient mathematical form to fit the data, while others choose to use the Arrhenius equation. This work chose to use the Arrhenius equation approach as it can relate tempering damage during welding to physical phenomena. The Arrhenius equation is then used to define the progression of the tempering reaction using the Johnson-Mehl-Avrami-Kolmogorov (JMAK) equation

$$ P\left(T,t\right)=1- \exp \left\{-{\left[k(T)t\right]}^n\right\} $$
(13)

where the non-dimensional softening damage, P, is related to k, the potential energy of the reaction, tempering time and the JMAK exponent n, which determines the rate of tempering. Then, k is defined by the Arrhenius equation

$$ k(T)={k}_0 \exp \left(-\frac{Q}{\mathrm{RT}}\right) $$
(14)

and is a function of the activation energy for softening, Q, the universal gas constant, R, and an arbitrary energy barrier at infinite temperature, k 0.

3.2.2 Accounting for the non-isothermal tempering cycle

In its current form, Eq. 14 can only calculate the tempering damage in isothermal cases, as the JMAK equation is nonlinear with respect to temperature. However, if the value within the exponential is viewed as the accumulated tempering damage over the welding cycle, then Eq. 13 may be rewritten as:

$$ P\left(T,t\right)=1-{e}^{-{Y}^n} $$
(15)
$$ Y\left(T,t\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}k\left[T(t)\right]} dt $$
(16)

This transformation assumes that the transformation products and mechanism, and therefore the activation energy, do not change with temperature. Although this assumption may be incorrect, as tempering rate is exponentially related to temperature (from the Arrhenius equation), the majority of the local tempering will occur near the peak temperature. Close to the peak temperature, the tempering mode will not change so for the vast majority of local tempering will be caused by a single mechanism, validating the use of a single tempering activation energy throughout the temperature history. With the transformation used in Eqs. 15 and 16, k(T)dt is assumed to be proportional to the number of atomic jumps that occur during time dt. The total tempering damage during the welding cycle may be determined by adding up all of these diffusion jumps during the characteristic time t HAZ defined below. This technique has been successfully used by many researchers to model tempering in non-isothermal cases [14, 16]. From these transformations, then, the general equation to calculate the softening progression occurring along any arbitrary point along the sub-critical HAZ is:

$$ {P}_{\mathrm{SCHAZ}}(r)=1- \exp \left\{-{\left[{\displaystyle \underset{0}{\overset{t_{\mathrm{HAZ}}}{\int }}{k}_0 \exp \left(-\frac{Q}{\mathrm{RT}\left(t,r\right)}\right)} dt\right]}^n\right\} $$
(17)

where P SCHAZ is the softening progression at a specific area in the sub-critical HAZ of a weld, and t HAZ is the time that the local area of the HAZ is above 400 °C, the temperature where stage 3 tempering occurs [17]. With Eq. 17, the tempering damage may easily be integrated. In this study, this was done numerically using the Middle Riemann sum method using a commercially available spreadsheet.

3.2.3 Calculating the final local hardness

Once the tempering progression has been calculated, the final hardness of the tempered region may be calculated. This may be done similarly as done in the literature [8, 15, 18] where it was assumed that the hardness tempered linearly from its as-quenched hardness to its fully tempered hardness. Using this assumption, the tempered hardness may easily be calculated as

$$ H(r)={H}_{\mathrm{q}}-{P}_{\mathrm{SCHAZ}}(r)\left({H}_{\mathrm{q}}-{H}_{\infty}\right) $$
(18)

where H(r) is the local tempered hardness, H q is the as-quenched or the base material martensite hardness and H ∞ is the minimum hardness of the tempered martensite after tempering for long times near its Ac 1 temperature. All of these values are known except for H ∞, which is typically found experimentally.

3.2.4 Relating material specific parameters to martensite chemistry

From the above technique, it is possible to calculate the final hardness in the sub-critical HAZ. However, to do this, the material hardness values of H q and H ∞ need to be known as well as the parameters Q, n and k 0 for the JMAK equation. H q may easily be found by either direct measurement or using Eq. 6; however, determining the other parameters requires extensive testing. To solve this general issue, a series of experiments were carried out to correlate these parameters to martensite chemistry [10]. Although this is out of the scope of the current study, it is summarized below.

To solve for H ∞, a series of furnace tempering experiments were carried out on several martensitic steels with varying chemistry. It was found that at long times the hardness of the tempered martensite approached the volume weighted average of the ferrite and cementite hardness values, 80 HV [19] and 1,270 HV [20], respectively. Therefore, H ∞ could be predicted by the lever law. Interestingly, no contribution to hardness was measured from solution strengthening of Cr, Mo and less than 2 % Mn. Therefore, H ∞ could be related directly to the martensite carbon content.

$$ {H}_{\infty }=\left(1-\frac{\mathrm{C}}{6.67}\right){H}_{\upalpha}+\frac{\mathrm{C}}{6.67}{H}_{\vartheta } $$
(19)

where H α is the ferrite hardness, and H θ is the cementite hardness.

The parameters for the JMAK equation were solved using a series of Gleeble rapid tempering experiments similar to those documented by Biro et al. [18]. The experiments used to define the JMAK parameters of this work were fitted to the form of the JMAK equation given in Eq. 13. From this work, it was found that the activation energy was related to Mn, Cr and Mo contents which are known to affect the thermodynamics of cementite formation as well as the difference in the as-quenched and tempered hardness. The inclusion of the base material hardness term H q implies that the increased internal stress decreases the thermal energy needed to advance the tempering reaction. It was found that n is purely a function of martensite hardness or internal stresses and k 0 is a constant. The correlations for activation energy (in kJ/mol), n (dimensionless) and k 0 (in 1/s) are below:

$$ Q=332-0.18\left({H}_{\mathrm{q}}-{H}_{\infty}\right)+14\mathrm{Mn}+34\mathrm{Cr}+72\mathrm{Mo} $$
(20)
$$ n=0.122-1.27\times {10}^{-4}\left({H}_{\mathrm{q}}-{H}_{\infty}\right) $$
(21)
$$ {k}_0={10}^{-14}{\mathrm{s}}^{-1} $$
(22)

It should be noted that a complete range of martensite chemistries could not be found to complete this work, so these relations are only valid for steels with 0.09–0.69 wt% C, 0.4–4.1 wt% Mn, 0–0.2 wt% Mo and 0–0.5 wt% Cr and 0.18–0.22 wt% Si [10]. Although the effect Si has on slowing cementite formation is well known, it was not accounted for in that study so work is ongoing to create a more complete correlation. The application of this model to dual phase grades (ferrite-martensite) is in progress.

4 Combining thermal history and hardness models to predict the hardness profile

4.1 Steps to predicting the hardness profile in a resistance spot weld

With the models to predict temperature history during welding, and the hardness of both the super-critical and sub-critical HAZ, the whole hardness profile may be modelled. Modelling the hardness profile requires:

  1. 1.

    Determining the Ac 1 and Ac 3 temperatures in the material. This may be done using experimental data or empirical relations such as those presented by Andrews [21].

  2. 2.

    Solving for the thermal efficiency, η, either by equating r Ac1 predicted by the Rosenthal equation to numerical or experimental data or by using an empirical relation such as Eq. 4.

  3. 3.

    Calculating r Ac1 using Eq. 3 if η in step 2 was determined by an empirical relation.

  4. 4.

    Determining the local temperature history across the weld using the Rosenthal equation (Eq. 1).

  5. 5.

    Solving for the hardness using either the Yurioka relations if the local peak temperature exceeds the Ac 3 temperature or the JMAK equation if the local temperature is below the Ac 1 temperature.

These results may then be laid out to form the hardness profile. It should be noted that in the area where the local peak temperature is between the Ac 1 and Ac 3 temperatures, it is assumed that the hardness profile linearly transitions from the peak hardness to the minimum hardness. An example of the arbitrary hardness profile along with the models used for each part of the prediction is laid out in Fig. 5.

Fig. 5
figure 5

Schematic of a hardness profile prediction

Full size image

4.2 Model validation

To validate whether this technique is able to adequately predict the hardness profiles seen in spot welding, welds were made on three industrial martensitic steels. These materials represent a variety of chemical compositions (see Table 1).

Table 1 Chemistry and thickness of materials used in model validation
Full size table

All of the materials were welded using a pedestal style 50 Hz AC spot welder. The welds were made according to ISO 18278-2 at welding currents near the expulsion limit of the joint. The welding parameters for each material may be seen below in Table 2. After welding, the welds were cross sectioned, polished and etched using standard metallographic techniques. The Vickers microhardness profile was then measured using a 500-g load at a 15-s dwell time. Hardness indentations were spaced far enough so as to not interfere with each other. The hardness profile pattern may be seen in Fig. 6.

Table 2 Welding parameters used for model validation
Full size table
Fig. 6
figure 6

Hardness indentation pattern used to create hardness profile

Full size image

The predicted hardness profiles agreed with the microhardness measurements (see Figs. 7, 8, 9). In the fusion zone and the super-critical HAZ, the data fits the model very well. However, as is typical, there is a high amount of scatter in the nugget hardness measurements. This, of course, could not be modelled. As well, there was a very good correlation between the predicted and the measured hardness values at the r Ac1. In general, the model had a tendency to slightly under predict the hardness in all locations where 95 % of the predictions fell between −8.5 % and 7.3 % of the measured values. Considering that hardness measurements will typically have a standard deviation of about 5–10 HV (about 1–2 % of 450 HV) and are spaced of 150 to 200 μm, it is believed that these results are well within acceptable limits.

Fig. 7
figure 7

Measured and predicted hardness profile across an RSW in Grade A

Full size image
Fig. 8
figure 8

Measured and predicted hardness profile across an RSW in Grade B

Full size image
Fig. 9
figure 9

Measured and predicted hardness profile across an RSW in Grade C

Full size image

The model also over and under predicted the hardness profiles for the fusion zones and super-critical HAZes in each of the steels differently. The martensite hardness of steel A, containing low C and high Mn and Cr, was largely over predicted, the hardness profile of steel B, with a medium C content, was generally under predicted and steel C with the highest C content was predicted well. It is not known why these discrepancies occurred; however, a more detailed hardness model may better fit the data. The hardness of the sub-critical HAZ was generally well predicted. The average error in predicting the minimum hardness was −2.5 %, with the worst prediction being steel A with an error of −4.8 %. Further from the r Ac1, the hardness prediction was also fairly good with the only exception being steel C where one side of the hardness profile being under predicted.

It was also seen that the assumption that the hardness transitioned linearly from r Ac3 to r Ac1 was proven to be correct. Two hardness points were measured in the intercritical HAZ of steel C. Both of these measurements fell on the hardness profile predicted by this model.

The most interesting observation, though, is that the hardness profile of a weld was predicted using three simple equations, with all of the calculations done using a widely available and low-cost spreadsheet program. This is contrary to the current state of the art, where a weld hardness profile must be calculated using complex and expensive modelling programs.

5 Further applications of this RSW hardness model

Although this model was designed to be used for RSW martensitic steels, it is believed that with very few changes it may be applied to other welding processes and other steels. For example, in other tests it has already been applied to laser welding by adapting the form of the Rosenthal equation that is used [10], and work is ongoing to adapt the model to gas metal arc welding. However, caution should be used if applying this model to other AHSS from the DP and TRIP families. These steels have a multiphase structure where some phases temper, while others are stable. Although work is ongoing to study how the softening of one part of the structure affects the overall hardness of the tempered material [7, 8], it has still not been generalized as was done with martensitic steels. If this model is applied to these steels, either the JMAK parameters must be solved for each steel individually or more work must be done to characterize the tempering properties of these steel families.

It is further believed that the model may be used to model weld strength as well as weld hardness. From the typical correlations between steel hardness and strength [22], this model may be used to predict local weld strength. Then, this data may be used to predict the tensile shear or cross-tension strength of modelled spot welds.

6 Conclusions

This study investigated how to predict the hardness profile across a resistance spot weld in martensitic steel. This was accomplished by applying the Rosenthal equation to determine the temperature history throughout the weld, Yurioka et al.’s hardness prediction to determine the hardness of the super-critically heated material and the JMAK equation to predict the hardness of the tempered material. Although the application of this was straightforward, the following was seen from the development and testing of this model.

  • The post-welded hardness of welds may be modelled by applying simple analytical models to the known metallurgical processes that occur during welding.

  • Although some of the assumptions that the Rosenthal equation is based on were violated, this temperature model may be used in this application because:

    • The temperature history was valid near the peak hardness where the majority of tempering occurs.

    • The prediction of t 8/5, which determines the phase transformations during cooling, was close to predict a similar phase distribution in the rapidly cooled structures of RSW.

  • Hardness predictions generally matched the hardness measurements along the weld profile with the error for individual measurements ranging from about −8.5 to 7.3 %.

  • The model predicted the hardness of the sub-critical HAZ very well with only an average −2.5 % error seen at r Ac1 where the minimum hardness is found.

  • Expensive modelling software is not needed to model the hardness profile in the RSW of martensitic steels. Modelling may be carried out using a typical personal computer and a spreadsheet on a wide process and product range.

  • Model has already been applied with success to laser welding.

  • Metallurgical model to describe martensite softening could be used for other applications such as post-weld induction heat treatment or surface softening.