Uncertainty Quantification and Propagation in Computational Materials Science and Simulation-Assisted Materials Design

Abstract

Significant advances in theory, simulation tools, advanced computing infrastructure, and experimental frameworks have enabled the field of materials science to become increasingly reliant on computer simulations. Theory-grounded computational models provide a better understanding of observed materials phenomena. At the same time, computational tools constitute an important ingredient of any framework that seeks to accelerate the materials development cycle. While simulations keep increasing in sophistication, formal frameworks for the quantification, propagation, and management of their uncertainties are required. Uncertainty analysis is fundamental to any effort to validate and verify simulations, which is often overlooked. Likewise, no simulation-driven materials design effort can be done with any level of robustness without properly accounting for the uncertainty in the predictions derived from the computational models. Here, we review some of the most recent works that have focused on the analysis, quantification, propagation, and management of uncertainty in computational materials science and ICME-based simulation-assisted materials design. Modern concepts of efficient uncertainty quantification and propagation, multi-scale/multi-level uncertainty analysis, model selection as well as model fusion are also discussed. While the topic remains relatively unexplored, there have been significant advances that herald an increased sophistication in the approaches followed for model validation and verification and model-based decision support.

Introduction

Motivation

Computer simulations are a 'comprehensive method for studying systems that are best modeled with analytically unsolvable equations. [the term also] refers to the entire process of choosing a model, finding a way of implementing that model in a form that can be run on a computer, studying the output of the resulting algorithm, and using this entire process to make inferences, and in turn trying to sanction those inferences, about the target system that one tries to model' [1]. In materials science, we use computer simulations to explore process–structure–property relationships that are too difficult/complex to express in closed analytical forms. These models or simulations usually incorporate background theories, numerical methods, and experimental data with varying degrees of uncertainty. Uncertainties (as discussed below) are mathematical representations of gaps in our knowledge about a system. These gaps arise because we do not have entire knowledge of the physical phenomena, our model parameterization is incomplete, and/or we only have partial knowledge of the state of a system when we attempt to simulate it.

Without a proper understanding of the origin and effect of uncertainties on the predictions associated with these models, it is impossible to assess their validity [2]. In simulation-assisted materials design, understanding how uncertainties in models propagate through model chains is critical in order to arrive at robust decision making [3, 4]. Unfortunately, in the field of materials science, computational modeling has been mostly deterministic or uncertainty-agnostic as it is often (implicitly) assumed that systems are not stochastic in nature, models are relatively complete, model parameters can be determined with absolute certainty, etc.

In deterministic calibration approaches, a single estimate for model parameters is proposed given available data for the system of interest—conventional deterministic approaches tend to rely on the minimization of the discrepancy between the mean response of the model and the available data through least-squares methods, for example. In practice, however, uncertainty in the models themselves, as well as the experimental data, is confronted against results in multiple suitable sets of plausible models and model parameterizations that can provide similar predictions (model outputs) for the system under study. This is particularly the case with highly complex models and highly uncertain data.

From a probabilistic perspective, each of these model/parameter combinations has a finite probability of being the most adequate representation of the ‘ground truth’ they all attempt to emulate [5]. In deterministic approaches for model building, however, all but one of the potentially infinite instances of model/parameter sets are ignored, resulting in predictions with no error bounds. Neglect of the uncertainty sources—i.e., model structure and model parameter uncertainties which are discussed later in "Uncertainty Categorization in Computational Modeling" section—is problematic because doing so makes it impossible, even in principle, to evaluate the consistency of the model with the data. Moreover, deterministic model predictions do not provide sufficient information for robust or reliability-based design, where properly quantified uncertainties in the predicted outcome of a design choice play a fundamental role [6,7,8].

Because of this reason, probabilistic calibration approaches that enable materials design under uncertainty have recently attracted considerable attention [9,10,11]. In these approaches, the uncertainties of the model parameters or input variables are first detected and then analytically or numerically quantified in the form of error bounds or probability distributions based on the available data for the system. The probabilistic calibration of model parameters is known as uncertainty quantification (UQ), while the propagation of these uncertainties forward through the model is known as uncertainty propagation (UP). Clearly, the assessment of the uncertainties associated with the model predictions is crucial because this results in higher confidence in the predictions themselves as well as in better estimation of risks associated with specific design choices, providing better decision support for robust or reliability-based design [7].

Relevance to Integrated Computational Materials Engineering

Integrated Computational Materials Engineering (ICME) [12] prescribes the integration of models with experiments as a strategy for the accelerated determination of process–structure–property–performance relationships. These relationships can then be inverted in order to design (optimize) the chemistry and synthesis/processing conditions necessary to achieve specific (multi-scale) microstructures with targeted properties or performance metrics [13,14,15]. In this framework, UQ of the multi-scale models/simulations has been recognized as one of the most critical elements to realize robust simulation-assisted materials design, although a more sustained research effort on this problem is warranted [16].

A major challenge to proper UQ/UP analysis along process–structure–property relationships is the realization of the linkages between different models. To date, the dominant paradigm relies on the use of ‘hand-shaking’ protocols between models, explicitly passing outputs of a simulation platform as inputs to the next element of the model chain. This approach is considerably challenging because often times, different simulation tools are developed by different groups/communities and between-model interfacing requires significant synchronicity in software development efforts [16].

An emerging solution to this issue relies on the linking models and simulations in a probabilistic sense, rather than through explicit input–output linkages [17]. By propagating uncertainties across models, as a transformation of probability distribution functions representing the input space to probability distribution functions over the output space, statistical correlations between inputs and outputs can be obtained. Model linkages can in turn be implemented as operations over probability distribution functions. Since risk analysis essentially operates on the probability space, the application of stochastic approaches for UP naturally leads to properly grounded robust materials design.

Connections along input–output spaces tend to be challenging not only because of the complexities associated with model ‘handshaking’ but also because of the computational costs of the individual models themselves. Explicitly sampling the model/parameter space with sufficient statistics to arrive at well-converged probability distribution functions is highly impractical in these cases. Here, machine learning (ML) models, such as Gaussian processes (GPs), can come into the picture to assist UQ/UP operations by providing cheap surrogate models that emulate the response of expensive models at much more reduced cost—at the expense of potentially losing information upon constructing these surrogate models.

In materials design under the ICME framework, there are often different models/simulations/experiments with different fidelities available that attempt to describe the same physical phenomenon. In these cases, information fusion techniques can be applied to effectively and smartly combine the information obtained from these sources for better probabilistic prediction of the system behavior [18,19,20]. An efficient information query of sources can also be performed by maximizing the information gain based on the consideration of a trade-off between their cost and precision. Knowledge gradient (KG) is identified as one of the most commonly used approaches for this efficient query [21,22,23].

Bayesian Inference as an Essential Tool to Uncertainty Quantification/Propagation

Despite the importance of UQ, UP, and uncertainty management (UM) in materials design and discovery, just few systematic studies have been performed for the analysis of uncertainty in computational materials modeling/simulation over the past years [10, 24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. In most of these works, Bayesian inference has been introduced as the main tool for UQ of the computational models, mainly due to the relative simplicity of implementation and the rigor of the resulting Bayesian analysis. In addition, Bayesian approaches enable the use of prior information derived from previous experience or expert knowledge within a framework that naturally leads to knowledge update when the models/theories are confronted with newly acquired information.

Gelman et al. [39] and a Sandia National Laboratories report published in the past decade [40] had already highlighted the significance of applying Bayesian inference in engineering design problems with no concerns about the philosophical and/or conceptual debates associated with the basic principles of this inference framework, i.e., the long-running debate between frequentist and Bayesian frameworks for inference [41]. In Bayesian inference, the process of updating prior knowledge upon acquisition of new information implies the quantification of uncertainties in the model parameter space. Practically, the quantification of such uncertainties is carried out by computing multi-dimensional integrals that are very difficult or often nonviable to evaluate through conventional integration techniques [42]. For this reason, Monte Carlo (MC) integration methods that take advantage of sampling techniques, such as Markov Chain Monte Carlo (MCMC), are usually used as a more robust and simpler solution to this problem [39, 43, 44].

Unfortunately, MC-based UQ/UP approaches require ${\mathcal{O}}\big (1\times 10^6\big )$ model evaluations for properly converged uncertainty analysis, and in these cases, sensitivity analysis (SA) can be used to reduce the complexity of the problem. SA helps reduce the cost of UQ by discarding the model parameters/input variables that have the least influence over model outputs, thus reducing the dimensionality of the problem—MCMC sampling, as any numerical integration approach, is subject to the curse of dimensionality [45]. In other words, SA helps to find the influential factors that are required to be determined more accurately in order to reduce the uncertainty of the model outputs [10]. Generally, SA can be performed locally or globally. Local SA usually includes the first partial derivatives of the model outputs with respect to the factors. Higher values of the partial derivatives correspond to a higher influence of the factors on the outputs. Although local SA is simple and relatively easy to implement, it disregards (possible) nonlinearities in the models—many common materials simulations tend to be nonlinear—the uncertainty of the factors, as well as their possible interactions. To solve these issues, global SA can be used. Variance-based methods as well as the elementary effects method are the most well-known global SA approaches [10, 46]. It should be noted, however, that the cost of each MCMC sample is high enough in some cases that even SA cannot make the total cost of the approach reasonable. In these cases, a less costly approach is to emulate the computer simulations with inexpensive, fast, ML surrogate models [40].

Overview of Present Work

The main goal of the present work is to highlight the importance of UQ and UP in computational modeling as they greatly improve the process of validation and verification of scientific simulation tools, and most importantly, they enable robust materials design under ICME frameworks. The present contribution starts with the description of different sources of uncertainty as well as the definition of fundamental concepts in two different statistical points of view for UQ—i.e., frequentist and Bayesian inference. Then, significant works on UQ/UP in materials modeling are reviewed and this is followed by the discussion of novel and advanced approaches to address some major issues associated with UQ/UP in computational modeling. Advances in model selection and model fusion are also discussed. The paper closes by providing some ideas on how the field can make further progress as methods/frameworks for UQ/UP are further developed.

The Importance of Uncertainty Quantification in Design

From an epistemological perspective, there will always be missing knowledge about a physical system because of: sparse and uncertain information about the system at the moment of observation, physical limits to the resolution of the measurements, incomplete underlying theories, fundamental or practical computational limitations. Incomplete knowledge necessarily leads to uncertainty, and it is thus expected that any simulation used to predict the behavior of a material will carry a number of uncertainties. The latter should be quantified and analyzed against any available experimental evidence in order to facilitate the process of validation and verification of the underlying theoretical frameworks. Moreover, such uncertainties should be propagated in order to provide decision support to the design/optimization of materials and materials systems.

From an engineering perspective, risk assessment is an essential task for decision making in robust- and reliability-based design [6, 47], which incorporates the probabilistic analysis of materials systems—i.e., UQ and UP. In robust design, the goal is to make the response of the system less sensitive to variations in the input variables. UQ/UP can provide information required to obtain a notion of confidence about the robustness of the system, as shown in Fig. 1. As can be observed in this figure, the variations in the design parameters (inputs) due to their uncertainties can reflect different variations in the responses (outputs) of the system. In robust design, it is important to determine the values of the design parameters such that their fluctuations have the least effects on the system outputs. The fundamental requirements of this analysis are UQ of the design parameters and subsequent UP from these parameters to the responses of the system.

Fig. 1

A schematic illustration of robust design based on the sensitivity of system outputs with respect to the variations (uncertainties) in its inputs

UQ is also highly relevant in safety analysis in design. Here, it should be noted that the conservative consideration of safety factors in an ad hoc manner to cover all the uncertainties in the system is no longer valid for the decision making in design. Instead, the probabilistic analyses (UQ) of the system’s response and its working conditions can provide a good quantitative measure for the probability of failure or reliability index which can be used to calculate the design safety factor in a systematic way. Therefore, probabilistic methods can provide a more precise and less conservative safety factor compared to their deterministic counterparts, resulting in a reduction in the design cost.

UQ is also important when designing materials and materials systems under constraints. In fact, there are a large number of materials design problems that include constraints in their input or output spaces—such as the design of functionally graded materials in additive manufacturing through path planning in the phase diagram in order to prevent the formation of undesirable phases in the final products [48]. (Here, the compositional constraints are defined by the boundaries of the undesirable phases in the phase diagram that contain some uncertainties.) Figure 2 schematically illustrates the need for UQ in such designs. In this figure, the red line surrounds the allowable (feasible) design region that satisfies the constraints in the given design problem. The dark green ellipsoidal region also shows the optimal design space that can be obtained in any ICME hierarchical scale of interest—i.e., process, structure or property space—based on the performance requirements. From a deterministic perspective (as shown in Fig. 2a), any point in this green region can be used for design; however, the entire green region may not be a reliable or safe design due to the absence of the UQ. In this regard, the quantification of the constraint uncertainties (confidence intervals) across the red boundary which is shown in blue in Fig. 2b can provide a level of confidence or reliability in design by excluding the intersecting area between the blue and green regions from the optimal green region suggested in the deterministic design. The reason is that any point in this intersecting area has a relatively high probability for design failure due to the violation of the design constraints. Therefore, UQ in this schematic example plays an important role in order to identify the optimal and reliable region in the design space, rather than just the optimal region recommended by the deterministic design.

Fig. 2

A schematic example to illustrate the importance of UQ in a reliable (safe) design

The importance of UQ can also be discussed in regard to efficient global optimization, which has emerged as one of the important tools in accelerated materials design and discovery [49,50,51]. Materials design/discovery requires the solution of an inverse problem that maps desired property outcomes to required materials configurations (as well as the processing steps necessary to achieve them). The vastness of the materials design space and the considerable cost associated with its exploration/exploitation via experimental or computational means makes it necessary to rely on efficient optimization approaches. In these sequential optimization frameworks, a probabilistic prediction of the system response is performed throughout the entire design space by ML regression techniques (e.g., GP regression) and then followed by the maximization of an acquisition function to identify the next point to query given the data already acquired. After the design space has been queried, the probabilistic predictions (i.e., models) over the design space are updated and the cycle is repeated until the discovery/design goal is achieved or resources are exhausted [52].

In all (Bayesian) optimization approaches for materials design, the efficient exploration and exploitation of the materials design space are carried out by maximizing acquisition functions that explicitly account for the uncertainties in the response of the system. While in most applications of such frameworks, the predicted uncertainties arise from the posterior distributions of the ML models used to emulate the system response, explicitly propagated uncertainty in model parameters and model inputs can certainly be used to arrive at more robust sequential experimental designs.

Classifications of Uncertainty Sources

Aleatoric Versus Epistemic Uncertainties

In order to ensure the rigorous analysis, quantification, and management of uncertainties in computer simulations, it is essential to understand their origin. The most well-known classifications of uncertainty are aleatoric vs epistemic uncertainty [9]. Both types of uncertainties exist in most scientific, engineering, and design problems, and it is thus necessary to understand their characteristics, origin as well as the extent to which they can be managed. Aleatoric uncertainty—also known as irreducible uncertainty—results from the inherent random variability in either the material structure or its behavior, which in principle can only be properly quantified in the form of a frequency (probability) distribution. For example, results obtained from two identical experiments/measurements are not necessarily the same due to the natural randomness or stochastic nature of the system—e.g., no two microstructures are identical and can only be compared in the aggregate. Proper quantification of this type of uncertainty requires extensive sampling of nominally identical instances of the system under study. However, random or mixed-effects models with factors representing random effects or the mix of fixed and random effects—such as the models used in sensitivity analysis (SA) through analysis of variance (ANOVA)—can be applied to reduce the cost of aleatoric UQ with a trade-off in precision. In these approaches, variance components that include the residual variance (aleatoric uncertainty) are estimated through expected mean squares (EMS) or restricted maximum likelihood (REML) techniques. Surrogate modeling approaches—e.g., Kennedy and O’Hagan’s GP-based approach which is explained further in "Uncertainty Categorization in Computational Modeling" section—can also be considered as cheap solutions for the determination of aleatoric uncertainty. As it is clear from its name, this type of uncertainty cannot be reduced but only managed. As the technology for UQ is advancing, it is likely to re-categorize some of these uncertainties as epistemic in the future.

Contrary to aleatoric uncertainty, epistemic or reducible uncertainty arises from the inadequate and/or inaccurate/incomplete knowledge of the system under investigation [24]. Epistemic uncertainty can potentially be reduced by improving/increasing our knowledge—accessed through simulations and/or experiments—about the system [53]. In experiments, better control of experimental conditions, better calibration of measuring tools, and fewer human errors through better design of experimental protocols contribute to reducing epistemic uncertainty. In computational modeling, the reduction in epistemic uncertainty can be achieved by acquiring more knowledge about the physics and parameters of the system as well as through modeling frameworks with higher fidelity, resolution, etc.

A better understanding of the characteristics of the uncertainty classes discussed above can be arrived through analogy by looking at precision and accuracy in target shooting. Figure 3 shows the aleatoric (precision) and epistemic (accuracy) uncertainty through the scattered and deviated shots on the target, respectively. As can be observed in this figure, there are different degrees of scatter and deviation which represent different contributions of these two uncertainties to the total uncertainty in this case. Here, the accuracy can be improved by changing the aim point from the target center to the point obtained by the point symmetry of the shot center on the target. This implies a reduction in epistemic uncertainty. On the other hand, aleatoric uncertainty is irreducible but describable in the form of a frequency distribution [10]. However, it should be noted that this analogy disregards the possibility of the random scatter appearance due to the epistemic uncertainty. In other words, the bias, in this case, is always clear based on the shooting condition, but in reality, some cases may show random biases.

Fig. 3

Reprinted with permission from [10]

An illustration of aleatoric and epistemic uncertainty through their analogy with precision and accuracy.

Uncertainty Categorization in Computational Modeling

From the perspective of computer simulation, uncertainty can be further classified into natural (NU), model parameter (MPU), model structure (MSU), and propagated uncertainty (PU). The first three classes were proposed earlier by Isukapalli et al. [53], while PU has been later added as a unique category of uncertainty [6], particularly due to its high relevance in the verification and validation of the theoretical underpinnings of simulation tools as well as in robust design of materials.

In the above classification, NU is the same as aleatoric uncertainty, as explained in "Aleatoric Versus Epistemic Uncertainties" section. This uncertainty is irreducible but manageable through robust design as the latter can be used to identify regions in the input space where the system’s performance exhibits the least possible sensitivity to uncertainty. MPU arises from insufficient or inaccurate information about the parameters with considerable influence on the response of the model. This type of uncertainty can be reduced by obtaining more data or more precise experiments/measurements. MSU, on the other hand, results from incomplete knowledge about the physics of the problem, incorrect assumptions or simplifications, and/or numerical inaccuracies. This type of uncertainty can also be reduced by improving the model structure, including better understanding of the physics of the given system, fewer simplifications, more accurate assumptions, and the application or development of more precise numerical methods [6]. In the case in which data on the ground truth are available, the Kennedy and O’Hagan’s approach can be applied to partition NU, MPU, and MSU [54]. In this approach, a linear correlation is considered between data and model prediction at any given point x in the design space, as follows:

$$\begin{aligned} D(x)=\rho M(x,\theta )+\delta (x)+\varepsilon (x) \end{aligned}$$

(1)

where D, $\rho$, M, $\theta$, $\delta,$ and $\varepsilon$ are data, a constant linear coefficient, the physical or GP fitted model, the model parameters (to account for MPU), a model discrepancy function (to account for MSU), and the data error (to account for NU), respectively. $\varepsilon$ is assumed to be a normally distributed function with a fixed variance—i.e., ${\mathcal{N}}(0,\sigma ^2)$. Based on Kennedy and O’Hagan’s approach, two GP models are constructed using the collected data and a sufficient number of results obtained from the physical model to estimate M and $\delta.$ (M can be considered as the physical model itself if it is not expensive.) Then, the vector of parameters in this framework, $\Phi =\{\rho ,\theta ,\beta ,\psi ,\sigma ^2\}$, is estimated by a probabilistic calibration technique such as MCMC, where $\beta$ and $\psi$ are the vectors of regressors and hyper-parameters in the constructed GP(s), respectively. This is how the above-mentioned classes of uncertainty can be quantified and differentiated from each other [54, 55].

Generally, this uncertainty partitioning is essential in computational modeling since it can provide an insight into potentially effective approaches to reduce uncertainty. For example, the ratio of MSU to MPU can help one determine which area in the modeling structure (physics or parameters) requires more information for uncertainty reduction. In the end, PU is the uncertainty that can be propagated along a chain of models to the final outputs. Analysis and quantification of this type of uncertainty are very important in materials design since the decision-making process must be performed according to the final uncertainty obtained from a chain of models, not from the individual models themselves [6].

Uncertainty Propagation Versus Uncertainty Quantification

Uncertainty Propagation

UP in computational models/simulations is a forward analysis that involves mapping the uncertainty in the inputs/parameters to uncertainty on the outputs of the model. This process is, in essence, one of the transformations as the uncertainties (of different kinds) in the inputs/parameters of a model are transformed into uncertainties in the model outputs. This process often involves sampling the input/parameter space and then propagating its uncertainties through the evaluation of the model or a surrogate.

The most basic approach to the propagation of uncertainty through computational models/simulations is based on numerical Monte Carlo (MC) sampling—e.g., Fig. 4. For a general computational model, $f({\mathbf{X}})$, where ${\mathbf{X}} = (X_1,X_2,\ldots ,X_d)^T$ and the ${\mathbf{X}}$ is a random vector, MC sampling works by sampling a point ${\mathbf{x}}$ from the distribution of ${\mathbf{X}}$ and then running the computational model to evaluate $f({\mathbf{x}})$. If this process is repeated (tens, hundreds of) thousands of times, then the strong law of large numbers and an application of Skorokhod’s representation theorem guarantee that the empirical distribution of the output evaluations converges in distribution to that of $f({\mathbf{X}})$ [56, 57]:

$$\begin{aligned} F^{n,f} ({\mathbf{t}}) = \frac{1}{n} \sum _{i=1}^n {\mathbb{I}}({\mathbf{x}}^i \le {\mathbf{t}}) \xrightarrow {D} F^{f}({\mathbf{t}}) \;\; \text{as } n \rightarrow \infty , \end{aligned}$$

(2)

where ${\mathbb{I}}({\mathbf{x}}^i \le {\mathbf{t}})$ is the maximum convention Heaviside step function defined as

$$\begin{aligned} {\mathbb{I}}({\mathbf{x}} \le {\mathbf{t}}) = \left\{ \begin{array}{l l} 1, &{} \quad \text{if } x_i \le t_i, \; \forall \, i \in \{1,2,\dots ,d\}\\ 0, &{} \quad \text{otherwise,} \end{array} \right. \end{aligned}$$

(3)

$F^{n,f}$ is the empirical distribution of $f({\mathbf{X}})$ generated by sampling, and $F^{f}$ is the cumulative distribution function of $f({\mathbf{X}})$. Given this convergence behavior, MC sampling is often considered the gold standard to compare against when developing new algorithms/frameworks for UP [58,59,60,61,62,63], although its slow convergence rate of $O(1/\sqrt{n})$ makes it impractical for most expensive models [57].

In cases in which direct sampling of the model space through MC-based approaches is impractical, analytical methods are often used to accelerate the process of UP. These methods usually utilize surrogate models to approximate the uncertainty of the model outputs. Therefore, choosing between these two alternatives of UP methods—i.e., numerical and analytical methods—results in a trade-off between cost and accuracy. Generally, it can be stated that analytical UP methods are faster but not as accurate as numerical counterparts. Among analytical methods, first-order second moment (FOSM) and second-order second moment (SOSM) techniques have commonly been used for nonlinear propagation of uncertainty in different scientific and engineering problems [31, 47, 64]. In these techniques, uncertainty is propagated along a first- or seconder-order series approximation of the (expensive) model at the input/parameter mean value rather than the model itself.

Fig. 4

Reprinted with permission from [29]

MC-based UP in CALPHAD-based thermodynamic modeling of the Hf–Si binary system.

Polynomial chaos expansion (PCE) and Kriging (GP regression) are two other analytical approaches that have become increasingly popular in recent years. In PCE, the computational model/simulation is considered as a black box where the inputs and outputs are the only known model features. This method creates a surrogate model by choosing a finite set of orthonormal polynomials (functions of the uncertain inputs) whose coefficients can be optimized against the available data for the system. The least-angle regression and the least-square algorithm are examples of approaches that can be used to select the polynomials in the basis and to optimize their coefficients, respectively [65]. GP is a supervised nonparametric regression approach that provides a probabilistic stochastic surrogate model based on weighted distance-based correlations between the errors of the input sample points. In essence, the closer the sample points are, the closer their errors will be. Here, the data obtained from the (expensive) model/simulation are utilized to optimize the hyper-parameters in the correlation function, mostly using the maximum likelihood method [65,66,67].

Uncertainty Quantification

UQ is an inverse analysis that determines the overall uncertainty over the model parameters/inputs based on the available data for the system and its error [43]. UQ approaches are usually capable of providing the full statistical property of the model parameters in the form of a multivariate probability distribution whose covariance matrix indicates the parameter correlations. As is the case in UP, MC-based numerical methods that will be discussed later in "Bayesian Inference" section tend to be the standard approaches to UQ—as an example, the marginal frequency distribution of two parameters resulting from an MCMC probabilistic calibration of a CALPHAD model for the Hf–Si binary system is shown in Fig. 5. Despite their straightforward nature, MC-based methods tend to be very expensive, especially in cases in which the models are very expensive and/or in which the input parameter space is highly dimensional.

Fig. 5

Reprinted with permission from [29]

Marginal frequency distribution of two CALPHAD parameters in the Hf–Si system after an MCMC probabilistic calibration against the available data.

As mentioned earlier in  "Uncertainty Propagation" section, surrogate-based approaches can be employed to address this computational cost. Figure 6, for example, shows a case study for a surrogate-based uncertainty analysis of a finite element-based thermal model in additive manufacturing. In that work, Mahmoudi et al. [68] have used a multi-output Gaussian process (MOGP) regression model to represent physically correlated outputs from a thermal model. The MOGP was used in turn to carry out MCMC-based model calibration against experimental data.

Fig. 6

Reprinted with permission from [68]

Surrogate-based uncertainty analysis of finite element-based thermal models in additive manufacturing. left: experimental characterization of melt pool dimensions; right: comparison between surrogate model predictions and finite element simulations.

Practically, surrogate-based approximations of model outputs are not always able to provide sound uncertainty analysis with high degree of confidence. In these cases, the model itself should be used directly in order to achieve higher precision in UQ. In cases in which the cost of MC-based methods arises from high dimensionality in the input space, it is possible to discard the model parameters less likely to impact the model output through SA. It should be noted that variance-based sensitivity analyses (VBSAs)—e.g., ANOVA—are the most commonly used approaches in engineering [30, 69,70,71,72]. ANOVA is a powerful global SA with a good performance in high-dimensional cases, where the influential parameters are identified through hypothesis testing built upon partitioning the total uncertainty of the model prediction into the uncertainties arisen from the individual parameters and their interactions [73].

Statistical Inference for Uncertainty Quantification

UQ can generally be understood through two different statistical paradigms—i.e., frequentist and Bayesian. The contrast between these two competing frameworks originates on fundamental differences in the definition of probability, the assumptions about data and parameters, as well as their reliance on fundamentally different foundations of statistical inference. We wish to point out that both views have benefits and drawbacks and are equally relevant in the wider field of statistical inference. However, UQ Bayesian inference has recently received considerable attention. As will be discussed below, engineering and scientific problems tend to be data sparse (physical realizations or simulations of design choices are costly), which makes frequentist approaches much less useful as compared with Bayesian frameworks.

Frequentist Inference

Probability, from a frequentist point of view, is described in terms of the occurrence frequency of a specific outcome over numerous iterations of a measurement/observation at a unique condition (or set of values of inputs). In this context, data are always assumed to be a realization (random sample) of a random variable, whereas parameters are considered to be fixed but usually unknown [74]. In other words, frequentist inference assumes that a single true vector of parameter values exists whose uncertainties can in principle, at least be mapped from an infinite number of samples of the underlying distribution. For this reason, more measurements/observations result in a better inference for the true parameter values and their uncertainties (UQ). When the frequentist paradigm is applied to model calibration and UQ, the true values and uncertainties of the parameters can be approximated through the average ($\langle \theta _F \rangle$) and variance–covariance matrix ($\hat{C_F}$) of the parameter estimates or best parameter values mapped from an ensemble of measurements/observations, as follows:

$$\begin{aligned} \langle \theta _F \rangle= {} \frac{1}{N_D}\sum _{i=1}^{N_D} \hat{\theta _i} \end{aligned}$$

(4)

$$\begin{aligned} \hat{C_F}= {} \frac{1}{N_D}\sum _{i=1}^{N_D} (\hat{\theta _i}-\langle \theta _F \rangle ) (\hat{\theta _i}-\langle \theta _F \rangle )^T \end{aligned}$$

(5)

where $N_D$ and $\hat{\theta _i}$ are the number of the measurements/observations and the parameter estimate mapped from the ith measurement/observation in the ensemble, respectively [44]. In frequentist inference, the most popular approach to the identification of parameter estimates is the maximum likelihood estimation (MLE). As it is clear from the name of this approach, the parameter values that maximize the likelihood function are considered as the parameter estimates:

$$\begin{aligned} {\hat{\theta }}_{i}^{\mathrm{MLE}} = \text{arg}_\theta \max \big [ L(\theta |D_i) \big ] \end{aligned}$$

(6)

where $\theta$, $D_i$, and $L(\theta |D_i)$ denote the parameter variable, the ith measurement/observation, and the corresponding likelihood function, respectively.

Another aspect of frequentist statistics is hypothesis testing based on the calculation of a p value after the definition of the null and alternative hypotheses. Here, the p value aims to quantify how likely a specific event is to occur if the null hypothesis is assumed to be correct. The purpose of frequentist hypothesis testing is to examine whether the null hypothesis is rejected in favor of the alternative hypothesis or not. For the rejection of the null hypothesis, the p value must be smaller than a significance level ($\alpha$) that is typically considered as 0.01, 0.05, or 0.1. For example, the Pearson linear correlations between model variables/parameters can be evaluated through the p test. Generally, these linear coefficients can alter between − 1 and 1, where the lower/upper bound indicates a perfect negative/positive linear correlation, and 0 indicates no correlation. In the above hypothesis testings, variables/parameters with no correlations are considered as null hypotheses. Here, the correlation coefficient obtained from any variable/parameter sample data can be used to calculate the corresponding p value and test whether there are significant linear correlations or not. In this regard, a p value less than the assumed significance level results in the rejection of the corresponding null hypothesis, which implies some correlations between variables/parameters. Another important application of the frequentist hypothesis testing with p value is in SA based on ANOVA decomposition to recognize the most influential parameters in the physical models. These influential parameters are determined by the rejection of the null hypotheses that are the zero contributions of the parameters and their interactions to the overall variation (uncertainty) of the model response.

Bayesian Inference

Within a Bayesian statistical paradigm, the degree of belief for a specific event to occur can be expressed in terms of a probability that can in turn be calculated by considering a combination of the current (prior) state of knowledge and newly given/acquired data/evidence [74]. In other words, the probability density of a specific value of an occurring quantity is obtained based on the prior knowledge and new data. Bayesian statistics are generally described as conditional probabilities due to the subjectivity of the prior belief. In the Bayesian view, unlike its frequentist counterpart, parameters and data are considered as random variables with (un)known prior probability distributions and a fixed constant with noise, respectively.

In this statistical framework, the prior probability distribution for the parameters is updated to a posterior probability distribution by the given data. It should also be noted that the posterior distribution is treated as a prior and updated to a new posterior distribution for the parameters as soon as other new data are provided. This sequential inference process is performed based on the Bayes’ theorem that is expressed as the following relationship derived from the fundamental definition of conditional probability:

$$\begin{aligned} P(\theta |M,D)=\frac{P(D|\theta ,M) P(\theta |M)}{P(D|M)} \end{aligned}$$

(7)

where $P(\theta |M)$, $P(D|\theta ,M)$, P(D|M), and $P(\theta |M,D)$ are the prior probability or prior knowledge for the parameters shown as the probability of the parameter vector $\theta$ given the model M, the likelihood function as the probability of acquiring the data D given the model M at the fixed parameters $\theta$, the evidence as the probability of getting the data D given the model M, and the posterior probability of the parameters shown as the probability of the parameter vector $\theta$ given the model M and the data D, respectively.

Figure 7 shows an illustration of Bayesian inference for model parameter calibration and UQ based on the given data, where the parameter prior distribution is updated to a posterior distribution using the likelihood function. Such a posterior distribution (or a representative sample of parameter vectors) is considered as the solution for the inverse UQ problem. In the case that a representative parameter sample is obtained for the posterior probability distribution, the mean and variance–covariance matrix of the sample can be used to assign probabilistically calibrated values to the model parameters. As can be observed in this figure and also in Eq. 7, the posterior probability is proportional to the likelihood multiplied by the prior probability. Therefore, the Bayesian inference is found upon the combined contributions of the likelihood and the prior, instead of just the likelihood, which is the main inference element in the frequentist approaches.

Fig. 7

Reprinted with permission from [24]

An illustration of the Bayesian inference framework.

In the Bayesian framework, prior probability distributions can be defined either as informative or non-informative. Non-informative priors are usually used in cases in which there is very little prior information about the system parameters. The most commonly used non-informative and informative priors in engineering problems are uniform and normal distributions, respectively. Here, normal distributions must include proper selections of the hyper-parameters—specifically finite proper standard deviations—in order to be recognized as informative priors since infinite standard deviations in these cases are equivalent to non-informative uniform priors. Beside normal distributions, the hyper-parameter choices are very important in the informativity of some other distributions. For example, informative inverse gamma prior distributions also need to have hyper-parameters greater than 1 [75]. Generally, the definition of the prior distribution in Bayesian inference is a very important task since an incorrect prior distribution may misdirect the inference process. The strong influence of priors on the outcome of the inference process is perhaps the major source of criticism of Bayesian frameworks [76].

The definition of the likelihood function is another important aspect of the Bayesian inference framework. This function can generally be described in terms of the residuals (errors) between the given data and their corresponding model outcomes as well as their variance. There are two general approaches—known as formal and informal—to the estimation of the likelihood function [77]. Formal approaches consider a statistical functional form for the residuals to derive the corresponding likelihood function [78]. Here, the parameters of this functional form can be calibrated against the measurements/observations. The explicit definition of the residual/likelihood function in the formal approaches enables the validation of the assumptions associated with the form of this function by new given measurements/observations. However, the assumptions of these approaches that consider the residuals to be formally distributed, uncorrelated, and/or stationary (homoscedastic) are not always true.

So-called informal likelihood functions have been developed to address these issues. One of the well-known approaches is the generalized likelihood uncertainty estimation (GLUE) [79] that implicitly defines a general and flexible likelihood function based on a fuzzy measure. In this approach, the likelihood monotonically changes from 0 to 1 as the similarity between the model prediction at the given parameter $\theta$ and the corresponding measurement/observation increases. This similarity can be defined in different measures of goodness in terms of the residuals and their variance. Although the informal approaches can handle complex structures for the residuals with no need for the definition of an explicit functional form, the assumptions for the residual function cannot be validated by new measurements/observations due to the implicit reference to the underlying residual structure in these approaches.

It is worth noting that the issues presented for both approaches have been addressed through a generalized formal likelihood function proposed by Schoups et al. [77]. Here, the residual function is defined as a general explicit formal function with parameters that can be calibrated and that can account for the residuals’ correlation, heteroscedasticity, and generality in the functional form.

The evidence or the marginal likelihood is a normalization constant in the Bayes’ theorem that can be calculated as:

$$\begin{aligned} P(D|M)=\int P(D|\theta , M)P(\theta |M) {\mathrm{d}}\theta \end{aligned}$$

(8)

The evidence is the key element in the calculation of the Bayes factor, which can be used as a metric for model comparison—in Bayesian model selection, BMS—as well as model fusion—in Bayesian model averaging, BMA. The Bayes factor and its application are discussed further in "Model Selection and Information Fusion" section. However, the above integration is not easy to solve when there are a large number of parameters in the model M. In these cases, asymptotic approximations—such as Laplace’s method, the variants of Laplace’s method, and the Schwarz criterion—or numerical methods— such as MC sampling methods, importance sampling methods, quadrature methods, and posterior sampling methods (e.g., MCMC sampling techniques)—can be applied to address this issue [80].

As mentioned earlier in this section, the posterior probability distribution determines the probability of the parameter vector $\theta$ given the data, which is proportional to likelihood times prior. In problems related to parameter calibration and UQ, the main goal is to find the mean value ($\langle \theta _B \rangle$) and variance–covariance matrix (${\hat{c}}_B$) of this distribution which can be determined as:

$$\begin{aligned} \langle \theta _B \rangle= {} \int \theta P(\theta |D) {\mathrm{d}}\theta \end{aligned}$$

(9)

$$\begin{aligned} {\hat{C}}_B= {} \int (\theta -\langle \theta \rangle )(\theta -\langle \theta \rangle )^T P(\theta |D) {\mathrm{d}}\theta \end{aligned}$$

(10)

The absence of closed-form solutions and the curse of high dimensionality in most cases make these integrations very hard to solve through conventional analytical and numerical approaches. The most well-known solution is MC integration where the samples from the posterior distribution ($P(\theta |D)$) are used to estimate the above integrations:

$$\begin{aligned}&\langle \theta \rangle \approx \frac{1}{N}\sum _{i=1}^{N} \theta _i \end{aligned}$$

(11)

$$\begin{aligned}&C^\theta \approx \frac{1}{N}\sum _{i=1}^{N} (\theta _i-\langle \theta \rangle )(\theta _i-\langle \theta \rangle )^T \end{aligned}$$

(12)

Therefore, a sampling tool is required for these approximations. Direct or rejection sampling can be applied for simple cases, but the complexity in most engineering models resulting from their high-dimensional parameter spaces brings a need for more practical and robust sampling methods. For this reason, MCMC approaches have been developed from the mid-twentieth century onwards [81]. However, the high cost of these sampling techniques limited their applications until recent decades due to lack of computing power. Now, MCMC methods are the most commonly used sampling techniques in Bayesian inference. Gibbs sampling and Metropolis–Hastings are two popular approaches to sample parameter vectors from the posterior distribution.

In the Gibbs sampling technique, the initial guess for the values of n given model parameters—i.e., $\theta ^0=\{\theta _0^1,\ldots ,\theta _0^n\}$—is updated by sampling a new value for each parameter from its corresponding conditional distribution—i.e., $P(\theta _1^i|\theta _1^1,\ldots ,\theta _1^{(i-1)},\theta _{0}^{(i+1)},\ldots ,\theta _0^{n},D)$. This sampling continues n times to generate the new parameter vector $\theta ^1$. It should be noted that these conditional distributions are defined based on the prior distributions for the parameters. The above process can sequentially be performed by sampling parameters one by one from their conditional distributions defined in general form as $P(\theta _z^i|\theta _z^1,\ldots ,\theta _z^{(i-1)},\theta _{z-1}^{(i+1)},\ldots ,\theta _{z-1}^{n},D)$ until the multivariate distribution obtained from the sampled parameter vectors tends to be stationary.

The Metropolis–Hastings algorithm also starts with an initial guess for the parameters, and then, parameter vector candidates are sequentially sampled from a posterior proposal distribution (q) that can be adaptive toward the target distribution during the sampling process. At each iteration of this sequential approach, the sampled candidate can be accepted or rejected based on the Metropolis–Hastings ratio (MH), unlike the Gibbs sampling, where all the samples are accepted. This ratio is defined as follows:

$$\begin{aligned} MH=\frac{P(\theta ^{\mathrm{cand}})P(D|\theta ^{\mathrm{cand}})}{P(\theta ^{z-1})P(D|\theta ^{z-1})} \frac{q(\theta ^{z-1}|\theta ^{\mathrm{cand}})}{q(\theta ^{\mathrm{cand}}|\theta ^{z-1})} \end{aligned}$$

(13)

In this equation, the first ratio, known as the Metropolis ratio, compares the likelihood times the prior probability for the sampled candidate with its counterpart for the last parameter vector in the chain at each MCMC iteration, which is technically equivalent to the comparison of their posterior probabilities. The second ratio, known as the Hastings ratio, considers the asymmetry effect of the proposal distribution. In essence, the probability for a forward move from $\theta ^{(z-1)}$ to $\theta ^{\mathrm{Cand}}$ is compared with the probability of the reverse move at each MCMC iteration. In the case that the proposal distribution is symmetric, the Hastings ratio becomes 1. The calculated MH helps to decide about the acceptance or rejection of the sampled candidate at each MCMC iteration. Here, $\mathrm {min}(MH, 1)$ indicates the acceptance probability of the candidate. $\theta ^z=\theta ^{\mathrm{Cand}}$ when the candidate is accepted, while $\theta ^z=\theta ^{(z-1)}$ in the case of rejection. This sequential sampling process continues until the proposal distribution becomes stationary.

Gibbs sampling is a particular case of the Metropolis–Hastings approach, where the proposal distribution is assumed to be the conditional distribution for each parameter. Sampling from the conditional distributions rather than directly from the high-dimensional posterior distribution of the parameters makes the Gibbs sampling technique very attractive in Bayesian inference. However, it is not always easy to obtain the conditional distributions or to inversely sample these distributions due to their uncommon distribution forms. Moreover, Gibbs sampling may become very slow in convergence by getting stuck in the low-density regions of the posterior distribution. In these cases, the Metropolis–Hastings approach can provide better performance. We note that advanced MC- and MCMC-based sampling approaches with better efficiency have been proposed over recent years. The MultiNest algorithm [82] and ensemble samplers with affine invariant [83] are two of the most important sampling approaches that have been developed to tackle the issues associated with sampling the multi-model and the badly scaled posterior distributions, respectively.

It is worth discussing how these methods work in principle to better comprehend their benefits. Nested sampling (NS) has mainly been developed for the calculation of the evidence (Eq. 8), but it can also be used to determine the posterior probability. In this approach, the multi-dimensional integral in Eq. 8 is transformed into a one-dimensional integral as where ${\mathcal{L}}$ is the transformed likelihood function as a function of prior volume X (see [82] for further details). Here, a prior volume is a region in the prior parameter space that satisfies an iso-contour constraint for the likelihood of the data given the model parameters. Practically, this transformed integral can be estimated by a standard quadrature method that sums up the transformed likelihood values (${\mathcal{L}}_i$) calculated for a sequential set of discrete prior volumes ($X_i$) times their corresponding weights ($w_i$)—i.e., . It should be noted that $X_i$ alters from 1 to close to 0 in descending order as $1 = X_0> X_1> \cdots> X_i> \cdots> X_N > 0$. The weights are also determined by the trapezium rule as $w_i=\frac{1}{2}(X_{i-1} - X_{i+1})$.

Since the transformed likelihood function in terms of the prior volume is typically unknown, the mentioned summation is performed through an MC-based technique. In this regard, a set of points called 'live points' are sampled from the prior distribution, and then, in a sequential process, the point with the lowest likelihood considered as ${\mathcal{L}}_i$ is discarded from these live points and substituted by a new point from the prior distribution with a likelihood value higher than ${\mathcal{L}}_i$. This strategy is used to find the prior volume $X_i$ at each iteration. This sampling process is repeated until the contribution of the current live points to the evidence value is less than a tolerance.

Efficient and robust sampling from the complex likelihood-constrained prior distributions remains a big challenge. In this regard, the MultiNest approach has mainly been developed for sampling from the multimodal distributions. This technique partitions the live points into a set of (overlapping) ellipsoids with different volumes at each iteration. These ellipsoids are constructed using an expectation-minimization method where the sum of the ellipsoid volumes is minimized by considering a lower bound for their total enclosed volumes. This lower bound is defined as a user-defined fraction of the expected prior volume calculated at each iteration. The new substitute point is uniformly sampled from the union of these ellipsoids such that the probability of selecting this point from a specific ellipsoid equals its volume over the sum of the ellipsoid volumes. If the new point has a likelihood larger than ${\mathcal{L}}_i$, it is accepted with the probability of $\frac{1}{q}$ where q is the number of ellipsoids containing the point; otherwise, it is rejected, and this sampling process continues till the acceptance of a new point. In addition to the evidence calculation, the importance weights associated to the individual discarded points during the above sequential process can be used to infer the posterior distribution and its important statistical features, which are obtained as follows:

(14)

Despite the ability of the MultiNest approach in sampling complex posterior distributions, there is a need for the proper choice of the user-defined parameter in order to provide an appropriate trade-off between the speed and bias in sampling [82].

In ensemble MCMC sampling, a set of walkers—i.e., $\overrightarrow{X} = (X^1,\ldots ,X^k,\ldots ,X^L) \in {\mathbb{R}}^{nL}$ where $X^k = (X_1^k,\ldots ,X_n^k) \in {\mathbb{R}}^n$—move in the parameter space, rather than just one walker in the standard MCMC approaches. This approach produces a chain of ensembles, starting from $\overrightarrow{X}(1)$ to $\overrightarrow{X}(t)$ in a sequential sampling manner. Here, each ensemble is consecutively sampled from a proposal probability density of independent walkers—i.e., $\Pi (\overrightarrow{X}) = \Pi (X^1,\ldots ,X^k,\ldots ,X^L) = \pi (X^1) \times \cdots \times \pi (X^k) \times \cdots \times \pi (X^L),$ where $\pi (X^k)$ is the proposal density for the walker $X^k$—by considering the current positions of other ensembles. Generally, the ensemble sampling can improve the efficiency of the MCMC technique in optimization/calibration problems. Goodman and Weare [83] have improved the ensemble sampling by an affine transformation that converts a bad-scaled distribution into a well-defined one in order to facilitate the sampling process. This transformation is defined in the form of $Y = AX + b$, which keeps the sampling process unchanged due to the proportionality of the transformed proposal distribution to the original one—i.e., $\pi _{A,b}(Y) = \pi _{A,b}(AX + b) \propto \pi (X)$. Let consider a 2D skewed proposal normal density as $\pi (X) \propto \exp (-\frac{(X_1 - X_2)^2}{2\epsilon }-\frac{(X_1 + X_2)^2}{2})$. In this instance, a proper MCMC method should move the walker(s) in order of $\sqrt{\epsilon }$ and 1 in the (1,− 1) and (1,1) directions, respectively. However, the affine transformation makes the sampling process easier and faster by providing a normal distribution in the form of $\pi (Y) \propto \exp (-\frac{(Y_1^2 + Y_2^2)}{2})$ where $Y_1 = \frac{(X_1-X_2)}{\sqrt{\epsilon }}$ and $Y_2 = X_1 + X_2$ [83].

The introduction of the posterior predictive distribution as another natural output of the Bayesian inference is also beneficial here. Unlike posterior distribution—i.e., $P(\theta |x_D)$ where $x_D$ shows the position of the available data—this distribution is independent of the parameters ($\theta$) and defined as a conditional probability of unobserved data points ($x^*$) given the observed data ($x_D$)—i.e., $P(x^*|x_D)$. Technically, the predictive distribution density is determined through the likelihood of unobserved data weighted by the posterior of the parameters given the observed data. One of the most important applications of the posterior predictive distribution is in GP surrogate modeling, where a normal distribution is predicted for any arbitrary $x^*$ given $x_D$.

In contrast to the hypothesis testing using the p values in the frequentist view, a Bayesian hypothesis testing using the Bayes factor has been proposed by Jeffreys [84]. Here, the hypothesis testing is not carried out based on the rejection of the null hypothesis. Instead, probabilities are assigned to the hypotheses using the calculation of Bayes factors that are the ratios of the posterior probabilities of all individual given hypotheses and a fixed arbitrary reference hypothesis. These probabilities indicate to what extent the given hypotheses are favored by the evidence. Therefore, they can act as a comparison measure in hypothesis testing. It is worth noting that hypotheses can be replaced by models in BMS and BMA, where the assigned probability to each model can be considered as the selection criterion and the model weight, respectively [80].

Frequentist Versus Bayesian Inference: Benefits and Drawbacks

There are a number controversial discussions about frequentist and Bayesian inference. However, without paying attention to the controversies, it is important to know what the advantages and disadvantages of each view are in order to make an appropriate decision about which approach to use in order to have the best inference for a given problem.

The main criticism of the Bayesian inference paradigms, as mentioned above, is the high degree of subjectivity in the choice of the prior distributions. In this case, the form of prior distribution should be selected by the user, even if some data are available for the parameters. Generally, improper selection of the prior distribution can mislead or slow down the Bayesian statistical inference. On the other hand, the selection of a reasonable prior distribution for the parameters provides better inference in the Bayesian approaches, especially when data are lacking. In this regard, it should be noted that increasing the data results in less effects of the prior on the posterior convergence, which makes the Bayesian inference less subjective to the prior selection.

In frequentist approaches, on the other hand, a large quantity of data is required to have a reasonable inference, which demands a careful experimental design beforehand in order to acquire the required data. However, engineering and design problems usually suffer a lack of data due to the high cost of experiments. Here, Bayesian approaches can be more useful since the inference can be made by whatever data are available and also updated by any newly acquired data.

The differences between these two approaches to statistical inference can also be discussed in relation to hypothesis testing. The frequentist hypothesis testing offers the benefit of being objective due to the global agreement on the inference from p value. This view also criticizes the probability assignments to the hypotheses in the Bayesian hypothesis testing since a hypothesis is, according to the frequentist view, philosophically either wrong or true and nothing in between. However, the probabilities obtained from the Bayes factor help to decide which hypothesis or model is more favored by the evidence in the case of model selection and averaging. This can be considered as one of the major drawbacks of the frequentist hypothesis testing when the null hypothesis is not rejected. In this case, it is unclear to what extent the null hypothesis is favored by the evidence. Moreover, Bayesian hypothesis testing can easily consider multiple alternative hypotheses, which is very difficult to manage in the frequentist case through multiple pair hypothesis testing. Unlike the frequentist testing approach, the hypotheses can be un-nested models in the Bayesian case—i.e., they can involve different sets of parameters [85].

Uncertainty Quantification/Propagation in Materials Modeling

In the past decade, as theories, codes, and computing infrastructure have reached increasingly advanced levels of sophistication and performance, UQ and UP in materials simulations have slowly gained steam. The increased interest in the topic is due to the need to improve validation and verification protocols as well as to better inform decision-making processes in materials design. Although much work remains to be done and some future directions will be pointed out in later sections of the review, the field already has several examples of UQ/UP in virtually all scales/frameworks available in the computational materials science repertoire. Most of the efforts that will be discussed here correspond to single-scale/single-level modeling along the process–structure–property forward materials science paradigm. Virtually, all examples discussed deal with problems related to inorganic materials (mostly alloys) and this is mostly because of our lack of familiarity with simulations in other materials classes, although it could be argued that computational materials science work on inorganic materials is slightly ahead of work in other materials classes.

Electronic and Alloy Theoretic Calculations

At the electronic/atomic scale, Mortensen et al. [27] and Hanke [28] have performed pioneering work on the probabilistic analysis of density functional theory (DFT) calculations. In the first work, the parameter uncertainties of an exchange–correlation functional used to account for electron–electron interactions have been quantified through a Bayesian approach. In this approach, an ensemble of the model parameter sets has been constructed given an experimental database for different quantities of interest (QoIs) that includes bond lengths, binding energy, and vibrational frequencies. The parameter uncertainties have been propagated to the mentioned QoIs through a forward analysis of the parameter ensemble [27]. In the latter work, the already known or calculated uncertainties for the parameters in a dispersion-corrected DFT model have been propagated to graphite inter-layer binding energies and distances using a standard analytical approach for the calculation of the second central moment associated with variance (uncertainty) [28].

In this field, another important UQ/UP work has recently been published by Aldegunde et al. [86]. In this work, ML surrogate models based on cluster expansions have been proposed as alternatives to expensive first-principles quantum mechanical simulations to accelerate the prediction of several thermodynamic QoIs for alloys, including the convex hull (or ground state set), phase transitions as well as phase diagrams. Here, the appropriate cluster expansion model has automatically been selected through the application of a relevant vector machine that identifies the most influential and relevant basis functions given the data. After finding these basis functions, a Bayesian framework has been used to quantify the uncertainties in the expansion coefficients. Then, the coefficient uncertainties have been propagated to the mentioned QoIs through an analytical calculation of their predictive distributions.

Figure 8, for example, compares the deterministic (least-squares approach in ATAT [87]) and probabilistic (Bayesian linear regression) predictions of the bond stiffness in terms of the bond length in the Si–Ge system for bending (blue dots) and stretching (red dots) elements of the force tensor resulting from eight different atomic configurations. These results have been obtained after the deterministic and probabilistic calibrations of the coefficients in each independent linear model considered for each of the tensor elements. It should be noted that both MPU and MSU show significant contributions in the QoI uncertainties in this work due to a lack of data for the training of the coefficients (parameters) and inaccuracy in the predictions resulting from the truncation of the cluster expansion model, respectively. Therefore, probabilistic predictions are required in order to be able to replace the first-principles calculations by the cluster expansion surrogate models [86].

We note that there were some similar works [88, 89] before this work, where a Bayesian approach was applied for the UQ of the cluster expansion coefficients, but those works did not consider using UP to determine uncertainties in the QoIs resulting from uncertainties in the model coefficients. Another important example of the use of UQ at the atomic scale is the work by Rizzi et al. [90] in which uncertainties in the diffusion coefficient in Ni/Al bilayers simulated through MD which was determined through an MCMC inference approach [90].

Fig. 8

Reprinted with permission from [86]

Comparison of the deterministic and probabilistic predictions of the bond stiffness in terms of the bond length in the Si–Ge system for both bending (blue dots) and stretching (red dots) elements of the force tensor, where left, middle, and right plots correspond to Si–Si, Ge–Si, and Ge–Ge bonds, respectively.

CALPHAD Modeling of Phase Stability

The CALculation of PHAse Diagram (CALPHAD) formalism [91] has emerged as one of the pillars in any ICME framework applied to the accelerated development of alloys [92]. Briefly, the CALPHAD framework enables the rigorous encoding of thermodynamic information about phases in a system in terms of easy to evaluate Gibbs energy functions which are then used to predict phase diagrams through Gibbs energy minimization. Since thermodynamic properties and phase diagrams are fundamental to understanding phase stability as well as phase constitution, their uncertainty greatly affects the outcome of forward models for microstructure evolution that in turn impact decision making in ICME-based alloy design. In order to confidently predict phase stability, phase constitution as well as microstructures and properties, UQ/UP of CALPHAD models is crucial. While notions of uncertainty analysis in CALPHAD models remained dormant for almost a decade, we note that there are some early pioneering studies by Konigsberger [93], Olbricht et al. [94], Chatterjee et al. [95], and Malakhov et al. [96] that performed probabilistic analyses of different thermodynamic QoIs through either simple Bayesian-based approaches or simplified analytical frameworks.

Stan and Reardon [37] proposed a rigorous Bayesian framework for the UQ of phase diagrams. Here, the thermodynamic parameters that include melting temperature and enthalpy of the individual phases are sampled from their posterior probability distributions by considering a multi-objective genetic algorithm (GA) scheme implemented in the context of Bayesian inference. In this scheme, a single fitness value is obtained for all the given objectives based on a fuzzy logic-weighting technique. When the proposed posterior distributions become almost stationary during GA—i.e., parameter convergence—the last population obtained from this process has been considered as the final posterior distribution of the parameters that has been utilized to find the parameter uncertainty bounds. The phase diagrams obtained from this population through model forward analyses have been used to find the uncertainty of the phase diagrams, as shown in Fig. 9 [37].

Fig. 9

Reprinted with permission from [37]

The calculated phase diagrams and their uncertainty bounds for a$\text{UO}_2$–$\text{PuO}_2$ and b$\text{UO}_2$–BeO binary systems.

In much more recent work, Otis and Liu [36] have proposed an automated high-throughput CALPHAD modeling framework that incorporates UQ of the model parameters. It should be noted that the parameter selection for the construction of these sublattice-based models is not fully objective and still requires the expert opinion because of the big challenge arisen from the very large degrees of freedom in CALPHAD modeling—i.e., high diversity in the model form. Here, the Akaike information criterion (AIC) and a univariate scoring approach—e.g., an F test—have been applied to find an appropriate set of parameters for the modeling of pure elements, end-members, or stoichiometric compounds, and the proper number of the sublattice interaction parameters of mixing in the presence of multi-phases, respectively. In that work, the identification of the appropriate set of parameters is followed by an MCMC probabilistic parameter calibration given the relevant data. This UQ approach has been bench-marked using a simple example for the excess Gibbs energy formulation in a binary system expressed as follows:

$$\begin{aligned} G_{mf}^E=x_A x_B (H_{\mathrm{ex}}-TS_{\mathrm{ex}}+L_{\mathrm{ex}} T^2) \end{aligned}$$

(15)

where $x_A$ and $x_B$ are the molar fractions of the constituents in the given system. $H_{\mathrm{ex}}$, $S_{\mathrm{ex}}$, and $L_{\mathrm{ex}}$ also denote the enthalpy of mixing, the entropy of mixing, and an interaction parameter, respectively. After the definition of the prior probability distribution for these parameters, the MCMC framework has been used to find the posterior parameter distribution given ten synthetic data. The marginal and joint posterior probability distributions of these parameters are shown in Fig. 10, where the solid blue and black dashed lines indicate the initial values of the parameters and their calibrated values with 95% credible intervals, respectively. The application of this framework for the quick construction of CALPHAD databases has also been shown through a case study on the Ni-Al binary system [36].

Fig. 10

Reprinted with permission from [36]

Marginal and joint posterior probability distributions for the parameters of the excess Gibbs free energy after MCMC sampling process. The solid blue and black dashed lines correspond to the initial values of the parameters and their calibrated values with 95% credible intervals, respectively.

Duong et al. [32, 97], Honarmandi et al. [29], and Attari et al. [34, 38] have also performed a systematic Bayesian UQ for the thermodynamic parameters of the phases modeled through either the sub-regular solution or line-compound model, the Gibbs free energies of the phases at any arbitrary temperature, and the phase diagram in the U–Nb, $\text{Ti}_2\text{AlC}{-}\text{Cr}_2\text{AlC}$, Hf–Si, and $\text{Mg}_2\text{Si}_x\text{Sn}_{1-x}$ systems. In these works, an adaptive MCMC Metropolis–Hasting technique has been utilized to update the prior distribution defined for the model parameters to their posterior distribution given the calculated and/or experimental data. It is worth noting that the initial parameter values have been considered as the optimized values obtained from the deterministic optimization process in the PARROT module of the Thermo-Calc to arrive at a faster parameter convergence in the high-dimensional CALPHAD parameter space—i.e., a lower cost for the MCMC sampling process.

A uniform prior distribution has also been assumed for each parameter over a reasonable range around its initial value. In the applied MCMC approach, the posterior proposal distribution is adapted during the sampling process based on the variance-covariance matrix of the previous samples in the MCMC chain. Moreover, the likelihood function has been defined as a Gaussian distribution centered at the given data with unknown error. Here, the likelihood error is considered as a hyper-parameter and updated with the rest of the model parameters during the MCMC process. The parameter uncertainties obtained after the MCMC sampling process have been propagated to the phase diagram in the mentioned works through either the analytical FOSM approach or the numerical forward analysis of the converged MCMC samples.

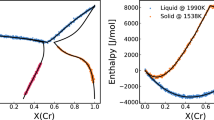
Honarmandi et al. [29] have shown how these uncertainties are propagated to the phase diagram at any specific temperature through the Gibbs free energy of phases as an intermediate step. This chain of UP can be observed in Fig. 11 for the results obtained from two different CALPHAD models for the Hf–Si binary system at two arbitrary temperatures. The applications of Bayesian model selection and information fusion approaches in materials design have also been illustrated in this work [29], which are discussed in "Model Selection and Information Fusion" section.

Fig. 11

Reproduced with permission from [29]

UP from the thermodynamic parameters to the Gibbs free energy of phases to the phase diagram of the Hf–Si system resulting from two different models at two different arbitrary temperatures.

In the most recent UQ work in CALPHAD, Paulson et al. [98] have applied an MCMC sampling technique in ESPEI [36, 99] to perform the calibration and UQ of the CALPHAD model parameters. This has been followed by a model forward analysis scheme for a specified number of parameter samples in order to propagate the parameter uncertainties to different thermodynamic QoIs, such as the compositions, phase fractions, sublattice site fractions, activities, Gibbs free energy of phases, all the thermodynamic properties resulting from the first and second derivatives of Gibbs free energy, and more importantly stable and metastable phase diagrams. This framework has been demonstrated through a case study on the Cu–Mg binary system.

As shown in Fig. 12, the stable phase diagrams obtained at discrete temperature points from 150 parameter sets have been superimposed to demonstrate the uncertainty bounds in the phase diagram. The application of metastable phase diagrams in materials processing under non-equilibrium conditions has been the main motivation for the probabilistic analysis of the Cu–Mg metastable phase diagram in this work. In this regard, the probabilistic metastable phase diagram for the liquid and FCC phase in the mentioned binary system can be obtained through different UP pathways. Figure 13 shows two of these pathways, where the parameter uncertainties have been propagated to the Gibbs free energy of the liquid and FCC phases to a superimposed metastable phase diagram (Fig. 13a, b), or the liquid and FCC phase fractions to a phase diagram representing the probability of nonzero phase fraction of the coexisting liquid and FCC phases (Fig. 13c, d). From the design perspective, one of the most significant contributions of this work [98] is the capability of determining the phase (meta)stability in a probabilistic way at any given point in composition, temperature, and pressure (X–T–P) space.

Fig. 12

Reprinted with permission from [98]

Cu–Mg superimposed equilibrium (stable) phase diagram obtained from 150 parameter sample sets at discrete temperature points.

Fig. 13

Reprinted with permission from [98]

Cu–Mg metastable phase diagram for the liquid and FCC phase in the system obtained through UP from a, b the Gibbs free energy of the liquid and FCC phases to a superimposed phase diagram, and c, d the liquid and FCC phase fractions to a phase diagram demonstrating the probability of nonzero phase fraction of the coexisting liquid and FCC phases. As a manner of illustration, just the Gibbs free energy of the phases at 650 K and the phase fractions at $x_{\mathrm {Mg}}=0.2$ are shown in a and c, respectively.

In other relevant work, Paulson et al. [100] have proposed a modified Bayesian framework for the calibration, UQ, and model selection in CALPHAD. Here, a MultiNest sampling technique has been used to find the posterior distribution of the thermodynamic model parameters given data. This framework attempts to address the issues associated with the presence of outliers, systematic errors, and inconsistencies between the thermodynamic models for different QoIs. The issue with outliers has been addressed through the consideration of an appropriate likelihood function—e.g., Student’s t distribution—rather than a normal distribution, which better accounts for the scattered data. The systematic errors have also been considered by weighting each data in the likelihood function by a hyper-parameter that is updated with the thermodynamic parameters from a proper choice of prior—e.g., an exponential function—to a posterior distribution during the sampling process. To address consistencies between the thermodynamic models, the data for all the thermodynamic QoIs have been taken into account in the likelihood, rather than just the data for one QoI in the ignorance of the others, with the consideration of the same prior distribution for the common parameters in these models. The proposed framework has been applied to the thermodynamic properties of Hf. In this case study, the issue of the model selection has also been addressed in the modeling of the specific heat for different existing phases in this system. Here, the potential models are compared by the calculation of their marginal likelihoods in the context of the Bayes factor [100], which is discussed further in "Model Selection and Information Fusion" section.

In a very recent work by Ricciardi et al. [101], the probabilistic estimation of the Redlich–Kister interaction parameters in the Gibbs free energy of the Ag–Cu binary system has been performed against the corresponding phase diagram data through a Bayesian random-effects Hierarchical model. In this model, where $D^{(s)}=M(\theta ^{(s)}) + \varepsilon$$(s=1,\ldots ,S)$, the random effects ($\theta ^{(s)}$)—resulting from the inherent parameter variability—and the observation error ($\varepsilon$) are assumed to be samples from multivariate normal distributions in the form of $\text{MVN}_d(\theta ,\Lambda ^{-1})$ and $\text{MVN}_n(0,\Psi ^{-1})$, respectively. Here, $\theta$ is the distribution mean value known as the overall effect, $\Lambda$ is a $d \times d$ matrix that denotes the dispersion of the parameters around $\theta$, $\Psi = \delta ^2 I$ is a diagonal $n \times n$ matrix that denotes the dispersion of the independent observation errors around 0, d is the parameter space dimension, and n is the number of data points. The variations in data can also be defined as $\text{MVN}_n(M(\theta ^{(s)}),\Psi ^{-1})$ based on the variations in the observation errors. In the next step, Bayesian inference has been applied for the UQ of the random and overall effects as well as the hyper-parameters in the multivariate normal distributions. After the proper definition of the prior distribution for the mentioned unknowns, $P(\theta ,\Lambda ,\Psi )$, their posterior distribution, $P(\theta ,\theta ^{(1)},\ldots ,\theta ^{(s)},\Lambda ,\Psi |D^{(1)},\ldots ,D^{(s)})$, and marginal posterior predictive distribution for unobserved data ($y^*$), $P(y^*|D^{(1)},\ldots ,D^{(s)})$, can be inferred using an MCMC sampling scheme. Among these unknowns, the posterior inference for the overall effect ($\theta$) is what determines the uncertainty of the interaction parameters in the above thermodynamic model. In this work, the posterior distribution of the total Gibbs free energy at 1000 K and the corresponding region in the phase diagram as a function of Cu atomic fraction has also been obtained through the forward model analysis of a set of MCMC samples after convergence [101].

Mesoscale Materials Simulations

At the micro/mesoscale, phase-field modeling is generally one of the most important approaches to model the microstructural features of material that result from specific processing conditions. To date, however, there are not very many examples of UQ applied to these types of simulations, primarily due to the complexities arisen from the high cost of microstructural modeling and high-dimensional parameter and objective (QoI) spaces. However, the issues for UQ/UP in this area can possibly be addressed using surrogate-based numerical approaches (e.g., Kennedy and O’Hagan’s approach), low-order models (e.g., FOSM or PCE), and efficient numerical techniques (e.g., importance weighting algorithm), which is worth the researchers’ attention in this area.

While there are not many examples of UQ/UP applied to this important simulation framework, two recent works are worth discussing. The work by Zhang et al. [102] has attempted to address the parameter calibration and UQ in phase-field modeling through a statistical framework. In this framework, the geometry of experimentally evolved 3D microstructures and their corresponding simulated 3D microstructures have been compared through two cost functions to find different optimum parameter values associated with different combinations of representative sub-domain sizes (k: the cube edge length in terms of the number of simulation grid points), initial times ($t_0$), and time step numbers ($t_n$). Then, the mean value and standard deviation of these deterministic optimum values have been introduced as the calibrated parameter values and their uncertainties. This framework has been utilized for the calibration of the liquid diffusion coefficient ($D^{\mathrm{L}}$) in a phase-field model implemented for the isothermal dendrite coarsening in a hypo-eutectic Al–Cu system.

The effects of k and $t_n$ on the optimum value of $D^{\mathrm{L}}$ at a constant $t_0$ are shown in Fig. 14. According to this figure, the k values between 160 and 250 can provide almost a uniform optimum value for $D^{\mathrm{L}}$ at all four time steps. At the k values greater than 160, there are statistically sufficient interface areas to well represent the microstructural features in the simulation domain, while the sub-domain becomes too close to the simulation domain at the k values greater than 250 that can misdirect the calibration process. Therefore, the calibration of $D^{\mathrm{L}}$ has been performed by considering different sub-domain sizes in the mentioned range—i.e., $160< k < 250$—as well as different values of $t_n$ and $t_0$. Two-parameter calibration has also been carried out in this work for $D^{\mathrm{L}}$ and capillary length $l^L$ using the same framework [102].

Despite the high value of this work, the thorough model parameterization with the proposed framework can be very costly, which may limit its applications. However, it seems that the surrogate-based calibration approaches—e.g., Kennedy and O’Hagan’s approach [54] discussed in "Uncertainty Categorization in Computational Modeling" section—can be good candidates to estimate the phase-field parameter values and their uncertainties given time-series experimental data at a reasonable cost.

Fig. 14

Reprinted with permission from [102]

The effects of k and $t_n$ on the optimum value of $D^{\mathrm{L}}$ at $t_0=10$.

In the second work, Attari et al. [34, 38] have addressed the UP challenge associated with the high-dimensional input and output space in phase-field modeling of microstructural evolution under chemical and elastic driving forces. In this work, an efficient sampling scheme based on Gaussian copulas [103] has been considered to propagate uncertainties from the high-dimensional model parameter space (20 parameters and model inputs) to a set of microstructural QoIs. It is worth noting that very high heterogeneity of microstructural output space brings a need for the definition of multiple QoIs to fully evaluate the influence of model inputs/parameters on the final microstructure features.

This high-throughput UP approach has been applied to an elasto-chemical phase-field model for $\text{Mg}_2\text{Si}_x\text{Sn}_{1-x}$ thermoelectric materials [104]. In this case, a reasonable number of the parameter vectors—i.e., 10,000—have been sampled from the thermodynamic parameter posterior distributions obtained from the MCMC calibration of a relevant CALPHAD model as well as the micro-elastic and kinetic parameter prior distributions defined based on the literature or expert’s intuition. Then, the microstructures and their corresponding QoIs obtained from the forward model analyses of the parameter samples are used to construct the open phase-field microstructure database (OPMD) [105] and the QoI distributions, respectively. 800 out of 10,000 generated microstructures are shown in Fig. 15. As observed in this figure, the variations in the model parameters can result in a broad variety of microstructure morphologies. Although the possibility of experimentally realizing the predicted microstructures remains to be investigated, the resulting microstructural variety demonstrates the capability of the proposed phase-field model to capture the similar morphologies that have already been observed in other materials system. It should be noted that the constructed database is very valuable and relevant to the scope of ICME since it can provide a better understanding of process–microstructure relationship in the given system.

Fig. 15

Reproduced with permission from [34, 38]

800 Examples from the generated microstructural database besides the morphological varieties obtained for the $\text{Mg}_2\text{Si}_x\text{Sn}_{1-x}$ system.

Another important microstructural modeling in the ICME framework is the second-phase precipitation modeling that has recently received some attention in the UQ/UP area of research. In this respect, Honarmandi et al. [106] have shown a thorough analysis of the parameter calibration and UQ in an Ni-Ti precipitation model implemented in MatCalc© using a multi-objective adaptive MCMC technique. Here, the precipitation model includes three inputs as the nominal Ni content, aging temperature, and aging time, five parameters as the matrix/precipitate interfacial energy, nucleation site density, precipitate aspect ratio, diffusion correction, and nucleation constant, and three outputs as the average Ni content in matrix, mean precipitate size, and precipitate volume fraction. All of these three outputs have been compared with the relevant experimental datasets at the same time in a multi-objective calibration framework.

In the work by Honarmandi et al. [106], the influential model parameters have been calibrated against each given dataset in a probabilistic way to find a relationship for the calibrated interfacial energy in terms of aging temperature and nominal Ni content. Then, the interfacial energy in the model has been replaced by the developed relationship for the probabilistic calibration of the other four parameters against all the datasets together. The model results calculated by the calibrated parameters showed noticeable discrepancies with the corresponding data due to very high uncertainties resulting from the model structure as well as from experiments. For this reason, an information fusion approach has been introduced to combine the model results and data points for better probabilistic prediction of the precipitation behavior [106], which is discussed further in "Model Selection and Information Fusion" section.

Tapia et al. [55] have probabilistically calibrated the same Ni-Ti precipitation model through a multi-objective Bayesian framework based on Kennedy and O’Hagan’s approach [54] that was discussed in "Uncertainty Categorization in Computational Modeling" section. However, just three model parameters—including the interfacial energy and two parameters for an exponential equation defined for the diffusion coefficient—have been taken into account in this work. Two probabilistic calibrations have been performed by considering the computational model and GP surrogate model as M in Eq. 1, while $\delta$ is estimated through another GP surrogate model in both cases. In these calibrations, an MCMC sampling method has been employed to determine the plausible optimum values of the model parameters and hyper-parameters as well as their uncertainties given the experimental data [55].

Materials Processing

Generally, the proper modeling of the materials processing is typically very complicated and expensive due to many involving physical mechanisms. Therefore, there are not many works in this area since UQ of these models is a challenging task and needs advanced analytical or surrogate-based numerical techniques. For example, approximating M in Eq. 1 with GP surrogate model is very useful in these cases. In this regard, Mahmoudi et al. [68] have used the same Bayesian framework where M is a GP model to calibrate the parameters of an expensive finite element method (FEM)-based thermal model in the additive manufacturing of the Ti–6Al–4V alloys. The marginal posterior distributions of the model parameters are shown in Fig. 16. In this case study, it has been shown that the constructed GP estimates the original model with a good degree of precision. In addition, the predictions obtained from the calibrated model are in good agreement with the relevant experimental data [68].

Fig. 16

Reprinted with permission from [68]

Marginal parameter posterior distributions after the MCMC calibration of the multivariate GP-based model fitted to the responses obtained from the FEM-based thermal model at some random spatial input points.

In a recent study, Acer [107] has applied an analytical approach (AUQLin) to quantify the uncertainties associated with the microstructural texture in the Ti–7Al alloy. AUQLin is an inverse approach based on the principle for the transformation of random variables. In that work, the experimental uncertainty of Young’s modulus has inversely been propagated to the volume-averaged compliance parameters through the mentioned analytical framework that has been followed by solving another inverse problem to propagate the uncertainties of the compliance parameters to the microstructural texture. Here, the uncertainties of the microstructural texture have been represented by the variations in a microstructural descriptor known as the Orientation Distribution Function (ODF). This descriptor determines the volume factions of various crystallographic orientations in the microstructure, which is linearly related to the compliance parameters. However, it should be noted that the latter inverse problem leads to multiple solutions for the ODF mean values and uncertainties. Therefore, an optimization approach has been applied to find the final analytical solution for the microstructural texture mean value and uncertainty based on the minimization of the differences between the mean values and uncertainties of the analytically computed ODFs and their corresponding experimental data. The experimental ODF mean values and uncertainties have been calculated from 150 EBSD samples taken from different specimens or different locations on the same specimen. The optimized ODF mean values and uncertainties show very good agreement with their experimental counterparts, as shown in Fig. 17 [107].

Fig. 17

Reprinted with permission from [107]

Comparison of a the mean value and b the uncertainty of the microstructural texture obtained from the applied analytical approach and the experiments.

Macroscopic Materials Properties

At the macro-scale, there are different UQ works on the macroscopic properties of different materials systems, some of which are discussed in this section. Generally, one of the most important materials properties—for structural applications—is the materials’ plastic response to external forces that directly contributes to the materials fabrication. In this respect, Honarmandi and Arroyave [31] have applied an adaptive MCMC sampling approach to calibrate and quantify the parameter uncertainties of a physical model that describes the plastic flow behavior of multi-phase transformation-induced plasticity (TRIP) steels. In this work, the calibration results obtained from sequential and simultaneous data training—i.e., calibrations with one data at a time and all data at the same time—have been compared to each other. Here, it should be noted that three stress–strain experimental data sets have been considered for the calibrations and the rest for the model validation. None of these data training strategies has shown any noticeable superiority over the other, except for slightly more defined posterior distribution in the case of simultaneous data training. In each case, the parameter uncertainties have been propagated to the stress–strain curves of different TRIP steels through the FOSM approach explained in  "Uncertainty Propagation" section. In both of the training cases, there were some discrepancies between the model predictions and their corresponding experimental data (see Fig. 18a, b) that have mostly been attributed to large experimental uncertainties in the measurement of the phase volume fractions (one of the model inputs). For this reason, these volume fractions have also been calibrated for each TRIP steel, while the model parameters are fixed and equal to the parameter posterior mean values after the sequential data training. The correction of the phase volume fractions leads to a very good consistency between the model results and experimental data for each alloy, or at least the 95% credible intervals of the predictions cover the experimental data (see Fig. 18c, d). The reproducibility of the applied MCMC approach has also been checked by the parameter recalibration against some generated synthetic data. The results have confirmed that no significant uncertainties have been added by the approach [31].

Fig. 18

Reproduced with permission from [31]

Probabilistic stress–strain curves obtained for two different TRIP steels (left and right columns) after a, b the sequential data training and c, d the correction of the phase volume fractions (considering fixed sequentially calibrated parameters).

In another work, Rizzi et al. [108] have used an MCMC approach to probabilistically calibrate the physical parameters in a surrogate model constructed upon the results obtained from a finite element-based plasticity simulation. In this work, the surrogate model is developed as a polynomial chaos expansion (PCE) of the parameter vector $\theta$. Then, a formulation called additive error formulation has been built by adding a measurement error (noise) to the surrogate model. Besides this measurement noise, a model discrepancy error has also been added to the parameter vector, which is called embedded error formulation. It should also be noted that multiple batches of tensile test specimens have been prepared to obtain the stress–strain experimental data for calibrations, where each batch has nominally identical specimens. Each of the above formulations has been utilized to calibrate five model parameters given one of the experimental batches as an example. Figure 19 shows 100 stress–strain curves obtained after the forward analysis of 100 parameter posterior samples (obtained from both of the MCMC calibrations) through the surrogate model with and without the consideration of the measurement noise term. A very small uncertainty of the stress–strain response in Fig. 19a implies that the calibration of the additive error formulation results in very small uncertainties for the parameters, and the variations in the response are mostly reflected in the measurement noise as observed in Fig. 19c. On the other hand, the calibration of the embedded error formulation provides an uncertainty partitioning between the model parameters and observation noise that leads to a much better consistency of the stress–strain results and observation error with their corresponding experimental data [108].

Fig. 19

Reprinted with permission from [108]

Comparison of 100 posterior realizations of the stress–strain curve obtained after the MCMC calibration of five model parameters using additive (left column) and embedded (right column) error formulations with (bottom row) and without (top row) the consideration of the measurement noise term.

Recently, Ricciardi et al. [101] have probabilistically calibrated the hardening parameters in a reduced-order viscoplastic self-consistent (VPSC) model by considering the inherent variability of the stress–strain response in the Bayesian random-effects Hierarchical framework discussed at the end of  "CALPHAD Modeling of Phase Stability" section. In this framework, the posterior probability density of the parameters and hyper-parameters, in addition to, the posterior predictive density for untested data has been inferred using an MCMC sampling technique. The uncertainty of the hardening parameters has also been propagated to the stress–strain curves through the forward model analysis of a set of MCMC posterior samples [101].

The UQ/UP study of shape memory alloy (SMA) properties is another topic of interest in robust design that has recently attracted some attention by the community. The main reason for the popularity of SMAs is their broad applications in engineering, such as micro-electro-mechanical systems, biomedical implants and devices, seismic protection tools, actuators and sensors, and aerospace structures and products [109, 110].

Oehler et al. [111] have used design of experiment (DOE) approaches based on MC simulation techniques to perform the SA and UP through a hierarchy of analysis tools and a numerical constitutive model for an SMA-actuated morphing structure. Here, the sensitivity of the outputs to the variations in normal-distributed input variables, as well as the propagated uncertainties for the outputs, has been determined through this framework.

Martowicz et al. [112] have also performed SAs and UP for a numerical model that describes the phase transformation in the super-elasticity phenomenon of an SMA bumper, as well as two regression-based surrogate models constructed based on some results obtained from the numerical model. In this work, the sensitivity of the output of the numerical and surrogate models to the variations in the uncertain input variables has been evaluated through a central finite difference (FD) that considers just one input at a time in its analysis. Moreover, an MC simulation technique has been adopted to propagate the uncertainties from the input variables to the output of the surrogate models.

Recently, Islam and Karadogan [113] have used an MC-based forward analysis scheme to propagate the uncertainties from the normally distributed input variables of two most commonly used models for super-elasticity—i.e., Tanaka [114] and Liang–Rogers [115] models—to their stress–strain outputs under different isothermal conditions. They have also evaluated the sensitivity of the stress–strain outputs to the inputs through global VBSAs—i.e., Extended Fourier Amplitude Sensitivity Test (eFAST) and Sobol—for both of the applied models. Here, the influential model inputs have been determined based on a criterion for the average of the sensitivity indices obtained at different maximum loading stresses and isothermal temperatures for each input. Both of the applied sensitivity approaches have been consistent in selecting the influential parameters.

In other works, Crews et al. [116, 117] have applied an MCMC approach known as the delayed rejection adaptive Metropolis (DRAM) method to find the posterior parameter distribution of a homogenized energy model for SMA bending actuators, given the relevant experimental data. It should be noted that the applied external voltage (for the purpose of Ohmic heating) and the bending angle of an SMA tendon are the input and output of this work, respectively. Figure 20 shows the comparisons between the 95% credible intervals obtained after the forward UP from the MCMC-calibrated model parameters to the temporal changes in the bending angle under two different input conditions—i.e., sinusoidal and step input voltages—and their corresponding experimental data. As shown in this figure, the majority of the experimental data fall into the uncertainty bounds in both of the cases, which highly validates the model for SMA robust design applications.

Fig. 20

Reprinted with permission from [117]

The probabilistic temporal changes in the bending angle in an SMA tendon obtained under a sinusoidal and b step input voltages, besides their corresponding experimental data.

Enemark et al. [118] have also utilized an adaptive MCMC approach to quantify the parameter uncertainties and linear correlations in a thermo-mechanical model that predicts the super-elastic behavior of SMA helical springs. In this work, some experimental isothermal cyclic responses have been considered for parameter calibration and UQ. The marginal parameter posterior frequency distributions and pairwise scatter plots obtained after the MCMC sampling process have been shown in the diagonal and off-diagonal plots of Fig. 21, respectively. According to this figure, it is clear that the marginal distributions for all the parameters are almost Gaussian, and parameter pairs exhibit significant variance in their degree of statistical correlation. It should be noted that a highly linear scatter plot with a positive or negative slope corresponds to a highly positive or negative linear correlation with a coefficient close to 1 or − 1; on the other hand, a close to circular scatter plot indicates a linear uncorrelation with a coefficient close to 0. However, in this work, there is no UP analysis from the model parameters to the isothermal cyclic response resulting from the loading and unloading process. In addition, there is no systematic SA to find the most influential parameters for the sake of the UQ cost reduction [118].

Fig. 21

Reprinted with permission from [118]

The marginal parameter posterior frequency distributions and pairwise scatter plots for the model parameters in the diagonal and off-diagonal plots, respectively.

In other relevant work, Honarmandi et al. [30] have adopted the same Bayesian framework and thermo-mechanical model as well as a systematic sensitivity analysis and a forward UP to predict the probabilistic thermal actuation response (isobaric cyclic response) of SMAs. In this work, applying a DOE that includes a complete factorial design (CFD) and a global VBSA known as ANOVA has resulted in the identification of the influential parameters for this model. These parameters have been used in the model calibration against three experimental isobaric cyclic responses. In this probabilistic calibration process, the cyclic curves obtained from the model and experiment have been compared in the likelihood function through the calculation of their squared euclidean distance, as proposed by Tschopp et al. [119].

The MCMC technique has also been modified in the work by Honarmandi et al. [30] in order to consider some constraints between the model parameters during the sampling process. This modification has been performed by penalizing the likelihood such that the MCMC sampled candidates are rejected as the defined constraints are not satisfied. Moreover, the UPs from the model parameters to the isobaric cyclic predictions have been performed for the three isobaric conditions using both of the FOSM and forward analysis approaches. Unlike the FOSM approach, the forward analysis approach is more precise but also more costly. Therefore, a trade-off exists between the precision and cost in the application of these methods. For example, the model prediction and its 95% credible interval are obtained by the forward UP analysis, and the corresponding experimental data have been shown for three different isobaric conditions in Fig. 22. As observed in this figure, there are good agreements between the isobaric cyclic loops obtained from the model and experiment, or at least the data are covered by the uncertainty bounds [30].

Fig. 22

Reprinted with permission from [30]

Probabilistic predictions of the isobaric hysteresis response of a Ni-Ti alloy obtained through forward UP analyses and the corresponding experimental data at three different isobaric conditions: a 100, b 150, and c 200 MPa.

Advanced Frameworks for Uncertainty Quantification/Propagation in Materials Simulations

Efficient Uncertainty Propagation

As mentioned in "Uncertainty Propagation vs. Uncertainty Quantification" section, the most basic and common approach to propagate uncertainty through computational models is via MC sampling. For expensive computational models, the use of sampling approaches is computationally prohibitive. A typical alternative is to create a surrogate or meta-model of the full model using a small set of samples from the full model. The result of developing a surrogate model is usually a much cheaper version of the computational model that can be used for various purposes—such as uncertainty propagation [120, 121]. The reduction in runtime, however, comes at the expense of loss in accuracy as well as of information on the full model output.

As mentioned in "Uncertainty Propagation vs. Uncertainty Quantification" section, other state-of-the-art and common approaches to uncertainty propagation are techniques such as generalized PCEs [122]. These methods require smooth functions that do not contain discontinuities and also face challenges in high dimensions when functions lack an additive structure [123]. For the case of discontinuities, a common issue that deteriorates accuracy is the presence of Gibbs-type phenomena. To overcome this challenge, multi-element stochastic collocation methods were developed [123, 124]. Unfortunately, such methods often require a large number of samples to detect discontinuities, rendering the approach computationally prohibitive. On the other hand, if there are no discontinuities—which for black-box simulation models are generally unknown a priori—significant computational effort is wasted.

Materials science simulations often result in highly discontinuous output spaces that result from the high nonlinearity of the applied theories/models. Moreover, as one of the main purposes of materials simulations is to uncover process–structure–property relationships, it is imperative to preserve as much information about the model output as possible. These challenges and requirements clearly preclude non-sampling-based UP approaches. MC sampling, however, is impractical when simulations are computationally expensive. The question then is whether it is possible to carry out UP by sampling directly from the actual simulation and obtain properly converged output distributions without having to sample the input space $1\times 10^5{-}1\times 10^6$ times.

Recall that each sample taken from the MC sampling chain has a weight of 1/n, where n corresponds to the total number of MC steps carried out so far. When $n \rightarrow \infty$, we are guaranteed to have a well-converged probability distribution in the output space. Since, on average, all samples are useful to construct the well-converged output distributions, logic dictates that some samples are more useful than others. A sampling-based approach for efficient UP can take advantage of this to arrive at well-converged predictive uncertainties, using much fewer direct evaluations of the (expensive) models than traditional MC methods—see Fig. 23. The central hypothesis here is that in small sample size regimes, this convergence can be achieved more quickly by carefully selecting points in the input space via assignment of non-uniform weights to individual UP samples. The challenge of evaluating statistics from a target distribution given random samples generated from a proposal distribution is known as the ‘change of measure’ and arises in a host of domains such as importance sampling, information divergence, and particle filtering [125, 126].

Fig. 23

Reproduced with permission from [127]

Importance sampling approach whereby proposal samples from a proposal distribution are re-weighted in order to generate the target distribution.

Sampling-based approaches for accelerated UP rest on the hypothesis stating, a more efficient convergence of the probability law ${\mathcal{L}}$ on the input space—i.e., probability and cumulative distribution functions (CDFs, PDFs)—will lead to improved convergence for certain statistical quantities of interest in the output space. These approaches can be used to identify the next sample to propagate through an expensive model. Generally, this next sample will be chosen such that the difference between the true input law and the current empirical law is minimized, by re-weighting the incorrect input (proposal) distribution in order to obtain the correct (target) distribution, as shown in Fig. 24 [33, 127].

Fig. 24

Reproduced with permission from [127]

Correcting the proposal distribution shown in the blue using importance weights and estimate the target distribution shown in the red as a weighted proposal distribution (dotted plot on the right).

Recently, Sanghvi et al. [33] have proposed an importance weighting algorithm that corrects UP results obtained from inaccurate proposal distributions of model inputs/parameters by re-weighting the previously available model evaluations. This approach is capable of achieving probability measure changes over many dimensions, which is ideal in materials science problems given the usually large-dimensional input space. To demonstrate their framework, Sanghvi et al. [33] considered a Johnson–Cook (J–C) model [128] for the high-strain deformation behavior of Ti–6Al–4V [129]. The J–C model has been considered to include five uncertain parameters, and the challenge was to re-weight already acquired samples in the input space (assuming uniform distributions) in order to estimate the target (normal) distributions as per prior parameterizations [129], as shown in Fig. 25. In that figure, it is shown how the probability law of the output of the model is well converged once the inputs have been reweighed to match the correct distributions.

Fig. 25

Reproduced with permission from [33]

Uncertainty propagation via change in measure for a five-dimensional Johnson–Cook model in which (incorrect) uniform distributions for the inputs have been transformed to (correct) normal distributions. (Left) proposal and target PDF; (center): proposal and target CDF; (right): convergence of the mean response of Johnson–Cook model as a function of sample size.

Uncertainty Quantification/Propagation in Multi-scale Modeling

As mentioned in  "Uncertainty Quantification/Propagation in Materials Modeling" section, the quantification of the parameter uncertainties and their propagation to the outcome of the individual models are important tasks in order to validate their outcome against data in a probabilistic way and find their sensitivity to the parameter variations (uncertainties) for the sake of their applications in materials design. However, the uncertainty of the outcome of a chain of multi-scale models—i.e., from the atomic/electronic level to the microstructural features to the macroscopic behavior—is required for the decision-making process in ICME design. In these types of problems, uncertainty must be propagated along multi-scale models, not just a single model. Despite the importance of UQ in multi-scale modeling, few relevant works exist in the recent literature that suggests much more effort in this area in order to fulfill the ICME promises. These few works are discussed in this section as follows.

Liu et al. [130] focused on the UQ of a developed multi-scale constitutive model that connects the microstructural features and defects in random heterogeneous composite materials to their failure in the context of structure–property–performance relationships of the ICME framework. In that work, probabilistic Bayesian calibration—where the statistical information obtained from direct numerical simulation as well as limited experimental data serves as the parameter prior—has been performed to quantify the parameter uncertainties of the constitutive model. Then, a stochastic projection method based on PCE has been applied to propagate the parameter uncertainties across the multi-scale model to the properties and performance of the composite materials.

There are also some important UQ/UP works in multi-scale modeling for plastic flow response in polycrystalline materials that have already been discussed by Chernatynskiy et al. [10]. In regard to predictive process–structure–property relationships, Kouchmeshky and Zabaras [131, 132] have investigated the variations in the macroscopic properties—such as Young’s, shear, and bulk modulus—resulting from the inherent uncertainties in the deformation processing conditions and initial microstructural texture of the given materials. In these works, a reduced-order model based on the Karhunen–Loeve expansion has been constructed to reduce the stochastic domain dimension for the initial texture from a random field to a few spatial modes (a set of random variables) that can highly represent the texture randomness in the microstructure. The information acquired from X-ray scattering techniques or a maximum entropy method (MaxEnt) in the lack of experimental data has been used to construct the distributions of these random variables. In the end, the propagated uncertainties from the initial texture and processing conditions to the properties have been presented in the form of distribution or convex hull plots. Here, convex hull is the smallest convex polygon surrounding all the samples in the property space obtained after the UP analysis. An example of these plots for Young’s–shear–bulk modulus is shown in Fig. 26. Generally, the convex hull provides a good graphical representation of the variations in QoIs, which can be a very useful tool for product designers [131, 132].

Fig. 26

Reprinted with permission from [10]

An illustration of the convex hull for Young’s, shear, and bulk modulus after the UP from the random initial texture and processing conditions.

Koslowski and Strachan [133] have also propagated uncertainties across different length scales in the plasticity modeling of a nano-crystalline Ni membrane. Figure 27 shows how the uncertainties have been propagated along the multi-scale models in this work. First, the microstructural texture and the distribution for the macroscopic residual stresses along the membranes’ axial direction have been derived experimentally. Then, an ensemble of 1000 residual stresses has been produced from the experimental distribution (see Fig. 27a) as the representation of 1000 membranes. For each residual stress, 5000 representative grains have been generated in agreement with the experimental texture. In the next step, the strain tensors calculated for each of the twelve slip systems in all the individual grains have been used to construct the distribution of the in-plane and out-of-plane strains for the considered slip system (see Fig. 27b). The strain distributions for all the slip planes have been converted into the distribution of unstable stacking fault energies using a molecular dynamics (MD) response surface (see Fig. 27c). The last step in this multi-scale UP is to predict the distribution of critical resolved shear stresses (CRSS) from the previous distribution through a phase-field method to dislocation dynamics (PFDD) (see Fig. 27d) [133].

Fig. 27

Reprinted with permission from [10]

A schematic illustration of UP along a chain of the multi-scale plasticity models for nano-crystalline Ni membranes.

Uncertainty Quantification/Propagation Through Model Chains

As mentioned in  "Introduction" section, the central paradigm behind ICME is the integration of multiple modeling tools and their coupling with experiments in order to accelerate the materials development cycle. While model integration has long been recognized as one of the most important enablers of fully realized ICME frameworks, the linkage between models is highly challenging in practice [16].

To date, there are relatively few examples of realizations of ICME frameworks with explicit linkage between different models through a physics-based model chain. The recent work by Attari et al. [34, 38] is a good example of a systematic analysis of uncertainty across a chain of models—i.e., a CALPHAD and phase-field model. As mentioned earlier in "Uncertainty Quantification/Propagation in Materials Modeling" section, the plausible optimum values and uncertainties of the thermodynamic parameters incorporated into a CALPHAD model for the $\text{Mg}_2\text{Si}_x\text{Sn}_{1-x}$ thermoelectric system have been quantified through an adaptive MCMC approach given the corresponding composition–temperature data in the phase diagram. Then, a Gaussian copula has been applied to efficiently sample from the posterior distribution of the thermodynamic parameters obtained after the MCMC calibration—which is technically a joint prior parameter distribution for the phase-field simulation—as well as the prior distributions of the micro-elastic and kinetic parameters defined based on the literature or expert’s intuition. These samples have been analyzed through a forward scheme to propagate the uncertainties of the mentioned parameters to a set of microstructural QoIs [34, 38].

In another recent work, Reddy et al. [134] have put forward an ontological framework for integrated computational materials engineering. In their framework, Reddy and collaborators have proposed a meta-model-based framework that consists of abstracting elements of the ICME model chain—i.e., materials, processes, structure, properties—and their relationships. The framework enables the linkage between models through pre-specified input/output protocols. Brough et al. [135] have proposed the Materials Knowledge Systems (MKSs) framework to capture process–structure–property linkages. In this framework, homogenization and localization methods have been used to express structure–property connections that are then abstracted in terms of surrogate/regression models. These works constitute valuable examples for model integration. Until recently, however, model integration efforts have seldom included protocols to quantify, propagate, and manage uncertainty through the model chains.

Consider, for example, a model chain consisting of two distinct models, ${\mathcal{M}}_1$ and ${\mathcal{M}}_2$—as mentioned above, one effective approach to decrease the computational expense associated with model evaluations is to replace the expensive simulations with surrogate models—e.g., GPs [17]. Each of these models has inputs x, parameters $\theta$, as well as outputs y, which can be computed in principle through a GP that emulates the original expensive model. This model chain is hierarchical and unidirectional as models ${\mathcal{M}}_1$ and ${\mathcal{M}}_2$ are connected through an (intermediate) output vector of model ${\mathcal{M}}_1$, which serves as input to model ${\mathcal{M}}_2$. In order to properly establish such a model chain as a plausible framework for uncertainty-aware model integration, several challenges must be overcome: First, the framework must be capable of providing the ability to probabilistically calibrate the individual models by comparing the QoIs they produce with available data from experiments; second, the framework should enable the propagation of information (uncertainty) across the model chain; third, the evaluation of the models should be sufficiently cheap to carry out a properly converged exploration of the input–output space; lastly, the framework should accommodate the challenges associated with the existence of unobservable QoIs produced from a model as inputs to models down the model chain.

Fig. 28

Reproduced with permission from [136]

ICME-based integration of a thermal model to a phase-field model in additive manufacturing.

To illustrate the problem, consider (see Fig. 28) an ICME model chain applied to additive manufacturing. Specifically, consider a finite element thermal model [137] capable of establishing the connection between processing conditions in a laser powder-bed fusion system (power, scanning velocity) and thermal history (thermal gradients and cooling rates) in different regions of a melt pool. The thermal histories can then be used as inputs to a phase-field simulation [138] of the solidification behavior of the alloy being processed. The practical integration of these two models is manifold: First, the output of the thermal model used by the phase-field model (thermal histories) is not easily accessible; second, each model has numerous parameters that are uncertain before confronting them with experimentally derived observables; third, each of the models is computationally expensive; fourth, explicit linkages between the outputs of the thermal models and the inputs to the phase-field models are infeasible.

Recently, Mahmoudi [136] and Mahmoudi et al. [139] have put forward a framework that addresses this type of problem. Their framework relies on the use of Bayesian networks (BNs) [140, 141]. As shown in Fig. 29, BN is a tool that captures causal relationships between the variables and parameters within a network of models using a directed acyclic probabilistic graph [142]. In the practical implementation of a BN-based approach to UQ/UP, the relationships between inputs and outputs through model chains are expressed in terms of coupled stochastic models. The calibration of the parameters has been done through Bayesian update schemes.

Fig. 29

Reproduced with permission from [136]

Bayesian network representation of AM-ICME (finite element–phase-field) model chain shown in Fig. 28. Models ${\mathcal{M}}_1$ (thermal history) and ${\mathcal{M}}_2$ (microstructure evolution) are represented as GPs with parameters $\theta _1$, $\theta _2$. The models are linked through unobservable intermediate outputs (cooling rate, thermal gradient), ${\hat{y}}_{1U}$. Model ${\mathcal{M}}_1$ has observable outputs ${\hat{y}}_{1Q}$ (melt pool width, depth, and peak temperature) that can be compared against data $D_{1Q}$. Similarly, model ${\mathcal{M}}_2$ has observable outputs (primary dendrite arm spacing, PDAS, and micro-segregation).

Mahmoudi has demonstrated his proposed framework [136] by linking a finite element model connecting processing conditions to thermal histories developed by Karayagiz et al. [137] with a phase-field model of microstructure evolution under rapid solidification conditions developed by Karayagiz et al. [138]. The models employed the materials properties of a binary Ni–Nb alloy that has then been printed using a laser powder-bed fusion machine. Macro-structural features of the melt pool (melt pool width and depth) as well as microscopic features of the solidified microstructure (primary dendrite arm spacing, PDAS) have been used to simultaneously calibrate the parameters of both models. Preliminary results in Fig. 30 have suggested that the proposed BN-based model chain is capable of predicting experimental observables at two scales (melt pool dimensions and solidification microstructure) with acceptable error bounds—better results have achieved in recent work by Mahmoudi et al. [139].

Fig. 30

Reproduced with permission from [136]

Errors associated with the model predictions of melt pool width (finite element model) and primary dendrite arm spacing (PDAs) during the additive manufacturing of Ni–Nb binary alloy.

Model Selection and Information Fusion

In numerical simulations and physical modeling as an essential element in materials design under the ICME framework, engineers and scientists typically have at their disposal multiple models at different levels of fidelity and/or physical sophistication describing the same physical system. Deciding on the most appropriate model to properly represent the given system is not necessarily an easy task when the model outcomes are comparable. Therefore, a systematic framework is required to address the issue of model selection in these cases. To address this problem, Bayesian model selection (BMS) based on the Bayes factor can be a good candidate to identify the model that is more favored by the given data—based on the Bayesian hypothesis testing discussed in "Bayesian Inference" section .

Honarmandi et al. [29] have applied this approach to compare four CALPHAD models with different numbers of parameters for the HF-Si system. As mentioned earlier in  "CALPHAD Modeling of Phase Stability" section, Paulson et al. [100] have also applied the same approach to select the best specific heat model as a function of temperature for each Hf phase. In this case, the Bayes factor has been obtained for each potential model by calculating its marginal likelihood over the marginal likelihood of a reference model for each phase. The results have implied that the combination of the Debye and a quadratic polynomial model, a quadratic polynomial model, and a linear model are the best models for the specific heats of the alpha, beta, and liquid Hf phases, respectively.

Generally speaking, it should be noted that the identification of the closest model to the data is not often the best strategy in the prediction of the system response since there is potentially some useful information in all the feasible models proposed to describe the response of the given system. For this reason, information fusion approaches have been developed to properly combine the information obtained from different sources (models and experiments) for better predictions of the system response [18,19,20]. In information fusion approaches, the information can be acquired from the given sources by optimally partitioning the total budget based on a reasonable balance between the cost and accuracy of the data queries from these sources. Co-Kriging and BMA are the most commonly used information fusion approaches in the engineering problems, which are briefly discussed in this section with some case studies.

In the co-Kriging approach proposed by Kennedy and O’Hagan [143], a linear relationship similar to Eq. 1 is assumed between each two closest ranked models in the hierarchy of multi-fidelity models. Here, GP surrogate models are constructed over some random results obtained from the lowest-ranked model and each error term in the mentioned hierarchy of linear relationships and then statistically correlated together to predict the response of the highest fidelity model. For example, consider the simple case of two fidelity models where the low- and high-fidelity models are a physical model/simulation and the corresponding experiment, respectively. In this case, two GP surrogate models are constructed over some random results obtained from the low-fidelity model/simulation—i.e., $f(x_i,\theta )$—and some other random results obtained from the error term—i.e., $\delta (x_j)+\varepsilon (x_j)$ in Eq. 1 that is equivalent to $D(x_j)-\rho M(x_j,\theta )$, M can be the low-fidelity physical or GP surrogate model. Ultimately, these two GP surrogate models are correlated through the construction of a variance–covariance matrix based on distance correlations between the input values of the applied random results, to find a fused model for the experimental response.

The mentioned correlation brings the expectation that co-Kriging surrogate models provide more precise predictions with lower uncertainties for the response of the high-fidelity model compared to the GP surrogate models. To confirm this, a 1D simple example of the martensite start temperature variation in terms of Ni content in Ni-Ti SMAs has been considered to compare the ordinary Kriging (GP) and co-Kriging predictions for the high-fidelity model. As shown in Fig. 31, 27 and four data points (red cross and green squares) with no noises have been sampled from the responses of a low-fidelity generated linear model and a high-fidelity relevant experiment, respectively. As can be observed in this figure, the co-Kriging surrogate model provides a much closer mean response (blue vs. red line) to the real response of the high-fidelity model (green line fitted on the experimental data from Frenzel et al. [144]) as well as a lower uncertainty (blue vs. red shaded region). It is worth noting that the plot has been designed for a sequential efficient Bayesian optimization problem, where an absolute value of $M_s-30$ has been considered to be able to find the Ni content resulting in an $M_s$ equal to 30C through the minimization process. In this case, the application of the co-Kriging surrogate model should lead to a more efficient optimization process compared to the commonly used GP surrogate model due to its higher accuracy.

Higher efficiency of the optimization process using co-Kriging modeling has also been shown in the case of high-dimensional design problems by Chung and Alonso [145]. In very recent works, Honarmandi et al. [106] and Patra et al. [146] have applied this information fusion approach for the probabilistic predictions of the precipitation behavior of Ni-Ti SMAs and polymer band-gaps, respectively.

Fig. 31

Comparison of the ordinary Kriging (GP) and co-Kriging surrogate model in a 1D example

BMA is also another well-known approach that combines the probabilistic responses of multi-fidelity sources to find a fused model with a more robust prediction of the system response. Here, a weighted average is taken over the response of all the models at any given set of input, where the weights are the probability of each model given data—i.e., $P(M_i|D)$—and calculated using the Bayes’ factors. The probabilistic information for BMA can be obtained through GP surrogate modeling or the Bayesian calibration of the original model against the given data. For example, Talapatra et al. [147] have applied BMA over the GP models obtained for the shear and/or bulk modulus of MAX phases as a function of several combinations of their selected features in order to autonomously perform single- and multi-objective Bayesian optimizations for materials discovery. Technically, at any specified input (feature set) values, a weighted average of all the GP acquisition values has been calculated in these optimization frameworks, rather than just the acquisition value of the best GP model that requires a priori knowledge of the best feature set.

Another example is the work by Honarmandi et al. [29], where a BMA-fused phase diagram has been produced by taking a weighted average (at any specified composition) over four MCMC-calibrated phase diagrams obtained from four CALPHAD models with different numbers of parameters. Here, a wider uncertainty bound has been obtained for the fused phase diagram compared to the phase diagrams constructed from the individual models. This wider uncertainty bound can provide some benefits for robust design in the safety–critical applications. However, it can be too conservative due to the BMA assumption about the statistical independence of the individual models.

When the assumption of statistical independence between models is not warranted, one can use, for example, the error correlation-based model fusion (CMF) framework developed by Allaire and Willcox [18]. CMF was used by Honarmandi et al. [29] to construct a more accurate fused phase diagram. CMF considers the correlations between the model errors (standard deviations) at any specified composition that result in a fused phase diagram with uncertainties lower than those of the applied individual models. The CMF-fused phase diagrams obtained from the fusions of three and four CALPHAD models are shown in Fig. 32. It should be noted that the best proposed model has been disregarded in the case of three-model fusion. The fused diagrams have provided closer mean values to the data (ground truth) and lower uncertainties compared to the phase diagrams obtained from the applied individual models in each case. Although the three-model fused phase diagram has not perfectly captured all the features and details in the phase diagram—e.g., sharp eutectic points, it has covered all the data points in its 95% credible intervals, unlike those three individual models. Finding such a reasonable phase diagram via the fusion of random CALPHAD models—that may have very low degrees of accuracy—can be the first step toward making the CALPHAD modeling more objective for the sake of autonomy in design rather than being subjective to model selection.

Fig. 32

Reprinted with permission from [29]

CMF-fused phase diagrams obtained from the fusions of a three and b four CALPHAD models.

Conclusions

Our inability to have complete models due to incomplete knowledge of the physical systems in question, as well as their inevitable inherent uncertainties, brings the need for a proper uncertainty analysis of the models. Identifying different sources of uncertainty, quantifying these uncertainties, and propagating them across different scales (levels) of process–structure–property–performance hierarchy in the ICME framework are very important tasks that enable not only the proper management of the uncertainties but also make robust/reliability-based materials design possible.

In computational materials modeling, most of the UQ works in the literature have focused on the quantification of the overall uncertainties—i.e., NU, MPU, and MSU—reflected on the model input variables/parameters given the relevant probabilistic data about the system outputs, or the propagation of the prior input variable/parameter uncertainties—i.e., NU and MPU—to the model outputs with no consideration of MSU. However, partitioning the uncertainties resulting from different sources seems to be essential in order to apply proper strategies for the reduction in the epistemic uncertainties. Kennedy and O’Hagan’s framework [54] for the calibration of computer models is one of the important approaches to tackle this problem.

Another issue that should be addressed in the UQ of computational models is a lack of systematic works for the uncertainty analysis across a chain of models in the ICME hierarchy. The reason is that the decision-making process in materials design depends on the probabilistic response obtained from the entire ICME chain and not just the response of a single model in this chain. Since the individual models in this chain can be very expensive, the challenge here is the cost of the UP across the chains of models through the conventional numerical approaches—e.g., MC-based sampling approaches. Although constructing surrogate models using a small number of samples from the outputs of these expensive models—e.g., GP surrogate models—are a typical solution for this problem, it usually comes at the cost of information and accuracy loss that is not always desirable. Therefore, efficient UP approaches—such as the importance weighting algorithm proposed by Sanghvi et al. [33]—should be developed to keep the balance between cost and accuracy. It should also be noted that BN is a powerful tool to provide the connections between the variables and parameters of the individual models in the chain—some of which can be unobservable—in order to perform a systematic UQ/UP in these types of problems.

In the case that multiple models with different fidelity and cost exist to describe the physical system of interest, the individual model predictions and their uncertainties can be combined statistically to find a fused model with either a more robustness or higher level of certainty in its prediction. In other words, UQ can be performed through the fusion of all the feasible models rather than just the best model in order to reduce either the risk or uncertainty in design depending on the required objectives in the given problems. Information fusion approaches are also capable of providing autonomous processes for the acceleration of materials design and discovery.

In recent years, the growing idea of data-to-knowledge due to the development of ML techniques has become an increasingly popular topic in materials science and engineering research. ML regression techniques can be useful tools in the accelerated materials design and discovery by substituting expensive models with much cheaper alternatives. Some of these regression techniques—e.g., GPs—already include predictive uncertainties in their estimations, but some others do not. For example, deep learning models—such as deep neural network models—with the ability of microstructural feature recognition have recently emerged in materials science as alternatives for expensive phase-field models. However, the proper UQ/UP in these surrogate models is necessary for their applications in materials design and discovery frameworks. It is our view that this can be one of the most promising research areas in UQ/UP.

In this review, it has been attempted to present a thorough overview of UQ/UP in materials design under the ICME framework and address different relevant issues that are required to be studied more in the future. While we recognize that the field of UQ/UP in materials modeling is in its infancy, there is much to learn from other fields of study that have already reached a much higher level of sophistication when it comes to the analysis, understanding, and management of uncertainties in computer simulations. The most advanced UQ/UP approaches discussed in this review have resulted from highly interdisciplinary collaborations between experts in statistics, UQ/UP, and materials science. We hope that such examples motivate further interdisciplinary work aimed at resolving the many outstanding issues that computational materials modeling faces. Although solutions to these problems are quite challenging, they will greatly and positively impact model validation and verification efforts as well as decision making in materials design.