Introduction

In recent times a number of studies on reliability evaluation of earth slopes have been reported in the literature that are aimed at emphasizing the importance of adopting a probabilistic approach of analysis of slopes. However, the vast majority of these studies have considered only one type of uncertainty, namely, the epistemic uncertainty (statistical uncertainty and measurement errors); in other words, the aleatory uncertainty due to spatial variability has received much less attention.

Studies reported on reliability analysis of earth slopes considering spatial variability were conducted under the framework of Limit Equilibrium Method (LEM) as well as the Finite Element Method (FEM). Those based on the Random Finite Element Method (RFEM) include Griffiths and Fenton [1], Schweiger and Peschl [2], Griffiths et al. [3], Hicks and Spencer [4], Le [5] and others. More recently, Jha [6] has studied the influence of spatial variation on slope reliability using the RFEM and the First Order Second Moment method combined with variance reduction theory. Based on this study, the author has recommended the use of RFEM and determination of realistic scales of fluctuation, coefficient of variation of soil properties for slope reliability analysis. In spite of its key advantage that no failure mechanism needs to be assumed, the RFEM suffers from excessive computational efforts since the strength reduction method calculates the factor of safety by progressively reducing or increasing the shear strength of the material in order to bring the slope to a state of limiting equilibrium [7]. Moreover, as pointed out by Ji et al. [8], the number of spatially correlated random variables assigned to elements is commonly very large in the advanced RFEM so that only Monte Carlo simulation can be employed.

On the other hand, a lot of researchers studied the influence of spatial variation on the slope reliability based on the LEM [8–17]. El-Ramly et al. [10] modeled the spatial variability of each input variable along the slip surface by a 1D stationary random field describing an elaborate spatial variability discretization model. A few others (e.g., Hong and Roh [15]; Wang et al. [16]; Li et al. [17]) also modeled the spatial variability of soil properties by a 1D random field; but they considered spatial variation along the vertical direction. It was, however, argued that if only the vertical autocorrelation distance is considered, it might result in some of the variables having no effect on the critical slip surface [17]. Low [11]; Cho [13]; Low et al. [14], and Ji et al. [8] adopted the slicewise discretization of the 2D random field. Cho [13], however, proposed a local averaging method combined with numerical integration to discretize random fields of soil properties in two-dimensional space; while Low [11]; Low et al. [14]; Ji et al. [8] used the midpoint discretization of random field known as the method of autocorrelated slices. Ji et al. [8], however, proposed another method known as the method of interpolated autocorrelations. The authors, however, have concluded that the method of autocorrelated slices is more accurate and it should be used as the benchmark for the development of the method of interpolated autocorrelations. However most of these models entail significant errors due to the unrealistic introduction of inter-layer correlation of soil properties. These models are also unable to handle different values of the scale of fluctuation from layer to layer. Moreover, with the exception of Ji et al. [8], most of these studies were made to determine the probability of failure (or reliability index) of a predetermined slip surface.

As stated before, all the above mentioned LEM based studies considered spatial variability but the reliability analyses were conducted on predetermined slip surfaces, specifically, the probabilistic critical slip surfaces determined without considering spatial variability. It may be stated that these studies are based on an indirect approach for taking the effect of spatial variability into account. Only one or two researchers (e.g., Ji et al. [8]) have addressed the problem of direct determination of the probabilistic critical slip surface considering spatial variability during the process of determination itself. It may be stated, therefore, that such a study is based on a direct approach for taking the effect of spatial variability into account. While the direct approach is a more logical of the two approaches, the indirect approach is computationally simpler. It is therefore necessary to investigate to what extent the results obtained based on the two approaches differ, as well as which approach leads to a more conservative estimate of the safety of a slope.

To this end, the purpose of the paper is to develop a computational procedure for reliability analysis of earth slopes under the framework of limit equilibrium principles, in which the spatial variability of soils has been taken into account based on a new discretization model which is free from the shortcomings associated with the available discretization models and using this model to draw a comparison between the results of reliability analysis of earth slope obtained from both the indirect and the direct approaches for considering spatial variability of soil properties. To elucidate the present analysis as well as to bring out the difference clearly, the case study of a complex slope in multi-layered soil has been reanalysed. A comparison of all the above studies are also been made using the discretization model proposed by Cho [13].

Adopted Methodologies

Evaluation of Factor of Safety

Out of the numerous limit equilibrium methods of slices currently available for slope stability analysis, the Spencer method valid for general slip surfaces [18] is regarded as one of the rigorous methods as it does not make any a priori assumption regarding the shape of the slip surface and satisfies both the force and the moment equilibrium conditions [19]. In this study, therefore, this method is chosen for calculation of the factor of safety (FS) and hence for evaluation of the performance function for the reliability analysis. The method of solution for FS of a given slip surface is cast as a mathematical programming problem and solved using the well-known Sequential Quadratic Programming (SQP) [20] technique in the MATLAB environment. The adoption of the SQP technique is based on Hong and Roh [15] who reported that ‘an extensive comparative study of nonlinear programming codes presented by Schittkowski [21] ranked the performance of the SQP method to be the highest’.

Deterministic Critical Slip Surface

The problem of determination of the critical slip surface and the associated minimum factor of safety (FSmin) is, as usual, cast as a mathematical programming problem, and, once again, the SQP technique in the MATLAB environment is employed to solve this problem.

Probabilistic Analysis

The First Order Reliability Method (FORM), being the most versatile among the FOSM methods of reliability analyses [22], has been adopted in this study. In this method, the reliability index β is defined as the minimum distance from the origin to the failure surface in the standard normal space, using a linearization of the performance function around the design point as originally proposed by Hasofer and Lind [23]. The limit state function for the slope stability is usually defined as g(X) = FS −1.0, X being a vector of basic state (or design) variables of the system consisting of the uncertain geotechnical parameters (i.e. geometry and soil properties). The most commonly used [24, 25] formulations of β is as follows.

$$ \upbeta = \mathop {\min }\limits_{{{\text{g}}({\text{X}}) = 0}} \sqrt {\left\{ {\frac{{{\text {X}}_{\text{i}} - \upmu_{\text{i}}^{\text{N}} }}{{\sigma_{\text{i}}^{\text{N}} }}} \right\}^{T} \left[ {\text{R}} \right]^{ - 1} \left\{ {\frac{{X_{\text{i}} - \upmu_{\text{i}}^{\text{N}} }}{{\sigma_{\text{i}}^{\text{N}} }}} \right\}} $$
(1)

where, μ N i and σ N i are the equivalent normal mean and standard deviation of the ith random variable Xi and [R] is the matrix of correlations coefficients between the standard normal variables. The determination of the reliability index β is, thus, a problem of optimization, and as indicated by Wang et al. [16], the successful application of FORM relies on the selection of a robust optimization algorithm for multi-dimensional minimization, the SQP technique in the MATLAB environment is employed again to solve this problem. The solution yields the design point on the failure surface and the corresponding reliability index β. Then the failure probability can be expressed as p F  = Φ(−β), where Φ (·) denotes the standard normal cumulative distribution function.

Search Algorithm for the Probabilistic Critical Slip Surface

In deterministic slope stability analysis, it is conventional to use an optimization based algorithm to search for the deterministic critical slip surface (surface with the minimum factor of safety) based on some suitable slope stability model. In most algorithms, the problem of locating the deterministic critical slip surface associated with the minimum factor of safety, FSmin, is formulated as an optimization problem as follows [Eq. (2)]:

$$ {\text{FS}}_{\min} = {\min}_{\mathbf{X}} {\text{FS}}\left( {{\mathbf{P}},{\mathbf{X}}} \right) $$
(2)

where, P = set of input geotechnical parameters: c1, ϕ 1, c2, ϕ 2, etc., X = set of co-ordinates defining the shape and location of the slip surface: x1, y1, x2, y2, etc., FS = factor of safety for a given set of geotechnical parameters P and a given geometry of the slip surface defined by the location parameters X.

Bhattacharya et al. [26] proposed a computational procedure for locating the probabilistic critical slip surface (surface of the minimum reliability index, β min) for earth slopes, which is conceptually no different from that of the deterministic critical slip surface. The problem of locating the probabilistic critical slip surface associated with the minimum reliability index, β min, had been formulated in exactly the same way as for the deterministic critical slip surface, viz.,

$$ \beta_{\min } = {\min}_{X} \beta \left( {{\mathbf{P}} ,{\mathbf{X}}} \right) $$
(3)

where, β = reliability index for a given set of geotechnical parameters (including the statistical properties) and a given geometry of the slip surface defined by its location parameters.

It is, thus, evident that the proposed computational procedure for the determination of the probabilistic critical slip surface involves a 3-tier analysis: (1) Evaluation of performance function requires the evaluation of Spencer’s factor of safety involves the first tier of analysis; (2) Evaluation of the reliability index, β based on FORM involves the second tier of analysis, and (3) Search for the probabilistic critical slip surface and the associated minimum reliability index β min involves the third tier of analysis. As mentioned before, for the first two tiers, the optimization problem has been solved using the SQP technique in the MATLAB environment. The third tier of analysis has also been solved using the SQP technique when the slip surfaces are assumed to be of circular shape. However, for the slip surface of general shape, an efficient random search technique [27] has been employed. The reason for such choice is based on experience. For slip surfaces of general shape, the random search technique of Greco [27] has been found to yield a lower minimum compared to the SQP technique. More detailed description of the above procedure can found elsewhere [28].

The Proposed Discretization Model for Modeling of Spatial Variability

In order to include the effect of spatial variability into the reliability analysis of earth slopes, it is required to discretize the random fields into finite number of random variables. Such a few models of discretization are available in the literature for two-dimensional (2D) spatial variability analysis (e.g., Cho [13]; Ji et al. [8]). However these models entail significant errors due to the unrealistic introduction of inter-layer correlation of soil properties. These models are also unable to handle different values of the scale of fluctuation from layer to layer. The above observations have provided the motivation for the proposed work to develop a new discretization model which is free from the above mentioned shortcomings.

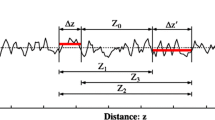
In the proposed model, for the arbitrary positions of trial slip surfaces within the search domain, the entire length of the slip surface is at first divided into segments lying entirely within each individual layer present in the soil profile. Then the total numbers of slices (as done in the method of slices) and strips (part of a slice) contained in each segment are then identified (Fig. 1). The field within each small element (either an entire slice or a strip) is described in terms of the spatial average of the field over the element length. As the lengths of these elements are different, the local averaging method combined with numerical integration as proposed by Cho [13] has been preferred over the midpoint discretization of random field [8, 11, 14] in order to discretize random fields of soil properties in two-dimensional space. In the proposed model, the discretization of random fields is made for each segment within a particular layer and, therefore, the random variables representing the concerned layers only are considered for the analysis.

Fig. 1
figure 1

Proposed discretization of the random fields over the slip surface

Full size image

In order to describe the 2D anisotropic random field, the widely used exponential auto-correlation function of the following form [13, 29] [Eq. (4)] is considered.

$$ \rho (x,y) = \exp \left\{ { - \left( {\frac{2}{{\delta_{x} }}\left| x \right| + \frac{2}{{\delta_{y} }}\left| y \right|} \right)} \right\} $$
(4)

where, δ x is the horizontal scale of fluctuation, and δ y is the vertical scale of fluctuation.

The variances of the average strength parameters are reduced by multiplying the variance function for each element by the point variance of the random field. The variance function for the anisotropic random field is as follows [13] [Eq. (5)]:

$$ \gamma (L) = \frac{{\left[ {2L\left( {\frac{\cos \alpha }{{\delta_{x} }} + \frac{\sin \alpha }{{\delta_{y} }}} \right) - 1 + \exp \left\{ { - 2L\left( {\frac{\cos \alpha }{{\delta_{x} }} + \frac{\sin \alpha }{{\delta_{y} }}} \right)} \right\}} \right]}}{{2L^{2} \left( {\frac{\cos \alpha }{{\delta_{x} }} + \frac{\sin \alpha }{{\delta_{y} }}} \right)^{2} }} $$
(5)

The correlation coefficients between these elements within a particular segment are estimated using Eq. (6) [13].

$$ \rho (L_{i} ,L_{j} ) = \frac{1}{{L_{i} ,L_{j} }}\int_{0}^{{L_{i} }} {\int_{0}^{{L_{j} }} {\rho (z)djdi} } $$
(6)

where z is the distance between the two arbitrarily situated points, one on element i and another on element j (Fig. 1).

To elucidate the proposed discretization model, a numerical example (Fig. 1) is taken from the ACADS study [30] in which the cohesions in each of the three soil layers are treated as random variables. For an arbitrary position of the trial or intermediate slip surface, there are three segments namely, segment A, segment B and segment C corresponding to the two intersections between layer boundaries and slice bases in slice 10 and 12. So the numbers of random variables for segments A, B and C become 10, 3 and 1 respectively. All these random variables and the correlation coefficients among them in each segment are generated. Random variables in each segment are uncorrelated with those in other segments. So, most of the correlation coefficient in the overall correlation matrix of the size (14 × 14) becomes zero. It may be mentioned here that El-Ramly et al. [10] also used similar framework of discretization; however his model considers only one-dimensional random field (along the slip surface).

Computational Advantages of the Proposed Discretization Model

The proposed model has the following advantages over the other discretization models available in the literature for 2D spatial variability analysis:

  1. 1.

    In the model proposed by Cho [13] or by Ji et al. [8], in cases of layered slopes, by assuming slice to slice correlation, inter-layer correlation of soil properties are implicitly considered which may not really exist. This does not arise in the proposed model.

  2. 2.

    In a layered slope, if the values of the scale of the fluctuation are different from layer to layer, Cho’s model and Ji et al.’s model cannot be used. However, the proposed model can automatically handle this situation.

  3. 3.

    The number of discretized random variables in Cho’s model or Ji et al.’s model equals the number of slices multiplied by the total number of random soil parameters in all the soil layers. In the proposed model, however, the discretization of random fields is made for each segment lying within a particular layer and hence the random variables within the concerned layers only are considered for analysis. It is seen that by doing so in the proposed model, not only the total numbers of discretized random variables are much smaller than that in Cho’s model or Ji et al.’s model but also most of the correlation coefficients in the overall correlation matrix becomes zero; which ultimately leads to substantial reduction of computational effort and time. For example, for the slope example considered, the total number of discretized random variables as per Cho’s model or Ji et al.’s model equals to 36 (=12 × 3) in place of 14 in the proposed model and the size of the overall correlation matrix becomes 36 × 36, whereas in proposed model it is only 14 × 14.

Developed Computer Programs

In order to carry out the computations involved in solving the numerical examples included in the paper, the following computer programs have been developed in the MATLAB environment:

  1. 1.

    Computer Program I: Computer Program to search for the deterministic critical slip surface.

  2. 2.

    Computer Program II: Computer Program based on FORM to search for the probabilistic critical slip surface without considering spatial variability.

  3. 3.

    Computer Program III: Computer Program to search for the probabilistic critical slip surface incorporating spatial variability based on the developed discretization model.

Illustrative Example

For the purpose of numerical demonstration of the results of the investigations proposed in this paper, a case study of the Bois Brule Levee has been selected from the literature [31] and is described in the following subsections.

Description

In this example, the probabilistic stability for the Bois Brule Levee, located along the west bank of the middle Mississipi River in Perry Country, Missouri, USA [32], has been studied. Figure 2 depicts a typical slope section showing the soil profile consisting of four zones, namely, Embankment Clay, Foundation Clay, Foundation Sand and Clay Blanket. This example was previously analysed by Hassan and Wolff [31] and Bhattacharya et al. [26]. In this respect it can be regarded as a benchmark problem.

Fig. 2
figure 2

Cross section of the Bois Brule Levee (after Hassan and Wolff [31])

Full size image

Following Hassan and Wolff [31], the reanalysis in this study has been carried out for steady seepage conditions under a flood on the levee to elevation 116.59 m (382.50 ft). Uncertainty in pore pressure is not considered in the analysis; in other words, the locations of the piezometric line are treated as deterministic. Consolidated-undrained (CU) strength parameters are used for the clay materials. Strength parameters of all the layers are considered as random variables and all these variables are assumed to be lognormally distributed in order to avoid negative values. The mean value, standard deviation, coefficient of variation (COV) and correlation coefficient for these parameters are given in Table 1 [32].

Table 1 Statistical properties of soil parameters
Full size table

In their analysis, Hassan and Wolff [31] considered both circular and non-circular slip surfaces. It was reported that β min for the circular surface was less than that for the non-circular surface. Bhattacharya et al. [26], however, considered only the noncircular surfaces. The present analysis has also been carried out for noncircular slip surfaces with a total of 12 slices.

Results of Deterministic Analysis

Using the computer program I and assuming the soil properties to be deterministic with values equal to their mean values in Table 1, the deterministic critical slip surface has been found out using Spencer method [18] coupled with the SQP technique available in the MATLAB environment and is as shown in Fig. 3. The associated minimum factor of safety is obtained as FSmin = 2.289, which is much lower than those reported by earlier investigators (Table 3).

Fig. 3
figure 3

Slope section and critical slip surfaces

Full size image

Results of Probabilistic Analysis

The results of probabilistic analysis are presented under the following sub-headings:

  1. 1.

    Determination of the probabilistic critical slip surface without considering spatial variability

  2. 2.

    Re-analysis of the above surface considering spatial variability

  3. 3.

    Determination of the probabilistic critical slip surface considering spatial variability

Determination of the Probabilistic Critical Slip Surface without Considering Spatial Variability

Using the probabilistic version of the developed computer program (computer program II) the probabilistic critical slip surface has been determined when all random variables are assumed to be lognormally distributed. Figure 3 shows the probabilistic critical slip surface alongside the deterministic critical slip surface. Here the two critical slip surfaces are markedly different in shape and location. While the deterministic critical slip surface extends well into the foundation sand layer, the probabilistic critical slip surface passes tangential to the thin clay blanket. The associated minimum reliability index (β min) is obtained as 2.657 and the associated probability of failure (pF) being 3.9 × 10−3 (Table 2). Table 2 also presents the details of sensitivity analysis based on the FORM method. The cohesion and friction angle of the thin clay blanket appear to have substantial effect on the slope stability, as these properties have the greater direction cosines. The reasonableness of the location of the probabilistic critical slip surface in Fig. 3, can be explained from the fact that the variation of shear strength parameters for the clay blanket layer is much higher than that for the foundation sand layer (as indicated by their COV values in Table 1 and also from the results of the sensitivity analysis in Table 2).

Table 2 Results of sensitivity analysis based on FORM
Full size table

Keeping in view that reliability analysis is sometimes performed on the deterministic critical slip surface, in the present analysis the reliability index for the deterministic critical slip surface, denoted as βFS, is also evaluated as 6.078 which, as expected, is greater than β min. Table 3 presents a comparison of the values of FSmin and β min obtained in the present analysis and those reported by the previous investigators using different methods of analyses. It is observed that the obtained value of β min using FORM is slightly lower than that reported by Bhattacharya et al. [26] using MVFOSM method and higher than that reported by Hassan and Wolff [31] using MVFOSM method. However, the obtained value of β min using MVFOSM in the present analysis is much lower than these results. Moreover, the probabilistic critical slip surface has been determined based on FORM assuming all random variables are truncated-normally distributed with left truncation point at 0.0 (in order to avoid negative values) and the associated minimum reliability index (β min) is obtained as 2.047 which is also much lower than those reported by previous investigators.

Table 3 Summary of reliability analysis without considering spatial variability
Full size table
Effect of Cross-Correlation Among the Basic Random Variables

Though in the present example problem, the cross-correlation between the cohesion and the friction angle for layers are given [32], it would be interesting to see how the results of the reliability analysis varies when these cross-correlations among the basic random variables are neglected. For the purpose of the above mentioned investigation, all the previous reliability analyses are repeated neglecting the cross-correlations and all the random variables are again assumed to be lognormally distributed. Table 4 presents a comparison of the results obtained with and without considering cross-correlation.

Table 4 Comparison between values of reliability index with and without consideration of cross-correlation
Full size table

It is seen from Table 4 that using both the methods (the FORM and the MVFOSM) the values of reliability index neglecting cross-correlation are higher than those considering cross-correlation. It is also observed that the trend of results between the FORM and the MVFOSM method remain same as before considering cross-correlation (Table 3).

Figure 4 shows the probabilistic critical slip surface neglecting those cross-correlations among the basic random variables based on the FORM method. For the sake of comparison, the probabilistic critical slip surface obtained previously considering cross-correlation is also included in the Figure. From Fig. 4, it is observed that the probabilistic critical slip surface neglecting those cross-correlations is shifted towards toe.

Fig. 4
figure 4

Slope section with probabilistic critical slip surfaces based on the FORM method

Full size image

Re-analysis of the Above Probabilistic Critical Slip Surface Considering Spatial Variability

Determination of the probabilistic critical slip surface(s) together with the associated minimum reliability index, as presented in the preceding section, was done without considering spatial variability of the soil properties. In this sub-section, the probabilistic critical slip surface obtained above has been re-analysed to consider the effect of spatial variability. As stated already, such an analysis may be referred to as the indirect procedure for considering spatial variability. Initially, an attempt has been made to incorporate the cross-correlation in the analysis together with the spatial correlation. However, such an attempt failed as convergence could not be achieved. Thus, the subsequent analyses were conducted considering spatial correlation only, neglecting cross-correlation. This is expected to result in “conservative” estimate of β. As before, the random variables were assumed to be lognormally distributed. But before doing this, it is desirable to validate the computer program developed for the proposed model.

Validation of the Proposed Model

For the purpose of validation, a few layered slope examples from Cho [13] and Ji et al. [8] (more specifically the example 1 of both Cho [13] and Ji et al. [8]) have been re-analysed using the proposed model. The results obtained from the re-analysis have been found to be comparable (Table 5) with those reported by the authors. It can be noted further that in case of layered slopes in which the entire slip surface lies within a single layer, the proposed model becomes the same as the Cho’s model. Therefore, in such a situation results obtained by using these two models should also be the same. Indeed, in the example 1 of Cho’s paper in which the entire slip surface lies within a single layer (upper layer), the two sets of results given in Table 5 are found to be rather close. The observations from Table 5 thus serve to validate the proposed model.

Table 5 Validation of the proposed model
Full size table
Re-analysis of the Probabilistic Critical Slip Surface

The proposed spatial variability discretization model is used in this re-analysis which is split up into (1) Study 1 and (2) Study 2. Study 1 considers equal set of values of scale of fluctuation for all the layers while study 2 considers different set of values of scale of fluctuations for the layers.

Study 1: Comparison of Reliability Index With and Without Consideration of Spatial Variability with Equal Set of Values of Scale of Fluctuations in all Soil Layers

For this study, the values of scale of fluctuation in the horizontal and the vertical direction (δ x and δ y) are taken as 20 m (assumed range: 10–50 m) and 2 m (assumed range: 1–5 m) respectively. Comparison of results are made based on the proposed discretization model and the model proposed by Cho [13]. The Results are presented in Table 6.

Table 6 Comparison between values of reliability index with and without consideration of spatial variability (Study 1)
Full size table

From Table 6 it is observed that for a given slip surface consideration of spatial variability increases the reliability index significantly. Further, for the particular combination of scale of fluctuations selected for this study, β value obtained from the proposed model is more conservative than the Cho’s model.

Study 2: Comparison of Reliability Index With and Without Consideration of Spatial Variability with Different Set of Values of Scale of Fluctuations for Different Soil Layers

An assumption needs to be made regarding different set of values of the scale of fluctuations for different soil layers. Such an assumption can be made from the results of the sensitivity analysis based on the FORM method (Table 2). It would be logical to assume higher values of scale of fluctuations for those soil layers whose strength parameters have greater sensitivity or higher level of uncertainty. The following set of values of scale of fluctuations are assumed merely for demonstration purpose as well as to show the applicability of the proposed discretization model (Table 7):

Table 7 Assumed set of values of scale of fluctuations (Study 2)
Full size table

The results of the analysis are presented in Table 8.

Table 8 Comparison between values of reliability index with and without consideration of spatial variability (Study 2)
Full size table

From the comparison of results presented in Table 6 and Table 8, it is observed that for a given slip surface, for the assumed different set of values of scale of fluctuations the reliability index decreases significantly from that corresponding to the equal set of values of scale of fluctuations in all the layers (given in parenthesis).

Determination of the Probabilistic Critical Slip Surface Considering Spatial Variability

In contrast to the ‘indirect procedure’ of reliability analysis considering spatial variability, as presented in the preceding sub-section, the ‘direct procedure’ for reliability analysis considering spatial variability is presented in this sub-section. Once again, for the sake of convenience, such an analysis is sub-divided into two parts: (1) Study 1 which corresponds to equal set of values of scale of fluctuations in all the layers and (2) study 2 which corresponds to unequal set of values of scale of fluctuations for the layers.

Study 1: Minimum Reliability Index with Equal Set of Values of Scale of Fluctuations in all Soil Layers

Using the developed computer program III, the probabilistic critical slip surfaces have been determined by using the proposed discretization model. For the sake of comparison, analysis has also been done by using the discretization model proposed by Cho [13]. For the particular case of δ x = 20 m and δ y = 2 m, the two critical slip surfaces are plotted in Fig. 5 which shows that these surfaces are not only quite different from each other but also substantially different from the probabilistic critical slip surface determined without considering spatial variability. Table 9 presents the values of β min associated with these surfaces. It is interesting to note that these values are markedly different from one another.

Fig. 5
figure 5

Slope section with probabilistic critical slip surfaces

Full size image
Table 9 Comparison between values of minimum reliability index with and without consideration of spatial variability (Study 1)
Full size table

A comparison between Table 6 and Table 9 indicates that the observations made from Table 6 for β values are also valid for β min values in Table 9. Further, values of β min in Table 9 are lower than the corresponding values of β in Table 6. The largest difference is nearly 26 % corresponding to the proposed discretization model.

Study 2: Minimum Reliability Index with Different Set of Values of Scale of Fluctuations for Different Soil Layers

Similar to studies made for given slip surface, using the developed computer programs III, the probabilistic critical slip surfaces based on the proposed discretization model has been determined for the selected set of values of scale of fluctuations for different soil layers (Table 7). The results are presented in Table 10.

Table 10 Comparison between values of minimum reliability index with and without consideration of spatial variability (Study 2)
Full size table

From Table 10 it is observed that for the assumed different set of values of scale of fluctuations the minimum reliability index also decreases significantly, which is as per expectation.

The two probabilistic critical slip surfaces respectively for the equal set of values of scale of fluctuations in all soil layers (study 1) and for the different set of values of scale of fluctuations in different soil layers (study 2) are plotted in Fig. 6, which shows that two surfaces are located quite differently from one another.

Fig. 6
figure 6

Slope section and probabilistic critical slip surfaces considering spatial variability for study 1 and 2

Full size image

Conclusions

Based on the studies undertaken in this paper, the following concluding remarks can be made:

  1. 1.

    The studies undertaken in this paper have revealed that the probabilistic critical slip surfaces obtained from the direct approach (considering the effect of spatial variability during the search for critical slip surface) are found to be substantially different from those from indirect approach (considering the effect of spatial variability on the critical slip surface already determined without considering spatial variability). Further, values of the minimum reliability indices (β min) associated with the probabilistic critical slip surfaces obtained from the direct approach are found to be considerably lower than those from the indirect approach. In other words, adoption of indirect approach might lead to an overestimation in the β min value (underestimation in the probability of failure, pF of a slope).

  2. 2.

    Based on the studies conducted in this paper, it is seen that the reliability results based on the proposed model is considerably more conservative than those based on the Cho’s model. Further, the analysis based on the proposed model drastically reduces the amount of computational effort and time. Reduction in computational time has been observed to be nearly 50 %.

  3. 3.

    The study has brought out certain computational advantages of the proposed model over the other discretization models available in the literature for 2D spatial variability analysis, and the results presented have demonstrated these advantages. These advantages would make the proposed model capable of handling those cases of layered slopes in which soils in different layers have different values of scale of fluctuation.