Introduction

Gravity retaining walls, especially with improvement of RCC structures though have become more or less obsolete in terms of construction (replaced by RCC cantilever or counter fort type retaining walls), yet in India, there exists a number of them that has been built in the past in many strategically important places (both post and pre independence era). This possibly started after 1857, when British East India Company took a major lesson learnt out of Sepoy Mutiny, especially with the massacre at Meerut and Lucknow [1]. Lord Canning, then Viceroy of India, realized that they needed to develop railways as means of rapid mass transport for quick deployment of military force to areas of unrest.

This resulted in construction of a number bridges and laying of tracks in many hilly and remote areas that required gravity type retaining walls for smooth operation of the rail movement. Many of these walls built about 150 years ago made out of stone masonry, bricks and plain concrete (reinforced concrete structure was yet to see its light of birth then) are still operational till date and has stood the test of time—though a number of them had yet been tested to a strong motion earthquake and examined as to how well these walls performed under it.

Evaluating their health in terms of a future strong motion earthquake remains an important exercise, now that our understanding of this fury of Mother Nature is far more profound. Damage to any of these walls due to earthquake (especially those built at strategic locations), can have serious problems in terms of logistics as well as trade, commodity movement and post-earthquake relief supply. Unfortunately tools available to asses its behavior as realistically as possible under seismic force even today is quite limited. Available tools are invariably marred by idealization, and simplified boundary conditions that may not reflect correctly the actual behavior in reality, and this needs a serious evaluation.

In Indian context, only tool available to assess a gravity type retaining wall’s performance under earthquake is by Mononobe and Mastsuo [2] and Okabe’s Method [3] (M–O method). This continues to dominate IS-1893 (2002) [4] and many other international codes for more than 90 years, irrespective of the fact that, many countries including US has now abandoned the method, as it has now been proved beyond any dispute that M–O based method gives a lower bound solution than reality [5–8].

Armed with M–O method only, it would become quite difficult for any investigator to convince the client or a governmental body that a gravity wall that has stood the test of time for more than 150 years or more is actually unsafe—if a strong motion earthquake hit the site, unless he comes up with a most realistic model that takes into cognizance almost all the parameters that could affect its performance notwithstanding the fact that despite M–O method’s popularity due to its ease in application can give highly misrepresentative results under many circumstances.

A number of researchers in other countries have investigated this problem, like Steedman and Zeng [9], Saran and Prakash [10], Saran and Gupta [11], Seed and Whitman [12], Whitman [13, 14], Richard and Elms [15], Das and Puri [16] etc. In India, this problem has been investigated by researchers like Choudhury et al. [17–19], Ghosh et al. [20–22], Sarkar [23], and sundry others. However, most of these researches are a variation of M–O method in one form or other, trying to incorporate other soil conditions like surcharge loading q or using logarithmic spiral curves etc. within the basic M–O frame work. Major lacunae that exists in M–O method can be summarized as hereafter.

  • M–O method assumes the wall to be perfectly rigid and only considerers the soil subjected to peak ground acceleration. This assumption is possibly not realistic, as because the wall may have high stiffness, but the stiffness is surely not infinite, and can affect the overall seismic response. Structural influence of the wall itself, on overall dynamic response is completely ignored in M–O method.

  • Its failure to predict the point of action of lateral thrust which at best remains an approximation.

  • M–O method was actually derived for dry cohesion less backfill and really does not cater to soil with additional surcharge over backfill, though the method has been rampantly used or abused in many such cases.

Present paper tries to address some of these shortcomings as proposed above and come up with a mathematical model that is more realistic, and which may be used for performance evaluation of such gravity retaining walls under future earthquakes.

Proposed Method

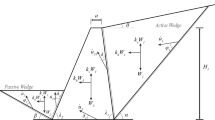
To understand the essence of the proposed approach, the simplest case of a gravity type retaining wall with cohesion less dry back fill, level with the wall as shown in Fig. 1 is considered. Boundary conditions like sloped soil will be imposed at a later stage.

Fig. 1
figure 1

A gravity retaining wall retaining dry cohesion less back fil

Full size image

Wall Retaining Cohesion Less ϕ Soil Only: Case-1

Shown in Fig. 1 is a cantilever gravity type retaining wall with dry sandy backfill, with ground having no slope. It is to be noted that the proposed mathematical model can also be derived from a more generalized soil condition but this has been considered first for sake of brevity and also to use it as a benchmark for more generalized cases that will be taken up subsequently. While performing the analysis it is assumed here that

  • The soil profile under active case is at incipient failure when the failure line OR make an angle tan (45 + ϕ/2) as shown in Fig. 1.

  • Since soil profile is already under failed condition under static load (i.e. the active earth pressure is already mobilized), it will not induce any stiffness to overall dynamic response but will only contribute to inertial effect.

  • Since the gravity cantilever wall is of significant thickness, its mass and stiffness contribution cannot be ignored. The wall thus contributes both to stiffness and inertia of the overall soil-structure system.

  • The retaining wall is assumed to be fixed at base and foundation compliance has been ignored for the time being.

It will be observed that assumptions made above are quite similar to what Mononobe and Mastsuo [2] or Steedman and Zeng [9] has assumed in their analysis. While Mononobe and Steedman both ignored effect of wall, this has been considered in the present analysis. Based on above assumptions the analysis is carried out as elaborated hereafter.

Dynamic Flexural Response

For this, we start with a uniform fixed base cantilever beam shown in Fig. 2 (ignoring the hydrostatic soil pressure impinging on it). Under free vibration condition the equation of equilibrium is expressed as

Fig. 2
figure 2

A cantilever beam under free vibration

Full size image
$$ EI\frac{{\partial^{4} u}}{{\partial z^{4} }} = \rho A\frac{{\partial^{2} u}}{{\partial t^{2} }} $$
(1)

where u is the lateral displacement of the beam, ρ mass density of beam material, A area of cross section of beam (assumed uniform over its length), I moment of inertia of the beam element and E Young’s modulus of the beam material. For solution of Eq. (1), let \( u(z,t) = Y(z)q(t) \). Based on separation of variable technique, Eq. (1) can be separated into two linear differential equation and one of which is Eq (2). The generic solution to this equation is given by Eq. (3). Imposing the four boundary conditions (Fig. 2) as Eq. (4) we have the shape function as Eq. (5). Where m is mode number 1, 2, 3 etc.

$$ EI\left( {\frac{{d^{4} Y}}{{dz^{4} }}} \right) - \lambda^{4} Y = 0\,\quad{\text{where}}\,\,\lambda^{4} = \frac{{\rho A\omega^{2} }}{EI} $$
(2)
$$ Y = C_{1} \sin \lambda z + C_{2} \cos \lambda z + C_{3} \sinh \lambda z + C_{4} \cosh \lambda z $$
(3)
$$ 1)\,\,Y = 0\,\,{\text{at}}\,z = \, 0; \; 2)\,\frac{dY}{dz} = 0\, {\text{at}}\,z = \, 0 \, \, 3)\,\frac{{d^{3} Y}}{{dz^{3} }} = 0\,{\text{at}}\,z = H; \; 4)\,\,\frac{{d^{2} Y}}{{dz^{2} }} = 0\,\,{\text{at}}\,z = H $$
(4)
$$ Y_{m} = \sin \frac{{\mu_{m} z}}{H} - \sinh \frac{{\mu_{m} z}}{H} - \alpha_{m} \left( {\cos \frac{{\mu_{m} z}}{H} - \cosh \frac{{\mu_{m} z}}{H}} \right) $$
(5)
$$ \mu_{m} = 1.875,\,4.694,\,7.855,\,\frac{2m - 1}{2}\pi ,\,\,\alpha_{m} = \frac{{\sin \mu_{m} + \sinh \mu_{m} }}{{\cos \mu_{m} + \cosh \mu_{m} }} $$
(6)
$$ f_{i}^{b} \left( z \right) = \sin \frac{{\mu_{i} z}}{H} - \sinh \frac{{\mu_{i} z}}{H} - \alpha_{i} \left( {\cos \frac{{\mu_{i} z}}{H} - \cosh \frac{{\mu_{i} z}}{H}} \right) $$
(7)

Equation (5) is actually the eigenvectors of the beam and is usually expressed as Eq. (7). Here the superscript ‘b’ stands for bending and subscripts i stands for mode numbers 1, 2, 3 etc. Equation (7) will now be used to determine the dynamic stiffness of the gravity wall cross section shown in Fig. 1. Here ψb is a dimensionless number \( \psi_{b} = \left( {B_{t} - B_{b} } \right)/B_{b} \), I b moment of inertia of the wall at base \( I(z) = I_{b} \left( {1 + \psi_{b} {z \mathord{\left/ {\vphantom {z H}} \right. \kern-0pt} H}} \right)^{3} \) and A b cross sectional area at base \( A(z) = A_{b} \left( {1 + \psi_{b} {z \mathord{\left/ {\vphantom {z H}} \right. \kern-0pt} H}} \right) \). Now for a wall of variable cross section under any loading q, the equation of equilibrium is expressed as Eq. (8). We assume \( u = u_{0} f_{i}^{b} (z) \) as the displacement profile to Eq. (8). If \( u_{0} f_{i}^{b} (z) \) would have been an exact solution then \( EI_{z} \left( {{{d^{4} u} \mathord{\left/ {\vphantom {{d^{4} u} {dz^{4} }}} \right. \kern-0pt} {dz^{4} }}} \right) - q = 0 \). Since it is not, we have a residual error R e expressed as Eq. (9). To minimize the error based on Galerkin’s weighted residual technique we integrate it over the domain, multiplying it by the weighted function \( f_{j}^{b} (z) \)when\( \int\nolimits_{0}^{H} {R_{e} } f_{j}^{b} (z)dz = 0 \).

$$ EI_{z} \left( {{{d^{4} u} \mathord{\left/ {\vphantom {{d^{4} u} {dz^{4} }}} \right. \kern-0pt} {dz^{4} }}} \right) = q $$
(8)
$$ R_{e} = EI_{z} \left( {{{d^{4} u} \mathord{\left/ {\vphantom {{d^{4} u} {dz^{4} }}} \right. \kern-0pt} {dz^{4} }}} \right) - q $$
(9)
$$ \int\limits_{0}^{H} {EI_{z} u_{0} \frac{{d^{2} }}{{dz^{2} }}} \left( {\frac{{d^{2} f_{i}^{b} (z)}}{{dz^{2} }}} \right)f_{j}^{b} (z)dz = \int\limits_{0}^{H} {qf_{j}^{b} (z)dz} $$
(10)

On successive integration of Eq. (10) by parts one can have Eq. (11). The first two terms of Eq. (11) cancels out leaving Eq. (12). Considering Eq. (12) in the form\( \left[ K \right]\left\{ \varDelta \right\} = \left\{ P \right\} \), we conclude that, as per Galerkinian basis, the dynamic stiffness matrix for a wall width varying linearly can be expressed as Eq. (13). The mass matrix [M] can be expressed as Eq. (14).

$$ \left[ {EI_{z} u_{0} \frac{{d^{2} }}{{dz^{2} }}\left( {\frac{{df_{i}^{b} (z)}}{dz}} \right)} \right]_{0}^{H} - \left[ {EI_{z} u_{0} \frac{{d^{2} }}{{dz^{2} }}\left( {\frac{{df_{i}^{b} (z)}}{dz}} \right)} \right]_{0}^{H} + \int\limits_{0}^{H} {EI_{z} u_{0} \frac{{d^{2} }}{{dz^{2} }}\left[ {\frac{{d^{2} f_{i}^{b} (z)}}{{dz^{2} }}} \right]} f_{j}^{b} (z)dz = \int\limits_{0}^{H} {qf_{j}^{b} (z)dz} $$
(11)
$$ \int\limits_{0}^{H} {EI_{z} u_{0} \frac{{d^{2} }}{{dz^{2} }}\left[ {\frac{{d^{2} f_{i}^{b} (z)}}{{dz^{2} }}} \right]} f_{j}^{b} (z)dz = \int\limits_{0}^{H} {qf_{j}^{b} (z)dz} $$
(12)
$$ \left[ K \right]_{ij} = EI_{b} \int\limits_{0}^{H} {\frac{{d^{2} }}{{dz^{2} }}\left[ {\left( {1 + \psi_{b} \frac{z}{H}} \right)^{3} \frac{{d^{2} }}{{dz^{2} }}f_{i}^{b} (z)} \right]} f_{j}^{b} (z)dz $$
(13)
$$ \left[ M \right]_{ij} = \frac{{\gamma_{c} A_{b} }}{g}\int\limits_{0}^{H} {\left( {1 + \psi_{b} \frac{z}{H}} \right)f_{i}^{b} (z)} f_{j}^{b} (z)dz + \left( {\frac{{K_{a} \gamma_{s} }}{g}} \right)\int\limits_{0}^{H} {\left( {H - z} \right)} f_{i}^{b} (z)f_{j}^{b} (z)dz $$
(14)

Here, \( \gamma_{c} \) weight density of gravity wall, \( \gamma_{s} \)Weight density of backfilled soil, \( K_{a} \)coefficient of active earth pressure, when either Rankine or Coulomb’s formulation can be used, \( g \) acceleration due to gravity. In natural co-ordinates [K] and [M] can be written as Eqs. (15) and (16). Where \( f_{i}^{b} \left( \xi \right) \) and \( f_{j}^{b} \left( \xi \right) \) are expressed in Eq. (7) where ξ = z/H and \( \varOmega \) is a dimensionless number expressed as \( \varOmega = K_{a} \left( {\gamma_{s} /\gamma_{c} } \right)\left( {H/B_{b} } \right) \). From Eqs. (15) and (16), it is observed that stiffness matrix is actually dependent on ψ b which is again a function of the ratio B t /B b and the mass matrix is a function of both B t /B b and soil parameter \( \varOmega \). For instance, for B t /B b  = 0.1 and \( \varOmega \)=0.3 one can have Eq. (17) for first three modes.

$$ \left[ K \right]_{ij} = \frac{{EI_{b} }}{{H^{3} }}\int\limits_{0}^{1} {\frac{{d^{2} }}{{d\xi^{2} }}} \left[ {\left( {1 + \psi_{b} \xi } \right)^{3} \frac{{d^{2} }}{{d\xi^{2} }}f_{i}^{b} (\xi )} \right]f_{j}^{b} (\xi )d\xi $$
(15)
$$ \left[ M \right]_{ij} = \frac{{\gamma_{c} A_{b} H}}{g}\left[ {\int\limits_{0}^{1} {\left( {1 + \psi_{b} \xi } \right)f_{i}^{b} (\xi )f_{j}^{b} (\xi )d\xi + \varOmega \int\limits_{0}^{1} {\left( {1 - \xi } \right)f_{i}^{b} (\xi )f_{j}^{b} (\xi )d\xi } } } \right] $$
(16)
$$ \left[ K \right]_{3 \times 3} = \left[ {\begin{array}{*{20}c} {13.965} & {24.495} & {23.911} \\ {24.495} & {165.589} & {289.033} \\ {23.911} & {289.033} & {1.167 \times 10^{3} } \\ \end{array} } \right]\frac{{EI_{b} }}{{H^{3} }}\,\,\left[ M \right]_{3 \times 3} = \left[ {\begin{array}{*{20}c} {0.616} & {0.246} & { - 0.033} \\ {0.246} & {0.566} & {0.225} \\ { - 0.033} & {0.225} & {0.662} \\ \end{array} } \right]\frac{{\gamma_{c} A_{b} H}}{g} $$
(17)

Considering the general Eigen value problem \( \left[ K \right]\left\{ \phi \right\} = \lambda \left[ M \right]\left\{ \phi \right\} \) and solving the same by Jacobi’s method [24], we finally have time period and scaling vector [\( \varphi_{i}^{b} \)] expressed as Eq. (18). The time period can thus be generically expressed by Eq. (19). Where, the term C TFi is given in Table 1 in terms of B t /B and \( \varOmega \). Based on Eq. (19) if one tries to estimate the time period of a gravity retaining wall one could well under estimate it, as because the slenderness ratio (H/B b ) for these type of wall are usually ≤2.0 and shear deformation can play a significant role on the final outcome [25].

Table 1 Values of CTFi for various Bt/Bb and Ω ratio
Full size table
$$ \left[ {T_{f} } \right]_{3 \times 3} = \frac{{H^{2} }}{{B_{b} }}\sqrt {\frac{{\gamma_{c} }}{gE}} \left[ {\begin{array}{*{20}c} {5.119} & 0 & 0 \\ 0 & {1.501} & 0 \\ 0 & 0 & {0.51} \\ \end{array} } \right]\,\left[ {\varphi_{i}^{b} } \right] = \left[ {\begin{array}{*{20}c} 1 & {0.297} & { - 0.16} \\ { - 0.165} & { - 1} & {0.218} \\ {0.019} & {0.226} & { - 1} \\ \end{array} } \right] $$
(18)
$$ \left[ {T_{f} } \right]_{i} = C_{TFi} \frac{{H^{2} }}{{B_{b} }}\sqrt {\frac{{\gamma_{c} }}{gE}} $$
(19)

Dynamic Shear Response

The free vibration equation of a shear beam of uniform cross sectional area A can be expressed as Eq. (20). Solving Eq. (20), it can be shown that the eigen vector of the problem [7] can be expressed as \( f_{i}^{s} = \cos \left[ {{{\left( {2i - 1} \right)\pi \left( {H - z} \right)} \mathord{\left/ {\vphantom {{\left( {2i - 1} \right)\pi \left( {H - z} \right)} {2H}}} \right. \kern-0pt} {2H}}} \right] \). Here the superscript s stands for the term shear and subscript i stands for mode 1, 2, 3 etc. Now since in this case the area of wall varies as A z  = A b (1 + ψ b z/H), it changes the characteristics of the differential equation when applying Galerkin’s technique it can be shown [26] that the stiffness matrix can be expressed as Eq. (21) and then by Eq. (22). In natural co-ordinates (ξ = z/H) this is expressed as Eq. (23) and mass matrix is expressed as Eq. (24). Where ψ b and Ω are dimensionless terms as explained before. Expanding Eqs. (23) and (24) for a typical value of B t /B b  = 0.1 and Ω = 0.3 we have Eq. (25) for first three modes.

$$ \to \frac{{\partial^{2} u}}{{\partial z^{2} }} = \frac{1}{{Vs^{2} }}\frac{{\partial^{2} u}}{{\partial t^{2} }} $$
(20)
$$ \left[ K \right] = - \int\limits_{0}^{H} {\frac{d}{dz}\left[ {GA_{z} \frac{d}{dz}f_{i}^{s} (z)} \right]f_{j}^{s} (z)} dz $$
(21)
$$ \to \left[ K \right] = - GA_{b} \int\limits_{0}^{H} {\frac{d}{dz}\left[ {\left( {1 + \psi_{b} \frac{z}{H}} \right)\frac{d}{dz}f_{i}^{s} (z)} \right]f_{j}^{s} (z)} dz $$
(22)
$$ \left[ K \right] = - \frac{{GA_{b} }}{H}\int\limits_{0}^{1} {\frac{d}{d\xi }\left[ {\left( {1 + \psi_{b} \xi } \right)\frac{d}{d\xi }f_{i}^{s} (\xi )} \right]f_{j}^{s} (\xi )} d\xi $$
(23)
$$ \to \left[ M \right]_{ij} = \frac{{\gamma_{c} A_{b} H}}{g}\left[ {\int\limits_{0}^{1} {\left( {1 + \psi_{b} \xi } \right)f_{i}^{s} (\xi )} f_{j}^{s} (\xi )d\xi + \varOmega \int\limits_{0}^{1} {\left( {1 - \xi } \right)} f_{i}^{s} (\xi )f_{j}^{s} (\xi )d\xi } \right] $$
(24)
$$ \left[ K \right] = \frac{{\eta GA_{b} }}{H}\left[ {\begin{array}{*{20}c} {0.904} & { - 0.675} & {0.125} \\ { - 0.675} & {6.332} & { - 3.375} \\ {0.125} & { - 3.375} & {17.188} \\ \end{array} } \right]\,\,\left[ M \right] = \frac{{\gamma_{c} A_{b} H}}{g}\left[ {\begin{array}{*{20}c} {0.228} & { - 0.122} & { - 0.014} \\ { - 0.122} & {0.336} & { - 0.122} \\ { - 0.014} & { - 0.122} & {0.345} \\ \end{array} } \right] $$
(25)

Here \( \eta = \) a shear correction factor = 2/3 for rectangular section. On Eigen-solution, this finally results in the time period for shear deformation and the corresponding scaling vector [\( \varphi_{i}^{s} \)] can be expressed as Eq. (26). Time period [T s ] i in Eq. (26) can be generically expressed as Eq. (27).

$$ \left[ {T_{S} } \right]_{i} = \frac{H}{{V_{s} \sqrt \eta }}\left[ {\begin{array}{*{20}c} {3.173} & 0 & 0 \\ 0 & {1.355} & 0 \\ 0 & 0 & {0.852} \\ \end{array} } \right]\,\,\left[ {\varphi_{i}^{s} } \right] = \left[ {\begin{array}{*{20}c} { - 1} & { - 0.49} & {0.288} \\ { - 0.037} & { - 1} & {0.413} \\ {4.467 \times 10^{ - 3} } & { - 0.057} & 1 \\ \end{array} } \right] $$
(26)
$$ \left[ {T_{S} } \right]_{i} = \left[ {C_{TS} } \right]_{i} \left[ {{H \mathord{\left/ {\vphantom {H {V_{s} \sqrt \eta }}} \right. \kern-0pt} {V_{s} \sqrt \eta }}} \right] $$
(27)

where [C TS ] i are the diagonal elements of the matrix in Eq. (26) of [T s ] i . The values of C TS for the first three modes for different Bt/B and soil parameter Ω are presented in Table 2. The time period of flexure and shear can be now combined. That is if a load vector P is applied on a body, the displacement of the body due to bending as well as shear deformation can be expressed as [27] Eq. (28). Where, δ t is total displacement of the system; δ b and δ s are displacement due to bending and shear. Eq. (28) can be expressed as Eq. (29). Where P total load; K b and K s are stiffness due to bending and shear deformation, respectively. Eq. (29) can be expressed as Eq. (30) then Eq. (31). Where ω e is combined frequency of the system due to bending and shear, ω b and ω s frequency due to bending and shear only.

Table 2 Values of C TS for various B t /B b and Ω ratio
Full size table
$$ \delta_{t} = \delta_{b} + \delta_{s} $$
(28)
$$ {P \mathord{\left/ {\vphantom {P {K_{e} }}} \right. \kern-0pt} {K_{e} }} = {P \mathord{\left/ {\vphantom {P {K_{b} }}} \right. \kern-0pt} {K_{b} }} + {P \mathord{\left/ {\vphantom {P {K_{s} }}} \right. \kern-0pt} {K_{s} }} $$
(29)
$$ {m \mathord{\left/ {\vphantom {m {K_{e} }}} \right. \kern-0pt} {K_{e} }} = {m \mathord{\left/ {\vphantom {m {K_{b} + {m \mathord{\left/ {\vphantom {m {K_{s} }}} \right. \kern-0pt} {K_{s} }}}}} \right. \kern-0pt} {K_{b} + {m \mathord{\left/ {\vphantom {m {K_{s} }}} \right. \kern-0pt} {K_{s} }}}} $$
(30)
$$ {1 \mathord{\left/ {\vphantom {1 {\omega_{e}^{2} }}} \right. \kern-0pt} {\omega_{e}^{2} }} = {1 \mathord{\left/ {\vphantom {1 {\omega_{b}^{2} }}} \right. \kern-0pt} {\omega_{b}^{2} }} + {1 \mathord{\left/ {\vphantom {1 {\omega_{s}^{2} }}} \right. \kern-0pt} {\omega_{s}^{2} }} $$
(31)

where m is total mass of the system. Equation (31) is precisely the classical Dunkerley’s equation [28] by which combined frequency of multi-body systems can be derived by treating each system in isolation and is often used in Dynamic soil structure interaction (DSSI) problems [29–31]. Equation (31) finally yields Eq. (32). Substituting Eqs. (19) and (27) in Eq. (32) and considering r s  = H/B b , the slenderness ratio of the wall, the time period is given by Eq. (33).

$$ T_{ei}^{2} = T_{bi}^{2} + T_{si}^{2} $$
(32)
$$ T_{ei} = C_{TFi} \frac{{H^{2} }}{{B_{b} }}\sqrt {\frac{{\gamma_{c} }}{gE}\left[ {1 + \left( {\frac{{C_{TSi} }}{{C_{TFi} }}} \right)^{2} \frac{{2\left( {1 + \nu } \right)}}{{\eta r_{s}^{2} }}} \right]} $$
(33)

Equation (33) is of particular interest as it explains the effect of shear deformation that goes on to elongate the time period. It will be observed from Eq. (33) that it is strongly dependent on slenderness ratio r s . As B b reduces, value r s increase rapidly (in terms of its square), and for large values of r s makes the second term within the parenthesis insignificant when flexural mode dominates the response. As per modal response analysis, \( S_{d} = S_{a} /\omega^{2} \), where S d modal amplitude; S a spectral acceleration corresponding to time period T. Based on definition as per IS-1893 (2002) [4], dynamic amplitude u t i can be expressed as Eq. (34). Here κ i is modal mass participation factor for ith mode and is expressed as Eq. (35).

$$ u_{i}^{t} = \kappa_{i}^{b} \beta \left( {{{S_{ai}^{b} T_{ei}^{2} } \mathord{\left/ {\vphantom {{S_{ai}^{b} T_{ei}^{2} } {4\pi^{2} }}} \right. \kern-0pt} {4\pi^{2} }}} \right)\left\{ {\varphi_{i}^{b} } \right\}^{T} \left\{ {f_{i}^{b} \left( \xi \right)} \right\} $$
(34)
$$ \kappa_{i}^{b} = {{\left( {\int\limits_{0}^{1} {\left( {1 + \psi_{b} \xi } \right)f_{i}^{b} (\xi )d\xi + \varOmega \int\limits_{0}^{1} {(1 - \xi )f_{i}^{b} (\xi )d\xi } } } \right)} \mathord{\left/ {\vphantom {{\left( {\int\limits_{0}^{1} {\left( {1 + \psi_{b} \xi } \right)f_{i}^{b} (\xi )d\xi + \varOmega \int\limits_{0}^{1} {(1 - \xi )f_{i}^{b} (\xi )d\xi } } } \right)} {\left( {\int\limits_{0}^{1} {\left( {1 + \psi_{b} \xi } \right)f_{i}^{b} (\xi )^{2} d\xi + \varOmega \int\limits_{0}^{1} {(1 - \xi )f_{i}^{b} (\xi )^{2} d\xi } } } \right)}}} \right. \kern-0pt} {\left( {\int\limits_{0}^{1} {\left( {1 + \psi_{b} \xi } \right)f_{i}^{b} (\xi )^{2} d\xi + \varOmega \int\limits_{0}^{1} {(1 - \xi )f_{i}^{b} (\xi )^{2} d\xi } } } \right)}} $$
(35)

Here, \( \beta = {{ZI} \mathord{\left/ {\vphantom {{ZI} {2R}}} \right. \kern-0pt} {2R}} \)where Z zone factor, I importance factor and R ductility or response reduction factor. \( \varphi_{i}^{b} \)is the scaling vector as expressed in Eq. (18) we have Eq (36). For dynamic, moment \( M = - EI_{z} \left( {d^{2} u/dz^{2} } \right) \), shear \( V = - EI_{z} \left( {d^{3} u/dz^{3} } \right) \) considering the gravity wall is predominantly a flexural member we have Eqs. (37) and (38).

$$ u_{i}^{t} = \left( {{\beta \mathord{\left/ {\vphantom {\beta {4\pi^{2} }}} \right. \kern-0pt} {4\pi^{2} }}} \right)\left[ {\kappa_{i}^{b} S_{ai}^{b} T_{ei}^{2} \left\{ {\varphi_{i}^{b} } \right\}^{T} \left\{ {f_{i}^{b} \left( \xi \right)} \right\}} \right] $$
(36)
$$ M_{i} (\xi ) = \frac{{ - EI_{b} \left( {1 + \psi_{b} \xi } \right)^{3} \beta }}{{4\pi^{2} H^{2} }}\left[ {\kappa_{i}^{b} S_{ai}^{b} T_{ei}^{2} \left\{ {\varphi_{i}^{b} } \right\}^{T} \frac{{d^{2} }}{{d\xi^{2} }}\left\{ {f_{i}^{b} \left( \xi \right)} \right\}} \right] $$
(37)
$$ V_{i} (\xi ) = \frac{{ - EI_{b} \left( {1 + \psi_{b} \xi } \right)^{3} \beta }}{{4\pi^{2} H^{3} }}\left[ {\kappa_{i}^{b} S_{ai}^{b} T_{ei}^{2} \left\{ {\varphi_{i}^{b} } \right\}^{T} \frac{{d^{3} }}{{d\xi^{3} }}\left\{ {f_{i}^{b} \left( \xi \right)} \right\}} \right] $$
(38)

For consideration of vertical acceleration, it has been shown by Chowdhury and Dasgupta [26] that Eq. (36) to (38) get multiplied by a factor 1.5 when as per IS-1893 (2002) [4], S av the vertical acceleration, is taken as half of horizontal acceleration S ax . Based on this, Eq. (36) to (38) gets modified to Eq. (39) to (41). For passive earth pressure case the steps remain exactly same, except use K p in lieu of K a .

$$ u_{i}^{t} = \left( {{{3\beta } \mathord{\left/ {\vphantom {{3\beta } {8\pi^{2} }}} \right. \kern-0pt} {8\pi^{2} }}} \right)\left[ {\kappa_{i}^{b} S_{ai}^{b} T_{ei}^{2} \left\{ {\varphi_{i}^{b} } \right\}^{T} \left\{ {f_{i}^{b} \left( \xi \right)} \right\}} \right] $$
(39)
$$ M_{i} (\xi ) = \frac{{3EI_{b} \left( {1 + \psi_{b} \xi } \right)^{3} \beta }}{{8\pi^{2} H^{2} }}\left[ {\kappa_{i}^{b} S_{ai}^{b} T_{ei}^{2} \left\{ {\varphi_{i}^{b} } \right\}^{T} \frac{{d^{2} }}{{d\xi^{2} }}\left\{ {f_{i}^{b} \left( \xi \right)} \right\}} \right] $$
(40)
$$ V_{i} (\xi ) = \frac{{3EI_{b} \left( {1 + \psi_{b} \xi } \right)^{3} \beta }}{{8\pi^{2} H^{3} }}\left[ {\kappa_{i}^{b} S_{ai}^{b} T_{ei}^{2} \left\{ {\varphi_{i}^{b} } \right\}^{T} \frac{{d^{3} }}{{d\xi^{3} }}\left\{ {f_{i}^{b} \left( \xi \right)} \right\}} \right] $$
(41)

Wall retaining cohesion less soil inclined at angle i with horizontal: Case-2

For soil inclined at an angle i with horizontal we consider the active and passive earth pressure coefficient as Eq. (42). Except for this change in K a and K p all other steps as explained earlier remains the same. An interesting point may be noted here is that, in Mononobe’s equation when \( \varphi - i - \theta < 0 \), where \( \theta = \tan^{ - 1} (\alpha_{h} /(1 - \alpha_{v} ) \) and α h and α v are seismic coefficients in horizontal and vertical direction, the active earth pressure equation fails to give a solution as it becomes imaginary number. In the proposed solution this problem is well circumvented.

$$ K_{a} = \cos i\frac{{\cos i - \sqrt {\cos^{2} i - \cos^{2} \varphi } }}{{\cos i + \sqrt {\cos^{2} i - \cos^{2} \varphi } }}\,\,{\text{and}}\,K_{p} = \cos i\frac{{\cos i + \sqrt {\cos^{2} i - \cos^{2} \varphi } }}{{\cos i - \sqrt {\cos^{2} i - \cos^{2} \varphi } }} $$
(42)

Results and Discussion

The procedure as proposed herein has been compared to a 2D finite element analysis (FEM) carried out by ANSYS [32]. The comparison has been carried out for both cases. Case-1 has also been compared with Mononobe’s expression as a cross check. The gravity wall examined herein has following properties:

Properties of gravity retaining wall -Height (H) 10 m, base width (B b ) 5 m, top width (B t ) 0.5 m, Modulus of Elasticity of retaining wall (E) 1.2 × 107 kN/m2, Poisson’s ratio (ν) 0.15, unit weight (γ) 24 kN/m3; Properties of Backfilled soil—Angle of internal friction (ϕ) 31.19o, unit weight of soil (γ s ) 17 kN/m3, angle of inclination (i) 10o; Seismic Code factors—As per IS 1893(2002) [4] zone factor Z 0.36, importance factor I 3.0 and response reduction factor R 1.5.

The FEM model chosen for the gravity wall is as shown in Fig. 3. Backfilled soil mass whose pressure is generically hydrostatic type in nature has been added as lumped mass at the vertical face of wall. Time periods for two cases based on proposed theory as well as by ANSYS are furnished in Table 3. It is observed that time periods based on proposed method are in commendable agreement with those obtained from ANSYS. The mode shapes for first three modes based on FEM analysis is shown for case 1 in Fig. 4. Figure 4 shows modal response of the fixed base gravity wall for the first three modes. Typical displacement, bending moment and shear force curve for case 1 based on proposed method for first three modes and their SRSS values are shown in Fig. 5. The static plus dynamic moment and shear has been derived for case-1 and compared with M–O method as shown in Table 4. It is evident from above that M–O method underrates the magnitude of moment and shear based on pseudo static approach. This is because while M–O method calculate moments and shear value based on presumed α h and α v value but here the time period effect plus modal mass participation combined with mode shapes produces a much higher value, which M–O method does not takes into consideration. Fixed base dynamic amplitude, moments and shear for two cases are as shown in Table 5. It is observed that the fundamental mode is the most predominant mode and for all of the case, a first mode modal analysis would suffice to evaluate its seismic performance.

Fig. 3
figure 3

Finite element model of the fixed base gravity wall

Full size image
Table 3 Comparison of fixed base time periods
Full size table
Fig. 4
figure 4

First three modes shapes of gravity wall by FEM for Case-1

Full size image
Fig. 5
figure 5

a Displacement plot of the wall for Case-1 by proposed method for first three modes (ue(ξ,1), ue(ξ,2), ue(ξ,3)) and its SRSS value (ueSRSS(ξ)) b Dynamic bending moment plot of the wall case-1 by proposed method for first three modes (Me(ξ,1), Me(ξ,2), Me(ξ,3)) and its SRSS value (MeSRSS(ξ)) c Dynamic shear force of the wall case-1 by proposed method for first three modes (Ve(ξ,1), Ve(ξ,2), Ve(ξ,3)) and its SRSS value (VeSRSS(ξ))

Full size image
Table 4 Comparison of moments and shear proposed versus M–O method case-1
Full size table
Table 5 Dynamic Amplitude, Moments and Shears based on proposed method
Full size table

The objective of this research here is to use the same boundary conditions as used by Mononobe, however incorporating the time period factor that is the basic key to dynamic response and develop a mathematical model that is more realistic, rather than assuming a maximum peak ground acceleration as assumed by M–O method which may or may not be true in all cases..

Mononobe assumed the wall under Coloumb’s failure condition and modified the earth pressure coefficient for Ka and Kp considering the pseudo static lateral and vertical force αhW and αvW acting on the wall. Here the soil profile makes and angle of 45 + ϕ/2 and 45 − ϕ/2 with horizontal plane for active and passive case respectively. The concept is reiterated further as here under.

  • After construction of the wall the soil has been back filled behind the wall.

  • After the backfilling is completed the wall is assumed to have yielded slightly either by miniscule sliding or tilting when the active earth pressure has already been mobilized making angle 45 + ϕ/2 and is under stable condition under this situation.

  • The earthquake comes and hits the wall under this situation.

  • Considering the active earth pressure is already generated (at the angle of 45 + ϕ/2), due to minuscule yielding of wall, the soil wedge acts as a rigid block getting locked to the wall and move in phase with it. The soil has no stiffness but contributes to the response by its own inertia only. The damping is contributed by the friction between the failed soil wedge and the soil below along line OR.

  • In case the wall remains unyielding after backfilling and no active line generates, the mathematical model becomes completely different when the dynamic pressure on the wall is guided by propagation of shear waves in a one dimensional infinite shear beam. The details of such behavior are furnished in the paper Chowdhury and Dasgupta [26].

Some Practical Remedial Measures

Based on 2D FEM analysis, or if analyzed by the proposed method it will not be surprising if investigated and found that many of the existing gravity retaining walls built earlier would be structurally found unsafe if subjected to a strong motion earthquake as per code. The question remains as to how to retrofit them and make them perform in a manner so that they can be attributed as seismically safe? For this some strengthening measures are suggested as in Fig. 6.

Fig. 6
figure 6

Schemes for retrofitting

Full size image

In case 1, if the design shear force due to seismic force is found to be more than the sliding capacity of the wall, then this additional shear force may be taken up by installing additional piles behind the retaining wall (provided space permits).The L shaped pile cap that connects the pile and the wall can be connected to the existing wall by Hilti bolts to transfer the thrust. The additional shear force can be taken up by the lateral load capacity of the piles.

In case II (when there is no space behind the wall to install piles) on can remove the back fill by about 1.5–2 m and then drill a hole through the wall inserting a tie road which is provided with a cap plate so that it may firmly abut by the wall, further, in order to ensure that the load transfer is smooth the hole surrounding the rod should filled with high strength grout to hold the rod in position. The rod is extended well beyond the active failure zone and connected to an anchor block cast in situ. The additional load is now taken up by the tied rod which in turn transmits this load to the anchor block that finally transfers it to the surrounding soil by passive pressure generated in the soil once it is backfilled and tamped properly. The depth to which the anchor block is to be provided would of course depend upon the magnitude of additional force it is expected to resist. Higher this force is deeper it should be placed. In case the soil is aggressive in nature, the tied rod my may be protected by providing corrosion resistive HVC sleeves around it. The behavior of the wall of course does not remain like a pure cantilever beam in this case, but acts as a propped cantilever and stresses at critical sections are to be checked accordingly.

Conclusion

A comprehensive analytical solution is proposed herein that can predict behavior of a gravity retaining wall with cohesion less ϕ soil inclined at angle i with horizontal as backfill. The results match well with a 2D finite element model especially in terms of time period which is the key controlling factor in terms of dynamic behavior of the soil-wall system. It would however be difficult to predict with authenticity as to whether FEM or the proposed method gives a more accurate result, as both FEM, and the proposed method has some simplifying assumption inherent in them. While FEM uses a conforming linear/non conforming bilinear polynomial shape function to arrive at the stiffness matrix, and based on isoparametric formulation, when subjected to reduced Gaussian integration would invariably have some error in it- as the procedure is essentially numerical and converges Lower bound [33].

The proposed method on the other hand models an essentially 2D plain stress problem by a 1D beam element, however the simplifying assumption is offset by considering the effect of shear deformation over and above the predominating flexural behavior and also assuming a trigonometric shape function which in essence is an infinite polynomial series that minimizes further error if any in the stiffness formulation (with no truncation error). Moreover, applying Galerkin’s weighted residual method at the level of differential equation significantly cuts down the computational effort compared to FEM where Rayleigh–Ritz’s method is actually applied, and a solution is sought based on algebraic solution to the stiffness matrix. It would perhaps suffice to say that both FEM and the proposed method gives comparable results and comprehensively establishes the fact that the simplifying assumption made in M–O method based on rigid body mechanics is not really realistic in terms of predicting seismic response of a gravity retaining wall and could be quite misleading.