Numerical simulations of Kuramoto–Sivashinsky equation in reaction-diffusion via Galerkin method

Abstract

Finite element methods have been frequently employed in seeking the numerical solutions of PDEs. In this study, a Galerkin finite element numerical scheme is constructed to explore numerical solutions of the generalized Kuramoto–Sivashinsky (gKS) equation. A quartic trigonometric tension (QTT) B-spline function is adapted as base of the Galerkin technique. The incorporation of B-spline Galerkin in space discretization generates the time-dependent system. Then, the use of Crank–Nicolson time integration algorithm to this system gives the wholly discretized scheme. The efficiency of the method is tested over several initial boundary value problems. In addition, the stability of the computational scheme is analyzed by considering Von Neumann technique. The computational results obtained by the suggested scheme are simulated and compared with the commonly existing numerical findings.

Introduction

Many phenomena are classified through constructing the nonlinear PDEs in many disciplines such as mathematical physics. The generalized Kuramoto–Sivashinksy (gKS) equation is one of these equations which has been widely used in modeling wave mechanism in the context of such fields. In this study, numerical simulations of wave patterns are investigated for the KS model which is given as the following nonlinear PDE in one dimension [22],

$$\begin{aligned}\frac{\partial u(x,t)}{\partial t}+u(x,t)\frac{\partial u(x,t)}{\partial x} +\alpha \frac{\partial ^{2}u(x,t)}{\partial x^{2}}\nonumber \\\quad +\beta \frac{\partial ^{3}u(x,t)}{\partial x^{3}}+\vartheta \frac{\partial ^{4}u(x,t)}{\partial x^{4}}=0, \quad x\in [a,b], \quad t\in (0,T] \end{aligned}$$

(1)

along with the initial condition (IC),

$$\begin{aligned} u(x,0)=u_{0}, \end{aligned}$$

(2)

and boundary conditions (BCs),

$$\begin{aligned} \begin{array}{ll} u(a,t)=f_{0}, & u(b,t)=f_{1}, \\ u_{x}(a,t)=0, & u_{x}(b,t)=0 \end{array} \end{aligned}$$

(3)

where $\alpha$, $\beta$ and $\vartheta$ are presented as real constants. The nonlinear advection term is given by $uu_{x}$, the dissipation term is known as $u_{xx}$ and dispersion term is presented as $u_{xxx}$ in the model description of the gKS equation. Plasma physics, concentration waves, flame propagation and reaction-diffusion dynamics, free surface film-flows and two face flows in plain or cylindrical geometries [16,17,18] are simulated computationally by the gKS equation. Tanh-function [11], Chebyshev spectral collocation [15], radial basis function-based mesh-free [26], Lattice Boltzmann [19], meshless method of lines [13], He’s variational iteration [24], finite difference and collocation [20], differential quadrature [23] and generalization of Gegenbauer Wavelet Collocation [6] methods are build up to calculate numerical and analytical solutions of the various classes of KS equation.

The gKS equation is classified by proper determination of $\beta$. For instance, when $\beta$ is zero, this type of the equation is named as Kuramoto–Sivashinsky (KS) equation which models wave pattern in various physical and chemical fields. When the parameters are chosen as $\alpha =\vartheta =1$ and $\beta =0$, the model represents the wave patterns in unstabilized flames and thin hydrodynamic films [12]. The special case without $u_{xxx}$ is handled numerically using collocation method via exponential cubic B-spline, trigonometric cubic B-spline and septic B-spline [9, 10, 29]. Local discontinuous Galerkin method and differential quadrature method are applied in [27, 28]. In this study, since gKS equation has derivatives of up to fourth order, it can be integrated using quartic trigonometric B-splines.

Splines are extensively used tools in many fields of applied mathematics. These functions are used not only to represent geometric design, but also to model scientific data. Thus, many splines have been proposed by researches to interpolate complex function, to fit curves at some given points and to solve differential equations [1,2,3]. Trigonometric tension B-splines are nonpolynomial splines consisting of two or more trigonometric functions having the form of bell-shaped curve. A quartic trigonometric tension (QTT) B-splines are introduced in the paper [4] to get numerical results of the Burgers–Huxley equation. Also, in that work, a QTT B-spline collocation method with Crank–Nicolson combination is build up for integrating the Burgers–Huxley equation. In another study, current splines are employed to the base of a collocation method to obtain computational solutions of regularized long wave equation [14]. Recent applications of present spline function to the nonlinear models are presented in [7, 8].

More recently, the KS model has been investigated by scholars in numerical and analytical sense. A study is conducted to find the numerical solutions of KS model via fourth-order Runge–Kutta method [5]. Analytical findings have been contributed in [25] by adopting Laplace transform and variational iteration methods for integer and fractional types of KS model. Another study has been devoted to explore the well-posedness of the KS equation in two dimensions [21].

The rest of the work is constructed as follows: In Sect. 2, the B–spline function is explored by considering the necessary higher-order derivative definitions. The employment of the methodology is also presented which gives the space-time discretized scheme in Sect. 3. Then, Sect. 4 serves the stability investigation of the scheme based on Von-Neumann stability method. Section 5 presents numerical experiments showing the capability of the current procedure. Depictions of the solutions are presented in one- or two-dimensional views. Physical pattern of the experimental cases is simulated. Section 6, therefore, reveals the advantages of the current scheme with conclusive notes and possible extensions of the study.

Description of QTT B-splines

In this section, the description of the newly proposed B-spline function is explored based on trigonometric and polynomial functions. First, consider the uniformly partitioned interval [a, b] as in $a=x_{0}<x_{1}<\ldots <x_{N}=b$ into finite elements $[x_{m},x_{m+1}]$ assuming mesh length as $h=x_{m+1}-x_{m},$ $m=0,1,\ldots ,N-1.$ The current QTT B-spline function of order $k=2$ is given as [4],

$$\begin{aligned} T_{m,k}(x)=\left\{ \begin{array}{ll} \frac{{\sin \tau (x-{x_{m-2}})}}{{\sin (\tau h)}}, & x\in \left[ {{x_{m-2}},{x_{m-1}}}\right) , \\ \frac{{\sin \tau ({x_{m}}-x)}}{{\sin (\tau h)}}, & x\in \left[ {{x_{m-1}},{x_{m}}}\right) , \\ 0, & \text {otherwise.} \end{array} \right. \end{aligned}$$

(4)

where $\tau = \sqrt{\eta },\mathrm{{ }}\eta = \frac{\pi }{h}\left( {\eta \in \mathbf{{R}}} \right)$ shows the tension parameter. When the order is given as $k\ge 3,$ the following recursive formula is presented to derive the higher-order QTT B-spline $T_{m,k}(x)$,

$$\begin{aligned} T_{m,k}(x)=\int \limits _{-\infty }^{x}(\gamma _{m,k-1}T_{m,k-1}(s)-\gamma _{m+1,k-1}T_{m+1,k-1}(s))ds \end{aligned}$$

(5)

where $\gamma _{m,k}=\left( \int \limits _{-\infty }^{\infty }T_{m,k}(s)ds\right) ^{-1},$ for $m=0,\pm 1,\ldots$.

Now, considering equations (4) and (5), QTT B-splines for $k=5$ are represented as,

$$\begin{aligned} T_{m,5}(x)=\theta \left\{ \begin{array}{ll} \tau ^{2}(-D_{m-2})^{2}+2C_{m-2}-2, & [x_{m-2},x_{m-1}] \\ -\tau ^{2}(3h^{2}+6hD_{m-2}+2(-D_{m-2})^{2})+2M(\tau ^{2}(D_{m-1})^{2}-2)-(6C_{m-1}+2C_{m}-4), & [ x_{m-1},x_{m}] , \\ \tau ^{2}( 13h^{2}+10hD_{m-2}+2(-D_{m-2})^{2})+M(2\tau ^{2}(11h^{2}+10hD(m-2)) \\ +4M\tau ^{2}(-D_{m-2})^{2}-8M+6C_{m}+6C_{m+1}-4), & [ x_{m},x_{m+1}] , \\ -\tau ^{2}(23h^{2}+14h(D_{m-2})+2(-D_{m-2})^{2})+2M(\tau ^{2}(D_{m+2})^{2}-2)-(2C_{m+1}+6C_{m+2}-4), & [x_{m+1},x_{m+2}] , \\ \tau ^{2}(D_{m+3})^{2}+2C_{m+3}-2, & [x_{m+2},x_{m+3}] , \\ 0, & \text {otherwise.} \end{array} \right. \end{aligned}$$

(6)

where $\theta =\frac{r}{2\tau ^{2}}$, $r=\frac{1}{2h^{2}(1-M)},$ $C_{m+j}=\cos (\tau (x_{m+j}-x))$, $D_{m+j}=(x_{m+j}-x),$ $M=\cos (\tau h)$. The detailed values of the QTT B-Spline function at the connected values are explored in Table 1.

Table 1 The B-spline function $T_{m,5}(x)$ and its accompanying derivative forms

where

• $\phi _{1} =r( h^{2}\tau ^{2}+2\cos (\tau h)-2) /2\tau ^{2}$,

• $\phi _{2} =r( h^{2}\tau ^{2}-2\cos (\tau h)( h^{2}\tau ^{2}+1) +2) /2\tau ^{2}$,

• $\phi _{3} =r( h\tau -\sin (\tau h)) /\tau$ ,

• $\phi _{4} =r( -h\tau +3\sin (\tau h)-2\cos (\tau h)h\tau )/\tau$ ,

• $\phi _{5} =r(1-\cos (\tau h))$,

• $\phi _{6} =r\tau \sin (\tau h)$,

• $\phi _{7} =-3r\tau \sin (\tau h)$.

The general form of the B-Spline functions depends on the distinct-free parameter $\tau$. The QTT B-splines over the domain $[-1,1]$ are depicted in Fig. 1 considering $\tau =9$.

Fig. 1

QTT B-splines over the interval for [0, 1] and $\tau =9$

Application of the method using QTT B-splines

The set of QTT B-splines given by $T_{m,5}(x),$ $m=-2,\ldots ,N+1$ is known to be a basis on the problem domain [a, b]. Therefore, the solutions given by U(x, t) are approximated by assembling the QTT B-splines $T_{m,5}(x)$ for the analytical solutions u(x, t) as,

$$\begin{aligned} u(x,t)\approx U(x,t)=\sum \limits _{m=-2}^{N+1}\gamma _{m}(t)T_{m,5}(x). \end{aligned}$$

(7)

The values given by $\gamma _{m}(t)$ are presented as unknown variables which will be evaluated with the treatment of Galerkin method. Over the sample finite element $[x_{m},x_{m+1}],$ approximated solution which is represented by Eq. (7) is given in terms of five QTT B-spline shape functions as the following,

$$\begin{aligned} U(x,t)=\sum \limits _{j=m-2}^{m+2}\gamma _{j}(t)T_{j,5}(x). \end{aligned}$$

(8)

The unknown function U and its related derivatives given by $U_{x},U_{xx},U_{xxx}$ on $[x_{m},x_{m+1}]$ are carried out in terms of $\gamma _{m}$ by using (8) and the QTT B-spline curve suggested in (6) as the following,

$$\begin{aligned} \begin{array}{l} U(x_{m},t_{n})\approx U_{m}^{n}=\phi _{1}\gamma _{m-2}+\phi _{2}\gamma _{m-1}+\phi _{2}\gamma _{m}+\phi _{1}\gamma _{m+1}, \\ U_{x}(x_{m},t_{n})\approx U_{m}^{\prime }=\phi _{3}\gamma _{m-2}+\phi _{4}\gamma _{m-1}-\phi _{4}\gamma _{m}-\phi _{3}\gamma _{m+1}, \\ U_{xx}(x_{m},t_{n})\approx U_{m}^{\prime \prime }=\phi _{5}\gamma _{m-2}-\phi _{5}\gamma _{m-1}-\phi _{5}\gamma _{m}+\phi _{5}\gamma _{m+1}, \\ U_{xxx}(x_{m},t_{n})\approx U_{m}^{\prime \prime \prime }=\phi _{6}\gamma _{m-2}+\phi _{7}\gamma _{m-1}-\phi _{7}\gamma _{m}-\phi _{6}\gamma _{m+1}. \end{array} \end{aligned}$$

(9)

Regarding the Galerkin methodology, the following integral from a to b is presented as,

$$\begin{aligned}&\int \limits _a^b w \left( x \right) \left( \frac{{\partial u(x,t)}}{{\partial t}} + u(x,t)\frac{{\partial u(x,t)}}{{\partial x}} \right. \nonumber \\&\quad \left. + \alpha \frac{{{\partial ^2}u(x,t)}}{{\partial {x^2}}} + \beta \frac{{{\partial ^3}u(x,t)}}{{\partial {x^3}}} + \vartheta \frac{{{\partial ^4}u(x,t)}}{{\partial {x^4}}} \right) {\mathrm {d}}x = 0 \end{aligned}$$

(10)

where w(x) is named as weight function. Over the typical element $[x_{m},x_{m+1}]$, the distribution of integral Eq. (10) is

$$\begin{aligned}&\int \limits _{{x_m}}^{{x_{m + 1}}} w \left( x \right) \left( \frac{{\partial u(x,t)}}{{\partial t}} + u(x,t)\frac{{\partial u(x,t)}}{{\partial x}} \right. \nonumber \\&\quad \left. + \alpha \frac{{{\partial ^2}u(x,t)}}{{\partial {x^2}}} + \beta \frac{{{\partial ^3}u(x,t)}}{{\partial {x^3}}} + \vartheta \frac{{{\partial ^4}u(x,t)}}{{\partial {x^4}}} \right) {\mathrm {d}}x = 0 \end{aligned}$$

(11)

Now, the transformation $\xi =x-x_{m}$, $0<\xi <h$ is applied to Eq. (11) which corresponds to

$$\begin{aligned}&\int \limits _{0}^{h}w\left( \xi \right) \dfrac{\partial u(\xi ,t)}{\partial t} {\mathrm {d}}\xi +\int \limits _{0}^{_{h}}w(\xi )u(\xi ,t)\dfrac{\partial u(\xi ,t)}{\partial \xi }{\mathrm {d}}\xi \nonumber \\&\quad +\alpha \int \limits _{0}^{h}w(\xi )\dfrac{\partial ^{2}u(\xi ,t)}{\partial \xi ^{2}}{\mathrm {d}}\xi +\beta \int \limits _{0}^{h}w(\xi )\dfrac{\partial ^{3}u(\xi ,t)}{\partial \xi ^{3}}{\mathrm {d}}\xi \nonumber \\&\quad +\vartheta \int \limits _{0}^{h}w(\xi )\dfrac{\partial ^{4}u(\xi ,t)}{\partial \xi ^{4}}{\mathrm {d}}\xi . \end{aligned}$$

(12)

Then, the QTT B-spline shape functions $T_{j}(x),$ $j=m-2,\ldots ,m+2$ on [0, h] can be obtained in terms of the local coordinate $\xi$ as,

$$\begin{aligned} T_{m-2}(\xi )= & \theta (\tau ^{2}(h-\xi )^{2}+2cos(\tau (h-\xi ))-2),\nonumber \\ T_{m-1}(\xi )= & \theta (-(\tau ^{2}(23h^{2}+14h(-3h-\xi )+2(3h+\xi )^{2})\nonumber \\&+2M(\tau ^{2}(h-\xi )^{2}-2)) \nonumber \\&-(2cos(\tau (-\xi ))+6cos(\tau (h-\xi ))-4)), \nonumber \\ T_{m}(\xi )= & \theta (\tau ^{2}(13h^{2}+10h(-2h-\xi )+2(2h+\xi )^{2})\nonumber \\&+M(2\tau ^{2}(11h^{2}+10h(-2h-\xi ))) \nonumber \\&+4M\tau ^{2}(2h+\xi )^{2}-8M+6cos(\tau (-\xi ))\nonumber \\&+6cos(\tau (h-\xi ))-4), \nonumber \\ T_{m+1}(\xi )= & \theta (-(\tau ^{2}(3h^{2}+6h(-h-\xi )+2(h+\xi )^{2})\nonumber \\&+2M(\tau ^{2}(-\xi )^{2}-2)) \nonumber \\&-(6cos(-\tau \xi )+2cos(\tau (h-\xi ))-4)), \nonumber \\ T_{m+2}(\xi )= & \theta (\tau ^{2}\xi ^{2}+2cos(\tau \xi )-2). \end{aligned}$$

(13)

Therefore, using Eqs. (13) into Eq. (8) and employing Eq. (8) into Eq. (12) entail to the following,

$$\begin{aligned}&\sum \limits _{j=m-2}^{m+2}\left\{ \begin{array}{c} \left( \int \limits _{0}^{h}T_{i}T_{j}{\mathrm {d}}\xi \right) \gamma _{j}^{n+1}+\left( \int \limits _{0}^{h}T_{i}\left( \sum \limits _{k=m-2}^{m+2}\gamma _{k}^{n+1}T_{k}\right) T_{j}^{\prime }{\mathrm {d}}\xi \right) \gamma _{j}^{n+1}+ \\ \alpha \left( \int \limits _{0}^{h}T_{i}T_{j}^{\prime \prime }{\mathrm {d}}\xi \right) \gamma _{j}^{n+1}+\beta \left( \int \limits _{0}^{h}T_{i}T_{j}^{\prime \prime \prime }{\mathrm {d}}\xi \right) \gamma _{j}^{n+1}+\vartheta \left( \int \limits _{0}^{h}T_{i}T_{j}^{\prime \prime \prime \prime }{\mathrm {d}}\xi \right) \gamma _{j}^{n+1} \end{array} \right\} \nonumber \\&\quad -\sum \limits _{j=m-2}^{m+2}\left\{ \begin{array}{c} \left( \int \limits _{0}^{h}T_{i}T_{j}{\mathrm {d}}\xi \right) \gamma _{j}^{n}+\left( \int \limits _{0}^{h}T_{i}\left( \sum \limits _{k=m-2}^{m+2}\gamma _{k}^{n}T_{k}\right) T_{j}^{\prime }{\mathrm {d}}\xi \right) \gamma _{j}^{n}+ \\ \alpha \left( \int \limits _{0}^{h}T_{i}T_{j}^{\prime \prime }{\mathrm {d}}\xi \right) \gamma _{j}^{n}+\beta \left( \int \limits _{0}^{h}T_{i}T_{j}^{\prime \prime \prime }{\mathrm {d}}\xi \right) \gamma _{j}^{n}+\vartheta \left( \int \limits _{0}^{h}T_{i}T_{j}^{\prime \prime \prime \prime }{\mathrm {d}}\xi \right) \gamma _{j}^{n} \end{array} \right\} \end{aligned}$$

(14)

in which $^{\prime }$ and $\cdot$ express space and time derivatives, respectively. Now, consider the following matrix forms for each $i,j,k=m-2(1)m+2$ as,

$$\begin{aligned} {\mathbf {A}}_{ij}^{e}= & \int \limits _{0}^{h}T_{i}T_{j}{\mathrm {d}}\xi , \nonumber \\ {\mathbf {B}}_{ij}^{e}(\gamma ^{e})^{n+1}= & \int \limits _{0}^{h}T_{i}\left( \sum \limits _{k=m-2}^{m+2}T_{k}\gamma _{k}^{n+1}\right) T_{j}^{\prime }{\mathrm {d}}\xi , \nonumber \\ {\mathbf {C}}_{ij}^{e}= & \int \limits _{0}^{h}T_{i}T_{j}^{\prime \prime }{\mathrm {d}}\xi , \nonumber \\ {\mathbf {D}}_{ij}^{e}= & \int \limits _{0}^{h}T_{i}T_{j}^{\prime \prime \prime }{\mathrm {d}}\xi , \nonumber \\ {\mathbf {E}}_{ij}^{e}= & \int \limits _{0}^{h}T_{i}T_{j}^{\prime \prime \prime \prime }{\mathrm {d}}\xi , \end{aligned}$$

(15)

where the matrices ${\mathbf {A}}^{e},$ ${\mathbf {C}}^{e},{\mathbf {D}}^{e},$ ${\mathbf {E}}^{e}$ are presented in $5\times 5$ dimension and the matrix ${\mathbf {B}}^{e}$ is the element matrix with the dimension $5\times 5\times 5,$ then with the representations of these element matrices Eq. (14) is reorganized as,

$$\begin{aligned} {\mathbf {A}}^{e}{\dot{\gamma }}^{e}+\left( {\mathbf {B}}^{e}\left( \gamma ^{e}\right) +\alpha {\mathbf {C}}^{e}+\beta \mathbf {D}^{e}+\vartheta {\mathbf {E}}^{e}\right) \gamma ^{e} \end{aligned}$$

(16)

where $\gamma =(\gamma _{m-2},\ldots ,\gamma _{m+2})^{T}.$ Now, the local element matrices given in Eq. (16) are assembled which yields the following global matrix equation,

$$\begin{aligned} \mathbf {A}{\dot{\gamma }}+\left( {\mathbf {B}}\left( \gamma \right) +\alpha \mathbf {C}+\beta \mathbf {D}+\vartheta {\mathbf {E}}\right) \gamma =0. \end{aligned}$$

(17)

Then, the unknown parameters $\gamma$ and its related derivative form ${\dot{\gamma }}$ are accomplished by the Crank–Nicolson formulation including the time stages $n+1$ with n as,

$$\begin{aligned} \gamma =\frac{\gamma ^{n+1}+\gamma ^{n}}{2}, \quad {\dot{\gamma }}=\frac{\gamma ^{n+1}-\gamma ^{n}}{\varDelta t}. \end{aligned}$$

(18)

Therefore, iterative formula is obtained for the time parameters $\gamma ^{n}$ as the following,

$$\begin{aligned}&\left[ A+\frac{\varDelta t}{2}\left( B(\gamma ^{n+1})+\alpha C+\beta D+\vartheta E\right) \right] \gamma ^{n+1}\nonumber \\&\quad =\left[ A-\frac{\varDelta t}{2}\left( B(\gamma ^{n})+\alpha C+\beta D+\vartheta E\right) \right] \gamma ^{n}. \end{aligned}$$

(19)

The last expression consists of $N+4$ linear equations and $N+4$ unknowns as $(\gamma _{-2}^{n+1},\gamma _{-1}^{n+1},\ldots ,\gamma _{N+1}^{n+1})$. Then, with the use of BCs and initial value of the problem, the vector $(\gamma _{-2}^{0},\gamma _{-1}^{0},\ldots ,\gamma _{N+1}^{0})$ is achieved. In addition, nonlinearity is handled by replacing the term ${\mathbf {B}}(\gamma ^{n})$ with ${\mathbf {B}}(\gamma ^{n+1})$ so that the system is obtained by the Gauss elimination method. In addition to increase the accuracy, and to tackle the nonlinearity, it is essential to apply the following iteration at each time steps as,

$$\begin{aligned} \left( \gamma ^{*}\right) ^{n+1}=\gamma ^{n}. \end{aligned}$$

Finally, the solutions of the resultant system of the linear equations give the desired computational solutions.

Stability analysis

The Von Neumann stability analysis is implemented to discuss the stable computational difference scheme. Firstly, the term U is assumed as local constant which is given as a part of the nonlinear term $UU_{x}$, so that Fourier stability method for Eq. (19) can be performed. In order to do so, a typical member of the (19) is considered as,

$$\begin{aligned}&\omega _{1}\gamma _{m-4}^{n+1}+\omega _{2}\gamma _{m-3}^{n+1}+\omega _{3}\gamma _{m-2}^{n+1}+\omega _{4}\gamma _{m-1}^{n+1}+\omega _{5}\gamma _{m}^{n+1}\\&\qquad +\omega _{6}\gamma _{m+1}^{n+1}+\omega _{7}\gamma _{m+2}^{n+1}+\omega _{8}\gamma _{m+3}^{n+1}+\omega _{9}\gamma _{m+4}^{n+1}\\&\quad =\omega _{9}\gamma _{m-4}^{n}+\omega _{8}\gamma _{m-3}^{n}+\omega _{7}\gamma _{m-2}^{n}+\omega _{6}\gamma _{m-1}^{n}+\omega _{5}\gamma _{m}^{n}\\&\qquad +\omega _{4}\gamma _{m+1}^{n}+\omega _{3}\gamma _{m+2}^{n}+\omega _{2}\gamma _{m+3}^{n}+\omega _{1}\gamma _{m+4}^{n} \end{aligned}$$

where the parameters $\omega _{i},$ $i=1,\ldots ,9$ are assembled from the system (19) in which these values are not explained since they include long and complicated expressions. Then, adressing the Fourier mode $\gamma _{m}^{n}=s^{n}e^{im\theta }$ for the linearized difference equation, following relation is written as,

$$\begin{aligned} \delta ^{n+1}=q\delta ^{n}. \end{aligned}$$

Thus, the growth factor quantity is obtained as the following equation,

$$\begin{aligned} q=\frac{c-id}{c+id} \end{aligned}$$

where

$$\begin{aligned} c= & (\omega _{1}+\omega _{9})\cos (4\theta )+(\omega _{2}+\omega _{8})\cos (3\theta )\\&+(\omega _{3}+\omega _{7})\cos (2\theta )+(\omega _{4}+\omega _{6})\cos (\theta )+\omega _{5} \\ d= & (\omega _{1}-\omega _{9})\sin (4\theta )+(\omega _{2}-\omega _{8})\sin (3\theta )\\&+(\omega _{3}-\omega _{7})\sin (2\theta )+(\omega _{4}-\omega _{6})\sin (\theta ). \end{aligned}$$

Obviously, the quantity in the last expression $\left| q\right|$ is less than or equal to 1 which, therefore, proves to preserve the unconditionally stable difference scheme. However, each parameter is preferred to give efficient numerical solutions.

Application of the suggested method to experimental cases

In this section, some experimental cases are considered to validate the results produced by suggested method. To measure the accuracy of the proposed method for a fair comparison, calculations are carried out with the global relative error (Gre) given by,

$$\begin{aligned} \text {Gre}=\frac{\sum \limits _{m=1}^{N+1}\left| U_{m}^{n}-u_{m}^{n}\right| }{\sum \limits _{m=1}^{N+1}\left| u_{m}^{n}\right| }, \end{aligned}$$

(20)

where u shows the exact and U represents the numerical solutions, respectively.

Solitary wave propagation

As a first case, numerical solution of Eq. (1) is given under the selection of parameters as $\alpha =\vartheta =1$ and $\beta =4$. Analytical solution is given by [19],

$$\begin{aligned} u(x,t)= & s+9-15\left[ \tanh \left( k\left( x-st-x_{s}\right) \right) \right. \nonumber \\&\left. +\tanh ^{2}\left( k\left( x-st-x_{s}\right) \right) \right. \nonumber \\&\left. -\tanh ^{3}\left( k\left( x-st-x_{s}\right) \right) \right] . \end{aligned}$$

(21)

The IC is determined by setting $t=0$ in the analytical solution and homogen Neumann BCs are used. The solution of this problem preserves the solitary wave profile with initial position $x_{s}$ and speed s. The parameters of $s=6,$ $k=\frac{1}{2},$ $x_{s}=-10$ in Eq. (21) are preferred in calculations. The program is carried out considering the interval $[-30,30]$ for $\varDelta t=0.0001$ and space step $h=0.1$ as in the study [19] . In Table 2, values of Gre at some times are documented to make comparison results of suggested method with ones for [19] and CPU time of the suggested Galerkin technique is calculated by considering time steps as 0.01 and 0.0001 to show the cost in Table 2. Suggested method gives far better results than the method given in the work [19]. In addition, solutions are much more efficient even the larger time step is preferred. For instance, with $\varDelta t = 0.01$, suggested algorithm gives error $3.1885 \times 10^{-3}$, whereas cubic spline Lattice Boltzmann method produces $3.5172 \times 10^{-2}$ at time stage $t=4$ using the time step $\varDelta t= 0.0001$.

Table 2 Gres for solitary wave propagation at different times

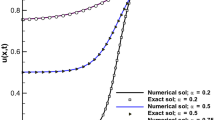
The solitary wave propagation is depicted in 3D at time $t=4$ in Fig. 2. And also, in Fig. 3, the solutions at $t=1,2,3,4$ are illustrated for $\varDelta t=0.001$ and $h=0.1$.

Fig. 2

Solitary wave propagation in 3D

Fig. 3

Solitary wave propagation in 2D

Shock wave profile of KS equation

The computational calculations are carried out for the numerical solution of Eq. (1) considering the following analytical solution:

$$\begin{aligned} u(x,t)= & s+\frac{15}{19}\sqrt{\frac{11}{19}}\left[ -9\tanh \left( k\left( x-st-x_{s}\right) \right) \right. \nonumber \\&\left. +11\tanh ^{3}\left( k\left( x-st-x_{s}\right) \right) \right] . \end{aligned}$$

(22)

The IC is determined by the closed-form solution given by Eq. (22), and homogen Neumann BCs are used. The numerical results are obtained on the finite interval $[-30,30]$ with $\varDelta t=0.01$ and $h=0.4$ and compared with the well-known existing methods such as quintic B-spline collocation method [22], exponential cubic B-spline collocation method [9] and the differential quadrature method [23]. Table 3 serves these numerical findings according to the parameters as $s=5,$ $k=\sqrt{\frac{11}{76}},$ $x_{s}=-12.$

Table 3 Gres for shock profile wave propagation at different times

Shock wave simulations of the KS equation are presented by Fig. 4 in 3D view over $0\le t \le 4$. In addition, generation of the shock waves is visualized in Fig. 5 considering at time levels $t=1,2,3,4$ with $\varDelta t=0.001$ and $h=0.1$. Depictions of the shock profile of KS equation exhibit the physical nature of the wave propagation.

Fig. 4

Shock profile wave propagation in 3D

Fig. 5

Shock profile wave propagation in 2D

The chaotic nature of KS equation

Numerical solution of Eq. (1) is get for $\alpha =\vartheta =1$ and $\beta =0$. This example is a special a case of gKS which is known to exhibit chaotic behavior when spatial domain is finite. Such model is given under the Gaussian IC as,

$$\begin{aligned} u(x,0)=-\exp (-x^{2}) \end{aligned}$$

BCs are determined by considering conditions given by (3). The computational domain is considered as $[-30,30]$ with $N=120,$ $\varDelta t=0.001$ space and time partitions. In Fig. 6, wave pattern is simulated over $0\le t \le 5$ and Fig. 8 shows the depiction of turbulent flow on $0\le t \le 20$ temporal domain in 3D views. In addition, in Figs. 7 and 9, depictions of the numerical solutions of the gKS equation are presented at time stages $t=5$ and $t=20$, respectively. It can be observed that the numerical results well exhibit chaotic behavior of the model as expected.

Fig. 6

Chaotic behavior in 3D

Fig. 7

Behavior at $t=5$

Fig. 8

Chaotic behavior in 3D

Fig. 9

Chaotic behavior at $t=20$

Conclusion

In this work, using QTT B-splines, Galerkin technique is constructed for the numerical solution of the gKS equation. The present method to simulate solitary wave propagation numerically provides less error than in comprasion with the Lattice Boltzmann method as given in Table 2. Shock profile wave propagation is presented to show accuracy of the method compared with the quintic collocation method and quintic B-spline-base differential quadrature. Table 3 also shows that the current scheme gives efficient results than those existing works. In the last experimental case, chaotic solution of the KS equation is simulated and proved to preserve turbulent wave nature of the current model. Thus, the proposed method is shown to be capable for generating numerical solution of high accuracy for the solution of the gKS equation. The experimental results are quite satisfactory when compared with the other results of the literature. So it can be concluded that the QTT B-spline Galerkin method is both efficient and reliable for getting the numerical findings of the PDEs. The proposed algorithm can be further considered as preferable for the numerical solution of the PDEs with derivatives of up to fourth order since it can be integrated using QTT B-splines quite efficiently.