Approximation Process Based on Parametric Generalization of Schurer–Kantorovich Operators and their Bivariate Form

Abstract

We construct the Schurer–Kantorovich operators depending on the shape parameter $\alpha \in [0,1]$ which we called $\alpha$-Schurer–Kantorovich operators, and estimate their moments and central moments. We discuss the uniform convergence as well as the rate of convergence in terms of modulus of smoothness and Lipschitz-type functions, and other related results for our new aforementioned operators. Further, we construct the bivariate $\alpha$-Schurer–Kantorovich operators and investigate the degree of convergence with the help of Lipschitz class for bivariate function. Moreover, we discuss the approximation behaviors of bivariate $\alpha$-Schurer–Kantorovich operators for functions having continuous partial derivatives. Statement: We constructed the $\alpha$-Schurer–Kantorovich operators and established several approximation results. Our operators coincide with $\alpha$-Bernstein–Kantorovich operators (for $\nu =0$), Schurer–Kantorovich operators (for $\alpha =1$), and Bernstein–Kantorovich operators (for $\alpha =1$ and $\nu =0$) which means that our operator is stronger than existing in the literature. Thus, we believe that the new operator will open new vistas in this field.

1 Introduction

Bernstein operators are one of the most significant and interesting operators on the space of continuous functions C[0, 1]. For any function h(z) in C[0, 1], the expression

$$\begin{aligned} B_{r}(h;z)=\sum _{p=0}^{r}h_{p}\left( {\begin{array}{c}r\\ p\end{array}}\right) z^{p}(1-z)^{r-p}\;\;\;\;\;\;\;(z\in [0,1],r\in \mathbb {N}) \end{aligned}$$

is called Bernstein operators [1] of order $r\in \mathbb N$ (the set of natural numbers), where $h_{p}=h\left( \frac{p}{r}\right)$. The linear positive operators $B_{r}(h;z)$ were constructed by Bernstein to demonstrate the simple proof of famous Weierstrass approximation theorem which asserts that for any function h(z) on C[a, b] and for any $\epsilon >0$ there is a polynomial b(z) such that $|h(z)-b(z)|<\epsilon$ for $a\le z\le b$.

Chen et al. [2] recently demonstrated the concept of $\alpha$-Bernstein operators $B_{r}^{\alpha }(h;z)$ which includes Bernstein operators for $\alpha =1$ as

$$\begin{aligned} B_{r}^{\alpha }(h;z)=\sum _{p=0}^{r}h_{p}\Delta _{r,p}^{\left( \alpha \right) }\left( z\right) \end{aligned}$$

(1.1)

for any $h\in C[0,1]$, $z\in [0,1]$, $r\in \mathbb N$ and showed that the operators (1.1) are linear and positive for the value of shape parameter $\alpha$ in [0, 1]. The $\alpha$-Bernstein polynomials $\Delta _{r,p}^{\left( \alpha \right) }\left( z\right)$ are defined as

$$\begin{aligned}&\Delta _{r,p}^{\left( \alpha \right) }\left( z\right) =\Bigg [\left( 1-\alpha \right) z\left( {\begin{array}{c}r-2\\ p\end{array}}\right) +\left( 1-\alpha \right) \left( 1-z\right) \left( {\begin{array}{c}r-2\\ p-2\end{array}}\right) \\&\quad +\alpha z\left( 1-z\right) \left( {\begin{array}{c}r\\ p\end{array}}\right) \Bigg ] z^{p-1}\left( 1-z\right) ^{r-(p+1)}\;\;\;\;\;\;\;\;\;\;\;(r\ge 2), \end{aligned}$$

and

$$\begin{aligned} \Delta _{1,0}^{\left( \alpha \right) }\left( z\right) =1-z,\;\;\;\Delta _{1,1}^{\left( \alpha \right) }\left( z\right) =z. \end{aligned}$$

Inspired by the work of Chen et al. [2], Mohiuddine et al. [3] introduced the Kantorovich modification of (1.1) including bivariate variant of this operator and discussed the uniform convergence of their operators as well as rate of convergence by means of modulus of continuity. The Stancu-type $\alpha$-Bernstein–Kantorovich operators have been defined by Mohiuddine and Özger [4] wherein several approximation results such as rate of convergence and Voronovskaja-type theorem were investigated. There are some other operators motivated by $\alpha$-Bernstein operators, namely $\alpha$-Bernstein–Durrmeyer operators [5], bivariate $\alpha$-Bernstein–Durrmeyer operators and their GBS operators [6], $\alpha$-Baskakov operators [7], $\alpha$-Baskakov–Durrmeyer operators [8] and many others. There are some researchers who modified and generalized Bernstein operators by means of Bézier bases [9,10,11,12,13]. For further details on related concept and statistical approximation, we refer to [14,15,16,17,18,19,20,21,22].

Let $\nu \in \mathbb Z_{0}^{+}$ $(\mathbb Z_{0}^{+}=\{0,1,2,\ldots \})$ and $r\in \mathbb N$. Then, Schurer [23] (also see [24]) defined the linear positive operators

$$\begin{aligned} S_{r,\nu }:C\left[ 0,\nu +1\right] \rightarrow C[0,1] \end{aligned}$$

by

$$\begin{aligned} S_{r,\nu }(h;z)=\sum _{p=0}^{r+\nu }h\left( \frac{p}{r}\right) \mathcal {P}_{r,\nu ,p}(z)\;\;\;\;\;(z\in [0,1]). \end{aligned}$$

(1.2)

for all $h\in [0,1+\nu ]$. For $p=0,1,\ldots ,r+\nu$, the polynomials $\mathcal {P}_{r,\nu ,p}(z)$ given by

$$\begin{aligned} \mathcal {P}_{r,\nu ,p}(z)=\left( {\begin{array}{c}r+\nu \\ p\end{array}}\right) z^{p}(1-z)^{r+\nu -p}. \end{aligned}$$

Keeping the $\alpha$-Bernstein operators together with Schurer modification of Bernstein operators into consideration, in the most recent past, Özger et al. [25] introduced the linear positive operators which they called $\alpha$-Bernstein–Schurer operators which are as follows:

Given a continuous function h on $\left[ 0,\nu +1\right]$, $\alpha \in [0,1]$, $z\in [0,1]$ and for each positive integer r, the $\alpha$-Bernstein–Schurer operator is given by

$$\begin{aligned} \Psi _{r,\nu }^{\alpha }\left( h;z\right) =\sum \limits _{p=0}^{r+\nu }h\left( \frac{p}{r}\right) \mathcal {P}_{r,\nu ,p}^{\left( \alpha \right) }\left( z\right) , \end{aligned}$$

(1.3)

where the $\alpha$-Bernstein–Schurer polynomials $\mathcal {P}_{r,\nu }^{(\alpha )}(z)$ are given as

$$\begin{aligned} \mathcal {P}_{1,\nu ,0}^{\left( \alpha \right) }\left( z\right) =1-z,\;\;\;\mathcal {P}_{1,\nu ,1}^{(\alpha )}(z)=z \end{aligned}$$

and

$$\begin{aligned} \mathcal {P}_{r,\nu ,p}^{\left( \alpha \right) }\left( z\right)= & {} \Bigg [\left( 1-\alpha \right) z\left( {\begin{array}{c}r+\nu -2\\ p\end{array}}\right) +\left( 1-\alpha \right) \left( 1-z\right) \left( {\begin{array}{c}r+\nu -2\\ p-2\end{array}}\right) \nonumber \\&+\alpha z\left( 1-z\right) \left( {\begin{array}{c}r+\nu \\ p\end{array}}\right) \Bigg ] z^{p-1}\left( 1-z\right) ^{r+\nu -(p+1)} \end{aligned}$$

(1.4)

for $r\ge 2$. Özger et al. [25] discussed in detail several basic properties, global approximation with the help of Ditzian-Totik uniform modulus of smoothness and rate of convergence of $\alpha$-Bernstein–Schurer operators. Further, they obtained Voronovskaja-type approximation results of aforesaid operators and investigated shape preserving properties which showed that $\Psi _{r,\nu }^{\alpha }\left( h;z\right)$ preserves convexity and monotonicity.

2 Generalized Schurer–Kantorovich Operators and Auxiliary Results

To approximate the Lebesgue integrable functions on [0, 1], in this section, we first construct the Kantorovich-type modification of (1.3) as follows.

Consider $\nu \in \mathbb Z_{0}^{+}$ and $\alpha \in [0,1]$. Then, we define the $\alpha$-Schurer–Kantorovich operators for any function $h\in C\left[ 0,1+\nu \right]$ and $r\in \mathbb N$ by

$$\begin{aligned} \mathcal {K}_{r,\nu }^{\alpha }\left( h;z\right) =(r+1)\sum \limits _{p=0}^{r+\nu }\mathcal {P}_{r,\nu ,p}^{\left( \alpha \right) }\left( z\right) \int _{\frac{p}{r+1}}^{\frac{p+1}{r+1}}h(t)\mathrm{d}t\;\;\;\;\;(z\in [0,1]) \end{aligned}$$

(2.1)

The operators considered by (2.1) are linear and positive, and $\mathcal {P}_{r,\nu ,p}^{\left( \alpha \right) }\left( z\right)$ is considered by (1.4).

Consider the test function $e_{\kappa }\left( t\right) =t^{\kappa -1}$ $(\kappa =1,2,3)$. Recall as in [25] that the moments of $\Psi _{r,\nu }^{\alpha }\left( e_{\kappa }\left( t\right) ;z\right)$ are obtained by

$$\begin{aligned} \Psi _{r,\nu }^{\alpha }\left( e_{\kappa }\left( t\right) ;z\right) = {\left\{ \begin{array}{ll} 1 &{} \quad \text {if }\quad \kappa = 1, \\ z+\frac{\nu }{r}z &{} \quad \text {if }\quad \kappa = 2,\\ z^2+\frac{(r+\nu +2(1-\alpha ))(z-z^2)}{r^2}+\frac{\nu (\nu +2r)z^2}{r^2}&{} \quad \text {if }\quad \kappa = 3. \end{array}\right. } \end{aligned}$$

(2.2)

Lemma 2.1

The operators $\mathcal {K}_{r,\nu }^{\alpha }\left( e_k;z\right)$ satisfy:

$$\begin{aligned} \mathcal {K}_{r,\nu }^{\alpha }\left( e_1(t);z\right)= & {} 1,\\ \mathcal {K}_{r,\nu }^{\alpha }\left( e_2(t);z\right)= & {} \left( \frac{r}{r+1}\right) \left( 1+\frac{\nu }{r}\right) z +\frac{1}{2(r+1)}, \\ \mathcal {K}_{r,\nu }^{\alpha }\left( e_3(t);z\right)= & {} \left[ \left( \frac{r}{r+1}\right) ^2+\frac{\nu (2r+\nu )}{r^2} -\frac{(r+\nu +2(1-\alpha ))}{r^2}\right] z^2\\&+\left[ \frac{(r+\nu +2(1-\alpha ))}{r^2}+\left( \frac{r}{r+1}\right) \left( 1+\frac{\nu }{r}\right) \right] z+\frac{1}{3(r+1)^2}. \end{aligned}$$

Proof

It follows from the definition of the operators (2.1) together with (2.2) that

$$\begin{aligned} \mathcal {K}_{r,\nu }^{\alpha }\left( e_1;z\right)= & {} (r+1)\sum \limits _{p=0}^{r+\nu } \mathcal {P}_{r,\nu ,p}^{\left( \alpha \right) }\left( z\right) \int _{\frac{p}{r+1}}^{\frac{p+1}{r+1}}\mathrm{d}t=1. \end{aligned}$$

Now,

$$\begin{aligned}&\mathcal {K}_{r,\nu }^{\alpha }\left( e_2;z\right) =(r+1)\sum \limits _{p=0}^{r+\nu } \mathcal {P}_{r,\nu ,p}^{\left( \alpha \right) }\left( z\right) \int _{\frac{p}{r+1}}^{\frac{p+1}{r+1}}t\mathrm {d}t \\&\quad =\frac{r}{r+1} \Psi _{r,\nu }^{\alpha }\left( e_2(t);z\right) +\frac{1}{2(r+1)} \Psi _{r,\nu }^{\alpha }\left( e_1(t);z\right) \\&\quad =\frac{r}{r+1}\left( 1+\frac{\nu }{r}\right) z +\frac{1}{2(r+1)},\\ \end{aligned}$$

Finally, we can find

$$\begin{aligned}&\mathcal {K}_{r,\nu }^{\alpha }\left( e_3;z\right) =(r+1)\sum \limits _{p=0}^{r+\nu } \mathcal {P}_{r,\nu ,p}^{\left( \alpha \right) }\left( z\right) \int _{\frac{p}{r+1}}^{\frac{p+1}{r+1}}t^2\mathrm {d}t \\&\quad =\left( \frac{r}{r+1}\right) ^2 \Psi _{r,\nu }^{\alpha } \left( e_3(t);z\right) + \frac{r}{(r+1)^2} \Psi _{r,\nu }^{\alpha }\left( e_2(t);z\right) \\&\quad +\frac{1}{3(r+1)^2} \Psi _{r,\nu }^{\alpha }\left( e_1(t);z\right) \\&\quad =\bigg (\frac{r}{r+1}\bigg )^2 \left\{ z^2+\frac{(r+\nu +2(1-\alpha ))(z-z^2)}{r^2} +\frac{\nu (2r+\nu )z^2}{r^2}\right\} \\&\quad +\frac{r}{(r+1)^2}\left( z+\frac{\nu }{r}z\right) +\frac{1}{3(r+1)^2}, \end{aligned}$$

which completes the proof. $\square$

Corollary 2.1

The operators $\mathcal {K}_{r,\nu }^{\alpha }\left( e_k;z\right)$ satisfy (central moments):

$$\begin{aligned} \mathcal {K}_{r,\nu }^{\alpha }\left( e_2(t)-z;z\right)= & {} \Bigg [\left( \frac{r}{r+1}\right) \left( 1+\frac{\nu }{r}\right) -1\Bigg ]z +\frac{1}{2(r+1)}, \\ \mathcal {K}_{r,\nu }^{\alpha }\left( (e_2(t)-z)^2;z\right)= & {} \Bigg [ \bigg ( \frac{r}{r+1}\bigg )^2+ \frac{\nu (2r+\nu )}{r^2}+1-2\bigg (\frac{r}{r+1}\bigg )\bigg (1+\frac{\nu }{r}\bigg )\\&-\frac{(r+\nu +2(1-\alpha ))}{r^2} \Bigg ]z^2+\frac{1}{3(r+1)^2}\\&+\Bigg [\frac{(r+\nu +2(1-\alpha ))}{r^2}+\bigg (\frac{r}{r+1}\bigg )\bigg (1+\frac{\nu }{r}\bigg )-\frac{1}{r+1}\Bigg ]z. \end{aligned}$$

3 Approximation Properties of the Operators $\mathcal {K}_{r,\nu }^{\alpha }$

Lemma 3.1

Let $z\in [0,1]$. Then, for all $h\in C_b[0,1+\nu ]$ and $\alpha \in [0,1]$, one gets

$$\begin{aligned} \left| \mathcal {K}_{r,\nu }^{\alpha }(h;z)\right| \le \Vert h \Vert _{C_b[0,1+\nu ]}, \end{aligned}$$

where $C_b[0,1+\nu ]$ is the class of continuous and bounded function on $[0,1+\nu ]$ and $\Vert .\Vert _{C_b[0,1+\nu ]}$ is the sup-norm on $[0,1+\nu ]$.

Proof

From the operators (2.1), we can easily see that

$$\begin{aligned} \left| \mathcal {K}_{r,\nu }^{\alpha }(h;z)\right|\le & {} (r+1)\sum _{p=0}^{r+\nu } \mathcal {P}_{r,\nu ,p}^{\left( \alpha \right) }\left( z\right) \int _{\frac{p}{r+1}}^{\frac{p+1}{r+1}}|h(t)|\mathrm{d}t\\\le & {} \sup _{t\in [0,1+\nu ]}|h(t)|~\mathcal {K}_{r,\nu }^{\alpha }(e_{2}(t);z)\\= & {} \Vert h \Vert _{C_b[0,1+\nu ]}, \end{aligned}$$

by Lemma 2.1. $\square$

Theorem 3.1

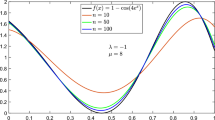
Assume that $h\in C_{b}[0,1+\nu ]$. Then, the operators $\mathcal {K}_{r,\nu }^{\alpha }(h;z)$ converge uniformly to the function h on [0, 1].

Proof

Clearly, by Korovkin theorem [26, 27], it is enough to prove our assertion that

$$\begin{aligned} \lim _{r \rightarrow \infty }\mathcal {K}_{r,\nu }^{\alpha }(e_\kappa (t);z)=z^{\kappa -1},\quad \kappa =1,2,3 \end{aligned}$$

uniformly on [0, 1]. Thus, from Lemma 2.1, one gets

$$\begin{aligned}\lim _{r \rightarrow \infty }\mathcal {K}_{r,\nu }^{\alpha }(e_1(t);z)=1,\;\;\lim _{r \rightarrow \infty }\mathcal {K}_{r,\nu }^{\alpha }(e_2(t);z)=z,\;\;\lim _{r \rightarrow \infty }\mathcal {K}_{r,\nu }^{\alpha }(e_3(t);z)=z^2\end{aligned}$$

uniformly on [0, 1]. Hence, $\alpha$-Schurer–Kantorovich operators converge uniformly to h on [0, 1]. $\square$

Consider a function h in $C[0,1+\nu ]$ and $\hat{\delta }>0$. Then, the modulus of smoothness of second-order of h is defined as

$$\begin{aligned} \omega _{2}\left( h;\hat{\delta }^{\frac{1}{2}}\right) =\sup _{0<\mu \le \hat{\delta } ^{\frac{1}{2} }}\sup _{z,z+2\mu \in [0,1+\nu ] }|h(z)-2h(z+\mu )+h(z+2\mu )| \end{aligned}$$

while the usual modulus of continuity is given by

$$\begin{aligned} \omega \left( h;\hat{\delta }\right) =\sup _{0<\mu \le \hat{\delta }}\sup _{z,z+\mu \in [0,1+\nu ] }|h(z+\mu )-h(z)|. \end{aligned}$$

(3.1)

For every $\hat{\delta }>0$ and $h\in C_b[0,1+\nu ]$, the Peetre’s K-functional is defined as:

$$\begin{aligned} K_{2}(h;\hat{\delta })=\inf \left\{ \Vert h-\varphi \Vert _{C_b[0,1+\nu ]}+\hat{\delta }\Vert \varphi ^{\prime \prime }\Vert _{C_{b}[ 0,1+\nu ]}:\varphi \in C_{b}^{2}[0,1+\nu ]\right\} , \end{aligned}$$

(3.2)

where

$$\begin{aligned} C_b^2[0,1+\nu ]=\left\{ \varphi \in C_b[0,1+\nu ]:\varphi ^{\prime },\varphi ^{\prime \prime }\in C_b[0,1+\nu ]\right\} . \end{aligned}$$

By Theorem 2.4 of [28], $\exists$ a constant $\mathcal {M}>0$ such that

$$\begin{aligned} K_{2}(h;\hat{\delta } )\le \mathcal {M}\omega _2\left( h;\hat{\delta }^{\frac{1}{2}}\right) . \end{aligned}$$

Theorem 3.2

For every $h\in C_{b}[0,1+\nu ]$ and $z\in [0,1],$ one has

$$\begin{aligned} |\mathcal {K}_{r,\nu }^{\alpha }(h;z)-h(z)|\le 2\omega \left( f;\hat{\delta }_{r,\nu }^{\alpha }(z)\right) , \end{aligned}$$

where $\hat{\delta }=\hat{\delta }_{r,\nu }^{\alpha }(z) =\sqrt{\mathcal {K}_{r,\nu }^{\alpha }\left( (e_2(t)-z)^2;z\right) }$ and given in Corollary 2.1.

Proof

Using (3.1) and employing Cauchy-Schwartz inequality to our operators (2.1), we have

$$\begin{aligned}&|\mathcal {K}_{r,\nu }^{\alpha }(h;z)-h(z)|\le (r+1)\sum \limits _{p=0}^{r+\nu } \mathcal {P}_{r,\nu ,p}^{\left( \alpha \right) }\left( z\right) \int _{\frac{p}{r+1}}^{\frac{p+1}{r+1}}|h(t)-h(z)|\mathrm{d}t\nonumber \\&\quad \le \left\{ 1+\frac{1}{\hat{\delta }}(r+1)\sum \limits _{p=0}^{r+\nu }\mathcal {P}_{r,\nu ,p}^{\left( \alpha \right) } \left( z\right) \int _{\frac{p}{r+1}}^{\frac{p+1}{r+1}}|t-z|\mathrm{d}t\right\} \omega (h;\hat{\delta })\nonumber \\&\quad \le \left\{ 1+\frac{1}{\hat{\delta }}\left( (r+1)\sum \limits _{p=0}^{r+\nu } \mathcal {P}_{r,\nu ,p}^{\left( \alpha \right) }\left( z\right) \int _{\frac{p}{r+1}}^{\frac{p+1}{r+1}} (t-z)^2\mathrm {d}t\right) ^{\frac{1}{2}}\right\} \omega (h;\hat{\delta })\nonumber \\&\quad =\left\{ 1+\frac{1}{\hat{\delta }}\sqrt{\mathcal {K}_{r,\nu }^{\alpha }\left( (e_2(t)-z)^2;z\right) }\right\} \omega (f;\hat{\delta }). \end{aligned}$$

(3.3)

Considering $\hat{\delta }=\hat{\delta }_{r,\nu }^{\alpha }(z)=\sqrt{\mathcal {K}_{r,\nu }^{\alpha }\left( (e_2(t)-z)^2;z\right) }$ in (3.3) leads us the assertion of Theorem 3.2. $\square$

Theorem 3.3

Let $\varphi \in C_{b}^{2}[0,1+\nu ]$. Then

$$\begin{aligned} |\mathcal {L}_{r,\nu }^{\alpha }\left( \varphi ;z\right) -\varphi (z)|\le \left[ \left( \hat{\delta }_{r,\nu }^{\alpha }(z)\right) ^2 +\left\{ \frac{1}{2(r+1)}+\left( \frac{\nu -1}{r+1}\right) z\right\} ^{2}\right] \Vert \varphi ^{\prime \prime }\Vert _{C_b[0,1+\nu ]}, \end{aligned}$$

where $\hat{\delta }_{r,\nu }^{\alpha }(z)=\sqrt{\mathcal {K}_{r,\nu }^{\alpha }\left( (e_2(t)-z)^2;z\right) }$, the operators $\mathcal {L}_{r,\nu }^{\left( \alpha \right) }$ considered as

$$\begin{aligned} \mathcal {L}_{r,\nu }^{\alpha }\left( \varphi ;z\right) =\mathcal {K}_{r,\nu }^{\alpha }\left( \varphi ;z\right) +\varphi (z)-\varphi \left( \Theta _{r,\nu }(z)\right) \end{aligned}$$

(3.4)

and

$$\begin{aligned}\Theta _{r,\nu } (z)=\mathcal {K}_{r,\nu }^{\alpha }\left( e_2(t);z\right) =\left( \frac{r}{r+1}\right) \left( 1+\frac{\nu }{r}\right) z+\frac{1}{2(r+1)}.\end{aligned}$$

Proof

Employing Lemma 2.1 in operators (3.4), we get

$$\begin{aligned} \mathcal {L}_{r,\nu }^{\alpha }\left( e_1(t);z\right) =1\;\;\text{ and }\;\;\mathcal {L}_{r,\nu }^{\alpha }\left( e_2(t);z\right) =\mathcal {K}_{r,\nu }^{\alpha }\left( e_2(t);z\right) +z-\Theta _{r,\nu } (z)=z. \end{aligned}$$

With a view of Lemma 3.1, the operators (3.4) satisfy the inequality

$$\begin{aligned} |\mathcal {L}_{r,\nu }^{\alpha }\left( h;z\right) |\le 3 \Vert h\Vert _{C_b[0,1+\nu ]}. \end{aligned}$$

(3.5)

Since $\varphi \in C_{b}^{2}[0,1+\nu ]$, Taylor’s expansion gives

$$\begin{aligned} \varphi (e_2(t))=\varphi (z)+(e_2(t)-z)\varphi ^{\prime }(z)+\int _{z}^{e_2(t)}(e_2(t)-\zeta )\varphi ^{\prime \prime }(\zeta )\mathrm {d}\zeta . \end{aligned}$$

It follows by operating $\mathcal {L}_{r,\nu }^{\alpha }$ that

$$\begin{aligned} \mathcal {L}_{r,\nu }^{\alpha }\left( \varphi ;z\right) -\varphi (z)= & {} \varphi ^{\prime }(z)\mathcal {L}_{r,\nu }^{\alpha }(e_2(t)-z;z)\\&+\mathcal {L}_{r,\nu }^{\alpha }\left( \int _{z}^{e_2(t)}(e_2(t)-\zeta )\varphi ^{\prime \prime }(\zeta ) \mathrm {d}\zeta ;z\right) \\= & {} \mathcal {L}_{r,\nu }^{\alpha }\left( \int _{z}^{e_2(t)}(e_2(t)-\zeta )\varphi ^{\prime \prime }(\zeta )\mathrm {d}\zeta ;z\right) \\= & {} \mathcal {K}_{r,\nu }^{\alpha }\left( \int _{z}^{e_2(t)}(e_2(t)-\zeta )\varphi ^{\prime \prime }(\zeta )\mathrm {d}\zeta ;z\right) \\&-\int _{z}^{\Theta _{r,\nu } (z)}\left( \Theta _{r,\nu }(z)-\zeta \right) \varphi ^{\prime \prime }(\zeta )\mathrm {d}\zeta \end{aligned}$$

which yields

$$\begin{aligned} \left| \mathcal {L}_{r,\nu }^{\alpha }\left( \varphi ;z\right) -\varphi (z)\right|\le & {} \left| \mathcal {K}_{r,\nu }^{\alpha }\left( \int _{z}^{e_2(t)}(e_2(t)-\zeta )\varphi ^{\prime \prime }(\zeta )\mathrm {d}\zeta ;z\right) \right| \nonumber \\&+\left| \int _{z}^{\Theta _{r,\nu } (z)}\left( \Theta _{r,\nu } (z)-\zeta \right) \varphi ^{\prime \prime }(\zeta )\mathrm {d}\zeta \right| . \end{aligned}$$

(3.6)

We see that

$$\begin{aligned} \left| \int _{z}^{e_2(t)}(e_2(t)-\zeta )\varphi ^{\prime \prime }(\zeta )\mathrm {d}\zeta \right| \le (e_2(t)-z)^{2}\Vert \varphi ^{\prime \prime }\Vert _{C_b[0,1+\nu ]} \end{aligned}$$

and

$$\begin{aligned} \left| \int _{z}^{\Theta _{r,\nu } (z)}\bigg (\Theta _{r,\nu } (z)-\zeta \bigg )\varphi ^{\prime \prime }(\zeta ) \mathrm {d}\zeta \right| \le \left\{ \frac{1}{2(r+1)}+\left( \frac{\nu -1}{r+1}\right) z\right\} ^{2} \Vert \varphi ^{\prime \prime }\Vert _{C_b[0,1+\nu ]}. \end{aligned}$$

Thus, the inequality (3.6) gives

$$\begin{aligned} |\mathcal {L}_{r,\nu }^{\alpha }\left( \varphi ;z\right) -\varphi (z)|\le \left[ \mathcal {K}_{r,\nu }^{\alpha }\left( (e_2(t)-z)^{2};z\right) +\left\{ \frac{1}{2(r+1)}+\left( \frac{\nu -1}{r+1}\right) z\right\} ^{2} \right] \Vert \varphi ^{\prime \prime }\Vert _{C_b[0,1+\nu ]}. \end{aligned}$$

$\square$

Theorem 3.4

For any $h\in C_{b}^{2}[0,1+\nu ]$, the inequality

$$\begin{aligned}&|\mathcal {K}_{r,\nu }^{\alpha }(h ;z)-h(z)|\le \mathcal {M}\omega _{2}\left( h;\frac{1}{2}\sqrt{\Omega _{r,\nu }^{\left( \alpha \right) }(z)}\right) \\&\quad +\omega \left( h;\frac{1}{2(r+1)}+\left( \frac{\nu -1}{r+1}\right) z\right) , \end{aligned}$$

holds, where

$$\begin{aligned}&\Omega _{r,\nu }^{\left( \alpha \right) }(z)=\left( \hat{\delta }_{r,\nu }^{\alpha }(z) \right) ^2 +\left\{ \frac{1}{2(r+1)}+ \left( \frac{\nu -1}{r+1}\right) z\right\} ^{2},\;\;\\&\quad \hat{\delta }_{r,\nu }^{\alpha }(z) =\sqrt{\mathcal {K}_{r,\nu }^{\alpha }\left( (e_2(t)-z)^2;z\right) }. \end{aligned}$$

Proof

Since $h\in C_{b}^{2}[0,1+\nu ]$, we can write from Eq. (3.4) that

$$\begin{aligned}&|\mathcal {K}_{r,\nu }^{\alpha }(h ;z)-h(z)|=\left| \mathcal {L}_{r,\nu }^{\alpha }(h ;z)-h(z)+h\left( \left( \frac{r}{r+1}\right) \left( 1+\frac{\nu }{r}\right) z+\frac{1}{2(r+1)}\right) -h(z)\right| \\&\quad \le \left| \mathcal {L}_{r,\nu }^{\alpha }(h-\varphi ;z)\right| +\left| \mathcal {L}_{r,\nu }^{\alpha }(\varphi ;z)-\varphi (z)\right| +\left| (h-\varphi )(z)\right| \\&\quad +\left| h(z)-h\left( \left( \frac{r}{r+1}\right) \left( 1+\frac{\nu }{r}\right) z+\frac{1}{2(r+1)}\right) \right| . \end{aligned}$$

By using Theorem 3.3, we obtain

$$\begin{aligned} |\mathcal {K}_{r,\nu }^{\alpha }(h ;z)-h(z)|\le & {} 4\Vert h-\varphi \Vert _{C_b[0,1+\nu ]}\\&+ \left[ \left( \hat{\delta }_{r,\nu }^{\alpha }(z) \right) ^2 +\left\{ \frac{1}{2(r+1)}+ \left( \frac{\nu -1}{r+1}\right) z\right\} ^{2}\right] \Vert \varphi ^{\prime \prime }\Vert _{C_b[0,1+\nu ]}\\&+\omega \left( h;\left( \frac{\nu -1}{r+1}\right) z+\frac{1}{2(r+1)}\right) . \end{aligned}$$

We are now applying $\inf _{\varphi \in C_{b}^{2}[0,1+\nu ]}$ and using (3.2), we fairly have

$$\begin{aligned} \left| \mathcal {K}_{r,\nu }^{\alpha }(h ;z)-h(z)\right| \le 4K_{2}\left( h;\frac{\Omega _{r,\nu }^{\left( \alpha \right) }(z)}{4}\right) +\omega \left( h;\frac{1}{2(r+1)}+\left( \frac{\nu -1}{r+1}\right) z\right) , \end{aligned}$$

where

$$\begin{aligned}\Omega _{r,\nu }^{\left( \alpha \right) }(z)=\left( \hat{\delta }_{r,\nu }^{\alpha }(z)\right) ^2 +\left\{ \frac{1}{2(r+1)}+ \left( \frac{\nu -1}{r+1}\right) z\right\} ^{2},\end{aligned}$$

yields

$$\begin{aligned} \left| \mathcal {K}_{r,\nu }^{\alpha }(h ;z)-h(z)\right| \le \mathcal {M}\omega _{2}\left( h;\frac{1}{2}\sqrt{\Omega _{r,\nu }^{\left( \alpha \right) }(z)}\right) +\omega \left( h;\left( \frac{\nu -1}{r+1}\right) z+\frac{1}{2(r+1)}\right) . \end{aligned}$$

This completes the proof. $\square$

The class of all Lipschitz functions $h\in C[0,1+\nu ]$ (the set of all continuous functions on $[0,1+\nu ]$) is defined as

$$\begin{aligned} Lip_{\mathcal {C}}(\theta )=\left\{ h:|h(\lambda _{1})-h(\lambda _{2})|\le \mathcal {C}|\lambda _{1}-\lambda _{2}|^{\theta };\;\lambda _{1},\lambda _{2}\in [0,1+\nu ]\right\} , \end{aligned}$$

(3.7)

where $0<\theta \le 1$ and $\mathcal {C}$ is a non-negative constant.

Theorem 3.5

For any $h\in Lip_{\mathcal {C}}(\theta )$, one has

$$\begin{aligned} \left| \mathcal {K}_{r,\nu }^{\alpha }\left( h;z\right) -h(z)\right| \le \mathcal {C}\left( \hat{\delta }_{r,\nu }^{\alpha }(z) \right) ^\theta \;\;\;\;\;\;\;(\theta \in (0,1],\mathcal {C}>0), \end{aligned}$$

where $\hat{\delta }_{r,\nu }^{\alpha }(z)=\sqrt{\mathcal {K}_{r,\nu }^{\alpha }\left( (e_2(t)-z)^2;z\right) }$.

Proof

To obtain the assertion of Theorem 3.5, we can use Eq. (3.7) and well-known Hölder inequality, and write

$$\begin{aligned} |\mathcal {K}_{r,\nu }^{\alpha }\left( h;z\right) -h(z)|\le & {} |\mathcal {K}_{r,\nu }^{\alpha }(h(e_2(t))-h(z);x)|\\\le & {} \mathcal {K}_{r,\nu }^{\alpha }\left( |h(e_2(t))-h(z)|;z\right) \\\le & {} \mathcal {C}\mathcal {K}_{r,\nu }^{\alpha }\left( |(e_2(t)-z)|^{\theta };z\right) \\\le & {} \mathcal {C}\left( \mathcal {K}_{r,\nu }^{\alpha }(e_1(t);z)\right) ^{\frac{2-\theta }{2}}\left( \mathcal {K}_{r,\nu }^{\alpha }(|(e_1(t)-z)|^{2};z)\right) ^{\frac{\theta }{2}} \\= & {} \mathcal {C}\left( \mathcal {K}_{r,\nu }^{\alpha }\left( \left( e_1(t)-z\right) ^2;z\right) \right) ^{\frac{\theta }{2}}, \end{aligned}$$

which completes the proof. $\square$

Theorem 3.6

For any $\varphi \in C_{b}^{2}[0,1+\nu ]$, one has the inequality

$$\begin{aligned} \left| \mathcal {K}_{r,\nu }^{\alpha }(\varphi ,z)-\varphi (z)\right| \le \left( \sqrt{\hat{\delta }_{r,\nu }^{\alpha }(z)}+\frac{\left( \hat{\delta }_{r,\nu }^{\alpha }(z) \right) ^2}{2}\right) \Vert \varphi \Vert _{C_{b}[0,1+\nu ]}, \end{aligned}$$

where $\hat{\delta }_{r,\nu }^{\alpha }(z)=\sqrt{\mathcal {K}_{r,\nu }^{\alpha }\left( (e_2(t)-z)^2;z\right) }$.

Proof

Since $\varphi \in C_{b}^{2}[0,1+\nu ]$, it follows from the Taylor’s expansion that

$$\begin{aligned} \varphi (e_2(t))=\varphi (z)+\varphi ^{\prime }(z)(e_2(t)-z)+\varphi ^{\prime \prime }(\psi )\;\frac{(e_2(t)-z)^2}{2}. \end{aligned}$$

Consequently,

$$\begin{aligned} \left| \varphi (e_2(t))-\varphi (z)\right| \le \mathcal {V}_{1}|(e_2(t)-z)|+\frac{1}{2}\mathcal {V}_{2}(e_2(t)-z)^2, \end{aligned}$$

where

$$\begin{aligned} \mathcal {V}_{1}=\sup _{z\in [0,1+\nu ]}\left| \varphi ^{\prime }(z)\right| =\Vert \varphi ^{\prime }\Vert _{C_{b}[0,1+\nu ]}\le \Vert \varphi \Vert _{C_{b}[0,1+\nu ]}, \end{aligned}$$

and

$$\begin{aligned} \mathcal {V}_2=\sup _{z\in [0,1+\nu ]} \left| \varphi ^{\prime \prime }(z)\right| =\Vert \varphi ^{\prime \prime }\Vert _{C_{b}[0,1+\nu ]}\le \Vert \varphi \Vert _{C_{b}[0,1+\nu ]}. \end{aligned}$$

We therefore obtain

$$\begin{aligned} \left| \varphi (e_2(t))-\varphi (z)\right| \le \left( |(e_2(t)-z)|+\frac{1}{2}(e_2(t)-z)^2\right) \Vert \varphi \Vert _{C_{b}[0,1+\nu ]}. \end{aligned}$$

From the linearity of operators (2.1), we obtain

$$\begin{aligned} \left| \mathcal {K}_{r,\nu }^{\alpha }(\varphi ,z)-\varphi (z)\right| \le \left( \mathcal {K}_{r,\nu }^{\alpha }\left( \left| (e_2(t)-z)\right| ;z\right) +\frac{1}{2}\mathcal {K}_{r,\nu }^{\alpha }\left( \left( e_2(t)-z\right) ^2;z\right) \right) \Vert \varphi \Vert _{C_{b}[0,1+\nu ]}. \end{aligned}$$

The Cauchy–Schwarz inequality gives

$$\begin{aligned} \mathcal {K}_{r,\nu }^{\alpha }\left( \left| \left( e_2(t)-z\right) \right| ;z\right) \le \left( \mathcal {K}_{r,\nu }^{\alpha }\left( \left( e_2(t)-z\right) ^2;z\right) \right) ^{\frac{1}{2}} \end{aligned}$$

and hence

$$\begin{aligned} \left| \mathcal {K}_{r,\nu }^{\alpha }(\varphi ,z)-\varphi (z)\right| \le \left( \sqrt{\mathcal {K}_{r,\nu }^{\alpha }\left( \left( e_2(t)-z\right) ^2;z\right) }+\frac{\mathcal {K}_{r,\nu }^{\alpha }\left( \left( e_2(t)-z\right) ^2;z\right) }{2}\right) \Vert \varphi \Vert _{C_{b}[0,1+\nu ]}, \end{aligned}$$

which gives Theorem 3.6. $\square$

4 Bivariate $\alpha$-Schurer–Kantorovich Operators

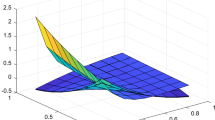
We demonstrate the bivariate case of our $\alpha$-Schurer–Kantorovich operators defined in Sect. 2. Let $\nu \in \mathbb {Z}_{0}^{+}$. Suppose $C\left( \mathcal {I}^2\right)$ is the class of all continuous functions on $\mathcal {I}^2$ $(\mathcal {I}^2:=\mathcal {I}\times \mathcal {I})$, where

$$\begin{aligned} \mathcal {I}^2=\{(u_1,u_2):0 \le u_1 \le 1+\nu , \; 0 \le u_2 \le 1+\nu \}.\end{aligned}$$

For $g\in C\left( \mathcal {I}^2\right)$, the norm of g is

$$\begin{aligned} \Vert g\Vert _{C\left( \mathcal {I}^2\right) }=\sup _{(u_1,u_2)\in \mathcal {I}^2 }|g(u_1,u_2)|.\end{aligned}$$

Consider $0\le \alpha _1,\alpha _2\le 1$. For any $g\in C\left( \mathcal {I}^2\right)$, $r_1,r_2\in \mathbb {N}$ and $(z_1,z_2)\in [0,1]\times [0,1]$, we define the bivariate form of (2.1), namely bivariate $\alpha$-Schurer–Kantorovich operators, by

$$\begin{aligned} \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( g;z_1,z_2\right)= & {} (r_{1}+1)(r_{2}+1)\sum \limits _{p_1=0}^{r_1+\nu } \sum \limits _{p_2=0}^{r_2+\nu }\mathcal {P}_{r_1+\nu ,r_2+\nu ,p_{1},p_{2}}^{\alpha _1,\alpha _2}\left( z_1,z_2\right) \nonumber \\&\times \int _{\frac{p_1}{r_1+1}}^{\frac{p_1+1}{r_1+1}}\int _{\frac{p_2}{r_2+1}}^{\frac{p_2+1}{r_2+1}}g(t,s)\mathrm{d}t\mathrm{d}s, \end{aligned}$$

(4.1)

where

$$\begin{aligned} \mathcal {P}_{r_1+\nu ,r_2+\nu ,p_{1},p_{2}}^{\alpha _1,\alpha _2}\left( z_1,z_2\right) =\mathcal {R}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(z_1)\mathcal {R}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(z_2)\end{aligned}$$

and

$$\begin{aligned}&\mathcal {R}_{r_i,\nu ,p_{i}}^{(\alpha _i)}(z_i)=\Bigg [\left( 1-\alpha _i \right) z_i\left( {\begin{array}{c}r_i+\nu -2\\ p_i\end{array}}\right) \\&\quad +\left( 1-\alpha _i \right) \left( 1-z_i\right) \left( {\begin{array}{c}r_i+\nu -2\\ p_i-2\end{array}}\right) \\&\quad +\alpha _{i}z_i\left( 1-z_i\right) \left( {\begin{array}{c}r_i+\nu \\ p_i\end{array}}\right) \Bigg ]z_i^{p_i-1}\left( 1-z_i\right) ^{r_i+\nu -(p_i+1)} \end{aligned}$$

for $i=1,2$ and $r_i\ge 2$. Note that (4.1) is linear positive operator and for bivariate $\alpha$-Bernstein–Schurer operators (see [29]).

Lemma 4.1

Let $0\le \alpha _1,\alpha _2\le 1$, $r_1,r_2\in \mathbb {N}$ and $(z_1,z_2)\in [0,1]\times [0,1]$. If

$$\begin{aligned} \mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(g;z_1,z_2)=(r_{1}+1)\sum \limits _{p_1=0}^{r_1+\nu }\mathcal {R}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(z_1)\int _{\frac{p_1}{r_1+1}}^{\frac{p_1+1}{r_1+1}}g(t,s)\mathrm{d}t, \end{aligned}$$

(4.2)

and

$$\begin{aligned} \mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)} (g;z_1,z_2) =(r_{2}+1)\sum \limits _{p_2=0}^{r_2+\nu }\mathcal {R}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(z_2)\int _{\frac{p_2}{r_2+1}}^{\frac{p_2+1}{r_2+1}} g(t,s)\mathrm{d}s, \end{aligned}$$

(4.3)

for any $g\in C\left( \mathcal {I}^2\right)$, then

$$\begin{aligned}&\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( g;z_1,z_2\right) =\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}\left( \mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(g;z_1,z_2) \right) \\&\quad =\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}\left( \mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(g;z_1,z_2) \right) . \end{aligned}$$

Proof

It is easy to see that

$$\begin{aligned}&\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}\left( \mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(g;z_1,z_2)\right) \\&\quad = \mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}\left( (r_{2}+1)\sum \limits _{p_2=0}^{r_2+\nu }\mathcal {R}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(z_2)\int _{\frac{p_2}{r_2+1}}^{\frac{p_2+1}{r_2+1}} g(t,s)\mathrm{d}s\right) \\&\quad =(r_{2}+1)\sum \limits _{p_2=0}^{r_2+\nu }\mathcal {R}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(z_2)\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}\left( \int _{\frac{p_2}{r_2+1}}^{\frac{p_2+1}{r_2+1}}g(t,s)\mathrm{d}s\right) \\&\quad = \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( g;z_1,z_2\right) . \end{aligned}$$

Similarly, we prove $\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}\left( \mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(g;z_1,z_2) \right) =\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( g;z_1,z_2\right)$. $\square$

Lemma 4.2

Let $0\le \alpha _1,\alpha _2\le 1$, $r_1,r_2\in \mathbb {N}$ and $(z_1,z_2)\in [0,1]\times [0,1]$. Suppose $e_{uv}(t,s)=t^{u-1}s^{v-1}$ for $(u,v)\in \mathbb N\times \mathbb N$ with $u+v\le 4$. The following identities hold:

$$\begin{aligned} \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(e_{11};z_1,z_2)= & {} 1,\\ \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(e_{21};z_1,z_2)= & {} \left( \frac{r_1}{r_1+1}\right) \left( 1+\frac{\nu }{r_1}\right) z_1 +\frac{1}{2(r_1+1)},\\ \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(e_{12};z_1,z_2)= & {} \left( \frac{r_2}{r_2+1}\right) \left( 1+\frac{\nu }{r_2}\right) z_2 +\frac{1}{2(r_2+1)},\\ \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(e_{31};z_1,z_2)= & {} \left[ \left( \frac{r_1}{r_1+1}\right) ^2+ \frac{\nu _1(2r_1+\nu )}{r_1^2} -\frac{(r_1+\nu +2(1-\alpha _1))}{r_1^2} \right] z_1^2\\&+\left[ \frac{(r_1+\nu +2(1-\alpha _1))}{r_1^2} +\left( \frac{r_1}{r_1+1}\right) \left( 1+\frac{\nu }{r_1}\right) \right] z_1\\&+\frac{1}{3(r_1+1)^2},\\ \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(e_{13};z_1,z_2)= & {} \left[ \left( \frac{r_2}{r_2+1}\right) ^2+ \frac{\nu _2(2r_2+\nu )}{r_2^2} -\frac{(r_2+\nu +2(1-\alpha _2))}{r_2^2}\right] z_2^2\\&+ \left[ \frac{(r_2+\nu +2(1-\alpha _2))}{r_2^2}\right. \\&\left. +\left( \frac{r_2}{r_2+1}\right) \left( 1+\frac{\nu }{r_2}\right) \right] z_2+\frac{1}{3(r_2+1)^2}. \end{aligned}$$

Proof

From Eq. (4.1), we write

$$\begin{aligned}&\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( e_{11};z_1,z_2\right) =(r_{1}+1)(r_{2}+1)\sum \limits _{p_1=0}^{r_1+\nu } \sum \limits _{p_2=0}^{r_2+\nu }\mathcal {P}_{r_1+\nu ,r_2+\nu ,p_{1},p_{2}}^{\alpha _1,\alpha _2}\left( z_1,z_2\right) \int _{\frac{p_1}{r_1+1}}^{\frac{p_1+1}{r_1+1}}\int _{\frac{p_2}{r_2+1}}^{\frac{p_2+1}{r_2+1}}\mathrm{d}t\mathrm{d}s\\&\quad =(r_{1}+1)\sum \limits _{p_1=0}^{r_1+\nu }\mathcal {R}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(z_1)\frac{1}{(r_{1}+1)}(r_{2}+1)\sum \limits _{p_2=0}^{r_2+\nu }\mathcal {R}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(z_2)\frac{1}{(r_{2}+1)}\\&\quad =\mathcal {K}_{r_{1},\nu }^{\alpha _{1}}\left( 1;z_{1}\right) \mathcal {K}_{r_{2},\nu }^{\alpha _{2}}\left( 1;z_{2}\right) \\&\quad =1=\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(e_{11};z_1,z_2)\;(or,\;\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(e_{11};z_1,z_2)). \end{aligned}$$

Again, using Eq. (4.1), we write

$$\begin{aligned}&\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( e_{21};z_1,z_2\right) =(r_{1}+1)(r_{2}+1)\sum \limits _{p_1=0}^{r_1+\nu } \sum \limits _{p_2=0}^{r_2+\nu }\mathcal {P}_{r_1+\nu ,r_2+\nu ,p_{1},p_{2}}^{\alpha _1,\alpha _2}\left( z_1,z_2\right) \int _{\frac{p_1}{r_1+1}}^{\frac{p_1+1}{r_1+1}}\int _{\frac{p_2}{r_2+1}}^{\frac{p_2+1}{r_2+1}}t\mathrm{d}t\mathrm{d}s\\&\quad =\frac{(r_{1}+1)}{2}\sum \limits _{p_1=0}^{r_1+\nu }\mathcal {R}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(z_1)\left[ \left( \frac{p_1+1}{r_1+1}\right) ^{2}-\left( \frac{p_1}{r_1+1}\right) ^{2}\right] \\&\quad \times (r_{2}+1)\sum \limits _{p_2=0}^{r_2+\nu }\mathcal {R}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(z_2)\frac{1}{(r_{2}+1)}\\&\quad =\mathcal {K}_{r_{1},\nu }^{\alpha _{1}}\left( t;z_{1}\right) \mathcal {K}_{r_{2},\nu }^{\alpha _{2}}\left( 1;z_{2}\right) \\&\quad =\left( \frac{r_{1}}{r_{1}+1}\right) \left( 1+\frac{\nu }{r_{1}}\right) z_{1} +\frac{1}{2(r_{1}+1)}=\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(e_{21};z_1,z_2) \end{aligned}$$

and similarly

$$\begin{aligned}&\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( e_{12};z_1,z_2\right) =\mathcal {K}_{r_{1},\nu }^{\alpha _{1}}\left( 1;z_{1}\right) \mathcal {K}_{r_{2},\nu }^{\alpha _{2}}\left( s;z_{2}\right) \\&\quad =\left( \frac{r_{2}}{r_{2}+1}\right) \left( 1+\frac{\nu }{r_{2}}\right) z_{2} +\frac{1}{2(r_{2}+1)}=\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(e_{12};z_1,z_2). \end{aligned}$$

Now

$$\begin{aligned}&\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( e_{31};z_1,z_2\right) =(r_{1}+1)(r_{2}+1)\sum \limits _{p_1=0}^{r_1+\nu } \sum \limits _{p_2=0}^{r_2+\nu }\mathcal {P}_{r_1+\nu ,r_2+\nu ,p_{1},p_{2}}^{\alpha _1,\alpha _2}\left( z_1,z_2\right) \int _{\frac{p_1}{r_1+1}}^{\frac{p_1+1}{r_1+1}}\int _{\frac{p_2}{r_2+1}}^{\frac{p_2+1}{r_2+1}}t^{2}\mathrm{d}t\mathrm{d}s\\&\quad =\frac{(r_{1}+1)}{3}\sum \limits _{p_1=0}^{r_1+\nu }\mathcal {R}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(z_1)\left[ \left( \frac{p_1+1}{r_1+1}\right) ^{3}-\left( \frac{p_1}{r_1+1}\right) ^{3}\right] \\&\quad \times (r_{2}+1)\sum \limits _{p_2=0}^{r_2+\nu }\mathcal {R}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(z_2)\frac{1}{(r_{2}+1)}\\&\quad =\mathcal {K}_{r_{1},\nu }^{\alpha _{1}}\left( t^{2};z_{1}\right) \mathcal {K}_{r_{2},\nu }^{\alpha _{2}}\left( 1;z_{2}\right) \\&\quad =\left[ \left( \frac{r_{1}}{r_{1}+1}\right) ^2+\frac{\nu (2r_{1}+\nu )}{r_{1}^2} -\frac{(r_{1}+\nu +2(1-\alpha _{1}))}{r_{1}^2}\right] z_{1}^2\\&\quad +\left[ \frac{(r_{1}+\nu +2(1-\alpha _{1}))}{r_{1}^2}+\left( \frac{r_{1}}{r_{1}+1}\right) \left( 1+\frac{\nu }{r_{1}}\right) \right] z_{1}+\frac{1}{3(r_{1}+1)^2}\\&\quad =\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(e_{31};z_1,z_2) \end{aligned}$$

and by following the same line, we obtain

$$\begin{aligned}&\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( e_{13};z_1,z_2\right) =\mathcal {K}_{r_{1},\nu }^{\alpha _{1}}\left( 1;z_{1}\right) \mathcal {K}_{r_{2},\nu }^{\alpha _{2}}\left( s^{2};z_{2}\right) \\&\quad =\left[ \left( \frac{r_{2}}{r_{2}+1}\right) ^2+\frac{\nu (2r_{2}+\nu )}{r_{2}^2} -\frac{(r_{2}+\nu +2(1-\alpha _{2}))}{r_{2}^2}\right] z_{2}^2\\&\quad +\left[ \frac{(r_{2}+\nu +2(1-\alpha _{2}))}{r_{2}^2}+\left( \frac{r_{2}}{r_{2}+1}\right) \left( 1+\frac{\nu }{r_{2}}\right) \right] z_{2}+\frac{1}{3(r_{2}+1)^2}\\&\quad =\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(e_{13};z_1,z_2). \end{aligned}$$

$\square$

Corollary 4.1

Suppose $\Psi _{uv}(t,s)=(t-z_1)^{u-1}(s-z_2)^{v-1}$ for $(u,v)\in \mathbb N\times \mathbb N$ with $u+v\le 4$. In view of Lemma 4.2, the following identities hold:

$$\begin{aligned}&\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(\Psi _{21}(t,s);z_1,z_2)\\&\quad =\left[ \left( \frac{r_1}{r_1+1}\right) \left( 1+\frac{\nu }{r_1}\right) -1\right] z_1 +\frac{1}{2(r_1+1)}\\&\quad =\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(\Psi _{21}(t,s);z_1,z_2),\\&\quad \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(\Psi _{12}(t,s);z_1,z_2) =\left[ \left( \frac{r_2}{r_2+1}\right) \left( 1+\frac{\nu }{r_2}\right) -1\right] z_2 +\frac{1}{2(r_2+1)}\\&\quad =\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(\Psi _{1,2}(t,s);z_1,z_2),\\&\quad \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(\Psi _{31}(t,s);z_1,z_2) = \Bigg [\left( \frac{r_1}{r_1+1}\right) ^2+ \frac{\nu (2r_1+\nu )}{r_1^2}+1\\&\qquad -2\left( \frac{r_1}{r_1+1}\right) \left( 1+\frac{\nu }{r_1}\right) -\frac{(r_1+\nu +2(1-\alpha _1))}{r_1^2} \Bigg ]z_1^2 \\&\qquad +\Bigg [\frac{(r_1+\nu +2(1-\alpha _1))}{r_1^2}+\bigg (\frac{r_1}{r_1+1}\bigg ) \left( 1+\frac{\nu }{r_1}\right) \\&\qquad -\frac{1}{r_1+1}\Bigg ]z_1 +\frac{1}{3(r_1+1)^2}\\&\quad =\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(\Psi _{31}(t,s);z_1,z_2),\\&\quad \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(\Psi _{13}(t,s);z_1,z_2) = \Bigg [\bigg ( \frac{r_2}{r_2+1}\bigg )^2+\frac{\nu (2r_2+\nu )}{r_2^2}+1\\&\qquad -2\left( \frac{r_2}{r_2+1}\right) \left( 1+\frac{\nu }{r_2}\right) -\frac{(r_2+\nu +2(1-\alpha _2))}{r_2^2} \Bigg ]z_2^2 \\&\qquad +\Bigg [\frac{(r_2+\nu +2(1-\alpha _2))}{r_2^2} +\bigg (\frac{r_2}{r_2+1}\bigg )\left( 1+\frac{\nu }{r_2}\right) \\&\qquad -\frac{1}{r_2+1}\Bigg ]z_2+\frac{1}{3(r_2+1)^2}\\&\quad =\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(\Psi _{13}(t,s);z_1,z_2). \end{aligned}$$

5 Approximation Properties of Bivariate $\alpha$-Schurer–Kantorovich Operators

For $g\in C(\mathcal {I}^2)$ and for any $\hat{\delta _1},\hat{\delta _{2}}>0$, the bivariate form of modulus of continuity is defined by

$$\begin{aligned} \hat{\omega }(g;\hat{\delta _1},\hat{\delta _{2}})=\sup \left\{ \left| g(t,s)-g(z_1,z_2)\right| :\left| t-z_1\right| \le \hat{\delta _1},\left| s-z_2\right| \le \hat{\delta _2};(t,s),(z_1,z_2)\in \mathcal {I}\times \mathcal {I}\right\} . \end{aligned}$$

Note that $\hat{\omega }(g;\hat{\delta _1},\hat{\delta _2})$ satisfies the following conditions:

• (i) $\hat{\omega }(g;\hat{\delta _1},\hat{\delta _2})\rightarrow 0$ as $\hat{\delta _1},\hat{\delta _2} \rightarrow 0$,

• (ii) $|f(t,s)-f(z_1,z_2)|\le \hat{\omega }(g;\hat{\delta _1},\hat{\delta _2})\left( \frac{|t-z_1|}{\hat{\delta _1}}+1 \right) \left( \frac{|s-z_2|}{\hat{\delta _2}}+1\right) .$

With respect to $z_{1}$ and $z_{2}$, the partial modulus of continuity is defined as

$$\begin{aligned}&\hat{\omega _1}\left( g;\hat{\delta _1}\right) = \sup \left\{ \left| g(u_1,z_2)-g(u_2,z_2)\right| :|u_1-u_2|\le \hat{\delta _1},z_{2}\in \mathcal {I}\right\} ,\\&\quad \hat{\omega _2}\left( g;\hat{\delta _2}\right) = \sup \left\{ \left| g(z_1,s_1)-g(z_1,s_2)\right| :|s_1-s_2|\le \hat{\delta _2},z_{1}\in \mathcal {I}\right\} . \end{aligned}$$

For more details, we refer to [30].

Theorem 5.1

Let $0\le \alpha _1,\alpha _2\le 1$, $r_1,r_2\in \mathbb {N}$ and $(z_1,z_2)\in [0,1]\times [0,1]$. For any $g\in C\left( \mathcal {I}^2\right)$, one has

$$\begin{aligned} \lim _{r_1,r_2 \rightarrow \infty }\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(g)=g\end{aligned}$$

uniformly on $[0,1]\times [0,1]$.

Proof

Taking Lemma 4.2 and letting limit $r_1,r_2\rightarrow \infty$ into our account, we see that

$$\begin{aligned}&\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(e_{11};z_1,z_2)\rightarrow 1,\;\;\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(e_{21};z_1,z_2)\rightarrow z_{1}\\&\quad \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(e_{12};z_1,z_2)\rightarrow z_{2},\;\;\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(e_{31}+e_{13};z_1,z_2)\rightarrow (z_{1}+z_{2}) \end{aligned}$$

uniformly on $[0,1]\times [0,1]$. It follows by Volkov’s theorem [31] that

$$\begin{aligned} \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(g)\rightarrow g\;(r_1,r_2\rightarrow \infty )\end{aligned}$$

uniformly on $[0,1]\times [0,1]$.

Theorem 5.2

For any $g \in C(\mathcal {I}^2)$, we have

$$\begin{aligned} \left| \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(g)-g(z_1,z_2)\right| \le 2\hat{\omega _1}(g;\hat{\delta _1})+2\hat{\omega _2}(g;\hat{\delta _2}), \end{aligned}$$

where

$$\begin{aligned}\hat{\delta _1}=\delta _{r_1,\nu ,p_{1}}^{(\alpha _1)}=\sqrt{\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(\Psi _{21}(t,s);z_1,z_2)}\end{aligned}$$

and

$$\begin{aligned}\hat{\delta _2}=\delta _{r_2,\nu ,p_{2}}^{(\alpha _2)}=\sqrt{\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(\Psi _{12}(t,s);z_1,z_2)}.\end{aligned}$$

Proof

The Cauchy–Schwarz inequality gives

$$\begin{aligned}&\left| \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(g;z_1,z_2)-g(z_1,z_2)\right| \\&\quad \le \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( |g(t,s)-g(z_1,z_2)|;z_1,z_2\right) \\&\quad \le \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( |g(t,s)-g(z_1,s)|;z_1,z_2 \right) \\&\qquad +\mathcal {J}_{r_1,r_2,\nu _1,\nu _2}^{\alpha _1,\alpha _2}\left( |g(z_1,s)-g(z_1,z_2)|;z_1,z_2 \right) \\&\quad \le \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( \hat{\omega _1}\left( g;|t-z_1|\right) ;z_1,z_2 \right) \\&\qquad +\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( \hat{\omega _2}\left( g;|s-z_2|\right) ;z_1,z_2\right) \\&\quad \le \hat{\omega _1}(g;\hat{\delta _1})\left( 1+\hat{\delta _1}^{-1}\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( |t-z_1|;z_1,z_2\right) \right) \\&\quad +\hat{\omega _2}(g;\hat{\delta _2})\left( 1+\hat{\delta _2}^{-1}\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( |s-z_2|;z_1,z_2\right) \right) \\&\quad \le \hat{\omega _1}(g;\hat{\delta _1})\left( 1+\frac{1}{\hat{\delta _1}} \sqrt{\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(\Psi _{21}(t,s);z_1,z_2)}\right) \\&\qquad +\hat{\omega _2}(g;\hat{\delta _2})\left( 1+\frac{1}{\hat{\delta _2}} \sqrt{\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(\Psi _{12}(t,s);z_1,z_2)}\right) . \end{aligned}$$

By choosing $\hat{\delta _1}=\delta _{r_1,\nu ,p_{1}}^{(\alpha _1)}=\sqrt{\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(\Psi _{21}(t,s);z_1,z_2)}$ and $\hat{\delta _2}=\delta _{r_2,\nu ,p_{2}}^{(\alpha _2)}=\sqrt{\mathcal {V}_{r_2,\nu ,p_{2}}^{\alpha _2}(\Psi _{12}(t,s);z_1,z_2)}$, we obtain the assertion of Theorem 5.2. $\square$

We now discuss the degree of convergence of (4.1) in terms of Lipschitz class. For $\theta _1,\theta _2 \in (0,1]$, the Lipschitz class for bivariate function defined by

$$\begin{aligned} Lip_{L}(\theta _1,\theta _2)= & {} \left\{ g: \left| g(t,s)-g(z_1,z_2)\right| \le L |t-z_1|^{\theta _1}|s-z_2|^{\theta _2}\right\} , \end{aligned}$$

where $(t,s),(z_1,z_2)\in \mathcal {I}^2$ and a constant $L>0$.

Theorem 5.3

Suppose that $g\in Lip_{L}(\theta _1,\theta _2)$ and $\theta _1,\theta _2 \in (0,1]$. Then, for every $(z_1,z_2)\in \mathcal {I}^2$, we have

$$\begin{aligned} \left| \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(g;z_1,z_2)-g(z_1,z_2)\right| \le L \left( \delta _{r_1,\nu ,p_{1}}^{(\alpha _1)}\right) ^{\frac{\theta _1}{2}} \left( \delta _{r_2,\nu ,p_{2}}^{(\alpha _2)}\right) ^{\frac{\theta _2}{2}}, \end{aligned}$$

where $\delta _{r_1,\nu ,p_{1}}^{(\alpha _1)}$ and $\delta _{r_2,\nu ,p_{2}}^{(\alpha _2)}$ are given in Theorem 5.2.

Proof

Since $g\in Lip_{L}(\theta _1,\theta _2)$, we obtain from the monotonicity and linearity of (4.1) that

$$\begin{aligned}&\left| \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(g;z_1,z_2)-g(z_1,z_2)\right| \le \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( \left| g\left( t,s\right) -g\left( z_1,z_2\right) \right| ;z_1,z_2 \right) \\&\quad \le L \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( \left| t-z_1\right| ^{\theta _1}\left| s-z_2\right| ^{\theta _2};z_1,z_2 \right) \\&\quad = L \mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)} \left( \left| t-z_1\right| ^{\theta _1};z_1,z_2\right) \mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)} \left( \mid s-z_2\mid ^{\theta _2};z_1,z_2 \right) . \end{aligned}$$

Applying Hölder inequality on the right-hand side of above inequality, we obtain

$$\begin{aligned}&\mid \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(g;z_1,z_2)-g(z_1,z_2)\mid \\&\quad \le L \mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)} \left( ( t-z_1)^2;z_1,z_2\right) ^{\frac{\theta _1}{2}}\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)} \left( ( t-z_1)^2;z_1,z_2\right) ^{\frac{\theta _2}{2}}\\&\quad = L \left( \delta _{r_1,\nu ,p_{1}}^{(\alpha _1)}\right) ^{\frac{\theta _1}{2}} \left( \delta _{r_2,\nu ,p_{2}}^{(\alpha _2)}\right) ^{\frac{\theta _2}{2}}, \end{aligned}$$

which completes the desired results. $\square$

For $g\in C(\mathcal {I}^2 )$, $C^{1}(\mathcal {I}^2)$ and $C^{2}(\mathcal {I}^2)$ are used to denote the spaces of continuous functions such that $\frac{\partial g}{\partial z_{1}},\frac{\partial g}{\partial z_{2}}\in C(\mathcal {I}^2)$ and $\frac{\partial ^ig}{\partial z_{1}^i},\frac{\partial ^ig}{\partial z_{2}^i}\in C(\mathcal {I}^2)$ $(i=1,2)$, respectively.

Theorem 5.4

Let $g\in C^{1}(\mathcal {I}^2 )$ and $(z_1,z_2)\in [0,1]\times [0,1]$. Then

$$\begin{aligned} \mid \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(g;z_1,z_2)-g(z_1,z_2)\mid \le \left\| \frac{\partial g}{\partial z_1}\right\| _{C(\mathcal {I}^2)}\sqrt{\delta _{r_1,\nu ,p_{1}}^{(\alpha _1)}} +\left\| \frac{\partial g}{\partial z_2}\right\| _{C(\mathcal {I}^2)}\sqrt{\delta _{r_2,\nu ,p_{2}}^{(\alpha _2)}}. \end{aligned}$$

Proof

Let $(z_1,z_2)\in [0,1]\times [0,1]$ be fixed. For any $g\in C^{1}(\mathcal {I}^2)$, the Taylor’s theorem gives

$$\begin{aligned} g(t,s)-g(z_1,z_2)= & {} \int _{z_1}^{t} \frac{\partial g(\xi ,s)}{\partial \xi } \mathrm {d}\xi +\int _{z_2}^{s} \frac{\partial g(z_1,\zeta )}{\partial \zeta }d\zeta . \end{aligned}$$

Therefore

$$\begin{aligned}&\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( g(t,s);z_1,z_2\right) -g(z_1,z_2)= \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2} \left( \int _{z_1}^{t}\frac{\partial g(\xi ,s)}{\partial \xi }d\xi ;z_1,z_2\right) \nonumber \\&\quad +\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( \int _{z_2}^{s} \frac{\partial g(z_1,\zeta )}{\partial \zeta }d\zeta ;z_1,z_2\right) . \end{aligned}$$

(5.1)

We can see that

$$\begin{aligned} \left| \int _{z_1}^{t}\frac{\partial g(\xi ,s)}{\partial \xi }d\xi \right| \le \int _{z_1}^{t}\left| \frac{\partial g(\xi ,s)}{\partial \xi }d\xi \right| \le \left\| \frac{\partial g}{\partial z_1} \right\| _{C(\mathcal {I}^2)}|t-z_1| \end{aligned}$$

(5.2)

and

$$\begin{aligned} \left| \int _{z_2}^{s}\frac{\partial g(z_1,\zeta )}{\partial \zeta }d\zeta \right| \le \int _{z_2}^{s}\left| \frac{\partial g(z_1,\zeta )}{\partial \zeta }d\zeta \right| \le \left\| \frac{\partial g}{\partial z_2}\right\| _{C(\mathcal {I}^2)}|s-z_2|. \end{aligned}$$

(5.3)

Employing inequalities (5.2) and (5.3) in the equality (5.1), we obtain

$$\begin{aligned}&\left| \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( g(z_1,z_2);z_1,z_2\right) -g(z_1,z_2)\right| \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\&\quad \le \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( \left| \int _{z_1}^{t}\frac{\partial g(\xi ,s)}{\partial \xi }d\xi \right| ;z_1,z_2\right) +\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( \left| \int _{z_2}^{s}\frac{\partial g(z_1,\zeta )}{\partial \zeta }d\zeta \right| ;z_1,z_2\right) \\&\quad \le \left\| \frac{\partial g}{\partial z_1}\right\| _{C(\mathcal {I}^2)}\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( |t-z_1|;z_1,z_2\right) +\left\| \frac{\partial g}{\partial z_2}\right\| _{C(\mathcal {I}^2)}\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( |s-z_2|;z_1,z_2\right) \\&\quad \le \left\| \frac{\partial g}{\partial z_1}\right\| _{C(\mathcal {I}^2)} \left( \mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(\Psi _{31}(t,s);z_1,z_2)\right) ^{\frac{1}{2}} \left( \mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(e_{11};z_1,z_2) \right) ^{\frac{1}{2}}\\&\qquad +\left\| \frac{\partial g}{\partial z_2}\right\| _{C(\mathcal {I}^2)}\left( \mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(\Psi _{13}(t,s);z_1,z_2)\right) ^{\frac{1}{2}} \left( \mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(e_{11};z_1,z_2) \right) ^{\frac{1}{2}} \\&\quad = \left\| \frac{\partial g}{\partial z_1}\right\| _{C(\mathcal {I}^2)}\sqrt{\delta _{r_1,\nu ,p_{1}}^{(\alpha _1)}} +\left\| \frac{\partial g}{\partial z_2}\right\| _{C(\mathcal {I}^2)}\sqrt{\delta _{r_2,\nu ,p_{2}}^{(\alpha _2)}}. \end{aligned}$$

$\square$

Theorem 5.5

For any $g\in C^{2}(\mathcal {I}^2)$, one has

$$\begin{aligned}&\mathcal {R}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( g;t,s\right) -g(z_1,z_2) \le \Big \{\delta _{r_1,\nu ,p_{1}}^{(\alpha _1)}+\delta _{r_2,\nu ,p_{2}}^{(\alpha _2)}+\left( \mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(\mu _{2,1};z_1,z_2)-z_1\right) ^2\\&\quad +\left( \mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(e_{12};z_1,z_2)-z_2\right) ^2\Big \}\left\| g\right\| _{C(\mathcal {I}^2)}. \end{aligned}$$

In the case, $\mathcal {R}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( g;t,s\right)$ is defined involving the bivariate $\alpha$-Schurer–Kantorovich operators by

$$\begin{aligned} \mathcal {R}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(g;z_1,z_2)=\mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(g;z_1,z_2)+g(z_1,z_2) -g\left( \mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(e_{21};z_1,z_2),\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(e_{12};z_1,z_2)\right) , \end{aligned}$$

where $\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(e_{21};z_1,z_2)$ and $\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(e_{12};z_1,z_2)$ are given in Lemma 4.2.

Proof

With the help of Lemma 4.2 and Corollary 4.1, we get

$$\begin{aligned}&\mathcal {R}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(e_{11}(t,s);z_1,z_2)=1, \mathcal {R}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(e_{21}(t,s);z_1,z_2)=z_1, \mathcal {R}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(e_{12}(t,s);z_1,z_2)=z_2,\\&\quad \mathcal {R}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(\Psi _{21}(t,s);z_1,z_2)=0, \mathcal {R}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}(\Psi _{12}(t,s);z_1,z_2)=0. \end{aligned}$$

For any $g\in C^{2}(\mathcal {I}^2)$ and from the Taylor series expansion, we observe that

$$\begin{aligned} g(t,s)-g(z_1,z_2)= & {} \frac{\partial {g(z_1,z_2)}}{\partial z_1}(t-z_1)+\int _{z_1}^t (t-\vartheta )\frac{\partial ^2 {g(\vartheta ,z_2)}}{\partial \vartheta ^2}d\vartheta \\&+\frac{\partial {g(z_1,z_2)}}{\partial z_2}(s-z_2)+\int _{z_2}^s (s-\varsigma )\frac{\partial ^2 {g(z_1,\varsigma )}}{\partial \varsigma ^2}d\varsigma . \end{aligned}$$

It follows by operating $\mathcal {R}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}$ in the last equality that

$$\begin{aligned}&\mathcal {R}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( g\left( t,s\right) ;z_1,z_2\right) -\mathcal {R}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( g(z_1,z_2 );z_1,z_2\right) \nonumber \\&\quad = \mathcal {R}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( \int _{z_1}^t (t-\vartheta )\frac{\partial ^2 {g(\vartheta ,z_2)}}{\partial \vartheta ^2}d\vartheta ;z_1,z_2\right) \nonumber \\&\qquad +\mathcal {R}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2} \left( \int _{z_2}^s (s-\varsigma )\frac{\partial ^2 {g(z_1,\varsigma )}}{\partial \varsigma ^2}d\varsigma ;z_1,z_2\right) \nonumber \\&\quad = \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2} \left( \int _{z_1}^t (t-\vartheta )\frac{\partial ^2 {g(\vartheta ,z_2)}}{\partial \vartheta ^2}d\vartheta ;z_1,z_2\right) \nonumber \\&\qquad + \mathcal {J}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2} \left( \int _{z_2}^s (s-\varsigma )\frac{\partial ^2 {g(z_1,\varsigma )}}{\partial \varsigma ^2}d\varsigma ;z_1,z_2\right) \nonumber \\&\qquad -\int _{z_1}^{\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(e_{21};z_1,z_2)} \left( \mathcal {U}_{r_1,\nu _1}^{\alpha _1}(e_{21};z_1,z_2)-\vartheta \right) \frac{\partial ^2 {g(\vartheta ,z_2)}}{\partial \vartheta ^2}d\vartheta \nonumber \\&\quad -\int _{z_2}^{\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)} (e_{12};z_1,z_2)}\left( \mathcal {V}_{r_2,\nu _2}^{\alpha _2}(e_{12};z_1,z_2) -\varsigma \right) \frac{\partial ^2 {g(z_1,\varsigma )}}{\partial \varsigma ^2}d\varsigma . \end{aligned}$$

(5.4)

Clearly,

$$\begin{aligned} \left| \int _{z_1}^t (t-\vartheta )\frac{\partial ^2 {g(\vartheta ,z_2)}}{\partial \vartheta ^2}d\vartheta \right| \le \int _{z_1}^t \left| (t-\vartheta )\frac{\partial ^2 {g(\vartheta ,z_2)}}{\partial \vartheta ^2}d\vartheta \right| \le \left\| g\right\| _{C(\mathcal {I}^2)}(t-z_1)^2 \end{aligned}$$

and

$$\begin{aligned} \left| \int _{z_2}^s (s-\varsigma )\frac{\partial ^2 {g(z_1,\varsigma )}}{\partial \varsigma ^2}d\varsigma \right| \le \int _{z_2}^s \left| (s-\varsigma )\frac{\partial ^2 {g(z_1,\varsigma )}}{\partial \varsigma ^2}d\varsigma \right| \le \left\| g\right\| _{C(\mathcal {I}^2)}(s-z_2)^2. \end{aligned}$$

Consequently,

$$\begin{aligned}&\left| \int _{z_1}^{\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(e_{21};z_1,z_2)} \left( \mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(e_{21};z_1,z_2)-\vartheta \right) \frac{\partial ^2 {g(\vartheta ,z_2)}}{\partial \vartheta ^2}d\vartheta \right| \\&\quad \le \left\| g \right\| _{C(\mathcal {I}^2)}\left( \mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(\mu _{2,1};z_1,z_2)-z_1\right) ^2 \end{aligned}$$

and

$$\begin{aligned}&\left| \int _{z_2}^{\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(e_{12};z_1,z_2)}\left( \mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(e_{12};z_1,z_2)-\varsigma \right) \frac{\partial ^2 {g(z_1,\varsigma )}}{\partial \varsigma ^2}d\varsigma \right| \\&\quad \le \left\| g \right\| _{C(\mathcal {I}^2)}\left( \mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(\mu _{1,2};z_1,z_2)-z_2\right) ^2. \end{aligned}$$

We therefore have from Eq. (5.4) that

$$\begin{aligned}&\left| \mathcal {R}_{r_1,r_2,\nu }^{\alpha _1,\alpha _2}\left( g;t,s\right) -g(z_1,z_2)\right| \le \Big \{\mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(\Psi _{31}(t,s);z_1,z_2)\\&\quad +\mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(\Psi _{13}(t,s);z_1,z_2)+\left( \mathcal {U}_{r_1,\nu ,p_{1}}^{(\alpha _1)}(e_{21};z_1,z_2)-z_1\right) ^2\\&\quad +\left( \mathcal {V}_{r_2,\nu ,p_{2}}^{(\alpha _2)}(e_{12};z_1,z_2)-z_2\right) ^2\Big \}\left\| g\right\| _{C(\mathcal {I}^2)}, \end{aligned}$$

which completes the proof. $\square$