Approximation of functions by Stancu variant of Bernstein–Kantorovich operators based on shape parameter ${\varvec{\alpha }}$

Abstract

We construct the Stancu variant of Bernstein–Kantorovich operators based on shape parameter $\alpha$. We investigate the rate of convergence of these operators by means of suitable modulus of continuity to any continuous functions f(x) on $x\in [0,1]$ and Voronovskaja-type approximation theorem. Moreover, we study other approximation properties of our new operators such as weighted approximation as well as pointwise convergence. Finally, some illustrative graphics are provided here by our new Stancu-type Bernstein–Kantorovich operators in order to demonstrate the significance of our operators.

1 Introduction

Bernstein polynomials are a powerful tool for replacing a lot of arduous calculations carried out for continuous functions with friendly calculations on approximating polynomials. For this reason, many researchers are interested to work on Bernstein operators with a view of studying end-points interpolation, convergence, shape preserving properties and many others.

In the recent past, Chen et al. [1] presented a new family of Bernstein operators for the continuous function f(x) on [0, 1]which includes the shape parameter $\alpha$ and called it $\alpha$-Bernstein operators. Let $\alpha$ be a fixed real number and let f(x) be a continuous function on [0, 1]. Then, for each positive integer n, the $\alpha$-Bernstein operators are given by

$$\begin{aligned} T_{n,\alpha }\left( f;x\right) =\sum \limits _{i=0}^{n}f\left( i/n\right) p_{n,i}^{\left( \alpha \right) }\left( x\right) \quad \left( x\in [0,1]\right) , \end{aligned}$$

(1.1)

where $\alpha$-Bernstein polynomials $p_{n,i}^{(\alpha )}(x)$ of order n are given by $p_{1,0}^{\left( \alpha \right) }\left( x\right) =1-x$, $p_{1,1}^{(\alpha )}(x)=x$,

$$\begin{aligned} p_{n,i}^{(\alpha )}(x)= & {} \Bigg [\left( 1-\alpha \right) x\left( {\begin{array}{c}n-2\\ i\end{array}}\right) +\left( 1-\alpha \right) \left( 1-x\right) \left( {\begin{array}{c}n-2\\ i-2\end{array}}\right) \\&+\alpha x\left( 1-x\right) \left( {\begin{array}{c}n\\ i\end{array}}\right) \Bigg ] x^{i-1}\left( 1-x\right) ^{n-i-1}\quad (n\ge 2). \end{aligned}$$

and the binomial coefficients in the last equality are given by the formula

$$\begin{aligned} \left( {\begin{array}{c}a\\ b\end{array}}\right) =\left\{ \begin{array}{ll} \frac{a!}{b!(a-b)!}&{}~~~(0\le b\le a), \\ {\bar{0}}&{}~~~(\mathrm{otherwise}). \end{array}\right. \end{aligned}$$

The choice of $\alpha =1$ in (1.1) gives the classical Bernstein operators [2] which shows that $\alpha$-Bernstein operators are stronger than classical one, in this case $p_{n,i}^{(\alpha )}(x)$ reduces to $p_{n,i}^{(1)}(x)$ which is a classical Bernstein basis function. Chen et al. discussed several approximation results of (1.1), namely, Voronovskaya type pointwise convergence, uniform convergence, shape preserving properties, rate of convergence and many others.

Motivated by the work of [1], Mohiuddine et al. [3] considered the mean values of f in the intervals $[ \frac{i}{n+1},\frac{i+1}{n+1}]$ instead of sample values and constructed the Kantorovich modification of $\alpha$-Bernstein operators which is given by

$$\begin{aligned} M_{n,\alpha }\left( f;x\right) =(n+1)\sum _{i=0}^{n}p_{n,i}^{\left( \alpha \right) }\left( x\right) \int _{\frac{i}{n+1}}^{\frac{i+1}{n+1}}f\left( s\right) ds. \end{aligned}$$

(1.2)

In particular, they studied the rate of convergence in local and global sense for the operators and also constructed the bivariate version of (1.2). For some recent work on generalized Kantorovich operators, we refer to [4,5,6,7,8,9].

Acar and Kajla [10] introduced the Durrmeyer type modification of the $\alpha$-Bernstein operators in (1.1). Later, Kajla and Miclăuş [11] defined and studied the bivariate version of $\alpha$-Bernstein–Durremeyer operators and, by taking these operators into their account, in the same paper, they also constructed generalized Boolean sum operators. Inspired from the operators introduced by Chen et al. [1], recently, Aral and Erbay [12] presented the generalization of classical Baskakov operators based on parameter $\alpha$ and then Nasiruzzaman et al. [13] constructed these operators on weighted spaces and studied their various approximation properties.

For each $n\in {\mathbb {N}}$ and $0\le \theta \le \beta$, Stancu [14] introduced the operator $S_{n}^{\theta ,\beta }:C[0,1]\rightarrow C[0,1]$ given by

$$\begin{aligned} S_{n}^{\theta ,\beta }(f;x)=\sum _{i=0}^{n}p_{n,i}(x)f \left( \frac{i+\theta }{n+\beta }\right) , \end{aligned}$$

where C[0, 1] denote the space of all real-valued continuous functions on [0, 1] and

$$\begin{aligned} p_{n,i}=p_{n,i}^{(1)}=\left( {\begin{array}{c}n\\ i\end{array}}\right) x^{i}(1-x)^{n-i} \end{aligned}$$

are the Bernstein basis functions. If we take $\theta =\beta =0$ in the last operators, then

$$\begin{aligned} S_{n}^{0,0}(f;x)=T_{n,1}(f;x). \end{aligned}$$

Several authors studied approximation results for these types of operators, we refer the interested reader to [15,16,17,18,19,20,21,22,23,24,25]. For recent work on statistical approximation of linear positive operators, we refer to [26,27,28,29,30].

We aim here to construct Stancu variant of Kantorovich type operators defined in (1.2). For this, consider two non-negative parameters $\theta$ and $\beta$ such that $0\le \theta \le \beta$ and define the following operators

$$\begin{aligned} S_{n,\alpha }^{\theta ,\beta }\left( f;x\right) =(n+\beta +1)\sum \limits _{i=0}^{n}p_{n,i}^{\left( \alpha \right) }\left( x\right) \int _{\frac{i+\theta }{n+\beta +1}}^{\frac{i+\theta +1}{n+\beta +1}}f\left( s\right) ds \end{aligned}$$

(1.3)

for $x\in [0,1]$, where $p_{n,i}^{(\alpha )}$ is same as defined earlier. We call (1.3) by Stancu-type Bernstein–Kantorovich operators based on shape parameter $\alpha$ and these operators are linear positive for any $\alpha \in [0,1]$.

2 Auxiliary results

Here, we calculate the moments of our new operators (1.3). We shall assume throughout this paper that $alpha\in [0,1]$.

Lemma 1

[1] Let $e_{i}\left( x\right) =x^{i},$ where $i=0,1,2,3,4.$ Then, moments of $T_{n,\alpha }$ are given by

$$\begin{aligned} T_{n,\alpha }\left( e_{0};x\right)= & {} 1, \\ T_{n,\alpha }\left( e_{1};x\right)= & {} x, \\ T_{n,\alpha }\left( e_{2};x\right)= & {} x^{2}+\frac{n+2\left( 1-\alpha \right) }{n^{2}}x\left( 1-x\right) , \\ T_{n,\alpha }\left( e_{3};x\right)= & {} x^{3}+\dfrac{3(n+2(1-\alpha ))}{n^{2}} x^{2}(1-x)+\dfrac{(n+6(1-\alpha ))}{n^{3}}x(1-x)(1-2x), \\ T_{n,\alpha }\left( e_{4};x\right)= & {} x^{4}+\dfrac{6(n+2(1-\alpha ))}{n^{2}} x^{3}(1-x)+\dfrac{4(n+6(1-\alpha ))}{n^{3}}x^{2}(1-x)(1-2x) \\&+\dfrac{\left( \left( 3n(n-2)+12(n-6)(1-\alpha )\right) x(1-x)+(n+14(1-\alpha ))\right) }{n^{4}}x(1-x). \end{aligned}$$

Lemma 2

For the operators $S_{n,\alpha }^{\theta ,\beta }\left( e_{i};x\right)$, $i=0,1,2$, we have

$$\begin{aligned} S_{n,\alpha }^{\theta ,\beta }\left( e_{0};x\right)= & {} 1, \\ S_{n,\alpha }^{\theta ,\beta }\left( e_{1};x\right)= & {} \frac{n}{n+\beta +1}x+\frac{2\theta +1}{2(n+\beta +1)}, \\ S_{n,\alpha }^{\theta ,\beta }\left( e_{2};x\right)= & {} \frac{n^2}{(n+\beta +1)^2}x^2+\frac{n+2(1-\alpha )}{(n+\beta +1)^2}x(1-x)+\frac{3n(2\theta +1)x+3\theta ^2+3\theta +1}{3(n+\beta +1)^2}. \end{aligned}$$

Proof

In view of the operators (1.3) and Lemma 1, we obtain

$$\begin{aligned} S_{n,\alpha }^{\theta ,\beta }\left( e_{0};x\right)= & {} (n+\beta +1)\sum \limits _{i=0}^{n}p_{n,i}^{\left( \alpha \right) }\left( x\right) \int _{\frac{i+\theta }{n+\beta +1}}^{\frac{i+\theta +1}{n+\beta +1}}ds \\= & {} T_{n,\alpha }\left( e_{0};x\right) =1.\\ S_{n,\alpha }^{\theta ,\beta }\left( e_{1};x\right)= & {} (n+\beta +1)\sum \limits _{i=0}^{n}p_{n,i}^{\left( \alpha \right) }\left( x\right) \int _{\frac{i+\theta }{n+\beta +1}}^{\frac{i+\theta +1}{n+\beta +1}}sds \\= & {} (n+\beta +1)\sum \limits _{i=0}^{n}p_{n,i}^{\left( \alpha \right) }\left( x\right) \frac{2(i+\theta )+1}{2(n+\beta +1)^2} \\= & {} \frac{n}{n+\beta +1} T_{n,\alpha }\left( e_{1};x\right) +\frac{2\theta +1}{2(n+\beta +1)} T_{n,\alpha }\left( e_{0};x\right) \\= & {} \frac{n}{n+\beta +1}x+\frac{2\theta +1}{2(n+\beta +1)} .\\ S_{n,\alpha }^{\theta ,\beta }\left( e_{2};x\right)= & {} (n+\beta +1)\sum \limits _{i=0}^{n}p_{n,i}^{\left( \alpha \right) }\left( x\right) \int _{\frac{i+\theta }{n+\beta +1}}^{\frac{i+\theta +1}{n+\beta +1}}s^2ds \\= & {} (n+\beta +1)\sum \limits _{i=0}^{n}p_{n,i}^{\left( \alpha \right) }\left( x\right) \frac{3i^2+3(2\theta +1)i+3\theta +1}{3(n+\beta +1)^3} \\= & {} \frac{n^2}{(n+\beta +1)^2} T_{n,\alpha }\left( e_{2};x\right) +\frac{(2\theta +1)n}{(n+\beta +1)^2} T_{n,\alpha }\left( e_{1};x\right) \\&+\frac{3\theta +1}{3(n+\beta +1)^2} T_{n,\alpha }\left( e_{0};x\right) \\= & {} \frac{n^2}{(n+\beta +1)^2}x^2+\frac{n+2(1-\alpha )}{(n+\beta +1)^2}x(1-x)+\frac{3n(2\theta +1)x+3\theta ^2+3\theta +1}{3(n+\beta +1)^2}. \end{aligned}$$

$\square$

The following corollary is an immediate consequence of Lemma 2.

Corollary 1

The central moments of the operators (1.3) are given by

$$\begin{aligned} S_{n,\alpha }^{\theta ,\beta }\left( e_{1}-x;x\right)= & {} \frac{2\theta +1-2(\beta +1)x}{2(n+\beta +1)},\\ S_{n,\alpha }^{\theta ,\beta }\left( \left( e_{1}-x\right) ^{2};x\right)= & {} \frac{1}{n+\beta +1}\left[ \frac{ x(\beta +1)(x(\beta +1)-(2\theta +1)) }{n+\beta +1}\right. \\&+\left. \frac{ (n+2(1-\alpha ))(x-x^2) }{n+\beta +1}+ \frac{3\theta ^2+3\theta +1}{3(n+\beta +1)}\right] \end{aligned}$$

Lemma 3

For given $f\in C\left[ 0,1\right]$ and $n\in {\mathbb {N}}$, we have

$$\begin{aligned} \left\| S_{n,\alpha }^{\theta ,\beta }\left( f\right) \right\| \le \left\| f\right\| , \end{aligned}$$

where $\left\| \cdot \right\|$ denote the uniform norm on [0, 1].

Proof

In view of Lemma 2, we have $\left| S_{n,\alpha }^{\theta ,\beta }\left( f;x\right) \right| \le S_{n,\alpha }^{\theta ,\beta }\left( e_{0};x\right) \left\| f\right\| =\left\| f\right\|$. $\square$

Theorem 1

If f is continuous on [0, 1], for any $\alpha \in [0, 1]$, then $S_{n,\alpha }^{\theta ,\beta }(f)$ converge uniformly to f on [0, 1], that is,

$$\begin{aligned} \lim _{n\rightarrow \infty }\left\| S_{n,\alpha }^{\theta ,\beta }(f)-f \right\| =0. \end{aligned}$$

Proof

We obtain from Lemma 2 that

$$\begin{aligned}&\displaystyle \lim _{n\rightarrow \infty }S_{n,\alpha }^{\theta ,\beta }(e_{0})=e_{0}, \\&\displaystyle \lim _{n\rightarrow \infty }S_{n,\alpha }^{\theta ,\beta }(e_{1};x)=\lim _{n\rightarrow \infty }\left( \frac{n}{n+\beta +1}x+\frac{2\theta +1}{2(n+\beta +1)}\right) =e_{1}(x) \end{aligned}$$

and similarly $\lim _{n\rightarrow \infty }\left\| S_{n,\alpha }^{\theta ,\beta }(e_{2})-e_{2}\right\| =0$. Hence, by the Korovkin theorem, we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\left\| S_{n,\alpha }^{\theta ,\beta }(f)-f \right\| =0. \end{aligned}$$

$\square$

3 Rate of convergence of $S_{n,\alpha }^{\theta ,\beta }$

Let $W^{2}=\left\{ g\in C\left[ 0,1\right] :g^{\prime },g^{\prime \prime }\in C\left[ 0,1\right] \right\} .$ For $f\in C\left[ 0,1\right]$ and $\varepsilon >0,$ the Peetre’s K-functional is defined by

$$\begin{aligned} K_{2}\left( f;\varepsilon \right) =\inf \left\{ \left\| f-g\right\| +\varepsilon \left\| g^{\prime \prime }\right\| :g\in W^{2}\right\} . \end{aligned}$$

Also, for $f\in C\left[ 0,1\right]$ and $\varepsilon >0,$ the second order modulus of smoothness for f is defined as

$$\begin{aligned} \omega _{2}\left( f;\sqrt{\varepsilon }\right) =\sup _{0<h\le \sqrt{\varepsilon } }\sup _{x,x+2h\in \left[ 0,1\right] }\left| f\left( x+2h\right) -2f\left( x+h\right) +f\left( x\right) \right| . \end{aligned}$$

The usual modulus of continuity for f is defined as

$$\begin{aligned} \omega \left( f;\sqrt{\varepsilon }\right) =\sup _{0<h\le \varepsilon }\sup _{x,x+h\in \left[ 0,1\right] }\left| f\left( x+h\right) -f\left( x\right) \right| . \end{aligned}$$

By [31, p.177, Theorem 2.4,], for $f\in C\left[ 0,1\right] ,$ there exists a constant $C>0$ such that

$$\begin{aligned} K_{2}\left( f;\varepsilon \right) \le C\omega \left( f;\sqrt{\varepsilon }\right) . \end{aligned}$$

(3.1)

Theorem 2

Let $f\in C\left[ 0,1\right]$ and $\alpha \in \left[ 0,1\right] .$ Then

$$\begin{aligned} \left| S_{n,\alpha }^{\theta ,\beta }\left( f;x\right) -f\left( x\right) \right| \le 2\omega \left( f;\rho _{n,\theta ,\beta ,\alpha }\left( x\right) \right) \;\;\;\;\;(x\in \left[ 0,1\right] ),\nonumber \\ \end{aligned}$$

where $\rho _{n,\theta ,\beta ,\alpha }^{2}\left( x\right) = S_{n,\alpha }^{\theta ,\beta }( \left( e_{1}-x\right) ^{2};x)$.

Proof

From the monotonicity of the operators $S_{n,\alpha }^{\theta ,\beta }$ and taking Lemma 2 into our account, one writes

$$\begin{aligned} \left| S_{n,\alpha }^{\theta ,\beta }\left( f;x\right) -f\left( x\right) \right| =\left| S_{n,\alpha }^{\theta ,\beta }\left( f\left( t\right) -f\left( x\right) ;x\right) \right| \le S_{n,\alpha }^{\theta ,\beta }\left( \left| f\left( t\right) -f\left( x\right) \right| ;x\right) . \end{aligned}$$

Since

$$\begin{aligned} \left| f\left( t\right) -f\left( x\right) \right| \le \left( 1+\varepsilon ^{-2}\left( t-x\right) ^{2}\right) \omega \left( f;\varepsilon \right) \end{aligned}$$

for any $x,t\in \left[ 0,1\right]$ and any $\varepsilon >0$, we have

$$\begin{aligned} \left| S_{n,\alpha }^{\theta ,\beta }\left( f;x\right) -f\left( x\right) \right| \le \left( 1+\varepsilon ^{-2}\rho _{n,\theta ,\beta ,\alpha }^{2}\left( x\right) \right) \omega \left( f;\varepsilon \right) . \end{aligned}$$

Thus, the conclusion of our result obtained by considering $\varepsilon =\rho _{n,\theta ,\beta ,\alpha }\left( x\right)$. $\square$

Theorem 3

Let $f\in C\left[ 0,1\right] .$ Then

$$\begin{aligned} \left| S_{n,\alpha }^{\theta ,\beta }\left( f;x\right) -f\left( x\right) \right| \le C\omega _{2}\left( f;\varepsilon _{n,\alpha ,\theta ,\beta }\left( x\right) \right) +\omega \left( f;\frac{\left| 2\theta +1-2(\beta +1)x\right| }{2(n+\beta +1)}\right) \quad (x\in \left[ 0,1\right] ),\nonumber \\ \end{aligned}$$

(3.2)

where C is a positive constant and

$$\begin{aligned} \varepsilon _{n,\alpha ,\theta ,\beta }\left( x\right) =\left[ \frac{\left( 2\theta +1-2(\beta +1)\right) ^2x^2}{4(n+\beta +1)^2}+\rho _{n,\theta ,\beta ,\alpha }^{2}\left( x\right) \right] ^{\frac{1}{2}}, \end{aligned}$$

and $\rho _{n,\theta ,\beta ,\alpha }^2\left( x\right)$ is given by Theorem 2.

Proof

For a given function $f\in C\left[ 0,1\right]$, let us consider the following auxiliary operators

$$\begin{aligned} \bar{S}_{n,\alpha }^{\theta ,\beta }\left( f;x\right) =S_{n,\alpha }^{\theta ,\beta }\left( f;x\right) -f\left( \frac{2nx+2\theta +1}{2(n+\beta +1)}\right) +f\left( x\right) \quad (x\in \left[ 0,1\right] ) . \end{aligned}$$

(3.3)

By using Lemma 2, we obtain

$$\begin{aligned} \bar{S}_{n,\alpha }^{\theta ,\beta }\left( 1;x\right) =1 \;\;\text{ and }\;\;\bar{S}_{n,\alpha }^{\theta ,\beta }\left( t;x\right) =x. \end{aligned}$$

With the help of Taylor’s formula and for $g\in W^{2}$, one writes

$$\begin{aligned} \bar{S}_{n,\alpha }^{\theta ,\beta }\left( g;x\right) =g\left( x\right) +\bar{S}_{n,\alpha }^{\theta ,\beta }\left( \int _{x}^{t}\left( t-u\right) g^{\prime \prime }\left( u\right) du;x\right) \;\;\;\;\;(x,t\in \left[ 0,1\right] ) . \end{aligned}$$

It follows from (3.3) and the last equality that

$$\begin{aligned} \bar{S}_{n,\alpha }^{\theta ,\beta }\left( g;x\right) -g\left( x\right) =S_{n,\alpha }^{\theta ,\beta }\left( \int _{x}^{t}\left( t-u\right) g^{\prime \prime }\left( u\right) du;x\right) -\int _{x}^{\frac{2nx+2\theta +1}{2(n+\beta +1)}}\left( \frac{2nx+2\theta +1}{2(n+\beta +1)}-u\right) g^{\prime \prime }\left( u\right) du. \end{aligned}$$

By using the fact

$$\begin{aligned} \left| \int _{x}^{t}\left( t-u\right) g^{\prime \prime }\left( u\right) du\right| \le \frac{\left\| g^{\prime \prime }\right\| }{2}\left( t-x\right) ^{2} \end{aligned}$$

we obtain

$$\begin{aligned} \left| \bar{S}_{n,\alpha }^{\theta ,\beta }\left( g;x\right) -g\left( x\right) \right| \le \frac{\left\| g^{\prime \prime }\right\| }{2} S_{n,\alpha }^{\theta ,\beta }\left( \left( t-x\right) ^{2};x\right) +\frac{\left\| g^{\prime \prime }\right\| }{2}\left( \frac{2nx+2\theta +1}{2(n+\beta +1)}-x\right) ^{2} \end{aligned}$$

which yields

$$\begin{aligned} \left| \bar{S}_{n,\alpha }^{\theta ,\beta }\left( g;x\right) -g\left( x\right) \right| \le \frac{\left\| g^{\prime \prime }\right\| }{2}\left( \frac{\left( 2\theta +1-2(\beta +1)\right) ^2x^2}{4(n+\beta +1)^2}+\rho _{n,\theta ,\beta ,\alpha }^{2}\left( x\right) \right) . \end{aligned}$$

On the other hand, since

$$\begin{aligned} \left| \bar{S}_{n,\alpha }^{\theta ,\beta }\left( f;x\right) \right| \le 3\left\| f\right\| \;\;\;\;\;\;(x\in \left[ 0,1\right] ). \end{aligned}$$

we obtain from Lemma 2 that

$$\begin{aligned} \left| S_{n,\alpha }^{\theta ,\beta }\left( f;x\right) -f\left( x\right) \right|\le & {} \left| \bar{S}_{n,\alpha }^{\theta ,\beta }\left( f-g;x\right) \right| +\left| \bar{S}_{n,\alpha }^{\theta ,\beta }\left( g;x\right) -g\left( x\right) \right| \\&+\left| g\left( x\right) -f\left( x\right) \right| +\left| f\left( \frac{2nx+2\theta +1}{2(n+\beta +1)}\right) -f\left( x\right) \right| \\\le & {} 4\left\| f-g\right\| +\frac{\left\| g^{\prime \prime }\right\| }{2}\left( \rho _{n,\theta ,\beta ,\alpha }^{2}\left( x\right) +\frac{\left( 2\theta +1-2(\beta +1)x\right) ^2 }{4(n+\beta +1)^2}\right) \\&+\,\omega \left( f;\frac{\left| 2\theta +1-2(\beta +1)x\right| }{2(n+\beta +1)}\right) . \end{aligned}$$

Next, by taking $\inf _{g\in W^{2}}$ on the right-hand side of the above inequality, we get

$$\begin{aligned} \left| S_{n,\alpha }^{\theta ,\beta }\left( f;x\right) -f\left( x\right) \right|\le & {} 4K_{2}\left( f;\rho _{n,\theta ,\beta ,\alpha }^{2}\left( x\right) +\frac{\left( 2\theta +1-2(\beta +1)x\right) ^2 }{(n+\beta +1)^2} \right) \\&+\,\omega \left( f;\frac{\left| 2\theta +1-2(\beta +1)x\right| }{2(n+\beta +1)}\right) , \end{aligned}$$

we easily find from (3.1) that

$$\begin{aligned} \left| S_{n,\alpha }^{\theta ,\beta }\left( f;x\right) -f\left( x\right) \right| \le C\omega _{2}\left( f;\varepsilon _{n,\alpha ,\theta ,\beta }\left( x\right) \right) +\omega \left( f;\frac{\left| 2\theta +1-2(\beta +1)x\right| }{2(n+\beta +1)}\right) , \end{aligned}$$

which proves the theorem completely. $\square$

Now we obtain global approximation formula in terms of Ditzian-Totik uniform modulus of smoothness of first and second order defined by

$$\begin{aligned} \omega _{\xi }(f, \varepsilon ):=\sup _{0<|h|\le \varepsilon } ~\sup _{x, x+ h\xi (x) \in [0,1]}\{|f(x+h\xi (x))-f(x)|\} \end{aligned}$$

and

$$\begin{aligned} \omega _2^{\phi }(f, \varepsilon ):=\sup _{0<|h|\le \varepsilon } ~\sup _{x,x\pm h\phi (x)\in [0,1]}\{|f(x+h\phi (x))-2f(x)+f(x-h\phi (x))|\}, \end{aligned}$$

respectively, where $\phi$ is an admissible step-weight function on [a, b], i.e. $\phi (x)=[(x-a)(b-x)]^{1/2}$ if $x \in [a, b]$. Corresponding K-functional is

$$\begin{aligned} K_{2, \phi (x)}(f,\varepsilon )=\inf _{g \in W^2(\phi )}\big \{||f-g||_{C[0,1]}+\varepsilon ||\phi ^2g''||_{C[0,1]}:g\in C^2[0 ,1]\big \}, \end{aligned}$$

where $\varepsilon >0$,

$$\begin{aligned} W^2(\phi )=\{g\in C[0,1]:g' \in AC[0,1],~ \phi ^2g'' \in C[0,1]\} \end{aligned}$$

and

$$\begin{aligned} C^2[0 ,1]=\{g\in C[0,1]:g', g'' \in C[0,1]\} . \end{aligned}$$

Here, $g' \in AC[0,1]$ means that $g'$ is absolutely continuous on [0, 1]. It is known from [32] that there exists an absolute constant $C > 0$, such that

$$\begin{aligned} C^{-1}\omega _2^{\phi }(f, \sqrt{\varepsilon })\le K_{2, \phi (x)}(f,\varepsilon )\le C \omega _2^{\phi }(f, \sqrt{\varepsilon }). \end{aligned}$$

(3.4)

Theorem 4

Let $\phi$ $(\phi \ne 0)$ be an admissible step-weight function of Ditzian–Totik modulus of smoothness such that $\phi ^2$ is concave and $f \in C[0, 1]$. Then, for any $x \in [0,1]$ and $C>0$, we have

$$\begin{aligned} | S_{n,\alpha }^{\theta ,\beta }(f; x)-f(x)|\le C \omega _2^{\phi }\bigg (f, \frac{\varepsilon _{n,\alpha ,\theta ,\beta }(x)}{2\phi (x)}\bigg )+\omega _{\xi }\bigg (f, \frac{2\theta +1-2(\beta +1)x}{2\xi (x)(n+\beta +1)}\bigg ), \end{aligned}$$

where $\varepsilon _{n,\alpha ,\theta ,\beta }$ is given by Theorem 3.

Proof

We again consider the operator $\bar{S}_{n,\alpha }^{\theta ,\beta }(f; x)$ defined in (3.3). Let $u=\rho x+(1-\rho )t$, $\rho \in [0,1]$. Since $\phi ^2$ is a concave function on [0, 1], it follows that $\phi ^2(u)\ge \rho \phi ^2(x)+(1-\rho )\phi ^2(t)$ and hence

$$\begin{aligned} \frac{|t-u|}{\phi ^2(u)}\le \frac{\rho |x-t|}{\rho \phi ^2(x)+(1-\rho )\phi ^2(t)}\le \frac{|t-x|}{\phi ^2(x)}. \end{aligned}$$

(3.5)

So

$$\begin{aligned} |\bar{S}_{n,\alpha }^{\theta ,\beta }(f; x)-f(x)|&\le |\bar{S}_{n,\alpha }^{\theta ,\beta }(f-g; x)|+|\bar{S}_{n,\alpha }^{\theta ,\beta }(g; x)-g(x)|+|f(x)-g(x)|\nonumber \\&\le 4\Vert f- g\Vert _{C[0 ,1]}+|\bar{S}_{n,\alpha }^{\theta ,\beta }(g; x)-g(x)|. \end{aligned}$$

(3.6)

By applying the Taylor’s formula, we obtain

$$\begin{aligned}&|\bar{S}_{n,\alpha }^{\theta ,\beta }(g; x)-g(x)|\nonumber \\&\quad \le S_{n,\alpha }^{\theta ,\beta } \bigg (\bigg |\int _{x}^{t}|t-u|~|g''(u)|du\bigg |; x\bigg )+\bigg | \int _{x}^{\frac{2\theta +1-2(\beta +1)x}{2(n+\beta +1)}}\big |\frac{2\theta +1-2(\beta +1)x}{2(n+\beta +1)}-u\big |~|g''(u)|~du\bigg |\nonumber \\&\quad \le \Vert \phi ^2 g''\Vert _{C[0,1]} S_{n,\alpha }^{\theta ,\beta } \bigg (\bigg |\int _{x}^{t}\frac{|t-u|}{\phi ^2(u)}du\bigg |; x\bigg ) +\Vert \phi ^2 g''\Vert _{C[0,1]}~\bigg |\int _{x}^{\frac{2\theta +1-2(\beta +1)x}{2(n+\beta +1)}}\frac{|\frac{2\theta +1-2(\beta +1)x}{2(n+\beta +1)}-u|}{\phi ^2(u)}~du\bigg |\nonumber \\&\quad \le \phi ^{-2}(x)\Vert \phi ^2 g''\Vert _{C[0,1]} S_{n,\alpha }^{\theta ,\beta }((t-x)^2; x)+ \phi ^{-2}(x)\Vert \phi ^2 g''\Vert _{C[0,1]}\frac{(2\theta +1-2(\beta +1))^2 x^2}{4(n+\beta +1)^2}. \end{aligned}$$

(3.7)

From (3.6), (3.7) and by using definition of K-functional along with the relation (3.4), we obtain

$$\begin{aligned}&|\bar{S}_{n,\alpha }^{\theta ,\beta }(f; x)-f(x)|\\&\quad \le 4\Vert f- g\Vert _{C[0 ,1]}+\phi ^{-2}(x)\Vert \phi ^2 g''\Vert _{C[0,1]}\Bigg (\rho _{n,\theta ,\beta ,\alpha }^2\left( x\right) +\frac{(2\theta +1-2(\beta +1))^2 x^2}{4(n+\beta +1)^2}\Bigg )\\&\quad \le C \omega _2^{\phi }\bigg (f, \frac{\varepsilon _{n,\alpha ,\theta ,\beta }(x)}{2\phi (x)}\bigg ). \end{aligned}$$

On the other hand, from the Ditzian–Totik uniform modulus of smoothness of first order we have

$$\begin{aligned} \left| f\left( \frac{2nx+2\theta +1}{2(n+\beta +1)}\right) -f(x)\right|&=\bigg |f\bigg (x+\xi (x) \frac{2\theta +1-2(\beta +1)x}{2\xi (x)(n+\beta +1)}\bigg )-f(x)\bigg |\\&\le \omega _{\xi }\bigg (f, \frac{2\theta +1-2(\beta +1)x}{2\xi (x)(n+\beta +1)}\bigg ). \end{aligned}$$

Hence

$$\begin{aligned} | S_{n,\alpha }^{\theta ,\beta }(f; x)-f(x)|&\le |\bar{S}_{n,\alpha }^{\theta ,\beta }(f; x)-f(x)|+\big |f\left( \frac{2nx+2\theta +1}{2(n+\beta +1)}\right) -f(x)\big |\\&\le C \omega _2^{\phi }\bigg (f, \frac{\varepsilon _{n,\alpha ,\theta ,\beta }(x)}{2\phi (x)}\bigg )+\omega _{\xi }\bigg (f, \frac{2\theta +1-2(\beta +1)x}{2\xi (x)(n+\beta +1)}\bigg ). \end{aligned}$$

This completes the proof. $\square$

Theorem 5

Let $f \in C^{1}[0 ,1]$. For any $x \in [0 ,1]$, the following inequality holds:

$$\begin{aligned} |S_{n,\alpha }^{\theta ,\beta }(f; x)-f(x)|&\le \left| \frac{2\theta +1-2(\beta +1)x}{2(n+\beta +1)}\right| ~|f'(x)|+2\rho _{n,\theta ,\beta ,\alpha }\left( x\right) w\big (f', \rho _{n,\theta ,\beta ,\alpha }\left( x\right) \big ), \end{aligned}$$

where $\rho _{n,\theta ,\beta ,\alpha }\left( x\right)$ is given by Theorem 2.

Proof

For any $t \in [0 ,1]$, $x \in [0 ,1]$, we have

$$\begin{aligned} f(t)-f(x)=(t-x)f'(x)+\int _{x}^{t}(f'(u)-f'(x))du. \end{aligned}$$

Applying $S_{n,\alpha }^{\theta ,\beta }(f; x)$ on both sides of the above relation, we obtain

$$\begin{aligned} S_{n,\alpha }^{\theta ,\beta }(f(t)-f(x); x)=f'(x)S_{n,\alpha }^{\theta ,\beta }(t-x; x)+S_{n,\alpha }^{\theta ,\beta }\bigg (\int _{x}^{t}(f'(u)-f'(x))du;x\bigg ). \end{aligned}$$

It is well known that for any $\varepsilon >0$ and each $u \in [0 ,1]$,

$$\begin{aligned} |f(u)-f(x)|\le w(f, \varepsilon )\bigg (\frac{|u-x|}{\varepsilon }+1\bigg ), ~~f \in C[0 ,1]. \end{aligned}$$

With above inequality we have

$$\begin{aligned} \bigg |\int _{x}^{t}(f'(u)-f'(x))du\bigg |\le w(f', \varepsilon )\bigg (\frac{(t-x)^2}{\varepsilon }+|t-x|\bigg ). \end{aligned}$$

Thus,

$$\begin{aligned} |S_{n,\alpha }^{\theta ,\beta }(f; x)-f(x)|\le |f'(x)|~|S_{n,\alpha }^{\theta ,\beta }(t-x; x)|+w(f', \varepsilon ) \bigg \{\frac{1}{\varepsilon }S_{n,\alpha }^{\theta ,\beta }((t-x)^2; x)+S_{n,\alpha }^{\theta ,\beta }(t-x; x)\bigg \}.\nonumber \\ \end{aligned}$$

(3.8)

Applying Cauchy–Schwarz inequality on the right hand side of (3.8), we have

$$\begin{aligned} |S_{n,\alpha }^{\theta ,\beta }(f; x)-f(x)|&\le f'(x) \left| \frac{2\theta +1-2(\beta +1)x}{2(n+\beta +1)}\right| \\&\quad +w(f', \varepsilon ) \bigg \{\frac{1}{\varepsilon }\sqrt{S_{n,\alpha }^{\theta ,\beta }((t-x)^2; x)}+1\bigg \}\sqrt{S_{n,\alpha }^{\theta ,\beta }(|t-x|; x)}. \end{aligned}$$

Choosing $\varepsilon =\rho _{n,\theta ,\beta ,\alpha }\left( x\right)$, we get the desired result. $\square$

4 Voronovskaja-type theorem

Theorem 6

For every $f\in C_B[0, 1]$ such that $f', f'' \in C_B[0,1]$. Then, for each $x \in [0 ,1]$, we have

$$\begin{aligned} \lim _{n \rightarrow \infty } n\big \{S_{n,\alpha }^{\theta ,\beta }(f; x)-f(x)\big \}=\frac{2\theta +1-2(\beta +1)x}{2}f'(x)+\frac{x(1-x)}{2}f^{''}(x) \end{aligned}$$

uniformly on [0, 1], where $C_B[0, 1]$ denotes the set of all real-valued bounded and continuous functions defined on [0, 1].

Proof

Let $x \in [0 ,1]$. By the Taylor’s expansion theorem of function f in $C_B[0, 1]$ we obtain:

$$\begin{aligned} f(t)=f(x)+(t-x)f^{'}(x)+\frac{1}{2}(t-x)^2f^{''}(x)+(t-x)^2~r_x(t), \end{aligned}$$

(4.1)

where $r_x(t)$ is Peano form of the remainder, $r_x\in C[0, 1]$ and $r_x(t)\rightarrow 0$ as $t\rightarrow x.$ Operating $S_{n,\alpha }^{\theta ,\beta }(f; x)$ to the identity (4.1), we get

$$\begin{aligned} S_{n,\alpha }^{\theta ,\beta }(f; x)-f(x)=f^{'}(x)S_{n,\alpha }^{\theta ,\beta }(t-x; x)+\frac{f^{''}(x)}{2} S_{n,\alpha }^{\theta ,\beta }((t-x)^2; x) + S_{n,\alpha }^{\theta ,\beta }((t-x)^2 r_x(t); x). \end{aligned}$$

Using Cauchy–Schwarz inequality, we have

$$\begin{aligned} S_{n,\alpha }^{\theta ,\beta }((t-x)^2 r_x(t); x)\le \sqrt{S_{n,\alpha }^{\theta ,\beta }((t-x)^4; x)}\sqrt{S_{n,\alpha }^{\theta ,\beta }(r^2_x(t); x)}. \end{aligned}$$

(4.2)

Since $\lim _{n \rightarrow \infty }n \{S_{n,\alpha }^{\theta ,\beta }((t-x)^4; x)\}$ is bounded by Lemma 2 we have $\lim _{n} S_{n,\alpha }^{\theta ,\beta }(r^2_x(t); x)=0$. It means

$$\begin{aligned} \lim _{n \rightarrow \infty }n\{S_{n,\alpha }^{\theta ,\beta }((t-x)^2 r_x(t); x)\}=0. \end{aligned}$$

Thus

$$\begin{aligned} \lim _{n \rightarrow \infty } n\{S_{n,\alpha }^{\theta ,\beta }(f; x)-f(x)\}&=\lim _{n \rightarrow \infty } n\big \{S_{n,\alpha }^{\theta ,\beta }(t-x; x)f'(x)+\frac{f^{''}(x)}{2} S_{n,\alpha }^{\theta ,\beta }((t-x)^2; x)\\&\quad +S_{n,\alpha }^{\theta ,\beta }((t-x)^2 r_x(t); x)\big \}. \end{aligned}$$

The result follows immediately by applying Corollary 1. $\square$

5 Weighted approximation of $S_{n,\alpha }^{\theta ,\beta }$

We use the notation $C({\mathbb {R}}_{+})$ to denote the space of all continuous functions f on ${\mathbb {R}}_{+}=[0,\infty )$ and $B_{2}({\mathbb {R}}_{+})$ denotes the set of all functions f on ${\mathbb {R}}_{+}$ having the property

$$\begin{aligned} |f(x)|\le C_{f}\rho (x),\;\;\rho (x)=1+x^{2}, \end{aligned}$$

where a constant $C_{f}>0$ depending on f. By $C_{2}({\mathbb {R}}_{+})$, we denote the subspace of all continuous functions in $B_{2}({\mathbb {R}}_{+})$ and define

$$\begin{aligned} C_{2}^{*}({\mathbb {R}}_{+})=\left\{ f\in C_{2}({\mathbb {R}}_{+}) :\lim _{x\rightarrow \infty }\frac{|f(x)|}{\rho (x)}<\infty \right\} . \end{aligned}$$

It is also known that $B_{2}({\mathbb {R}}_{+})$ is a Banach space. For $f\in B_{2}({\mathbb {R}}_{+})$, the norm of f is defined by

$$\begin{aligned} \Vert f\Vert _{2}=\sup _{x\ge 0}\frac{|f(x)|}{\rho (x)}. \end{aligned}$$

Theorem 7

Let $\rho (x)=1+x^{2}$ be a weight function. Then, for all $f\in C$, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert S_{n,\alpha }^{\theta ,\beta }f-f\Vert _{2}=0 \end{aligned}$$

Proof

In view of weighted Korovkin theorem, it is sufficient to see that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert S_{n,\alpha }^{\theta ,\beta }(e_{i})-e_{i}\Vert _{2}=0\;\;\;\;\;\;(i=0,1,2). \end{aligned}$$

(5.1)

It is easy to see from Lemma 2 that

$$\begin{aligned} \Vert S_{n,\alpha }^{\theta ,\beta }(e_{0})-e_{0}\Vert _{2}\rightarrow 0\quad (n\rightarrow \infty ). \end{aligned}$$

(5.2)

Again, with the help of Lemma 2, one can write

$$\begin{aligned} \Vert S_{n,\alpha }^{\theta ,\beta }(e_{1})-e_{1}\Vert _{2}&\le \left( \frac{n}{n+\beta +1}-1\right) \sup _{x\ge 0}\left( \frac{x}{1+x^{2}}\right) +\frac{2\theta +1}{2(n+\beta +1)}\\&\le \frac{n}{n+\beta +1}-1+\frac{2\theta +1}{2(n+\beta +1)} \end{aligned}$$

which yields

$$\begin{aligned} \Vert S_{n,\alpha }^{\theta ,\beta }(e_{1})-e_{1}\Vert _{2}\rightarrow 0\quad (n\rightarrow \infty ). \end{aligned}$$

(5.3)

Proceeding along the same lines as above, we obtain

$$\begin{aligned} \Vert S_{n,\alpha }^{\theta ,\beta }(e_{2})-e_{2}\Vert _{2}\le & {} \left( \frac{n^2}{(n+\beta +1)^2}-\frac{n+2(1-\alpha )}{(n+\beta +1)^2}-1\right) \sup _{x\ge 0}\left( \frac{x^{2}}{1+x^{2}}\right) \\&+\left( \frac{n+2(1-\alpha )}{(n+\beta +1)^2}+\frac{3n(2\theta +1)}{3(n+\beta +1)^2}\right) \sup _{x\ge 0}\left( \frac{x}{1+x^{2}}\right) +\frac{3\theta ^2+3\theta +1}{3(n+\beta +1)^2}\\\le & {} \frac{n^2}{(n+\beta +1)^2}-\frac{n+2(1-\alpha )}{(n+\beta +1)^2}-1+\frac{3\theta ^2+3\theta +1}{3(n+\beta +1)^2}\\&+\frac{n+2(1-\alpha )}{(n+\beta +1)^2}+\frac{3n(2\theta +1)}{3(n+\beta +1)^2}. \end{aligned}$$

Letting limit as $n\rightarrow \infty$ in the last inequality, we get

$$\begin{aligned} \Vert S_{n,\alpha }^{\theta ,\beta }(e_{2})-e_{2}\Vert _{2}\rightarrow 0\quad (n\rightarrow \infty ). \end{aligned}$$

(5.4)

Hence, in view of (5.2)–(5.4), we conclude that (5.2) holds for $i=0,1,2$. $\square$

Theorem 8

For each $f\in C$, one has

$$\begin{aligned} \lim _{n\rightarrow \infty }\sup _{x\ge 0}\frac{|S_{n,\alpha }^{\theta ,\beta }(f;x)-f(x)|}{(1+x^{2})^{1+\theta }}=0. \end{aligned}$$

(5.5)

Proof

For any fixed $\gamma >0$, one writes

$$\begin{aligned} \sup _{x\ge 0}\frac{|S_{n,\alpha }^{\theta ,\beta }(f;x)-f(x)|}{(1+x^{2})^{1+\theta }}\le & {} \sup _{x\le \gamma }\frac{|S_{n,\alpha }^{\theta ,\beta }(f;x)-f(x)|}{(1+x^{2})^{1+\theta }}+\sup _{x\ge \gamma }\frac{|S_{n,\alpha }^{\theta ,\beta }(f;x)-f(x)|}{(1+x^{2})^{1+\theta }}\nonumber \\\le & {} \Vert S_{n,\alpha }^{\theta ,\beta }(f)-f\Vert _{C[0,\gamma ]}+\Vert f\Vert _{2}\sup _{x\ge \gamma }\frac{|S_{n,\alpha }^{\theta ,\beta }(1+t^{2};x)|}{(1+x^{2})^{1+\theta }}\nonumber \\&+\sup _{x\ge \gamma }\frac{|f(x)|}{(1+x^{2})^{1+\theta }} \end{aligned}$$

(5.6)

It follows from the fact $|f(x)|\le M(1+x^{2})$ that

$$\begin{aligned} \sup _{x\ge \gamma }\frac{|f(x)|}{(1+x^{2})^{1+\theta }}\le \frac{\Vert f(x)\Vert _{2}}{(1+\gamma ^{2})^{1+\theta }}. \end{aligned}$$

Let $\epsilon >0$ be given. We can choose $\gamma$ to be so large that the inequality

$$\begin{aligned} \frac{\Vert f(x)\Vert _{2}}{(1+\gamma ^{2})^{1+\theta }}<\epsilon /3. \end{aligned}$$

(5.7)

With the help of Lemma 2, one gets

$$\begin{aligned} \Vert f\Vert _{2}\frac{|S_{n,\alpha }^{\theta ,\beta }(1+t^{2};x)|}{(1+x^{2})^{1+\theta }}\rightarrow 0\quad (n\rightarrow \infty ). \end{aligned}$$

Thus

$$\begin{aligned} \Vert f\Vert _{2}\sup _{x\ge \gamma }\frac{|S_{n,\alpha }^{\theta ,\beta }(1+t^{2};x)|}{(1+x^{2})^{1+\theta }}<\epsilon /3 \end{aligned}$$

(5.8)

for the choice of $\gamma$ as large as enough. Moreover, the first term on the right-hand side of inequality (5.6) in virtue of Korovkin theorem becomes

$$\begin{aligned} \Vert S_{n,\alpha }^{\theta ,\beta }(f)-f\Vert _{C[0,\gamma ]}<\epsilon /3. \end{aligned}$$

(5.9)

Consequently, in virtue of (5.7)–(5.9), we proves the assertion (5.5) of Theorem 8. $\square$

6 Pointwise estimates of $S_{n,\alpha }^{\theta ,\beta }$

To prove our next result concerning the point convergence of our new operators, we first recall the Lipschitz condition as follows: let us consider $0<\lambda \le 1$ and $H\subset [0,\infty )$. Then, a function f in $C_{B}[0,\infty )$ belongs to $Lip(\lambda )$ if the condition

$$\begin{aligned} |f(s)-f(x)|\le C_{\lambda ,f}|s-x|^{\lambda }\;\;\;\;\;(x\in [0,\infty ],s\in H) \end{aligned}$$

holds, where the constant $C_{\lambda ,f}$ is depending on both $\alpha$ and f.

Theorem 9

Assume that $0<\lambda \le 1$, $H\subset [0,\infty )$ and $f\in C_{B}[0,\infty )$. Then, for each $x\in [0,\infty )$,

$$\begin{aligned} |S_{n,\alpha }^{\theta ,\beta }(f;x){-}f(x)|\le & {} C_{\lambda ,f}\Biggl \{\biggl (\frac{(n+2(1-\alpha ))x(1{-}x)}{(n{+}\beta +1)^2}+\frac{ x(\beta +1)(x(\beta +1)-(2\theta +1)) }{(n+\beta +1)^2}\nonumber \\&+\frac{3\theta ^2+3\theta +1}{3(n+\beta +1)^2}\biggl )^{\frac{\lambda }{2}}+2(d(x,H))^{\lambda }\Bigg \}, \end{aligned}$$

(6.1)

where d(x, H) is the distance between x and H, defined by

$$\begin{aligned} d(x,H)-\inf \{|t-x|:t\in H\}. \end{aligned}$$

Proof

Let ${{\bar{H}}}$ be a closure of H. Suppose that $s\in {{\bar{H}}}$ such that $|x-s|=d(x,H)$. Then

$$\begin{aligned} |f(t)-f(x)|\le |f(t)-f(s)|+|f(s)-f(x)|\;\;\;\;(x\in [0,\infty )). \end{aligned}$$

Consequently, we write

$$\begin{aligned} |S_{n,\alpha }^{\theta ,\beta }(f;x)-f(x)|\le S_{n,\alpha }^{\theta ,\beta }(|f(t)-f(s)|;x)+S_{n,\alpha }^{\theta ,\beta }(|f(x)-f(s)|;x) \end{aligned}$$

and therefore we find that

$$\begin{aligned} |S_{n,\alpha }^{\theta ,\beta }(f;x)-f(x)|\le & {} C_{\lambda ,f}\Big \{S_{n,\alpha }^{\theta ,\beta }(|t-s|^{\lambda };x)+|x-s|^{\lambda }\Big \}\nonumber \\\le & {} C_{\lambda ,f}\Big \{S_{n,\alpha }^{\theta ,\beta }(|t-x|^{\lambda }+|x-s|^{\lambda };x)+|x-s|^{\lambda }\Big \}\nonumber \\= & {} C_{\lambda ,f}\Big \{S_{n,\alpha }^{\theta ,\beta }(|t-x|^{\lambda };x)+2|x-s|^{\lambda }\Big \}. \end{aligned}$$

(6.2)

Applying the Holder inequality for $p=2/\lambda$ and $q=2/(2-\lambda )$ to (6.2), we obtain

$$\begin{aligned} |S_{n,\alpha }^{\theta ,\beta }(f;x)-f(x)|\le & {} C_{\lambda ,f}\left\{ \left( S_{n,\alpha }^{\theta ,\beta }(|t-x|^{p\lambda };x)\right) ^{\frac{1}{p}}\left( S_{n,\alpha }^{\theta ,\beta }(1^{q};x)\right) ^{\frac{1}{q}}+2\left( d\left( x,H\right) \right) ^{\lambda }\right\} \nonumber \\= & {} C_{\lambda ,f}\left\{ \left( S_{n,\alpha }^{\theta ,\beta }(|t-x|^{2};x)\right) ^{\frac{\lambda }{2}}+2\left( d\left( x,H\right) \right) ^{\lambda }\right\} \end{aligned}$$

(6.3)

In view of the condition (ii) of Corollary 1, the last inequality (6.3) leads us the inequality (6.1) which proves the result. $\square$

In order to prove our next result, recall that the Lipschitz-type maximal function of order $\lambda$ [33] is given by

$$\begin{aligned} \omega _{\lambda }(f;x)=\sup _{s\in [0,\infty ),s\not =x}\frac{|f(s)-f(x)|}{|s-x|^{\lambda }} \end{aligned}$$

(6.4)

for $x\in [0,\infty )$ and $0<\lambda \le 1$. We are now ready to prove a local direct estimate of $S_{n,\alpha }^{\theta ,\beta }$.

Theorem 10

Assume that $f\in C_{B}[0,\infty )$ and $0<\lambda \le 1$. Then, for all $x\in [0,\infty )$, one has

$$\begin{aligned} |S_{n,\alpha }^{\theta ,\beta }(f;x)-f(x)|\le & {} \omega _{\lambda }(f;x)\biggl (\frac{ x(\beta +1)(x(\beta +1)-(2\theta +1)) }{(n+\beta +1)^2}\nonumber \\&+\frac{ (n+2(1-\alpha ))(x-x^2) }{(n+\beta +1)^2}+\frac{3\theta ^2+3\theta +1}{3(n+\beta +1)^2}\biggl )^{\frac{\lambda }{2}}. \end{aligned}$$

(6.5)

Proof

In view of (6.4), we can write

$$\begin{aligned} |S_{n,\alpha }^{\theta ,\beta }(f;x)-f(x)|= & {} |S_{n,\alpha }^{\theta ,\beta }(f;x)-f(x)S_{n,\alpha }^{\theta ,\beta }(1;x)|\\\le & {} S_{n,\alpha }^{\theta ,\beta }(|f(t)-f(x)|;x)\\\le & {} \omega _{\lambda }(f;x)S_{n,\alpha }^{\theta ,\beta }(|t-x|^{\lambda };x) \end{aligned}$$

By applying the Holder inequality for

$$\begin{aligned} p=2/\lambda \;\;\;\text{ and }\;\;\;q=2/(2-\lambda ) \end{aligned}$$

to the last inequality, we immediately see that

$$\begin{aligned} |S_{n,\alpha }^{\theta ,\beta }(f;x)-f(x)|\le & {} \omega _{\lambda }(f;x)\left( S_{n,\alpha }^{\theta ,\beta }(|t-x|^{2};x)\right) ^{\frac{\lambda }{2}}. \end{aligned}$$

(6.6)

We can easily find from the last inequality together with Corollary 1 that the assertion (6.5) holds true. $\square$

7 Numerical analysis

We use MATLAB to numerically analyse the theoretical results of the previous sections by demonstrating convergence and error of approximation of Stancu variant of Bernstein–Kantorovich operators (1.3).

We first consider the function given in [3]:

$$\begin{aligned} f(x)=\cos ^3\left( 2 \pi x-\frac{\pi }{2}\right) +2\sin \left( \frac{\pi x}{2}\right) \end{aligned}$$

(7.1)

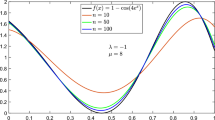
on the interval [0, 1]. The graph of f(x) given above, approximation of our operators and the corresponding error of approximation are given in Fig. 1.

Fig. 1

Function, its best approximation and error of approximation

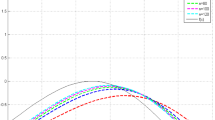
For any non-negative real values of $\beta$ and $\theta$ in the interval [0, 1], we get the best approximation for our Stancu-type Bernstein–Kantorovich operators (1.3). When the values of $\beta ,\theta \in [0,1]$ increase, the maximum error for $n=20,50,100$ increases too. In general, the choice of $\beta =\theta$ and for any fixed $\alpha$, the maximum error increases for $n=20$ when the values of $\beta , \theta$ increase. On the other hand, if $\beta \ne \theta$ for any fixed $\alpha$ then the error of approximation oscillates and increases, in general. If we choose $\alpha =0.9$ to compare the error of approximation of our operators and the operators defined in [3], we see that the parameters $\beta$ and $\theta$ give us the flexibility to have a better maximum error of approximation. The case $\alpha =0.9$ is given in Table 1 to compare the approximation of our operators and the operators defined in [3] for the above considered function. Table 1 shows that maximum error of approximation of our operators is less than the error of approximation of operators defined in [3].

Table 1 Error of approximation

We also demonstrate the convergence of our operators by choosing $f(x)=\cos (2\pi x )$ on the interval [0, 1]. In Fig. 2, we give the graph of $f(x)=\cos (2\pi x ) ,$ approximation of our operators and the corresponding error of approximation. Moreover, we provide Table 2 to see the error of approximation of our operators for the function $f(x)=\cos (2\pi x )$.

Fig. 2

Function, its best approximation and error of approximation

Table 2 Error of approximation

8 Concluding remarks and observations

In our present investigation, we defined the sequence of Stancu-type Bernstein–Kantorovich linear positive operators depends on shape parameter $\alpha \in [0,1]$ (or, Stancu-type $\alpha$-Bernstein–Kantorovich) by

$$\begin{aligned} S_{n,\alpha }^{\theta ,\beta }\left( f;x\right)= & {} (n+\beta +1)\sum \limits _{i=0}^{n}\Bigg [\left( 1-\alpha \right) x\left( {\begin{array}{c}n-2\\ i\end{array}}\right) +\left( 1-\alpha \right) \left( 1-x\right) \left( {\begin{array}{c}n-2\\ i-2\end{array}}\right) \nonumber \\&+\, \alpha x\left( 1-x\right) \left( {\begin{array}{c}n\\ i\end{array}}\right) \Bigg ] x^{i-1}\left( 1-x\right) ^{n-i-1}\int _{\frac{i+\theta }{n+\beta +1}}^{\frac{i+\theta +1}{n+\beta +1}}f\left( s\right) ds. \end{aligned}$$

(8.1)

We established several approximation results such as rate of convergence, Voronovskaja-type approximation theorem, weighted approximation as well as pointwise estimates of (8.1). However, if we take $\theta =0$ and $\beta =0$ then

$$\begin{aligned} S_{n,\alpha }^{0,0}\left( f;x\right) =M_{n,\alpha }\left( f;x\right) \end{aligned}$$

which means that Stancu-type $\alpha$-Bernstein–Kantorovich operators include $\alpha$-Bernstein–Kantorovich operators (1.2). We also provide Table 3 to numerically demonstrate the advantages of our new operators. We are now reconsidering the function f(x) defined by (7.1) in previous section and take $\theta =0.25$ and $\beta =0.75$ to compare $S_{n,\alpha }^{\theta ,\beta }$ and $M_{n,\alpha }$.

Table 3 Error of approximation for different values of $\theta$ and $\beta$

Furthermore, if $\alpha =1$ then (1.1), (1.2) and (8.1) will be read (respectively) as Bernstein operators $T_{n,1}\left( f;x\right)$ [2], Bernstein–Kantorovich operators $M_{n,1}\left( f;x\right)$ [34] and Stancu-type Bernstein–Kantorovich operators $S_{n,1}^{\theta ,\beta }\left( f;x\right)$ [35]. We therefore conclude that (8.1) contains $M_{n,\alpha }\left( f;x\right)$, $M_{n,1}\left( f;x\right)$ and $S_{n,1}^{\theta ,\beta }\left( f;x\right)$. Hence (8.1) is a nontrivial generalization of some widely-studied linear positive operators existing in the literature and so our results as well.