A Comparative Study of Cubic B-spline-Based Quasi-interpolation and Differential Quadrature Methods for Solving Fourth-Order Parabolic PDEs

Abstract

In this work, we present two approaches for simulation of fourth-order parabolic partial differential equations. In the first method, cubic B-spline quasi-interpolation is used to approximate the spatial derivative of the dependent variable and forward difference to approximate the time derivative. In the second method, we have used modified cubic B-spline functions-based differential quadrature method (DQM) for space discretization to get a system of ODEs and then this system is solved by SSP-RK43 method to get the results at knots. The numerical results demonstrate the accuracy of the proposed method. The stability analysis of the methods has also been discussed. It is observed that quasi-interpolation-based method is unconditionally stable, whereas for DQM, the stability has to be checked for a large number of space points. Moreover, for the small number of grid points, DQM gives better results, while for a large number of grid points, quasi-interpolation-based method is better.

1 Introduction

Consider the forth-order parabolic equation governing the transverse vibrations of a beam,

$$\begin{aligned} \dfrac{\partial ^2 v}{\partial t^2} + \dfrac{\partial ^4 v}{\partial x^4}=G(x,t),\quad x\in (a, b),\quad t>0, \end{aligned}$$

(1)

with initial conditions

$$\begin{aligned} \left\{ \begin{array}{l} v(x,0)=f_0(x),\quad \; x\in (a, b),\\ v_t(x,0)=f_1(x),\quad x\in (a, b), \end{array} \right. \end{aligned}$$

(2)

and boundary conditions being

$$\begin{aligned} \left\{ \begin{array}{l} v(a,t)=g_a(t),\qquad \quad v(b,t)=g_b(t),\qquad t>0\\ v_{xx}(a,t)=p_a(t),\qquad v_{xx}(b,t)=p_b(t),\quad \, t>0 \end{array} \right. \end{aligned}$$

(3)

where v(x, t) is the transverse displacement of the beam, t and x are time and space variables, G(x, t) is the dynamic force per unit mass, $f_0(x),$ $f_1(x),$ $g_a(t),$ $g_b(t),$ $p_a(t)$ and $p_b(t)$ are sufficiently smooth functions.

We solve Eq. (1) by rewriting it as a system of two second-order equations, for which we are introducing two new variables $\phi$ and $\psi$ as

$$\begin{aligned} \phi =\dfrac{\partial {v}}{\partial {t}},\qquad \psi =\dfrac{\partial ^2v}{\partial x^2} \end{aligned}$$

(4)

Now, we get two simultaneous partial differential equations in the following form

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial {\phi }}{\partial {t}}=-\dfrac{\partial ^2\psi }{\partial {x}^2}+G\\ \\ \dfrac{\partial {\psi }}{\partial {t}}=\dfrac{\partial ^2\phi }{\partial {x}^2} \end{array} \right. \end{aligned}$$

(5)

Equations (2) and (3) now become

$$\begin{aligned} \phi (x,0) = \, & {} f(x),\quad \phi (a,t)=a_0(t),\quad \phi (b,t)=b_0(t). \end{aligned}$$

(6)

$$\begin{aligned} \psi (x,0) = \, & {} h(x),\quad \psi (a,t)=a_1(t),\quad \psi (b,t)=b_1(t). \end{aligned}$$

(7)

Equation (1) has been solved by several authors using finite difference method after splitting into a system of second-order equation [1,2,3,4,5,6]. Fairweather and Gourlay [7] developed an explicit and implicit scheme which is based on the semi-explicit method of Lees [8]. Mohanty et al. [9] solved a special type of fourth-order parabolic PDE by two-level implicit methods. Mittal and Jain [10] solved Eq. (1) by cubic B-spline collocation method with redefined basis functions. Dehghan and Manafian [11] used the homotopy perturbation method to solve the fourth-order parabolic PDE.

For the approximation of a function and its derivatives, Sablonnière [12, 13] developed a discrete univariate B-spline quasi-interpolation method and verified that the approximation of first derivative of a certain class of functions by this method is better than the approximation by finite difference method. Moreover, he demonstrated that for cubic spline interpolation, the first derivative of certain functions represents the convergence of order $O(h^4)$. Based on this motivation, the research community has tried to implement this technique to develop numerical algorithms for a few partial differential equations. Zhu and Kang [14, 15] solved hyperbolic conservation laws using the quasi-interpolation-based method. Kumar and Baskar [16] developed higher-order numerical schemes for particular one-dimensional Sobolev-type equations by implementing quadratic and cubic B-spline technique for quasi-interpolation and compared the performance of the proposed algorithm in terms of accuracy and the rate of convergence.

Bellman et al. [17] were the first to introduce DQM for the solution of PDEs. Quan and Chang [18] used DQM to develop explicit formulae for approximation of weighting coefficients. There are various types of test functions that have been used in DQM to compute the weighting coefficient, viz. B-spline functions (quadratic, cubic, quintic, etc.), Legendre polynomials, Lagrange interpolation polynomials, sine–cosine function, etc. B-spline functions are piece-wise polynomials and their curves have the property to maintain the smoothness and continuity of higher-order derivatives, and due to the local support property, B-spline functions are commonly used as a test function. Mittal and Jiwari [19, 20] solved nonlinear one-dimensional Berger–Huxley-, Fisher- and Burgers-type equations by DQM, also see [21,22,23,24]. Dehghan and Abbaszadeh [25, 26] solved Brusselator reaction–diffusion model and Klein–Gordon Zakharov equations by different methods, also see [27,28,29].

The main objective of this work is to present a study of CBSQI and DQM for solving fourth-order parabolic PDEs.

2 Univariate B-spline Quasi-interpolants

Let us consider an interval [a, b] with the uniform partition $X_n=\{x_j=a+jh:j=0,1,\ldots ,n\},$ where $h=(b-a)/n$. Let $B^d(X_n)$ be the spline space of degree d, and let $\{B_j^d: j=1,2,\ldots ,n+d\}$ form a basis for $B^d(X_n)$, which can be formulated by the de Boor-Cox recursive formula [30]. As we know that support of a B-spline is a subset of the interval $[x_{j-d-1}, x_j],$ we need to add multiple knots at the endpoints in such a way that $x_{-d}=x_{-d+1}=\ldots =x_{-1}=x_{0}=a$ and $b=x_n=x_{n+1}=\ldots =x_{n+d}$.

B-spline quasi-interpolant of degree d for a function v has been defined as [13]

$$\begin{aligned} Q_dv(x)=\sum _{j=1}^{n+d}\mu _j(v)B_j^d(x). \end{aligned}$$

(8)

Let $\mathbb {P}_n^d$ be the space of polynomial of degree at most d. In general, we impose the condition that quasi-interpolant $Q_dv$ is exact on $\mathbb {P}_n^d$, i.e. $Q_dv=v$ for all $v\in \mathbb {P}_n^d$. The coefficients $\mu _j$ are obtained using this condition. Sablonnière [31] used this technique called the discrete quasi-interpolant. The main advantage of BSQI is that it is very easy to implement as it has direct construction, i.e., we do not need to solve any system of linear equations. Moreover, it is local, i.e., the value $Q_dv(x)$ depends only on the values of v in a neighborhood of x. We also show that derivatives of B-spline quasi-interpolants are approximated as the derivatives of a corresponding function.

2.1 Cubic B-spline Quasi-Interpolation

For a function v, cubic B-spline quasi-interpolant is defined from Eq. (8) by taking $d=3$ as

$$\begin{aligned} Q_3v(x)=\sum _{j=1}^{n+3}\mu _j(v)B_j^3(x), \end{aligned}$$

(9)

where nodes are taken to be the same as knots, i.e., $\xi _j=x_j$ $(j=0,1,\ldots ,n)$ and define the coefficients $\mu _j(v)$ $(j=1,2,\ldots ,n+3)$

$$\begin{aligned} \left\{ \begin{array}{l} \mu _1(v)=v_0 \qquad \; \mu _2(v)=\dfrac{1}{18}\Big [7v_0+18v_1-9v_2+2v_3\Big ],\\ \mu _j(v)=\;\dfrac{1}{6}\Big [-v_{j-3}+8v_{j-2}-v_{j-1}\Big ],\quad \text {for}\; 3\le {j}\le (n+1) \\ \mu _{n+2}(v)=\dfrac{1}{18}\Big [2v_{n-3}-9v_{n-2}+18v_{n-1}+7v_n\Big ],\quad \mu _{n+3}(v)=v_n, \end{array} \right. \end{aligned}$$

(10)

and the corresponding B-spline functions are generated by using de Boor-Cox recursive formula [30]

$$\begin{aligned} B_j^3(\xi )= \left\{ \begin{array}{l} {\dfrac{(\xi -x_{j-4})^3}{(x_{j-3}-x_{j-4})(x_{j-2}-x_{j-4})(x_{j-1}-x_{j-4})},\qquad \qquad \qquad \qquad \qquad \text {if}\; x_{j-4}<{\xi }\le {x_{j-3}}}, \\ \dfrac{(\xi -x_{j-4})^2(x_{j-2}-\xi )}{(x_{j-2}-x_{j-4})(x_{j-2}-x_{j-3})(x_{j-1}-x_{j-4})}\\ +\dfrac{(\xi -x_{j-4})(x_{j-1}-\xi )(\xi -x_{j-3})}{(x_{j-1}-x_{j-4})(x_{j-1}-x_{j-3})(x_{j-2}-x_{j-3})} \\ +\dfrac{(x_{j}-\xi )(\xi -x_{j-3})^2}{(x_{j}-x_{j-3})(x_{j-1}-x_{j-3})(x_{j-2}-x_{j-3})},\qquad \qquad \qquad \qquad \qquad \text {if}\; x_{j-3}<{\xi }\le {x_{j-2}} \\ \dfrac{(\xi -x_{j-4})(x_{j-1}-\xi )^2}{(x_{j-1}-x_{j-4})(x_{j-1}-x_{j-3})(x_{j-1}-x_{j-2})}\\ + \dfrac{(\xi -x_{j-3})(x_{j-1}-\xi )(x_j-\xi )}{(x_{j-1}-x_{j-3})(x_{j-1}-x_{j-2})(x_j-x_{j-3})}\\ + \dfrac{(x_j-\xi )^2(\xi -x_{j-2})}{(x_{j}-x_{j-3})(x_{j}-x_{j-2})(x_{j-1}-x_{j-2})}, \qquad \qquad \qquad \qquad \qquad \quad \text {if}\; x_{j-2}<{\xi }\le {x_{j-1}},\\ {\dfrac{(x_j-\xi )^3}{(x_j-x_{j-3})(x_j-x_{j-2})(x_j-x_{j-1})}, \qquad \qquad \qquad \qquad \qquad \qquad \quad \text {if}\; x_{j-1}<{\xi }\le {x_{j}}}\\ 0,\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \text {otherwise} \end{array} \right. \end{aligned}$$

(11)

The different B-spline functions are represented in Fig. 1.

Fig. 1

Cubic B-spline functions for the knot $X_{10}=(1,1,1,2,3,4,5,6,7,8,9,10,11,11,11),\,B_j^3,j=1,2,\ldots ,13$

The first and the second derivatives of $Q_3v$ are calculated as

$$\begin{aligned} (Q_3v)'(x)=\sum _{j=1}^{n+3}\mu _j(v){(B_j^3)}'(x), \end{aligned}$$

(12)

and

$$\begin{aligned} (Q_3v)''(x)=\sum _{j=1}^{n+3}\mu _j(v){(B_j^3)}''(x), \end{aligned}$$

(13)

where $(B_j^3)'$ and $(B_j^3)''$ are obtained from Eq. (11).

$$\begin{aligned} \left. \begin{array}{l} (Q_3v)'(\xi _0)=\dfrac{1}{h}\Big [-\dfrac{11}{6}v_0+3v_1-\dfrac{3}{2}v_2+\dfrac{1}{3}v_3\Big ],\\ (Q_3v)'(\xi _1)=\dfrac{1}{h}\Big [-\dfrac{1}{3}v_0-\dfrac{1}{2}v_1+v_2-\dfrac{1}{6}v_3\Big ],\\ (Q_3v)'(\xi _{n-1})=\dfrac{1}{h}\Big [\dfrac{1}{6}v_{n-3}-v_{n-2}+\dfrac{1}{2}v_{n-1}+\dfrac{1}{3}v_{n}\Big ],\\ (Q_v)'(\xi _{n})=\dfrac{1}{h}\Big [-\dfrac{1}{3}v_{n-3}+\dfrac{3}{2}v_{n-2}-3v_{n-1}+\dfrac{11}{6}v_{n}\Big ], \end{array} \right\} \end{aligned}$$

(14)

and

$$\begin{aligned}&(Q_3v)'(\xi _j)\nonumber \\&\quad =\dfrac{1}{h}\Big [\dfrac{1}{12}v_{j-2}-\dfrac{2}{3}v_{j-1}+\dfrac{2}{3}v_{j+1}-\dfrac{1}{12}v_{j+2}\Big ],\quad 2\le {j}\le (n-2). \end{aligned}$$

(15)

The approximation of $v'$ can be written in terms of matrix form as

$$\begin{aligned} (Q_3v)'=\dfrac{1}{h}D_3^{(1)}v, \end{aligned}$$

(16)

where $D_3^{(1)}$ is the $(n+1)\times (n+1)$ coefficient matrix that is obtained from Eqs. (14)–(15) and $v=(v_0,v_1,\ldots ,v_n)^T.$

For the second derivative, we have

$$\begin{aligned} \left. \begin{array}{l} (Q_3v)''(\xi _0)=\dfrac{1}{h^2}\Big [2v_0-5v_1+4v_2-v_3\Big ],\\ (Q_3v)''(\xi _1)=\dfrac{1}{h^2}\Big [v_0-2v_1+v_2\Big ],\\ (Q_3v)''(\xi _{n-1})=\dfrac{1}{h^2}\Big [v_{n-2}-2v_{n-1}+v_n\Big ],\\ (Q_3v)''(\xi _{n})=\dfrac{1}{h^2}\Big [-v_{n-3}+4v_{n-2}-5v_{n-1}+2v_{n}\Big ], \end{array} \right\} \end{aligned}$$

(17)

and

$$\begin{aligned}&(Q_3v)''(\xi _j)\nonumber \\&\quad =\dfrac{1}{h^2}\Big [-\dfrac{1}{6}v_{j-2}+\dfrac{5}{3}v_{j-1}-3v_{j}+\dfrac{5}{3}v_{j+1}-\dfrac{1}{6}v_{j+2}\Big ],\quad 2\le {j}\le (n-2). \end{aligned}$$

(18)

Similarly, we write the above expressions in terms of matrix form as

$$\begin{aligned} (Q_3v)''=\dfrac{1}{h^2}D_3^{(2)}v, \end{aligned}$$

(19)

where $D_3^{(2)}$ is the $(n+1)\times (n+1)$ coefficient matrix that is obtained from Eqs. (17)–(18).

3 Description of Cubic B-spline Quasi-interpolation Method (CBSQI)

Now we implement the CBSQI method, discretizing the time derivative as forward difference scheme and for space derivative applying $\theta$-weighted scheme in Eq. (5), where $0\le \theta \le 1,$ giving

$$\begin{aligned}&\dfrac{\phi ^{m+1}-\phi ^m}{\Delta {t}}=-\Big [\theta \psi _{xx}^{m+1}+(1-\theta )\psi _{xx}^m\Big ]\nonumber \\&\quad +\Big [\theta {G}^{m+1}+(1-\theta )G^m\Big ], \end{aligned}$$

(20)

$$\begin{aligned}&\dfrac{\psi ^{m+1}-\psi ^m}{\Delta {t}}=\Big [\theta \phi _{xx}^{m+1}+(1-\theta )\phi _{xx}^m\Big ]. \end{aligned}$$

(21)

$$\begin{aligned}&\phi ^{m+1}+\dfrac{\Delta {t}\theta }{h^2}D_3^{(2)}\psi ^{m+1}=\phi ^m-\dfrac{\Delta {t}(1-\theta )}{h^2}D_3^{(2)}\psi ^m\nonumber \\&+\Delta {t}\Big [\theta {G}^{m+1}+(1-\theta )G^m\Big ],\qquad \end{aligned}$$

(22)

$$\begin{aligned}&\psi ^{m+1}-\dfrac{{\Delta {t}}\theta }{h^2}D_3^{(2)}\phi ^{m+1}=\psi ^m+\dfrac{{\Delta {t}}(1-\theta )}{h^2}D_3^{(2)}\phi ^{m} \end{aligned}$$

(23)

Although Eqs. (22) and (23) are valid for all $\theta \in [0,1]$, we will use $\theta =\dfrac{1}{2}$(the famous Crank–Nicolson scheme)

$$\begin{aligned}&\phi ^{m+1}+\dfrac{\Delta {t}}{2h^2}D_3^{(2)}\psi ^{m+1}=\phi ^m-\dfrac{\Delta {t}}{2h^2}D_3^{(2)}\psi ^m\nonumber \\&\quad +\frac{\Delta {t}}{2}\Big [G^{m+1}+G^m\Big ], \end{aligned}$$

(24)

$$\begin{aligned}&\psi ^{m+1}-\dfrac{\Delta {t}}{2h^2}D_3^{(2)}\phi ^{m+1}=\psi ^m+\dfrac{\Delta {t}}{2h^2}D_3^{(2)}\phi ^m \end{aligned}$$

(25)

Let $\mu =\dfrac{\Delta {t}}{2h^2}$

$$\begin{aligned}&\phi ^{m+1}+{\mu }D_3^{(2)}\psi ^{m+1}=\phi ^m-{\mu }D_3^{(2)}\psi ^m\nonumber \\&\quad +\dfrac{\Delta {t}}{2}\Big [G^{m+1}+G^m\Big ] \end{aligned}$$

(26)

$$\begin{aligned}&\psi ^{m+1}-{\mu }D_3^{(2)}\phi ^{m+1}=\psi ^m+{\mu }D_3^{(2)}\phi ^m \end{aligned}$$

(27)

$$\begin{aligned}&\left[ {\begin{array}{cc} {\mu }D_3^{(2)} &{} I\\ I &{} -{\mu }D_3^{(2)} \end{array}}\right] \left[ {\begin{array}{cc} \psi ^{m+1}\\ \phi ^{m+1} \end{array}}\right] = \left[ {\begin{array}{cc} -{\mu }D_3^{(2)} &{} I\\ I &{} {\mu }D_3^{(2)} \end{array}}\right] \left[ {\begin{array}{cc} \psi ^m\\ \phi ^m \end{array}}\right] \nonumber \\&+\frac{\Delta {t}}{2} \left[ {\begin{array}{cc} G^{m+1}+G^m\\ \mathbf {0} \end{array}}\right] \quad \end{aligned}$$

(28)

where

$$\begin{aligned} D_3^{(2)}=\begin{pmatrix} 2 &{}-5 &{}4 &{}-1 &{}0 &{}0 &{}\cdots &{}0 &{}0\\ 1 &{}-2 &{}1 &{}0 &{}0 &{}0 &{}\cdots &{}0 &{}0\\ \dfrac{-1}{6} &{}\dfrac{5}{3} &{}-3 &{}\dfrac{5}{3} &{}\dfrac{-1}{6} &{}0 &{}\cdots &{}0 &{}0\\ 0 &{}\dfrac{-1}{6} &{}\dfrac{5}{3} &{}-3 &{}\dfrac{5}{3} &{}\dfrac{-1}{6} &{}\cdots &{}0 &{}0\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ 0 &{}0 &{}\cdots &{}\dfrac{-1}{6} &{}\dfrac{5}{3} &{}-3 &{}\dfrac{5}{3} &{}\dfrac{-1}{6} &{}0 \\ 0 &{}0 &{}\cdots &{}0 &{}\dfrac{-1}{6} &{}\dfrac{5}{3} &{}-3 &{}\dfrac{5}{3} &{}\dfrac{-1}{6}\\ 0 &{}0 &{}\cdots &{}0 &{}0 &{}0 &{}1 &{}-2 &{}1\\ 0 &{}0 &{}\cdots &{}0 &{}0 &{}-1 &{}4 &{}-5 &{}2 \end{pmatrix}_{(n+1)\times (n+1)} \end{aligned}$$

(29)

where ${D_3^{(2)}}$ and I (identity) are $(n+1)\times (n+1)$ matrices and $\varvec{\phi }^m=(\phi _1^m,\phi _2^m,\ldots ,\phi _{n+1}^m)^T$ and $\varvec{\psi }^m=(\psi _1^m,\psi _2^m,\ldots ,\psi _{n+1}^m)^T$ are the column vectors. When $m=0$, the vectors $\varvec{\phi }^0$ and $\varvec{\psi }^0$ are obtained from the initial conditions and solutions of Eq. (5) at time level $t=(m+1)\Delta {t}$ are calculated by solving the linear system Eq. (28). After calculating the value of $\psi$ at each time level, we again apply the CBSQI on Eq. (4) to get the final result.

4 Stability of CBSQI

Since stability does not depend on G(x, t), so in stability discussion we ignore G(x, t). By using the coefficients of CBSQI from Eqs. (17)–(18) to approximate the space derivative, Eqs. (26)–(27) are written for internal nodes as

$$\begin{aligned}&\phi _i^{m+1}+\mu \Big [-\dfrac{1}{6}\psi _{i-2}^{m+1}+\dfrac{5}{3}\psi _{i-1}^{m+1}-3\psi _i^{m+1}+\dfrac{5}{3}\psi _{i+1}^{m+1}-\dfrac{1}{6}\psi _{i+2}^{m+1}\Big ] \nonumber \\&\quad =\phi _i^m-\mu [-\frac{1}{6}\psi _{i-2}^m+\frac{5}{3}\psi _{i-1}^m-3\psi _i^m+\frac{5}{3}\psi _{i+1}^m\nonumber \\&\qquad -\frac{1}{6}\psi _{i+2}^m\Big ],\;\text {for}\,i=2,\ldots ,n-1\qquad \end{aligned}$$

(30)

$$\begin{aligned}&\psi _i^{m+1}-\mu \Big [-\dfrac{1}{6}\phi _{i-2}^{m+1}+\dfrac{5}{3}\phi _{i-1}^{m+1}-3\phi _i^{m+1}+\dfrac{5}{3}\phi _{i+1}^{m+1}-\dfrac{1}{6}\phi _{i+2}^{m+1}\Big ]\qquad \qquad \qquad \qquad \quad \nonumber \\&\quad =\psi _i^m+\mu \Big [-\dfrac{1}{6}\phi _{i-2}^m+\dfrac{5}{3}\phi _{i-1}^m-3\phi _i^m+\dfrac{5}{3}\phi _{i+1}^m\nonumber \\&\qquad -\dfrac{1}{6}\phi _{i+2}^m\Big ],\;\text {for}\,i=2,\ldots ,n-1\qquad \end{aligned}$$

(31)

$$\begin{aligned}&\phi ^{m+1}+{\mu }T\psi ^{m+1}=\phi ^m-{\mu }T\psi ^m \end{aligned}$$

(32)

$$\begin{aligned}&-{\mu }T\phi ^{m+1}+\psi ^{m+1}=\psi ^m+{\mu }T\phi ^m \end{aligned}$$

(33)

where

$$\begin{aligned} T=\begin{pmatrix} -3 &{}\dfrac{5}{3} &{}\dfrac{-1}{6} &{}0 &{}0 &{}\cdots &{}0 &{}0\\ \dfrac{5}{3} &{}-3 &{}\dfrac{5}{3} &{}\dfrac{-1}{6} &{}0 &{}\cdots &{}0 &{}0\\ \dfrac{-1}{6} &{}\dfrac{5}{3} &{}-3 &{}\dfrac{5}{3} &{}\dfrac{-1}{6} &{}\cdots &{}0 &{}0\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ 0 &{}0 &{}\cdots &{}\dfrac{-1}{6} &{}\dfrac{5}{3} &{}-3 &{}\dfrac{5}{3} &{}\dfrac{-1}{6} \\ 0 &{}0 &{}\cdots &{}0 &{}\dfrac{-1}{6} &{}\dfrac{5}{3} &{}-3 &{}\dfrac{5}{3} \\ 0 &{}0 &{}\cdots &{}0 &{}0 &{}\dfrac{-1}{6} &{}\dfrac{5}{3} &{}-3 \end{pmatrix}_{(n-3)\times (n-3)} \end{aligned}$$

(34)

We write above equation as

$$\begin{aligned}&\left[ {\begin{array}{cc} I &{} {\mu }T\\ -{\mu }T &{} I \end{array}}\right] _{2(n-3)\times 2(n-3)} \left[ {\begin{array}{cc} \phi ^{m+1}\\ \psi ^{m+1} \end{array}}\right] \nonumber \\&\quad = \left[ {\begin{array}{cc} I &{} -{\mu }T\\ {\mu }T &{} I \end{array}}\right] _{2(n-3)\times 2(n-3)} \left[ {\begin{array}{cc} \phi ^m\\ \psi ^m \end{array}}\right] \end{aligned}$$

(35)

$$\begin{aligned}&\left[ {\begin{array}{cc} \phi ^{m+1}\\ \psi ^{m+1} \end{array}}\right] \nonumber \\&\quad =(I+\mu ^2T^2)^{-1} \left[ {\begin{array}{cc} I &{} -{\mu }T\\ {\mu }T &{} I \end{array}}\right] \left[ {\begin{array}{cc} I &{} -{\mu }T\\ {\mu }T &{} I \end{array}}\right] \left[ {\begin{array}{cc} \phi ^m\\ \psi ^m \end{array}}\right] \end{aligned}$$

(36)

$$\begin{aligned}&\left[ {\begin{array}{cc} \phi ^{m+1}\\ \psi ^{m+1} \end{array}}\right] \nonumber \\&\quad =(I+\mu ^2T^2)^{-1} \left[ {\begin{array}{cc} I-{\mu ^2}T^2 &{} -2{\mu }T\\ 2{\mu }T &{} I-{\mu ^2}T^2 \end{array}}\right] \left[ {\begin{array}{cc} \phi ^m\\ \psi ^m \end{array}}\right] \end{aligned}$$

(37)

$$\begin{aligned}&W^{m+1}=\mathbb {M}W^{m} \end{aligned}$$

(38)

where

$$\begin{aligned} W^{m+1}= \left[ {\begin{array}{cc} \phi ^{m+1}\\ \psi ^{m+1} \end{array}}\right] , \mathbb {M}=(I+\mu ^2T^2)^{-1} \left[ {\begin{array}{cc} I-{\mu ^2}T^2 &{} -2{\mu }T\\ 2{\mu }T &{} I-{\mu ^2}T^2 \end{array}}\right] \end{aligned}$$

If the eigenvalues of T be $\tau _i, i=1,2,\ldots ,n-1,$, then the eigenvalues $\lambda _i$ of $\mathbb {M}$ are obtained as

$$\begin{aligned} \lambda _i=\dfrac{1-{\mu ^2}\tau _i^2}{1+{\mu ^2}\tau _i^2}\pm 2j\dfrac{\mu \tau _i}{1+{\mu ^2}\tau _i^2},\qquad j=\sqrt{-1} \end{aligned}$$

(39)

The modulus of the above expression is equal to unity, which shows that the method is unconditionally stable.

5 Modified Cubic B-spline Differential Quadrature Method

In DQM, the approximation of the derivatives of a certain function is achieved by writing it as the weighted sum of its values at discrete points over the considered domain. The remaining work is to calculate the weighting coefficients. For this, we consider uniformly distributed n knots: $a=x_0<x_1<\cdots<x_{n-1}<x_n=b$ such that $x_{i+1}-x_i=h$. For a given function v(x, t), first- and second-order spatial derivatives at any node $x_i$ for $i=0,1,\ldots ,n$ are approximated by

$$\begin{aligned} v_x(x_i,t)= & {} \sum _{j=0}^{n}\alpha _{ij}v(x_j,t),\qquad \text {for}\;i=0,1,\ldots ,n, \end{aligned}$$

(40)

$$\begin{aligned} v_{xx}(x_i,t)= & {} \sum _{j=0}^{n}\beta _{ij}v(x_j,t),\qquad \text {for} \;i=0,1,\ldots ,n. \end{aligned}$$

(41)

where $\alpha _{ij}$ and $\beta _{ij}$ are the weighting coefficients of the first- and second-order derivatives with respect to space variable. We have cubic B-spline function from Eq. (11), from which set $\{ B_{-1}^3(x), B_0^3(x),\ldots, B_{n}^3(x),B_{n+1}^3(x)\}$ forms a basis over the considered domain. By using these functions, we define the modified cubic B-spline functions at any node as

$$\begin{aligned} \left. \begin{array}{l} \check{B}_0(x)=B_0^3(x)+2B_{-1}^3(x),\quad \quad \,\; \\ \check{B}_1(x)=B_1^3(x)-B_{-1}^3(x),\qquad \quad \\ \check{B}_i(x)=B_i^3(x), \qquad \qquad \qquad \quad i=2,4,\ldots ,n-2, \\ \check{B}_{n-1}(x)=B_{n-1}^3(x)-B_{n+1}^3(x),\; \\ \check{B}_{n}(x)=B_{n}^3(x)+2B_{n+1}^3(x), \qquad \quad \end{array} \right\} \end{aligned}$$

(42)

where set $\{\check{B}_0(x), \check{B}_1(x),\ldots ,\check{B}_{n-1}(x),\check{B}_{n}(x)\}$ forms a basis over the considered interval. The values of cubic B-splines and its derivatives at the nodes are presented in Table 1.

Table 1 Cubic B-splines and its derivatives at knots

5.1 Computation of the Weighting Coefficients

The first-order derivative is approximated as

$$\begin{aligned} \check{B_k}'(x_i)=\sum _{j=0}^{n}\omega _{ij}^{(1)}\check{B_k}(x_j), \quad i=0,1,\ldots ,n\; \text {and} \; k=0,1,\ldots ,n \end{aligned}$$

(43)

At the first knot $x_0$, the approximation is given as

$$\begin{aligned} \check{B_k}'(x_0)=\sum _{j=0}^{n}\omega _{0j}^{(1)}\check{B_k}(x_j), \quad k=0,1,\ldots ,n.\qquad \qquad \qquad \quad \; \end{aligned}$$

(44)

For $x=x_0$, the value of $\check{B_k}'(x_0)$ is given by 6/h at $x_1$ knot and $-6/h$ at $x_0$ knot.

This results in a tridiagonal system of equations as

$$\begin{aligned} \begin{pmatrix} 6 &{}1 &{} 0 &{} &{} &{} \\ 0 &{}4 &{}1 &{}0 &{} &{}\\ &{} &{}1 &{}4 &{}1 &{} &{}\\ \cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots \\ &{} &{}1 &{}4 &{}1 &{}\\ &{} &{}0 &{}1 &{}4 &{}0\\ &{} &{} &{} 0 &{}1 &{}6 \end{pmatrix} \begin{pmatrix} \omega _{00}^{(1)}\\ \omega _{01}^{(1)}\\ .\\ .\\ .\\ \omega _{0n}^{(1)} \end{pmatrix} =\begin{pmatrix} -\dfrac{6}{h}\\ \dfrac{6}{h}\\ .\\ .\\ .\\ 0 \end{pmatrix} \end{aligned}$$

(45)

We note that the above coefficient matrix is nonsingular. So to solve the above system, we apply Thomas algorithm whose solution gives us the coefficients $\omega _{00}^{(1)}, \omega _{01}^{(1)},\ldots , \omega _{0n}^{(1)}$.

Similarly, for second knot $x_1$, the approximation is given as

$$\begin{aligned} \check{B_k}'(x_1)=\sum _{j=0}^{n}\omega _{1j}^{(1)}\check{B_k}(x_j), \quad k=0,1,\ldots ,n \end{aligned}$$

(46)

which again results in a tridiagonal system of equations as follows

$$\begin{aligned} \begin{pmatrix} 6 &{}1 &{} 0 &{} &{} &{} \\ 0 &{}4 &{}1 &{}0 &{} &{}\\ &{} &{}1 &{}4 &{}1 &{} &{}\\ \cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots \\ &{} &{}1 &{}4 &{}1 &{}\\ &{} &{}0 &{}1 &{}4 &{}0\\ &{} &{} &{} 0 &{}1 &{}6 \end{pmatrix} \begin{pmatrix} \omega _{10}^{(1)}\\ \omega _{11}^{(1)}\\ .\\ .\\ .\\ \omega _{1n}^{(1)} \end{pmatrix} =\begin{pmatrix} \dfrac{3}{h}\\ 0\\ -\dfrac{3}{h}\\ .\\ .\\ 0 \end{pmatrix} \end{aligned}$$

(47)

The solution of the above system provides the coefficients $\omega _{10}^{(1)}, \omega _{11}^{(1)},\ldots ,\omega _{1n}^{(1)}$. In the same way, the weighting coefficients corresponding to $x_i, i =2, 3, \ldots , n-1$ are determined. Finally, for the last knot, $\check{B_k}'(x_n)$ is given by 6/h at $x_n$ and $-6/h$ at $x_{n-1}$.

$$\begin{aligned}&\check{B_k}'(x_{n})=\sum _{j=0}^{n}\omega _{nj}^{(1)}\check{B_k}(x_j), \quad k=0,1,\ldots ,n \end{aligned}$$

(48)

$$\begin{aligned}&\begin{pmatrix} 6 &{}1 &{} 0 &{} &{} &{} \\ 0 &{}4 &{}1 &{}0 &{} &{}\\ &{} &{}1 &{}4 &{}1 &{} &{}\\ \cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots &{}\cdots \\ &{} &{}1 &{}4 &{}1 &{}\\ &{} &{}0 &{}1 &{}4 &{}0\\ &{} &{} &{} 0 &{}1 &{}6 \end{pmatrix} \begin{pmatrix} \omega _{n0}^{(1)}\\ \omega _{n1}^{(1)}\\ .\\ .\\ .\\ \omega _{nn}^{(1)} \end{pmatrix} =\begin{pmatrix} 0\\ 0\\ .\\ .\\ -\dfrac{6}{h}\\ \dfrac{6}{h} \end{pmatrix} \end{aligned}$$

(49)

for which solution provides the coefficients $\omega _{n0}^{(1)}, \omega _{n1}^{(1)}, \ldots , \omega _{nn}^{(1)}$. Thus, we have calculated the first-order weighting coefficient $\omega _{ij}^{(1)}$ of B-spline functions for $0\le i,j\le n$.

In the same way, the weighting coefficient $\omega _{ij}^{(2)}, 0\le i,j\le n$ for the second-order partial derivative, is determined. Second- or higher-order weighting coefficients are computed by using Shu recursion formula [32]:

$$\begin{aligned} \omega _{ij}^{(k)} = \, & {} k\Big [\omega _{ij}^{(1)}\omega _{ii}^{(k-1)}-\dfrac{\omega _{ij}^{(k-1)}}{(x_i-x_j)}\Big ], \end{aligned}$$

(50)

$$\begin{aligned} \omega _{ii}^{(k)}= & {} -\sum _{j=0,j\ne i}^{n}\omega _{ij}^{(k)}, \,i=j\, \text {and} \,i=0,1,\ldots ,n \end{aligned}$$

(51)

6 Implementation of Differential Quadrature Method (DQM)

Applying the DQM to Eq. (5) , we get

$$\begin{aligned}&\frac{\mathrm{d}\phi (x_i,t)}{\mathrm{d}t}\nonumber \\&\quad =-\sum _{j=1}^{n-1}\omega _{ij}^{(2)}\psi (x_i,t)+G(x_i,t),\quad \text {for} \; i=1,\ldots ,n-1, \end{aligned}$$

(52)

$$\begin{aligned}&\frac{\mathrm{d}\psi (x_i,t)}{\mathrm{d}t}\nonumber \\&\quad =\sum _{j=1}^{n-1}\omega _{ij}^{(2)}\phi (x_i,t),\qquad \qquad \qquad \;\text {for} \; i=1,\ldots ,n-1, \end{aligned}$$

(53)

with initial conditions and boundary conditions Eqs. (6) and (7). Now the above system is written as

$$\begin{aligned} \frac{\mathrm{d}\varOmega }{\mathrm{d}t}=\mathbb {P}\varOmega +\mathbb {Q} \end{aligned}$$

(54)

where

$$\begin{aligned} \mathbb {P}=\left[ {\begin{array}{cc} 0 &{} -A\\ A &{} 0 \end{array}}\right] ,\;\varOmega = \left[ {\begin{array}{cc} \phi \\ \psi \end{array}}\right] \text {and}\; \mathbb {Q}=\left[ {\begin{array}{cc} G_1\\ 0 \end{array}}\right] \end{aligned}$$

(55)

where A is a matrix of the weighting coefficients $\omega _{ij}^{(2)}$ and $\mathbb {Q}$ contains boundary and other values. Then, the above system of ODE is integrated w.r.t. time deploying an appropriate method. Here, strong stability-preserving fourth-order RK method is preferred for its inherent advantages such as correctness of solution, numerical stability and compact memory requirements.

7 Stability of DQM

From Eq. (54), we have system

$$\begin{aligned} \frac{\mathrm{d}\varOmega }{\mathrm{d}t}=\mathbb {P}\varOmega +\mathbb {Q} \end{aligned}$$

(56)

where $\varOmega =[\phi \;\psi ]^T=[\phi _2,\phi _3, \ldots , \phi _{n-1}\;\; \psi _2,\psi _3, \ldots , \psi _{n-1}]^T$ is the solution vector at the internal nodes, $\mathbb {P}$ is the coefficient matrix and the vector $\mathbb {Q}$ representing the boundary and other values.

Assume that $\lambda _i$ is the eigenvalue of $\mathbb {P}$. Asymptotically, for the stable solution of $\varOmega$, we must have

• 1. $-2.78<\Delta t\lambda _i <0$, if eigenvalues are real.

• 2. $-2\sqrt{2}<\Delta t\lambda _i<2\sqrt{2}$, if eigenvalues have complex part only.

• 3. $\Delta t\lambda _i$ should be in a region as shown in Fig. 2, if eigenvalues are complex.

Fig. 2

Stability region

Eigenvalues of $\mathbb {P}$ depend upon the eigenvalues of A, which are found to be within the stability region. Similarly, we can check the stability of nonlinear problems.

8 Numerical Experiments

This section presents the results obtained by CBSQI and DQM in graphical and tabular forms with the brief description. The accuracy and efficiency of the proposed method are calculated for four test problems by maximum absolute error norm, which is defined as follows.

$$\begin{aligned} L_\infty =\Vert {v^{\rm exact}-v^{\rm cal}}\Vert =\max _{\begin{array}{c} i \end{array}}\mid {v_i^{\rm exact}-v_i^{c\rm al}}\mid \end{aligned}$$

(57)

where $v^{\rm exact}_i$ and $v^{\rm cal}_i$ denote the exact and calculated solutions at knot $x_i$, respectively.

The convergence rate of the DQM is to be evaluated, which is obtained by $L_\infty$ error norm. The following formula has been used to compute the order of convergence:

$$\begin{aligned} \text {Order}=\frac{\log{(E(N_1)/E(N_2)})}{\log({N_1/N_2)}} \end{aligned}$$

(58)

where $E(N_1)$ is the error and $N_1$ is the count of partitions.

We have calculated the rate of convergence of the CBSQI method for Problem 1. Figure 3 shows that CBSQI provides the second-order approximation.

Fig. 3

Log–log plot between errors and space step

Problem 1

Consider a fourth-order nonhomogeneous PDE

$$\begin{aligned} \frac{\partial ^2 v}{\partial t^2} + \frac{\partial ^4 v}{\partial x^4}=(\pi ^4-1)\sin {\pi x}\cos {t},\quad x\in [0, 1],\quad t>0 \end{aligned}$$

along with initial conditions

$$\begin{aligned} v(x,0)=\sin {\pi x},\quad v_t(x,0)=0,\quad x\in [0, 1] \end{aligned}$$

and boundary conditions

$$\begin{aligned} v(0,t)=v(1,t)=v_{xx}(0,t)=v_{xx}(1,t)=0, \quad t\ge {0}. \end{aligned}$$

The analytical solution is $v(x,t)=\sin {\pi x}\cos {t}.$ From Eq. (4), initial and boundary conditions are derived as

$$\begin{aligned}&\phi (x,0)=0,\quad \phi (0,t)= \phi (1,t)=0.\\&\psi (x,0)=-\pi ^2\sin {\pi x},\quad \psi (0,t)=\psi (1,t)=0. \end{aligned}$$

The computed results obtained by both methods and analytical solution are compared in Table 2.

In Table 2, displacement v(x, t) and bending moment $v_{xx}(x,t)$ are computed for different values of $t = 0.02$ and 0.1 for each $n = 20, 40, 60$ and $\Delta t = 0.0001$. We observe that computed results by DQM for $n = 20, 40, 60$ are better than CBSQI. But instead of this, we also observe that CBSQI produces good results for large $n=90, 180, 270$, while DQM becomes unstable for such large n.

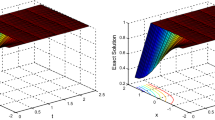
Figure 4 depicts the computed numerical results for $n = 60$, $\Delta t = 0.0001$ at $t = 0.1$. In Table 3, we compare our results with Mittal and Jain [10], and it is clear that CBSQI method gives good results.

Table 2 Maximum absolute errors in v(x, t) and $v_{xx}(x,t)$ for Problem 1

Table 3 Maximum absolute errors in v(x, t) for Problem 1

Fig. 4

Displacement for $t\le 0.1$ ($n=60$, $\Delta t=0.0001$)

Problem 2

Consider the singularly perturbed problem of the form:

$$\begin{aligned} \frac{\partial ^2 v}{\partial t^2} + \epsilon \frac{\partial ^4 v}{\partial x^4}=f(x,t),\quad 0<{\epsilon }< < {1},\quad x\in (0, 1),\quad t>0 \end{aligned}$$

The analytical solution is $v(x,t)=\text {e}^{-\epsilon \pi ^2t}\sin {\pi x}.$ From this, we get initial conditions

$$\begin{aligned} v(x,0)=\sin {\pi x},\quad v_t(x,0)=-\epsilon \pi ^2\sin {\pi x},\quad x\in [0, 1] \end{aligned}$$

and boundary conditions

$$\begin{aligned} v(0,t)=v(1,t)=v_{xx}(0,t)=v_{xx}(1,t)=0, \quad t\ge {0}. \end{aligned}$$

From Eq. (4), initial and boundary conditions are derived as

$$\begin{aligned}&\phi (x,0)=-\epsilon \pi ^2\sin {\pi x},\quad \phi (0,t)=0 =\phi (1,t)=0.\\&\psi (x,0)=-\pi ^2\sin {\pi x},\quad \psi (0,t)=\psi (1,t)=0. \end{aligned}$$

The computed results obtained by both methods and analytical solution are compared in Table 4.

In Table 4, using $h = 1/8, 1/16, 1/32$ and corresponding $\Delta t =0.025, 0.00625, 0.0015625$, we compute displacement v(x, t) and bending moment $v_{xx}(x,t)$ for different values of $\epsilon =0.1, 0.01, 0.001$ and time level $t=1$ by applying both methods. We found that for $\epsilon = 0.01, 0.001$ computed results by DQM are better than CBSQI. But instead of this, we also observe that CBSQI produces good results for large $\epsilon = 0.1$, while DQM becomes unstable.

Figure 5 depicts the computed numerical results for $n = 32$, $\Delta t = 0.0015625$ at $t = 1$.

Table 4 Maximum absolute errors in v(x, t) and $v_{xx}(x,t)$ for Problem 2

Fig. 5

Displacement for $t\le$1 ($n=32$, $\Delta t=0.0015625$, $\epsilon =0.001$)

Problem 3

Consider a fourth-order nonhomogeneous PDE

$$\begin{aligned} \frac{\partial ^2 v}{\partial t^2} + \frac{\partial ^4v }{\partial x^4}=[24-x^2(1-x)^2]\cos {t},\quad x\in [0, 1],\quad t>0 \end{aligned}$$

along with initial conditions

$$\begin{aligned} v(x,0)=x^2(1-x)^2,\quad v_t(x,0)=0,\qquad \qquad x\in [0, 1] \end{aligned}$$

and boundary conditions

$$\begin{aligned} v(0,t)=v(1,t)=0,\quad v_{xx}(0,t)=v_{xx}(1,t)=2\cos {t}, \quad t\ge {0} \end{aligned}$$

The analytical solution is $v(x,t)=x^2(1-x)^2\cos {t}$. From Eq. (4), initial and boundary conditions are derived as

$$\begin{aligned}&\phi (x,0)=0,\quad \phi (0,t)= \phi (1,t)=0.\\&\psi (x,0)=2-12x+12x^2,\quad \psi (0,t)=\psi (1,t)=2\cos {t}. \end{aligned}$$

The computed results obtained by both methods and analytical solution are compared in Table 5.

Figure 6 depicts the computed numerical results for $n = 60$, $\Delta t = 0.0001$ at $t = 0.1$.

Table 5 Maximum absolute errors in v(x, t) and $v_{xx}(x,t)$ for Problem 3

Fig. 6

Displacement for $t\le 0.1$ ($n=60$, $\Delta t=0.0001$)

Problem 4

Consider a fourth-order nonhomogeneous PDE

$$\begin{aligned}&\frac{\partial ^2 v}{\partial t^2} + (1+x)\frac{\partial ^4 v}{\partial x^4}=f(x,t), \quad x\in [0, 1],\quad t>0\\&\text {where}\;f(x,t)=-72(1+x)(1-5x+5x^2)t\sin {t}+(x-x^2)^3(2\cos {t}-t\sin {t}). \end{aligned}$$

The initial and boundary conditions are as follows

$$\begin{aligned}&v(x,0)=0,\quad v_t(x,0)=0,\qquad \qquad \qquad \quad x\in [0, 1],\\&v(0,t)=v(1,t)=v_{xx}(0,t)=v_{xx}(1,t)=0,\ \qquad t\ge {0}, \end{aligned}$$

The analytical solution is $v(x,t)=(x-x^2)^3t\sin {t}$. From Eq. (4), initial and boundary conditions are derived as

$$\begin{aligned}&\phi (x,0)=0,\quad \phi (0,t)= \phi (1,t)=0.\\&\psi (x,0)=0,\quad \psi (0,t)=\psi (1,t)=0. \end{aligned}$$

The computed results obtained by both methods and analytical solutions are compared in Table 6.

Figure 7 depicts the computed numerical results for $n = 60$, $\Delta t = 0.0001$ at $t = 1$.

Table 6 Maximum absolute errors in v(x, t) and $v_{xx}(x,t)$ for Problem 4

Fig. 7

Displacement for $t\le 1.0$ ($n=60$, $\Delta t=0.0001$)

Thus, according to the given tabular results and figures, we conclude that for each problem, DQM gives better solutions than CBSQI for the small number of grid points, but we also found that for a large number of grid points, DQM becomes unstable, whereas CBSQI produces good solutions.

9 Conclusions

In this paper, we have presented two numerical methods named CBSQI and DQM for solving fourth-order parabolic PDEs. The proposed methods are tested on four test problems, and on the basis of these results, we summarize the final outcomes as

• 1. DQM gives better solutions than CBSQI when the number of grid points is small, but we also found that for a large number of grid points, DQM becomes unstable, whereas CBSQI produces good solutions.

• 2. The stability of both the methods is discussed, and it is found that DQM is conditionally stable, whereas CBSQI is unconditionally stable.

• 3. To the best of the authors' knowledge, CBSQI Crank–Nicholson scheme technique has been used for the first time for solving fourth-order parabolic PDEs. The main advantage of CBSQI is that it is very easy to implement.

• (iv) The proposed methods can be applied for higher dimensional problems.