A chaotic salp swarm algorithm based on quadratic integrate and fire neural model for function optimization

Abstract

Real-world problems generally do not possess mathematical features such as differentiability and convexity and thus require non-traditional approaches to find optimal solutions. SSA is a meta-heuristic optimization algorithm based on the swimming behaviour of salps. Though a novel idea, it suffers from a slow convergence rate to the optimal solution, due to lack of diversity in salp population. In order to improve its performance, chaotic oscillations generated from quadratic integrate and fire model have been augmented to SSA. This improves the balance between exploration and exploitation, generating diversity in the salp population, thus avoiding local entrapment. CSSA has been tested against twenty-two bench mark functions. Its performance has been compared with existing standard optimization algorithms, namely particle swarm optimization, ant–lion optimization and salp swarm algorithm. Statistical tests have been carried out to prove the superiority of chaotic salp swarm algorithm over the other three algorithms. Finally, chaotic SSA is applied on three engineering problems to demonstrate its practicability in real-life applications.

1 Introduction

In recent times, meta-heuristic techniques have become very popular. At a time when engineering problems are engulfed in the midst of gargantuan complexity, meta-heuristic approaches have offered a safe haven by providing reliable, computationally fast and efficient methods for generating solutions. One of the reasons for this enormous demand for the use of meta-heuristic approaches is that they provide a simple black-box approach, whereby the problem of interest is defined only in terms of inputs and outputs. No special care needs to be taken to fit the problem to the meta-heuristic algorithm for generating solutions. Also, these approaches handle the case of constrained optimization problems quite elegantly.Constraint optimization problems are problems in which the target function is minimized or maximized based on constraints. Constraints define the feasible domain space wherein the solution has to be looked for [1]. While conventional deterministic approaches suffer from increased complexity, meta-heuristic approaches are not affected by the same. On top of that, accuracy of the solution generated is quite high and is obtained within a very reasonable amount of time. Again, in this case, the problem of local minima entrapment also is not present. Local minima entrapment refers to the entrapment of the algorithm in a local minimum solution. This prevents the algorithm from finding out the global optimum solution in the search domain. Therefore, it is not difficult to see why this class of techniques has won hearts of researchers from various domains of engineering and sciences. Meta-heuristic approaches belong to the family of stochastic optimization techniques as they take random operators into account during optimization.

In the broadest sense, stochastic optimization algorithms can be based on inspiration of an algorithm and the number of random solutions generated in each step of optimization process [2, 3]. The first category includes swarm intelligence-based algorithms [4], evolutionary algorithms [5] and physics-based algorithms [6]. The second category can be divided into two sub-categories, namely (1) individual-based algorithms and (2) population-based algorithms [3]. In individual-based algorithms, a single random solution is chosen and is iteratively improved so as to obtain an optimal solution. These algorithms are faster as they have lesser computational costs and fewer function evaluations. Popular algorithms of these categories include tabu search [7], hill climbing [8], iterated local search [9] and simulated annealing [10]. One of the major disadvantages of these algorithms is that they are susceptible to premature convergence. This prevents them from attaining global optimum solutions. Premature convergence occurs when the algorithm gets trapped in a local minimum and is unable to find the global minima.

The population-based algorithms start with an initial set of candidate solutions, expressed as $\overrightarrow{y} = \{ \overrightarrow{y_1} , \overrightarrow{y_2} , \overrightarrow{y_3} , \ldots , \overrightarrow{y_n} \},$ where n denotes the number of candidate solutions. Each solution is evaluated against a fitness function. The algorithm then proceeds to obtain better solutions with higher fitness values by modifying or updating or combining the candidate solutions. The new obtained solutions are again tested with the fitness function. The process continues until a solution with desirable accuracy is obtained. One of the major advantages of these algorithms over individual-based approach is that they are not susceptible to premature convergence. Since many particles are computed at a time, chances of getting trapped into a local optimum is minimum. Two popular sub-categories of population-based algorithms are evolutionary computing and swarm intelligence.

Evolutionary category of meta-heuristic algorithms that start out with a set of randomly chosen solutions and better solutions is generated from the chosen set. These algorithms mimic the Darwinian theory of evolution, whereby weaker solutions are eliminated. Some of the prominent examples include genetic algorithm [12], differential evolution [13], evolutionary Programming [14], evolutionary strategy [16], human evolutionary model [38], evolutionary membrane algorithm [39] and asexual reproduction optimization [40].

The second category of meta-heuristic algorithms, i.e. swarm intelligence algorithms, is inspired by the collective behaviour of a group of creatures, such as ants, birds, grey wolves and whales. In a swarm, each creature keeps track of its own position, as well as the position of its neighbours. The whole group cooperates with each other to find resources, protects itself from enemies and sustains itself in the long run. Moving along the same train of thought, swarm intelligence algorithms use intelligence of individual elements of the swarm to compute the most optimal solution in the search space. Advantages of using swarm intelligence algorithms can be stated as follows. First, there are only a few parameters to adjust, compared to evolutionary algorithms. Second, during the course of iteration, information regarding the search space is not lost. Third, there are comparatively lesser operators to adjust. Fourth, implementation is quite easy. Some of the most popular examples of these algorithms include particle swarm optimization [31], whale optimization [42], grey wolf optimization [25], ant colony optimization [30], artificial bee colony algorithm [11], firefly algorithm [32], cuckoo search algorithm [28], democratic particle swarm optimization [29], Dolphin Echolocation [41], ant–lion optimization [57], cuckoo optimization algorithm [34], fruit fly optimization algorithm [35], bat algorithm [36], moth-flame optimization algorithm [47], mushroom reproduction optimization (MRO) [48], butterfly optimization algorithm [49], Andean Condor Algorithm [51].

A third category of meta-heuristic algorithms is based on the principles of physics operating in the universe. Examples of this category include gravitational search algorithm [23], charged system search [24], ray optimization [26], colliding body optimization [54], blackhole optimization algorithm [55], big-bang big crunch algorithm [27], gravitational local search [17], central force optimization [18], artificial chemical reaction optimization algorithm [19],small world optimization algorithm [20], galaxy-based search algorithm [21], curved space optimization [22].

To further improve the performance of these existing algorithms, chaotic behaviour can be incorporated. Chaotic behaviour is generally displayed by nonlinear dynamic systems which are highly sensitive to initial conditions. These systems display chaotic behaviour by performing infinite unstable periodic motions across a range of permissible values [33]. Chaotic behaviour has been augmented in algorithms like genetic algorithms [52], harmonic search [56], PSO [43], ABC [44], FA [45], BOA [53], GWO [33].

In the presented work, we propose a chaotic salp swarm algorithm driven by 1D poincare map of quadratic leaky integrate and fire model for generating chaotic oscillations. To our knowledge, our work is the first to empower a meta-heuristic algorithm with a neural model. This new approach opens the immense possibilities for developing a whole spectrum of algorithms based on neural models.

The rest of the section is divided as follows: In Sect. 2, a background study has been presented. In Sect. 2.1, an overview of salp swarm optimization algorithm has been presented. In Sect. 2.2, an overview of quadratic integrate and fire model has been presented. In Sect. 2.3, an overview of chaos theory and chaos maps has been presented. In Sect. 3, the chaotic SSA(CSSA) algorithm has been described. Section 4 contains results and discussions regarding CSSA, which includes benchmark function testing and statistical testing. Section 5 presents the application of CSSA on three real-life engineering problems, namely gear train design problem, cantilever beam design problem and welded beam design problem. Section 6 presents the conclusion and future scope of the algorithm.

2 Background

In this section, an overview of salp swarm algorithm, quadratic integrate and fire neural model and chaos theory and chaos maps has been presented.

2.1 Overview of salp swarm algorithm

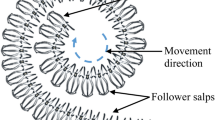
Salp swarm optimization algorithm [37] is a recently developed algorithm based on the swarm behaviour of the salps. Salps are deep sea creatures belonging to the family of Salpidae. Like many deep sea creatures, they have transparent barrel-shaped body and propagate by pumping water through their body to move forward. Salps form a chain structure called salp chain. The swarm coordination between salps in the chain helps them to perform better coordination in movement and foraging.

Salp chains have two types of population groups: leader and followers. The leader is at the front of the salp chain. It leads the group and is responsible for maintaining a balance between the exploration and exploitation ratio. Followers follow each other and the leader. The position of the salps is defined in n-dimensional search space, where n is the number of variables in the given optimization problem. The food source is denoted as F, which is the swarm’s target.

The position of the leader is defined as:

$$\begin{aligned} f(x) = \left\{ \begin{array}{ll} F_i +c_1((ub_i -lb_j)c_2+lb_j), &{} \text{ if } c_3 \ge 0;\\ F_i -c_1((ub_i -lb_j)c_2+lb_j) ,&{} \text{ if } c_3 < 0;\end{array} \right. \end{aligned}$$

(1)

where $x_j^1$ is the position of the first salp in the $j\mathrm{th}$ dimension, $F_j$ is the position of the food in the jth dimension and $ub_{j}$ and $lb_{j}$ are the upper and lower bounds in the $j\mathrm{th}$ dimension. c1,c2,c3 are random numbers. Also,

$$\begin{aligned} c_1=2e^{-\left( \frac{4l}{L}\right) ^2} \end{aligned}$$

(2)

l is the current iteration, and L is the maximum number of iterations. $c_2$, $c_3$ are random numbers generated from $\left[ 0,1 \right]$.

The position of the followers is given by:

$$\begin{aligned} x_j^i=\frac{1}{2}\big ( x_j^i + x_j^{i-1}\big ) \end{aligned}$$

(3)

where i $\ge$ 2 and $x_j^i$ is the $i\mathrm{th}$ follower salp in the $j\mathrm{th}$ dimension. Algorithm for salp optimization is shown in Fig. 1.

Fig. 1

Algorithm for SSA [3]

2.2 Overview on quadratic integrate and fire neural model

Neurons are the basic building blocks of the brain and the central nervous system. There are about 86 billion neurons within the nervous system to communicate with rest of the body. They are usually classified into three broad types: sensory neurons, motor neurons and interneurons. The fundamental function of a neuron is to convert an incoming stimuli into a train of electrical events called as spikes. Spikes are sudden upsurges in membrane potential when the membrane potential reaches a specific value, called threshold voltage. Some popular models for replicating the firing behaviour of neurons are leaky integrate and fire model [69], modified leaky integrate and fire model [68], Hodgkin–Huxley model [69], compartment model [69].

Quadratic integrate and fire model [69] is a variant of leaky integrate and fire model. Compared to traditional leaky integrate and fire model, quadratic integrate and fire model can provide a better replication of dynamic behaviour of biological neurons. QIF model can be represented as

$$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}t}= & {} y^2 +a +y \end{aligned}$$

(7)

$$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}t}= & {} \frac{b-y}{\tau (y)} \end{aligned}$$

(8)

and spike rules are:

$$\begin{aligned} \left\{ \begin{array}{ll} x(t^+)=q, &{} {\hbox {if}}\;x(t)=h;\\ y(t^+)=cy(t)+p ,&{} {\hbox {if}}\; x(t)=h;\end{array} \right. \end{aligned}$$

(9)

and $t^+=\mathrm{lim}_{\epsilon \rightarrow 0, \epsilon >0} (t+\epsilon )$. h is the peak of the spike, q is the reset value, p, c, b describe the adaptive current and c $\ge$ 0. $\tau (x)$ defines the voltage-dependent adaptive time constant and is defined as $\tau (x)=\tau /x$, where $\tau$ is a constant.

2.2.1 Chaotic behaviour in QIF model

Considering the poincare section: $S=\{(x,y)| x=h\}$, chaotic behaviour is displayed in QIF model if the parameters follow the following 6 conditions [46]:

$$\begin{aligned}&(cQ+H)^2 -(Q^2-H^2+L)(c^2-1) \ge 0 \end{aligned}$$

(10)

$$\begin{aligned}&l \ge 0 \end{aligned}$$

(11)

$$\begin{aligned}&c > 1 \end{aligned}$$

(12)

$$\begin{aligned}&H> f(y_z)=y_A > y_*; \end{aligned}$$

(13)

$$\begin{aligned}&f(y_A)=y_B < y_1 \end{aligned}$$

(14)

$$\begin{aligned}&y_k \ne \frac{Q}{c} \end{aligned}$$

(15)

where

$L=(2a + h^2 +q^2 -b)$,

$H=(a+h^2)$ ,

$Q=(p-a-q^2)$,

$y_z=\frac{-Q}{c}$,

$y_A=f(y_z)$,

$y_* = \frac{\sqrt{(cQ+ H )^2 -(Q^2-H^2+L)(c^2-1)}-(cQ+H)}{c^2 -1}$

a, q, b, p, h, c are parameters as defined in the previous section. The poincare map for quadratic integrate and fire model is given by:

$$\begin{aligned} y_{i+1}=f(y_i)=H-\sqrt{(cy_i+Q)^2 + L} \end{aligned}$$

(16)

2.3 Chaos theory and chaotic maps

In its most general form, a chaos is a deterministic, random-like method found in nonlinear, dynamic system, which is non-periodic, bounded and-nonconverging. Mathematically, chaos is the randomness of a simple deterministic dynamical system and chaotic system may be considered as a source of randomness [50]. Chaos is apparently random, but possesses an element of regularity. It is due to this regularity that chaotic variables can be used to perform searches at higher speeds compared to pure stochastic searches. In addition, a change in only a few variables and an alteration in initial state is required to obtain an entirely different sequence. So, chaotic maps have been used in number of meta-heuristic search algorithms. Some popular chaotic maps are included in Table 1. Some popular chaotic algorithm includes chaotic krill herd optimization algorithm [63], chaotic grasshopper optimization algorithm [64], chaotic whale optimization algorithm [65], chaotic grey wolf optimization algorithm [66], chaotic bee colony algorithm [67].

Table 1 Examples of chaotic maps

3 Proposed quadratic integrate and fire model-driven salp swarm optimization

In the proposed work, SSA [37] is forged with chaotic oscillations arising from quadratic integrate and fire model [61]. This helps SSA to avoid local optimum solutions. Also, ergodicity and non-repetition properties of chaos ensure that overall searches are done at faster rate compared to stochastic searches. The proposed algorithm is shown in Fig. 2. In the first step, the salp population is initialized with random values. QIF model parameters are initialized as well. After this, fitness of each search agent is calculated. The position of leader salp is updated, and the positions of follower salps are calculated by augmenting the chaotic map value. The chaotic map sequence is then updated, and position of salps is adjusted based on upper and lower bounds. This process continues till the termination condition is not fulfilled. The chaotic map value helps to avoid local minima entrapment and ensures faster convergence.

Fig. 2

Algorithm for chaotic SSA

4 Results and discussion

In this section, two experiments have been performed to prove that CSSA performs better than the standard meta-heuristic algorithms. For comparison purposes, we have chosen three standard nature-inspired heuristic algorithms, namely PSO, ALO and SSA. The experiment can be divided into two broad categories: (1) testing against benchmark functions and (2) statistical testing. In the first test, all the four algorithms are tested against a set of 22 benchmark functions. The best-case performance, worst-case performance, average-case performance and standard deviation of each algorithm are compared with those of CSSA. Relevant conclusions are drawn based on these parameters.

Since meta-heuristic algorithms are probabilistic in nature, comparison based on mean and standard deviation is not sufficient. So, statistical testing methods are used to prove the hypothesis that CSSA performs better than the other three algorithms. Friedman test was used for this purpose in the presented work. Further, Holms test was employed to show that CSSA performs the best. All simulations were performed on a Intel(R) Core(TM) i7-5500U CPU with a clock rate of 2.40GHz. Finally, an asymptotic complexity analysis of the algorithm has been performed.

4.1 Test against standard benchmark functions

CSSA, SSA, PSO, ALO were tested against a set of benchmark functions. The details of the benchmark functions are stated in appendix A. Maximum number of iterations used for all the algorithms is 1000. The details of the performance of all the mentioned algorithms are shown in Table 2. It can be observed that CSSA has clearly surpassed the performance of all other algorithms based on the best-case and average-case parameters. The standard deviation is also minimum, indicating that the algorithm is stable near the global optimum. CSSA performs better than other algorithms in functions F1, F2, F3, F4, F5, F6, F8, F9, F10, F12, F13, F15, F19, F20, F21, F22 in terms of average fitness values. In F7, its performance is equivalent to SSA, and in functions F16 and F17, all algorithms perform equally. In F11, CSSA performs worse than all other algorithms. Also, in terms of best-case values, CSSA performs better than other algorithms in F1, F2, F3, F4, F5, F6, F7, F9, F10, F11, F12, F13, F15, F21. It performs equivalent to SSA in F8 and F15. In F18, F19, F20, F22, CSSA, SSA and ALO perform equivalently. In F14, F16, F18, all algorithms perform equivalently. Further, standard deviation is minimum for most cases in CSSA, when compared with other algorithms.

The convergence graphs of the functions with respect to the functions are shown in Fig. 3. The convergence graphs have been drawn with respect to the best-case performances obtained from the benchmark functions. It can be clearly seen that CSSA has outperformed all other algorithms in most of the benchmark functions. These improved results can be attributed to the enhanced balance between exploration and exploitation ratio obtained from integrating chaotic oscillations.

4.2 Statistical measures for performance evaluation

Statistical techniques are used to prove the significant differences between results of optimization algorithms. Friedman test has been used in our work. Friedman test is a nonparametric test which is used to find differences among groups for ordinal dependent variables [60]. The null hypothesis is stated as:

$H_0: {\text {All the optimization algorithms are equivalent}}$

The confidence level $\alpha$ is taken as 0.05. Ranks are assigned based on the value of the best-case results obtained in the test functions. The ranks are assigned from 1 to 4. The average rank is calculated as:

$$\begin{aligned} R_j=\frac{\text {Sum of total ranks obtained by}\,j_\mathrm{th} \text { algorithm}}{\text {Total number of functions.}} \end{aligned}$$

(20)

Table 2 Results from tests against benchmark functions

Fig. 3

Convergence curves

Friedman statistics is represented as:

$$\begin{aligned} F_F=\frac{(N-1)X_F^2}{N(k-1)-X_F^2} \end{aligned}$$

(21)

where

$$\begin{aligned} X_F^2=\frac{12N}{k(k+1)}\left[ \sum _{j}R_j^2 - \frac{k(k+1)^2}{4} \right] \end{aligned}$$

(22)

Here N is the number of test functions, and k is the number of algorithms used. The Friedman statistic $F_F$ is distributed according to the F-distribution with ($k-1$) and ($k-1$) ($N-1$) degree of freedom. For 4 algorithms and 22 test functions, the degree of freedom is from 3 to 63. Therefore, the critical value of F(3,63) for $\alpha$ for $\alpha =0.05$ is 2.75. If $F_F$ value is less than the critical value, then the null hypothesis is accepted, otherwise it is rejected. Clearly, the value of $F_F=6.833$ is greater than the critical value. Therefore, the null hypothesis is rejected. This implies there exists some difference between the algorithms (Table 3).

Since the null hypothesis is rejected, Holm’s test is performed. It determines whether performance of CSSA is better than the other algorithms.

$H_0:\hbox {The}$ pair algorithms being compared are different

z value is computed as

$$\begin{aligned} z=\frac{R_i-R_j}{SE} \end{aligned}$$

(23)

where

$$\begin{aligned} SE=\sqrt{\frac{k(k+1)}{6N}} \end{aligned}$$

(24)

Here, CSSA is the control algorithm. After computing the z value, probability, p is computed from the normal distribution. If the computed p value is less than $\left( \frac{\alpha }{k-i} \right)$, then the hypothesis is rejected, else it is accepted. The results of Holm’s test are shown in Table 4.

Since the all the other algorithms are rejected, it is proved that CSSA performs better than the other algorithms.

Table 3 Average ranking of algorithms based on the evaluations from benchmark functions

Table 4 Holms test

4.3 Asymptotic complexity analysis of CSSA

In this section, an asymptotic analysis of running time of CSSA has been presented. Asymptotic analysis is concerned with the change in running time of an algorithm based on the input size [62]. It does not involve actual experimentation to find the running time of an algorithm. It is based on a theoretical analysis where running time of an algorithm is represented as a function of input size.

There are five asymptotic notations used during the analysis, namely $\theta$, O, $\omega$, o, $\Omega$, which are as follows:

For a given function g(n),

$\theta (g(n))=\{f(n): \text {There exist positive constants }c_1, c_2, \text {and}\ n_o\ \text {such that}\ 0 \le c_1g(n)\le f(n) \le c_2 g(n)\ \text {for all }\ n \ge n_0\}$

$O(g(n))=\{f(n): \text {There exist positive constants }c\ \text {and}\ n_o \text {such that}\ 0 \le f(n) \le c g(n)\ \text {for all }\ n \ge n_0\}$

$\Omega =(g(n))=\{f(n): \text {There exist positive constants } c \ \text {and} n_o \ \text {such that}\ 0 \le cg(n)\le f(n)\ \text {for all }\ n \ge n_0\}$

$o(g(n))=\{f(n): \text {For any positive constant }c> 0, \text {there exists a constant}\ n_o >0\ \text {such that}\ 0 \le f(n) < c g(n)\ \text {for all }\ n \ge n_0\}$

$\omega (g(n))=\{f(n): \text {For any positive constant }c> 0, \text {there exists a constant}\ n_o >0\ \text {such that}\ 0 \le c g(n) < f(n) \ \text {for all }\ n \ge n_0\}$

Major contributing factors for complexity analysis of CSSA include number of iterations involved, number of salps, chaotic map generation and updations. Initializing the position of the salps in step 1 has complexity O(n). Similarly, chaotic map calculation has complexity O(n). Now, for each iteration, fitness calculation has a complexity of O(n). Updation of c1 has complexity O(1). Also, position update for each iteration has complexity O(n). Now, involving the total number of iterations in the analysis, it can be concluded that asymptotic complexity of CSSA is $O(n^2)$. Thus, CSSA is a polynomially bound algorithm.

Fig. 4

Structure of gear train design

Table 5 Gear design problem

Fig. 5

Cantilever beam design problem

Table 6 Cantilever problem

5 Applications in engineering problems

In this section, CSSA algorithm has been applied to three engineering problems, namely gear train design problem, cantiliver problem and welded beam design problem. A brief description of the three problems has been provided, followed by results from simulation with SSA and CSSA.

5.1 Gear train design problem

This problem has been formulated to find the minimum number of tooth for four gears of a train in order to reduce the cost of gear ratio [59]. It can be depicted as shown in Fig. 4. It has four decision variables, namely $\eta _A( x_1)$, $\eta _B(x_2)$, $\eta _C(x_3)$ and $\eta _D(x_4)$.

The minimization function can be described as:

$$\begin{aligned} Min \ F(x)=\left( \frac{1}{6.931}- \frac{x_3 x_2}{x_1x_4} \right) ^2 \end{aligned}$$

(25)

where $12 \le x_i \le 60$ and $i=1,2,3,4$.

The results obtained for the minimization problem from SSA and CSSA are depicted in Table 5. Clearly, CSSA has outperformed all other algorithms.

5.2 Cantilever beam

This problem is formulated to minimize the weight of the cantilever beam [59]. The beam consists of hollow elements of square cross section, where the thickness of the elements is constant. The right end of the beam is rigidly supported, and a load is applied on the free end. Figure 5 shows the described configuration.

The minimization problem can be shown as:

$$\begin{aligned} \mathrm{Min} F(x)=0.06224(x_1+x_2+x_3+x_4+x_5) \end{aligned}$$

(26)

subject to the constraints:

$$\begin{aligned} g(x)=\frac{61}{x_1^3}+\frac{37}{x_2^3}+\frac{19}{x_3^3}+\frac{7}{x_4^3}+\frac{1}{x_5^3} \le 1 \end{aligned}$$

(27)

where $0.01 \le x_i \le 100$, ${i}=1,2,\ldots ,5$

The results obtained from CSSA have been compared with PSO, ALO, SSA and are depicted in Table 6.

CSSA was able to obtain the most optimal value for the objective function F.

5.3 Welded beam design

In this problem, the cost of fabrication of welded beam is to be minimized [59]. The structure consists of a beam A and the weld for holding it onto member B. The schematic diagram is shown in Fig. 6.

Fig. 6

Structure of welded beam design problem

The minimization function can be defined as:

(28)

subject to constraints:

where

$$\begin{aligned}&0.1\le h\le 2.0,\\&0.1 \le l \le 10\\&0.1 \le t \le 10\\&0.1 \le b \le 2.0\\&G=12\times 10^6 psi\\&E=30\times 10^6 psi\\&P =6000 lb \\&L = 14 in{:} \end{aligned}$$

Also,

$$\begin{aligned} \tau= & {} \sqrt{\tau _1^2 + 2\tau _1\tau _2 \left( \frac{l}{2R}\right) + \tau _2^2}\\ \mathrm{tau}_1= & {} \frac{P}{\sqrt{2}hl}\\ \mathrm{tau}_2= & {} \frac{MR}{J}\\ M= & {} P(L+0.5)\\ J= & {} 2\left( \frac{lh}{\sqrt{2}} \left[ \frac{l^2}{12} + \left( \frac{h+t}{2}\right) ^2 \right] \right) \\ R= & {} \frac{1}{2} \sqrt{l^2 + (h+t)^2}\\ \sigma (x)= & {} \frac{6PL}{bt^2}\\ \delta (x)= & {} \frac{4PL^3}{Ebt^3}\\ P_c(x)= & {} \frac{4.013 \sqrt{EFt^2b^6}}{6L^2} \left( 1-\frac{t}{2L} \sqrt{\frac{E}{4G}}\right) \end{aligned}$$

where $h=$ weld thickness, $\hbox {l}=\hbox {length}$ of bar attached to the weld, ${t}=\hbox {bar's}$ height, $\hbox {b}=\hbox {bar's thickness}$, $\sigma =\hbox {bending}$ stress, $\tau =\hbox {shear}$ stress, $P_c=\hbox {buckling}$ load on the bar and side constraints, $\mathrm{tau}_{\max }=\hbox {maximum stree}$ on the beam $\hbox {allowed}=13{,}600 \hbox {psi}$, $\sigma =\hbox {normal}$ stress on the $\hbox {beam}=30{,}000\,\hbox {psi}$, $P_c=\hbox {bar}$ buckling load, $P=\hbox {load}=6000\hbox {lb}$, $\tau =$ beam-end deflection, $\tau _1=$ primary stress, $\tau _2=$ secondary stress, $M=\hbox {moment of inertia}$, $J=\hbox {polar}$ moment of inertia.

The results from simulations with CSSA, SSA, PSO and ALO are provided in Table 7.

Table 7 Welded beam design

Here, CSSA obtains the most optimal value for the objective function as compared to the other 3 algorithms.

6 Future scope and conclusion

Proposed chaotic SSA opens up a huge scope for the incorporation of neural models into the working mechanisms of optimization algorithms to enhance their performance. Neural models are known to exhibit a variety of behaviours which can be augmented with optimization algorithms to improve their performance. More biologically realistic models, such as Hodgkin–Huxley model, compartment model, modified leaky integrate and fire model, can generate more complicated chaotic behaviours, which can further aid in improving the convergence rate of the meta-heuristic algorithms.

In the presented work, we have incorporated quadratic integrate and fire model for improving the performance of SSA. We used the chaotic oscillations generated from the model to calculate the position of the follower salps. The proposed chaotic SSA was compared with SSA, PSO and ALO based on standard benchmark functions and statistical tests, and it was proved that chaotic SSA performs better than the other optimization algorithms. Asymptotic complexity analysis was also presented to show that the algorithm is polynomially bound. CSSA was also implemented in three real-life engineering problems to demonstrate its ability to solve complicated problems of practical importance.

Benchmark functions

In this section, details of the function used in Table 2 have been described.

• Function F1

  • Mathematical expression: $\sum _{i=1}^{n} x_i^2$

  • Lower bound: $-100$

  • Upper bound: 100

  • Dimensions: 30

• Function F2

  • Mathematical expression: $\sum _{i=1}^{n} \left| x_i \right| + \prod _{i=1}^{n} \left| x_i \right|$

  • Upper bound: -10

  • Lower bound: 10

  • Dimensions: 10

• Function F3

  • Mathematical expression: $\sum _{i=1}^{n}\left( \sum _{j=1}^{i} x^{j}\right) ^2$

  • Upper bound: -100

  • Lower bound: 100

  • Dimensions: 10

• Function F4

  • Mathematical expression: $max_i\{ \left| x_i \right| , 1\le i \le n \}$

  • Upper bound: -100

  • Lower bound: 100

  • Dimensions: 10

• Function F5

  • Mathematical expression: $\sum _{i=1}^{n-1}[100(x_{i+1}-x_{i}^2)^2 +(x_i -1)^2 ]$

  • Upper bound: $-30$

  • Lower bound: 30

  • Dimensions: 10

• Function F6

  • Mathematical expression: $\sum _{i=1}^{n}([x_i +0.5])^2$

  • Upper bound: $-100$

  • Lower bound: 100

  • Dimensions: 10

• Function F7

  • Mathematical expression: $\sum _{i=1}^{n} ix_i^4+\hbox {random}[0,1)$

  • Upper bound: $-1.28$

  • Lower bound:1.28

  • Dimensions: 10

• Function F8

  • Mathematical expression: $\sum _{i=1}^{n} ix_i^4+random[0,1)$

  • Upper bound: $-500$

  • Lower bound: 500

  • Dimensions: 10

• Function F9

  • Mathematical expression: $\sum _{i=1}^{n} [x_i^2-10\cos (2\pi x_i)+10]$

  • Upper bound: $-5.12$

  • Lower bound: 5.12

  • Dimensions: 10

• Function F10

  • Mathematical expression: $-20exp\left( {-}0.2\sqrt{\frac{1}{n}\sum _{i{=}1}^{n}x_i^2} \right) -exp\left( \frac{1}{n}\sum _{i=1}^{n}\cos (2\pi x_i) \right) +20 +e$

  • Upper bound: $-32$

  • Lower bound: 32

  • Dimensions: 10

• Function F11

  • Mathematical expression: $\frac{1}{400} \sum _{i=1}^{n}x_i^2 - \prod _{i=1}^{n}\cos \left( \frac{x_i}{\sqrt{i}} \right) +1$

  • Upper bound: $-600$

  • Lower bound: 600

  • Dimensions: 10

• Function F12

  • Mathematical expression: $\frac{\pi }{n} \left\{ \right. 10 \sin (\pi y_1) +\sum _{i=1}^{n-1}(y_i -1)^2 [1 + 10 \sin ^2 (\pi y_{i+1})]+(y_n-1)^2\} + \sum _{i=1}^{n} u(x_i,10,100,4)$

    $y_i=1+\frac{x_i+1}{4}$

    $u(x_i,a,k,m)=\left\{ \begin{array}{ll} k(x_i-a)^m &{} x_i >a\\ 0 &{} -a<x_i<a\\ k(-x_i-a)^m &{} x_i < -a \end{array}\right.$

  • Upper bound: $-50$

  • Lower bound: 50

  • Dimensions: 10

• Function F13

  • Mathematical expression:

    $0.1 \left\{ \sin ^2\left( 3 \pi x_1 \right) \right. + \sum _{i=1}^{n} (x_i-1)^2[1+\sin ^2(3 \pi x_i +1)]+(x_n -1)^2 [1+\sin ^2(2 \pi x_n)]\left. \right\} + \sum _{i=1}^{n} u(x_i,5,100,4)$

    $y_i=1+ \frac{x_i + 1 }{4}$

    $u(x_i,a,k,m)=\left\{ \begin{array}{ll} k(x_i-a)^m &{} x_i >a\\ 0 &{} -a<x_i<a\\ k(-x_i-a)^m &{} x_i < -a \end{array}\right.$

  • Upper bound: $-50$

  • Lower bound: 50

  • Dimensions: 10

• Function F14

  • Pseudocode:

    $\hbox {aS}=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,\ldots$

    $-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];$

    $\mathbf{for }\hbox { j}=1:25$

    $\hbox {bS(j)}=\mathbf{sum }(({x}'-\hbox {aS}(:,\hbox {j})).\hat{\,}6)$;

    end

    $\hbox {o}=(1/500+\mathbf{sum }(1./([1:25]+\hbox {bS}))).\hat{\,}(-1)$;

    end

  • Upper bound: $-65.536$

  • Lower bound: 65.536

  • Dimensions: 2

• Function F15

  • Pseudocode:

    $\hbox {aK}=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246]$;

    $\hbox {bK}=[.25 .5 1 2 4 6 8 10 12 14 16]$;

    $\hbox {bK}=1./\hbox {bK}$;

    $\hbox {o}=\mathbf{sum }((\hbox {aK}-(({x}(1).^{*}(\hbox {bK}.\hat{\,}2 +{x}(2).^{*}\hbox {bK}))./(\hbox {bK}.\hat{\,}2+{x}(3).^{*} \hbox {bK}+{x}(4)))).\hat{\,}2)$;

    end

  • Upper bound: $-5$

  • Lower bound: 5

  • Dimensions: 4

• Function F16

  • Pseudocode:

    $$\begin{aligned} O&=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3\\&\quad +x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4); \end{aligned}$$

  • Upper bound: $-5$

  • Lower bound: 5

  • Dimensions: 4

• Function F17

  • Pseudocode:

    $\hbox {o}=(1+({x}(1)+{x}(2)+1)\hat{\,}2^{*}(19-14^{*}{x}(1) +3^{*}({x}(1)\hat{\,}2)-14^{*}{x}(2)+6^{*}{x}(1)^{*}{x} (2)+3^{*}{x}(2)\hat{\,}2))^{*}\ldots (30+(2^{*}{x}(1)-3^{*}{x}(2))\hat{\,}2^{*}(18-32^{*}{x}(1) +12^{*}({x}(1)\hat{\,}2)+48^{*}{x}(2)-36^{*}{x}(1)^{*}{x} (2)+27^{*}({x}(2)\hat{\,}2)))$;

  • Upper bound: $-2$

  • Lower bound: 2

  • Dimensions: 2

• Function F18

  • Pseudocode:

    $\hbox {aH}=[3 10 30;.1 10 35;3 10 30;.1 10 35]$;

    $\hbox {cH}=[1 1.2 3 3.2]$;

    $\hbox {pH}=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547; .03815 .5743 .8828]$;

    $\hbox {o}=0$;

    for $\hbox {i}=1:4$

    $\hbox {o}=\hbox {o}-\hbox {cH(i)}^{*}\hbox {exp}(-(\mathbf{sum }(\hbox {aH}(\hbox {i},:). ^{*}((\hbox {x-pH}(\hbox {i},:)).\hat{\,}2))))$;

    end

  • Upper bound: 0

  • Lower bound: 1

  • Dimensions: 3

• Function F19

  • Pseudocode: $\hbox {aSH}=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3; 8 1 8 1;6 2 6 2;7 3.6 7 3.6]$;

    $\hbox {cSH}=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5]$;

    $\hbox {o}=0$;

    for $\hbox {i}=1:5$

    $\hbox {o}=\hbox {o-((x-aSH(i,:))}^{*}(\hbox {x-aSH}(\hbox {i},:))'+\hbox {cSH}(\hbox {i}))\hat{\,} (-1)$;

    end

  • Upper bound: 0

  • Lower bound: 1

  • Dimensions: 6

• Function F20

  • Pseudocode:

    $\hbox {aH}=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14]$;

    $\hbox {cH}=[1 1.2 3 3.2]$;

    $\hbox {pH}=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991$; $\ldots \, .2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381]$;

    $\hbox {o}=0$;

    for $\hbox {i}=1:4$

    $\hbox {o}=\hbox {o}-\hbox {cH(i)}^{*}\mathbf{exp }(-(\mathbf{sum }(\hbox {aH}(\hbox {i},:).^{*} ((\hbox {x-pH}(\hbox {i},:)).\hat{\,}2))))$;

    end

  • Upper bound: 0

  • Lower bound: 10

  • Dimensions: 4

• Function F21

  • Pseudocode: $\hbox {aSH}=[4 4 4 4;1 1 1 1;8 8 8 8; 6 6 6 6;3 7 3 7; 2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6]$;

    $\hbox {cSH}=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5]$;

    $\hbox {o}=0$;

    for $\hbox {i}=1:7$

    $\hbox {o}=\hbox {o}-((\hbox {x-aSH}(\hbox {i},:))^{*}(\hbox {x-aSH}(\hbox {i},:)) '+\hbox {cSH}(\hbox {i}))\hat{\,}(-1)$;

    end

  • Upper bound: 0

  • Lower bound: 10

  • Dimensions: 4

• Function F22

  • Pseudocode:

    $\hbox {aSH}=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6; 3 7 3 7;2 9 2 9;5 5 3 3; 8 1 8 1;6 2 6 2;7 3.6 7 3.6]$;

    $\hbox {cSH}=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5]$;

    $\hbox {o}=0$;

    for $\hbox {i}=1:10$

    $\hbox {o}=\hbox {o}-((\hbox {x-aSH}(\hbox {i},:))^{*}(\hbox {x-aSH}(\hbox {i},:))' +\hbox {cSH}(\hbox {i}))\hat{\,}(-1)$;

    end

  • Upper bound: 0

  • Lower bound: 10

  • Dimensions: 4