Introduction

Materials are used at different strain rates which most of them show different responses to the change of loading rates. Polymeric materials are also known as sensitive materials to the loading rates [1]. Therefore, to analyze their behavior, many experiments should be done at different strain rates. However, determining the mechanical behavior of materials at different strain rates are costly and time consuming; thus, a model is necessary to determine the mechanical behavior of these materials at different dynamic loading conditions.

The strain rate-dependent mechanical behavior of metals was investigated by many research groups [2, 3]. Johnson and Cook [2] by performing torsion and tension tests had presented an empirical constitutive model that predicted the mechanical properties of various metallic materials at various strain rates. Zerilli and Armstrong [3] based on the framework of thermally activated dislocation motion, proposed three micro-structurally based constitutive equations for BCC, FCC and HCP metals. However, it was shown [4, 5] that Johnson–Cook(JC) and Zerilli–Armstrong (ZA) models did not predict the strain rate-dependent strength of some metals with an acceptable accuracy. For this reason, some of researchers modified constitutive models to predict the mechanical behavior of special materials. Meyer [4] claimed that the ZA model was found to be inadequate for the Ti–6Al–4V material. Thus, by modification of the ZA model for metals with a hexagonal closely packed crystal structure, at a strain rate range of 10,000–50,000 1/s, a good agreement with the experimental data was obtained.

Holmquist and Jonson [6] showed that the strain rate effect on the material strength was not properly modeled in the JC model. Thus, they substituted the linear term of the JC model by an exponential term. Kang and Huh [7] replaced the linear term of the JC constitutive model with a quadratic term for considering the strain rate effects. Lin et al. [8] based on the experimental results of uniaxial tensile tests at low strain rates (0.0001–0.01 1/s) and the temperature range of 1123–1373 K proposed a modified JC model that considered the effects of strain, strain rate and temperature for alloy steels. Zhang et al. [9] modified the JC model by introducing a temperature effect function and neglecting the coupling effect. Lin et al. [5] combined the JC and ZA models to obtain the coupling effects of strain rate–temperature–strain of a high-strength steel alloy.

The strain rate-dependent mechanical behavior of polymers was also investigated by other research groups [10–12]. Arruda et al. [10] studied the effects of strain rate, temperature and thermo-mechanical coupling on the inelastic response of a glassy polymer (polymethacrylate) over a strain rate range of 0.01–0.1 1/s. Tervoort [11] with a thermodynamic view proposed a constitutive equation for elasto-viscoplastic deformation of glassy polymers. However, his model could not describe the full linear and nonlinear viscoelastic regions but explained the strain-hardening and strain-softening responses. Plaseied and Fatemi [12] studied the deformation behavior of vinyl ester polymer under a monotonic tensile loading. They used a standard linear solid model and modified it to represent the mechanical behavior of vinyl ester over a strain rate range of 0.0001–1 1/s and at temperature range between room temperature and 100 °C. It should be noted that their model has been applied just for vinyl ester polymer and was not approved to be a general model.

To analyze the nonlinear strain rate-dependent behavior of polymers, Goldberg et al. [13, 14] modified the Bodner–Partom viscoplastic state variable model [15] which was originally developed to analyze the viscoplastic deformation of metals above one-half of the melting temperature. Goldberg et al. model included eight material parameters that should be calculated experimentally. But, obtaining these material parameters is a difficult task. Furthermore, effect of temperature changes was not considered [16]. Duan et al. [17] proposed a phenomenological uniaxial constitutive model that was able to describe entire range of deformation for glassy and semi-crystalline polymers. Similar to Goldberg et al. model, three tests at different strain rates and different temperatures should be conducted to determine the eight material constants.

In comparison with neat polymers, nano-phased polymeric composites show remarkable enhancement in mechanical, electrical and thermal properties [18]. Due to their polymeric matrix strain rate dependency, these types of composites are sensitive to the loading rates. Ingram et al. [19] studied the tensile behavior of polypropylene (PP) filled with carbon nano-fibers at strain rate range of 0.02–2 1/min. Their experimental results indicated that both neat and nano-phased PP were strain rate-dependent materials, and the tensile modulus and yield strength increased by increasing the strain rate. Shokrieh et al. [20] by combining a micromechanical approach and the Goldberg et al. model, presented a strain rate-dependent micromechanical model to predict the mechanical behavior of carbon nanotube (CNT)/polymer nanocomposites under various loading rates. They achieved an acceptable accuracy on predicting the stress–strain behavior and ultimate strength of neat and reinforced polymers. In addition, they [21] modified the JC model to predict the nonlinear shear mechanical behavior of neat and nano-phased epoxy at low loading rates. However, the proposed modified JC model is limited to low loading rates and is not capable of predicting the ultimate strength as a function of the applied strain rate.

In the present study, at first, the mechanical behavior of neat and nano-phased epoxy have been studied experimentally. Then, the JC constitutive model was modified to develop a new generalized strain rate-dependent constitutive model to predict the mechanical properties of neat polymers at a wide range of applied strain rate. The dynamic constitutive model predicts the linear elastic and inelastic regions of stress–strain behavior and the ultimate strength of polymers at arbitrary loading rates. Finally, the new modified JC dynamic constitutive model is combined with the modified Halpin–Tsai micromechanics model to predict the mechanical behavior of the nano-phased polymers. The present model is called the combined dynamic constitutive-micromechanical model. To verify the present model, the results obtained by the model are compared with experimental data.

Experimental

Materials

The ML-506 epoxy resin (bisphenol-A), the hardener HA-11 (polyamine) and the vapor-grown carbon nano-fibers (VGNCFs) were used to conduct the required experiments. The epoxy resin and hardener were supplied by Mokarrar Engineering Materials Co., Iran and the VGNCF was supplied by Grupo Antolin SL, Spain.

Preparation of specimens and test procedure

The epoxy resin and vapor-grown carbon nano-fibers (VGNCFs) were used to conduct the required experiments. The influence of adding VGNCFs on shear mechanical properties of epoxy resin at quasi-static and dynamic loading rates has been studied by the authors recently and reported in detail [21, 22]. In this research, the effect of adding VGCNFs on the tensile mechanical properties of epoxy resin at dynamic strain rate was also studied.

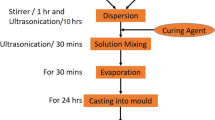
To produce the nanocomposites, a special procedure was followed [23]. The epoxy resin was mixed with 0.25 wt% of VGCNF and stirred for 15 min at 2000 rpm. Then, to break the residual aggregates, the mixture was sonicated for 60 min. During the sonication, the mixture container was held in a cold water bath to prevent overheating. The hardener was added to the mixture and then was vacuumed at 10 mbar to degas the polymer. Specimens were cured for 24 h at room temperature followed by a post-curing for 2 h at 80°C and 1 h at 110°C.

It was shown that the tensile modulus and strength of ML-506 epoxy were 2.42 GPa and 50.87 MPa, respectively. In addition, its shear modulus and shear strength were 0.98 GPa and 33.41 MPa, respectively. It was also found that the tensile and shear strengths of CNF/epoxy nanocomposites were enhanced by adding 0.25 wt% of VGNCFs [22]. The technical data of VGCNF samples used in this study are shown in Table 1. The density of CNF and epoxy are 2 and 1.11 g/cm3, respectively. The tensile modulus of the CNF is 240 GPa [24], its Poisson’s ratio is equal to 0.21 [25] and its shear modulus is 98.36 GPa. Also its shape factor is 300 [24].

Table 1 Technical data of used vapor-grown carbon nano-fibers (VGCNF)
Full size table

The tensile tests were conducted using Santam universal apparatus (Iran). The static test was conducted according to ASTM: D638-10 while there is no standard instruction for dynamic tests of polymers. In addition, a torsion testing machine (TecQuipment-SM21, UK) was used to conduct the torsional tests according to the instruction of TecQuipment-SM21 apparatus. It should be noted that at least five and three specimens were tested for tensile tests and shear tests, respectively. The tensile tests were performed at three different strain rates 0.00167, 0.1 and 0.2 1/s. The gage length of tensile specimens was 12.7 mm and cylindrical samples with height of 78 and 9.2 mm diameter were prepared from epoxy specimens for torsion tests. In addition, the shear tests were done at three different strain rates, 0.848, 2.56 and 4.27 1/s. Figure 1 shows the intact tensile and torsional specimens of neat ML-506 epoxy (Fig. 1a) and its 0.25 wt% VGCNF/epoxy nanocomposites (Fig. 1b).

Fig. 1
figure 1

Intact neat and reinforced ML-506 with CNF specimens for a tensile and b shear tests

Full size image

Experimental results

Using the tensile and torsional experiments, the tensile and shear mechanical behavior of the neat epoxy and 0.25 wt% VGCNF/epoxy nanocomposites were characterized. The typical tensile stress–strain curves of the neat and VGCNF/epoxy nanocomposites at different strain rates are shown in Fig. 2. Furthermore, the average values of tensile elastic modulus and ultimate strength of the neat and VGCNF/epoxy nanocomposites at different strain rates are given in Table 2.

Fig. 2
figure 2

Typical tensile stress–strain curves of a pure epoxy ML-506 and b 0.25 wt% VGCNF/epoxy nanocomposite

Full size image
Table 2 Average amounts of tensile elastic moduli and strengths of the neat epoxy and 0.25 wt% VGCNF/epoxy nanocomposites at different strain rates
Full size table

It can be seen that addition of CNFs increased the tensile modulus and strength of nanocomposite samples. Adding 0.25 wt% of CNF to the epoxy at static strain rate increased its tensile modulus and strength to 12.40 and 11.03 %, respectively; whereas at low loading rates, the tensile elastic moduli of the neat epoxy and epoxy reinforced with CNFs were constant. Moreover, the tensile strength showed an increase at the first stage, but it decreased at relatively higher applied strain rates. It should be mentioned that the experimental results of ultimate strength indicated a considerable scatter at relatively higher loading rates.

The typical shear stress–strain curves of neat and nano-phased ML-506 epoxy at different strain rate are shown in Fig. 3. Table 3 also presents the shear moduli and strength of the neat ML-506 epoxy and 0.25 wt% CNF/epoxy nanocomposites at different strain rates. As can be seen, adding CNFs or increasing the strain rate increased the shear mechanical properties of the nanocomposite samples compared to that of neat ML-506. At a strain rate of 0.85 1/s, adding 0.25 wt% of CNF to neat epoxy increased its shear modulus and strength to 13.27 and 23.97 %, respectively. Shear modulus of neat ML-506 epoxy at the strain rate range of 0.85–4.27 1/s was increased 40.82 %; while the shear strength was increased up to 19.22 %. In addition, the shear modulus and the shear strength of nanocomposite samples were increased up to 39.64 and 25.54 % at the same strain rate range.

Fig. 3
figure 3

Typical shear stress–strain curves of a pure epoxy ML-506 and b 0.25 wt% VGCNF/epoxy nanocomposite

Full size image
Table 3 Average amounts of shear elastic moduli and strengths of the neat epoxy and 0.25 wt% VGCNF/epoxy nanocomposites at different strain rates
Full size table

Dynamic constitutive-micromechanical model

In the present research, at first a generalized strain rate-dependent constitutive model has been developed by modifying the Johnson–Cook constitutive model [2] to represent the strain rate-dependent mechanical behavior of neat polymers. Then, the developed strain rate-dependent constitutive model was combined with a micromechanical model to obtain a dynamic constitutive-micromechanical model. This present model can be used to describe the dynamic behavior of nano-phased polymers.

Traditional Johnson–Cook constitutive model

In this section, first the original JC model is discussed and then it is modified to develop a dynamic constitutive model for polymeric materials. The JC model is expressed as Eq. (1) [2]:

$$\sigma = \left[ {A + B(\varepsilon )^{n} } \right]\left[ {1 + C{ \ln }(\dot{\varepsilon }^{*} )} \right]\left[ {1 - (T^{*} )^{m} } \right]$$
(1)

where σ is equivalent stress, ε is equivalent plastic strain, A is yield stress of the material under reference deformation conditions (MPa), B is strain-hardening constant (MPa), n is strain-hardening coefficient, C is strain rate strengthening coefficient and m is thermal softening coefficient. Parameter \(\dot{\varepsilon }^{*}\) is dimensionless strain rate and is defined as \(\dot{\varepsilon }^{*} = \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}\) in which \(\dot{\varepsilon }\) and \(\dot{\varepsilon }_{0}\) are strain rate and reference strain rate, respectively. Moreover, T * is the dimensionless homologous temperature and can be given as \(T^{*} = \frac{{T - T_{\text{r}} }}{{T_{\text{m}} - T_{\text{r}} }}\) where T, T m and T r are current absolute temperature, melting temperature and reference temperature, respectively. By neglecting the temperature changes, the equivalent stress is described by the following simplified Eq. (2) [26]:

$$\sigma = [A + B\varepsilon^{n} ][1 + C{ \ln }\dot{\varepsilon }^{*} ]$$
(2)

Since the JC model is defined based on the true stress and strain, to determine the unknown coefficients, first the engineering stress and strain must be converted to the true stress and strain, respectively. For this purpose, the following relations are used:

$$\varepsilon = {\text{ln(}}1 + \varepsilon_{\text{nom}} ), \quad \gamma = \ln (1 + \gamma_{\text{nom}} )$$
(3)
$$\sigma = \sigma_{\text{nom}} (1 + \varepsilon_{\text{nom}} ), \quad \tau = \tau_{\text{nom}} (1 + \gamma_{\text{nom}} )$$
(4)

where ε nom, σ nom, ε, σ are engineering strain, engineering stress, true strain, true stress, respectively. In addition, γ nom, τ nom, γ, τ are the engineering shear strain, engineering shear stress, true shear strain, true shear stress, respectively. In Eq. (2) the material coefficient A is the yield stress at zero true plastic strain for the reference strain rate, and can be obtained directly from the stress–strain curve of quasi-static loading rate. When the strain rate is equal to the reference strain rate, Eq. (2) is rewritten as follows:

$$\sigma = A + B\varepsilon^{n}$$
(5)

Equation (5) is plotted for two true stress–strain points to calculate the B and n parameters. To determine C constant, the JC model is rewritten in the following form:

$$\frac{\sigma }{{A + B\varepsilon^{n} }} = 1 + C{ \ln }\dot{\varepsilon }^{*}$$
(6)

The variations of \(\frac{\sigma }{{A + B\varepsilon^{n} }}\) versus \({ \ln }\dot{\varepsilon }^{*}\) must be plotted at different strain rates and then by averaging the results at some arbitrary strain values, the C constant can be determined.

Generalized strain rate-dependent constitutive model for neat polymers

Strain rate-dependent elastic modulus

The JC constitutive model has been presented to predict the plastic stress–strain curve. However, to study the entire stress–strain curves of materials, it is essential to know the elastic mechanical properties variations versus the loading rate. In the present study, to consider the elastic mechanical properties of polymers in the generalized strain rate-dependent constitutive model, an empirical equation is proposed to consider the strain rate effects on tensile and shear moduli of polymers as follows:

$$H(\dot{\varepsilon }) = \alpha_{1} ({ \ln }\dot{\varepsilon }^{*} )^{{\beta_{1} }} + \gamma_{1}$$
(7)

where α 1, β 1, and γ 1 are scaling material constants. Variable \(H(\dot{\varepsilon })\) is the desired dynamic elastic modulus.

Modifying the JC model for polymers

By considering the stress–strain behavior of pure polymers, the JC model was modified by replacing its exponential and logarithmic functions with two polynomial terms. This modification has been proposed according to the mechanical behavior of epoxy resins at different loading rates. Therefore, the modified JC model is presented as follows:

$$\sigma = [A + a\varepsilon^{3} + b\varepsilon^{2} + c\varepsilon ]\left[ {1 + C_{1} { \ln }\dot{\varepsilon }^{*} + C_{2} ({ \ln }\dot{\varepsilon }^{*} )^{2} } \right]$$
(8)

where A, a, b, c, C 1 and C 2 are material constants.

Similar to the JC model, at least two tests at different strain rates should be performed to determine the material constants. It is worth to mention that the quasi-static strain rate has been selected as the reference strain rate. To determine other parameters, the modified JC equation can be rewritten in the reference strain rate as the following equation:

$$[\sigma - A] = [a\varepsilon^{3} + b\varepsilon^{2} + c\varepsilon ]$$
(9)

where A is defined similar to the JC model and a, b, c are obtained by a least square fitting method with a polynomial curve of order three.

To calculate parameters C 1 and C 2, the modified JC equation is written in the following form:

$$\left[ {\frac{\sigma }{{A + ax^{3} + bx^{2} + cx}} - 1} \right] = \left[ {C_{1} { \ln }\dot{\varepsilon }^{*} + C_{2} ({ \ln }\dot{\varepsilon }^{*} )^{2} } \right]$$
(10)

At different values of strain, graphs of \(\frac{\sigma }{{A + ax^{3} + bx^{2} + cx}} - 1\) versus \({ \ln }\dot{\varepsilon }^{*}\) were plotted and by averaging the results, C 1 and C 2 can be determined.

Prediction the ultimate strength under tensile and shear loadings

To predict the entire stress–strain behavior of polymers, new criteria were required to define the ultimate stress and strain. First of all, the trends of variation of tensile and torsional ultimate strengths of different types of polymers at different strain rates were studied. Then, an empirical material model to predict the ultimate tensile and shear strengths as a function of applied strain rate was presented. The strain rate effects on the ultimate strength can be expressed adequately using a regression function defined as follows:

$$S_{\text{f}} \left( {\dot{\varepsilon }} \right) = \alpha_{2} ({ \ln }\dot{\varepsilon }^{*} )^{{\beta_{2} }} + \gamma_{2}$$
(11)

where \(S_{\text{f}} \left( {\dot{\varepsilon }} \right)\) is the ultimate strength as a function of strain rate and α 2, β 2 and γ 2 are material constants and \(\dot{\varepsilon }^{*}\) is the predefined dimensionless strain rate value.

Development of a combined dynamic constitutive-micromechanical model

The present combined dynamic constitutive-micromechanical model for nanocomposites can predict the stress–strain behavior of polymers reinforced with nanoparticles. In other words, it is possible to determine the mechanical properties of polymer reinforced with nanoparticles at arbitrary volume fractions of nanoparticles and loading rates. Using the generalized strain rate-dependent constitutive model, the stress–strain curve of nanocomposites can be modeled; but with any change in the CNF volume fraction, all characterization tests should be repeated. It is obvious that this is a time-consuming and expensive task. Therefore, a micromechanical model is implemented in this section to consider the CNF volume fraction changes. This model using the stress–strain behavior of neat polymer and mechanical properties of the CNF predicts the stress–strain behavior of nanocomposites at arbitrary strain rates and CNF volume fractions.

Figure 4 shows the algorithm of the present model. As can be seen, to simulate the stress–strain behavior of nanocomposites, first the tensile and shear stress–strain behavior of the pure epoxy was predicted by the generalized strain rate-dependent constitutive model at the applied strain rate. Polymers showed nonlinear mechanical behaviors even at low strain rates. Thus, tangent modulus concept was used. Using a micromechanical model and having the tangent modulus of the pure polymer and mechanical properties of nanocomposites, the tangent modulus of nanocomposites could be determined in an arbitrary strain range. Finally, using the tangent modulus of nanocomposites, their stress–strain behavior was simulated. It was assumed that mechanical properties of nanoparticles were not sensitive to the loading rate [20].

Fig. 4
figure 4

Algorithm of the combined dynamic constitutive-micromechanical model

Full size image

It should be mentioned that there are different micromechanical methods to predict the elastic properties of composites. In this study, the modified Halpin–Tsai equation as a semi-empirical micromechanical equation was considered as follows [27]:

$$\frac{P}{{P_{\text{m}} }} = \frac{{1 + \xi \eta V_{\text{f}} }}{{1 - \eta V_{\text{f}} }}$$
(12)

and

$$\eta = \left (\frac{{\alpha \frac{{P_{f} }}{{P_{m} }} - 1}}{{\frac{{P_{f} }}{{P_{m} }} + \xi }}\right)$$
(13)

where m and f stand for the matrix and fibers, respectively. The term of ξ = 2 l/d in tensile loading is the shape factor in which l is the length and d is the diameter of the nanoparticle and ξ is equal to 1 for the shear loading. Moreover, V f is the volume fraction of nanoparticles. In addition, α is the orientation factor and is equal to 0.184 for CNF [28]. Using Tables 2 and 3 data and processing algorithm explained in Fig. 4, the stress–strain behavior of CNF/epoxy nanocomposites can be predicted.

Results and discussion

In following sections, at first, the traditional JC model has been evaluated by predicting the dynamic mechanical behavior of neat polymers. Then, the predicted results by the generalized strain rate-dependent constitutive model are presented and compared with experimental data to verify the present model for neat polymers. Finally, using combined dynamic constitutive-micromechanical model, the dynamic tensile and shear stress–strain behaviors of epoxy reinforced with VGCNF have been predicted and compared with conducted experiments.

Assessment of the traditional JC model

The accuracy of the traditional JC model for modeling the behavior of epoxy under dynamic loading conditions was evaluated. To evaluate the JC model, as well as the ML-506 epoxy tested in this work, test results of PR520 and 977-2 as toughened epoxies and E-862 as a standard brittle epoxy were utilized [16]. Table 4 shows calculated material constants of the JC model for these four epoxy samples. In Fig. 5, the experimental results and the results of the JC model for the shear stress–strain behavior of these polymers at different stain rates are compared. As shown in Fig. 5, the JC model is not able to predict the experimental results of polymers well. Moreover, it should be noted that the JC model cannot predict the linear tensile behavior of neat polymers because of their relatively brittle behavior especially at high strain rate.

Table 4 Material constants of the JC model for different epoxy resins
Full size table
Fig. 5
figure 5

Comparison between experimental data and JC model predictions for shear stress–strain behavior of a ML-506, b PR520, c 977-2, and d E-862 epoxy resins at room temperature

Full size image

Assessment of the generalized strain rate-dependent constitutive model

A comparison between experimental and simulated data with the generalized strain rate-dependent constitutive model for neat polymers is presented in this section. First, the empirical model to predict elastic section and strength of polymers is evaluated. Using the conducted experimental data in this research and the available experimental data in the literature [16], the parameters α i, β i and γ i, where i = 1, 2, were calculated and are given in Tables 5, 6, 7, and 8. Figures 6 and 7 show the variation of tensile and shear moduli and strength of polymers in terms of the applied strain rates. As shown in these figures, Eqs. (7) and (11) well fitted the experimental results.

Table 5 Material constants of strain rate-dependent elastic model for tensile loading
Full size table
Table 6 Material constants of strain rate-dependent elastic model for torsional loading
Full size table
Table 7 Material constants of Eq. (11) to predict the ultimate strength under tensile loading
Full size table
Table 8 Material constants of Eq. (11) to predict the ultimate strength under torsional loading
Full size table
Fig. 6
figure 6

Effect of strain rate on tensile and shear moduli of a ML-506, b PR520, c 977-2, and d E-862 epoxy resins

Full size image
Fig. 7
figure 7

Effect of strain rate on true ultimate strength of a ML-506, b PR520, c 977-2, and d E-862 epoxy resins

Full size image

As it was discussed, using the generalized strain rate-dependent constitutive model, the linear and nonlinear segments of mechanical behavior of neat polymers can be predicted at the arbitrary loading rate. Moreover, the strain rate-dependent ultimate strength can be also determined.

Equation (8) predicts the nonlinear mechanical behavior of polymers. In addition, Eqs. (7) and (11) describe the elastic behavior and ultimate strength of polymers under dynamic loading rate, respectively.

Calculated material constants of generalized strain rate-dependent constitutive model for different epoxy resins are shown in Tables 9 and 10. A comparison between the predicted and experimental stress–strain behavior of polymers has been shown in Figs. 8 and 9. As shown, the generalized strain rate-dependent constitutive model showed an acceptable agreement with the experimental data at different strain rates. In other words, this dynamic constitutive model could predict the entire stress–strain behavior of polymers at a wide range of applied loading rates.

Table 9 Material constants of the generalized strain rate-dependent constitutive model for different epoxy resins under tensile loading
Full size table
Table 10 Material constants of the generalized strain rate-dependent constitutive model for different epoxy resins under shear loading
Full size table
Fig. 8
figure 8

Comparison between the tensile experimental data and the generalized strain rate-dependent constitutive model predictions at room temperature for a ML-506, b PR520, c 977-2, and d E862 epoxy resins

Full size image
Fig. 9
figure 9

Comparison between the torsional experimental data and the generalized strain rate-dependent constitutive model predictions at room temperature for a ML-506, b PR520, c 977-2, and d E862 epoxy resins

Full size image

Assessment of the dynamic constitutive-micromechanical model

Using the proposed dynamic constitutive-micromechanical model, the tensile and shear stress–strain behavior of 0.25 wt% VGCNF/epoxy nanocomposites under different strain rates have been predicted and compared with experimental data shown in Fig. 10. This figure indicates that the proposed model predicts well the strain rate-dependent mechanical behavior of the nanocomposites especially for torsional loadings. However, it should be noted that at relatively higher strain rates, the tensile strength of VGCNF/epoxy nanocomposites cannot be predicted adequately because of different trends of tensile strength of neat and nano-phased epoxy versus the applied strain rate.

Fig. 10
figure 10

Comparison between predicted and experimental results of 0.25 wt% VGCNF/epoxy nanocomposite at various strain rates for a tensile and b torsional behaviors

Full size image

The stress–strain curve of VGCNF/epoxy nanocomposites shows a linear behavior beside a nonlinear behavior. Therefore, the model should be able to predict these behaviors up to final failure. In Fig. 10, a good agreement between the results of the model and experiments data is shown. Although there are several micromechanical models to predict the elastic behavior of nanocomposites, to the best knowledge of the present authors there is not a generalized model to be able to predict the strength of nanocomposites in various strain rates. The present dynamic constitutive-micromechanical model is capable of predicting the entire linear and nonlinear behaviors of VGCNF/epoxy nanocomposites and the ultimate strength at any arbitrary strain rates and nanoparticle volume fractions.

Conclusion

In the present study, first a generalized strain rate-dependent constitutive model has been proposed to predict the entire tensile and shear stress–strain behaviors of different epoxy resins. For this purpose the traditional Johnson–Cook model was modified. To consider the elastic behavior of polymers, an empirical equation was presented to consider the effects of strain rate on the elastic behavior of epoxy resin. Furthermore, a material model for prediction of the ultimate strength at the arbitrary loading rate has been proposed. Finally, the generalized strain rate-dependent constitutive model and the modified Halpin–Tsai micromechanical approach were combined to establish a new strain rate-dependent micromechanical model to predict the mechanical properties of nanocomposites at different strain rates. A comparison between predicted and experimental results showed the capability of the proposed model in simulation of the mechanical behavior of nanocomposites under dynamic loading conditions. The model developed in the present research is able to predict mechanical behavior of nanocomposites at any arbitrary volume fraction of nanoparticles and loading rates.