Introduction

Curing or vulcanization process is a fundamental step during the manufacturing of rubber articles, especially tires and other high thickness products. It plays an important role in achieving accurate and low tolerance shape and also pre-designed physical and mechanical properties of the final product. Therefore, optimum determination of time arrangements and temperature variations during heating and cooling or post-cure steps is of prime importance. Moreover, due to high energy consumption of this stage, optimization also leads to more economical process. However, owing to the low thermal diffusivity in rubbers and also applying time-varying operating conditions, the temperature field inside the article is not only non-uniform but also changes with time. Therefore, difficulties arise when a simple cure evaluation curve, generally obtained by a disk rheometer at constant temperature, is intended to be used to predict the time and temperature required for the completeness of a curing process. Traditionally, a full experimental method is adopted in which the thermal history at various points inside the article (especially high thickness zones) is measured. The measured temperature can be converted to state of cure or degree of cure by the use of a kinetics equation, and thus, the time required to achieve a complete cycle is determined. Obviously, this method is time-consuming and expensive since for every experiment at least a rubber article should be damaged. Alternatively, determination of the thermal history and its variation inside a product by solving heat transfer equation using an appropriate numerical method in conjunction with a computer code are the preferred methods in today’s rubber industry. Recently, we have briefly reviewed the numerical simulation of the curing process of rubber articles [1] and presented some practical techniques to predict the temperature distribution and state of cure in molded rubber articles. In order to accomplish this task, the results of a comprehensive and up-to-date review of this topic in a more informative approach are presented in this review. Some aspects of rubber vulcanization process that had not been dealt with in previous work are also considered.

This paper has been divided into six parts. After introduction and giving a brief overview, the second part deals with the historical background of the selected topic. Owing to the common background and theoretical aspect of rubber curing process with curing of thermoset composites, the computer simulation of the curing process in composite materials will also be briefly reviewed. The third section that is also the largest part of this work is concerned with mathematical modeling of the vulcanization process of rubbery materials. In this part, the governing relations including those of heat transfer and cure reaction kinetics in conjunction with mathematical relations developed for the description of the variations of the thermal and physical properties are introduced. Then, the numerical solution techniques and algorithms developed so far for the simulation of this process are discussed in detail. In addition, different aspects of the modeling and solution strategies are presented. The fourth part will examine the application of the developed methods for two series of productions: first, the application of computer simulation in tire industry is considered and second modeling approaches adopted for non-tire applications are taken into account. The fifth section gives a brief summary and conclusions, and finally in the last part the references and bibliography of the work are drawn.

Historical background

Preliminary work on the subject of heat transfer in rubber technology was undertaken by Gehman [2]. Different aspects of these topics including mixing, handling of raw materials, molding and shaping were covered. Ambelang et al. [3] performed the first practical work for the curing of a tire. They solved the heat transfer and kinetics equations by the use of a developed computer code, which was based on the finite difference method. Their model consisted of the shoulder zone of a tire, and the thermal properties were also assumed to be constant. A series of parametric study on the ambient temperature and shoulder thickness were carried out using the developed model. Prentice et al. [4] extended this work in 1981 and developed a more realistic numerical model for the vulcanization process of a pneumatic tire. Their model consisted of a two-dimensional heat transfer equation in Cartesian coordinates in conjunction with an empirical integral equation for the determination of the state of cure (SOC) from temperature profile. The bladder and mold were also included in their model. Both heating and cooling stages in mold and ambient temperature were taken into account. The energy (heat) equation was solved using the finite difference technique. The main drawbacks of this model were: (1) the finite difference was selected as the solution technique, (2) only the shoulder zone of the tire was considered in the model (the layout of the tire was selected form Ambelang et al. [3] work) and (3) although the geometry of tire in mold was nearly axisymmetric, a rectangular coordinate system was chosen for the description of the heat equation. However, the comparison between experimental measurements and the predicted temperature profile showed that there were very good agreements between them. Further, Schlanger [5] developed a simple one-dimensional numerical model for the simulation of the tire vulcanization process. Kong et al. [6] developed a 1D model and used it for the study of heat transfer in a rubber slab. The governing equation was analytically solved. The curing process was analyzed based on two dimensionless numbers (Fourier and Damkohler). The main weaknesses of the introduced model so far were: (1) they were either a simple 1D or 2D model without details of the tire or rubber article and (2) non-accurate techniques were used to solve the equations so that the variations of the parameters of the governing equations and geometrical details were not taken into consideration.

Development of more intricate mathematical models and use of a sophisticated technique such as finite element method started in early 90s. Marzocca [7] developed a one-dimensional finite element model for the simulation of curing process in a rubber cylinder. A first-order kinetics model was also assumed for the curing reaction. The simulation of the tire curing process by the finite element method was first started by Toth et al. [8] and published in 1991. Comparing with previously published works, it was a complete work in which they used the Abaqus code in conjunction with a user subroutine (HETVAL) to solve the coupled problem of heat transfer and cure kinetics in a single simulation step. The model was still two dimensional, and the heat flow in circumferential direction was not considered. The kinetics of the rubber compounds were studied by a moving die rheometer (MDR), and the variation in thermal properties was also taken into consideration. Despite the model developed by Prentice et al. [4], although the finite element model of their work was developed in a two-dimensional axisymmetric framework, the mold and bladder were not included in the model. Therefore, the boundary temperature profiles needed in the simulation were determined by use of thermocouples inserted between tire mold and tire bladder, respectively.

Han et al. [9] developed a two-dimensional axisymmetric finite element model in 1996 to simulate the curing process of tires. The working equations were solved using an in-house developed code. It was tried to take the most important aspects of the process such as complex geometry of tire, mold and bladder, time-varying boundary condition, heat and cooling steps and complicated cure kinetics model to be taken into account. The numerical results were also compared with experimental measurements. Later in 1999, this model was used [10] in conjunction with an optimization algorithm to determine the optimal cure steps for product quality assessment. The application of finite element method for simulation of rubber vulcanization was continued in 2000s. A complete two-dimensional axisymmetric finite element model was developed for the simulation of a passenger tire using HSTAR code (a module in COSMOS/M finite element package) by Ghoreishy [11] in conjunction with an in-house code to carry out cure kinetics calculations. The computed results were also compared with experimentally measured temperature profile. The bladder and mold were also included in that model. Tong et al. [12] and more recently Yan [13] gave a report on development of two-dimensional axisymmetric finite element model for the simulation of tire curing process. Having compared with other published works on two-dimensional models, there was no novelty presented in their works. The development of the finite element modeling of curing process in a three-dimensional framework has been extensively studied by Ghoreishy et al. [14–16]. They created a complete and comprehensive three-dimensional finite element model for the simulation of rubber curing process. An in-house developed computer code written in Visual Basic was used to simulate both a rubber article and a truck tire with complex tread pattern. The former was a molded rubber article with two inserted metal pieces. Both the mold and rubber were considered. Comparisons of the predicted temperature profiles with their corresponding experimentally measured values were also performed to check the validity and applicability of the developed models. It was shown that ignoring the flow in third direction (or solving the heat equation in two or one dimension) would give rise to significant errors in predicting temperature and extent of cure reaction for complex rubber articles such as tires with tread patterns. Since 2009, there have been advances in different aspects of mathematical modeling of curing process. Rafei et al. [17] publication is a breakthrough in which they have substantially improved the existing models. They have modeled the curing process of a thick rubber–metal composite part using Abaqus coupled with a user-defined subroutine (UMATHT). This subroutine allowed to take the variation of the physical and thermal properties with temperature and state of cure into consideration, which was not possible previously using HETVAL. In addition, the use of incompatible meshes and considering thermal contact effect as well as experimental verification on predicted state of cure were performed. A modified version of Kamal and Sourour kinetics model was also introduced in which the fitting of predicted data to experimental data has been improved comparing to the traditional model. These topics will be covered in the next section in detail. These advanced developed methodologies were further used for the modeling of a large rubber bearing [18], a truck tire [19] and also optimization of the mechanical properties of a thick industrial part [20]. Recently, Tang [21] used the modified kinetics model introduced in [17] in conjunction with a newly developed model called parabola model to simulate the curing process of a rubber fender. It is claimed that the use of parabola model would give rise to more accurate results.

In addition to the above-mentioned works, there are a few numbers of miscellaneous publications that have been devoted to the solution of heat transfer equation and cure reaction progress in rubbers. For example, Bin et al. [22] used the Abaqus code for the simulation of the curing of a radial tire, and Likozar et al. [23] have studied the heat transfer in different rubber compounds during molding using finite difference method. Recently, Wang et al. [24] published the results of a simple 2D heat transfer analysis for a NR molded article in conjunction with an empirical kinetic model. The results of this research have no novelty compared to previous works.

Rubber cure simulation was also studied and performed during processing and shaping operations. In these simulations, the flow and energy equations have been simultaneously solved in conjunction with appropriate rheological and kinetics equations. The first study in this field was carried out by Isayev et al. [25, 26] in which they have simulated the mold-filling process of a carbon black-filled rubber black compound. Finite element and finite difference methods were used for the solution of the flow and heat equations, respectively. Isayev et al. [27–29] have further improved these models to take the effect of vulcanization and state of cure on the rheological properties of the compounds into account. Both SBR and NR compounds were investigated in their work, and the effects of viscoelasticity and flow-induced crystallization were also studied. More recent attentions have focused on this topic. Ramorino et al. [30] and Arrillaga et al. [31] used the mold flow package to simulate the flow, filling and curing of a rubber compound during an injection molding process. Yao et al. [32] also reported the use of finite element method for the modeling of the flow and curing of a natural rubber compound in an injection mold. No significant advancement was obtained compared to previously published works.

Cure simulations were also extensively performed for non-rubber thermoset materials, especially reinforced polymer composites. The main difference between cure simulation in rubbers and composite material is that in the latter case the thermal conductivity of the composites changes in different directions. In other words, the tensor of material constants must be taken into consideration. Although the main purpose of this paper is to review the cure simulation of rubbers, due to similarity of this topic with cure simulation of composite materials this subject is briefly reviewed. Bogetti et al. [33] developed a two-dimensional simple model based on the finite difference method for the cure simulation of glass/polyester and graphite/epoxy composites. The application of finite element method for the simulation of curing thermoset composites was first reported by Yi et al. [34]. Since then, several papers were published on this topic using both in-house developed and commercial codes. Joshi et al. [35], Park et al. [36], Park et al. [37] developed their own codes based on Galerkin finite element method and finite difference technique to treat the time derivative and solved the cure simulation problem. In the latter work, the data given in Bogetti et al. [33] were used and the three-dimensional heat transfer equation was solved in conjunction with a cure kinetics equation. The same methodology was adopted by Guo et al. [38] for the simulation of the curing of thermoset matrix laminates manufactured by autoclave vacuum bag process. They have compared their results with experimentally measured temperature profiles and showed that there is a good agreement between actual and predicted data. Similarly, Yan [39] developed an in-house code to carry out similar cure simulations. Recent works are mainly based on the use of commercial software in conjunction with appropriate small code developed for the calculation of the cure kinetics. Behzad et al. [40] and Zhang et al. [41] have used COMSOL and Abaqus codes, respectively, to perform cure simulations for composites prepared from prepreg materials. Zhang et al. [42] also used Abaqus code for the cure simulation of a thermoset composite made of epoxy resin and studied the effect of degree of cure on mechanical properties. Similar simulations were also carried out during processing operations. For example, Lin et al. [43] and Cheung et al. [44] have developed finite element models for pultrusion and RTM (resin transfer molding) process, respectively. In a recent work, Aktas et al. [45] have used the PAM-RTM software to model the curing of unsaturated polyester resin in a vacuum infusion process. This software is a mold-filling codes based on the use of finite element technique. Analytical solution of heat transfer equation in composites was also studied by Amiri et al. [46]. They solved the transient heat transfer equation in a cylindrical coordinate system for an axisymmetric composite laminate with orthotropic materials. Computer simulation of rubber curing for continuous process such as extrusion is also a subject of interest for some researchers. In a relatively substantial work, Milani et al. [47–49] developed a robust mathematical model and written their own code using finite element method for simulation of the continuous curing of an EPDM production line. They have also applied their model for different rubber articles.

In addition to classical approximated and deterministic methods, statistical approaches are also used for the modeling of cure simulation. Rai et al. [50] have used artificial neural network (ANN) model for the simulation of the fabricating process of a thermoset composite in autoclave. The training stage was conducted based on the data from numerical simulation. Comparison of the predicted results with actual data confirmed their methodology and solution algorithm. In a more rigorous work, Karaağaç et al. [51] used the ANN method for the simulation and determination of the optimum cure cycle of rubber compounds in a tire. They have used three different ANN architectures and compared their results with conventional equivalent cure method. The results showed that the ANN technique can be used as a powerful tool to find the optimum cure condition. Later on, these authors extended their work and used adaptive neuro-fuzzy inference system (ANFIS) and compared the results from traditional equivalent cure method, ANN and ANFIS [52]. They have shown that ANFIS gives more accurate results with less error than the other methods.

Mathematical modeling

Computer simulation of the curing process of rubbers and thermoset materials is based on the solution of heat transfer equation in solids (conduction) and kinetics of the cure reaction in conjunction with different types of boundary conditions. The details of the mathematical modeling including governing equation, empirical models and numerical techniques are described in the following sections.

Heat transfer equation

The conduction heat transfer equation is a classic transport equation, which can be found in many text books and literature sources [53–55]. This equation can be described in different coordinate systems depending on the geometry and degree of simplification adopted for the modeling of the process. Two most common forms are as follows:

  1. 1.

    Three-dimensional coordinate system:

    $$\rho C\frac{\partial T}{\partial t} = \frac{\partial }{\partial x}\left( {k\frac{\partial T}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {k\frac{\partial T}{\partial y}} \right) +\frac{\partial }{\partial z}\left( {k\frac{\partial T}{\partial z}} \right) + \dot{Q}$$
    (1)
  2. 2.

    Two-dimensional axisymmetric (r, z):

    $$\rho C\frac{\partial T}{\partial t} = \frac{1}{r}\frac{\partial }{\partial r}\left( {rk\frac{\partial T}{\partial r}} \right) + \frac{\partial }{\partial z}\left( {k\frac{\partial T}{\partial z}} \right) + \dot{Q}$$
    (2)

In these equations, ρ is the material density, C is the specific heat capacity, T is the temperature, k is the thermal conductivity and \(\dot{Q}\) is the rate of generated heat per unit volume of the material due to the curing reaction, and thus, it is a function of both state of cure and temperature. Implementation of an appropriate equation for this parameter in the mathematical model is not trivial and needs sophisticated methods, which are described in detail in Sect. “(Cure kinetics)”.

Thermal properties

There are three physical properties, density, heat capacity and thermal conductivity (ρ, C, k) in Eqs. 1 and 2, which are referred to thermal or transport properties. The variation of these properties with solution variables (temperature and state of cure) is a very important aspect of this subject. The degree of deviation between predicated data and experimental values is strongly dependent on the type of the selected relations to describe these parameters.

Density of the rubber compounds is normally assumed to be decreased with the increase in temperature. However, for molded article in which the volume of mold cavity is nearly constant, the density of rubber can also be taken to be constant. In addition, experimental measurements revealed that density is also dependent on crosslink density. On the other hand, specific heat capacity of rubber is generally found to be increased with temperature. Moreover, similar to density it is also dependent on the crosslink density and so the effect of the degree of cure (extent of reaction) should also be taken into consideration. Consequently, different approaches are usually adopted. For example, Prentice et al. [4] assumed a constant value for the product of density and specific heat capacity (ρC). In another approach, density is assumed to be a function of crosslink density, while the specific heat capacity is considered to be a function of temperature and degree of cure (e.g., Yan [13], Tong et al. [12], Han et al. [9, 10]). For both variables, a linear law of mixture is considered as:

$$\rho_{m} = \left( {1 - \alpha } \right)\rho_{u} + \alpha \rho_{c}$$
(3)
$$C_{m} = \left( {1 - \alpha } \right)C_{u} \left( T \right) + \alpha C_{c} \left( T \right)$$
(4)

where α is the degree of cure, ρ m , ρ u and ρ c are the density of the partially, uncured and fully cured compounds, respectively. Similarly, C m , C u and C c are the specific heat capacity of partially, uncured and fully cured compounds, respectively. The dependency of each latter three parameters to temperature is taken into consideration as follows:

$$C_{u} \left( T \right) = C_{u,1} + C_{u,2} T$$
(5)
$$C_{c} \left( T \right) = C_{c,1} + C_{c,2} T$$
(6)

Experimental works have verified that due to the use of different compounding ingredients and complicated interactions between them, variations in specific heat capacity and thermal conductivity with degree of cure and temperature are too complicated to be described by simple equations. More recently, Ghoreishy et al. [17, 19, 20] have considered the variations of the specific heat capacity and the other thermal properties via a tabular data determined by experimental technique and implemented them into finite element model via an advanced user subroutine, UMATHT. This technique may enable us to take into account any complicated variation of the transport properties in relation to temperature and degree of cure.

Several studies have been made in the past to measure the thermal conductivity of rubber compounds and its variation with temperature and degree of cure. The first published study in this area was carried out by Frumkin et al. [56]. They have investigated the effects of different types of base polymer (natural and synthetic), filler loading and degree of cure on thermal conductivity. Rehner [57] published a paper and reported the measured thermal conductivity of a series of rubbers and studied the relationship between structures of the materials such as crosslinking; branching in polymer backbone and interactions between molecules and atoms; and thermal conductivity values. Eiermann [58] studied the thermal conductivity of rubbery materials from morphology point of view and investigated the variations of thermal conductivity with temperature in amorphous polymers. In another study, Crawile et al. [59] have studied the thermal conductivity of natural rubber compounds. The results of these preliminary works showed that the polymer base and filler content have the highest influence on this parameter while the degree of vulcanization did not significantly change the behavior of the variation in thermal conductivity with temperature. Hands et al. [60–62] published some comprehensive works on the thermal conductivity of carbon black-filled natural rubber compounds. They have studied the effects of several parameters including type and content of carbon black on the thermal conductivity and diffusivity and their variation with temperature. They have shown that both thermal conductivity and diffusivity of carbon black-filled compounds drop with rise in temperature with a relatively linear relationship. This confirms to some extent the previously mentioned finding in which it was assumed that density and specific heat capacity of the product were constant. They have also found that increases in carbon black loading also increase the slope of the thermal conductivity reduction with temperature rise. In other words, the higher carbon black content increases the sensitivity of the thermal conductivity to temperature variation. Sircar et al. [63] also studied the effects of the above parameters on the variations in thermal conductivity of both single and blended rubbers and found similar results. They used for the first time the DSC (differential scanning calorimetry) for the determination of the thermal conductivity. Kong et al. [6] studied the effects of different carbon black types and loadings, oil content, sulfur concentration and two non-black fillers (clay and aluminum powder) on the thermal conductivity of a series of rubber compounds based on SBR, BR IR and NR. Similar results and trends were found in accordance with previous publications. Saxena et al. [64] studied the effect of the addition of fine powder of waste NR product on the thermal conductivity of a SBR compound. It has been found that the thermal conductivity of the SBR composites falls to its minimum level at 10 phr of NR particle content. Further addition of NR particles results in challenging this fall in thermal conductivity due to lower crosslinking density of the composites with increases in filler content. The main novelty of their work in comparison with other publications is that they have studied the thermal conductivity variations in a broad range of temperature. They have also found that the thermal conductivity increases with temperature rise below the glass transition temperature (T g) while at above T g, thermal conductivity decreases with increases in temperature. The application of numerical techniques such as finite element method in combination with the measured temperature profile in relatively simple systems was an interesting subject for the determination of the transport properties. This type of problem is called “inverse problem” in which the known temperature profile is used as an input to the mathematical model to determine the transport properties such as thermal conductivity or diffusivity. Ghoreishy et al. [65] developed a finite element model for the heat transferred into a two-piece rubber disk via a platen heated press and converted the measured temperature profiles at the middle of this system and determined the thermal conductivity of the material. Recently, Li et al. [66, 67] developed a new method for the prediction of thermal conductivity of filled E-SBR. They have developed a micro-finite element model using Abaqus based on a representative volume element (RVE) to model the filler inside the polymer matrix. This model was used to predict the thermal conductivity of a series of polymer composites including E-SBR filled with silicon carbide, carbon nanotube, zinc oxide and alumina. Rafei et al. [17, 19] measured the thermal conductivity of carbon black-filled natural rubber compound using an inverse method and used them for simulation of the curing process of a thick rubber article. They have shown that due to the complicated interaction between constituents used in an industrial compound, the variation of thermal conductivity with temperature (especially for uncured compound) cannot be described by simple equations. Therefore, they have used tabular data of transport properties and used them inside the model via an in-house developed user subroutine.

Cure kinetics

Rubber curing process is an exothermic chemical reaction, and thus, a kinetic model is required to quantitatively describe the extent of reaction or degree of cure as a function of time and temperature. Degree of cure that is denoted by α can be described by the relation of generated heat up to time t, i.e., Q t to the total heat of reaction, i.e., Q ∞ (per unit volume) as:

$$\alpha = \frac{{Q_{t} }}{{Q_{\infty } }}$$
(7)

Differentiation of the above equation with respect to time yields:

$$\frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = \frac{1}{{Q_{\infty } }}\left( {\frac{{dQ_{t} }}{{{\text{d}}t}}} \right) = \frac{{\dot{Q}}}{{Q_{\infty } }}$$
(8)

By a simple rearrangement on the above equation, the rate of generated heat per unit volume, i.e., the source term in Eqs. 1 or 2, is found as:

$$\dot{Q} = Q_{\infty } \frac{{{\text{d}}\alpha }}{{{\text{d}}t}}$$
(9)

Therefore, describing the extent of reaction by a kinetics model not only predicts the degree of cure but also determines the source term in heat transfer equation.

The parameters in a cure kinetics model are determined in rubber industry by either a DSC or a torque rheometer. In the latter method, torque versus time is measured using a MDR (moving die rheometer) or ODR (oscillating disk rheometer). In this case, the degree of cure is calculated from toque profile using \(\alpha = \left( {\varGamma \left( t \right) - \varGamma_{\hbox{min} } } \right)/\left( {\varGamma_{\hbox{max} } - \varGamma_{\hbox{min} } } \right)\), where (t), Γ min and Γ max are instantaneous, minimum and maximum torques, respectively (Fig. 1). On the other hand, in a DSC experiment, the rate of reaction, dα/dt, is directly measured in conjunction with the total heat of vulcanization, i.e., Q ∞ (Vergnaud et al. [68] and Barzier et al. [69] for more details). However, it should be noted that the measured Q ∞ in a DSC experiment corresponds to both main crosslinking reaction and the side reactions that take place in rubber. As it is not an easy task to distinguish between the shares of each of these reactions, the obtained data via this approach are not fully reliable [70].

Fig. 1
figure 1

A typical isothermal torque rheometer curve with reversion

Full size image

It is generally known that there are three basic steps in curing process of rubber compounds. As it can be seen in Fig. 1, there is usually an induction time period during which the chemical reaction does not take place, and thus, the measured torque relatively remains constant. After this period, the curing stage starts, which can be characterized by rising of torque until reaching a maximum value. At the end of this stage, torque remains constant (or in some cases it goes for further increase; referred to marching stage). The last step is the reversion period which the cured rubber begins to degrade, and thus, the mechanical properties fail due to deterioration of polymer structure and destruction of its crosslinks. The kinetics models for each of the mentioned steps are as follows:

* Induction time

Based on the original work performed by Claxton et al. [71], the prediction of the induction time can be carried out by an Arrhenius-type temperature dependence as:

$$t_{i} = t_{0} e^{T_0/T}$$
(10)

where t 0 and T 0 are two material constants, which are independent of temperature. For non-isothermal process in which temperature continuously changes with time, a cumulative model is proposed, which is given as [72]:

$$\bar{t} = \int_{0}^{t} {\frac{{{\text{d}}t}}{{t_{i} \left( T \right)}}}$$
(11)

where t i (T) is the dependence of induction time to temperature described by Eq. 10. When the value of dimensionless time, \(\bar{t}\), becomes equal to one, the upper limit of t (in the integral) is considered as induction time. It should be noted that since during this step no cure reaction takes place and the source term in heat transfer equation is equal to zero. The above equation was extensively used for the prediction of the onset of cure reaction both in solid and flow problems (e.g., Ghoreishy et al. [14, 17], Isayev et al. [29], Launay et al. [73]).

* Curing stage

Kinetics of curing stage is totally different from induction period, and a number of studies have examined this topic to give an accurate and reliable model. Cure kinetic models are generally categorized into phenomenological and mechanistic models. Phenomenological models are normally developed based on the fitting of experimentally obtained data (degree or the rate of reaction) using appropriate equation. On the other hand, the latter models are based on the balance of chemical species participating during the curing or vulcanization reaction. Mechanistic models can give better physical sense to their users and also provide better relationship between compound formulation and its cure behavior, due to the very complicated nature of curing reaction especially for rubber compounds with several ingredients for which the phenomenological models are usually adopted to study the kinetics of vulcanization of rubbers.

The most common form of phenomenological models for the kinetics of chemical reactions is the nth-order model given as:

$$\frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = k\left( {1 - \alpha } \right)^{n}$$
(12)

where n is the order of reaction and k is a rate constant generally described by an Arrhenius-type temperature dependence of the form as:

$$k = k_{0} e^{{\left( {{\raise0.7ex\hbox{${ - E}$} \!\mathord{\left/ {\vphantom {{ - E} {RT}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${RT}$}}} \right)}}$$
(13)

where k 0 is a constant called pre-exponential factor, E is the activation energy, and R is the gas constant. Although the determination of the parameters of the first-order model is an easy task, it cannot predict the accelerating stage of the cure reaction, which normally takes place at degrees of cure less than about 0.25. In an nth-order model, the maximum rate of cure occurs at the beginning of the reaction. However, this is not true for rubber vulcanization as the cure curve clearly shows an inflection point, which corresponds to maximum rate of cure. This means that the maximum cure rate occurs at a conversion greater than zero. This phenomenon is known as the autocatalytic reaction in the context of chemical reaction. A more complex model of this type was first suggested by Piloyan et al. [74]. It has been later used by Kamal et al. [75, 76] for the description of the curing of two most common thermosets, i.e., unsaturated polyester and epoxy resins. This model was then suggested by Isayev et al. [72] to be used for rubber curing reaction. This equation is expressed by the following form:

$$\frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = k\alpha^{m} \left( {1 - \alpha } \right)^{n}$$
(14)

where m and n are two parameters representing the order of reaction. This model was used by several researchers for rubbery materials (e.g., Toth et al. [8], Han et al. [9, 10] and Yan [13]). Furthermore, Kamal et al. [77] extended the idea of using two parameters for reaction order (m, n) to the use of two rate constants and proposed the following model:

$$\frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = \left( {k_{1} + k_{2} \alpha^{m} } \right)\left( {1 - \alpha } \right)^{n}$$
(15)

They have successfully used this model for the prediction of the cure state of epoxy and polyester resins in injection molding process. This model is also used by Lopez et al. [78] to describe the vulcanization kinetics of a natural rubber nanocomposites based on nanoclay to study the effect of the interaction between clay and accelerator functional groups on the rate of curing reaction.

Obviously, neither of these models can be integrated analytically to produce an explicit form for the degree of cure. To overcome this drawback, Isayev et al. [72] suggested to use a growth or sigmoidal model, which was firstly proposed by Kamal et al. [75], in which the rate of reaction and degree of cure are, respectively, given by:

$$\frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = \frac{n}{k}\left( {t - t_{i} } \right)^{ - 1 - n} \alpha^{2}$$
(16)
$$\alpha = \frac{{k(t - t_{i} )^{n} }}{{1 + k\left( {t - t_{i} } \right)^{n} }}$$
(17)

A modified form of Eq. 16 was proposed by Ghoreishy et al. [17, 20] as:

$$\alpha = \frac{{A_{1} - A_{2} }}{{1 + \left[ {k\left( {t - t_{i} } \right)} \right]^{n} }} + A_{2}$$
(18)

where, A 1 and A 2 are the values of the state of cure (α) at the start and end of reactions, respectively. It is assumed in this work that A 1 is equal to 0.05, which is a standard value for α at the beginning of the cure reaction in rubber industries, and A 2 should theoretically be taken equal to 1 (α = 1 when t → ∞). However, in this model it is allowed to be determined numerically to reduce the error of curve fitting operation. The above-mentioned models were extensively used for the modeling of rubber curing process (e.g., Isayev et al. [26, 29], Ghoreishy et al. [14–17, 20], Sepehri et al. [79] and Khang et al. [80]).

The application of the above-mentioned models for a non-isothermal curing process is not a simple task, and several researchers have tried to propose a reliable and robust methodology to achieve it (e.g., [14, 17, 20, 72, 81–85]). The simplest adopted form is a quasi-isothermal approach in which rate constant (k) at every time step is calculated at the mean temperature between two successive time steps, i.e.,:

$$\alpha_{i} = \alpha_{i - 1} + \int_{{t_{i - 1} }}^{{t_{i} }} {\left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} \right)_{{T = T_{m} }} {\text{d}}t}$$
(19)

where

$$T_{m} = \left( {\frac{{T_{i} + T_{i - 1} }}{2}} \right)$$
(20)

In a more rigorous method, Isayev et al. [72] proposed a total differential approach, which is given as:

$$\alpha_{i} = \alpha_{i - 1} + \int_{{t_{i - 1} }}^{{t_{i} }} {\left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} \right)}_{{T = T_{m} }} {\text{d}}t + \int_{{T_{i = 1} }}^{{T_{i} }} {\left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}T}}} \right)} {\text{d}}T$$
(21)

However, it is generally known that during the curing process the temperature at some steps (such as cooling stage) decreases with time. Our numerical studies [14] showed that none of these models are capable of considering the effect of temperature decrease on rate of cure and state of cure; thus, these models fail to accurately predict the state of cure. In order to overcome this controversial condition, two approaches are usually adopted. In the first approach, a cure kinetics equation in the form of \({\text{d}}\alpha /{\text{d}}t = k\left( T \right)f\left( \alpha \right)\) is used where f (α) [e.g., for Kamal and Sourour model in Eqs. 16 and 17] is expressed as:

$$\frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = nk^{{\frac{1}{n}}} \alpha^{{\frac{n - 1}{n}}} \left( {1 - \alpha } \right)^{{\frac{n + 1}{n}}}$$
(22)

Therefore, the state of cure can be computed by the solution of the ordinary differential Eq. 22. However, since the right-hand side (RHS) of this equation is dependent on α, either a predictor–corrector technique should be used or the RHS of Eq. 22 must be evaluated at the previous time step to solve this nonlinear equation. It should be noted that temperature is implicitly embedded in this equation via k. On the other hand, since α at the start of calculation is equal to zero (initial condition), the RHS of Eq. 22 cannot be expressed in terms of α and k at the previous time step (i.e., α i−1 and k i−1); otherwise, a zero profile for α is obtained. In another method [81, 82], a reduced time approach is used to predict the state of cure. The numerical expression for the cumulative state of cure in this method based on the sigmoidal model (Eq. 17) is given as:

$$\left( {\frac{{\alpha_{i} }}{{1 - \alpha_{i} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}} = \left( {\frac{{\alpha_{i - 1} }}{{1 - \alpha_{i - 1} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}} + \int_{{t_{i - 1} }}^{{t_{i} }} k^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}} {\text{d}}t$$
(23)

As it can be seen, in this approach, the initial condition for α (i.e., α = 0 at time = t i ) does not affect the calculation of the α at next time step. The non-isothermal rate of cure is also computed as:

$$\left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}}\right)_{\text{non - isothermal}} = \frac{{\alpha_{i} - \alpha_{i - 1} }}{{\Delta t}}$$
(24)

Recently, isoconversional kinetic analysis was used for the treatment of non-isothermal kinetics of curing reaction in rubber and the other thermoset polymers [83, 86, 87]. This approach is based on the use of so-called model free technique in which the kinetics is assumed to be described by a global equation described as:

$$\frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = A_{\alpha } e^{\left(-E_{a}/\text{RT}\right)}f(\alpha)$$
(25)

where A α and E α are the apparent pre-exponential factor and apparent activation energy for the degree of cure α, respectively. f (α) can be an appropriate form such as the form proposed in Eq. 16. By integration of the Eq. 25, the time required to obtain a degree of cure equal to \(\alpha_{j,i}\) at a given reaction temperature T i , i.e., \(t_{{\alpha_{j,i} }}\), is derived by:

$$\ln \left( {t_{{\alpha_{i,j} }} } \right) = \ln \left[ {\frac{{\mathop \smallint \nolimits_{0}^{{\alpha_{j} }} \frac{{{\text{d}}\alpha }}{f\left( \alpha \right)}}}{{A_{\alpha } }}} \right] + \frac{{E_{\alpha } }}{{RT_{i} }}$$
(26)

For a given value of α j , the term in the bracket, i.e., \(\left[ {\frac{{\mathop \smallint \nolimits_{0}^{{\alpha_{j} }} \frac{{{\text{d}}\alpha }}{f\left( \alpha \right)}}}{{A_{\alpha } }}} \right]\), does not depend on temperature, and thus, by plotting \(\ln \left( {t_{{\alpha_{i,j} }} } \right)\) as a function of \(\frac{1}{{RT_{i} }}\), a straight line with s slope equal to E α is obtained. It can be seen that regardless of form of function f (α), the apparent pre-exponential factor and activation energy are computed. This technique was used by Leroy et al. [86, 87] and Vafayan et al. [83] to predict the non-isothermal kinetics of the curing of a natural rubber compound and an epoxy prepreg, respectively. More recently, Yeoh [88] reviewed and examined several kinetics models for rubbery materials including the previously mentioned equations and also Sestak-Berggren [89] autocatalytic model, which is given as:

$$\frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = k\alpha^{m} \left( {1 - \alpha } \right)^{n} \left( { - \ln \left( {1 - \alpha } \right)} \right)^{p}$$
(27)

This model was extensively used by many researchers, especially for the study of kinetics of crystallization in polymeric systems.

A number of good mechanistic models are also developed. Ding et al. [70] proposed a mechanistic model based on the chemistry of vulcanization for a NR-based rubber compound. Their model accounts cure stage and reversion phenomena for induction time period. The latter is a common behavior for NR-based compounds during over-cure stage. The proposed model consists of a series of first-order reaction for the induction time, main crosslinking reactions, side reactions that produce inactive species and also reversion stage in which a decrease in modulus is usually obtained. In order to quantify this kinetic model, five parameters need to be determined from isothermal cure tests. These are three rate constants (k1, k2, k6) that correspond to induction time period, rate of cure and reversion during over-cure stage, respectively, and two adjusting parameters that represent the initial rate of curing and measurement of competition between main crosslinking and side reactions. These parameters are also considered to be temperature dependent. Comparison of the fitted experimental data for mentioned compound data on the suggested model confirms the applicability of this approach. The same approach without reversion reactions was also adopted by Ding et al. [90] for a SBR rubber compound as it showed a plateau behavior during its over-cure stage.

The mechanistic approach was used in another work by Nozu et al. [91] for the simulation of the vulcanization of a rubber cylinder. They have used a five-reaction kinetic model in conjunction with a 1D conduction heat transfer equation expressed in cylindrical coordinate. They have predicted the temperature distribution and crosslink density inside the rubber and compared them with experimental data, which showed good agreement. Their model was so simple and thus limited to uncomplicated articles.

* Reversion stage

It is well known that over-cure of many rubber compounds (especially NR based) gives rise to decrease in the physical and mechanical properties compared to their optimum values. Traditionally, this phenomenon is characterized through a decline in torque–time curve determined by rheometer, which is known as reversion (Fig. 1). The first systematic study of the kinetics of reversion stage was reported by Rimondi et al. [92]. They have assumed that there are three simple schemes during a reversion-type curing reactions. These are: (1) formation of the strong crosslinks, (2) formation of weak crosslinks and (3) disruption of weak crosslinks. The kinetics of each of these reactions is also assumed to be described by an nth-order equation. Considering the torque to be the sum of a viscous component and a component resulting from chemical formation of crosslinks, a mathematical model is proposed and verified for two different compounds with and without reversion. This model is given as:

$$\varGamma \left( t \right) = \varGamma_{0} e^{{ - \left( {K_{\alpha }^{n} + K_{\beta }^{n} } \right)/\left( {\varGamma_{e} t^{n} /\varGamma_{0} n} \right)}} + \varGamma_{e} \chi \left( t \right)$$
(28)

where Γ(t), Γ0 and Γe are the instantaneous, initial and final torques corresponding to fully viscous state and fully crosslinked states, respectively. \(K_{\alpha }^{n}\) and \(K_{\beta }^{n}\) are the rate constants for the reaction of the formation of strong and weak crosslinks, respectively; t is the time, n is the order of reaction, and χ(t) is the degree of cure. Similar studies were performed based on this approach, and modified equations for the cure kinetics of the reversion stage are proposed (Han et al. [93] and Fan et al. [94]).

Solution methods

Analytical methods

Due to the complex shape of most rubber parts and tires, only a few works are devoted to the use of analytical methods for the solution of heat transfer and cure kinetics. Moreover, the nonlinear nature of the equation which is due to the dependency of the thermal properties and heat of reaction to temperature and state of cure prevents exact solutions to be achieved. An early publication by Gehman [2] contains some results of the application of a classical analytic method for the heat transfer in a rubber article.

Finite difference method

Finite difference method (FDM) is the simplest technique among the various numerical techniques given so far for the solution of the partial differential equations. It is used by some researchers to solve the heat transfer equation for rubber curing process. The first practical application of FDM in rubber curing was the simulation of the vulcanization process of the shoulder section of a tire by Prentice et al. [4]. Figure 2 shows the solution domain with FD grid. Although the developed model and adopted approach were simple, the differences between simulation results and experimental measurements, as reported in that paper, were very minor. The major drawbacks of this approach are difficulty in modeling of complex geometries and inability in solution of highly nonlinear problems such as rubber curing. Finite difference method was also used in conjunction with finite element method for the simulation of the curing process of rubber during injection molding (e.g., Isayev et al. [25]). In a recent work, Abhilash et al. [95] presented the results of solving one-dimensional heat equations in a rubber slab using MATLAB software. No significant results or in improvement methods are given.

Fig. 2
figure 2

Discretized finite difference form of the shoulder and mold used by Prentice et al. [4]

Full size image

Finite element method

Finite element method is a powerful and robust numerical technique that has been widely used to solve the heat transfer equation during curing process of rubber and other thermoset polymers. There are many published textbooks that can be referred for extensive details of the mathematical description of this method. For example, Comini [96], Lewis et al. [97], Huebner [98], Nassehi [99], Reddy [100, 101] and Bathe [102] are some of these references. There are several published works which most of them have been reviewed in historical background section. Due to the importance, its vast application in engineering analysis, the mathematical background of this technique and its features in relation to rubber curing process are concisely described here. Finite element method is based on the construction of an integral in which the integrand is an inner product of residual and weight functions and set the integral to zero. The residual is obtained by substitution of interpolation functions as approximate solutions. Standard Galerkin method is the most common form in which the weight functions are selected to be the same as the interpolation relations. In this approach, the approximate form of the governing Eqs. 1 or 2 is multiplied by weight functions and their integrals over the domain of a typical element (Ω e) are assumed to be equal to zero as given below:

$$\int_{{\varOmega_{e} }}^{{}} w \left[ {\rho C\frac{{\partial \tilde{T}}}{\partial t} - \frac{\partial }{\partial x}\left( {k\frac{{\partial \tilde{T}}}{\partial x}} \right) - \frac{\partial }{\partial y}\left( {k\frac{{\partial \tilde{T}}}{\partial y}} \right) - \frac{\partial }{\partial z}\left( {k\frac{{\partial \tilde{T}}}{\partial z}} \right) - \dot{Q}} \right]{\text{d}}\varOmega_{e}$$
(29)
$$\int_{{\varOmega_{e} }}^{{}} w \left[ {\rho C\frac{{\partial \tilde{T}}}{\partial t} - \frac{1}{r}\frac{\partial }{\partial r}\left( {rk\frac{{\partial \tilde{T}}}{\partial r}} \right) - \frac{\partial }{\partial z}\left( {k\frac{{\partial \tilde{T}}}{\partial z}} \right) - \dot{Q}} \right]{\text{d}}\varOmega_{e}$$
(30)

In the above equations, w is the weight function and \(\left( {\tilde{T}} \right)\) is an approximated form of the temperature distribution, which is generally given by a series relation generally belonging to the family of Lagrange interpolation polynomials. Using the divergence theorem, the weak form is obtained. Then, by selecting an appropriate interpolation function for the solution variable (temperature), the finite element working equations are derived as:

$$\left[ {M^{\left( e \right)} } \right]\left\{ {\dot{T}^{\left( e \right)} } \right\} + \left[ {K^{\left( e \right)} } \right]\left\{ {T^{\left( e \right)} } \right\} = \left\{ {F^{\left( e \right)} } \right\}$$
(31)

where {T (e)} and {T •(e)} are the vector of unknown (temperature) and its first derivative with respect to time, [M (e)], [K (e)], {F (e)} are elemental mass matrix, stiffness matrix and load vector, respectively. These matrices and vector are generally functions of temperature and state of cure and their components are given as follows [1]:

For three-dimensional model

$$M_{ij}^{\left( e \right)} = \iiint_{{\varOmega_{e} }} {\rho C\psi_{i} \psi_{j} {\text{d}}x{\text{d}}y{\text{d}}z}$$
(32)
$$K_{ij}^{\left( e \right)} = \iiint_{{\varOmega_{e} }} k\left( {\frac{{\partial \psi_{i} }}{\partial x}\frac{{\partial \psi_{j} }}{\partial x} + \frac{{\partial \psi_{i} }}{\partial y}\frac{{\partial \psi_{j} }}{\partial y} + \frac{{\partial \psi_{i} }}{\partial z}\frac{{\partial \psi_{j} }}{\partial z}} \right){\text{d}}x{\text{d}}y{\text{d}}z$$
(33)
$$F_{i}^{\left( e \right)} = \iiint_{{\varOmega_{e} }} {\psi_{i} \dot{Q}{\text{d}}x{\text{d}}y{\text{d}}z} + \oint_{{T_{e} }} {\psi_{i} } k\left( {\frac{\partial T}{\partial x}n_{x} + \frac{\partial T}{\partial y}n_{y} + \frac{\partial T}{\partial z}n_{z} } \right){\text{d}}\varGamma_{e}$$
(34)

For axisymmetric model

$$M_{ij}^{\left( e \right)} = \iint_{{\varOmega_{e} }} \rho C\psi_{i} \psi_{j} r{\text{d}}r{\text{d}}z$$
(35)
$$K_{ij}^{\left( e \right)} = \iint_{{\varOmega_{e} }} k\left( {\frac{{\partial \psi_{i} }}{\partial r}\frac{{\partial \psi_{j} }}{\partial r} + \frac{{\partial \psi_{i} }}{\partial z}\frac{{\partial \psi_{j} }}{\partial z}} \right)r{\text{d}}r{\text{d}}z$$
(36)
$$F_{i}^{\left( e \right)} = \iint_{{\varOmega_{e} }} {\psi_{i} \dot{Q}r{\text{d}}r{\text{d}}z} + \oint_{{\varGamma {}_{e}^{{}} }} {\psi_{i} } k\left( {\frac{\partial T}{\partial r}n_{r} + \frac{\partial T}{\partial z}n_{z} } \right)r{\text{d}}\varGamma_{e}$$
(37)

In these equations, Ψ i and Ψ j are the weight and interpolation functions, n x , n y and n z (for three-dimensional model) and n r and n z (for the axisymmetric model) are the components of the unit vector normal to the boundary and (e) represents the boundary of the element. In order to solve the first-order ordinary matrix differential of Eq. 31, the implicit θ time stepping scheme is usually used [101]. The final form of the working equations in this scheme is given as:

$$\left( {\left[ {M^{\left( e \right)} } \right]^{a} + \theta \Delta t\left[ {K^{\left( e \right)} } \right]^{a} } \right)\left\{ T \right\}^{n + 1} = \left( {\left[ {M^{\left( e \right)} } \right]^{a} - \left( {1 - \theta } \right)\Delta t\left[ {K^{\left( e \right)} } \right]^{a} } \right)\left\{ T \right\}^{n} + \left( {\left\{ {F^{\left( e \right)} } \right\}^{a} } \right)\Delta t$$
(38)

where superscripts n and n + 1 refer to the time t n and t n+1, respectively. The superscript a also indicates a time level between t n and t n+1, defined as:

$$\left\{ T \right\}^{a} = \left( {1 - \theta } \right)\left\{ T \right\}^{n} + \theta \left\{ T \right\}^{n + 1}$$
(39)

This means that depending on selected value for θ, the mass and stiffness matrices as well as load vector (i.e., \(\left[ {M^{\left( e \right)} } \right]^{a}\), \(\left[ {K^{\left( e \right)} } \right]^{a}\) and \(\left\{ {F^{\left( e \right)} } \right\}^{a}\)) should be calculated at this point. θ is a parameter which its values vary between 0 (explicit) and 1 (full implicit) and has significant influence on both convergence and stability of the numerical results [101]. Numerical experiments showed that a value of one for θ is the best compromise between accuracy and stability against computational cost and efforts.

Boundary conditions

The governing Eqs. 1 and 2 must be solved in conjunction with appropriate boundary conditions. Among the different types of boundary conditions that can be used for the solution of heat transfer equations, the first type, third type and radiation boundary conditions are normally used for the rubber curing process. The first-type boundary condition is used to directly impose temperature on the model. This type is mainly used during the heating stage in the mold. The third-type boundary condition that is also known as the convection boundary condition is generally used during the post-cure or cooling stage. The radiation boundary condition is primarily employed when the difference between temperatures on the surfaces of the rubber article and the surrounding media is very high. For example, at the early stage of the cooling step of a molded tire in the air or during the heating step of a rubber article in a high-temperature autoclave, radiation boundary condition should be applied in conjunction with convection boundary condition to obtain accurate solutions. The mathematical description of the third type and radiation boundary conditions are given as below:

For three-dimensional model

$${\text{Convection}}\quad \quad - k\left( {\frac{\partial T}{\partial x}n_{x} + \frac{\partial T}{\partial y}n_{y} + \frac{\partial T}{\partial z}n_{z} } \right) = h\left( {T - T_{\infty } } \right)$$
(40)
$${\text{Radiation}}\quad - k\left( {\frac{\partial T}{\partial x}n_{x} + \frac{\partial T}{\partial y}n_{y} + \frac{\partial T}{\partial z}n_{z} } \right) = F_{\varepsilon } F_{G} \sigma \left( {T^{4} - T_{\infty }^{4} } \right)$$
(41)

For axisymmetric model

$${\text{Convection}}\quad \quad - k\left( {\frac{\partial T}{\partial r}n_{r} + \frac{\partial T}{\partial z}n_{z} } \right) = h\left( {T - T_{\infty } } \right)$$
(42)
$${\text{Radiation}}\quad\quad- k\left( {\frac{\partial T}{\partial r}n_{r} + \frac{\partial T}{\partial z}n_{z} } \right) = F_{\upvarepsilon} F_{\text{G}} \sigma \left( {T^{4} - T_{\infty }^{4} } \right)$$
(43)

where h is the convection heat transfer coefficient, F ε is the emissivity function, F G is the geometric view factor, σ is the Stefan–Boltzmann constant (5.669 × 10−8 W/m2 K4), T is the absolute surface temperature of the body, and T ∞ is the absolute ambient (surrounding) temperature. Determination of proper values for h is not an easy task and needs several considerations with regard to the geometry, forced versus natural convection, cooling or heating media and temperature difference. It is one of the most challenging jobs in this field and requires several research works to be carried out to propose reliable and accurate equations. For the cooling stage, Gehman [2] proposed a semiempirical relation in which connective heat coefficient is given as:

$$h = C\left( {\frac{{\Delta T}}{L}} \right)^{0.25}$$
(44)

where C is a constant and dependent on geometry of the article, ΔT is the temperature difference between molded surface and ambient and L is a characteristic length. The above relation was also adopted by Prentice et al. [4] and Han et al. [9] during the simulation of the curing process of tires and by Ghoreishy et al. [14] for the cure simulation of a complex non-tire molded article. It is also worth to refer to the work carried out by Kennedy et al. [103] in which they have used their own empirical relation derived from laboratory data to simulate the post-cure stage of tire. Rafei et al. [17] used another empirical form for the calculation of the h during the cure simulation of a relatively thick and multi-part molded rubber article. Their approach was based on the calculation of the dimensionless Nusselt numbers for different surfaces and changing to heat transfer coefficient. Another important item is the determination of proper heat transfer coefficient for the flow of hot and cold media (steam and water) in bladder during curing and shaping of pneumatic tires. However, there are no published works on how to properly determine this parameter, and thus, it is another non-studied topic particularly in this field.

Thermal contact

Most of the rubber articles and also tires are shaped in molds. The heat transfer from hot mold to rubber may be influenced by the thermal resistance between mold and rubber surfaces, which is direct result of the roughness of surface profile. This introduces an additional conductance term, known as thermal contact conductance. Improvements in simulation software and more accurate modeling of heat transfer in design application have led to the study of thermal contact conductance at interface between metals and polymers [104]. Marotta et al. [105] measured the thermal contact conductance of several widely available thermoplastic and thermosetting polymers in contact with metals. The conductive heat transfer between the contact surfaces is assumed to be defined by:

$$Q = k_{c} \left( {T_{A} - T_{B} } \right)$$
(45)

where Q is the heat flux crossing the interface from point A on one surface to point B on the other, T A and T B are the temperatures of the points on the surfaces, and k c is the gap conductance. The value of thermal contact conductance between polymer–metal surfaces is in the range of 0.125−0.25 × 105 W/m2 K [104]. This relation was used by Rafei et al. [17] for the simulation of the curing process of a thick molded rubber. The results showed that taking the effect of thermal contact between the metal surfaces and rubber into consideration has led to obtain more accurate results. However, precise determination of the gap conductance (k c ) and its variation with temperature, pressure and surface roughness are still another challenge for an accurate cure simulation.

Incompatible mesh

As stated before, tire and most rubber articles have complex shapes. They are normally formed in molds with complicated geometries. More specifically, the shape and topology of the tread patterns in pneumatic tires are quite different from the other parts. Consequently, in many applications the use of meshes with different geometries and refinement is inevitable. Figure 3 shows a finite element mesh developed for the cure simulation of a thick rubber article. As can be seen, incompatible mesh is used to accurately discretize rubber and mold.

Fig. 3
figure 3

Incompatible meshes developed for cure simulation of a complex rubber article with mold [17]

Full size image

A tying algorithm is needed to take the incompatibility between meshes into account. General procedure is to equalize the calculated degree of freedom on contact line. This ensures that the variables (temperature) in contact line (or surface) have identical values.

Solution algorithm and computer codes

Two solution strategies are usually adopted by researchers to solve the rubber curing process via finite element method. The first one is based on the development of in-house code using a high-level language such as Fortran, Visual Basic, C or using software with computational language such as MATLAB. On the other hand, with advancement of commercial codes, especially from computational and CAD/CAE points of view, there is a great tendency to use advanced computer package to do this job. We briefly review both approaches and discuss their advantages and disadvantages in the following sections.

In-house development

A number of researchers have used their own developed codes to solve heat transfer and cure kinetics for rubber vulcanization. For example, Ghoreishy et al. [14–16] have simulated the curing process of a rubber article and also a truck tire using their own codes developed in Visual Basic. Han et al. [9, 10], Yan [13] and Marzocca [7] simulated the rubber curing using in-house developed codes (mainly in Fortran). The main advantage of developing a computer code from scratch is to implement kinetics of curing reactions in an integrated environment with finite element solution of the heat transfer equations. However, it is very time-consuming and requires commercial preprocessor and post-processor programs for the development of finite element mesh and also graphical visualization of the results. We will show some results of using in-house codes in application section.

Commercial software

Owing to the reduced computational cost and effort in conjunction with available preprocessing and post-processing routines, commercial codes are preferred to be used for the solution of rubber curing problems. A number of powerful finite element codes such as Abaqus [106], ANSYS [107] and MARC [108] are available in the market and can be used for this purpose. Although this technique reduces the computational cost and effort associated with the first method, the problem of computing the rate of cure and heat source as well as state of cure remains unsolved. Therefore, a supplementary calculating system is necessary for this part of calculation. The ability to include extra codes (as a user-defined subroutine) into a finite element code is a great advantage among the different computer programs [1, 19]. Abaqus is a powerful commercial code that has been extensively used for this purpose. It has two different subroutines to perform this task. HETVAL and UMATHT are two user subroutines, which can be tailored based on the selected kinetics and implemented into the finite element model. Toth et al. [8] and Ghoreishy [1] have used HETVAL subroutine for the simulation of the vulcanization process of a tire and a molded rubber articles, respectively. It was shown in those works that the HETVAL is a powerful and reliable subroutine, which can be used for the calculation of the cure kinetics and heat of reaction in conjunction with the heat transfer solution algorithm of Abaqus. UMATHT is more robust than the HETVAL as it can be used not only for the calculation of kinetics and heat of reaction but also the variations of the thermal properties (thermal conductivity, specific heat capacity and density) with temperature and state of cure that can be included in the model. Since most industrial compounds contain several ingredients, their properties show intricate variations with temperature and the other process variables such as state of cure. Consequently, UMATHT is the best choice that can be used to take the real-time variations of material properties into account. Ghoreishy et al. [17, 20] and Tang [21] have used UMATHT in conjunction with Abaqus code and simulated the curing process of rubber articles and showed its high capability in cope with nonlinear nature of the heat transfer equations encountered in rubber curing process. In addition to the mentioned subroutines, Wang et al. [109] and Su et al. [110] used VARM, which is another user subroutine, and simulated the vulcanization process of a giant radial tire with tread pattern. However, UVARM is not able to take the heat of reaction and its variations with temperature and state of cure into consideration. It can only be used to define new output variables such as induction time, rate and state of cure, and therefore, the use of this subroutine for cure simulation is restricted and is not suggested. In a recent comprehensive and novel work carried out by Vafayan et al. [111], the thermal cure cycle has been optimized for a complex-shape composite part made from epoxy/glass prepreg. Abaqus software has been linked with MATLAB software to allow coupling of simulation and optimization results, which leads to automatically designed thermal cure cycle. A complete objective function has been defined based on six sub-objective functions including maximum degree of cure, maximum temperature, crossover after gel point, cure gradients after gel point, temperature gradients and curing time. For the minimization of the objective function, genetic algorithm has been used as a more efficient search strategy.

Applications

Most of the published works devoted to this topic are reviewed in the previous section. In this part, we consider those works from application point of view and show that how this technique can be used for analysis and optimization of a cure process. We study them in two parts. The first is the application in tire curing process, and the in second the shaping and vulcanization of non-tire rubber parts are taken into account.

Tires

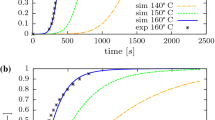
Numerical simulation of the curing process during tire shaping stage was studied by many researchers as reviewed and reported in background section. Here, we select few of them and present some of their results. The first practical modeling of tire curing process belongs to Prentice et al. [4], which is based on the finite difference method. Figure 4 shows and compares the actual temperature and the predicted data at different locations depicted in Fig. 2. As it can be seen, there are good agreements between actual temperature profiles and simulation results. This is in spite of using a relatively simple geometry and numerical technique. Early works on the use of finite element method in tire simulation start with Toth et al. [8]. The ability of their work in predicting the temperature profiles is shown in Fig. 5a, b. It was also shown that there are good confirmations between experimental and predicted temperature profiles. Both of these models were two dimensional. Ghoreishy et al. [15] for the first time developed a three-dimensional finite element model for the cure simulation of truck tire with pattern. They have, however, used a consistent mesh throughout the model including tread and body of the tire. Figure 6 shows the finite mesh of the tire. An in-house code was used to simulate the curing process. Figure 7 compares the temperature profiles at two points inside the tire, which confirmed the applicability of the model and developed code. The profiles of temperature and state of cure for two points with the same radius but different distance from mold surfaces (located inside and outside of the lug in the pattern) are shown in Figs. 8 and 9. As it can be seen, there is quite significant difference between the results obtained at these points which means that a three-dimensional model is necessary when dealing with complicated geometry such as tire pattern. In a more recent work, they have developed another three-dimensional model for a truck tire with inconsistent mesh as shown in Fig. 10. It can be seen that due to the complexity in tire geometry, tetrahedral mesh was utilized for the discretization of the tread part while hexahedral elements are used for the side wall and main body of the tire. Figure 11a–f shows the distributions of the temperature at 650, 1300, 1950, 2600, 3250 and 3900 s after the start of vulcanization in the mold, respectively. Also, Fig. 12a–d presents the distributions of the state of cure inside the tire at 2600 and 3900 s after start of vulcanization in the mold as well as 1300 and 2600 s after mold opening or start of post-cure stage. In all figures, it can be clearly found that there are significant differences in values of (T) and (α) at various positions.

Fig. 4
figure 4

Comparison of the actual temperature with simulation results as given in [4]

Full size image
Fig. 5
figure 5

Comparison between predicted and measured temperature profiles a top of belt edge [8] and b top of bead filler [8]

Full size image
Fig. 6
figure 6

Three-dimensional finite element mesh of a truck tire with consistent elements [15]

Full size image
Fig. 7
figure 7

Comparison between predicted and measured temperature profiles for two locations in the tire shown in Fig. 6 [15]

Full size image
Fig. 8
figure 8

Temperature profiles for two points located at different tread locations but with same radii [15]

Full size image
Fig. 9
figure 9

Profiles of state of cure for two points located at different tread locations but with same radii [15]

Full size image
Fig. 10
figure 10

Finite element mesh of a truck tire with inconsistent elements [19]

Full size image
Fig. 11
figure 11

Distribution of the temperature: a 650, b 1300, c 1950, d 2600, e 3250 and f 3900 s after start of molding [19]

Full size image
Fig. 12
figure 12

Distribution of the state of cure: a 2600 s after start of molding [19], b 3900 s after start of molding [19], c 1300 s after start of post-cure [19] and d 2600 s after start of post-cure [19]

Full size image

Non-tires

An advanced computer model was developed by Rafei et al. [17] for the modeling and simulation of the rubber curing process of a large and thick rubber article with metal insert. The developed model includes mold, and the thermal contact between metal and rubber is also taken into consideration as shown in Fig. 13. The simulated temperature profile for a point inside the molded rubber is compared with simulated data and presented in Fig. 14. As it is shown, there is excellent agreement between actual and predicted data. They have also used this model for the simulation and optimization of the curing process of another industrial part which its finite element mesh is shown in Fig. 15 [20]. Two molding times were selected. The first one was 3600 s, which has been initially chosen in the production line. Having simulated and examined the distribution of the temperature and state of cure, the molding was reduced to 2000 s and completion of the curing reaction was postponed to cooling stage. The profiles of temperature and state of cure obtained with these molding times for a point inside the rubber part are shown in Figs. 16 and 17, respectively. As it can be seen, both molding times give the same state of cure, and since the second one (i.e., 2000 s) is shorter than the first one, the cost would be much lower. In addition, the measurement of hardness on the final product revealed that the lower molding time produces an article with a hardness of five Shore A greater the part which was produced with longer molding time.

Fig. 13
figure 13

A thick and large rubber part with metal insert and mold [17]

Full size image
Fig. 14
figure 14

Comparison between experimentally measured and predicted temperature profiles for the rubber part shown in Fig. 13 [17]

Full size image
Fig. 15
figure 15

Finite element mesh of a thick industrial rubber article used in [20]

Full size image
Fig. 16
figure 16

Predicted temperature profiles for a point inside the rubber article shown in Fig. 15 using two molding times [20]

Full size image
Fig. 17
figure 17

Predicted profiles of state of cure for a point inside the rubber article shown in Fig. 15 using two molding times [20]

Full size image

Summary and conclusion

Computer simulation of rubber and thermoset polymers is an interesting and critical subject in polymer processing operations. This is because that by using this technique not only the optimization cost and efforts are substantially reduced but also distribution of the extent of crosslinking is found. Study of this subject is carried in this paper from several points of view to enhance our understanding from its theoretical background and current state of the art. This work reviewed development and solution of the governing heat transfer equations, cure kinetics and proposed equations, thermal properties, solution algorithm and computer code and also presented some limited results obtained for industrial applications. This review showed that there are some features in this topic that needs more attention and study. Among them, we can point to relations for accurate description of the heat transfer coefficients, especially for tire curing bladder, more rigorous cure kinetics equations, modeling of highly complicated geometries such as radial tires with complex tread patterns and finally more accurate measurement and determination of the thermal conductivity, heat capacity and density of the rubber, especially for cord–rubber composites.