Capacitated vehicle routing problem with sequence-based pallet loading and axle weight constraints

Abstract

In this paper, we introduce and study the capacitated vehicle routing problem with sequence-based pallet loading and axle weight constraints. To the best of our knowledge, it is the first time that axle weight restrictions are incorporated in a vehicle routing model. The aim of this paper is to demonstrate that incorporating axle weight restrictions in a vehicle routing model is possible and necessary for a feasible route planning. Axle weight limits impose a great challenge for transportation companies. Trucks with overloaded axles represent a significant threat for traffic safety and may cause serious damage to the road surface. Transporters face high fines when violating these limits. A mixed integer linear programming formulation for the capacitated vehicle routing problem with sequence-based pallet loading and axle weight constraints is provided. Results of the model are compared to the results of the model without axle weight restrictions. Computational experiments demonstrate that the model performs adequately and that the integration of axle weight constraints in vehicle routing models is required for a feasible route planning.

1 Introduction

One of the most studied combinatorial optimization problems in transport and logistics is the vehicle routing problem (VRP). The VRP concerns the distribution of goods between depots and customers (Toth and Vigo 2002). Its goal is to find a set of routes for a fleet of vehicles to satisfy customer demands. The objective function typically aims to minimize routing costs. The basic version of the vehicle routing problem is the capacitated vehicle routing problem (CVRP). The CVRP considers a homogeneous vehicle fleet with a fixed capacity (in terms of weight or number of items) which delivers goods from a depot to customer locations. Split deliveries are not allowed.

This paper focuses on the integration of loading constraints in VRPs. A survey conducted by the authors among several Belgian logistics service providers pointed out that they are faced with loading problems in their route planning. Current commercial route planning programs do not take into account most of these loading constraints, which makes the planning often not feasible in practice. This gives rise to last-minute changes in planning which may result in additional costs. The development of vehicle routing models that incorporate loading constraints is, therefore, vital for a more efficient planning of routes. The combination of VRP and loading problems is a fairly recent domain of research. For a detailed overview of literature on this topic up to 2010 the reader is referred to Iori and Martello (2010).

The focus of this paper is on the combination of a VRP with the loading of homogeneous pallets inside a vehicle, since this is a problem setting often encountered by distributors. Pallets may be placed in two rows inside the vehicle but cannot be stacked on top of each other because of their weight, fragility or customer preferences. Sequence-based loading is assumed which ensures that when arriving at a customer, no items belonging to customers served later on the route block the removal of the items of the current customer. The problem has similarities with the multi-pile VRP (MP-VRP), the double traveling salesman problem with multiple stacks (DTSPMS) and the traveling salesman pickup and delivery problem (TSPPD) with multiple stacks. Doerner et al (2007) develop a tabu search (TS) method and ant colony optimization (ACO) method to solve the MP-VRP, based on a real-world transportation problem regarding the transport of wooden chipboards. For every order, chipboards of the same type (small or large) are grouped into a unique item, which is placed onto a single pallet. The vehicle is divided into three piles on which pallets can be stacked. Pallets containing large chipboards can extend over multiple piles. The other pallets can be placed into a single pile. Because of this specific configuration of pallets placed into multiple piles, the original three-dimensional problem can be reduced to a one-dimensional one. Tricoire et al (2011) develop a combination of VNS and branch-and-cut to solve the MP-VRP exactly for small-size instances and heuristically for large-size instances. In both papers concerning the MP-VRP, sequence-based loading is taken into account. The DTSPMS, proposed by Petersen and Madsen (2009), considers pickup and delivery of goods performed in two separate networks in vehicles with multiple stacks. All pickups must be made before any delivery can take place. The goods cannot be repacked, nor vertically stacked. The goods can be placed in several rows (horizontal stacks). In each row, sequence-based loading (which equals last-in-first-out since only a single dimension is considered) is assumed. It is assumed that each order consists of a single item. The problem is based on a real-world application in which in a first phase, a container is loaded onto a truck to perform pickup operations and returned by that truck to a depot or terminal. In a second phase, the container is loaded onto a train, ship, plane or another truck and transported to another depot or terminal. In the depots or terminals, there are no facilities to repack the items inside the container. In the final phase, the container is again transferred to a truck which performs the delivery operations (Petersen and Madsen 2009). Petersen and Madsen (2009), Felipe et al (2009) and Felipe et al (2011) develop heuristic methods to solve the DTSPMS, while Lusby et al (2010), Petersen et al (2010), Lusby and Larsen (2011), Alba et al (2013) and Carrabs et al (2013) propose an exact algorithm. Côté et al (2012a) and Côté et al (2012b) consider the TSPPD with multiple stacks with LIFO loading with respectively a heuristic method and a branch-and-cut algorithm. Øvstebø et al (2011) examine a similar problem on roll-on/roll-off (RoRo) ships that transport cargo on wheels. The decks on the ship may be divided into lanes in which the cargo may be placed. The lanes may be compared to stacks in a truck. Sequence-based loading is considered as a soft constraint. A penalty cost is incurred if the constraint is violated.

To our knowledge, axle weight constraints have never been incorporated in a routing model. However, our survey pointed out that axle weight limits impose a great challenge for transportation companies. Trucks with overloaded axles represent a significant threat for traffic safety and may cause serious damage to the road surface. Transporters face high fines when violating these limits. Weigh-in-motion (WIM) systems on highways increase the chances that axle weight violations are detected. A WIM system monitors axle weight violations of trucks while driving. The authorities can thereby focus on trucks with violations according to the WIM system, to do a precise measurement. This leads to an enormous efficiency gain of the controls (Jacob and Feypell-de La Beaumelle 2010).

Legislation about axle weight limits varies by country (for an overview of the axle weight limits in Europe, the reader is referred to the International Transport Forum). The axle weight is the weight that is placed on the axles of the truck. A truck with five axles is illustrated in Fig. 1. The first axle, also called the steering axle, and the second axle, called the driving axle, both belong to the tractor. The axles of the trailer are tridem axles. Tridem axles are three successive axles with a distance between the middle of the first axle and the middle of the second axle and between the middle of the second axle and the middle of the third axle of less than 1.8 and more than 1 m. When item $j$ is placed onto a vehicle, the weight of the item is divided over the axles of the tractor and the axles of the trailer. $a_{ij}^F$ represents the weight of the items of customer $j$ placed on the coupling of the truck (which is the link between the tractor and the trailer). The weight on the coupling is carried by the axles of the tractor. $a_{ij}^R$ represents the weight of the items of customer $j$ on the axles of the trailer. As a truck delivers items to several customers on a single route, the weight on the axles of the truck changes. A load that is placed at the rear of the vehicle (behind the axles of the trailer) has a negative weight on the axles of the tractor. For this reason, it is possible that by unloading this item a violation of the weight limits of the axles of the tractor is induced. It is, therefore, important that axle weights are considered also during the whole trip of the vehicle and not only when the vehicle departs from the depot. To our knowledge, Lim et al (2013) are the only authors who address axle weight constraints in a container loading problem. They develop a heuristic method to tackle the single container loading problem with axle weight constraints. Axle weight limits have not yet been investigated in a VRP.

Fig. 1

Axle weight tractor (steering axle, driving axle) and trailer (tridem axles) (figure adapted from TruckScience)

In this paper, to the authors’ knowledge, for the first time axle weight restrictions are included in a VRP model. To ensure the relevance of the model, it is based on a survey conducted among Belgian logistics service providers. A problem formulation of a CVRP with sequence-based pallet loading and axle weight constraints is provided. The model is tested on networks of 10–25 customers and compared to a model without axle weight restrictions. In Sect. 2, the problem is described and illustrated with an example. The calculation of the axle weight is described in Sect. 3. A mixed integer linear programming formulation for the CVRP with sequence-based pallet loading and axle weight constraints is presented in Sect. 4. In Sect. 5, computational results are provided to illustrate the functioning of the model. In the final section, conclusions and future research opportunities are discussed (Sect. 6).

2 Problem description

The problem of interest in this paper is a CVRP with sequence-based pallet loading and axle weight constraints. To the best of our knowledge, it is the first time that axle weight restrictions are incorporated into a VRP model. The problem is based on a real-world problem. Information on the vehicle fleet (measurements, capacity, mass, axle weight limits) is derived from the information from a Belgian logistics service provider. The vehicle type that is considered in this article is a 30-foot truck that consists of a two-axle tractor (steering axle and driving axle) and a trailer with tridem axles. All vehicle types with the same axle configuration but different dimensions (for example, 40-foot trucks) may be handled by the model by modifying vehicle-specific parameters such as distance between the beginning of the truck and the middle of the rear axles. The idea behind the calculation of the center of gravity and the axle weights is also applicable on vehicles with a different axle configuration, but depending on the type of change in axle configuration it may be necessary to modify or add some equations and constraints to the model.

The VRP consists of a set of customers and a central depot. Customer demands need to be fulfilled and vehicle capacities need to be respected. Each customer has to be visited exactly once. Multiple homogenous 30-foot trucks are considered which consist of a tractor, a trailer and a container. The length, width and height of the inside dimensions of the container are, respectively, 9.12, 2.44 and 2.44 m. The mass of the empty tractor is 6.82 t of which 4.88 t is carried by the steering axle and 1.97 t is supported by the driving axle. The tare weight of the container is 3 t of which 2 t is supported by the coupling and 1 t is supported by the axles of the trailer. The mass of the empty trailer is 2 t. The maximum weight on the coupling of the tractor is 13.6 t. This is subtracted by the weight of the container carried by the coupling (2 t), which leads to a maximum weight of the load that may be placed on the coupling of 11.6 t. 80 % of the weight on the coupling is supported by the driving axles of the tractor, while the remaining 20 % is carried by the steering axle. The maximum weight capacity of the tridem axles of the trailer is 24 t. This is subtracted by the weight of the trailer (2 t) and the weight of the empty container carried by the axles of the trailer (1 t) which gives a total of 21 t. This is the maximum weight of the load that may be carried by the axles of the trailer. The maximum weight of the vehicle is 44 t. This is subtracted by the empty weight of the tractor (6.82 t), the tare weight of the container (3 t) and the weight of the trailer (2 t), which results in a maximum weight of the load of 32.2 t.

The demand of the customers is heterogeneous and consists of europallets ($80 \times 120$ cm). In total, 22 pallets may be placed inside a truck in two horizontal rows. Pallets are packed dense in the truck. This means there cannot be a gap between two consecutive pallets inside the truck. Pallets are alternately packed in the left and right row. This implies that the pallets of a single customer cannot be aligned in a single row. Moreover, the pallets of the last customer are placed at the deepest portion of the loading area. This pallet configuration is often used in practice since the stability of the load is much higher when the pallets are packed dense than when gaps are allowed between the pallets. It is assumed that all pallets of a single customer have the same weight and that the weight is uniformly distributed inside each pallet, i.e., the center of gravity of a pallet lies in its geometric midpoint. The container can only be unloaded at the rear side. To avoid moving pallets of other customers when arriving at a customer, sequence-based loading is imposed. Vertical stacking is not allowed, due to fragility of goods and customer preferences. Customers usually do not want goods of other customers to be packed on top of their goods.

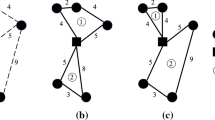
In the remaining of this section, the impact of incorporating axle weight restrictions in a routing model with sequence-based loading is illustrated with an example. In Fig. 2, a depot with four customers is presented. Each customer has a demand of five europallets. The total mass of the pallets of customer 1, 2, 3 and 4 is, respectively, 12, 2, 2 and 12 t. The distance matrix of the customer nodes and the depot may be found in Table 1. The shortest route between the depot and customer locations is computed with and without taking axle weight restrictions into account. For the computation of the weight on the axles, the reader is referred to Sect. 3.

Fig. 2

Graphical representation of a depot with four customers

Table 1 Distance matrix illustrative example

An optimal vehicle route when axle weight restrictions are not considered is graphically represented in Fig. 3a. The vehicle starts in the depot, visits customer nodes 1, 2, 3, 4 and returns to the depot. The loading scheme of the container may be found in Fig. 4a. Total distance traveled is 12.8. In Table 2, the total mass of the load as well as the weight of the load on the coupling and on the axles of the trailer when the truck arrives at each customer node is given. The total mass of the load is well below the maximum weight capacity (32.2 t) of the vehicle. Weight on the coupling is greater than the weight limit (11.6 t) when the vehicle departs from the depot until it arrives at the last customer. This means that the axle weight limits on the axles of the tractor are surpassed on the vehicle route. The highest axle weight violation takes place between between customer 1 and customer 2. When the vehicle departs from customer 1, the weight on the coupling is 18 % higher than the limit, which is substantial and could lead to a significant fine. It is, therefore, not a feasible solution for the distribution company. In this symmetric VRP without axle weight restrictions, visiting sequence 4-3-2-1 (the reverse order of customers from the first solution) is also an optimal route with the same total distance traveled as visiting sequence 1-2-3-4. This solution generates the same axle weight violations.

Fig. 3

Graphical representation of an optimal vehicle route a without axle weight restrictions, b with axle weight restrictions

Fig. 4

Loading scheme of a container (in top view) of the optimal route a without axle weight restrictions, b with axle weight restrictions. The load of, respectively, customer 1, 2 , 3 and 4 is indicated by C1, C2, C3 and C4

Table 2 Results of illustrative example without axle weight restrictions

In Fig. 3b, the optimal vehicle route when axle weight restrictions are considered is graphically represented. The vehicle starts in the depot, visits customer nodes 1, 2, 4, 3 and returns to the depot. In Table 3, the total mass of the load and the weight of the load on the coupling and on the axles of the trailer when the truck arrives at each customer node are given. Total distance traveled is 14, which is an increase of 9 % compared to the optimal solution in the model without axle weight restrictions. The maximum weight on the coupling is 10.2 t which does not exceed the weight limit on the coupling (11.6 t). The maximum load on the axles of the trailer is 18.8 t which is still below the weight limit on the axles of the trailer (21 t). In Fig. 4b, the loading scheme of the container is presented. Note that although the change only exists in swapping two customers (customer 3 and 4) on the route, all axle weight violations have disappeared. This is because the heavy pallets of customer 4 are not anymore at the beginning of the vehicle and are therefore not only carried by the coupling, but also partially by the trailer. To conclude, integrating axle weight restrictions in the model may lead to a higher distance traveled, but ensures a feasible weight distribution of the load inside the vehicle.

Table 3 Results of illustrative example with axle weight restrictions

3 Axle weight calculation

The calculation of the weight of the pallets of customer $j$ when traveling from customer $i$ to customer $j$ on the coupling point or the axles of the tractor ($a_{ij}^F$) and on the axles of the trailer ($a_{ij}^R$) is presented in Eqs. (1) and (2). Figure 5 graphically presents the parameters in Eqs. (1) and (2). The weight of the pallets of customer $j$ is denoted by $w_j$. Parameter $\mathrm{CG}_j$ represents the distance from the beginning of the container to the center of gravity of the pallet of customer $j$. Parameter $c$ denotes the distance from the beginning of the container to the coupling. The final parameter $d$ represents the distance between the coupling and the central axle of the trailer.

$$\begin{aligned} a_{ij}^R&=\frac{({\text {CG}}_j-c)}{d} w_j \end{aligned}$$

(1)

$$\begin{aligned} a_{ij}^F&=w_j- a_{ij}^R \end{aligned}$$

(2)

The weight of the pallets is divided over the axles of the trailer and the axles of the tractor. The distribution of the weight over the axles depends on the distance between the pallet and the axles. In the first part of Eq. (1), the percentage of the weight that is assigned to the axles of the trailer is computed by dividing the distance between the coupling and the center of gravity of the item by the distance between the coupling and the central axle of the trailer. In the second part of Eq. (1), this percentage is multiplied by the weight of the item to compute the weight that is carried by the axles of the trailer. The larger the distance between the item and the coupling, the higher the percentage of weight that is distributed to the axles of the trailer will be. The weight on the coupling is computed in Eq. (2) by subtracting the weight on the axles of the trailer from the weight of the item.

Based on real-world information, parameters $c$ and $d$, respectively, have a value of 1 and 5.5 m. In the next paragraphs, calculations are expressed in pallet places instead of meters. The europallets ($1.20 \times 0.8$ m) are placed in two rows with a width of 1.20 m, which makes the length of each pallet inside the container (= a single pallet place) equal to 0.8 m. The value of $c$ becomes 1.25 (= $\frac{1\,{\text {m}}}{0.8\,{\text {m}}/{\text {palletplace}}}$) pallet places and $d$ has a value of 6.875 (= $\frac{5.5\,{\text {m}}}{0.8\,{\text {m}}/{\text {palletplace}}}$) pallet places.

Fig. 5

Tractor (with two axles) and trailer (with tridem axles)

While $c$, $d$ and $w_j$ are parameters which are known beforehand, determining the value of $\mathrm{CG}_j$ is less straightforward since the center of gravity depends on where the item is placed in the truck. The calculation of the center of gravity is illustrated in Fig. 6 in which the gray pallets represent pallets that are already in the truck when arriving at customer $j$ and the black shaded pallets represent the pallets of customer $j$. Since it is assumed that the center of gravity lies in the geometric midpoint of the pallets of customer $j$, the center of gravity of the eight pallets of customer $j$ in Fig. 6 equals $3$. The starting point ($S_j$) is the point at which the first pallet of customer $j$ (when coming from customer $i$) is placed inside the vehicle, which is at point $1$ in Fig. 6. The number of pallets that are already in the truck when arriving at customer $j$ is denoted by $l_{ij}$ and $L_j$ represents the number of pallets of customer $j$.

Fig. 6

Top view of a container with indication of starting point ($S_j$) and center of gravity ($\mathrm{CG}_j$)

In the following paragraphs, a formula is presented to calculate the center of gravity of the pallets of a customer. The authors are not aware of other sources that use a similar approach.The calculation of the center of gravity is composed of two parts. The first part determines the starting point ($S_j$) at which the first pallet of customer $j$ will be placed. This depends on $l_{ij}$. If the number of pallets in the truck is even, $S_j$ equals $\frac{l_{ij}}{2}$. When the number of pallets already in the truck is odd, $S_j$ equals $\frac{l_{ij}}{2} -0.5$. In Fig. 6, $l_{ij}$ equals $2$ which results in a $S_j$ of $1$ $(=2/2)$. The second part of the calculation of the center of gravity determines the distance between the center of gravity of the pallets of customer $j$ and $S_j$. This depends on the value of $l_{ij}$ and $L_j$. When $l_{ij}$ is even, the second part of the equation for the center of gravity equals $E_j$. $E_j$ is the center of gravity of the pallets of customer $j$ when the truck is empty upon arrival ($l_{ij}$ = 0). $E_j$ corresponds to Eq. (3) or (4) depending on whether $L_j$ is, respectively, even or odd. The center of gravity of every pallet separately is added up and divided by the number of pallets of customer $j$ ($L_j$). The last term in the numerator in the formulas is ${\rm Max}[0, (L_j-21)]$ or ${\rm Max}[0, (L_j-20)]$ because vehicle capacity is 22 pallets. The value of $L_j$, therefore, has to be equal or lower than 22. The following terms ($\mathrm{Max}[0, (L_j-22)], \mathrm{Max}[0, (L_j-23)], \mathrm{Max}[0, (L_j-24)] \ldots$) will always yield zero and are thereby not added to the numerator.

If $L_j$ even:

$$\begin{aligned} E_j= \frac{({\text {Max}}[0, (L_j-1)]+{\text {Max}}[0, (L_j-3)]+ \cdots + {\text {Max}}[0, (L_j-21)])}{L_j} \end{aligned}$$

(3)

If $L_j$ odd:

$$\begin{aligned} E_j= \frac{\left( \frac{L_j}{2}+{\text {Max}}[0, (L_j-2)]+{\text {Max}}[0, (L_j-4)]+\cdots +{\text {Max}}[0, (L_j-20)]\right) }{L_j} \end{aligned}$$

(4)

When $l_{ij}$ is odd, the second part of the equation for the center of gravity equals $O_j$. $O_j$ is the center of gravity of the pallets of customer $j$ when a single pallet is placed in the truck upon arrival ($l_{ij} = 1$). $O_j$ equals Eqs. (5) or (6) depending on whether $L_j$ is respectively even or odd. The calculation of $O_j$ is analogous to the calculation of $E_j$. The last term in Eq. (5) +0.5 equals the center of gravity of the first pallet of customer $j$ that is placed inside the truck. The last term in Eq. (6) $-0.5$ added up with the term right before it also equals the center of gravity of the first pallet of customer $j$ that is placed inside the truck.

If $L_j$ even:

$$\begin{aligned} O_j= \frac{\left( \frac{L_j - 1}{2} + {\text {Max}}[0, (L_j-1)]+{\text {Max}}[0, (L_j-3)]+ \cdots + {\text {Max}}[0, (L_j-21)] + 0.5\right) }{L_j} \end{aligned}$$

(5)

If $L_j$ odd:

$$\begin{aligned} O_j= \frac{(L_j + {\text {Max}}[0, (L_j-2)]+{\text {Max}}[0, (L_j-4)]+\cdots +{\text {Max}}[0, (L_j-20)] - 0,5)}{L_j} \end{aligned}$$

(6)

Since the number of pallets of customer $j$ is known in advance, $O_j$ and $E_j$ can be treated as parameters or constants in the model. To integrate Eqs. (3)–(6) and the calculation of $S_j$ into a single formula to define the center of gravity, parameter $P_j$ and variable $C_{ij}$ are created. $P_j$ equals 1 if $L_j$ is even and equals $-1$ when $L_j$ is odd. Variable $C_{ij}$ is defined to keep track of the variable $l_{ij}$. When a vehicle travels from $i$ to $j$, $C_{ij}$ has a value of 1 when $l_{ij}$ is even and a value of $-1$ when $l_{ij}$ is odd. When a vehicle does not travel from $i$ to $j$, $C_{ij}$ is $0$. For the formulation of $C_{ij}$ the reader is referred to Sect. 4.

The integrated formula of $\mathrm{CG}_j$ is displayed in Eq. (7). Note that this is a linear formula.

$$\begin{aligned} \mathrm{CG}_j&= \frac{\sum _{i\in V} l_{ij}}{2} - \frac{1}{4}*\left( 1- \sum _{i\in V}{C_{ij}}\right) + O_j*\frac{1}{2}*\left( 1- \sum _{i\in V}{C_{ij}}\right) \nonumber \\&\quad + E_j*\frac{1}{2}*\left(1+ \sum _{i\in V}{C_{ij}}\right) \forall i\in V \end{aligned}$$

(7)

The formula is composed of two parts.

$$\begin{aligned} \frac{\sum _{i\in V} l_{ij}}{2} - \frac{1}{4}*\left( 1- \sum _{i\in V}{C_{ij}}\right) \end{aligned}$$

(7.1)

$$\begin{aligned} O_j*\frac{1}{2}*\left( 1- \sum _{i\in V}{C_{ij}}\right) + E_j*\frac{1}{2}*\left( 1+ \sum _{i\in V}{C_{ij}}\right) \end{aligned}$$

(7.2)

In Eq. (7.1), the starting point $S_j$ at which the first pallet of customer $j$ will be placed is determined. When $l_{ij}$ is even, $C_{ij}$ equals 1 and the second term will become $0$. Only the first term will remain. When $l_{ij}$ is odd, $C_{ij}$ equals $-1$ and the second term will become $-0.5$. Equation (7.2) calculates the distance between the center of gravity of the pallets of customer $j$ and the beginning of the truck, when no or a single pallet is inside the truck. This equals the distance between the center of gravity of the pallets and the beginpoint $S_j$. When $l_{ij}$ is even, $C_{ij}$ equals $1$ and the first term will become zero while the second term will become $E_j$. When $l_{ij}$ is odd, $C_{ij}$ equals $-1$ and the first term will become $O_j$ while the second term will turn to zero.

4 Problem formulation

In this section, a mixed integer linear programming formulation of a CVRP with sequence-based pallet loading and axle weight constraints is given. Note that the considered problem is a delivery problem, as illustrated in Sect. 2. The calculation for the center of gravity is, however, less complex when formulated as a pickup problem. Therefore, the problem formulation given in this section is for a pickup problem. Since we consider a symmetrical problem (symmetrical distance matrix) and do not assume time windows, the optimal visiting sequences of the pickup problem can be reversed to determine the optimal visiting sequences of the delivery problem.

To formulate the problem the following notation is used:

$$\begin{aligned}&V = \{0,1,\ldots ,n+1\} \text {set \, of \, vertices \, with \, customers\, (node \, 1, } \ldots , n) \hbox { and}\\&\qquad \text { depot \, (node }\, 0, \, n+1) \, (\hbox {indices }\, i,j,k) \\&E = \text { set \, of \, edges } \\&c_{ij} = \text {traveling \, cost \, on \, link}\, (i,j) \\&L_j = \text {number \, of \, pallets \, demanded \, by \, customer } j \\&L = \text {maximum \, amount \, of \, pallets \, per \, vehicle} \\&Q_j = \text {total \, mass \, of \, the \, pallets \, of \, customer } j \\&Q = \text {maximum \, mass \, capacity \, of \, each \, vehicle} \\&E_j = \text {center \, of \, gravity \, of \, the \, pallets \, of \, customer } j \text { when \, the \, truck \, is \, empty}\\&O_j = \text {center \, of \, gravity \, of \, the \, pallets \, of \, customer } j \text { when \, 1 \, pallet \, is \, in\, the \, truck}\\&A^F = \text {maximum \, weight \, on \, the \,coupling}\\&A^R = \text {maximum \, weight \, on \, the \, axles \, of \, the \, trailer}\\&W^T = \text {mass \, of \, the \, empty \, truck}\\&W^{TD} = \text {weight \, of \, the \, empty \, truck \, on \, the \, driving \, axle}\\&W^{TR} = \text {weight \, of \, the \, empty \, truck \, on \, the \, axles \, of \, the\, trailer}\\&h = \text {percentage \, of \, weight \, on \, the\, coupling \, that \, is \, carried \, by \, the \, driving \, axle}\\&c = \text {distance \, between \, the \, beginning \, of \, the \, truck \, and \, the \, coupling}\\&d = \text {distance \, between \, the \, coupling \, and \, the \, center \, of \, the \, axles \, of \, the \, trailer} \\&P_{j} = \left\{ \begin{array}{ll} 1 &{}\quad \text {if }\, L_j \, \text {even } \\ -1 &{}\quad \text {if }\, L_j \, \text {odd } \end{array} \right. \\ \end{aligned}$$

The decision variables are defined as:

$$\begin{aligned}&X_{ij} = \left\{ \begin{array}{ll} 1 &{}\quad \text {if \, a \, vehicle \, travels \, from }\,i\,\text { to}\, j \\ 0 &{}\quad \text {otherwise } \end{array} \right. \\&\mathrm{CG}_{j} = \text {center \, of \, gravity \, of \, the \, pallets \, of \, customer } j \\&l_{ij} = \left\{ \begin{array}{ll} \text {total \, number \, of \, pallets \, on \, this \, link} &{}\quad \text { if \, a \, vehicle \, travels \, from } \, i \text { to }\, j \\ 0 &{}\quad \text {otherwise } \end{array} \right. \\&q_{ij} = \left\{ \begin{array}{ll} \text {total \, cargo \, mass \, on \, this \, link} &{} \text { if \, a \, vehicle \, travels \, from }\, i \text { to }\, j \\ 0 &{} \text {otherwise } \end{array} \right. \\&a_{ij}^F = \left\{ \begin{array}{ll} \text {total \, cargo \, weight \, on \, the \, coupling \, on \, this \, link} &{} \text { if \, a \, vehicle \, travels \, from }\, i \, \text { to }\, j \\ 0 &{} \text {otherwise } \end{array} \right. \\&a_{ij}^R = \left\{ \begin{array}{ll} \text {total \, cargo \, weight \, on \, the \, axles \, of \, the \, trailer \, on \, this \, link} &{} \text { if \, a \, vehicle \, travels \, from }\, i \, \text { to }\, j \\ 0 &{} \text {otherwise } \end{array} \right. \\&C_{ij} = \left\{ \begin{array}{ll} 1 &{} \text {if } \,l_{ij} \, \text { even \, and \, a \, vehicle \, travels \, from } \, i \, \text { to }\, j \\ -1 &{} \text {if }\, l_{ij} \,\text { odd \, and \, a \, vehicle \, travels \, from }\, i \, \text { to }\, j \\ 0 &{} \text {otherwise } \end{array} \right. \\ \end{aligned}$$

$$\begin{aligned}&\min \sum _{(i,j)\in E}c_{ij}x_{ij} \end{aligned}$$

(8)

$$\begin{aligned} \text {Subject \, to} \nonumber \\&\sum _{i\in V} x_{ij} = 1 \quad \forall j\in V\backslash \{0,n+1\} \end{aligned}$$

(9)

$$\begin{aligned}&\sum _{j\in V} x_{ij} = 1 \quad \forall i\in V\backslash \{0,n+1\} \end{aligned}$$

(10)

$$\begin{aligned}&x_{n+1,j} = 0 \quad \forall j\in V \end{aligned}$$

(11)

$$\begin{aligned}&x_{j,0} = 0 \quad \forall j\in V \end{aligned}$$

(12)

$$\begin{aligned}&l_{0j} = 0 \quad \forall j\in V \end{aligned}$$

(13)

$$\begin{aligned}&l_{ij} \le L x_{ij} \quad \forall (i,j)\in E \end{aligned}$$

(14)

$$\begin{aligned}&\sum _{i\in V} l_{ij} + L_j = \sum _{k\in V} l_{jk} \quad \forall j\in V\backslash \{0,n+1\} \end{aligned}$$

(15)

$$\begin{aligned}&q_{0j} = 0 \quad \forall j\in V \end{aligned}$$

(16)

$$\begin{aligned}&q_{ij} \le Q x_{ij} \quad \forall (i,j)\in E \end{aligned}$$

(17)

$$\begin{aligned}&\sum _{i\in V} q_{ij} + Q_j = \sum _{k\in V} q_{jk} \quad \forall j\in V\backslash \{0,n+1\} \end{aligned}$$

(18)

$$\begin{aligned}&C_{0j} = x_{oj} \quad \forall j\in V \end{aligned}$$

(19)

$$\begin{aligned}&C_{ij} \le x_{ij}\quad \forall (i,j)\in E \end{aligned}$$

(20)

$$\begin{aligned}&C_{ij} \ge -x_{ij}\quad \forall (i,j)\in E \end{aligned}$$

(21)

$$\begin{aligned}&\sum _{i\in V} C_{ij} P_j = \sum _{k\in V} C_{jk} \quad \forall j\in V\backslash \{0,n+1\} \end{aligned}$$

(22)

$$\begin{aligned}&a_{0j}^F = 0 \quad \forall j\in V \end{aligned}$$

(23)

$$\begin{aligned}&a_{0j}^R = 0 \quad \forall j\in V \end{aligned}$$

(24)

$$\begin{aligned}&a_{ij}^F \le A^F x_{ij}\quad \forall (i,j)\in E \end{aligned}$$

(25)

$$\begin{aligned}&a_{ij}^R \le A^R x_{ij}\quad \forall (i,j)\in E \end{aligned}$$

(26)

$$\begin{aligned}&a_{ij}^F \ge - W^{TD} x_{ij} \quad \forall (i,j)\in E \end{aligned}$$

(27)

$$\begin{aligned}&a_{ij}^R \ge - W^{TR} x_{ij} \quad \forall (i,j)\in E \end{aligned}$$

(28)

$$\begin{aligned}&a_{ij}^F h + W^{TD} \ge 0.25 (W^{T} + q_{ij}) \quad \forall (i,j)\in E \end{aligned}$$

(29)

$$\begin{aligned}&\sum _{i\in V} a_{ij}^F + Q_j - \frac{({\text{CG}}_j - c) Q_j }{d} = \sum _{k\in V} a_{jk}^F \quad \forall j\in V\backslash \{0,n+1\} \end{aligned}$$

(30)

$$\begin{aligned}&\sum _{i\in V} a_{ij}^R + \frac{({\text{CG}}_j - c) Q_j }{d} = \sum _{k\in V} a_{jk}^R \quad \forall j\in V\backslash \{0,n+1\} \end{aligned}$$

(31)

$$\begin{aligned} {\rm CG}_j=&\frac{\sum _{i\in V} l_{ij}}{2} - \frac{1}{4}*\left(1- \sum _{i\in V}{C_{ij}}\right) + O_j*\frac{1}{2}*\left(1- \sum _{i\in V}{C_{ij}}\right) \nonumber \\&+ E_j*\frac{1}{2}*\left(1+ \sum _{i\in V}{C_{ij}}\right) \forall j\in V \end{aligned}$$

(32)

$$\begin{aligned}&x_{ij}\in \{0,1\} \end{aligned}$$

(33)

$$\begin{aligned}&l_{ij} \ge 0 \quad \forall (i,j)\in E \end{aligned}$$

(34)

$$\begin{aligned}&q_{ij} \ge 0 \quad \forall (i,j)\in E \end{aligned}$$

(35)

The objective function (8) aims to minimize transport costs. Constraints (9) and (10) ensure that each customer is visited exactly once. Constraint (11) makes sure that no route begins in the end depot (node $n+1$), while constraint (12) ensures that no route arrives in the start depot (node $0$). Constraints (13) and (16) initialize the values of $l_{0j}$ and $q_{0j}$ to $0$, since a container is empty when it departs from the start depot. Constraint (14) limits $l_{ij}$ to the maximum number of pallets that may be placed in each vehicle. Constraint (15) keeps track of $l_{ij}$ by adding up the number of pallets when arriving at customer $j$ ($l_{ij}$) with the number of pallets of customer $j$ ($L_j$). Constraint (18) keeps track of $q_{ij}$ in a similar way. Note that dense packing of the pallets into the vehicle is imposed. This means that there may not be a gap between two consecutive pallets in the truck. To relax the dense packing constraint, the equality sign in constraint (15) should be changed in a less-than-or-equal-to sign. Constraint (17) limits $q_{ij}$ to the maximum mass capacity (Q) of the vehicle. In constraint (19), the value of the variable $C_{0j}$ is set to 0 if $x_{0j}=0$ and set to 1 if $x_{0j}=1$. Since a container is empty when it departs from the start depot, it has an even number of pallets (0 pallets). Constraints (20) and (21) guarantee that $C_{ij}$ can only have a non-zero value when a vehicle travels from $i$ to $j$. Constraint (22) keeps track of $C_{ij}$ by multiplying the value of $C_{ij}$ when arriving at customer $j$ with parameter $P_j$ which equals $1$ if the number of pallets of customer $j$ is even, and $-1$ when the number of pallets of customer $j$ is odd. Constraints (23) and (24) initialize the values of the weight on the coupling ($a_{ij}^F$) and the weight on the rear axles ($a_{ij}^R$) to zero. Constraints (25), (26), (27) and (28) ensure that $a_{ij}^F$ and $a_{ij}^R$ only have a non-zero value when a vehicle travels from $i$ to $j$. Constraints (25) and (26) also specify the upper bounds of, respectively, $a_{ij}^F$ and $a_{ij}^R$. The values of the upper bounds $A^F$ and $A^R$ depend on the vehicle characteristics and are specified in legislation. The lower bound of $a_{ij}^F$ may also be fixed in legislation. Belgian legislation (KB 15.03.1968 art 32 bis) specifies that the mass corresponding to the load on the driving axle must be at least 25 % of the total mass of the loaded truck which is captured in constraint (29). On the left-hand side of constraint (29), the weight of the empty truck on the driving axle ($W^{TD}$) is added up with parameter $h$ (percentage of the weight on the coupling that is carried by the driving axle of the tractor) multiplied by the weight of the load that is placed on the coupling ($a_{ij}^F$). On the right-hand side, 25 % of the total mass of the empty truck and the total weight of the load is computed. Since there are no guidelines concerning the lower bound of the weight on the axles of the trailer, constraint (28) ensures that this should be at least equal to $-W^{TR}$ to avoid a negative axle weight on the rear axles. Constraint (30) keeps track of $a_{ij}^F$ by adding up the weight on the coupling when arriving at customer $j$ ($a_{ij}^F$) with the weight on the coupling of the pallets of customer $j$. Constraint (31) keeps track of $a_{ij}^R$ in a similar way. Constraint (32) determines the center of gravity of the pallets of customer $j$ ($\mathrm{CG}_j$) as a function of $C_{ij}$ and $l_{ij}$. This constraint is the same as Eq. (7) and is explained in Sect. 3.

5 Computational experiments

In this section, computational tests are described as an illustration of the functioning of the CVRP with sequence-based pallet loading and axle weight constraints. The model is compared to a CVRP with sequence-based pallet loading without axle weight restrictions. This is the model described in Sect. 4 without Eqs. (19)–(32). Different problem classes are constructed to demonstrate the performance of the model under various problem characteristics. In the model with axle weight restrictions, the constraints concerning the axle weight limits [Eqs. (25)–(29)] are defined as lazy constraints in Cplex to decrease the computation time. Lazy constraints are initially not part of the active model. The model is solved without the lazy constraints and each solution is checked to see if any of the constraints in the lazy pool is violated. If a lazy constraint is violated, this constraint is added to the active model. The instances with ten customers are tested both with and without the use of lazy constraints. The test shows that using lazy constraints considerably reduces computation time (by up to 50%). All problems are solved with Cplex 12.5 on a 2.5 GHz Intel Core i5 laptop with 4 GB RAM.

5.1 Test setting

The model formulated in the previous section is used to perform computational experiments on networks of 10, 15, 20 and 25 customers. Each network consists of a start depot (node 0), 10 to 25 customers and an end depot (the last node). It is assumed that the start depot and the end depot are located at the same location. To test differences in output between the two models (CVRP with sequence-based pallet loading with and without axle weight restrictions), four different problem classes are created by varying the values for the number of pallets of each customer ($L_i$) and the total mass of the pallets of each customer ($Q_i$). The number of pallets may have a low variation (between 4 and 7 pallets per customer) or a high variation (between 1 and 15 pallets per customer). With regards to the weight of the pallets, axle weight restrictions do not play a role when only light pallets (under 500 kg) are considered. Therefore, a distinction is made between customer demands of only heavy pallets (between 1,000 and 1,500 kg) and a fifty–fifty percent mix between customer demands with light pallets (between 100 and 500 kg) and customer demands with heavy pallets. In Table 4, four problem classes are presented. For each number of customers in the network (10, 15, 20 and 25) 32 instances are created (8 in each problem class). This means in total 128 instances are tested with both models.

Instances are created in the following way. First, the $x$ and $y$ coordinates of the customers are randomly generated between 0 and 10. The position of the depot is fixed to $(5,5)$. Routing costs $c_{ij}$ are computed by taking the Euclidean distance between the coordinates of each $(i,j)$ pair. Values for parameters $L_i$ and $Q_i$ are generated randomly in the intervals specified in Table 4, depending on the problem class. All the instances can be found on the following website http://alpha.uhasselt.be/kris.braekers/. Vehicle characteristics are defined in Sect. 2.

Table 4 Problem classes based on parameters $Q_i$ and $L_i$

5.2 Results

Results of the two models (with and without axle weight restrictions) for each problem class on networks of 10, 15 and 20 customers are presented in Tables 5, 6 and 7. Total cost and computation time are given for both models. For the networks of ten customers, the computation times of the model with axle weight restrictions are presented for the regular model and for the model in which constraints (25)–(29) are defined as lazy constraints. The cost increase from the model with axle weight restrictions compared to the model without axle weight restrictions is presented in the last column. With regards to the model without axle weight restrictions, the number of axle weight violations ($\#$ V) and maximum violation (Max V) (in percentage) are also provided. All violations that are reported are violations of the weight limit on the coupling (and thus on the axles of the tractor). There are no violations of the weight limit on the axles of the trailer. This may be explained by the higher weight capacity of the axles of the trailer (21 t) in comparison to the weight capacity of the coupling (11.6 t). The number of violations represents the number of arcs traveled by a vehicle in which the coupling is overloaded. The total number of arcs traveled in which the vehicle is loaded equals the number of customers in the network.

Table 5 Results of the CVRP with sequence-based pallet loading with and without axle weight constraints on network of ten customers

Table 6 Results of the CVRP with sequence-based pallet loading with and without axle weight constraints on instances with 15 customers

Table 7 Results of the CVRP with sequence-based pallet loading with and without axle weight constraints on instances with 20 customers

Table 5 shows that for the instances with 10 customers, the computation time is higher in the model with axle weight restrictions, but still acceptable with a maximum computation time of 250 s in the regular model and 142 s in the model with lazy constraints. On average, the computation time reduces with 45 % when axle weight restrictions are defined as lazy constraints. The instances with 15, 20 and 25 customers are, therefore, all solved with lazy constraints. Tables 6 and 7 show that the computation times increase considerably when the number of customers increases. The models with axle weight restrictions (with lazy pool constraints) find a solution within 2 h for 29 out of 32 instances with 15 customers, and for 22 out of 32 instances with 20 customers. The average computation time for the instances in which a solution is found within 2 h is 502 s in the instances with 15 customers and 1,940 s for the instances with 20 customers. Besides the increase in computation time, there is also a decrease of average cost increment when the number of customers increases. In Table 8 the average cost increase and maximum cost increase for the networks of 10, 15 and 20 customers are presented. While the average cost increase in the instances with 10 and 15 customers is, respectively, 2.98 and 2.77 %; it decreases with more than 60 to 1.10 % in the instances with 20 customers. Also the maximum cost increase is considerably higher in the instances with 10 and 15 customers (17.77 and 21.63 % respectively) than in the instances with 20 customers (6.41 %). This may indicate that with a larger number of customers in the network, the effect of incorporating axle weight restrictions on the routing costs is less prominent since there are generally more alternatives for feasible routes and packing schemes.

Table 8 Comparison of cost increase between the networks with 10, 15 and 20 customers

A comparison of the cost increase per problem class and number of customers in the network is graphically presented in Fig. 7. It is clear that the cost increase is the highest in problem class 2 where only heavy pallets are considered and the number of pallets per customer lies between 1 and 15. The cost increase is the lowest (nearly zero for the networks with 20 customers) in problem class 3 where a mix between heavy and light pallets is considered and the number of pallets per customer lies between 4 and 7. The positive effect of mixing light pallets with heavy pallets on the costs can be explained by the fact that this allows for more flexibility in the packing process. If lighter pallets are packed first in the truck, the weight of the heavy pallets will mostly be carried by the axles of the trailer, which have a higher weight capacity. Heavy pallets are, therefore, better transported together with light pallets even though the total weight capacity of the vehicle is sufficient to transport solely heavy pallets. A possible explanation for the negative effect on the cost of a higher variation in number of pallets per customer may be that a variation between 1 and 15 pallets per order leads to on average half of the orders which have more than 8 pallets which is much less flexible than orders between 4 and 7 pallets per customer. An order of 15 pallets with a pallet weight of 1.4 t, leads to a total weight of the order of 21 t, which is less flexible to position on a truck than several smaller orders with a high pallet weight. In Figs. 8 and 9, the cost increase in relation to the average weight of the demand and to the mass of the largest demand in terms of weight for the instances with 20 customers is graphically presented. A relationship between the cost increase and the largest demand can be clearly distinguished in Fig. 8: the cost increments that are higher than 1 % are all from instances where the largest demand is higher than 18 t. In Fig. 9, a relationship between cost increase and average weight of the demand of the customers can not be observed.

Fig. 7

Average cost increase in each problem class in networks with 10, 15 and 20 customers

Fig. 8

Cost increase in networks of 20 customers for each problem class related to the mass of the largest demand in terms of weight

Fig. 9

Cost increase in networks of 20 customers for each problem class related to the average weight of the demands

In Figs. 10 and 11, the cost increase for the instances with 20 customers is related to the maximum axle weight violation and the number of axle weight violations. The graphs indicate that there is no direct relationship between the height of the maximum violation or the number of violations and cost increase. Instances with a solution that involves a high axle weight violation in the model without axle weight restrictions may have a feasible solution in the model with axle weight restrictions for a similar routing cost, while vice versa, a small maximum axle weight violation may introduce a high increase in cost. Similarly, instances in which there are many axle weight violations do not necessarily have a large cost increment when integrating axle weight restrictions.

Fig. 10

Cost increase in networks of 20 customers for each problem class related to the maximum axle weight violation

Fig. 11

Cost increase in networks of 20 customers for each problem class related to the number of axle weight violations

Both models (with and without axle weight restrictions) did not find a solution for the instances with 25 customers within 2 h. The instances are nevertheless available on website http://alpha.uhasselt.be/kris.braekers/ to be used by future researches. The CVRP is known to be NP-hard, opening the way to heuristics.

6 Conclusions and future research

Axle weight limits have become an increasingly important issue for transportation companies. Transporters are faced with high fines when violating these limits, while commercial planning programs do not incorporate these constraints. Although research has been done on VRP combined with loading constraints, the literature is still silent about axle weight limits.

This paper proposes a problem formulation for the CVRP with sequence-based pallet loading and axle weight constraints. The performance of the model is illustrated with computational tests on networks of 10, 15, and 20 customers for different problem instances. Not including axle weight restrictions may induce major violations of axle weight limits which may lead to considerable fines. Integrating axle weight restrictions does not necessarily lead to a cost increase. Computational experiments show that the increase in routing costs decreases considerably to 1.10 % when the number of customers in the network increases from 10 to 20 customers. In several instances axle weight violations can even be avoided without a cost increment. The effect of including axle weight restrictions on the cost depends on the number of pallets per customer and the weight of the pallets. When only light pallets are packed, axle weight limits do not play a role in the packing process. The effect of integrating axle weight limits is higher when only heavy (1,000–1,500 kg) pallets are considered compared to a fifty–fifty percent mix of heavy and light pallets. The computational experiments also show a relationship between cost increment and the weight of the customer with the largest demand in terms of weight. When the weight of the largest demand is high, chances increase that the cost increment is higher than 1 %. Finding an exact solution within a reasonable time limit, for instances with 25 customers has proven to be difficult. Therefore, we aim to develop a heuristic method to solve larger instances.

Since this is the first paper that incorporates axle weight restrictions in a VRP and because of the relevance of the issue in practice, there are numerous opportunities for future research on the topic. Future research could integrate other realistic features in the current problem such as time windows, time-dependent routing and legal driving hours. Additionally, other loading constraints may be added to the current model. Another line of possible future research could be to integrate axle weight restrictions in other types of VRPs such as three-dimensional loading VRP, multi-compartment VRP and pickup and delivery problems. A promising research direction is to develop a branch-and-cut method to improve the efficiency of the formulation. In the literature concerning VRP with loading constraints, good results are attained with branch-and-cut algorithms [e.g., (Iori et al 2007; Tricoire et al 2011; Cordeau et al 2010; Alba et al 2013; Côté et al 2012b)]. Finally, since the CVRP is NP-hard, heuristics may be developed to be able to solve large instances.