Introduction

Harmonic generation in plasma by different laser profiles has been studied by many researchers in past. The profiles like Gaussian, Hermite Gaussian and Hermite–Cosh–Gaussian has been mainly used. The type of plasma and the intensity of incident laser decide the nature and amplitude enhancement of harmonic generated. The work in this field includes gaseous plasma of different types like collisional, collisionless, magneto-collisional plasma as well as metals, semiconductors etc. The factors like magnetic field, density ripple supports amplitude enhancement. The focusing and defocusing action of laser accounts for the presence of non-linearity which facilitates the harmonic generation phenomenon [1,2,3,4,5,6,7,8,9,10,11,12]. The ability of laser beam to undergo self-focusing helps to get a focused output with enhanced amplitude. The work in this field also includes the generation of harmonic with double frequency by a self-focused laser with Gaussian profile [13,14,15]. By this work, it has been observed that the metallic surface like metal–semiconductor interface is also a good choice for harmonic generation with Gaussian profile. The presence of free electrons in metals and n-type semiconductors supports nonlinear interactions of laser with matter and leads to harmonic generation. Researchers have studied harmonic generation with different plasmas using profiles other than Gaussian profile for lasers [16,17,18,19,20,21,22]. Nanda et al. [23] studied harmonic generation with Hermite–Cosh–Gaussian beam in magneto plasma. Their work showed that the presence of magnets promotes the laser’s self-focusing action which leads to efficient output wave. Patil et al. [24] examined differential equations of beam width parameter under paraxial approximations using Hermite–Cosh–Gaussian beam and their results explain collisionless heating of plasma which is useful for laser fusion.

The organization of the paper is as: "Analytical considerations" section contains derivations of differential equation for SHG amplitude and beam width parameter using ponderomotive mechanism. "Results and discussion" section encloses results and discussions. Concluding views are in "Conclusions" section.

Analytical considerations

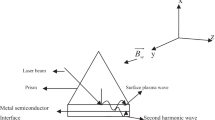
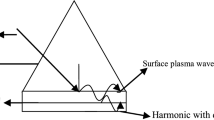
The glass prism of high refractive index with layer of metal and semiconductor is considered as shown in Fig. 1. The beam is made to strike metal–glass interface from glass side at an acute angle depending upon the nature of metal. Most of the light gets reflected but few photons could penetrate into the metal and can exert ponderomotive mechanism on electrons leading to the generation of surface plasma waves (SPW).

Fig. 1
figure 1

Glass prism with metal and semiconductor

Full size image

The electrons of semiconductor experience acceleration due to the interaction of these waves in metal. The laser is considered to be comprising of fields given byand

$$\vec{E}_{H} ^{\prime} = \hat{x} \, A^{\prime}(z,t)e^{ - i(\omega ^{\prime}t - k^{\prime}z)}$$
$$\overrightarrow {{B_{H} }} ^{\prime} = \left( {\overrightarrow {k^{\prime}} \times \overrightarrow {{E_{H} ^{\prime}}} } \right)/\omega ^{\prime}$$
(1)

with, \(k^{\prime}\) and \(\omega ^{\prime}\) as the constant of propagation and incident frequency.

The amplitude of electric field is taken as \(A^{\prime} = A_{0} e^{ - ik^{\prime}S}\) with,

$$A_{0} = \frac{{E_{0} }}{f(z)}H_{p} \left( {\frac{\sqrt 2 r}{{r_{0} f(z)}}} \right)e^{{\frac{{b^{2} }}{4}}} \left[ {\exp - \left( {\frac{r}{{r_{0} f(z)}} + \frac{b}{2}} \right)^{2} + \exp - \left( {\frac{r}{{r_{0} f(z)}} - \frac{b}{2}} \right)^{2} } \right]{}$$
(2)

where \(A_{0}\,\, {\text{ and}} \,\,S\) are functions of \({\text{r}\,\, and\,\, \text{z,}}\) \(f\) represents laser beam width, b represents the decentred parameter and \(r_{0}\) is the spot size of the laser at \(z = 0.\) The wave propagation has been considered along z-axis. \(\vec{E}_{s} = \hat{x}A_{s} e^{{ - i(\omega t - k_{s \, } z)}}\) be the wave equation for the surface plasma wave where, \(k_{s} = \left( {\omega /c} \right)\left( {\varepsilon_{m} \varepsilon_{s} /\left( {\varepsilon_{m} + \varepsilon_{s} } \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}\) with \(\omega\) and \(k_{s}\) as the frequency of surface plasma wave and propagation constant. The permittivities of mediums are \(\varepsilon_{m}\)(metal) and \(\varepsilon_{s}\)(semiconductor) respectively. The amplitude of SPW is related to the laser’s amplitude as \(A_{s} = f\left( {A^{\prime}} \right)\) with \(A_{s} = J^{\prime}A^{\prime}\)[25] where, \(J^{\prime}\) represents a positive real number and also \(\omega = \omega ^{\prime}\). The acceleration experienced by the electrons can be calculated using relation \(m \, \left( {d\overrightarrow {{v_{1} }} /dt} \right) = - e\overrightarrow {{E_{s} }} - e\overrightarrow {{E_{H} ^{\prime}}}\). The ponderomotive force exerted on electrons by the magnetic field of laser is, \(\overrightarrow {F} = - e\left( {\overrightarrow {{v_{1} }} \times \overrightarrow {{B_{H} ^{\prime}}} } \right)\) and the velocity \(\overline{v}\) is imparted to electrons which is given by

$$\overrightarrow {v} = - \frac{{e^{2} k_{l} }}{{m^{2} }}\left[ {\frac{{\overrightarrow {A} ^{{\prime}{2}} J^{\prime}e^{{ - i\left[ {\left( {2\omega ^{\prime}} \right)t - \left( {k_{s} + k^{\prime}} \right)z} \right]}} }}{{2\omega ^{\prime {3}} }} + \frac{{\overrightarrow {A} ^{\prime {2}} e^{{ - i\left( {2\omega ^{\prime}t - 2k^{\prime}z} \right)}} }}{{2\omega ^{\prime{3}} }}} \right]$$
(3)

This nonlinear velocity couples with density ripple \(n_{r^{\prime}} = n_{0} e^{ir^{\prime}z}\) where, \(n_{0}\) is the fundamental electron density, \(r^{\prime}\) represents the wave number and propagation distance is given by \(z\). The wave equation for second harmonic is considered as

$$\vec{E}^{\prime}_{2} = A^{\prime}_{2} e^{{ - i(2\omega ^{\prime}t - k_{2} z)}} \hat{x}$$
(4)

here, \(A^{\prime}_{2}\) defines the peak value of the electric component of the wave generated with double frequency as that of laser. The current density due to \(\vec{E}^{\prime}_{2}\) at \(\left( {2\omega ^{\prime},k_{2} } \right)\) is \(\vec{J}_{2L} = n_{0} e\vec{v}^{\prime}_{2}\).The term, \(\vec{v}^{\prime}_{2}\) is velocity and is obtained from relation \(m(d\vec{v}^{\prime}_{2} /dt) = - e\vec{E}^{\prime}_{2} .\) The linear and nonlinear current density sum up to give total current density,

$$\vec{J} = n_{r} e\vec{v} + n_{0} e\vec{v}^{\prime}_{2}$$
(5)

The equation governing wave motion is,

$$\nabla^{2} \overline{{E_{H} ^{\prime}}} + \frac{{\omega^{2} (\varepsilon_{m} + \varepsilon_{s} )\overrightarrow {{E_{H} ^{\prime}}} }}{{c^{2} \left( {\varepsilon_{m} \varepsilon_{s} } \right)}} = 0$$

Using the values of Eqs. 1 and 2 in Eq. 5 and equalising imaginary and real parts also by using paraxial approximations, we get

$$2ik^{\prime}\frac{\partial A^{\prime}}{{\partial z}} = \frac{{1}}{{{r}}}\frac{\partial A^{\prime}}{{\partial r}} + \frac{{\partial^{2} A^{\prime}}}{{\partial r^{2} }} + k^{{\prime}{2}} \left( {\frac{{\varepsilon_{{\text{m}}} \varepsilon_{s} }}{{\varepsilon_{m} + \varepsilon_{s} }}} \right)A^{\prime}{}$$
(6)

with \(A^{\prime} = A_{0} e^{ - ik^{\prime}S}\) and \(S = \frac{{r^{2} }}{2}\frac{1}{f}\frac{df}{{dz}} + \beta (z)\) where the first term is related to the curvature of the wave front. Here, \(A_{0}\) represents the initial value of amplitude, \(S\) is a function of r and z which takes into account the self-focusing effect also. \(\beta\) is a parameter which depends on z and accounts for the variations in S. Using values of all variables in Eq. 6 and on comparing the coefficients of \(r^{2}\) we get,

For \(p = 0\) mode

$$\frac{{d^{2} f}}{{dz^{{\prime}{2}} }}\left( \frac{1}{2f} \right) + \left( {\frac{{df }}{dz^{\prime}}} \right)^{2} \left( {\frac{1}{{4f^{3/2} }} - \frac{1}{{2f^{2} }}} \right) + - \frac{{2\xi_{0}^{2} }}{{r_{0}^{2} f^{2} }} + \left( {\frac{{\varepsilon_{m} + \varepsilon_{s} }}{{\varepsilon_{m} \varepsilon_{s} }}} \right)\frac{{\xi_{0}^{2} \omega_{l}^{2} }}{{c^{2} }}\exp \left( {\frac{{b^{2} }}{2}} \right) = {0 }$$
(7)

For \(p = 1\) mode

$$\frac{{d^{2} f}}{{dz^{{\prime}{2}} }}\left( \frac{1}{2f} \right) + \left( {\frac{{df }}{dz^{\prime}}} \right)^{2} \left( {\frac{1}{{4f^{3/2} }} - \frac{1}{{2f^{2} }}} \right) + - \frac{{2\xi_{0}^{2} }}{{r_{0}^{2} f^{2} }} + \left( {\frac{{\varepsilon_{m} + \varepsilon_{s} }}{{\varepsilon_{m} \varepsilon_{s} }}} \right)\frac{{\xi_{0}^{2} \omega_{l}^{2} }}{{c^{2} }}\left( {b^{2} - 2} \right)\exp \left( {\frac{{b^{2} }}{2}} \right) = {0}$$
(8)

where \(z^{\prime} = z/\xi_{0}\).

The equation for wave propagation for wave with double frequency is considered as,

$$\nabla^{2} \overrightarrow {E}_{2} = \frac{{4\pi \left( {\varepsilon_{m} + \varepsilon_{s} } \right)\partial \overrightarrow {{J }} }}{{c^{2} \left( {\varepsilon_{m} \varepsilon_{s} } \right)\partial t}} + \frac{{\partial^{2} \overrightarrow {{E_{2} }} }}{{c^{2} \partial t^{2} }}$$
(9)

Using Eqs. (4) and (5) in Eq. (9) the relation is obtained as,

$$\begin{aligned} &\frac{{\partial^{2} (A^{\prime}_{2} /A^{\prime}_{0} )}}{{\partial z^{{\prime}{2}} }} - \left( {k^{\prime}_{2} \xi_{0} } \right)^{2} \left( {\frac{{A^{\prime}_{2} }}{{A^{\prime}_{0} }}} \right) - \frac{{\omega_{p}^{2} \xi_{0}^{2} (\varepsilon_{m} + \varepsilon_{s} )}}{{c^{2} \left( {\varepsilon_{m} \varepsilon_{s} } \right)}}\exp \left( {\frac{{b^{2} }}{2}} \right)\left( {\frac{{A^{\prime}_{2} }}{{A^{\prime}_{0} }}} \right) \hfill \\ &\qquad - i\left( {\frac{{\omega_{p}^{2} }}{{\omega ^{\prime {2}} }}} \right)\left( {\frac{{\varepsilon_{m} + \varepsilon_{s} }}{{\varepsilon_{m} \varepsilon_{s} }}} \right)\left( {\frac{{eA_{0} }}{mc\omega ^{\prime}}} \right)\left( {1 + J^{\prime}} \right) \quad\quad \left( {k_{l} \xi_{0} } \right)\left( {\frac{{\omega ^{\prime}\xi_{0} }}{c}} \right)\exp \left( {\frac{{b^{2} }}{2}} \right) = 0 \hfill \\ \end{aligned}$$
(10)

wheres variables used are \(\omega_{p}^{^{\prime}2} = 4\pi n_{0} e^{2} /m\) and \(z^{\prime} = z/\xi_{0}\).

Results and discussion

Graphical analysis is done for Eqs. 7 and 10 with two decentered parameter \(b = 0\,\,{\text{ and }}\,b = {1}\) and other parameters are taken as \(\xi_{0} /r_{0} = 0.01, \, k_{l} \xi_{0} = 0.7,{{ J^{\prime}}} = {1}{{.5,}}\)\(\, \omega_{p} \xi_{0} /c = 0.2,k_{2} \xi_{0} = 1.4,\)\(\omega_{p} /\omega_{l} = 0.8.\) \(eA_{0} /mc\omega_{l} = 5 \, {.}\) The laser considered for the present work is Nd:YaG laser with frequency \(2.8 \times 10^{14} s^{ - 1}\) and the permitivities at this value of frequency are taken as 106.82 for Al, 57.909 for Ag and 19.5 for InSb at given frequency [25, 26]. Figure 2 depicts the graphical relation of beam width parameter and normalized propagation distance and it is clearly observed that under given conditions laser beam focuses well in case of Ag-InSb interface as compared to Al-InSb.

Fig. 2
figure 2

Graphical relationship of normalized propagation distance and beam width parameter

Full size image

The effect observed can be due to higher conduction electron density of Ag than Al. The propagation of Hermite–Cosh–Gaussian beam studied by Patil et al. [24] in n-InSb shows that as b increases the value of \(f\) decreases, we have observed the similar effect for metal–semiconductor interface. Figure 3a, b shows the amplitude variation with distance for Ag-InSb and Al-InSb for \(p = 0\,\,{\text{ and}} p = {1}\) modes of Hermite–Cosh–Gaussian beam and one could observe that for both the modes at different values of b, Ag-InSb gives better output. The decrease in amplitude accompanied with increases the value of b may be due to the collisions of charge carriers but at higher modes also the beam width parameter shows minimum for Ag-InSb and amplitude is also comparatively more for Ag-InSb. The self-focusing action of laser influences the generation of SPW which in turn makes the harmonic generated focused and efficient. The present analysis put forwards the metal–semiconductor as a material of choice for studying harmonic generation.

Fig. 3
figure 3

Graphical relationship of amplitude in normalized form with normalized distance a b = 0, b b = 1

Full size image

Conclusions

The metal’s interaction with laser gives rise to surface plasma waves which could further show nonlinear interactions with the electrons of semiconductor and lead to generation of harmonics with double frequency as of laser. The present study is based on the action of laser with Hermite–Cosh–Gaussian beam profile on metal–semiconductor interface for two different modes. The increase in the amplitude of double frequency harmonics takes place with the decrease in beam width parameter. The amplitude and focusing is observed to be better for Ag-InSb in both the modes as compared to Al-InSb. Hence, metal–semiconductor interface can be considered as a good option for second order harmonic generation.