1 Introduction

Scientific development has been advancing in new microtechnologies, inducing a positive perspective in the field of engineering. Thus, the development of mobile and energy-efficient electronic devices caught the attention of many researchers, as they do not require an electrical or chemical charge for their operation.

One way to power these electronic devices is through natural sources in the environment, such as heat, vibration, sunlight, and wind, since they are usually dissipative sources and freely available. Some works present an energy harvest vibration studies, and in [1,2,3], there are a review of these devices. The vibration energy conversion can occur through electromagnetic, electrostatic, and piezoelectric methods, the latter being the most often used.

Many works in the current literature related to mechanical energy harvest systems using piezoelectric have been published, providing relevant results [4,5,6]. A power harvest device review can be seen in [7]. Also, there is a book that deals only with piezoelectric energy harvesting, as written by [9].

This paper proposes a model of energy harvesting in the portal structure excited by a non-ideal DC motor with an unbalanced mass, which can generally be observed in practical cases. A major challenge in theoretical and experimental scientific research is to consider the non-ideal source of excitation and to understand the behavior of the dynamic system [10]. Research on non-ideal excitation has been studied in [11,12,13,14].

This structure was selected to have nonlinearities as duffing. Duffing stiffness describes a nonlinear spring with restorative force. According to [9], nonlinearities in the energy harvesting system increase the harvested power over a higher frequency bandwidth. Besides, the piezoelectric was modeled to have a nonlinear coupling, as shown in [15,16,17]. Studies indicate that the nonlinear modeling of piezoelectric coupling is an approximation to experimental, since there is a nonlinear relationship between deformation and electric field in the piezoceramic material [18, 19].

The study of the nonlinear energy harvesting model requires a detailed investigation of the dynamic response since nonlinear systems can be sensitive to initial conditions, unstable, and exhibit chaotic behavior. On the other hand, they have a higher power output over a wide frequency range [8]. Thus, it is necessary to characterize the dynamic response under different excitation conditions. An important tool is the bifurcation diagram that analyzes the effect of varying control parameters on dynamics. Another evaluation to be performed is the sensitivity to the initial conditions, where the calculation of the Lyapunov exponent provides this evaluation. They are important tools for qualifying and quantifying the stability of a system, making it possible to find periodic and chaotic behaviors. Thus, it allows verifying the characteristics of the dynamic response and system application conditions.

Further, frequency domain analyses are used to observe the dynamic responses. And for this case, a non-stationary analysis is required, since the behaviors studied vary over time and may present chaos. In this manner, a Fourier analysis made using the fast Fourier transform (FFT) method, seen in [20], is not effective because this analysis is more applicable in periodic signals or stationary cases [21]. However, some methods allow a time-frequency analysis in a non-stationary regime, more precisely, such as the short-time Fourier transform (ST-FT). Short-time Fourier transform (ST-FT) is a Fourier-related transformation used to determine the sinusoidal frequency and phase content of local sections of a signal as it varies over time [22]. This spectral analysis is time-dependent and the function is partitioned at smaller intervals, so that the spectrum can be considered constant within each one. Then, the variation of the Fourier transform is applied at each interval. In [23], there is an overview and presents an algorithm for estimating ST-FT signal.

The wavelet transform (WT) can be used for multi-scale analysis of the signal, providing features extracted from the frequency and time of the signal. An important wavelet transform feature is that the frequency varies in proportion to the change in center frequency and makes this method suitable for the non-stationary and discontinuous signal [24, 25]. It can be deepened in studies in [26]. One extension is the synchrosqueezed wavelet transform (SWT), which is a time-frequency analysis proposed by [27]. It is an empirical mode decomposition tool and has enhanced anti-noise capability and improved frequency and time resolution compared with WT [29]. SWT was applied in engineering in [28], and in [30] presented an analysis for low-frequency oscillations, and all obtained satisfactory results.

Another widely used time-frequency signal processing tool is the Wigner-Ville distribution (WVD), which can generalize the relationship between the power spectrum and autocorrelation function applied to the non-stationary signal [31]. The WVD can be deepened in [32,33,34].

The purpose of this paper is to evaluate the different responses of the mechanical system based on the mentioned time-frequency methods and, through this evaluation, conclude which time-frequency tool is best suited to characterize a dynamic behavior and verify the highest power harvested.

The article is organized as follows. Some definitions are presented in Section 2 as the proposed mathematical model, the equations of motion, and nonlinearities introduction. The dynamic response of the system is performed through the numerical solution, the bifurcation diagram, and the calculation of Lyapunov exponents that are presented in Section 3. Section 4 describes the energy harvesting analysis and Section 5 presents the time-frequency methods used to characterize the system and to distinguish it quantitatively between periodic and non-periodic. Section 6 shows the numerical results of a non-ideal energy harvesting system in terms of classical qualitative indicators, as well as its quantitative characterization through time-frequency analysis methods. The article ends with some conclusions.

2 Mathematical Background

2.1 Mechanical System and Equations of Motion

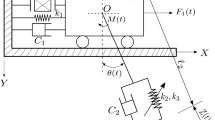
In this paper, a portal frame structure with layers of piezoelectric element (piezoceramic) on both sides of a column is proposed and an electric DC motor as a non-ideal excitation with an unbalanced mass is attached as shown in Fig. 1. It is considered the horizontal motion of a portal frame structure and rotation angle of the DC motor.

Fig. 1
figure 1

Mechanical system studied

Full size image

The configuration of the non-ideal mechanical system consists of the unbalanced mass (m2), structure mass (m1), linear damping (b), displacement of oscillator (X(t)), angular displacement of the rotor (φ(t)), inertia moment (J), and eccentricity (r). Also, P1 and P2 represent the piezoelectric film of the bi-morph configuration.

The columns of the portal frame structure are a duffing type that has a cubic nonlinearity; likewise, the system’s stiffness is represented as klX(t) + klnX(t)3, where kl is a linear stiffness and knl is a non-linear stiffness, representing the term of restorative force. There are several studies about the cubic nonlinearity, and in [35,36,37], models are proposed and validated experimentally.

The non-ideal excitation is represented by an equation, which describes the interaction of power supply with the driven system. In this paper, the function that defines the energy source is linear and represents the curve of torque versus velocity of DC motor based on [38, 39]. Thus, \(L(\dot {\varphi })-H(\dot {\varphi }) = V_{1} - V_{2}\dot {\varphi }\), where V1 is the voltage applied and V2 is a constant for each model of the DC motor.

Besides, there is an electrical circuit that represents the piezoelectric coupling to the mechanical component, that in according to [17] is given by \(\frac {d(X)}{C}q\), where q is the electrical charge, d(X) is a strain-dependent coupling coefficient, and C represents the piezoelectric capacitance. Thus, the voltage V across the piezoelectric material has the form by (1). And the voltage can also be represented as \(V = R \dot {q}\), where R is the piezoelectric resistance.

$$ V = -\frac{d(X)}{C} X+\frac{q}{C} $$
(1)

Therefore, the equations of motion are given by (2).

$$ \begin{array}{llll} (m_{1}+m_{2})\ddot{X}+b\dot{X} + k_{l} X + k_{ln} X{^{3}} = ... \\ ... m_{2} r (\ddot{\varphi} \sin{\varphi} - \dot{\varphi}^{2} \cos{\varphi}) + \frac{d(X)}{C}q \\ (J + m_{2} r^{2}) \ddot{\varphi} = m_{2} r \ddot{X} \cos{\varphi} + V_{1} - V_{2}\dot{\varphi} \\ R \dot q - \frac{d(X)}CX +\frac qC=0 \end{array} $$
(2)

And based on [38], it is valid to normalize the coordinates and time.

$$ \begin{array}{@{}rcl@{}} \tau = \omega_{1} t, x = r X, \omega_{1} = \sqrt{\frac{k_{l}}{m_{1}+m_{2}}}, \alpha = \frac{b}{(m_{1}+m_{2})\omega_{1}} \\ \beta_{1} = \frac{k_{l}}{(m_{1}+m_{2}){\omega_{1}^{2}}} , \beta_{3} = \frac{k_{n}l r^{2}}{(m_{1}+m_{2}){\omega_{1}^{2}}} \\ \delta_{1} = \frac{m_{2}\omega_{1}}{m_{1}+m_{2}} , \rho_{1}=\frac{V_{1}}{(J+r^{2}m_{2}){\omega_{1}^{2}}} \\ \rho_{2}=\frac{V_{2}}{(J+r^{2}m_{2}){\omega_{1}^{2}}}, \rho = R C \omega_{1}, \widehat{d}(X) = \theta(1+{\Theta}\left|X\right|) \\ \widehat{d}(X) = \frac{r}{q_{o}}d(r), \theta = \frac{r}{q_{o}}d_{lin}, {\Theta} = r d_{nlin} \end{array} $$

According to [16, 17], they are considered the function to dimensionless piezoelectric coupling coefficient as \(\widehat {d}(X) = \theta (1+{\Theta }\left |X\right |)\), where 𝜃 is a linear part and Θ is a non-linear part. Consequently, we may reduce the governing equations of motions as (3).

$$ \begin{array}{llll} x^{\prime\prime}+\alpha x^{\prime} + \beta_{1} x + \beta_{3} x^{3} - \theta(1+ {\Theta} \left|x\right|)v = ... \\ ... \delta_{1} \varphi^{\prime\prime} \sin (\varphi) + \delta_{1} \varphi^{\prime2} \text{cos}(\varphi) \\ \varphi^{\prime\prime} = \rho_{2} - \rho_{3} \varphi^{\prime} + \rho_{1} x^{\prime\prime} \sin (\varphi) \\ \rho v^{\prime} - \theta(1+ {\Theta} \left|x\right|)x + v = 0 \end{array} $$
(3)

3 Dynamic Response Analysis

3.1 Bifurcation Diagram

The bifurcation diagram is a classic tool used in dynamic behavior studies. It employs to evaluate the system dynamic behavior as a function of the variation of the control parameter. This evaluation is made qualitatively, representing only the orbit of each control parameter. Therefore, in this work, we obtain the bifurcation diagram, in which the control parameter is the term as a function of the voltage applied to the DC motor (ρ2), in other words, the external excitation applied to the structure.

3.2 Lyapunov Exponents

The Lyapunov exponent of a dynamic system describes the phase velocity which two close points in the physical space approach or move apart. The study of the Lyapunov exponent is interesting to observe only the largest Lyapunov exponent because it determines the overall system behavior. A negative exponent represents the convergence of two temporal signals with close initial conditions, being characterized as insensitive to the initial conditions. However, a positive exponent represents the divergence of these signals, demonstrating a sensitivity to the initial conditions. Therefore, the Lyapunov exponent provides the quantification of the dynamic behavior, in which the larger, the more sensitive to the initial conditions.

4 Power Harvesting

The piezoelectric coupling is considered as an equivalent circuit, as shown by the third equation of (3). Therefore, to determine the power harvested, the electrical power of the circuit is calculated.

Thus, knowing that power from the electrical circuit is V2/R. Then, the non-dimensional power harvested is obtained from (4) by [17].

$$ P = \rho v^{\prime2} $$
(4)

5 Time Frequency Analysis

5.1 Short-Time Fourier Transform

Firstly, the power spectral density (PSD), which describes how the energy of a signal will be distributed across the frequency, is studied. Thus, this tool assists in frequency capture and periodicity identification. The power spectral density is using fast Fourier transform (FFT).

In sequence, the short-time Fourier transform (ST-FT) is calculated, which is an extension of the Fourier transform and, however, provides the time-localized frequency information, as for situations that frequency components of a signal vary over time. The STFT mathematical formulation is written as [22]:

$$ \text{STFT}(\tau,\omega) = {\int}_{-\infty}^{\infty} x\left( t\right)w\left( t-\tau\right)e^{-j\omega t}dt $$
(5)

where w is the Hanning window, note that there is a difference between the window function w and frequency ω and x(t) is the signal to be transformed.

5.2 Continuous Wavelet Transform

The continuous wavelet transform (CWT) was studied to overcome the window size limitation, the resolutions Δt and Δf, which vary in the time-frequency plane to obtain all the information contained in the frequency plane [26].

And the CWT of signal F is defined as:

$$ W_{F}(u,s)= {\int}_{-\infty}^{\infty} F(t) \psi_{u,s}^{\ast}(t) dt $$
(6)

where \(\psi _{(u,s)}^{\ast } \) is:

$$ \psi_{(u,s)}^{\ast} = \frac1{\sqrt s}\psi\left( \frac{t-u}s\right) $$
(7)

For u ∈ R and s > 0.

Thus, it is possible to obtain the scalogram of F in according to (8), denoted by ς as [40]:

$$ \varsigma:=\left|\left|W_{F}(u,s)\right|\right|=\sqrt{{\int}_{-\infty}^{\infty}\left|F(t) \psi_{u,s}^{\ast}(t) du\right|^{2}} $$
(8)

where the parameter u refers to the scale and s a translation or location of the wavelet analyzed ψ. The parameter u controls a dilation/contraction of the function. As the parameter s varies, the signal F and analyzed locally around it. Thus, one can analyze the multi-scale aspects of the non-stationary signals studied. And the ς is known as the wavelet coefficient.

5.3 Synchrosqueezed Wavelet Transform

The synchrosqueezed wavelet transform (SWT) is a time-frequency analysis method that was based on an empirical mode decomposition (EMD)–like tool. According to [27], the corresponding frequency of each scale from WT is given by the derivative of the wavelet coefficients concerning time. Add the scale of the same frequency to obtain the higher resolution time-frequency curve. In this way, it allows improving the energy divergence of WT and time-frequency resolution.

Thus, taking partial derivative of instantaneous frequency WF(u,s) with respect to s and get ωs(u,s):

$$ \omega_{s}(u,s) = -i(W_{F}(u,s))^{-1}\frac{\partial W_{F}(u,s)}{\partial s} $$
(9)

Through (9) and calculation u, s and ωs(u,s) as discretized, it is determined the SWT as:

$$ \begin{array}{llll} T_{s}(\omega_{s_{1}},s) = \left( {\Delta}\omega_{s}\right)^{-1}{\sum}_{\epsilon}W_{F}\left( u_{k},s\right) ... \\ ... u_{k}^{-3/2}{\left( {\Delta} u\right)}_{k} \end{array} $$
(10)

which \(\epsilon = {u_{k}:\left |\omega _{s}\left (u_{k},s\right )-\omega _{s_{l}}\right |\leq {\Delta }\omega _{s}/2}\), \(({\Delta } u)_{k} = u_{k} - u_{k-1}\) and \({\Delta }\omega _{s} = \omega _{s_{l}}-\omega _{s_{l-1}}\).

5.4 Wigner-Ville Distribution

In recent years, alternative time-frequency representations have been studied and the Wigner-Ville distribution (WVD) has received great attention in the signal processing researchers.

According to [41, 42], the WVD can be derived by generalizing the relationship between the power spectrum and the autocorrelation function for the non-stationary signal.

For a continuous signal x(t), the Wigner-Ville distribution is defined as:

$$ \text{WVD}_{x}\left( t,f\right)={\int}_{-\infty}^{\infty} x\left( t+\frac\tau2\right)x^{\ast}\left( t-\frac\tau2\right)e^{-j2\pi f_{\tau}}d\tau $$
(11)

A deeper study on the method is presented in [43].

6 Results

To perform the numerical simulation, the parameters considered for dynamic system are α = 0.1, β1 = 1, β3 = 2, δ1 = 8.373, ρ1 = 0.05, ρ3 = 200, 𝜃 = 0.2, and Θ = 0.6, and ρ2 is the control parameter that represents the voltage applied on the DC motor. The equations of motion were solved by the Runge-Kutta scheme (4th order).

Figure 2 shows the bifurcation diagram to the model proposed.

Fig. 2
figure 2

Bifurcation diagram ranging the parameter of voltage applied

Full size image

Then, it can check which parameter (ρ2) will exhibit a periodic and chaotic behavior. The range of ρ2, between 82 and 92, has a periodic behavior, and chaotic behavior is found in the ranges 75 to 82 and 92 to 105.

Besides, the largest Lyapunov exponents were calculated by varying the control parameters, as shown in Fig. 3, where (λ1) is the first most significant and (λ2) is the second most significant. For the variation of the control parameter, the system presented only one positive Lyapunov exponent (for chaotic behavior) or all negative exponents (for periodic behavior).

Fig. 3
figure 3

Largest Lyapunov exponents. (λ1) the first most significant and (λ2) the second most significant

Full size image

Investigating Fig. 3 and the bifurcation diagram, periodic behaviors show that all the largest exponents are negative and, in chaotic cases, all the largest exponents are positive. Also, it is possible to quantify sensitivity to initial conditions as mentioned above. Thus, the largest Lyapunov exponents provide important information to complement the analysis of the bifurcation diagram and to characterize the dynamic behavior.

To analyze the energy harvesting system, it is required to determine the output energy, as in (4). And Fig. 4 shows the power harvested for periodic behaviors and chaotic behaviors.

Fig. 4
figure 4

Power harvesting, periodic cases: aρ2 = 87 and bρ2 = 93 and chaotic cases: cρ2 = 82 and dρ2 = 100

Full size image

Therefore, it can evaluate which behavior will harvest the most energy. It is noteworthy that the angular velocity of the DC motor in chaotic cases (Fig. 4c and d) is higher than that in periodic cases (Fig. 4a and b). Thus, the torque applied to the structure with higher speeds tends to provide higher vibration amplitudes. However, according to Fig. 4, it can be seen that the average power collected in chaotic cases is lower than that in periodic cases, due to its instability observed in the temporal response, resulting in high amplitude variations.

Figure 5 shows the power spectral density.

Fig. 5
figure 5

Power spectral density, periodic cases: aρ2 = 87 and bρ2 = 93 and chaotic cases: cρ2 = 82 and dρ2 = 100

Full size image

Through the power spectral density, it is not possible to analyze the signal, and only a greater amount of energy is noted in 0- to 3-Hz frequency range, which are the internal and external frequencies of the system.

In sequence, Fig. 6 shows the SFTF.

Fig. 6
figure 6

STFT, periodic cases: aρ2 = 87 and bρ2 = 93 and chaotic cases: cρ2 = 82 and dρ2 = 100

Full size image

Using STFT makes it possible to verify the energy and frequency spectrum varying over time, providing a more refined analysis than PSD analysis. Thus, the STFT graph shows that over time, the frequency band with the most energy is the same, 0 to 3 Hz. The spectra for the periodic and chaotic cases are indistinguishable, making their analysis unfeasible.

Figure 7 shows the CWT for two different behaviors. In all simulations based on the wavelet transform, the Morlet wavelet was used.

Fig. 7
figure 7

CWT, periodic cases: aρ2 = 87 and bρ2 = 93 and chaotic cases: cρ2 = 82 and dρ2 = 100

Full size image

The use of CWT allowed observing regions with energy concentrations. In the frequency domain, the region with the highest concentration (yellow regions) implies higher energy harvest, and it can be observed that the periodic cases (Fig. 7a and b) have larger amplitudes than in chaotic cases (Fig. 7c and d), as noted in Fig. 4. Moreover, there is a discontinuous and continuous variation in the frequency spectrum for chaotic and periodic behaviors, respectively, thus allowing explicit characterization of chaotic behaviors.

Figure 8 shows the time-frequency analysis using SWT for two different behaviors.

Fig. 8
figure 8

SWT, periodic cases: aρ2 = 87 and bρ2 = 93 and chaotic cases: cρ2 = 82 and dρ2 = 100

Full size image

The use of SWT also allows the visualization of the frequency domain. Thus, it was possible to notice in cases of periodic orbits ρ2 = 87 (Fig. 8a) and ρ2 = 93 (Fig. 8b), the stability, and predominance of the natural frequency of the system. And for the chaotic case ρ2 = 82 (Fig. 8c) and ρ2 = 100 (Fig. 8d), besides showing the natural frequency, other frequencies that damage the energy intensity due to its instability, as can be observed in the spectrum. Also, it is possible to characterize the nonlinearity effects of the system. Then, the SWT is better suited to characterize the dynamics of the system; however, the power harvest is not well characterized.

Applying the WVD to periodic and chaotic signal, it is possible to vizualize in Fig. 9.

Fig. 9
figure 9

WVD, periodic cases: aρ2 = 87 and bρ2 = 93 and chaotic cases: cρ2 = 82 and dρ2 = 100

Full size image

WVD allows verifying the energy concentration around the natural frequency of the system in the analyzed cases. In the chaotic case, there is a shift in frequencies, explicitly at higher frequencies, seen through the discontinuity of energy concentration. Therefore, WVD can characterize the frequency change shown by chaotic signals, but this tool is not efficient to evidence higher energy concentration in the periodic case, as seen in CWT.

7 Conclusions

In this paper, a mathematical model of an energy harvester and a portal frame structure with a non-ideal drive was studied. The nonlinearity included in the system provides higher power over a wide frequency range. Thus, the analysis was carried out through the bifurcation diagram to evaluate the dynamic behavior and determine the periodic and chaotic orbits. Besides, the largest Lyapunov exponent allowed us to verify some system characteristics, such as periodicity and sensitivity to initial conditions. And through these important nonlinear dynamic study tools, an analysis was made to harvest vibration energy for two different dynamic behaviors, periodic and chaotic.

Time-frequency analysis was also used to contribute to frequency spectrum verification for both dynamic behaviors, chaotic response characterization, and energy harvest analysis, using the following methods: STFT, CWT, SWT, and WVD.

It is recognizable that classical signal processing methods based on the Fourier transform are not suitable for this type of analysis. However, STFT is a tool that makes it possible to analyze transient signals due to their short-range partition. And its application made to characterize a chaotic behavior was not adequate, featuring no difference between periodic and chaotic signal, as already expected according to the literature cited previously.

On the other hand, wavelet transform analysis was adequate for the studied mechanical systems. Wavelet transform analysis has the advantage of identifying the dynamic behavior of nonlinear systems based on time response, energy harvest analysis, and the ability to detect short transients.

The synchrosqueezed wavelet transform method is an extension of the wavelet transform that adds empirically decomposed elements and frequency reassignment techniques. This new tool produces a well-defined frequency representation over time, allowing the identification of instantaneous frequencies in non-stationary signals to highlight individual components, allowing for improved nonlinearity characterization. However, like STFT, it was not efficient in analyzing the harvested energy spectrum.

Finally, WVD allowed us to verify the energy concentration around the natural frequency and to characterize the chaotic behavior through frequency spectrum discontinuities. However, for energy harvest analysis, it was not efficient to present energy concentration as seen in CWT.

Therefore, the study makes it possible to examine the energy harvested by two different behaviors and excitations. In the periodic case, more energy is harvested than chaotic, even with a lower excitation charge. In periodic behavior, the system frequencies are stable, as analyzed in the time-frequency spectrum, which allows the piezoelectric element layers to deform more and generate more energy.

Overall, results presented using STFT, CWT, SWT, and WVD break down an input signal into time-varying harmonic signal sets. Generally, STFT is the first option to be applied to a signal due to its versatility, ease, and low-cost computation; however, it is not suitable for the proposed application. CWT’s variable time and frequency resolution allow the characterization of chaotic behavior and very explicit verification and differentiation of energy concentration for two different dynamic behaviors. SWT and WVD presented satisfactory results only in the identification of chaotic dynamics characteristics. Each transformation used, therefore, has its strengths and weaknesses, making them strongly complementary and widely applied in nonlinear signal analysis.