Influence of Ion-Slip and Hall Current on Magneto Hydrodynamic Free Convective Flow Past an Accelerated Plate with Dufour Effect and Ramped Temperature

Abstract

An analytical solution is proclaimed the significance of ion-slip and Hall current on magnetohydrodynamic convective free flow of radiation absorbing as well as a chemical reacting fluid past an accelerated affecting vertical porous plate with ramped temperature and Dufour effect. The modelling equations are reformed into dimensionless equations, further illuminated systematically by multiple standard perturbation law. Appraisals were operationalized graphically to scrutinize the performance of fluid velocity, temperature as well as concentration on the vertical plate by means of the disparity of emerging physical parameters.

1 Introduction

Due to multifaceted industrial as well as manufacturing applications, it is a great understanding to examine the MHD flow. The noteworthy purpose of MHD principles is to interrupt the flow field in a requisite way by fluctuating the formation of the point of the confinement layer. Thus, with the intention to modify the flow kinematics, the idea to execute MHD seems to be more flexible and consistent. In pharmaceutical as well as ecological science, MHD has been playing a critical role in the application of fluid dynamics and therapeutic sciences, owing to its implications in chemical fluids as well as metallurgical fields. The production of an extra prospective dissimilarity transverse to the direction of accumulating free charge and applied magnetic field among the opposite surfaces induces an electric current vertical to both the fields, magnetic as well as electric. This current is renowned as Hall current. Numerous explorers have been reviewed on Ion-slip as well as Hall current. Vijayaragavan and Karthikeyan [1] examined the significance of Hall current effect on MHD Casson fluid in presence Dufour as well as thermal radiation effects by means of chemically reaction. The noteworthiness of double diffusion, Ion-slip and Hall current on MHD free convection flow of couple stretch fluid during porous channels through chemical reaction and Dufour along with soret effects scrutinized [2, 3].

The impact of Hall and ion-slip current on unsteady 2D fluid flow in presence of Dufour as well as heat source described by [4]. In this study, the modelling equations are reformed into dimensionless equations, further illuminated systematically by multiple standard perturbation law and a consistent magnetic field is employed perpendicularly to the way of the flow. Abuga et al. [5] have discussed prominence of Hall current along with rotating system on magnetohydrodynamic fluid flow through an infinite plate affecting which is perpendicular, with externally heating as well as cooling of the plate in the occurrence of ramped wall temperature and isothermal in the aspect of thermal diffusion as well as diffusion thermo. The implication of hall current on convective double diffusion flow past stretching sheet along with dissipation as well as radiation contemplated by [6, 7]. Based on this scrutiny it was confirmed that Galerkin finite element was employed for solving nonlinear coupled equations. Makinde [8] has explored numerically, ion-slip and hall current importance on transient MHD flow by means of convective external boundary conditions in the presence of an infinite porous plate. Based on the outcomes it was perceived that the explicit finite difference method was employed for solving unsteady coupled nonlinear PDE’s. Seth et al. [9] have dissected, affect of a rotational system on unsteady hydromagnetic flow which is natural convective flow over impulsively affecting erect plate thereby ramped temperature implanted in a permeable medium by taking thermal diffusion as well as heat absorption. Deka and Das [10], Seth [11] and Rajesh and Chamkha [12] have analyzed the significance of ramped wall temperature on transient 2D, passes through a vertical surface with radiation as well as a chemical reaction.

Objective of present study mainly discussed effect of Hall as well as ion-slip current on MHD natural convective with double diffusion of a chemical reacting and radiation absorbing past fluid an accelerated moving vertical porous plate with ramped temperature in presence of Dufour effect. Natural convection emerging from such a plate temperature profile is probable to be of importance in numerous manufacturing applications particularly where the underlying temperature is of noteworthiness in the design of electromagnetic gadgets as well as a number of natural phenomena occurring owing to convection as well as heat generation/absorption.

2 Formulation and Solution of the Problem

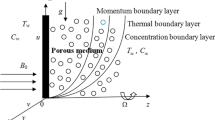
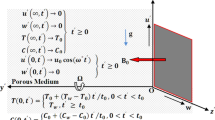
Contemplate transient 2D MHD natural convection stream with the help of double diffusion, synthetically responding with temperature-dependent heat retaining fluid past an accelerated boundless orthogonal affecting porous plate in a homogeneous of a stress grading in the aspect of thermal as well as mass diffusions. Contemplate x^*-axis is along the permeable in the upward surface way and z^*-axis in the way of non-parallel to the plane of the plate also y^* is normal to the x^*z^*—plane. The fluid is saturated by uniform crosswise appealing field B₀ employing parallel to z^*-axis. Initially, i.e. at the time $t^{*} \le 0$; the fluid as well as plate are at rest and retained at uniform temperature $T_{\infty }^{*}$ uniform surface concentration $C_{\infty }^{*}$. At time $t^{*} > 0$, plate starts affecting in x^*- direction opposite the gravitational field with time-dependent velocity $U_{0}^{*} \cos \omega^{*} t^{*}$. Temperature of the surface is accelerated or else declined to $T^{*} = T_{\infty }^{*} - t^{*} (T_{\infty }^{*} - T_{w}^{*} )/t_{{_{0} }}$ and the scale of concentration at the surface of the plate is accelerated or declined to $C^{*} = C_{\infty }^{*} - t^{*} (C_{\infty }^{*} - C_{w}^{*} )/t_{{_{0} }}$ when $(0,t_{0} ]$ thereafter i.e. at $(t_{0} ,\infty )$. The schematic outline assumed flow setup is shown in Fig. 1: The Hall current and Ion-slip was contemplated in the equation of momentum. Furthermore, Dufour as well as radiation absorption was reflected in the equation of energy.

Fig. 1

Schematic outline assumed flow setup

On the basis of the exceeding hypothesis, the transient fluid is represented by the consequent partial differential equations.

Equation of Momentum:

$$\left. \begin{aligned} \left[ {\frac{{\partial u^{*} }}{{\partial t^{*} }}} \right] = \vartheta \left[ {\frac{{\partial^{2} u^{*} }}{{\partial z^{{*^{2} }} }}} \right] + v_{\text{r}} \left[ {\frac{{\partial^{2} u^{*} }}{{\partial z^{{*^{2} }} }}} \right] - \beta \left[ {T_{\infty }^{*} - T^{*} } \right]g - \beta^{*} \left[ {C_{\infty }^{*} - C^{*} } \right]g \hfill \\ \quad \quad \quad \quad \quad - u^{*} \vartheta \left[ {K^{*} } \right]^{ - 1} - \frac{{v_{\text{r}} }}{{K^{*} }}\left[ {u^{*} } \right] - \frac{{\left[ {\beta_{e} w^{*} + \alpha_{e} u^{*} } \right]B_{0}^{2} \sigma_{e} }}{{\rho \left[ {\beta_{e}^{2} + \alpha_{e}^{2} } \right]}} \hfill \\ \end{aligned} \right\}$$

(1)

$$\begin{aligned} \left[ {\frac{{\partial w^{*} }}{{\partial t^{*} }}} \right] & = \vartheta \left[ {\frac{{\partial^{2} w^{*} }}{{\partial z^{{*^{2} }} }}} \right] + v_{\text{r}} \left[ {\frac{{\partial^{2} w^{*} }}{{\partial z^{{*^{2} }} }}} \right] - \frac{\vartheta }{{k^{*} }}\left[ {w^{*} } \right] \\ & \quad - \frac{{v_{\text{r}} }}{{K^{*} }}\left[ {w^{*} } \right] + \frac{{B_{0}^{2} \sigma_{e} \left[ {\beta_{e} u^{*} - \alpha_{e} w^{*} } \right]}}{{\rho \left[ {\alpha_{e}^{2} + \beta_{e}^{2} } \right]}} \\ \end{aligned}$$

(2)

Equation of Energy:

$$\begin{aligned} \frac{{\partial T^{*} }}{{\partial t^{*} }} & = \frac{k}{{\rho C_{p} }}\left( {\frac{{\partial^{2} T^{*} }}{{\partial z^{{*^{2} }} }}} \right) + \frac{{Q_{0} }}{{\rho C_{p} }}\left( {T^{*} - T_{\infty }^{*} } \right) \\ & \quad + \frac{{16\sigma_{s}^{*} T_{\infty }^{{*^{3} }} }}{{3\rho C_{\text{p}} k_{e}^{*} }}\frac{{\partial^{2} T^{*} }}{{\partial z^{{*^{2} }} }} + \frac{{D_{\text{m}} K_{\text{T}} }}{{C_{\text{s}} C_{\text{P}} }}\frac{{\partial^{2} C^{*} }}{{\partial z^{{*^{2} }} }} + R^{*} \left( {C^{*} - C_{\infty }^{*} } \right) \\ \end{aligned}$$

(3)

Equation of Concentration:

$$\frac{{\partial C^{*} }}{{\partial t^{*} }} = \tilde{D}\frac{{\partial^{2} C^{*} }}{{\partial y^{{*^{2} }} }} + K_{\text{r}} (C_{\infty }^{*} - C^{*} )$$

(4)

The relevant confinement conditions are

$$\left. \begin{aligned} u^{*} = 0,T^{*} = T_{\infty }^{*} ,C^{*} = C_{\infty }^{*} \quad {\text{if}}\;t^{*} \le 0\;{\text{for}}\;z \ge 0 \hfill \\ \left\{ \begin{aligned} \left. \begin{aligned} u^{*} = \left[ {U_{0}^{*} \cos \omega^{*} t^{*} } \right],\frac{{\left[ {T^{*} - T_{\infty }^{*} } \right]}}{{\left[ {T_{\text{w}}^{*} - T_{\infty }^{*} } \right]}} = t^{*} \left[ {t_{{_{0} }} } \right]^{ - 1} \hfill \\ \quad \quad \quad \frac{{\left[ {C_{\infty }^{*} - C^{*} } \right]}}{{\left[ {C_{\infty } - C_{\text{w}}^{*} } \right]}} = \left[ {\frac{{t^{*} }}{{t_{{_{0} }} }}} \right] \hfill \\ \end{aligned} \right\}\quad {\text{if}}\,(0,t_{0} ]\;{\text{at}}\;z^{*} = 0 \hfill \\ u^{*} \to 0,T^{*} \to T_{\infty }^{*} ,C^{*} \to C_{\infty }^{*} \;{\text{as}}\;z^{*} \to \infty \hfill \\ \end{aligned} \right. \hfill \\ \end{aligned} \right\}$$

(5)

Presently, non-dimensional amounts are characterized as

$$\left. \begin{aligned} f = \frac{{u^{*} }}{{U_{0} }},g = \frac{{w^{*} }}{{U_{0} }},U_{\infty } = \frac{{U_{\infty }^{*} }}{{U_{0} }},z = \frac{{V_{0} y^{*} }}{\vartheta },t = \frac{{V_{0}^{2} t^{*} }}{\vartheta },t_{0} = \frac{\upsilon }{{U_{0}^{2} }} \hfill \\ K^{*} = \frac{{K\vartheta^{2} }}{{V_{0}^{2} }},n^{*} = \frac{{V_{0}^{2} n}}{\vartheta },\frac{{\left( {T_{\infty }^{*} - T^{*} } \right)}}{{\left( {T_{\infty }^{*} - T_{\text{w}}^{*} } \right)}} = \theta ,\frac{{\left( {C_{\infty }^{*} - C^{*} } \right)}}{{\left( {C_{\infty }^{*} - C_{\text{w}}^{*} } \right)}} = C \hfill \\ \end{aligned} \right\}$$

(6)

After substituting the confinement conditions and non-dimensional variables in the governing Eqs. (1)–(4) then we obtain:

$$\frac{\partial f}{\partial t} = \left( {1 + \beta } \right)\frac{{\partial^{2} f}}{{\partial z^{2} }} + G_{\text{r}} \theta + G_{\text{m}} C - \left( {1 + \beta } \right)\left[ f \right] - \frac{{B_{0}^{2} \sigma_{e} \left[ {\alpha_{e} f + \beta_{e} g} \right]}}{{\rho \left[ {\alpha_{e}^{2} + \beta_{e}^{2} } \right]}}$$

(7)

$$\left[ {\frac{\partial g}{\partial t}} \right] = \left( {1 + \beta } \right)\left[ {\frac{{\partial^{2} g}}{{\partial z^{2} }}} \right] + v_{\text{r}} \left[ {\frac{{\partial^{2} g}}{{\partial z^{2} }}} \right] - \left( {1 + \beta } \right)\left[ g \right] + \frac{{B_{0}^{2} \sigma_{e} \left[ {\beta_{e} f - \alpha_{e} g} \right]}}{{\rho \left[ {\alpha_{e}^{2} + \beta_{e}^{2} } \right]}}$$

(8)

$$\frac{\partial \theta }{\partial t} = \left( {\Pr } \right)^{ - 1} \left( {1 + \frac{4R}{3}} \right)\frac{{\partial^{2} \theta }}{{\partial z^{2} }} + \eta \theta + Du\frac{{\partial^{2} C}}{{\partial z^{2} }} + R_{\text{a}} C$$

(9)

$$\frac{\partial C}{\partial t} = \left( {Sc} \right)^{ - 1} \frac{{\partial^{2} C}}{{\partial z^{2} }} - K_{\text{r}} C$$

(10)

The corresponding confinement conditions are

$$\left. \begin{aligned} f = g = \theta = C = 0\quad \forall z,t \le 0 \hfill \\ \left. \begin{aligned} u = \cos \omega t,\quad g = 0,\quad \theta = C = t\;{\text{at}}\;z = 0 \hfill \\ u,\theta ,C \to 0\;{\text{as}}\;z \to \infty \hfill \\ \end{aligned} \right\}:t > 0 \hfill \\ \end{aligned} \right\}$$

(11)

$$\left. \begin{aligned} M = \frac{{\sigma B_{0}^{2} \vartheta }}{{\rho V_{0}^{2} }},G_{\text{m}} = \frac{{\vartheta \beta^{*} g\left( {C_{w}^{*} - C_{\infty }^{*} } \right)}}{{V_{0}^{2} U_{0} }},G_{\text{r}} = \frac{{\vartheta \beta g\left( {T_{\text{w}}^{*} - T_{\infty }^{*} } \right)}}{{V_{0}^{2} U_{0} }},R = \frac{{4\sigma T_{\infty }^{{*^{{^{3} }} }} }}{{k_{e} k}} \hfill \\ Sc = \frac{\vartheta }{{\tilde{D}}},{\text{Dr}} = \frac{{D_{\text{m}} K_{\text{T}} \left[ {C_{\text{w}}^{*} - C_{\infty }^{*} } \right]}}{{\vartheta C_{\text{S}} C_{\text{P}} \left[ {T_{\text{w}}^{*} - T_{\infty }^{*} } \right]}},R_{\text{a}} = \frac{{R^{*} \vartheta \left( {C_{\text{w}}^{*} - C_{\infty }^{*} } \right)}}{{V_{0}^{2} \left( {T_{\text{w}}^{*} - T_{\infty }^{*} } \right)}},\Pr = \frac{{\rho \vartheta C_{\text{p}} }}{k} \hfill \\ \xi = \left[ {\frac{{M\left[ { - \alpha_{e} + i\beta_{e} } \right]}}{{\left[ {\alpha_{e}^{2} + \beta_{e}^{2} } \right]}} + \frac{1 + \beta }{K}} \right],K_{\text{r}} = \frac{{k_{1} \vartheta }}{{V_{0}^{2} }}\beta = \frac{{v_{\text{r}} }}{\vartheta }\eta = \frac{{\vartheta Q_{0} }}{{\rho V_{0}^{2} C_{\text{P}} }},\varGamma = \left( {\frac{3 + 4R}{3\Pr }} \right) \hfill \\ \end{aligned} \right\}$$

(12)

$$\frac{\partial \chi }{\partial t} = \left( {1 + \beta } \right)\frac{{\partial^{2} \chi }}{{\partial z^{2} }} + G_{\text{r}} \theta + G_{\text{m}} C - \chi \xi$$

(13)

Here $\chi = f + ig$

The relevant confinement conditions are

$$\left. \begin{aligned} \chi = \theta = C = 0\quad \forall z,t \le 0 \hfill \\ t > 0:\left\{ \begin{aligned} \chi = \cos \omega \,t,\theta = C = t\;{\text{at}}\;z = 0 \hfill \\ \chi ,\theta ,C \to 0,\;{\text{as}}\;z \to \infty \hfill \\ \end{aligned} \right. \hfill \\ \end{aligned} \right\}$$

(14)

Equations (9), (10) and (13) are illuminated systematically with the help of single perturbation method subject to initial and confinement conditions (14).

$$\left. {\chi = \chi_{0} \left( z \right){ \exp }(i\omega t) \ldots ,\quad \theta = \theta_{0} \left( z \right){ \exp }(i\omega t) \ldots ,\quad C = C_{0} \left( z \right){ \exp }(i\omega t) \ldots } \right\}$$

(15)

Substituting Eq. (15) in Eqs. (9), (10) and (13) then we obtain:

$$\left( {1 + \beta } \right)\chi_{0}^{{\prime \prime }} - (\xi - i\omega )\quad \chi_{0} = - G_{\text{r}} \theta_{0} - G_{\text{m}} C_{0}$$

(16)

$$\varGamma \theta_{0}^{{\prime \prime }} - \left( {i\omega - \eta } \right)\theta_{0} = - DuC_{0}^{{\prime \prime }} - R_{\text{a}} C_{0}$$

(17)

$$C_{0}^{{\prime \prime }} - Sc\left( {K_{\text{r}} + i\omega } \right)C_{0} = 0$$

(18)

The appropriate confinement conditions are

$$\left. {\left\{ \begin{aligned} \chi_{0} = e^{ - i\omega t} \cos (\omega t),\theta_{0} = C_{0} = te^{ - i\omega t} \;{\text{at}}\;z = 0 \hfill \\ \chi_{0} ,\theta_{0} ,C_{0} \quad \to 0\;{\text{as}}\;z \to \infty \hfill \\ \end{aligned} \right.} \right\}$$

(19)

Solve Eqs. (16)–(18) by using (19) then we get,

$$\chi = \left( \begin{aligned} \left( {(\cos \omega t)e^{ - i\omega t} - \psi_{2} - \psi_{3} } \right)\exp ( - \left( {\sqrt {\frac{(S - i\omega )}{1 + \beta }} } \right)z) \hfill \\ + \psi_{2} \exp ( - \left( {\sqrt {\frac{(i\omega - \eta )}{\varGamma }} } \right)z) + \psi_{3} \exp ( - \left( {\sqrt {Sc(K_{\text{r}} + i\omega )} } \right)z) \hfill \\ \end{aligned} \right)e^{i\omega t}$$

(20)

$$\theta = \left( {\left( {te^{ - i\omega t} - \psi_{1} } \right)e^{{ - \left( {\sqrt {\frac{(i\omega - \eta )}{\varGamma }} } \right)z}} + \psi_{1} e^{{ - \left( {\sqrt {Sc(K_{\text{r}} + i\omega )} } \right)z}} } \right)e^{i\omega t}$$

(21)

$$C = \left( {t\text{e}^{ - i\omega t} e^{{ - \left( {\sqrt {Sc\left( {K_{\text{r}} + i\omega } \right)} } \right)z}} } \right)e^{i\omega t} .$$

(22)

3 Discussion of Ideal Convergence

Figures 2, 3 and 4 Reaffirmed that the sway of time (t) on the velocity and temperature as well as concentration. From this figure, it was identified that as the values of “t” rises then it leads to rise in temperature and concentration as well as velocity. Figures 5, 6, 7 and 8 Illustrated that the performance of velocity and temperature for disparate estimators of Dufour (Dr) and radiation absorption (R_a). The results obtained from this figure it was perceived that enhance in temperature as well as velocity. Representative dissimilarity of the velocity along the spanwise coordinate yare exhibit in Figs. 9 and 10: From these figures, it was recognized that for diverse values of Ion-slip estimator ($\beta_{i}$) rises then it leads to enhance in velocity, but reverse effect occurred in case of Hall current ($\beta_{e}$). Figures 11 and 12: demonstrated that the impact of C.R. (K_r) as well as S.nu. (Sc) on concentration. On the basis of figures, it was perceived that velocity and concentration reduced with the raise of K_r and Sc.

Fig. 2

Performance of t on χ(z)

Fig. 3

Performance of t on θ(z)

Fig. 4

Performance of t on C(z)

Fig. 5

Performance of Dr on χ(z)

Fig. 6

Performance of Dr on θ(z)

Fig. 7

Performance of R_a on χ(z)

Fig. 8

Performance of R_a on θ(z)

Fig. 9

Performance of $\beta_{e}$ on χ(z)

Fig. 10

Performance $\beta_{i}$ on χ(z)

Fig. 11

Performance of Kr on C(z)

Fig. 12

Performance of Sc on C(z)

4 Conclusions

• As velocity, temperature as well as concentration rises with rise in time t.

• Temperature and velocity rises owing to the enhancement of Dufour Dr as well as radiation absorption R_a

• As rise in chemical reaction K_r leads to decline in velocity as well as concentration.

• As Velocity rises with the enhancement of Hall parameter ($\beta_{e}$), but inverse effect was occurred in case of Ion-slip current ($\beta_{i}$).