The split common fixed point problem for multivalued demicontractive mappings and its applications

Abstract

In this article, we consider the split common fixed point problem for two infinite families of multivalued mappings in real Hilbert spaces. We introduce an algorithm based on the viscosity method for solving the split common fixed point problem for two infinite families of multivalued demicontractive mappings. We establish a strong convergence result under some suitable conditions. As applications, we also apply our main result to the split variational inequality problem and the split common null point problem. Finally, we give the numerical example for supporting our main theorem.

1 Introduction

Let $\mathcal {H}_1$ and $\mathcal {H}_2$ be real Hilbert spaces and let $A : \mathcal {H}_1 \rightarrow \mathcal {H}_2$ be a bounded linear operator. Given nonempty closed covex subsets $C_{i} \subseteq \mathcal {H}_1$$(i = 1, 2,\ldots , t)$ and $Q_{j} \subseteq \mathcal {H}_2$$(j = 1, 2,\ldots , r)$ of $\mathcal {H}_1$ and $\mathcal {H}_2$, respectively. The multiple-set split feasibility problem (MSSFP) which was introduced by Censor et al. [12] is formulated as finding a point

$$\begin{aligned} \hat{x} \in \bigcap _{i=1}^{t}C_{i} \quad \text {such that}\; A\hat{x} \in \bigcap _{j=1}^{r}Q_{j}. \end{aligned}$$

(1.1)

In particular, if t = r = 1, then the MSSFP (1.1) is reduced to find a point

$$\begin{aligned} \hat{x} \in C \quad \text {such that}\; A\hat{x} \in Q, \end{aligned}$$

(1.2)

where C and Q are nonempty closed convex subsets of $\mathcal {H}_1$ and $\mathcal {H}_2$, respectively. The problem (1.2) is known as the split feasibility problem (SFP) which was first introduced by Censor and Elfving [7] for modeling inverse problems in finite-dimensional Hilbert spaces. It is known that $\hat{x}$ solves the SFP (1.2) if and only if $\hat{x}$ solves the fixed point equation:

$$\begin{aligned} P_{C}(I - \gamma A^{*}(I - P_{Q})A)\hat{x} = \hat{x}, \end{aligned}$$

(1.3)

where $A^{*}$ is the adjoint operator of A and $\gamma > 0$. Byrne [2] proposed the so-called CQ algorithm for solving the SFP and many authors studied the SFP and the MSSFP, see, for instance [1, 12, 17, 18, 24, 31, 34,35,36].

The split common fixed point problem (SCFP) is a generalization of the MSSFP, and is formulated as finding a point:

$$\begin{aligned} \hat{x} \in \bigcap _{i=1}^{t}Fix(S_{i}) \quad \text {such that}\; A\hat{x} \in \bigcap _{j=1}^{r}Fix(T_{j}), \end{aligned}$$

(1.4)

where $S_{i} : \mathcal {H}_1 \rightarrow \mathcal {H}_1$$(i = 1, 2,\ldots , t)$ and $T_{j} : \mathcal {H}_2 \rightarrow \mathcal {H}_2$$(j = 1, 2,\ldots , r)$ are nonlinear mappings with nonempty fixed point sets $Fix(S_{i})$ and $Fix(T_{i})$, respectively. In the case $t = r = 1$, the SCFP (1.4) is reduced to find a point

$$\begin{aligned} \hat{x} \in Fix(S) \quad \text {such that}\; A{x} \in Fix(T), \end{aligned}$$

(1.5)

where $S : \mathcal {H}_1 \rightarrow \mathcal {H}_1$ and $T : \mathcal {H}_2 \rightarrow \mathcal {H}_2$ are nonlinear mappings with nonempty fixed point sets Fix(S) and Fix(T), respectively. The problem (1.5) is usually called the two-set SCFP. Similarly, the SFP (1.2) becomes a special case of the two-set SCFP (1.5). The SCFP was studied by many authors (see [6, 10, 13, 20,21,22, 26, 28, 29, 32]) due to its applications are desirable and can be used in real-world applications, for example, in signal processing, in image processing, in image reconstruction, in modeling inverse problems, in computerized tomography, in the intensity-modulated radiation therapy, see [3, 7, 11, 12, 23].

In 2009, Censor and Segal [10] invented an algorithm to solve the two-set SCFP (1.5) for directed mappings in finite-dimensional Hilbert spaces as follows:

$$\begin{aligned} x_{n+1} = S(x_{n} + \gamma A^{*}(T-I)Ax_{n}), \quad n \in \mathbb {N}. \end{aligned}$$

(1.6)

In 2011, by modification of Mann’s iteration, Moudafi [21] introduced an algorithm for solving the two-set SCFP (1.5) in the infinite-dimensional real Hilbert spaces as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n = x_n + \gamma \beta A^{*}(T-I)Ax_n,\\ x_{n+1} = (1-\alpha _{n})y_{n} + \alpha _{n}Sy_{n},\quad n \in \mathbb {N}, \end{array}\right. } \end{aligned}$$

(1.7)

where S and T are quasi-nonexpansive mappings such that $I-S$ and $I-T$ are demiclosed at zero. He also proved a weak convergence result of this algorithm under some suitable control conditions.

In [28, 29, 32], they developed algorithms for solving the two-set SCFP (1.5) to cyclic algorithms and simultaneous algorithms for solving the SCFP (1.4).

Recently, the SCFP for multivalued mappings was considerd by Latif and Eslamian [16]. They proposed an algorithm based on the viscosity method to solve the SCFP for a finite family of multivalued quasi-nonexpansive mappings and a finite family of multivalued mappings such that the best approximation operators are quasi-nonexpansive, and also proved a strong convergence result as shown below.

Theorem 1.1

[16] Let $\mathcal {H}_{1}$ and $\mathcal {H}_{2}$ be two real Hilbert spaces, $A : \mathcal {H}_1 \rightarrow \mathcal {H}_2$ be a bounded linear operator. For $i = 1, 2,\ldots , t$, let $S_{i} : \mathcal {H}_{1} \rightarrow CB(\mathcal {H}_{1})$ and $T_{i} : \mathcal {H}_2 \rightarrow CC(\mathcal {H}_2)$ be multivalued mappings such that $S_{i}$ and $P_{T_{i}} : \mathcal {H}_2 \rightarrow \mathcal {H}_2$ are quasi-nonexpansive. Suppose that $I - S_{i}$ and $I - P_{T_{i}}$ are demiclosed at zero, and $S_{i}$ satisfies the endpoint condition. Assume that $\varOmega = \left\{ x \in \bigcap _{i=1}^{t}Fix(S_{i}) : Ax \in \bigcap _{i=1}^{t}Fix(T_{i}) \right\} \ne \emptyset$. Let $f : \mathcal {H}_{1} \rightarrow \mathcal {H}_{1}$ be a contraction. Let $\{x_n\} \subset \mathcal {H}_1$ be a sequence generated by $x_{0} \in \mathcal {H}_{1}$ and

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n = x_n + \sum _{i=1}^{t}\frac{1}{t}\gamma \beta A^{*}(P_{T_{i}} - I)Ax_{n},\\ u_n = \alpha _{n,0}y_n + \sum _{i=1}^{t}\alpha _{n,i}z_{n,i},\\ x_{n+1} = \vartheta _{n}f(u_n) + (1 - \vartheta _{n})u_n,\quad n \ge 0, \end{array}\right. } \end{aligned}$$

(1.8)

where $z_{n,i} \in S_{i}y_n$, $\beta \in (0, 1)$, $\gamma \in \left( 0,\frac{1}{\beta \Vert A\Vert ^2}\right)$, $\liminf _{n}\alpha _{n,0}\alpha _{n,i} > 0$, $\sum _{i=0}^{t}\alpha _{n,i} = 1$, $\lim _{n \rightarrow \infty } \vartheta _{n} = 0$, and $\sum _{n=0}^{\infty } \vartheta _{n} = \infty$. Then the sequence $\{x_{n}\}$ converges strongly to $\hat{x} \in \varOmega$ which solves the variational inequality:

$$\begin{aligned} \langle f(\hat{x}) - \hat{x}, x - \hat{x} \rangle \le 0\quad \text {for all} \; x \in \varOmega . \end{aligned}$$

Recently, Eslamian [13] studied and proposed an algorithm for solving the SCFP for two infinite families of single-valued demicontractive mappings and also proved a strong convergence theorem.

In this article, inspired and motivated by these works, we are interested to study the SCFP for two infinite families of multivalued mappings which is more general than the problem in Theorem 1.1. We introduce an algorithm based on the viscosity method to solve the SCFP for two infinite families of multivalued demicontractive mappings, and prove a strong convergence theorem of the proposed algorithm under some suitable conditions such that some assumptions in our main result is weaker than the common endpoint condition. Furthermore, our main result generalizes and improves the results of Latif and Eslamian [16] and Eslamian [13]. As applications, we also apply our main result to the split variational inequality problem and the split common null point problem. In the last section, we give the numerical example to demonstrate the convergence of our algorithm.

2 Preliminaries

Throughout this paper, let $\mathbb {N}$ be the set of positive integers and $\mathbb {R}$ the set of real numbers. We shall assume that $\mathcal {H}$ is a real Hilbert space with the inner product $\langle \cdot , \cdot \rangle$ and the norm $\Vert \cdot \Vert$, and let I be the identity operator on $\mathcal {H}$. We denote the strong and weak convergence of a sequence $\{x_{n}\}$ in $\mathcal {H}$ to an element $x \in \mathcal {H}$ by $x_{n} \rightarrow x$ and $x_{n} \rightharpoonup x$, respectively. Let K be a nonempty closed convex subset of $\mathcal {H}$. Recall that the (metric) projection from $\mathcal {H}$ onto K, denoted by $P_{K}$ is defined for each $x \in \mathcal {H}$, $P_{K}x$ is the unique element in K such that

$$\begin{aligned} \Vert x - P_{K}x \Vert = d(x, K) := \inf \{ \Vert x - y \Vert : y \in K \}. \end{aligned}$$

It is known that $P_{K}x \in K$ is characterized by the following property:

$$\begin{aligned} \langle x - P_{K}x, y - P_{K}x \rangle \le 0 \text {for all} \ y \in K. \end{aligned}$$

Let C be a nonempty subset of $\mathcal {H}$ and $k \in [0, 1)$. A mapping $f : \mathcal {H} \rightarrow \mathcal {H}$ is called a k-contraction with respect to C if $\Vert f(x) - f(z)\Vert \le k\Vert x - z \Vert$ for all $x \in \mathcal {H}$, $z \in C$; f is called a k-contraction if f is a k-contraction with respect to $\mathcal {H}$. It is easy to check that if $f : \mathcal {H} \rightarrow \mathcal {H}$ is a k-contraction with respect to C, where $0 \le k < 1$ and C is closed and convex, then $P_{C}f$ is a k-contraction on C.

A subset D of $\mathcal {H}$ is said to be proximal if for each $x \in \mathcal {H}$, there exists $y \in D$ such that

$$\begin{aligned} \Vert x - y \Vert = d(x, D). \end{aligned}$$

We denote by $CB(\mathcal {H})$, $CC(\mathcal {H})$, and $P(\mathcal {H})$ the families of all nonempty closed bounded subsets of $\mathcal {H}$, nonempty closed convex subsets of $\mathcal {H}$, and nonempty proximal bounded subsets of $\mathcal {H}$, respectively. The Pompeiu-Hausdorff metric on $CB(\mathcal {H})$ is defined by

$$\begin{aligned} H(A, B) := \max \bigg \{ \sup _{x \in A} d(x, B), \sup _{y \in B} d(y, A)\bigg \} \end{aligned}$$

for all $A, B \in CB(\mathcal {H})$. Let $T : \mathcal {H} \rightarrow 2^{\mathcal {H}}$ be a multivalued mapping. An element $p \in \mathcal {H}$ is called a fixed point of T if $p \in Tp$. The set of all fixed points of T is denoted by Fix(T). We say that T satisfies the endpoint condition if $Tp = \{p\}$ for all $p \in Fix(T)$. For multivalued mappings $T_{i} : \mathcal {H} \rightarrow 2^{\mathcal {H}}$$(i \in \mathbb {N})$ with $\bigcap _{i=1}^{\infty } Fix(T_{i}) \ne \emptyset$, we also say that $\{T_{i}\}_{i=1}^{\infty }$ satisfies the common endpoint condition if $T_{i}(p) = \{p\}$ for all $i \in \mathbb {N}$, for all $p \in \bigcap _{i=1}^{\infty } Fix(T_{i})$.

Now let us recall the definitions of multivalued mappings concerned in our study.

Definition 2.1

A multivalued mapping $T : \mathcal {H} \rightarrow CB(\mathcal {H})$ is said to be

• (i) nonexpansive if

  $$\begin{aligned} H(Tx, Ty) \le \Vert x - y \Vert \quad \text {for all} \; x, y \in \mathcal {H}, \end{aligned}$$

• (ii) quasi-nonexpansive if $Fix(T) \ne \emptyset$ and

  $$\begin{aligned} H(Tx, Tp) \le \Vert x - p \Vert \quad \text {for all} \; x \in \mathcal {H}, \quad p \in Fix(T), \end{aligned}$$

• (iii) demicontractive [9, 14] if $Fix(T) \ne \emptyset$ and there exists $k \in [0,1)$ such that

  $$\begin{aligned} H(Tx, Tp)^{2} \le \Vert x - p \Vert ^{2} +kd(x, Tx)^{2} \quad \text {for all} \; x \in \mathcal {H}, \quad p \in Fix(T). \end{aligned}$$

Note that the class of demicontractive mappings includes several common types of classes of mappings occurring in optimization problems, such as a class of nonexpansive mappings with nonempty fixed point set and a class of quasi-nonexpansive mappings.

The following example inspired by [9, Example 11] and [14, Example 3.4] shows that the class of quasi-nonexpansive mappings is properly contained in the calss of demicontractive mappings.

Example 2.2

Let $\mathcal {H} = \mathbb {R}$. For each $i \in \mathbb {N}$, define $T_{i} : \mathbb {R} \rightarrow 2^{\mathbb {R}}$ by

$$\begin{aligned} T_{i}x = \left\{ \begin{array}{ll} {\Bigg [} -\frac{(2i + 1)x}{2}, -(i+1)x \Bigg ], &{}\quad \text {if}\; x \le 0,\\ {\Bigg [} -(i+1)x, -\frac{(2i + 1)x}{2} \Bigg ], &{}\quad \text {if}\; x > 0.\\ \end{array}\right. \end{aligned}$$

Then $Fix(T_{i}) = \{0\}$. For each $0 \ne x \in \mathbb {R}$,

$$\begin{aligned} H(T_{i}x, T_{i}0)^{2} = | -(i+1)x - 0|^{2} = (i+1)^{2}|x - 0|^{2}= |x - 0|^{2} + (i^{2}+2i)|x|^{2}. \end{aligned}$$

Clearly, $T_{i}$ is not quasi-nonexpansive. We also have

$$\begin{aligned} d(x, T_{i}x)^{2} = \left| x - \left( -\frac{(2i + 1)x}{2} \right) \right| ^{2} = \left| \frac{(2i + 3)x}{2} \right| ^{2} = \left( \frac{4i^{2}+12i + 9}{4}\right) |x|^{2}. \end{aligned}$$

Therefore,

$$\begin{aligned} H(T_{i}x, T_{i}0)^{2} = |x - 0|^{2} + \left( \frac{4i^{2}+8i}{4i^{2}+12i + 9}\right) d(x, T_{i}x)^{2}. \end{aligned}$$

Hence $T_{i}$ is demicontractive with a constant $k_{i} = \frac{4i^{2}+8i}{4i^{2}+12i + 9} \in (0, 1)$.

For a multivalued mapping $T : \mathcal {H} \rightarrow P(\mathcal {H})$, the best approximation operator $P_{T}$ is defined by

$$\begin{aligned} P_{T}(x) := \{ y \in Tx : \Vert x - y\Vert = d(x, Tx)\}. \end{aligned}$$

We can easily prove that $Fix(T) = Fix(P_{T})$ and $P_{T}$ satisfies the endpoint condition. Song and Cho [25] gave an example for the best approximation operator $P_{T}$ which is nonexpansive, but T is not necessary to be nonexpansive.

Definition 2.3

Let $T : \mathcal {H} \rightarrow CB(\mathcal {H})$ be a multivalued mapping. The multivalued mapping $I - T$ is said to be demiclosed at zero if for any sequence $\{x_{n}\}$ in $\mathcal {H}$ which converges weakly to x and the sequence $\{\Vert x_{n} - y_{n}\Vert \}$ converges strongly to 0, where $y_{n} \in Tx_{n}$, then $x \in Fix(T)$.

Next, we give some significant tools for proving our main results.

Lemma 2.4

[27] For a real Hilbert space $\mathcal {H}$, the following inequality holds:

$$\begin{aligned} \Vert x + y \Vert ^{2} \le \Vert x\Vert ^{2} + 2\langle y, x + y\rangle \quad \text {for all}\; x , y \in \mathcal {H}. \end{aligned}$$

The following lemma shows the properties of demicontractive mappings which are inspired by [28, Lemma 1].

Lemma 2.5

Let $T : \mathcal {H} \rightarrow CB(\mathcal {H})$ be a multivalued k-demicontractive mapping. If $p \in Fix(T)$ such that $Tp = \{p\}$, then the following two inequalities hold: for all $x \in \mathcal {H}$, $y \in Tx$

• (i) $\langle x - y, p - y \rangle \le \frac{1+k}{2} \Vert x - y \Vert ^{2}$;

• (ii) $\langle x - y, x - p \rangle \ge \frac{1-k}{2} \Vert x - y \Vert ^{2}$.

Proof

Since T is k-demicontractive, we have

$$\begin{aligned} \langle x - y, p - y\rangle&= \frac{1}{2}\left( \Vert x - y\Vert ^{2} + \Vert p - y\Vert ^{2} - \Vert x - p\Vert ^{2} \right) \\&= \frac{1}{2}\left( \Vert x - y\Vert ^{2} + d(y, Tp)^{2} - \Vert x - p\Vert ^{2} \right) \\&\le \frac{1}{2}\left( \Vert x - y\Vert ^{2} + H(Tx, Tp)^{2} - \Vert x - p\Vert ^{2} \right) \\&\le \frac{1}{2} \left( \Vert x - y \Vert ^{2} + \Vert x - p\Vert ^{2} + kd(x, Tx)^{2} - \Vert x - p\Vert ^{2} \right) .\\&\le \frac{1}{2} \left( \Vert x - y \Vert ^{2} + k\Vert x - y|^{2} \right) = \frac{1+k}{2} \Vert x - y \Vert ^{2}. \end{aligned}$$

Similarly, we can prove the other inequality: $\langle x - y, x - p \rangle \le \frac{1-k}{2} \Vert x - y \Vert ^{2}$. $\square$

Lemma 2.6

[8] Let $\mathcal {H}$ be a real Hilbert space, $x_{i} \in \mathcal {H}$, $(1 \le i \le m)$ and $\{ \alpha _{i}\}_{i=1}^{m} \subset (0, 1)$ with $\sum _{i=1}^{m}\alpha _{i} = 1$. Then the following identity holds:

$$\begin{aligned} \left\| \sum _{i=1}^{m}\alpha _{i}x_{i} \right\| ^{2} = \sum _{i=1}^{m}\alpha _{i}\Vert x_{i}\Vert ^{2} -\!\! \sum _{i,j=1,i\ne j}^{m}\!\!\alpha _{i}\alpha _{j} \Vert x_{i} - x_{j}\Vert ^{2}. \end{aligned}$$

Lemma 2.7

[33] Suppose that $\{a_{n}\}$ is a sequence of nonnegative real numbers such that

$$\begin{aligned} a_{n+1} \le (1 - \lambda _{n})a_{n} + \lambda _{n}\sigma _{n} + \beta _{n},\quad n \in \mathbb {N}, \end{aligned}$$

where $\{\lambda _{n}\}, \{\sigma _{n}\}$ and $\{\beta _{n}\}$ satisfy the following conditions:

• (i) $\{\lambda _{n}\} \subset [0, 1]$, $\sum _{n=1}^{\infty } \lambda _{n} = \infty$;

• (ii) $\limsup _{n}\sigma _{n} \le 0$ or $\sum _{n=1}^{\infty } | \lambda _{n} \sigma _{n} | < \infty$;

• (iii) $\beta _{n} \ge 0$ for all $n \in \mathbb {N}$, $\sum _{n=1}^{\infty } \beta _{n} < \infty$.

Then $\lim _{n \rightarrow \infty } a_{n} = 0$.

Lemma 2.8

[19] Let $\{t_{n}\}$ be a sequence of real numbers such that there exists a subsequence $\{n_{i}\}$ of $\{n\}$ which satisfies $t_{n_{i}} <t_{n_{i}+1}$ for all $i \in \mathbb {N}$. Also consider the sequence of positive integers $\{\rho (n)\}$ defined by

$$\begin{aligned} \rho (n) := \max \{ k \le n : t_{k} < t_{k+1}\} \end{aligned}$$

for all $n \ge n_{0}$ (for some $n_{0}$ large enough). Then $\{\rho (n)\}$ is a nondecreasing sequence such that $\lim _{n \rightarrow \infty } \rho (n) = \infty$ and it holds that

$$\begin{aligned} t_{\rho (n)} \le t_{\rho (n)+1},\quad t_{n} \le t_{\rho (n)+1}. \end{aligned}$$

3 Main results

In this section, we present an algorithm for solving SCFP for two infinite families of multivalued demicontractive mappings and prove a strong convergence theorem.

Throughout this paper, let $\Gamma$ be the solution set of the SCFP for two infinite families of mappings $\{S_{i}\}_{i=1}^{\infty }$ and $\{T_{i}\}_{i=1}^{\infty }$, that is,

$$\begin{aligned} \Gamma := \left\{ x \in \bigcap _{i=1}^{\infty }Fix(S_{i}) : Ax \in \bigcap _{i=1}^{\infty }Fix(T_{i}) \right\} . \end{aligned}$$

In [30], it was shown that the fixed point set Fix(S) of a multivalued demicontractive mapping S, where S satisfies the endpoint condition is closed and convex. Hence we can prove the following lemma in the same way as [30, Lemma 3.2].

Lemma 3.1

Let $\mathcal {H}_{1}$ and $\mathcal {H}_{2}$ be two real Hilbert spaces, $A : \mathcal {H}_1 \rightarrow \mathcal {H}_2$ be a bounded linear operator. For each $i \in \mathbb {N}$, let $S_{i} : \mathcal {H}_{1} \rightarrow CB(\mathcal {H}_{1})$ and $T_{i} : \mathcal {H}_2 \rightarrow CB(\mathcal {H}_2)$ be multivalued demicontractive mappings with constants $k_{i}$ and $k_{i}^{\prime }$, respectively. Suppose that $\Gamma \ne \emptyset$. Then

• (i) $\Gamma$ is closed;

• (ii) If for each $p \in \Gamma$, $S_{i}(p) = \{p\}$ and $T_{i}(Ap) = \{Ap\}$ for all $i \in \mathbb {N}$, then $\Gamma$ is convex.

We now prove our main theorem.

Theorem 3.2

Let $\mathcal {H}_{1}$ and $\mathcal {H}_{2}$ be two real Hilbert spaces, $A : \mathcal {H}_1 \rightarrow \mathcal {H}_2$ be a bounded linear operator. For each $i \in \mathbb {N}$, let $S_{i} : \mathcal {H}_{1} \rightarrow CB(\mathcal {H}_{1})$ and $T_{i} : \mathcal {H}_2 \rightarrow CB(\mathcal {H}_2)$ be multivalued demicontractive mappings with constants $k_{i}$ and $k_{i}^{\prime }$, respectively, such that $I - S_{i}$ and $I - T_{i}$ are demiclosed at zero. Suppose that $\Gamma \ne \emptyset$ and for each $p \in \Gamma$, $S_{i}(p) = \{p\}$ and $T_{i}(Ap) = \{Ap\}$ for all $i \in \mathbb {N}$. Let $f : \mathcal {H}_{1} \rightarrow \mathcal {H}_{1}$ be a $\tau$-contraction with respect to $\Gamma$, where $0 \le \tau < 1$. Let $\{x_n\} \subset \mathcal {H}_1$ be a sequence generated by $x_{1} \in \mathcal {H}_{1}$ and

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n = x_n + \sum \nolimits _{i=1}^{n}\beta _{n,i}\gamma A^{*}(w_{n,i} - Ax_n),\\ u_n = \alpha _{n,0}y_n + \sum \nolimits _{i=1}^{n}\alpha _{n,i}z_{n,i},\\ x_{n+1} = \xi _{n}f(x_n) + (1 - \xi _{n})u_n,\quad n \in \mathbb {N}, \end{array}\right. } \end{aligned}$$

(3.1)

where $z_{n,i} \in S_{i}y_n$, $w_{n,i} \in T_{i}(Ax_{n})$, the parameter $\gamma$, and the sequences $\{\alpha _{n,i}\}_{n=1}^{\infty }$ for all $i \ge 0$, $\{\beta _{n,i}\}_{n=1}^{\infty }$ for all $i \in \mathbb {N}$ and $\{\xi _{n}\}_{n=1}^{\infty }$ satisfy the following conditions:

• (C1) $\gamma \in \left( 0,\frac{1 - k^{\prime }}{\Vert A\Vert ^2}\right)$, where $k^{\prime } = \sup \{k_{i}^{\prime } : i \in \mathbb {N} \}$;

• (C2) $\alpha _{n,i} \in [0, 1)$ such that $\alpha _{n,0} \in (k, 1)$ where $k = \sup \{k_{i} : i \in \mathbb {N} \}$, $\alpha _{n,i} \ne 0$ for all $i \le n$, $\liminf _{n}(\alpha _{n,0}-k)\alpha _{n,i} > 0$ for all $i \in \mathbb {N}$, and $\sum _{i=0}^{n}\alpha _{n,i} = 1$;

• (C3) $\beta _{n,i} \in [0, 1]$ such that $\beta _{n,i} \ne 0$ for all $i \le n$, $\liminf _{n}\beta _{n,i} > 0$ for all $i \in \mathbb {N}$, and $\sum _{i=1}^{n}\beta _{n,i} = 1$;

• (C4) $\xi _{n} \in (0, 1)$ such that $\lim _{n \rightarrow \infty } \xi _{n} = 0$ and $\sum _{n=1}^{\infty } \xi _{n} = \infty$.

Then the sequence $\{x_{n}\}$ defined by (3.1) converges strongly to $\hat{x} \in \Gamma$ which solves the variational inequality:

$$\begin{aligned} \langle f(\hat{x}) - \hat{x}, x - \hat{x} \rangle \le 0\quad \text {for all} \; x \in \Gamma . \end{aligned}$$

(3.2)

Proof

By Lemma 3.1, we have $\Gamma$ is closed and convex. It is easy to see that $P_{\Gamma }f$ is a $\tau$-contraction on $\Gamma$. Then by Banach fixed point theorem, $P_{\Gamma }f$ has unique fixed point $\hat{x} \in \Gamma$, i.e., $\hat{x} = P_{\Gamma }f(\hat{x})$. Hence $\hat{x}$ solves the variational inequality (3.2). We first show that $\{x_{n}\}$ is bounded. Since $\hat{x} \in \Gamma$, we obtain that $S_{i}(\hat{x}) = \{\hat{x}\}$ and $T_{i}(A\hat{x}) = \{A\hat{x}\}$ for all $i \in \mathbb {N}$. Applying Lemma 2.6, we have

$$\begin{aligned} \Vert y_{n} - \hat{x} \Vert ^{2}&= \left\| x_n + \sum _{i=1}^{n}\beta _{n,i}\gamma A^{*}(w_{n,i} - Ax_n) - \hat{x} \right\| ^{2} \nonumber \\&= \left\| \sum _{i=1}^{n}\beta _{n,i}( x_{n} - \hat{x} + \gamma A^{*}(w_{n,i} - Ax_n) ) \right\| ^{2} \nonumber \\&\le \sum _{i=1}^{n}\beta _{n,i} \Vert x_{n} - \hat{x} + \gamma A^{*}(w_{n,i} - Ax_n) \Vert ^{2} \nonumber \\&= \sum _{i=1}^{n}\beta _{n,i} \big ( \Vert x_{n} - \hat{x} \Vert ^{2} + \gamma ^{2} \Vert A^{*}(w_{n,i} - Ax_n) \Vert ^{2} \nonumber \\&\quad + 2\gamma \langle x_{n} - \hat{x}, A^{*}(w_{n,i} - Ax_n) \rangle \big ) \nonumber \\&\le \sum _{i=1}^{n}\beta _{n,i} \big ( \Vert x_{n} - \hat{x} \Vert ^{2} + \gamma ^{2} \Vert A\Vert ^2 \Vert w_{n,i} - Ax_n \Vert ^{2} \nonumber \\&\quad + 2\gamma \langle x_{n} - \hat{x}, A^{*}(w_{n,i} - Ax_n) \rangle \big ). \end{aligned}$$

(3.3)

Now we set

$$\begin{aligned} \mathcal {U}_{n} := 2\gamma \langle x_{n} - \hat{x}, A^{*}(w_{n,i} - Ax_n) \rangle . \end{aligned}$$

Since $T_{i}$ is $k_{i}^{\prime }$-demicontractive, then, by Lemma 2.5, we have

$$\begin{aligned} \mathcal {U}_{n}&= 2\gamma \langle A(x_{n} - \hat{x}), w_{n,i} - Ax_n \rangle \nonumber \\&= 2\gamma \langle A(x_{n} - \hat{x}) + (w_{n,i} - Ax_n) - (w_{n,i} - Ax_n), w_{n,i} - Ax_n \rangle \nonumber \\&= 2\gamma \left( \langle w_{n,i} - A\hat{x}, w_{n,i} - Ax_n \rangle - \Vert w_{n,i} - Ax_n \Vert ^{2} \right) \nonumber \\&\le 2\gamma \left( \frac{1+k_{i}^{\prime }}{2}\Vert w_{n,i} - Ax_n \Vert ^{2} - \Vert w_{n,i} - Ax_n \Vert ^{2} \right) \nonumber \\&= -(1 - k_{i}^{\prime })\gamma \Vert w_{n,i} - Ax_n \Vert ^{2}\nonumber \\&\le -(1 - k^{\prime })\gamma \Vert w_{n,i} - Ax_n \Vert ^{2}. \end{aligned}$$

(3.4)

By (3.3) and (3.4), we obtain

$$\begin{aligned} \Vert y_{n} - \hat{x} \Vert ^{2} \le \Vert x_{n} - \hat{x} \Vert ^{2} - \sum _{i=1}^{n}\beta _{n,i}\gamma (1 - k^{\prime } - \gamma \Vert A\Vert ^2)\Vert w_{n,i} - Ax_n\Vert ^{2}. \end{aligned}$$

Since $S_{i}$ is $k_{i}$-demicontractive and by using Lemma 2.6, we have

$$\begin{aligned} \Vert u_{n} - \hat{x} \Vert ^{2}&= \left\| \alpha _{n,0}y_n + \sum _{j=1}^{n}\alpha _{n,j}z_{n,j} - \hat{x} \right\| ^{2} \nonumber \\&\le \alpha _{n,0} \Vert y_{n} - \hat{x} \Vert ^{2} + \sum _{j=1}^{n}\alpha _{n,j}\Vert z_{n,j} - \hat{x} \Vert ^{2} - \sum _{j=1}^{n}\alpha _{n,0}\alpha _{n,j}\Vert y_{n} - z_{n,j} \Vert ^{2} \nonumber \\&= \alpha _{n,0} \Vert y_{n} - \hat{x} \Vert ^{2} + \sum _{j=1}^{n}\alpha _{n,j}d( z_{n,j}, S_{j}\hat{x} )^{2} - \sum _{j=1}^{n}\alpha _{n,0}\alpha _{n,j}\Vert y_{n} - z_{n,j} \Vert ^{2} \nonumber \\&\le \alpha _{n,0} \Vert y_{n} - \hat{x} \Vert ^{2} + \sum _{j=1}^{n}\alpha _{n,j}H( S_{j}y_{n}, S_{j}\hat{x} )^{2} - \sum _{j=1}^{n}\alpha _{n,0}\alpha _{n,j}\Vert y_{n} - z_{n,j} \Vert ^{2} \nonumber \\&\le \alpha _{n,0} \Vert y_{n} - \hat{x} \Vert ^{2} + \sum _{j=1}^{n}\alpha _{n,j}(\Vert y_{n} - \hat{x} \Vert ^{2} + k_{j}d(y_{n}, S_{j}y_{n})^{2})\nonumber \\&\quad - \sum _{j=1}^{n}\alpha _{n,0}\alpha _{n,j}\Vert y_{n} - z_{n,i} \Vert ^{2}\nonumber \\&\le \alpha _{n,0} \Vert y_{n} - \hat{x} \Vert ^{2} + \sum _{j=1}^{n}\alpha _{n,j}\Vert y_{n} - \hat{x} \Vert ^{2} + \sum _{j=1}^{n}\alpha _{n,j}k\Vert y_{n} - z_{n,j} \Vert ^{2}\nonumber \\&\quad - \sum _{j=1}^{n}\alpha _{n,0}\alpha _{n,j}\Vert y_{n} - z_{n,j} \Vert ^{2}\nonumber \\&= \Vert y_{n} - \hat{x} \Vert ^{2} - \sum _{j=1}^{n}(\alpha _{n,0} - k)\alpha _{n,j}\Vert y_{n} - z_{n,j}\Vert ^{2} \nonumber \\&\le \Vert y_{n} - \hat{x} \Vert ^{2} - (\alpha _{n,0} - k)\alpha _{n,i}\Vert y_{n} - z_{n,i}\Vert ^{2} \nonumber \\&\le \Vert x_{n} - \hat{x} \Vert ^{2} - \sum _{j=1}^{n}\beta _{n,j}\gamma (1 - k^{\prime } - \gamma \Vert A\Vert ^2)\Vert w_{n,j} - Ax_n\Vert ^{2} \nonumber \\&\quad - (\alpha _{n,0} - k)\alpha _{n,i}\Vert y_{n} - z_{n,i}\Vert ^{2} \end{aligned}$$

(3.5)

for all $1 \le i \le n$. It follows that $\Vert u_{n} - \hat{x} \Vert \le \Vert x_{n} - \hat{x}\Vert$. Thus, we have

$$\begin{aligned} \Vert x_{n+1} - \hat{x} \Vert&= \Vert \xi _{n}(f(x_{n}) - \hat{x}) + (1 - \xi _{n})(u_{n} - \hat{x}) \Vert \\&\le \xi _{n}\Vert f(x_{n}) - \hat{x} \Vert + (1-\xi _{n})\Vert u_{n} - \hat{x}\Vert \\&\le \xi _{n}( \Vert f(x_{n}) - f(\hat{x}) \Vert + \Vert f(\hat{x}) - \hat{x} \Vert ) + (1-\xi _{n})\Vert x_{n} - \hat{x}\Vert \\&\le \xi _{n}( \tau \Vert x_{n} - \hat{x} \Vert + \Vert f(\hat{x}) - \hat{x} \Vert ) + (1-\xi _{n})\Vert x_{n} - \hat{x}\Vert \\&= (1 - \xi _{n}(1-\tau )) \Vert x_{n} - \hat{x} \Vert + \xi _{n}(1-\tau ) \frac{\Vert f(\hat{x}) - \hat{x} \Vert }{1-\tau } \\&\le \max \left\{ \Vert x_{n} - \hat{x} \Vert , \frac{\Vert f(\hat{x}) - \hat{x} \Vert }{1-\tau } \right\} . \end{aligned}$$

By continuous taking this process, we obtain that

$$\begin{aligned} \Vert x_{n} - \hat{x} \Vert \le \max \left\{ \Vert x_{1} - \hat{x} \Vert , \frac{\Vert f(\hat{x}) - \hat{x} \Vert }{1-\tau } \right\} \end{aligned}$$

for all $n \in \mathbb {N}$. Therefore, $\{x_{n}\}$ is bounded. This implies that $\{f(x_{n})\}$ is also bounded. It follows from (3.5) that

$$\begin{aligned} \Vert x_{n+1} - \hat{x} \Vert ^{2}&= \Vert \xi _{n}(f(x_{n}) - \hat{x}) + (1 - \xi _{n})(u_{n} - \hat{x}) \Vert ^{2} \nonumber \\&\le \xi _{n} \Vert f(x_{n}) - \hat{x} \Vert ^{2} + (1 - \xi _{n}) \Vert u_{n} - \hat{x} \Vert ^{2} \nonumber \\&\le \xi _{n} \Vert f(x_{n}) - \hat{x} \Vert ^{2} + \Vert x_{n} - \hat{x} \Vert ^{2} \nonumber \\&\quad - \sum _{j=1}^{n}\beta _{n,j}\gamma (1 - k^{\prime } - \gamma \Vert A\Vert ^2)\Vert w_{n,j} - Ax_n\Vert ^{2} \nonumber \\&\quad - (\alpha _{n,0} - k)\alpha _{n,i}\Vert y_{n} - z_{n,i}\Vert ^{2} \end{aligned}$$

(3.6)

for all $1 \le i \le n$. By (3.6), we get the following two inequalities

$$\begin{aligned} \sum _{i=1}^{n}\beta _{n,i}\gamma (1 - k^{\prime } - \gamma \Vert A\Vert ^2)\Vert w_{n,i} - Ax_n\Vert ^{2}&\le \Vert x_{n} - \hat{x} \Vert ^{2} - \Vert x_{n+1} - \hat{x} \Vert ^{2} \nonumber \\&\quad + \xi _{n} \Vert f(x_{n}) - \hat{x} \Vert ^{2}, \end{aligned}$$

(3.7)

and

$$\begin{aligned} (\alpha _{n,0} - k)\alpha _{n,i}\Vert y_{n} - z_{n,i}\Vert ^{2}&\le \Vert x_{n} - \hat{x} \Vert ^{2} - \Vert x_{n+1} - \hat{x} \Vert ^{2} + \xi _{n} \Vert f(x_{n}) - \hat{x} \Vert ^{2} \end{aligned}$$

(3.8)

for all $1 \le i \le n$. Now we divide the rest of the proof into two cases.

Case 1. Assume that there exists $n_{0} \in \mathbb {N}$ such that $\{ \Vert x_{n} - \hat{x} \Vert \}_{n \ge n_{0}}$ is either nonincreasing or nondecreasing. Since $\{ \Vert x_{n} - \hat{x} \Vert \}$ is bounded, then it converges and $\Vert x_{n} - \hat{x} \Vert ^{2} - \Vert x_{n+1} - \hat{x} \Vert ^{2} \rightarrow 0$ as $n \rightarrow \infty$. Since $\xi _{n} \rightarrow 0$ as $n \rightarrow \infty$, then by (3.7) we deduce that

$$\begin{aligned} \lim _{n \rightarrow \infty } \sum _{i=1}^{n}\beta _{n,i}\Vert w_{n,i} - Ax_n\Vert ^{2} = 0. \end{aligned}$$

(3.9)

Since $\liminf _{n}\beta _{n,i} > 0$ for all $i \in \mathbb {N}$, then by (3.9) we have

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert w_{n,i} - Ax_n \Vert = 0 \end{aligned}$$

(3.10)

for all $i \in \mathbb {N}$. Similarly, in view of (3.8), since $\liminf _{n}(\alpha _{n,0}-k)\alpha _{n,i} > 0$ for $i \in \mathbb {N}$, we have

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert y_{n} - z_{n,i} \Vert = 0 \end{aligned}$$

(3.11)

for all $i \in \mathbb {N}$. From (3.9) and by using Lemma 2.6, we get

$$\begin{aligned} \Vert y_{n} - x_{n} \Vert ^{2}&= \gamma ^{2} \left\| \sum _{i=1}^{n}\beta _{n,i}A^{*}(w_{n,i} - Ax_n)\right\| ^{2} \nonumber \\&\le \gamma ^{2} \sum _{i=1}^{n}\beta _{n,i} \Vert A^{*}(w_{n,i} - Ax_n) \Vert ^{2} \nonumber \\&\le \gamma ^{2} \Vert A\Vert ^2\sum _{i=1}^{n}\beta _{n,i} \Vert w_{n,i} - Ax_n \Vert ^{2} ~\rightarrow 0 \end{aligned}$$

as $n \rightarrow \infty$, which implies that $\Vert y_{n} - x_{n} \Vert \rightarrow 0$ as $n \rightarrow \infty$. Next, we show that

$$\begin{aligned} \limsup _{n \rightarrow \infty } \langle f(\hat{x}) - \hat{x}, x_{n} - \hat{x} \rangle \le 0. \end{aligned}$$

To show this, let $\{x_{n_{j}}\}$ be a subsequence of $\{x_{n}\}$ such that

$$\begin{aligned} \lim _{j \rightarrow \infty }\langle f(\hat{x}) - \hat{x}, x_{n_{j}} - \hat{x} \rangle = \limsup _{n \rightarrow \infty }\langle f(\hat{x}) - \hat{x}, x_{n} - \hat{x} \rangle . \end{aligned}$$

Since $\{x_{n_{j}}\}$ is bounded, there exists a subsequence $\{x_{n_{j_{k}}}\}$ of $\{x_{n_{j}}\}$ and $x \in \mathcal {H}_{1}$ such that $x_{n_{j_{k}}} \rightharpoonup x$. Without loss of generality, we can assume that $x_{n_{j}} \rightharpoonup x$. Since $\Vert y_{n} - x_{n}\Vert \rightarrow 0$ as $n \rightarrow \infty$, we have $y_{n_{j}} \rightharpoonup x$. From (3.11) and by the demiclosedness of $I - S_{i}$ at zero for all $i \in \mathbb {N}$, we obtain that $x \in \bigcap _{i=1}^{\infty }Fix(S_{i})$. Since A is a bounded linear operator, we have $\langle y, Ax_{n_{j}} - Ax\rangle = \langle A^{*}y, x_{n_{j}} - x\rangle \rightarrow 0$ as $j \rightarrow \infty$, for all $y \in \mathcal {H}_{2}$, this implies that $Ax_{n_{j}} \rightharpoonup Ax$. From (3.10) and by the demiclosedness of $I - T_{i}$ at zero for all $i \in \mathbb {N}$, we get $Ax \in \bigcap _{i=1}^{\infty }Fix(T_{i})$. Therefore, $x \in \Gamma$. Since $\hat{x}$ satisfies the inequality (3.2), we have

$$\begin{aligned} \limsup _{n \rightarrow \infty } \langle f(\hat{x}) - \hat{x}, x_{n} - \hat{x} \rangle = \lim _{j \rightarrow \infty }\langle f(\hat{x}) - \hat{x}, x_{n_{j}} - \hat{x} \rangle = \langle f(\hat{x}) - \hat{x}, x - \hat{x} \rangle \le 0. \end{aligned}$$

By using Lemma 2.4, we have

$$\begin{aligned} \Vert x_{n+1} - \hat{x} \Vert ^{2}&= \Vert (1 - \xi _{n})(u_n - \hat{x}) + \xi _{n}(f(x_n) - \hat{x}) \Vert ^{2} \\&\le (1 - \xi _{n})^{2} \Vert u_n - \hat{x} \Vert ^{2} + 2\xi _{n} \langle f(x_{n}) - \hat{x}, x_{n+1} - \hat{x} \rangle \\&= (1 - \xi _{n})^{2} \Vert u_n - \hat{x} \Vert ^{2} + 2\xi _{n} \langle f(x_{n}) - f(\hat{x}), x_{n+1} - \hat{x} \rangle \\&\quad + 2\xi _{n} \langle f(\hat{x}) - \hat{x}, x_{n+1} - \hat{x} \rangle \\&\le (1 - \xi _{n})^{2} \Vert x_n - \hat{x} \Vert ^{2} + 2\xi _{n}\tau \Vert x_{n} - \hat{x}\Vert \Vert x_{n+1} - \hat{x} \Vert \\&\quad + 2\xi _{n} \langle f(\hat{x}) - \hat{x}, x_{n+1} - \hat{x} \rangle \\&\le (1 - \xi _{n})^{2} \Vert x_n - \hat{x} \Vert ^{2} + \xi _{n}\tau ( \Vert x_{n} - \hat{x}\Vert ^{2} + \Vert x_{n+1} - \hat{x} \Vert ^{2})\\&\quad + 2\xi _{n} \langle f(\hat{x}) - \hat{x}, x_{n+1} - \hat{x} \rangle . \end{aligned}$$

Thus,

$$\begin{aligned} \Vert x_{n+1} - \hat{x} \Vert ^{2}&\le \frac{(1 - \xi _{n})^{2} + \xi _{n}\tau }{1 - \xi _{n}\tau } \Vert x_n - \hat{x} \Vert ^{2} + \frac{2\xi _{n}}{1 - \xi _{n}\tau } \langle f(\hat{x}) - \hat{x}, x_{n+1} - \hat{x} \rangle \nonumber \\&= \left( 1 - \frac{(1-\tau )\xi _{n}}{1 - \xi _{n}\tau }\right) \Vert x_n - \hat{x} \Vert ^{2} + \frac{(\xi _{n} - (1-\tau ))\xi _{n}}{1 - \xi _{n}\tau }\Vert x_n - \hat{x} \Vert ^{2} \nonumber \\&\quad + \frac{2\xi _{n}}{1 - \xi _{n}\tau } \langle f(\hat{x}) - \hat{x}, x_{n+1} - \hat{x} \rangle \nonumber \\&\le \left( 1 - \frac{(1-\tau )\xi _{n}}{1 - \xi _{n}\tau }\right) \Vert x_n - \hat{x} \Vert ^{2} \nonumber \\&\quad +\frac{(1-\tau )\xi _{n}}{1 - \xi _{n}\tau } \left\{ \left( \frac{\xi _{n}}{1 - \tau } - 1 \right) M + \frac{2}{1 - \tau } \langle f(\hat{x}) - \hat{x}, x_{n+1} - \hat{x} \rangle \right\} \nonumber \\&= (1-\lambda _{n})\Vert x_n - \hat{x} \Vert ^{2} + \lambda _{n}\sigma _{n}, \end{aligned}$$

(3.12)

where $M = \sup \{ \Vert x_n - \hat{x} \Vert ^{2} : n \in \mathbb {N} \}$, $\lambda _{n} = \frac{(1-\tau )\xi _{n}}{1 - \xi _{n}\tau }$, and $\sigma _{n} = \left( \frac{\xi _{n}}{1 - \tau } - 1 \right) M + \frac{2}{1 - \tau } \langle f(\hat{x}) - \hat{x}, x_{n+1} - \hat{x} \rangle$. Clearly, $\{\lambda _{n}\} \subset [0, 1]$, $\sum _{n=1}^{\infty } \lambda _{n} = \infty$ and $\limsup _{n}\sigma _{n} \le 0$. From (3.12) and by applying Lemma 2.7, we can conclude that $x_{n} \rightarrow \hat{x}$ as $n \rightarrow \infty$.

Case 2. Suppose that $\{ \Vert x_{n} - \hat{x} \Vert \}$ is not a monotone sequence. Then there exists a subsequence $\{n_{l}\}$ of $\{n\}$ such that $\Vert x_{n_{l}} - \hat{x} \Vert < \Vert x_{n_{l}+1} - \hat{x} \Vert$ for all $l \in \mathbb {N}$. Now we define a positive interger sequence $\{\rho (n)\}$ by

$$\begin{aligned} \rho (n) := \max \{ k \le n : \Vert x_{k} - \hat{x} \Vert < \Vert x_{k+1} - \hat{x} \Vert \} \end{aligned}$$

for all $n \ge n_{0}$ (for some $n_{0}$ large enough). By Lemma 2.8, we have $\{\rho (n)\}$ is a nondecreasing sequence such that $\rho (n) \rightarrow \infty$ as $n \rightarrow \infty$ and

$$\begin{aligned} \Vert x_{\rho (n)} - \hat{x} \Vert ^{2} - \Vert x_{\rho (n)+1} - \hat{x} \Vert ^{2} \le 0 \end{aligned}$$

for all $n \ge n_{0}$. From (3.7), we obtain that

$$\begin{aligned} \lim _{n \rightarrow \infty } \sum _{i=1}^{\rho (n)}\beta _{\rho (n),i}\Vert w_{\rho (n),i} - Ax_{\rho (n)} \Vert ^{2} = 0 \end{aligned}$$

(3.13)

and

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert w_{\rho (n),i} - Ax_{\rho (n)} \Vert = 0 \end{aligned}$$

(3.14)

for all $i \in \mathbb {N}$. From (3.8), we have

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert y_{\rho (n)} - z_{\rho (n),i}\Vert = 0 \end{aligned}$$

(3.15)

for all $i \in \mathbb {N}$. By using (3.13)–(3.15)

and by the same proof as in case 1, we obtain that

$$\begin{aligned} \limsup _{n \rightarrow \infty } \langle f(\hat{x}) - \hat{x}, x_{\rho (n)} - \hat{x} \rangle \le 0. \end{aligned}$$

By the same computation as in case 1, we deduce that

$$\begin{aligned} \Vert x_{\rho (n)+1} - \hat{x} \Vert ^{2} \le (1-\lambda _{\rho (n)})\Vert x_{\rho (n)} - \hat{x} \Vert ^{2} + \lambda _{\rho (n)}\sigma _{\rho (n)}, \end{aligned}$$

where $\lambda _{\rho (n)} = \frac{(1-\tau )\xi _{\rho (n)}}{1 - \xi _{\rho (n)}\tau }$, $\sigma _{\rho (n)} = \left( \frac{\xi _{\rho (n)}}{1 - \tau } - 1 \right) M + \frac{2}{1 - \tau } \langle f(\hat{x}) - \hat{x}, x_{\rho (n)+1} - \hat{x} \rangle$ and $M = \sup \{ \Vert x_{\rho (n)} - \hat{x} \Vert ^{2} : n \in \mathbb {N} \}$. By utilizing Lemma 2.7, we obtain that $\Vert x_{\rho (n)} - \hat{x} \Vert \rightarrow 0$ as $n \rightarrow \infty$. It follows from Lemma 2.8 that

$$\begin{aligned} 0 \le \Vert x_{n} - \hat{x} \Vert \le \Vert x_{\rho (n)+1} - \hat{x} \Vert \rightarrow 0 \end{aligned}$$

as $n \rightarrow \infty$. Hence $\{x_{n}\}$ converges strongly to $\hat{x}$. This completes the proof.$\square$

Remark 3.3

We have the following notices of Theorem 3.2.

• (i) By taking $f \equiv u$ for some $u \in \mathcal {H}_{1}$, then the algorithm (3.1) becomes the Halpern-type algorithm. In particular, if $u = 0$, then $\{x_{n}\}$ converges strongly to $\hat{x} \in \Gamma$, where $\Vert \hat{x}\Vert = \min \{ \Vert x\Vert : x \in \Gamma \}$.

• (ii) The assumption “for each $p \in \Gamma$, $S_{i}(p) = \{p\}$ and $T_{i}(Ap) = \{Ap\}$ for all $i \in \mathbb {N}$” is weaker than the statement “$\{S_{i}\}_{i=1}^{\infty }$ and $\{T_{i}\}_{i=1}^{\infty }$ satisfies the common endpoint condition”.

By properties of the best approximation operator, we obtain the following result.

Corollary 3.4

Let $\mathcal {H}_{1}$ and $\mathcal {H}_{2}$ be two real Hilbert spaces, $A : \mathcal {H}_1 \rightarrow \mathcal {H}_2$ be a bounded linear operator. For each $i \in \mathbb {N}$, let $S_{i} : \mathcal {H}_{1} \rightarrow P(\mathcal {H}_{1})$ and $T_{i} : \mathcal {H}_2 \rightarrow P(\mathcal {H}_2)$ be multivalued mappings such that $P_{S_{i}}$ and $P_{T_{i}}$ are multivalued demicontractive mappings with constants $k_{i}$ and $k_{i}^{\prime }$, respectively. Suppose that $I - P_{S_{i}}$ and $I - P_{T_{i}}$ are demiclosed at zero for all $i \in \mathbb {N}$. Assume that $\Gamma \ne \emptyset$. Let $f : \mathcal {H}_{1} \rightarrow \mathcal {H}_{1}$ be a $\tau$-contraction with respect to $\Gamma$, where $0 \le \tau < 1$. Let $\{x_n\} \subset \mathcal {H}_1$ be a sequence generated by $x_{1} \in \mathcal {H}_{1}$ and

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n = x_n + \sum \nolimits _{i=1}^{n}\beta _{n,i}\gamma A^{*}(w_{n,i} - Ax_n),\\ u_n = \alpha _{n,0}y_n + \sum \nolimits _{i=1}^{n}\alpha _{n,i}z_{n,i},\\ x_{n+1} = \xi _{n}f(x_n) + (1 - \xi _{n})u_n, \quad n \in \mathbb {N}, \end{array}\right. } \end{aligned}$$

(3.16)

where $z_{n,i} \in P_{S_{i}}(y_n)$, $w_{n,i} \in P_{T_{i}}(Ax_{n})$, the parameter $\gamma$, and the sequences $\{\alpha _{n,i}\}$, $\{\beta _{n,i}\}$ and $\{\xi _{n}\}$ satisfy (C1)–(C4) in Theorem 3.2. Then the sequence $\{x_{n}\}$ defined by (3.16) converges strongly to $\hat{x} \in \Gamma$ which solves the variational inequality (3.2).

Proof

Since $P_{S_{i}}$ and $P_{T_{i}}$ satisfy the end point condition, and $Fix(S_{i}) = Fix(P_{S_{i}})$ and $Fix(T_{i}) = Fix(P_{T_{i}})$ for all $i \in \mathbb {N}$, so the result is obtained directly by Theorem 3.2. $\square$

The following result for solving the SCFP for multivalued quasi-nonexpansive mappings is a consequence of Theorem 3.2.

Corollary 3.5

Let $\mathcal {H}_{1}$ and $\mathcal {H}_{2}$ be two real Hilbert spaces, $A : \mathcal {H}_1 \rightarrow \mathcal {H}_2$ be a bounded linear operator. For each $i \in \mathbb {N}$, let $S_{i} : \mathcal {H}_{1} \rightarrow CB(\mathcal {H}_{1})$ and $T_{i} : \mathcal {H}_2 \rightarrow CB(\mathcal {H}_2)$ be multivalued quasi-nonexpansive mappings such that $I - S_{i}$ and $I - T_{i}$ are demiclosed at zero. Suppose that $\Gamma \ne \emptyset$ and for each $p \in \Gamma$, $S_{i}(p) = \{p\}$ and $T_{i}(Ap) = \{Ap\}$ for all $i \in \mathbb {N}$. Let $f : \mathcal {H}_{1} \rightarrow \mathcal {H}_{1}$ be a $\tau$-contraction with respect to $\Gamma$, where $0 \le \tau < 1$. Let $\{x_n\} \subset \mathcal {H}_1$ be a sequence generated by $x_{1} \in \mathcal {H}_{1}$ and

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n = x_n + \sum \nolimits _{i=1}^{n}\beta _{n,i}\gamma A^{*}(w_{n,i} - Ax_n),\\ u_n = \alpha _{n,0}y_n + \sum \nolimits _{i=1}^{n}\alpha _{n,i}z_{n,i},\\ x_{n+1} = \xi _{n}f(x_n) + (1 - \xi _{n})u_n,\quad n \in \mathbb {N}, \end{array}\right. } \end{aligned}$$

(3.17)

where $z_{n,i} \in S_{i}y_n$, $w_{n,i} \in T_{i}(Ax_{n})$, the parameter $\gamma$, and the sequences $\{\alpha _{n,i}\}_{n=1}^{\infty }$ for all $i \ge 0$, $\{\beta _{n,i}\}_{n=1}^{\infty }$ for all $i \in \mathbb {N}$ and $\{\xi _{n}\}_{n=1}^{\infty }$ satisfy the following conditions:

• (C1) $\gamma \in \left( 0,\frac{1}{\Vert A\Vert ^2}\right)$;

• (C2) $\alpha _{n,i} \in [0, 1)$ such that $\alpha _{n,i} \ne 0$ for all $i \le n$, $\liminf _{n}\alpha _{n,0}\alpha _{n,i} > 0$ for all $i \in \mathbb {N}$, and $\sum _{i=0}^{n}\alpha _{n,i} = 1$;

• (C3) $\beta _{n,i} \in [0, 1]$ such that $\beta _{n,i} \ne 0$ for all $i \le n$, $\liminf _{n}\beta _{n,i} > 0$ for all $i \in \mathbb {N}$, and $\sum _{i=1}^{n}\beta _{n,i} = 1$;

• (C4) $\xi _{n} \in (0, 1)$ such that $\lim _{n \rightarrow \infty } \xi _{n} = 0$ and $\sum _{n=1}^{\infty } \xi _{n} = \infty$.

Then the sequence $\{x_{n}\}$ defined by (3.17) converges strongly to $\hat{x} \in \Gamma$ which solves the variational inequality (3.2).

If $S_{i}$ and $T_{i}$ in Theorem 3.2 are single-valued mappings, we obtain the following result to solve the SCFP for two infinite families of single-valued demicontractive mappings.

Corollary 3.6

Let $\mathcal {H}_{1}$ and $\mathcal {H}_{2}$ be two real Hilbert spaces, $A : \mathcal {H}_1 \rightarrow \mathcal {H}_2$ be a bounded linear operator. For each $i \in \mathbb {N}$, let $S_{i} : \mathcal {H}_{1} \rightarrow \mathcal {H}_{1}$ and $T_{i} : \mathcal {H}_2 \rightarrow \mathcal {H}_2$ be demicontractive mappings with constants $k_{i}$ and $k_{i}^{\prime }$, respectively, such that $I - S_{i}$ and $I - T_{i}$ are demiclosed at zero. Suppose that $\Gamma \ne \emptyset$. Let $f : \mathcal {H}_{1} \rightarrow \mathcal {H}_{1}$ be a $\tau$-contraction with respect to $\Gamma$, where $0 \le \tau < 1$. Let $\{x_n\} \subset \mathcal {H}_1$ be a sequence generated by $x_{1} \in \mathcal {H}_{1}$ and

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n = x_n + \sum \nolimits _{i=1}^{n}\beta _{n,i}\gamma A^{*}(T_{i} - I)Ax_{n},\\ u_n = \alpha _{n,0}y_n + \sum \nolimits _{i=1}^{n}\alpha _{n,i}S_{i}y_n,\\ x_{n+1} = \xi _{n}f(x_n) + (1 - \xi _{n})u_n,\quad n \in \mathbb {N}, \end{array}\right. } \end{aligned}$$

(3.18)

where the parameter $\gamma$, and the sequences $\{\alpha _{n,i}\}$, $\{\beta _{n,i}\}$ and $\{\xi _{n}\}$ satisfy (C1)–(C4) in Theorem 3.2. Then the sequence $\{x_{n}\}$ defined by (3.18) converges strongly to $\hat{x} \in \Gamma$ which solves the variational inequality (3.2).

4 Applications

4.1 The split variational inequality problem

Let K be a nonempty closed convex subset of $\mathcal {H}$, and let $F : \mathcal {H} \rightarrow \mathcal {H}$ be a mapping. Recall that the variational inequality problem is to find a point $x^{*} \in K$ such that

$$\begin{aligned} \langle Fx^{*}\!, y - x^{*} \rangle \ge 0 \quad \text {for all}\; y \in K. \end{aligned}$$

(4.1)

The solution set of the problem (4.1) is denoted by VIP(K, F). It is not difficult to show that $Fix(P_{K}(I-\lambda F)) = VIP(K, F)$, where $\lambda > 0$. It was shown [15] that if F is $\delta$-inverse strongly monotone, where $\delta > 0$, i.e.,

$$\begin{aligned} \langle x - y, Fx - Fy \rangle \ge \delta \Vert Fx - Fy \Vert ^{2} \quad \text {for all} \; x, y \in \mathcal {H}, \end{aligned}$$

and $\lambda \in (0, 2\delta )$, then $P_{K}(I - \lambda F)$ is a nonexpansive mapping and $I - P_{K}(I - \lambda F)$ is demiclosed at zero.

Let $\mathcal {H}_{1}$ and $\mathcal {H}_{2}$ be two real Hilbert spaces, $A : \mathcal {H}_1 \rightarrow \mathcal {H}_2$ be a bounded linear operator. Given nonempty closed convex subsets $C \subseteq \mathcal {H}_{1}$ and $Q \subseteq \mathcal {H}_{2}$, and mappings $g : \mathcal {H}_{1} \rightarrow \mathcal {H}_{1}$ and $h : \mathcal {H}_{2} \rightarrow \mathcal {H}_{2}$. The split variational inequality problem (SVIP) is to find a point $x^{*} \in C$ such that

$$\begin{aligned} x^{*} \in VIP(C, g) \quad \text {and} \quad Ax^{*} \in VIP(Q, h). \end{aligned}$$

(4.2)

We obtain the following result which extends [16, Theorem 5.1].

Theorem 4.1

Let $\mathcal {H}_{1}$ and $\mathcal {H}_{2}$ be two real Hilbert spaces, $A : \mathcal {H}_1 \rightarrow \mathcal {H}_2$ be a bounded linear operator. For each $i \in \mathbb {N}$, let $C_{i}$ and $Q_{i}$ be nonempty closed convex subsets of $\mathcal {H}_{1}$ and $\mathcal {H}_{2}$, respectively, and let $g_{i} : \mathcal {H}_{1} \rightarrow \mathcal {H}_{1}$ and $h_{i} : \mathcal {H}_2 \rightarrow \mathcal {H}_2$ be inverse strongly monotone operators with constants $\delta _{i}$ and $\delta _{i}^{\prime }$, respectively. Assume that $\Theta := \left\{ x \in \bigcap _{i=1}^{\infty }VIP(C_{i}, g_{i}) : Ax \in \bigcap _{i=1}^{\infty }VIP(Q_{i}, h_{i}) \right\} \ne \emptyset$. Let $f : \mathcal {H}_{1} \rightarrow \mathcal {H}_{1}$ be a contraction with respect to $\Theta$. Let $\{x_n\} \subset \mathcal {H}_1$ be a sequence generated by $x_{1} \in \mathcal {H}_{1}$ and

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n = x_n + \sum \nolimits _{i=1}^{n}\beta _{n,i}\gamma A^{*}(P_{Q_{i}}(I - \lambda h_{i}) - I)Ax_{n},\\ u_n = \alpha _{n,0}y_n + \sum \nolimits _{i=1}^{n}\alpha _{n,i}P_{C_{i}}(I - \lambda g_{i}) y_n,\\ x_{n+1} = \xi _{n}f(x_n) + (1 - \xi _{n})u_n,\quad n \in \mathbb {N}, \end{array}\right. } \end{aligned}$$

(4.3)

where $\lambda \in (0, 2\delta )$ with $\delta := \inf \{\delta _{i}, \delta _{i}^{\prime } : i \in \mathbb {N}\}$, the parameter $\gamma$, and the sequences $\{\alpha _{n,i}\}$, $\{\beta _{n,i}\}$ and $\{\xi _{n}\}$ satisfy (C1)–(C4) in Corollary 3.5. Then the sequence $\{x_{n}\}$ defined by (4.3) converges strongly to $x^{*} \in \Theta$, where $x^{*}$ is the unique fixed point of a contraction $P_{\Theta }f$.

4.2 The split common null point problem

Byrne et al. [5] introduced and studied the split common null point problem (SCNP) as follows: Given two multivalued mappings $B_{1} : \mathcal {H}_{1} \rightarrow 2^{\mathcal {H}_{1}}$ and $B_{2} : \mathcal {H}_{2} \rightarrow 2^{\mathcal {H}_{2}}$, a bounded linear operator $A : \mathcal {H}_{1} \rightarrow \mathcal {H}_{2}$, the SCNP for two multivalued mappings is to find a point $x^{*} \in \mathcal {H}_1$ such that

$$\begin{aligned} x^{*} \in B_{1}^{-1}0 \quad \text {and} \quad Ax^{*} \in B_{2}^{-1}0, \end{aligned}$$

(4.4)

where $B_{1}^{-1}0 := \{ x \in \mathcal {H}_1 : 0 \in B_{1}x \}$ and $B_{2}^{-1}0$ are null point sets of $B_{1}$ and $B_{2}$, respectively. Byrne et al. [5] proposed algorithms and proved convergence theorems for finding such a solution of the SCNP (4.4) when $B_{1}$ and $B_{2}$ are maximal monotone operators.

Let us recall the maximal monotone operator: Let B be a multivalued mapping of $\mathcal {H}$ into $2^{\mathcal {H}}\!$, then B is called a maximal monotone operator if B is monotone, i.e.,

$$\begin{aligned} \langle x - y, u - v \rangle \ge 0 \quad \text {for all} \quad x,y \in D(B), u \in Bx, v \in By, \end{aligned}$$

where $D(B) := \{ x \in \mathcal {H} : Bx \ne \emptyset \}$, and the graph G(B) of B,

$$\begin{aligned} G(B) := \{ (x, u) \in \mathcal {H} \times \mathcal {H} : u \in Bx \}, \end{aligned}$$

is not properly contained in the graph of any other monotone operator. For a maximal monotone operator $B : \mathcal {H} \rightarrow 2^{\mathcal {H}}$ and $\lambda > 0$, the resolvent of B with parameter $\lambda$ is denoted and defined by

$$\begin{aligned} J_{\lambda }^{B} := ( I + \lambda B)^{-1}: \mathcal {H} \rightarrow D(B). \end{aligned}$$

It is known [4] that if $B : \mathcal {H} \rightarrow 2^{\mathcal {H}}$ is a maximal monotone operator and $\lambda > 0$, then $J_{\lambda }^{B}$ is single-valued, firmly nonexpansive, that is,

$$\begin{aligned} \Vert J_{\lambda }^{B}x - J_{\lambda }^{B}y \Vert ^{2} \le \Vert x - y \Vert ^{2} - \Vert x - J_{\lambda }^{B}x\Vert ^{2} \quad \text {for all} \quad x, y \in \mathcal {H}, \end{aligned}$$

and $Fix(J_{\lambda }^{B}) = B^{-1}0$. Moreover, $I - J_{\lambda }^{B}$ is demiclosed at zero.

By applying Theorem 3.2 and properties of the resolvent of maximal monotone operators, we obtain the following theorem.

Theorem 4.2

Let $\mathcal {H}_{1}$ and $\mathcal {H}_{2}$ be two real Hilbert spaces, $A : \mathcal {H}_1 \rightarrow \mathcal {H}_2$ be a bounded linear operator. Let $B_{1} : \mathcal {H}_{1} \rightarrow 2^{\mathcal {H}_{1}}$ and $B_{2} : \mathcal {H}_{2} \rightarrow 2^{\mathcal {H}_{2}}$ be maximal monotone operators, and let $J_{\lambda _{1}}^{B_{1}}$ and $J_{\lambda _{2}}^{B_{2}}$ be resolvents of $B_{1}$ and $B_{2}$, respectively for $\lambda _{1}, \lambda _{2} > 0$. For each $i \in \mathbb {N}$, let $S_{i} : \mathcal {H}_{1} \rightarrow CB(\mathcal {H}_{1})$ and $T_{i} : \mathcal {H}_2 \rightarrow CB(\mathcal {H}_2)$ be multivalued demicontractive mappings with constants $k_{i}$ and $k_{i}^{\prime }$, respectively, such that $I - S_{i}$ and $I - T_{i}$ are demiclosed at zero. Assume that $\Theta := \Gamma \cap \Omega \ne \emptyset$, where $\Gamma = \left\{ x \in \bigcap _{i=1}^{\infty }Fix(S_{i}) : Ax \in \bigcap _{i=1}^{\infty }Fix(T_{i}) \right\}$ and $\Omega = \left\{ x \in B_{1}^{-1}0 : Ax \in B_{2}^{-1}0 \right\}$, and for each $p \in \Theta$, $S_{i}(p) = \{p\}$ and $T_{i}(Ap) = \{Ap\}$ for all $i \in \mathbb {N}$. Let $f : \mathcal {H}_{1} \rightarrow \mathcal {H}_{1}$ be a contraction with respect to $\Theta$. Let $\{x_n\} \subset \mathcal {H}_1$ be a sequence generated by $x_{1} \in \mathcal {H}_{1}$ and

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n = x_n + \gamma \big ( \beta _{n-1,0}A^{*}( J_{\lambda _{1}}^{B_{1}} - I) Ax_{n} + \sum \nolimits _{i=1}^{n-1}\beta _{n-1,i} A^{*}( w_{n,i} - Ax_{n})\big ),\\ u_n = \alpha _{n-1}y_n + \alpha _{n-1,0}J_{\lambda _{2}}^{B_{2}}y_{n} + \sum \nolimits _{i=1}^{n-1}\alpha _{n-1,i}z_{n,i},\\ x_{n+1} = \xi _{n}f(x_{n}) + (1 - \xi _{n})u_n,\quad n \in \mathbb {N}, \end{array}\right. } \end{aligned}$$

(4.5)

where $z_{n,i} \in S_{i}y_n$, $w_{n,i} \in T_{i}(Ax_{n})$, the parameter $\gamma$, and the sequences $\{\alpha _{n}\}_{n=0}^{\infty }$, $\{\alpha _{n,i}\}_{n=0}^{\infty }$, $\{\beta _{n,i}\}_{n=0}^{\infty }$ for all $i \ge 0$, and $\{\xi _{n}\}_{n=1}^{\infty }$ satisfy the following conditions:

• (C1) $\gamma \in \left( 0,\frac{1 - k^{\prime }}{\Vert A\Vert ^2}\right)$, where $k^{\prime } = \sup \{k_{i}^{\prime } : i \in \mathbb {N} \}$;

• (C2) $\alpha _{n} \in (k, 1)$ where $k = \sup \{k_{i} : i \in \mathbb {N} \}$ and $\alpha _{n,i} \in [0, 1)$ such that $\alpha _{n,i} \ne 0$ for all $i \le n$, $\liminf _{n}(\alpha _{n}-k)\alpha _{n,i} > 0$ for all $i \in \mathbb {N}$, and $\alpha _{n} + \sum _{i=0}^{n}\alpha _{n,i} = 1$;

• (C3) $\beta _{n,i} \in [0, 1]$ such that $\beta _{n,i} \ne 0$ for all $i \le n$, $\liminf _{n}\beta _{n,i} > 0$ for all $i \ge 0$, and $\sum _{i=0}^{n}\beta _{n,i} = 1$;

• (C4) $\xi _{n} \in (0, 1)$ such that $\lim _{n \rightarrow \infty } \xi _{n} = 0$ and $\sum _{n=1}^{\infty } \xi _{n} = \infty$.

Then the sequence $\{x_{n}\}$ defined by (4.5) converges strongly to $x^{*} \in \Theta$, where $x^{*}$ is the unique fixed point of a contraction $P_{\Theta }f$.

Proof

We set $S_{0} := J_{\lambda _{1}}^{B_{1}}$ and $T_{0} := J_{\lambda _{2}}^{B_{2}}$. Then $S_{0}$ and $T_{0}$ are single-valued mappings. By properties of the resolvent of maximal monotone operators, we have $S_{0}$ and $T_{0}$ are 0-demicontractive, $I - S_{0}$ and $I - T_{0}$ are demiclosed at zero, $Fix(S_{0}) = B_{1}^{-1}0$ and $Fix(T_{0}) = B_{2}^{-1}0$. Thus,

$$\begin{aligned} \Theta = \left\{ x \in \bigcap _{i=0}^{\infty }Fix(S_{i}) : Ax \in \bigcap _{i=0}^{\infty }Fix(T_{i}) \right\} . \end{aligned}$$

Therefore, we can conclude from Theorem 3.2 that $\{x_{n}\}$ defined by (4.5) converges strongly to $x^{*} \in \Theta$, where $x^{*}$ is the unique fixed point of a contraction $P_{\Theta }f$. $\square$

5 A numerical example

In this section, we give a numerical result to demonstrate the convergence of our algorithm in Theorem 3.2.

Example 5.1

Let $\mathcal {H}_1 = \mathbb {R} = \mathcal {H}_2$. For each $i \in \mathbb {N}$, we define multivalued mappings $S_{i}$ and $T_{i}$ as follows:

$$\begin{aligned} S_{i}x = {\left\{ \begin{array}{ll} \{0\}, \quad &{}\text {if}\; x < 0,\\ \big [ \frac{x}{i+1}, x \big ], \quad &{}\text {if}\; x \ge 0,\\ \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} T_{i}x =\left\{ \begin{array}{ll} \big [ 0, \frac{|x|}{i+2} \big ], \quad &{}\text {if}\; x < i+2,\\ {[} 1, i+1 ], &{}\text {if}\; x \ge i+2.\\ \end{array}\right. \end{aligned}$$

It is not difficult to show that $S_{i}$ and $T_{i}$ are 0-demicontractive, and $I - S_{i}$ and $I - T_{i}$ are demiclosed at zero for all $i \in \mathbb {N}$. We also define a bouned linear operator $A: \mathbb {R} \rightarrow \mathbb {R}$ by $Ax = 3x$. Thus, $A^{*}x = 3x$ and $\Vert A\Vert = 3$. It is clear that $0 \in \Gamma$, where $\Gamma = \big \{ x \in \bigcap _{i=1}^{\infty }Fix(S_{i}) : Ax \in \bigcap _{i=1}^{\infty }Fix(T_{i}) \big \}$. For each $n \in \mathbb {N}$, $i \ge 0$, let

$$\begin{aligned} \alpha _{n,i} = {\left\{ \begin{array}{ll} \frac{1}{2^{i+1}}\big ( \frac{n}{n+1} \big ), \quad &{}\text {if}\; n > i,\\ 1 - \frac{n}{n+1}\left( \sum _{k=1}^{n}\frac{1}{2^{k}}\right) , &{} \text {if}\; n = i,\\ 0, &{}\text {otherwise}.\\ \end{array}\right. } \end{aligned}$$

Table 1 Numerical experiment of the algorithm (5.1)

Fig. 1

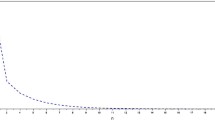
A gragh of error of the algorithm (5.1)

For each $n, i \in \mathbb {N}$, we let $\beta _{n,i} = \alpha _{n-1,i-1}$. It is easy to see that $\lim _{n \rightarrow \infty }\alpha _{n,i} = \frac{1}{2^{i+1}}$, $\lim _{n \rightarrow \infty }\beta _{n,i} = \frac{1}{2^{i}}$ and $\sum _{i=0}^{n}\alpha _{n,i} = 1 = \sum _{i=1}^{n}\beta _{n,i}$. Put $\gamma = \frac{1}{18}, \xi _{n} = \frac{1}{4500n}$ and let a contraction $f : \mathbb {R} \rightarrow \mathbb {R}$ be such that $f(x) = \frac{1}{2}$, then all conditions of Theorem 3.2 hold. Taking

$$\begin{aligned} z_{n,i} = {\left\{ \begin{array}{ll} 0, \quad &{}\text {if}\; y_{n}< 0,\\ \frac{2y_{n}}{i+1}, &{}\text {if}\; y_{n} \ge 0,\\ \end{array}\right. }\quad w_{n,i} = {\left\{ \begin{array}{ll} \frac{|3x_{n}|}{2i+4} , &{}\text {if}\; 3x_{n} < i+2,\\ 1, &{}\text {if}\; 3x_{n} \ge i+2,\\ \end{array}\right. } \end{aligned}$$

then an algorithm (3.1) becomes

$$\begin{aligned} x_{n+1} = \frac{1}{9000n} + \left( 1 - \frac{1}{4500n}\right) \left\{ \frac{n}{2n+2} \left( y_{n} - z_{n,n} + \sum _{i=1}^{n-1}\frac{1}{2^{i}}(z_{n,i}-z_{n,n}) \right) + z_{n,n} \right\} , \end{aligned}$$

(5.1)

where $y_n = \frac{1}{6}\left( 3x_{n} + w_{n,n} + \big ( \frac{n-1}{n}\big ) \sum _{i=1}^{n-1}\frac{1}{2^{i}}(w_{n,i} - w_{n,n}) \right)$, $n \in \mathbb {N}$. We first start with the initial point $x_{1} = 2$. The stopping criterion for our testing method is taken as: $|x_{n+1}-x_{n}| < 10^{-6}$. Now, a convergence of the algorithm (5.1) is shown by Table 1 and Fig. 1. It is observed that $x_{n} \rightarrow 0 \in \Gamma$.