This paper reports on a study exploring the use of an elastic strip (Fig. 1), which can be viewed as a flexible number line, and acts as a manipulative for supporting and extending fraction concepts. It reports on teaching experiments that investigated the effectiveness of the elastic strip to challenge and give support to developing the content knowledge and pedagogical content knowledge of prospective elementary teachers.

Fig. 1
figure 1

Elastic strip divided into 10 intervals being used to find 7/9 of length of a table

Full size image

Literature shows that that the teaching of fractions in elementary schools is difficult and that many teachers and prospective teachers have weak personal content knowledge of the topic. Research literature about mathematical understanding and the importance of teacher subject content and teaching knowledge is reviewed broadly before looking at the specific topic of teaching and learning about fractions from the perspectives of teachers, prospective teachers, and children. The use of manipulatives in teaching mathematics, firstly in general and then specifically in the context of teaching fractions, is described before discussing the specific model of the number line.

Mathematical understanding

Skemp (1976) argued that the word “understanding” is used in two quite different ways: instrumental understanding is characterised by uncritical use of rules and procedures based on the authority of an outside source such as a textbook or teacher, whereas a learner acquires relational understanding by adapting their own schema for the concept. Relational understanding has the potential for organic growth and is associated with depth of understanding and the ability to apply knowledge in novel situations (Skemp 1976, 1979). Relational mathematical understanding develops from physical and image-based experiences through cycles of acting and expressing and may lead to formalisations that enable the learner to reason in ways which appear independent of the physical or image-based experiences (Pirie and Kieren 1994). The understanding developed at each level provides the basis for new mental actions which are consolidated by expressing new understanding, either mentally or to others (Pirie and Kieren 1994).

Variation theory posits that such learning is potentially enhanced when the learner is exposed to, and perceives, variation in one factor while other factors are considered to be constant. The different aspects of a topic that become the focus for variation enable different possibilities for learning (Marton et al. 2004; Runesson 2005, 2006).

Mathematical knowledge for teaching

The exposition of the knowledge that is needed for effective teaching is a comparatively recent field: “[w]ith few exceptions, research of teachers’ subject matter knowledge (level, organisation, and understanding) has been alluded to but not studied” (Leinhardt and Smith 1985, p. 248). Shulman’s (1986) introduction of the term pedagogical content knowledge (PCK) as the specialist knowledge of content and of teaching that content, which differs from the knowledge held by non-experts, has stimulated mathematics educators to explore the nature of PCK required for effective mathematics teaching and the impact of that knowledge on student achievement. In this vein, mathematical knowledge for teaching (MKT) has been defined as “the mathematical knowledge used to carry out the work of teaching mathematics” (Hill et al. 2005, p. 373) such as introducing concepts, interpreting and responding to student work, and contributing to discussion. Studies of mathematics teaching in the USA have shown MKT is an important factor in lesson quality and student achievement in the junior elementary school (Hill et al. 2005) and in the middle school (Tchoshanov 2011). Similarly, a UK study indicated that poor subject knowledge was a contributing factor to weak planning and teaching of elementary mathematics (Goulding et al. 2002).

Elementary teachers’ knowledge about fractions

The term fraction has multiple inter-related meanings (Charalambous and Pitta-Pantazi 2007), and developing the understanding of fractional concepts occurs over many years of schooling. The teaching and learning of fractions is the most challenging topic of the school mathematics curriculum (Lamon 2007). Many studies have shown that a high proportion of elementary teachers lack content knowledge and PCK to teach the fraction concepts of elementary mathematics effectively (e.g. Leinhardt and Smith 1985; Ward 2010; Ward and Thomas 2007). The depth of MKT has been shown to vary between countries; for example, elementary teachers in the USA lacked the rich understanding of the content (and ways to teach that content) that was held by their Chinese counterparts in several aspects of mathematics, including fraction concepts (Ma 1999).

Chinese grade three teachers were shown to have considerably better MKT for teaching fractions than their USA counterparts in three areas: concepts, calculations, and solving word problems. The Chinese and US teachers had comparable skills at articulating difficulties that students might experience in their learning about fractions and in expressing ways of overcoming these; however, the Chinese teachers were more knowledgeable than their USA counterparts in identifying key fractional concepts, understanding the students’ prior knowledge, and developing ways for students to understand (Zhou et al. 2006). When explaining upper elementary students’ errors in addition of fractions, caused by apparent lack of prior knowledge, Chinese teachers commonly attributed these errors to lack of understanding of prior concepts whereas the US teachers more commonly suggested that the students had forgotten prior work. The difference in response illustrates a distinction between conceptions of learning. The suggestion that students had forgotten prior knowledge indicates a view of learning as remembering or forgetting, whereas the explanation that students had not understood indicates that the teachers were more aware of student thinking and the challenges of learning to work with fractions. The difference in MKT was also illustrated when questioning students about errors that revealed misconceptions. Chinese teachers asked questions that highlighted revealed engagement with the misconceptions; in comparison, the USA teachers tended to ask more generic questions (An et al. 2004).

The New Zealand context

Weakness in fraction MKT has also been identified in New Zealand-based research. In a study in which 53 New Zealand elementary teachers self-assessed their knowledge for teaching fractions, 27 % rated themselves as very weak or weak compared to 20 % who rated themselves as strong or very strong (Ward and Thomas 2007). Ward (2010) investigated the fraction MKT of 78 New Zealand teachers from years 1 to 9 using questions that examined concepts that would typically be taught to students between years 7 and 10. In the study, 78 % of teachers correctly recognised a rectangle that was divided into six equal parts, four of which were shaded to show 2/3; however, just 30 % of these teachers was able to describe how to demonstrate this relationship to students using materials or diagrams. Whereas 85 % of teachers correctly ordered fractions 3/5, 1/3, and 4/8, just 30 % was able to describe how they could support students to order these fractions using a conceptual approach. Ward found that greater fraction MKT was associated with greater student achievement gains. This study is conducted with prospective teachers in one New Zealand university. In New Zealand, as in many other countries, elementary teachers teach all curriculum subjects.

Studies of fractions MKT of prospective teachers

In a self-assessment of their knowledge of elementary school mathematics, third year prospective teachers in one UK university frequently listed fractions as one of their weakest topics (Ainley and Briggs 1998). In evaluating the fraction component of a course designed to deepen prospective teachers’ mathematical knowledge in a USA programme for prospective elementary teachers, Newton (2008) found that there were modest gains in skill at understanding basic concepts, computation, and work with word problems over the duration of the course. The researchers looked for evidence of flexibility, defined as an inclination to use procedures other than the standard algorithms, but found that flexibility was low in both the pre-test and post-test with, for example, 72 of 99 students solving the problem of 2/4–3/6 by expressing both fractions as 6/12 and identifying a common denominator before subtracting. The reliance on the use of algorithms, rather than a more flexible use of knowledge, may indicate that the students have not developed a rich understanding of the topic (Newton 2008). Berk et al. (2009) found that prospective elementary teachers in the USA showed limited flexibility in answering proportional reasoning problems, and they tended to solve many of the problems by the use of cross-multiplication rather than being alert to other methods that reduced the complexity of calculations and were unable to come up with multiple methods for solving such problems. A four-session intervention raised these measures of flexibility, with a greater range of methods, and more efficient methods were used to complete the problems. A delayed post-test administered to 45 participants 6 months after the intervention indicated that the increased flexibility had been retained.

Elementary school-based studies of fraction learning

Prospective education and professional development of teachers need to be informed by the research on children’s learning. This section will give a brief review of findings from a selection of studies that investigated elementary school children’s learning of fraction ideas. Despite the concern expressed about the lack of detail in the elaboration of the specialised knowledge required to support teaching (Hill 2010) and insufficient research into the learning of rational number ideas (Behr et al. 1992; Lamon 2007), there are studies which provide useful guidance to inform fraction instruction in elementary school.

In an analysis of the strategies school students used when solving fraction tasks, Smith (1995) found that the competent performers used a rich range of approaches, well matched to specific tasks. Weaker students tended to use a narrower range of taught strategies which were performed in an algorithmic manner. In an Australian study, 323 grade 6 children were required to select the larger fraction from pairs of fractions and explain their answers. Benchmarking, whereby fractions are ordered by considering the relationship of each one to common benchmarks such as 0, 1/2, and 1, and using of residual strategies, whereby fractions just less than 1 are compared by consideration of the difference of each of them from 1, were two strategies that demonstrated good number sense that were used effectively and successfully. Neither of these strategies was familiar to many of the teachers of these children indicating that they were likely to have been developed by individual children (Clarke and Roche 2009).

Results from empirical studies have suggested that the teaching of fractions in elementary school should be guided by the following:

  • an increase in emphasis on the meaning of rational numbers rather than on calculation procedures (Charalambous and Pitta-Pantazi 2007; Clarke and Roche 2009; Moss and Case 1999);

  • making the process of constructing fraction equivalence more explicit in a range of fractional situations (Ni 2001);

  • explicit sharing of benchmarking (Clarke and Roche 2009; Moss and Case 1999) which, for example, supports the ordering of 3/7 and 11/20 by comparing them both with 1/2;

  • a decrease in the use of pie graphs as a representation of fractions, and an increase in the use of other forms of visual representation (Moss and Case 1999);

  • building on children’s self-developed solution strategies (Moss and Case 1999);

  • careful definition of numerator and denominator so that the improper fractions fit naturally within the definition (Clarke and Roche 2009);

  • explicit sharing of residual thinking which, for example, allows reasoning such as 7/8 is greater than 4/5 by comparing the amount by which each is less than 1 (Clarke and Roche 2009); and

  • an increase in emphasis on estimation and approximation when representing and operating with rational numbers in order to develop number sense (Clarke and Roche 2009).

Transforming elementary mathematics teaching so that it aligns with these goals requires analysis of the approaches to teaching that can support such instruction. Fraction concepts can be introduced through the use of manipulatives. The next section provides an overview of research about the use of manipulatives for teaching mathematical concepts and then looks at the use of manipulatives for teaching fraction ideas.

Manipulatives and models in mathematics education

The use of manipulatives in mathematics instruction has a long history (Sowell 1989); however, research on the effectiveness of their use in assisting mathematics learning is mixed. A meta-analysis conducted by Sowell indicated that long-term use of manipulatives in elementary school generally has positive effects. In some circumstances using manipulatives can aid learning; however, learners may not perceive the link between the manipulatives and the mathematical concept that is being illustrated unless the relationship is specifically highlighted. There is evidence that in some classrooms lessons can become focused around the use of the manipulatives rather than the use of manipulatives to foster mathematical growth (Puchner et al. 2008). Furthermore, if the teacher lacks sufficient knowledge to demonstrate how the use of the manipulatives illuminates the concept, then the use of manipulatives can become a distraction (Moyer 2001). Relationships that may seem obvious to the teacher may be opaque to the learners.

When appropriate manipulatives are used effectively, they can support learning; however, their use needs to be accompanied by instruction linking the actions with the manipulatives to broader understanding of the underlying concepts (Kaminsky et al. 2009; Uttal et al. 1997). Perceptually rich, realistic manipulatives can assist learners to see mathematical tasks as more than classroom exercises and linked to the real world, for example prompting students to reject unrealistic answers. However, the realism of such manipulatives is potentially distracting and can make the task of generalising and abstracting more demanding for students (McNeil et al. 2009).

Some students who are apparently successful using prepared diagrams such as pre-partitioned circles to exemplify and order fractions are unable to create their own diagrams to support their thinking (Hodgen et al. 2010). This indicates that the creation of diagrams to support thinking is demanding and an indication of the depth of mathematical understanding. Such diagrams are most useful when considered as aids to thinking rather than as faithful representations (Hodgen et al. 2010).

Models for teaching fraction concepts

There is a range of manipulatives and models commonly used to support fraction instruction, for example, discrete objects such as sets of counters, pattern blocks,Footnote 1 fraction wall,Footnote 2 number lines, double number lines,Footnote 3 and area models such as circles and rectangles. The selection of the most effective models for use in instruction is paramount. For example, pattern blocks were found to be ineffective for assisting fourth and fifth grade children in the USA to build mental models of fractions, whereas fraction walls were effective for reinforcing part-whole constructs and supported mental models for ordering fractions. However, fraction walls were not effective for developing concepts of fractions greater than 1 or for developing estimation skills and pattern blocks were found not to support the building of mental models (Cramer and Wyberg 2009). Instruction in US fourth and fifth grade classrooms that focused on investigating through use of multiple representations over an extended period and that required students to make connections between different modes of representation such as manipulatives, diagrams, symbols, words, and contextualised problems resulted in more effective development of conceptual understanding of fractions than traditional textbook-based instruction (Cramer et al. 2002). An important feature of effective instruction is the explicit discussion of the attribute on which the model is based, such as relative length for linear models, relative area for two-dimensional models, and relative number in the set model (Steinle and Price 2008).

Number lines

Number lines are widely used in teaching and assessment of fraction concepts. Initial fraction instruction often emphasises part-whole construct and students experience difficulties translating concepts to the number line (Hannula 2003). This is illustrated by children in upper elementary schools who have greater success at shading a fraction of a rectangle than they do in locating a comparable fraction on a number line (Stephens and Pearn 2003).

Use of number lines requires understanding of the measure construct of fractions whereby multiples of a unit fraction (1/n) are used to determine the distance from a starting point (Charalambous and Pitta-Pantazi 2007). Effective use of number lines requires the learner to co-ordinate information provided pictorially by the marked line together with the numbers which give information about scale (Bright et al. 1988). Bright et al. suggested that use of multiple number lines, partitioned in different ways but all showing the same fraction, would assist learners to construct richer understandings of number lines. Number line instruction can be enhanced by use of models which progressively become more abstract. For example, a model to support percentage calculation, which initially consists of a bar modelling specific problems, can be developed to be a double number line, which may be applied more generally and can serve as a model for performing percentage calculations (Van Den Heuvel-Panhuizen 2003). Similarly, Abels (1991) used a calibrated elastic strip as a tool for supporting the introduction to calculating percentage change. This tool is similar to the tool used in the current study (Fig. 1).

Background to the study

The idea that stimulated my thinking about using an elastic strip to challenge and consolidate thinking about fractions came from a teacher’s poster demonstrating a piece of elastic secured at one end with one quarter of the length of elastic shaded. The instructions were to stretch this elastic strip to find one quarter of the distance from the fixed point to certain points on the poster. This initial idea has led to consideration of a range of ways in which an elastic strip can be used to challenge and extend fraction ideas such as equivalent fractions, ordering fractions, and conversion of fractions to decimals. Informal observation when using these ideas in classes has raised the question of whether the novel nature of tasks, when working with the elastic strip, requires learners to think deeply about fraction ideas as they are unable to successfully complete these tasks by using routines learned by rote. This study aims to ascertain how the elastic strip challenges and extends prospective teacher understanding of ordering fractions and equivalent fractions.

Description of the elastic strips

The elastic strips used in the teaching experiment (see Steffe 1991) are graduated scales with equal intervals. The strips are each about 1 m in length. Under slight tension, each strip is marked in equal intervals. The initial scale that participants in the study used was marked off in ten intervals. Later in the teaching experiment, two other strips were introduced: one strip with graduations labelled from 0 to 25 (Fig. 2) and the other with graduations labelled from 0 to 20. The elastic used to make the strips was able to be stretched to approximately double its un-stretched length. When the strips are used to find fractions of lengths, the physical restriction imposed by the limits on the elasticity necessitates the use of equivalent fractions to complete some of the tasks.

Fig. 2
figure 2

Elastic strip being used to find 5/6 of the length of a table using the equivalent fraction 20/24

Full size image

Method

The research model used was that of a teaching experiment in which the researcher had a participatory role as well as the role of data collector (Steffe 1991). Thirteen participants were recruited from two cohorts of prospective teacher education programmes at one New Zealand university. All participants entered teacher education as graduates in a range of disciplines and were students in a 1-year course for elementary school teaching. One cohort of five students was in their final month of their teacher education programme and had completed their mathematics education course 5 months earlier. The other cohort consisted of eight students in the first month of their teacher education course who had not started their mathematics education course, but were participating in an optional mathematics content course for elementary teaching which was taught by the researcher. Prospective teachers were encouraged to participate if they felt that their own knowledge of fractional concepts was weak. This purposive sampling was used in order that the study could report in depth on how such prospective teachers would respond to the teaching experiment.

To investigate their understanding of fraction ideas, each participant completed a written questionnaire (Fig. 3) and then took part in a teaching experiment either individually or in pairs. The teaching experiment consisted of a series of activities involving the use of an elastic number line for developing ideas of equivalent fractions and ordering fractions. No definition of the term fraction was given to participants during the study; however, the use of the tool to find proper fractions as points in an interval from zero to one required understanding of the measure construct. In this study, the unit was fixed, often as the length of the desk, and through varying the degree of stretch of the elastic, the number of equal parts that the unit was partitioned into was altered.

Fig. 3
figure 3

Chris’s answers to the questionnaireFootnote

The questionnaire attempted to establish an indication of the competence of each of the participants at dealing with equivalent fractions and with ordering fractions. The sets of fractions to be ordered consisted of one set of fractions with the same denominator, one set with the same numerator, and two sets that could be ordered using benchmarks, with the final using less familiar fractions than the initial question.

Full size image

The sessions were video recorded for later analysis. Completion of the questionnaire took approximately 5 min and the duration of the teaching experiment was typically within the range of 30 to 40 min.

Teaching experiment protocol

Initially the participants were told how the elastic strip was created, pointing out that it was divided into ten equal segments. The participants were asked to use a ten-segmented strip to find a point that was 7/10 of the way along a desk. They were then required to find 5/8 of the length of the table and 2/3 of the length of the desk. Intentionally, the strip was not sufficiently elastic to stretch along the table using just three segments. When they achieved this, they were asked what mathematical ideas they had used. Other elastic strips were introduced, which had been graduated and numbered into 20 and 25 segments, respectively, and similar tasks were undertaken. Participants were then asked to describe how they could find approximate fractions of lengths without using the elastic strip.

Next participants were asked to use the strips to compare pairs of equivalent fractions such as 3/7 and 5/8. This led to the discussion of the use of benchmarks to help order fractions. Examples of benchmarks included close to 0, close to 1, and close to 1/2, with additional probing to see if fractions were greater than or less than 1/2. After the teaching experiment, the participants were asked to describe what they had learned from participating in the teaching experiment and their views on the effectiveness of the use of an elastic strip for learning about fractions.

The teaching experiment was informed by the results of the initial questionnaire and conducted in a flexible way depending on the skill and needs of the prospective teachers. The use of the elastic strip required students to cooperate in order to complete the physical task. The physical nature of the task required discussion between participants when students were interviewed in pairs and between the participant and the researcher during an individual interview. When pairs of students undertook the tasks, they worked together, and when individuals undertook the tasks, they were required to give instructions to the researcher to act as partner in carrying out the tasks. When appropriate, students were asked to support the instructions and actions with reasoning.

Results

Themes emerging from the data (discovering a misconception, equivalence, ordering, and benchmarks) are presented below to illustrate ways in which prospective teachers’ knowledge was challenged and extended through the initial questionnaire and the interview.

Discovering a misconception

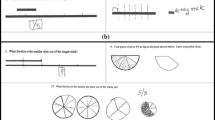
In the process of discussing Chris’sFootnote 5 incorrect answers to the questionnaire (see Fig. 3), a misconception that had very recently been acquired by Chris was uncovered. In the questionnaire, Chris wrote 4/8, 3/5, and 1/3 as the order from smallest to largest as shown in Fig. 3. He explained the answer by looking at the difference between the numerator and the denominator: 4/8 had a difference of 4, 3/5 had a difference of 2, and 1/3 had a difference of 2.

Chris successfully ordered a set of fractions with the same denominator, and a different set which had the same numerator; his explanation in each case was based on the difference between the numerator and denominator. He gave 9/40, 12/23, 5/11, and 11/13 as a correct ordering from smallest to largest. Again he appealed to the differences.

When asked where he had developed the idea of using this difference to order fractions, Chris said “It only came from yesterday’s class really. Someone explained her way of doing it and it seemed better for ordering these harder ones and seemed to work.”

This illustrates the fragile nature of the knowledge held by Chris. Chris listened to a method for comparing some fractions articulated by another prospective teacher, and applied it inappropriately to the fractions he was asked to order. On reviewing the video, it was clear that he had alluded to an episode in the mathematical content class on the previous day when prospective teachers had explained their approaches to ordering the fractions 2/3, 19/20, and 7/8. One prospective teacher had explained that each differs from 1 by a unit fraction and therefore we can order the fractions using knowledge about the ordering of the unit fractions, that is, residual thinking (Clarke and Roche 2009). Chris appears to have incorrectly generalised this to ordering fractions using “gap thinking” (Pearn and Stephens 2004) in which the fractions are ordered by the size of the difference between denominator and numerator for each. It appears that at this point he was regarding fractions as pairs of numbers which appeared not to be related to any visual representation of fractions. Challenging this misconception was achieved through use of the elastic tool and discussion of equivalent fractions and benchmarks.

The demonstration of how a learner over-generalised ideas presented by others and developed a misconception serves as a reminder of the care that needs to be taken in any teaching using a range of methods to ascertain the meaning that participants take from teaching.

Equivalence

In order to use the elastic strip to find fractions of a given length, the participants needed to use ideas of equivalent fractions. That this could be done successfully is shown in this section from the sessions with Monique and Hayley.

Monique was introduced to the strip by finding 7/10.

She was asked to find 2/3.

M: Ok, 2/3 on this, because it doesn’t stretch very well it is 4/6 so it must be 8/12.

Hayley easily used the strip to find 4/10 of the length of a table. When asked if she could find four sevenths of the length of the table, she suggested dividing each interval into seven. She was prompted by the researcher to consider stretching the tool, and then was able to see that she needed to stretch it so that the table matched seven intervals.

When asked to find 2/3, she quickly responded: “I can do a similar thing. You could stretch it so that it used nine” and identified the location of 2/3 by pointing to the six. When asked what idea she had used she hesitated and was prompted by the interviewer that she had used equivalent fractions.

H: For 3/4 I know that half of ten is 5 so half of that is 2 1/2. So 3/4 is 7 1/2 tenths.

R: If you weren’t allowed to cut any divisions in half.

H: If the strip was longer you could find 3/4 as 9 out of 12.

R: Could you consider using eighths?

H: Oh yes 3/4 is 6/8.

In contrast, the idea of equivalent fractions proved demanding for Chris as is shown in his response to the questionnaire and interview (see Fig. 3).

Chris correctly identified diagrams with 2/3 of their area shaded, but also included a circle where two of three non-equal parts had been shaded. He correctly named two fractions equivalent to 15/25, but his initial answers for fractions equivalent to 18/20 were 9/40 and 6/10. When asked to check these answers, after a pause he recognised that he had doubled the denominator and halved the numerator to get the incorrect answer of 9/40; at that point he corrected his answer.

When the elastic strip was introduced, Chris was asked to find 3/10 of the length of the table. When the researcher suggested stretching the strip, Chris then had the concern that the strip would be longer than it was initially, but he was reminded that we were trying to find a fraction of the length of the table, not of the strip. After thinking about this, Chris successfully used the strip to find 3/10 of the length of the table and also 4/9:

R: How do we find 2/3?

C: Not too sure. I have the idea of marking of 2/3 and then moving it along the table. I am not too sure where I am going with that.

R: You told me that equivalent fractions are fractions that name the same amount. We are looking for 2/3. Can you give me some equivalent fractions for 2/3?

C: 2/3, 4/6, 8/12. (with hesitation)

R: Is there one between those two?

C: 2/3 (hesitation).

R: You can write on here if it helps.

C: Yes, my head is getting sore.

Wrote down 2/3, 4/6 and 8/12 (pause).

R: I don’t want you getting stuck on that so how about we multiply the 2 by 3 and the 3 by 3.

C: 6/9.

R: Is that 2/3?

With that information Chris was able to create 2/3.

R: Can we make 3/4? How can we make 3/4 using this tool?

C: (pause). 3/4, I would just estimate it.

R: That’s fine. Can we find it using this tool?

C: I guess we can use the same idea.

R: (Pause) Thinking of equivalent fractions. 3/4 is the same as what?

C: 6/8.

The use of the elastic strip required prospective teachers to use the concept of fraction equivalence in a novel manner. When finding sets of equivalent fractions, several participants appeared to create successive fractions by doubling the denominator and numerator of the previous fraction. This created difficulties when the most useful equivalent fraction would have been found by multiplying the denominator and numerator of the original fraction by 3.

Ordering fractions with the same numerator but different denominators

Another prospective teacher, Greg (see Fig. 4), incorrectly ordered the fractions \( \frac{3}{{11}},\frac{3}{{14}},\frac{3}{{17}} \)as going from smallest to largest in question (e). He appears to have attempted to support his answer with diagrams; however, he has not been able to maintain equal sized pieces. He explained his ordering:

Fig. 4
figure 4

Greg’s answers to part of the questionnaire

Full size image

G: I was thinking 3 pieces shaded out of 11, 3 out of 14, and 3 out of 17. But I think the order might be reversed. I really struggle with that one.

Later the question was revisited with the aid of the strip. Initially 3/17 of the length of the table was found, and then 3/14 and 3/11.

R: Now we are going to find 3/14. Before we do it, what is going to happen to each of the pieces?

G: It’s going to stretch forward. So it is going to go (hand gesture indicating that the fraction was larger).

After the three fractions had been found using the strip, Greg proposed a rule:

G: So it is actually the other way round from my answer. I am just wondering when we have got the same number on top. Is that a general rule that you could follow, if you have the same number on top, and the denominator is bigger, the smaller the value?

Following a discussion about the ordering of unit fractions and then fractions with the same denominator, Greg was asked if the elastic strip had helped his thinking.

G: It just totally changed my way of thinking about fractions. It’s a visual for me that I like to see.

The use of the tool in this section seems successful in consolidating understanding of fractions with the same numerator and different denominators. A factor that may have contributed to the success is the restriction on the variation to changes in the denominator (see Marton et al. 2004; Runesson 2005, 2006), which may have enabled Greg to focus on and link the changes in denominator and the change in size of the fraction with the associated physical actions of stretching the elastic.

Ordering fractions

Greg incorrectly ordered the fractions from questionnaire part (d) (Fig. 4) as 1/3, 3/5, 4/8 and explained:

G: I tried to draw pictures to help me work it out. 1/3 is quite easy to visualise. I just see one piece shaded out of three. The same with 3 out of 5, so I thought 1/3 is smaller. 3/5 is getting more pieces so if I have 3 pieces out of 5 shaded, I can see more pieces being shaded with less left over. And 4/8 is 1/2. So you are getting 1/2 of something, and that is the biggest.

R: Are you happy with that order?

G: I think it is wrong. Maybe I might change it to 1/3, 1/2, 3/5. I feel I should change it, I feel that 3/5 is more than 1/2, but I am not confident. This is where I really struggle.

After using the elastic strip to correctly order these fractions, Greg again commented that using the strip had helped his understanding as he was now starting to visualise the relative size of fractions.

Benchmarking

Benchmarking is a technique for finding approximate values of fractions. When used for ordering fractions, benchmarking involves comparing the fractions to be ordered with familiar values or benchmarks. One example of benchmarking is sorting fractions into those which are close to, but greater than, zero, those which are just less than a half, those which are just greater than a half, and those which are nearly 1. The mathematically stronger participants demonstrated methods to order fractions that required converting to percentages or decimals, or by converting all fractions to a common denominator. In discussing how they had ordered fractions in the questionnaire they did not suggest they had used benchmarks.

After using the strip to compare fractions, Monique was able to use benchmarking to order fractions, as illustrated in the next excerpt which is a discussion about ordering two fractions:

R: After a while we will discard this tool and need to develop benchmarks.

M: 8/17 is just under 1/2, and 10/17 would be just over 1/2.

Monique very quickly moved to comparing fractions with benchmarks such as 1, 1/2, and 1/4 without the need to use the elastic strip.

In the questionnaire, Greg answered question (g) correctly as 9/40, 5/11, 12/23 and 11/13; however, he was not confident about his answer:

G: 9/40 is the smallest seems a ridiculous amount shaded out of 40. Littlest amount I could think of. Seems small to me. 5/11, that is quite close to1/2 12/23 is quite close to 1/2 5/11 and 12/23 seem almost the same. Both close to 1/2 11/13 seems quite close to 3/4. There is a lot more shaded out of that proportion. If we did that stretchy thing we might actually be quite close.

Greg used the elastic tool to locate each of the fractions in this set. He recognised that 9/40 was approximately 1/4, and after prompting to compare 9/40 to 10/40, recognised 9/40 was just less than 1/4. Similarly, the strip was used to find 5/11, and it was pointed out that 5.5 out of 11 would be 1/2, so 5/11 is just less than 1/2.

R: These two (5/11 and 12/23) were pretty close and you said they were both about 1/2.

Tell me about 12/23.

G: 12/24 would be 1/2. Half of 23 is 12.5, sorry 11.5. So 12/23 is slightly more than 1/2.

So it is more than this one (5/11) because it (5/11) is slightly less than 1/2.

So if I was to work this out again knowing this now, I could do it. Half of 11 is 5.5. Half of 23 is 11.5, and so I could compare them to a half and see that one was slightly more than half and one was just less than half.

This idea of benchmarks was discussed and consolidated by considering \( \frac{{11}}{{13}} \). Greg was asked to order a similar set of fractions and then asked if he had learnt anything from the session.

G: Yes I have. I have got more of an understanding of fractions and how they work. I’d love to take this strip into an exam and sit down and stretch it out. Now I have some kind of visual measurement in my brain that I can see; I can see that is close to 1, that is close to 0, that is more than a quarter, or less than quarter. Those are now my measuring blocks. 0, 1/4, 1/2, 3/4 and 1. I can work within those boundaries to work out what the answer might be. I might borrow it now and go home and practise it so I re-illustrate it in my head again.

Final comments from participants

Two of the participants who had better content knowledge about fractions than the others described how they intended to use the elastic strip during their teaching of elementary mathematics:

I like the elastic strip. I haven’t seen this before. I think it’s a really good way to teach equivalent fractions as you can use strips with different scales to find the same fraction. (Ella)

We always talk in terms of the concrete and the image in the mind; this is probably a good way, especially with the younger ones, to make that leap. You say something to them, and they just look at you and say ‘what!” If you can get them to do something in groups, it would be a great little group activity, they see if they can discover if there are connections. A starting point, they might be able to work out something. Rather than just give them the knowledge, give them 5 min to work with it, if they don’t get it you need to scaffold them towards it. (Grant)

I am used to calculating in time-consuming ways. Now I see that I can use approximations to give me an idea of the size of fractions and help me order them. (Amelia)

Other participants whose mathematical knowledge was not as strong made these comments about the sessions which indicate that they had personally consolidated their understanding during the teaching experiment:

I found the elastic very effective because I could see how it was working. (Jayne)

It is good to make equivalent fractions. When trying to make 1/3 you have to actively think about other ways of making 1/3 so that it will stretch across the table. (Warren)

Initially I just had the size of the number in my heads. I had no image at all. I can now see fractions as a length. Using the tool has given me a mental image, something solid, rather than just knowing it. (Ross)

These participants’ comments illustrate the potential uses of the elastic strip to challenge and extend their knowledge of fractions, with the novel nature of experience requiring the participants to think carefully about the concepts rather than relying on routine procedures.

Discussion and conclusions

The study showed that the fraction strip has the potential to assist learners in consolidating and reinforcing the images of the number line. The sessions showed the various depths at which students understood fraction concepts and reinforced the research (e.g., Leinhardt and Smith 1985; Ward 2010; Ward and Thomas 2007), which shows that some prospective teachers have significant gaps in their fractional content knowledge, casting doubt on their ability to effectively teach these concepts in elementary classrooms. These concerns are illustrated in the vignettes from the interview with Chris who was one of the weakest students in the study and who needs ongoing support to help him develop robust understanding of the key ideas of elementary school fraction knowledge. For other participants, using the elastic strip was an effective activity to challenge, consolidate, and extend their fraction thinking. The novel and the physical nature of the activity made it harder to recall rote routines, and the need to communicate in order to complete the task required the participants to re-engineer their knowledge of fractions.

When using this strip, care would be required to keep the learner’s attention on the size of the unit. Work with manipulatives carries the potential for the manipulative to become the focus of the teaching rather than the concept that it is designed to support. It is essential that the teaching does not stop with the use of the strip, but rather starts with it and moves on to developing images of the strip, and then to the key fraction ideas.

The strip was used in this study with adults who had previously encountered fraction ideas many times in their learning. The fact that several of the participants and many other prospective elementary mathematics teachers have at best fragile understanding of key fraction ideas for the elementary mathematics curriculum is concerning. The discussion illustrating how a participant had developed a misconception about the ordering of fractions serves as a reminder of the need to check what learners take from teaching. The novel nature and the requirement for cooperation and communication means that the elastic strip has the potential to assist teacher educators to get the students’ ideas about fractions into the public domain and to assist in addressing those ideas.

The transcript of Greg’s response to use of the tool to explore fractions with the same numerator but different denominators indicates further research informed by variation theory (Marton et al. 2004; Runesson 2005, 2006), investigating whether controlling variation in a more systematic way can enhance prospective teachers’ learning of fractional concepts would be productive.

This research was undertaken with prospective teachers who were recruited on the basis that they had limited understanding of fractions. Further research should be undertaken with a more representative group of prospective teachers and children to explore whether using the elastic tool is useful for developing relational understanding of fractions in other settings.

There have been calls for the teaching of elementary school mathematics to have a greater focus on concepts (Charalambous and Pitta-Pantazi 2007; Clarke and Roche 2009; Moss and Case 1999; Ni 2001). Achieving these goals requires teachers with sound subject knowledge (Goulding et al. 2002); however, a significant number of teachers have weak knowledge of fractional concepts (Ward 2010; Ward and Thomas 2007) and groups of prospective elementary teachers identified fractions as a specific mathematics content area where they lacked confidence. Programmes that enhance the MKT of prospective teachers in fractional concepts need to be considered as one way to lift the teaching skill in this area. The use of the elastic strip offers the potential to challenge and extend the knowledge of fractions of prospective teachers.