Introduction

Learning and teaching geometry proof

Understanding proof, including disproof, is always an uneasy task for most students. Students may view an inductive argumentation as a validated proof because this argumentation makes sense, and use inductive reasoning to show what is right (Morris 2002; Chazan 1993). Students may see a validated proof as a pseudo-validated proof, which requires trying one or several examples for confirming its correctness (Healy and Hoyles 2000). Moreover, it is hard for students to start a proof or to write down a logical process of argumentation. The formal representation of mathematical proofs is one factor resulting in students’ difficulties in learning mathematical proofs. Explicitly, the content of proofs is related to both its precision and status (Duval 2002), and the form of proofs follows the logical rule and the status of each argument rather than the thinking process of producing proofs.

For learning geometry content, visualisation, and dynamic construction have been suggested by some researchers (e.g., Hanna 2000; Leung and Lopez-Real 2002). For learning to construct proofs, investigation of propositions or conjecturing has also been considered to inspire the need for proof, to enhance understanding proofs and further to construct a valid proof (e.g., Koedinger 1998). In addition, transforming the verbal representation of dialogue into the literal and symbolic representation of proof is an obstacle which students must overcome for understanding the nature of proof (Harel and Sowder 1998; Sfard 2000). These kinds of activities are based on the practice of mathematicians, and they require students to find some patterns or properties from several numerical examples, geometric figures, or situational phenomena, and to validate properties formulated by students.

We agreed that mathematical proof is not a generic logical process, but a substantive methodological tool for developing concepts, for finding out properties, and for validating theorems (Herbst 2002). In addition to conjecturing or inquiry, reading is a necessary approach to learning what counts as a mathematical proof. The crucial question should be not only whether students could express their arguments, but whether they could read others' arguments. We need to develop learning tasks so as to keep a balance between proof substance and proof form. Specifically, the challenge was how to design tasks which could help students not merely write but also read proofs.

Accordingly, the purpose of this study was to design reading-oriented tasks comparative to writing-oriented tasks in current mathematics classrooms, and then compare the effects of reading-oriented instruction and writing-oriented instruction on students’ reading comprehension of geometry proof (RCGP) by quasi-experimental study. Two quasi-experimental questions were addressed in this study:

  1. (1)

    Regarding a short-term effect, would students who get reading-oriented instruction perform better at the post-test on RCGP as a whole and on each facet of RCGP than students who get writing-oriented instruction?

  2. (2)

    Regarding a long-term effect, would students who get reading-oriented instruction perform better at the delayed post-test on RCGP as a whole and on each facet of RCGP than students who get writing-oriented instruction?

Related literature

Reading comprehension of geometry proof

The goals of learning mathematics proofs could be both to develop the abilities of constructing knowledge and to enhance the understanding of deductive validation (Mariotti 2007). Many approaches are proposed to reach the learning goals. For learning to understand deductive validity, validating proofs is suggested to be helpful to unpack the logic of mathematical statements (Alcock and Weber 2005; Selden and Selden 2003). Alcock (2009) designed a set of resources to demonstrate how one might go about understanding proofs by examining their internal logical relationships and overall structures. In addition, cognitive reading strategies for elaborating proof and metacognitive reading strategies for planning what to identify and for monitoring comprehension of logical coherence are suggested for teaching how to read geometry proof (Yang 2011). For learning to construct knowledge, the construct of cognitive unity is recommended as a tool for predicting and analysing some difficulties met by students when they have to construct a proof based on the notion of making the connection between conjecturing and proving (Garuti et al. 1998). On the other hand, Leikin (2009) designed multiple proof tasks to build up students’ collective proof spaces and then to develop more connected mathematical knowledge.

Unlike the integration of conjecturing and proving, our study focussed on the understanding of deductive validation. Yang and Lin (2009) argued that reading to learn the validity of proofs was complementary to listening, speaking, writing, and doing to learn argumentation. Thus, they (2008) conceptualised and justified a model of RCGP to investigate what could be comprehended by reading a geometry proof. This model was composed of five facets of RCGP which were structured into four levels. The four comprehension levels—surface, recognising elements, chaining elements, and encapsulation—and the description of the five facets of RCGP—basic knowledge, logical status, summarisation, generality, and application—are shown in Table 1.

Table 1 Comprehension level and facets of RCGP
Full size table

Comprehension of the surface level is characterised as epistemic understanding without analysing the elements of an argument in a proof. The elements of an argument could be premises, conclusions, or applied properties. Comprehension of the recognising elements level is characterised as recognition of premises, conclusions, or properties that may be implicitly applied in a proof. Comprehension of chaining elements level is characterised in terms of understanding the logical chaining of premises, properties, and conclusions in a proof and to view figures as referential objects. The comprehension of encapsulation level is characterised as interiorising a proposition and its proof as a whole, which implies that one can apply it, as well as distinguish different premises related to other similar propositions.

In other words, one who understands most of the terms and sentences (basic knowledge) in a proposition and its proof is beyond comprehension of the surface, and is towards comprehension of recognising elements; one who correctly identifies the statuses of statements as premises, conclusions, or applied properties (logical status), and catching the core of the proof or the critical proof idea (summarisation) is beyond comprehension of recognising elements, and is towards comprehension of chaining elements; one who correctly identifies what is validated by the proof (generality) and knows how to apply this proposition or the proof (application) is beyond comprehension of chaining elements, and is towards comprehension of encapsulation.

Reading strategies

Few empirical studies have aimed at enhancing students’ understanding of proof by reading strategies. Literature about reading strategies in language instruction may shed some light on this issue. Sequencing events in a story, predicting outcomes of a story, drawing conclusions, and finding main ideas are examples of comprehension strategies (Smith 1965). Traditional strategy instruction assumes that a set of hierarchically ordered sub-strategies are sequentially acquired to improve reading comprehension. On the contrary, cognitive-based views of reading comprehension concern the constructive and interactive nature of reading and assume that readers actively construct the meaning of texts by integrating existing and new knowledge and flexibly using strategies to plan, monitor, and regulate comprehension (Dole et al. 1991).

Kintsch’s (1998) construction-integration model also emphasises that knowledge activation is a bottom-up, associative process, followed by contextual integration in a situation model. Once knowledge has been activated and a text base has been constructed, an integration process takes over to ensure that only related items play a role in the final knowledge representation, and that all the irrelevant and contradictory information that has necessarily been included in the bottom-up construction process is rejected. Other researchers further emphasise the importance of text processing strategies in reading comprehension. The findings from studies such as those of Palincsar and Brown (1984) have provided important experimental evidence that reciprocal teaching method can facilitate reading comprehension.

Reciprocal teaching refers to teaching students specific comprehension-fostering strategies by which students can improve their reading comprehension and apply these strategies to reading new texts, and has been one of the most outstanding approaches of strategy instruction (Alfassi 1998; Rosenshine and Meister 1994). It is designed to improve reading comprehension by teaching cognitive strategies, such as question generation, clarification, summarisation, and prediction. Both reciprocal teaching only (in which the instruction consisting of models, prompts and hints, and instruction occurs in dialogues between the teacher and students) and explicit teaching before reciprocal teaching (in which there is extensive teacher-led instruction in cognitive strategies before dialogues begin) focus on the cognitive strategies in the instruction and students’ practice of these strategies. Most of the reciprocal teaching studies show that learning these strategies requires at least three lessons (Rosenshine and Meister 1994). It may be worth trying to use cognitive strategies to design tasks instead of instructing students about these strategies if teachers are to improve students’ RCGP with less teaching time. However, studies on students’ reading strategies for comprehending geometry proofs are still scarce.

Method

Process for developing tasks

For designing reading-oriented instruction and justifying its effectiveness on RCGP in this study, four phases were conducted. First, the literature about reading strategies of reciprocal teaching method was reviewed. Second, an original task was designed according to four cognitive reading strategies (question generation, clarification, summarisation, and prediction) of reciprocal teaching methods and one metacognitive reading strategy (reflection). Third, this task was then implemented in one class, and it was found that students still had difficulty in RCGP (Yang and Lin 2009). Lastly, the original task and the statement-posing task which could compel students to distinguish the logical statuses of arguments and motivate their reading strategies (Yang 2010) were combined to improve students’ RCGP.

The two reading-oriented tasks were carried out in two of the five lessons of the unit for teaching secondary school geometric proofs in grade-nine classes of the participating teachers. Why were the tasks set in only two 45-minute lessons? In Taiwan’s junior high mathematics curriculum, there are five 45-minute lessons for learning the unit of secondary school geometry proofs in grade nine, and 10 of the 12 participating teachers agreed to use at most two lessons for the comprehension instruction of reading proofs under the pressure of limited instructional time. Therefore, the design of a reading-oriented instruction in the study did not follow reading strategy instruction which took much more time (Rosenshine and Meister 1994). Practically, the reading-oriented tasks were expected to be integrated into the curriculum and textbooks so the limited time—in the two 45-minute lessons for conducting this quasi-experiment of the reading tasks—was a research constraint.

Iterative refinement of task design

According to schema theory (Anderson and Pearson 1984), a reader can derive meaning from texts based on the reader’s preexisting knowledge, and can better understand meaning when appropriate schemas are triggered. For example, information must be processed in working memory before modified schemas are stored in long-term memory (Nassaji 2002). Thus, according to reading strategies used in reciprocal teaching methods, we designed a task of reading mathematics proofs for triggering or structuring students’ schemas, and for revealing their cognitive processes which their peers can acquire during class discussion. One mathematics teacher and her two classes of 66 ninth-graders (14 to 15 years old) participated in the quasi-experimental study of 2009 (Yang and Lin 2009).

In our study of 2009, it was found that there was no significant main effect of the task on the post-test for the two groups; however, there was a significant main effect on the delayed post-test for the two groups. We then reflected that the reading task designed for the experimental group might be insufficient to initiate students to think more carefully about what they had read, and that the reading task should be re-designed to move students from a conception of focussing on the epistemic values of each argument to one in which a logically validating process is embedded in how they should read these arguments. Thus, we tried to refine the reading task.

How would we modify the task for helping students to experience and understand the deductive and validating method of formal proof? Students might evaluate arguments whether they knew them or not, but might not evaluate their understanding based on logical chaining of the arguments. On the other hand, students of instrumental comprehension performed better on applying a proposition than on identifying logical chains of arguments. Thus, the idea of problem posing (Silver 1994) was adapted to mathematical proof, and statement-posing tasks were proposed to help students both distinguish the logical statuses of arguments and execute reading strategies (Yang 2010).

In a statement-posing task, a proof is given without its corresponding propositions and students are asked to think what these arguments can prove. The potential benefits of statement-posing tasks include guiding students to distinguish the logical status from the epistemic status of arguments, which is necessary for readjusting students’ understanding of proofs; providing them opportunities to understand the logical function of proof methods; facilitating their dialectical reading strategies; and giving them a generic example of reading tasks.

One the other hand, instructional designs that aim at increasing germane cognitive load are beneficial for students’ learning because students are guided to focus on cognitive processes that are necessary for accommodating schemas (Sweller et al. 1998), and increasing variability is one strategy to increase germane cognitive load (Paas and Van Merrienboer 1994). The statement-posing tasks (SP) are one variation of the tasks of reading mathematics proofs (RP), and the RP tasks provide more complete information than do the SP tasks. Accordingly, a RP task is assumed to more easily trigger relevant knowledge whereas a SP task is assumed to more easily increase germane cognitive load.

Furthermore, some of the participating teachers in our previous studies believed that students could easily lose focus when trying to understand proof by using the SP task because the task required readers to evaluate each argument and predict what it claims simultaneously, and this work might exceed students’ cognitive loads. Other participating teachers further suggested that the original reading task should be used first in instruction because this task was easier than the statement-posing task. Therefore, on the basis of both theoretical and practical perspectives, the RP task was used in instruction prior to the SP task.

The RP and SP tasks are given in Appendix A, and the ideas of using these reading strategies to design the worksheets are described in the following sections Questioning for structuring schemas to Reflecting for readjusting schemas and revealing cognitive processes.

Questioning for structuring schemas

Questioning involves asking questions related to the text for the purpose of monitoring and regulating comprehension of written materials. Students might have difficulties in creating their own questions while reading proofs. Therefore, in this study we adopted this strategy to provide generic questions (e.g., Q1-1 and Q1-2 in the RP task) to prompt students to recognise the logical statuses of related statements and to determine whether students could identify them. In the RP task, students were asked to determine what the given and the conclusion were. In the SP task, students were asked to identify the key points in the arguments (Q2-3), or the properties or definitions that were used in the proof (Q2-4). This might be helpful to structure students’ schemas of understanding proofs regarding the logical instead of epistemic value (Duval 2002). It should be noted that the initiating questions in the RP task are designed to structure students’ schemas because the students are assumed to focus on the content meaning of arguments in the task, and thus supporting them to structure arguments based on the logical status is required.

Predicting for triggering relevant knowledge

Nolan (1991) demonstrated that a self-questioning plus predicting treatment is more effective than a vocabulary treatment and self-questioning only treatment for facilitating reading comprehension. Predicting involves anticipating what will come next in the text as one is reading. While reading a proposition and its proof, one should predict what can be inferred based on the given (forward, Q1-3 in RP) or on the conclusion (backward, Q1-4 in RP) in the RP task. In the SP task (Q1-1) of this study, students were asked to predict what these arguments can prove at a macro level. This might be helpful to trigger relevant knowledge. It should be noted that the initiating questions in the SP task focus on predicting in order to trigger students’ relevant knowledge because the students are assumed to focus on the logical status of arguments in the task, thus triggering their relevant knowledge to understand the content meaning of proofs is required.

Clarifying for modifying schemas

Asking for clarification if needed is one approach to modifying schemas in reciprocal teaching methods. For example, readers should point out what they do not understand or clarify whether their understanding is coherent. Questions are designed to check if students understand the meaning of a proof through self-evaluation after questioning and predicting guidance. In both of the RP (Q2-1 to Q2-3) and SP (Q2-1 and Q2-2) tasks of this study, students were asked to identify which proof steps were not easy to understand by themselves, and which proof steps were redundant or unnecessary.

Summarising for restructuring schemas

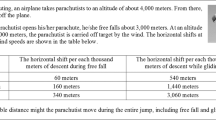
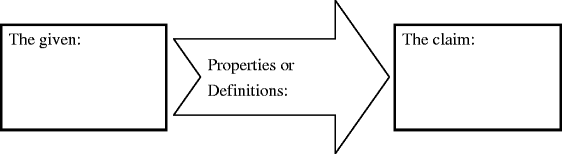
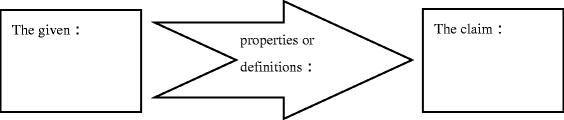
Summarisation involves summarising, in one or two sentences, several statements or paragraphs. The ability to summarise information requires readers to identify the important concepts, pick up ideas, and develop a holistic view of the text. To help students understand a proof structure and synthesise the proposition and its proof steps in this study, we provided a proof mapping as a visual display. Students were asked to identify important proof steps and chain proof steps logically by structuring the critical elements of a proof through the proof mapping. In both of the RP and SP tasks (Q3-1 and Q3-2), students were asked to use brief sentences to write down the main elements of the proof in the mapping (see Fig. 1) and discuss with each other.

Fig. 1
figure 1

A proof mapping for summarisation

Full size image

Taking Q 3-1 of the SP task in Appendix A as an example, the given is “O is the circumcentre of △ABC”; the claim is “\( \overline {\text{OA}} = \overline {\text{OB}} = \overline {\text{OC}} \)”; and properties or definitions include “O must lie on the perpendicular bisector of each side of △ABC.”, and “The distance between a point lying on the perpendicular bisector of one segment and one endpoint of this segment is equal to that between this point and the other endpoint of this segment.”.

Reflecting for readjusting schemas and revealing cognitive processes

In addition, in this study we designed reflecting questions to ask students to think over the predicting questions again and to compare their answers with the initial answers, to describe the logical relationship of a proof mapping and to reflect upon their reading strategies based on their metacognition of what they had understood and how they had read. In the RP task (Q4-1), students were asked to answer the question of, if they were teachers themselves, what problem they could pose that would be answered by the arguments in the proof. In the SP task, students were asked to rethink about their answer of what these arguments could prove (Q4-1). In both of the RP (Q4-4 to 4-6) and SP (Q4-2 to 4-4) tasks, students were asked to describe the relationship between the given, properties/definitions, and the conclusion, to point out what one should notice while applying the properties or definitions, and to suggest how one should read for comprehending proofs. All of the reflecting questions were designed to reveal and acquire cognitive processes of reading geometry proofs.

Taking Q4-1 and Q 4-2 of the SP task in Appendix A as an example, students might find they misunderstood “O must lie on the perpendicular bisector of \( \overline {\text{BC}} \)” as the given, and notice that “the given refers to original premises which warrant if some properties could be applied,” and “the claim refers the final conclusion which is derived from the given via some properties.”

In sum, the design of reading-oriented proof instruction in this study did not actually follow reading strategy instruction, but the four reading strategies emphasised within reciprocal teaching were adopted in designing the RP and SP tasks for RCGP.

Dependent measures

The geometrical content chosen to develop the instrument for the pre-test and the post-test in this study was the same (see Appendix B). The proposition and its proofs were adopted from one standard Taiwanese Grade 9 mathematics textbook. The structure of the designed items in the test regarding the operational definition of RCGP and its scoring scheme were developed in a previous study on RCGP (Yang and Lin 2008) (see the outline in Table 2), in which it took about 30 minutes for students to complete this test. Moreover, the teachers spent about 15 minutes discussing the answers of this test with the students in their experimental or control classes.

Table 2 Structure of reading comprehension of geometry proof (RCGP) test
Full size table

Sixteen items from RCGP were included in the instrument (see Table 2 and Appendix B). Except for Items 1 and 2, all were in the multiple-choice format. Some items contained multiple correct choices, so partial scores of 1, 2, or 3 were given. For example, Item 7 asked which properties are applied in the proof. There are three correct answers among the four choices. If students selected just the three correct choices, they would get a score of 3. If students selected the three correct choices and one wrong choice, they would get a score of 2. If students selected one of the three correct choices and one wrong choice, they would get a score of zero. The geometrical content chosen to develop the items in the instrument for the delayed post-test was shown in Appendix C. The 16 items of RCGP for the delayed post-test were modified from the items in Appendix B but according to the problem and its proof in Appendix C.

Quantitative measures regarding the five facets were derived from the 16 corresponding question items: basic knowledge comprehension, logical status comprehension, summarisation comprehension, generality comprehension, and application comprehension (see Table 2). The Cronbach alpha reliability coefficients of the pre-test, the post-test, and the delayed post-test were respectively 0.834, 0.866, and 0.856 for the Grade 9 participants in this study.

Participants

Twenty-two classes of 683 ninth-graders (14- to 15-years old), who were learning geometry proof in school participated in this quasi-experimental classroom study. Each class was randomly assigned to either the experimental group or the control group. Eleven classes of ninth-graders (n = 345) in the experimental group were instructed with the innovative worksheets with reading-oriented tasks while the other 11 classes of ninth-graders (n = 338) were instructed with regular proof instruction. The numbers of students in the two groups who completed the pre-test, the post-test, the delayed post-test, and all three tests are shown in Table 3. Only 295 and 311 students, respectively, of the experimental and the control groups completed all the three tests. The rate of complete data among the 683 participants in this study was 88.7 %.

Table 3 Numbers of participants that completed pre-test, post-test, delayed post-test and all three tests
Full size table

Twelve mathematics teachers participated in this study. Eight teachers taught the 11 classes in the experimental group while nine teachers taught the 11 classes in the control group. Of these 12 participating teachers, five teachers instructed both the experimental and the control classes. All the 12 participating teachers had experience of teaching geometry proof for ninth-graders. In addition, the first author discussed two instructional methods—how to implement the two types of tasks, RP and SP, in the experimental group; as well as how to guide students to write proofs and apply properties related to proofs—with the twelve participating teachers before this study.

Instruction

In the experimental group, there were two types of tasks. For the RP task (see Appendix A), students were asked to answer questions 1-1 to 1-4. The instructor asked one or two students to show their answers to the class, and then discussed with all students in the class the plausibility of the answers; questions 2-1 to 2-3 were adopted to check if students had sufficient pre-knowledge for understanding the proof. The instructor could explain to the students some properties of the proof (e.g., ASA) if they did not know those properties. Questions 3-1 and 3-2 provided a framework for summarising proof steps and asked students to discuss this with their peers. After peer discussions and presentations, the instructor explained how to summarise proof steps with the given, the applied properties, and the conclusions. Questions 4-1 to 4-4 asked students to rethink what the proof proves and to clarify their initial understanding and their summarisation. For students to reflect upon their strategies of comprehending proofs, questions 4-5 to 4-6 asked them to point out the conditions for applying a property and to describe how to understand proofs.

For the SP task (see Appendix A), the role of the instructor was the same as the role in the RP task. The questions in the SP task were also divided into four parts—predicting what the proof proves; questioning if students understand relevant concepts in the proof by themselves; summarising proof steps; reflecting what the proof proves, the conditions for applying a property, and how to understand proofs. The main difference between the SP task and the RP task was the predicting questions. The RP task asked students to think what could be inferred based on the given or the conclusion, and the SP task asked students to think what could be proved according to these arguments.

In the control group, teachers firstly guided students to write a proof for the proposition in the RP task. Then, teachers directed students to validate each proof step for explaining proof ideas and its meaning. Next, students were given the following task: “Given that O is the circumcentre of △ABC, prove that \( \overline {\text{OA}} = \overline {\text{OB}} = \overline {\text{OC}} \)”. About five to ten minutes later, one correct answer was written on the blackboard. Students were then asked to discuss their answers with each other. Lastly, some application questions were provided for students to practise how to apply the two proofs. The instruction in the control group was similar to teachers’ usual instruction.

Procedure

The reading-oriented and writing-oriented instructions were conducted about two weeks after the pre-test. Next, students did the post-test. After post-test, centroid, orthocentre, and circumcentre of a triangle were taught in about four weeks. Then, after the three weeks of the winter vacation, the graph of a quadratic function was taught in the first week of the new semester, and the students took the RCGP delayed post-test in the second week.

Analysis

In order to express the students’ score on each facet as a percentage, their score on each facet of RCGP was divided by the total score of that facet, and then the sum of the students’ five facet scores represented their performance of RCGP. The method of generalised estimating equation (GEE) is particularly well suited for testing hypotheses regarding the influence of factors on binary and other exponentially distributed response variables collected within participants over time, because it adjusts for the inherent correlation in scores on longitudinal dependent measures and covariates (Zeger and Liang 1986).

In this study, GEE was used with the model of a log link, gamma distribution, and the covariate of pre-test. Wald chi-square statistics (Rotnitzky and Jewell 1990) were used to judge whether the two groups had different performance on their mean scores of RCGP and those of each RCGP facet. For all tests performed, the significance level was set at 0.05, two-tailed. Repeated measures ANCOVA approaches to the problem were inadequate in this study because our data sets were not complete, and students’ scores with respect to each facet were not normally distributed.

Results

Performance on reading comprehension of geometry proof (RCGP)

Although the experimental and control groups have different mean scores of RCGP at pre-test, students’ scores of RCGP at the post-test and the delayed post-test could be adjusted for their pre-test scores. The adjusted means and standard deviations on the total RCGP scores of the two tests for the experimental and the control groups are presented in Table 4. The estimated marginal mean RCGP scores of the two tests for the experimental group were higher than those mean scores for the control group. The Wald chi-squared test revealed no significant difference between the two groups for the post-test (Wald chi-square = 2.299, p = 0.129) but a significant difference between the two groups for the delayed post-test (Wald chi-square = 5.831, p < 0.025).

Table 4 Adjusted means and standard errors on the total RCGP scores of post-test and delayed post-test with pre-test as a covariate for experimental and control groups
Full size table

Performance on each facet of reading comprehension of geometry proof (RCGP)

The means and standard deviations of the pre-test scores on each facet of RCGP for the experimental and the control groups are presented in Table 5. Because students’ scores on each facet had been divided by the total score of that facet, their scores could be interpreted as their percentages of comprehension on each facet. For example, the control group comprehended about 69 % of the meaning of mathematical terms and symbols in this proof, about 50 % of the meaning of the logical order of properties (logical status), or of the identification of critical ideas of the proof (summarisation), but comprehended below 50 % of the identification of the generality, or of correct application.

Table 5 Means and standard deviations of the pre-test scores on each facet of RCGP for experimental and control groups
Full size table

Although the experimental and control groups have different mean scores on each RCGP facet at pre-test, students’ scores on each RCGP facet at the post-test and the delayed post-test could be adjusted for their pre-test scores. The adjusted means and standard deviations of the post-test and the delayed post-test scores on the five facets for the experimental and the control groups are presented in Table 6. The estimated marginal mean scores on basic knowledge, logical status, summarisation, and generality facets of both post-test and delayed post-test for the experimental group were higher than those mean scores for the control group. However, at post-test, the estimated marginal mean scores on the application facet for the experimental group were lower than those mean scores for the control group; and at delayed post-test, the estimated marginal mean scores on the application facet for the experimental group were higher than those mean scores for the control group.

Table 6 Adjusted mean and standard deviation of post-test and delayed post-test scores on the five facets of RCGP
Full size table

The Wald chi-squared tests for comparing the difference in each facet of RCGP between the experimental and the control groups are presented in Table 7. Regarding the facets of basic knowledge, logical status, summarisation, and generality, the Wald chi-squared tests revealed significant differences for the post-test and the delayed post-test between the two groups. However, the Wald chi-squared test revealed no significant difference for the post-test and the delayed post-test regarding the facet of application.

Table 7 Wald Chi-squared tests for comparing the difference in each facet of RCGP between experimental and control groups
Full size table

Interpretation and reflection

This study compared the effects of the reading-oriented tasks and the writing-oriented tasks on students’ RCGP. With pre-test scores as covariates, significant difference in the total scores of RCGP was observed between the experimental and the control groups at the delayed post-test, but no significant difference in the total scores of RCGP was observed between the two groups at the post-test. This suggested that the instruction using the RP and SP tasks had better effects on students’ RCGP than did the usual instruction of the writing-oriented tasks after about 8 weeks even though the RCGP instruction was given to the students in just two 45-minute lessons.

We argue that there are some explanations for the absence of short-term effects. First, the test-retest condition might produce statistically equal progress in the two groups for a short period of time, because reviewing a test is also a kind of learning. Second, the test-retest condition might produce statistically equal regression in the two groups for a short period of time, because students might lose attention when answering the same questions. Thus, the delayed post-test is always more likely to show the difference between the two instructions.

In this paper, we also try to explain the relative ineffectiveness of the usual instruction based on schema theory, which assumes that knowledge representation consists of nodes and networks, and that meaningful learning interconnects the nodes by links (see Norman et al. 1976). The usual instruction might not enable students to store logical statuses of arguments in long-term memory. On the other hand, the instruction of the RP and SP tasks might benefit students’ cognitive operations, for example, chunking (Batting and Bellezza 1979) or inference making (Pressley 2000), which might further affect students’ learning after instruction. However, these explanations require further studies on tracking students’ understanding and cognitive operations over time.

Whereas performance on each facet of RCGP was comparable between the two groups of students, the experimental group demonstrated more comprehension in the facets of knowledge, logical status, summarisation, and generality than did the control group. However, there was no significant difference between the two groups for the post-test and for the delayed post-test regarding the facet of application. Several factors could have contributed to this result. First, the reading-oriented (RP and SP) tasks respectively required students to recognise and identify the claim, the given, and the applied properties, which are related to comprehension of the facet of logical status. Second, the experimental group students could structure and visualise these arguments with a proof mapping, which is related to comprehension of the facet of summarisation. Third, the reading-oriented tasks might initiate more schemas, which are good for knowledge organisation (Sweller et al. 1998). Lastly, the writing-oriented tasks provided some application questions for students to practise. Although the reading-oriented tasks did not emphasise the application of the proposition or its arguments, the potential of the SP task may initiate students’ germane cognitive load which is good for knowledge application (Sweller et al. 1998). Accordingly, this might be one reason for the lack of significant difference between the application scores of the experimental and the control groups. Further studies can be designed to combine reading-oriented and writing-oriented tasks for enhancing both knowledge organisation and application.

Nonetheless, the effect of reading-oriented instruction on RCGP was less than what we expected. There are several possible reasons for this unexpected finding. First, it was found that some students did not like to answer reflecting questions. They seemed unaware of the meaning of reflecting how they read proof. Second, reading strategies for comprehending geometry proof were not taught explicitly in this study. We suggest that reflecting questions could be revised for comparing the reading strategies used while reading the RP and the SP tasks; and this might make students explicitly aware of whether or not their reading strategies were adaptive to RCGP.

On the other hand, the experimental results did not match teachers’ expectations. Although some of the participating teachers who implemented reading-oriented instruction showed that they were still unfamiliar with reading tasks and queried the effect of the new tasks, most of the participating teachers predicted that the experimental group should perform better than did the control group on each facet of RCGP because they believed that writing proofs involved greater cognitive demand than did the RP or SP task, and that the high cognitive demand would result in low motivation and poor learning results. Teachers’ beliefs may be one factor which influences the effect of instructions (Ernest 1989). However, study of how teachers’ beliefs positively or negatively influence the effect is still required. Therefore, we suggest that teachers’ beliefs about innovative tasks are taken into account in experimental studies, and that teachers are asked to reflect upon their beliefs after the studies in order to develop teachers’ professional expertsise and adapt innovative tasks for their students.

Several possible limitations of this study need to be considered. First, some important factors or moderators were not included. It was found that learning materials intended to increase coherence benefitted low-knowledge readers but impeded high-knowledge readers (McNamara et al. 1996). If the possible interaction between RCGP ability and the task type is taken into account, what and how students with high or poor reading abilities learn from the RP and SP tasks will be of interest. In addition, as many studies have indicated, other important factors may influence the learning of proof—for example, proof scheme (Harel and Sowder 1998), epistemologies of mathematics and mathematics learning (Solomon 2006), affective factors (Furinghetti and Morselli 2009), and developmental types (Lin and Yang 2007)—but they were not investigated in our study.

Second, students receiving reading-oriented instruction performed significantly, but not highly significantly, better on RCGP at delayed post-test than those receiving writing-oriented instruction after controlling for the difference in their pre-test scores. Moreover, the two approaches did not actually improve students’ RCGP because their performance in the post-test was a little worse than that in the post-test. Alternative approaches to RCGP are required. Like DNR-based instruction (based on “duality,” “necessity,” and “repeated-reasoning”) which was developed for helping students to construct desirable ways of understanding (reading) and ways of thinking (writing) (Harel 2008), instructions should be more comprehensive and be informed by crucial factors of beliefs, affect, and learning over time.

Clearly, additional research is needed to investigate these issues. It is important to note that these limitations do not invalidate the usefulness of the present results. The reading-oriented tasks used in the present study represent specific reading materials that can be applied to textbooks and are more likely to facilitate students’ comprehension of geometry proof than writing-oriented instruction.