1 Introduction

Rotating discs are essential parts of many engineering applications (e.g., turbines, compressors, propellers, brake discs, electronic devices). Colossal trials are executed to decrease their weights and to increase their load capacity. Thus, fabricating discs with nonuniform thickness is found to be highly beneficial for load capacity escalation and weight reduction [1, 2]. Similarly, functionally graded materials (FGMs) are used to allow discs withstanding higher loads than monomaterials' discs. They were considered by many researchers while investigating, for example, buckling [3] and vibration of different structures [4, 5].

In general, FGMs are used with a specific function controlling the variation of a property [6,7,8,9]. However, in this study, a novel FGMs fabrication approach is considered to overcome the deleterious consequences of having any abrupt changes of common FGMs' volume fractions [2, 10, 11]. It relies on using number of layers with a unique volume fraction for each one. These layers are stacked together to form a multilayer (sandwich) disc [2, 10, 11]. Also, these layers are assumed to be perfectly bonded (no delamination present). Recently, there have been enormous efforts exploring the behaviors of such structures [10, 12, 13].

Rotating FGM discs were vastly investigated in many researches. Their behaviors were substantially impacted by many parameters under various loads (e.g., thermal and/or mechanical) [14,15,16], and this was proven through various methods, such as the finite difference method (FDM), the finite element method, and homotopy analysis method [2, 10, 11, 17, 18]. Generally, most articles revealed that circumferential stress is the critical stress for the disc behaviors compared to the radial stress [19,20,21]. In addition, various researches indicated that the temperature dependency of the material properties had paramount influences on the behaviors of single-layer discs/cylinders [21,22,23], and multilayer discs [2]. On the other hand, Eldeeb et al. [11] investigated the influences of deceleration on a multilayer disc made of functionally graded (FG) layers. They posed that circumferential stress-jumps were induced at the layers' interfaces, motivating occurrence of delamination (failure). Their analysis was conducted through the simple FDM, which proved its stability and ability to have a convergence for the asymptotic solution. The severity of such deleterious impacts could be reduced through increasing the number of layers and performing optimization [2, 10, 11].

Regarding optimization, several methods were used to detect the optimal solution of distinct problems [24,25,26]. Over the past 25 years, new optimization methods were developed, and their usage skyrocketed. For instance, the particle swarm optimization (PSO) [27], a hysteresis method, known for its straightforwardness, and capability to find the global optimum of any problem in numerous fields [28, 29]. It also requires less computational size compared to the other methods, i.e. the classical Karush–Kuhn–Tucker method [30]. PSO was a reliable option while optimizing the performance of different multilayer structures [31,32,33]. Some researchers illuminated that PSO outcomes had substantial effects on lowering the weights of monolayer rotating discs that is advantageous for their performance [30, 34]. Furthermore, it was referred that the proper selection of certain geometry and/or material parameters led to striking impacts on decreasing the failure likelihood of a sandwich disc [11] and cylinder [10].

In view of the foregoing review, sandwich structures are gaining remarkable attention. Therefore, a nonuniform thickness rotating FGM disc is considered in this study to enhance its behaviors through applying PSO, which is used in the forms of single-objective (SOPSO), and multi-objective (MOPSO). Those objectives of the PSO are: the disc's weight, maximum absolute circumferential stress, and maximum circumferential stress-jump. In addition, a suitable penalty function used to apply proper three constraints. In terms of the design variables, they included the thickness parameters and the volume fractions of the intermediate layers (ILs) that represent the disc's core. On the other hand, the innermost and outermost layers are made of metal and ceramic (represent the faces), respectively. The related governing differential equations (GDEs) are solved numerically through the FDM while considering the presence of external pressure and thermal load.

2 General Equations

The considered disc in this study has a nonuniform thickness. Many models are available in the literature describing the variation of the disc's thickness (\({h}_{\mathrm{r}}\)) versus the radius (\(r\)) [1, 35]. In this study, the power-law model was adopted. Thus, \({h}_{\mathrm{r}}\) for an annular disc with inner and outer radii \({r}_{0}\) and \({r}_{\mathrm{L}}\), respectively, is be expressed as [35]:

$${h}_{\mathrm{r}}=H{\left[1-\xi \left(r/{r}_{\mathrm{L}}\right)\right]}^{\varphi }$$
(1)

where \(\xi\) and \(\varphi\) are two geometrical parameters, and \(H\) is the thickness of the disc at \(r=0\). Table 1 presents the different convergent disc profiles obtained by altering the values of \(\xi\) and \(\varphi\).

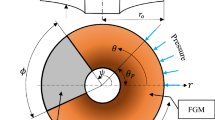
Table 1 Disc Profiles variation with the geometrical parameters [1]
Full size table

On the other hand, the proposed disc is composed of number of FG layers (\(L\)) as depicted in Fig. 1a. Referring to a certain layer is done through using subscript \(l\), where \(1\le l\le L\). In other words, any layer within the disc starts with \(r={r}_{l-1}\) and ends at \({r}_{l}\).

Fig. 1
figure 1

a Sandwich (multilayer) disc general configuration, and b Face and core of three- and five-layer discs. (IL(s): intermediate layer(s))

Full size image

The innermost layer of the disc (\(l=1\)) is chosen to be made of metal (\(m\)), whereas the outermost layer (\(l=L\)) is pure ceramic (\(C\)). Additionally, the ILs are treated as FGM layers composed of both \(m\) and \(C\). These ILs' volume fractions (\(V\)) altere radially according to the simple rule of mixture (Eq. 2). However, \(V\) is assumed to be constant within each layer. Hence, a material property (\(\beta\)) through each layer can be written as:

$${\beta }_{l}\left(r\right)={\beta }^{C} {V}_{l}^{C}+{\beta }^{m} {V}_{l}^{m}, {r}_{1}\le r\le {r}_{L-1}$$
(2)

Here \(\beta\) comprises elastic modulus \(E\), density \(\rho\), thermal expansion coefficient \(\alpha\), Poisson's ratio \(v\), and yield strength \({\sigma }_{y}\). Another formula, presented in Eq. 3, is used to describe the variation of the \(V\) for a nonoptimized case, which is used for the sake of comparison. It allows having constant \(V\) within the one layer with constant property mismatch between the layers [2, 11].

$${V}_{l}^{C}=(l-1)/(L-1) , {V}_{l}^{m}=1-{V}_{l}^{C}$$
(3)

Based on this description, it can be stated that the disc consists of a face and core. The face is represented by two layers: the inner (\({V}_{1}^{C}=0\)) and outer (\({V}_{L}^{C}=1\)) layers, and the core is made of number of ILs having different \(V\). For example, and as shown in Fig. 1b, the core of a three-layer disc is composed of only one layer, while for a five-layer disc; it is made up of three layers.

Regarding loading, and in addition to rotation, a thermal load prescribed by a polynomial function of the third order acts through the radial direction of the disc as follows:

$${T}_{\mathrm{r}}={K}_{0}+{K}_{1}r+{K}_{2}{r}^{2}+{K}_{3}{r}^{3}$$
(4)

where \(T\) is the temperature in \(^\circ{\rm C}\), and \({K}_{0}\), \({K}_{1}\), \({K}_{2}\) and \({K}_{3}\) are temperature coefficients [1].

3 Mathematical Modeling

3.1 Problem Formulation

For axisymmetric conditions, the GDE of a rotating nonuniform thickness disc in the polar coordinates (\(r\theta z\)) can be written as follows [1]:

$${\left(r{h}_{r}{\sigma }_{r}\right)}^{^{\prime}}-{h}_{r}{\sigma }_{\theta }+{h}_{r}{\rho }_{r}{\omega }^{2}{r}^{2}=0$$
(5)

where the subscript \(r\) denotes radial variation (e.g., \({h}_{r}=h(r)\)) Also, \(\omega\) is the angular speed. In addition, \({\sigma }_{r}\) and \({\sigma }_{\theta }\) are the radial and circumferential stresses, which are evaluated via Hooke's law for an isotropic material under plane stress hypothesis as [1]:

$$\begin{aligned} & \left\{\begin{array}{c}{\sigma }_{r}\\ {\sigma }_{\theta }\end{array}\right\}=\left[\begin{array}{cc}{\mathcal{C}}_{11}& {\mathcal{C}}_{12}\\ {\mathcal{C}}_{12}& {\mathcal{C}}_{11}\end{array}\right]\left\{\begin{array}{c}{\varepsilon }_{r}\\ {\varepsilon }_{\theta }\end{array}\right\}-{\mathscr{Y}}_{r}{T}_{r}\left\{\begin{array}{c}1\\ 1\end{array}\right\}, \\ & \left\{\begin{array}{c}{\mathcal{C}}_{11}\\ {\mathcal{C}}_{12}\\ {\mathscr{Y}}_{r}\end{array}\right\}=\frac{{E}_{r}}{1-{v}_{r}^{2}}\left\{\begin{array}{c}1\\ {v}_{r}\\ {\alpha }_{r}\left(1+{v}_{r}\right)\end{array}\right\} \end{aligned} $$
(6)

where \(\varepsilon _{r} = u^{\prime }\) and \({\varepsilon }_{\theta }=u/r\) are the radial and circumferential strains, respectively, calculated in terms of the radial displacement \(u\). Also, \({\mathcal{C}}_{11}\), \({\mathcal{C}}_{12}\) and \({\mathcal{C}}_{22}\) are the coefficients of the material stiffness tensor. Then, Eq. 6 is substituted in Eq. 5 to yield:

$$\left\{\begin{array}{c}{A}_{1}{u}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}+{A}_{2}{u}^{\mathrm{^{\prime}}}+{A}_{3}u={A}_{0}\\ {A}_{1}=r{h}_{r}{\mathcal{C}}_{11} , {A}_{2}={A}_{1}^{^{\prime}}\\ {A}_{3}={\left({h}_{r}{\mathcal{C}}_{12}\right)}^{^{\prime}}-{h}_{r}{\mathcal{C}}_{22}{r}^{-1}\\ {A}_{0}=r{\left({h}_{r}{\mathscr{Y}}_{r}{T}_{r}\right)}^{^{\prime}}-{h}_{r}{\rho }_{r}{\omega }^{2}{r}^{2}\end{array}\right.$$
(7)

where the single and double primes refer to the first and second derivatives, in turns, with respect to \(r\).

Before proceeding and looking at Fig. 1a, it is seen that the disc domain in \(r\)-direction is discretized into number of nodes \(n\), and symbol \(i\) refers to the node number, i.e. \(1\le i\le n\). Thus, Eq. 7 is usable through the whole nodes except for the ones at \(r={r}_{0}\) (\(i=1\)), \(r={r}_{L}\) (\(i=n\)), and any interface node. At \(i=1\), the disc is free to deform (\(u\ne 0\) and \({\sigma }_{r}=0\)), and at \(i=n\), there is an acting external pressure of \(P\) (\({\sigma }_{r}=-P\)) [2]. On the other hand, at every interface, it is always ensured to have two coincident nodes (\(i\), \(i+1\)) to detect the value of the circumferential stress-jumps (\(\Delta {\sigma }_{\theta }\)) occurring there. The boundary conditions at such nodes can be expressed as below while considering the continuity of \(u\) and \({\sigma }_{r}\) [2, 10, 11]:

$$u{|}_{i}^{l}=u{|}_{i+1}^{l+1}$$
(8a)
$${\sigma }_{r}{|}_{i}^{l}={\sigma }_{r}{|}_{i+1}^{l+1}$$
(8b)

3.2 Numerical Solution

In this study, the simple and effective FDM is used to solve the foregoing set of equations. Table 2 presents the proper FDM terms used to substitute the first and second derivatives, where \(\Psi\) and \(\updelta\) represent any parameter in the previous equations and radial distance between any two consecutive noncoincident nodes, respectively [2].

Table 2 FDM terms for first and second derivatives [10, 36]
Full size table

Consequently, Eq. 7 can be written in the following simplified FDM form:

$${u}_{i\pm 1}{\left[\frac{{A}_{1}}{{\updelta }^{2}}\pm \frac{{A}_{2}}{2\updelta }\right]}_{i}+{u}_{i}{\left[{A}_{3}-\frac{2{A}_{1}}{{\updelta }^{2}}\right]}_{i}={\left[{A}_{0}\right]}_{i}$$
(9)

Also, the boundary conditions at the disc's inner and outer surfaces are, respectively written as:

$${u}_{i}{\left(\frac{{\mathcal{C}}_{12}}{r}-\frac{3{\mathcal{C}}_{11}}{2\updelta }\right)}_{i}+{u}_{i+1}{\left(\frac{2{\mathcal{C}}_{11}}{\updelta }\right)}_{i}+{u}_{i+2}{\left(-\frac{{\mathcal{C}}_{11}}{2\updelta }\right)}_{i}={\mathscr{Y}}_{i}{T}_{i}, i=1$$
(10a)
$${u}_{i-2}{\left(\frac{{\mathcal{C}}_{11}}{2\updelta }\right)}_{i}+{u}_{i-1}{\left(-\frac{2{\mathcal{C}}_{11}}{\updelta }\right)}_{i}+{u}_{i}{\left(\frac{{\mathcal{C}}_{12}}{r}+\frac{3{\mathcal{C}}_{11}}{2\updelta }\right)}_{i}={\mathscr{Y}}_{i}{T}_{i}-P, i=n$$
(10b)

Similarly, Eqs. 8a and 8b are expressed as:

$$u{|}_{i+1}^{l+1}-u{|}_{i}^{l}=0$$
(11a)
$$\begin{aligned}&\begin{array}{l}{u}_{i-2}{\left[\frac{{\mathcal{C}}_{11}}{2\updelta }\right]}_{i}^{l}+{u}_{i-1}{\left[\frac{-2{\mathcal{C}}_{11}}{\updelta }\right]}_{i}^{l}+{u}_{i}\left[{\left[\frac{3{\mathcal{C}}_{11}}{2\updelta }+\frac{{\mathcal{C}}_{12}}{r}\right]}_{i}^{l}+{\left[\frac{3{\mathcal{C}}_{11}}{2\updelta }-\frac{{\mathcal{C}}_{12}}{r}\right]}_{i+1}^{l+1}\right] \end{array}\\ & \,\,\, +{u}_{i+2}{\left[\frac{-2{\mathcal{C}}_{11}}{\updelta }\right]}_{i+1}^{l+1}+{u}_{i+3}{\left[\frac{{\mathcal{C}}_{11}}{2\updelta }\right]}_{i+1}^{l+1}={\left[\mathscr{Y}T\right]}_{i}^{l} -{\left[\mathscr{Y}T\right]}_{i+1}^{l+1}\end{aligned}$$
(11b)

Thereafter, Eqs. 9–11 are solved simultaneously to yield the distribution of \(u\) across the disc. Afterwards, the distributions of stresses and strains are obtained based on their definitions and using Table 2. Then, the equivalent stress (\({\sigma }_{\mathrm{eq}}\)) is obtained based on the von Mises yielding criterion as shown below:

$${\sigma }_{\mathrm{eq}}={\left({\sigma }_{r}^{2}-{\sigma }_{r}{\sigma }_{\theta }+{\sigma }_{\theta }^{2}\right)}^{\frac{1}{2}}$$
(12)

3.3 Optimization

A typical optimization problem can be described as follows:

$$\left\{\begin{array}{l}\mathrm{find}\to\Phi =\left\{{\phi }_{1}, {\phi }_{2}, \dots ,{\phi }_{\mathrm{nv}}\right\} \\ \mathrm{min }\to F\left(\Phi \right)=\left\{{f}_{1}\left(\Phi \right), {f}_{2}\left(\Phi \right),\dots ,{f}_{\mathrm{no}}\left(\Phi \right)\right\}\\ \mathrm{Subject to }\to {M}_{{q}_{1}}\left(\Phi \right)\le 0, {q}_{1}=1, 2, \dots .,\mathrm{ni}\\ \mathrm{Subject to }\to {\psi }_{{q}_{2}}\left(\Phi \right)=0, {q}_{2}=1, 2, \dots .,\mathrm{ ne}\end{array}\right.$$
(13)

where \(\Phi\) represents the design variables (\({\phi }_{1}, {\phi }_{2}, \dots ,{\phi }_{nv}\)), \(F\left(\Phi \right)\) resembles all the objective functions of the optimization problem, \({M}_{q1}(\Phi )\) and \({\psi }_{q2}(\Phi )\) are the inequality and equality constraints, respectively. Besides, \(nv\), \(no\), \(ni\) and \(ne\) are the numbers of the design variables, objectives, inequality constraints and equality constraints, respectively.

In this study, the considered disc is composed of a number of layers, metal-FGMs-ceramic, with different \({V}^{m}\) for the ILs. In other words, the properties of these layers are dependent on these volume fractions. Accordingly, the optimal \({V}^{m}\) values for the ILs are to be determined according to certain objectives. Additionally, as the thickness of the disc has profound impacts on its behaviors, the two geometrical parameters (\(\xi\) and \(\varphi\)), shown in Eq. 1, comprise the rest of the design variables. Therefore, it could be stated that the current optimization problem is a multi-variable problem, where \(nv=3\) when \(L=3\), and \(nv=10\) when \(L=10\).

Additionally, three objectives are to be minimized individually or simultaneously. Firstly, minimizing the maximum absolute value of the circumferential stress (\(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\)) within the disc. Secondly, the value of the maximum circumferential stress-jump (\(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\)) is also considered for its serious consequences [2, 10, 37]. Finally, and for its crucial role, the weight of the disc (\(W\)) is the third objective that can be estimated through Eq. 14a. For convenience, it would be expressed in a dimensionless form (\(\overline{W}\)) through dividing by the weight of a complete ceramic disc as shown in Eq. 14b [34]:

$$W=2\pi g{\int }_{{r}_{0}}^{{r}_{L}}r{\rho }_{r}{h}_{r}dr=2\pi g\sum_{l=1}^{L}{\rho }_{l}{\int }_{{r}_{l-1}}^{{r}_{l}}r{h}_{r} \mathrm{d}r$$
(14a)
$$\overline{W}=\left(\sum_{l=1}^{L}{\rho }_{l}{\int }_{{r}_{l-1}}^{{r}_{l}}{h}_{r} r dr\right)/\left({\rho }^{C}{\int }_{{r}_{0}}^{{r}_{L}}{h}_{r} r \mathrm{d}r\right)$$
(14b)

where the gravitational acceleration \(g\) equals \(9.81\mathrm{m}/{\mathrm{s}}^{2}\).

On the other hand, several constrains are considered, in order to limit the search space of the optimization problem. The first two ones, Eqs. 15a and 15b, are thickness-related. The former is introduced to prevent the disc from having more than \(80\mathrm{\%}\) thickness reduction at \(r={r}_{L}\) compared to \(H\), and hence a stress concentration edge is formed [20, 21].

The latter one prevents the disc from excessive increase of \({h}_{r}{|}_{r={r}_{L}}\), which has a negative impact on \(\overline{W}\). The third constraint, Eq. (15c), is related to the occurrence of plasticity. It is desired to prevent any area through the disc from being plastically deformed. This is achieved via ensuring that \({\sigma }_{eq}\) of each node is less than \({\sigma }_{y}\).

$${h}_{r}{|}_{r={r}_{L}}\ge 0.2 H$$
(15a)
$${h}_{r}{|}_{r={r}_{L}}\le H$$
(15b)
$${\sigma }_{eq}<{\sigma }_{y}$$
(15c)

4 Particle Swarm Algorithm

Based on our previous research experience, PSO is a reliable method able to attain the global optimal for such similar problems; therefore, it is used in the current analyses. Moreover, a comparison between its results and other methods' outputs is illustrated in Sect. 5.1.

PSO is a population-based method that rests on a hypothesis of sharing social information among conspecifics, which simulates the behaviors of birds' flocks or schools of fish [27]. It solves a problem by having a population of candidate solutions (particles) randomly and homogeneously distributed in the solution space. Each particle (\(k\)) uses its local best position (\({B}_{k}\)) and the global best position (\({G}^{\left(\tau \right)}\)) of the solution set to decide its next movement during the following iteration. In each iteration (\(\tau\)), particles' positions (\({x}_{k}\)) and velocities (\({\vartheta }_{k}\)) are updated by the subsequent equations [38]:

$${x}_{k}^{\left(\tau +1\right)}={x}_{k}^{\left(\tau \right)}+{\vartheta }_{k}^{\left(\tau +1\right)}$$
(16a)
$${\vartheta }_{k}^{\left(\tau +1\right)}=\left(Y\times {\vartheta }_{k}^{\left(\tau \right)}\right)+\left({\zeta }_{1}\times {R}_{1}\times \left({B}_{k}^{\left(\tau \right)}-{x}_{k}^{\left(\tau \right)}\right)\right)+\left({\zeta }_{2}\times {R}_{2}\times \left({G}^{\left(\tau \right)}-{x}_{k}^{\left(\tau \right)}\right)\right)$$
(16b)

where \({\zeta }_{1}\) and \({\zeta }_{2}\) are the cognitive and social acceleration components, respectively, and \(Y\) is the inertia (constriction) coefficient. In addition, \({R}_{1}\) and \({R}_{2}\) are uniformly distributed numbers between zero and one.

However, Eq. 16b is only used for SOPSO, and it is modified to the form presented in Eq. 17 for the sake of MOPSO, where an external repository (\({\mathcal{R}}^{\left(\tau \right)}\)) to store the nondominated solutions of the randomly generated particles through each \(\tau\) is used [38].

$${\vartheta }_{k}^{\left(\tau +1\right)}=\left(Y\times {\vartheta }_{k}^{\left(\tau \right)}\right)+\left({\zeta }_{1}\times {R}_{1}\times \left({B}_{k}^{\left(\tau \right)}-{x}_{k}^{\left(\tau \right)}\right)\right)+\left({\zeta }_{2}\times {R}_{2}\times \left({\mathcal{R}}^{\left(\tau \right)}-{x}_{k}^{\left(\tau \right)}\right)\right)$$
(17)

For MOPSO, there cannot be one unique solution. There exists multiple points that graphically represented by the Pareto optimal solutions curve. Designers can select any point on the curve based on the desired requirements [10]. Furthermore, a death penalty method is employed to penalize particles that violates any of the priorly mentioned constraints [39].

5 Results and Discussion

The following section is divided into a number of subsections; the first one presents the verification of the solution scheme. The rest subsections are related to the optimization process of the disc behaviors.

5.1 Solution Scheme Verification

In this study, two separate MATLAB codes were used. The first was developed by the authors to solve the GDEs through the FDM. For the sake of brevity, this code was previously validated with different case studies in the literature. This can be found at length in Ref. [2, 11].

For the optimization process, four methods were examined at the beginning: PSO, genetic algorithm (GA), sequential quadratic programming (SQP), and ant lion optimizer (ALO). Both of GA and SQP are built-in functions in MATLAB, while freely online-available MATLAB codes for PSO [40] and ALO [41] were used. For each method, five trials for minimizing \(\Delta {{\sigma }_{\theta }}_{max}\) were executed considering the same stopping criterion (minimum function tolerance of \(1e-6\)).

As prescribed in Table 3, (i) PSO had the tiniest variations range (more stability) and managed to reach a unique value compared to the other three methods. (ii) GA, SQP and ALO were not as stable as PSO due to their different variation ranges. (iii) SQP managed to obtain a value very close to the minimum value of PSO, but it has the drawback of being dependent on initial guess to start searching that may result in stucking in a local optima. Such results confirm the great reliability and stability of PSO in such problems.

Table 3 Comparison between the results of different optimization algorithms for minimizing \({\Delta}{{\sigma}_{\theta}}_{\mathrm{max}}\) of a ten-layer disc
Full size table

5.2 Disc Parameters

In the following subsections, discs' optimal designs in terms of \({h}_{r}\) and \({V}_{l}^{m}\) for minimum objectives are assayed, depicted, and discussed. The considered disc has a nonuniform profile (Eq. 1), where \(H=0.1 m\), \({r}_{0}=0.1 m\) and \({r}_{L}=1 m\) [2]. It is composed of number of laminated equal width layers, i.e. \(L=3,\) \(5,\) \(8\) and \(10\). The innermost and outermost layers are always made of metal (Aluminum alloy 7075) and ceramic (Zirconia), respectively, and their properties are prescribed in Table 4. These materials are assumed to be completely isotropic.

Table 4 Properties of metal (aluminum alloy 7075) and ceramic (Zirconia) [42]
Full size table

Conversely, the ILs are made of FGMs of these two constituents with constant \(V\) within each layer. For loadings, the disc rotates with \(\omega =500\mathrm{ rad}/\mathrm{s}\), and is subjected to \(P=50 \mathrm{MPa}\) at \(r={r}_{L}\). Also, it is exposed to a thermal load defined by Eq. 4, and the coefficients \({K}_{0}\), \({K}_{1}\), \({K}_{2}\) and \({K}_{3}\) are set to \(20\mathrm{^\circ{\rm C} }\), \(10\mathrm{^\circ{\rm C} }/\mathrm{m}\), \(100\mathrm{^\circ{\rm C} }/{\mathrm{m}}^{2}\) and \(100\mathrm{^\circ{\rm C} }/{\mathrm{m}}^{3}\), respectively.

In this study, three objectives are sought: minimalizing \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\), \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) and \(\overline{W}\). It is aspired to find the optimal values of the two geometrical parameters (\(\xi\) and \(\varphi\)) and \({V}^{m}\) of the ILs. The range of \(\xi\) is \([0, 1]\), \(0\le \varphi \le 2\) [1], and \({V}^{m}\in \{\mathrm{0,1}\}\). Additionally, three constraints, prescribed in Eqs. 15a–15c, are used. Moreover, at the same loading, a nonuniform disc is provided to act as a comparing (nonoptimized) case. The distribution of \({\sigma }_{\theta }\) and \(\overline{{\sigma }_{\mathrm{eq}}}={\sigma }_{\mathrm{eq}}/{\sigma }_{y}\) for this case are shown in Fig. 2.

Fig. 2
figure 2

Nonoptimized case for comparison: a \({\sigma }_{\theta }\), and b \(\overline{{\sigma }_{\mathrm{eq}}}\)

Full size image

5.3 Solution Scheme Stability

To ensure the outcomes' reliability of the proposed algorithms, their stability should be assured primarily. For the FDM, it is found that the solution stability is influenced by \(\delta\). For similar problems, results showed that the convergence of the FDM asymptotic solution occurs at \(\delta =0.0005\mathrm{ m}\) [2, 11]. For the PSO, the values of \(Y\), \({\zeta }_{1}\) and \({\zeta }_{2}\) are set to \(0.729\), \(1.49\) and \(1.49\) that are chosen based on previous researches' experience [10, 38, 43], and also proved high stability as shown in Table 3.

Afterwards, the proper values of \(k\) and \(\tau\) need to be found. Several values were tested while minimizing, for instance, both of \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) and \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) for the extreme case (\(L=10\)). At the beginning, different numbers of \(k\) are examined, and \(k=800\) is assigned to be used. By moving to \(\tau\) while \(k=800\), Fig. 3a shows Pareto frontiers at different values starting from \(\tau =150\) until \(\tau =1500\). At small values, for instance \(\tau =150\) and \(300\), it is crystal clear that the increase of \(\tau\) yielded better Pareto optimal solutions. Therefore, stabilization is still absent, and rising \(\tau\) is compulsory for improved results. From \(\tau =750\), the range of the optimal solutions started to remain approximately static. This range almost has the same divergence as \(\tau\) goes up, but with relatively dissimilar diversity.

Fig. 3
figure 3

Convergence of Pareto frontier of optimal designs for minimizing \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) and \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\): a For different values of \(\tau\), and b For \(\tau =1500\)

Full size image

It is decided that \(\tau =1500\) would be used throughout the whole study. As beyond these two values (\(k=800\) and \(\tau =1500\)), no substantial enhancement occurred for the Pareto frontiers. This can be proven by exploring Fig. 3b. It shows the variation of the optimal solutions with each individual iteration when \(\tau\) is set to \(1500\). Stabilization is noticed to occur starting from \(\tau =800\), and continues to improve by the end of the 1500th iteration. Also, it is time-consuming to increase either of them, which resembles a major drawback for PSO in certain problems that requires great values of \(\tau\) and \(k\).

5.4 Single-Objective Optimization (SOPSO)

In subsections 5.4 and 5.5, a series of optimization models is conducted to enhance certain objective(s). In this subsection, \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\), \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) and \(\overline{W}\) are minimized individually through SOPSO with \(k\) and \(\tau\) set to \(800\) and \(1500\), respectively. These two values are assigned for this SOPSO problem since it is less complicated than the previous problem discussed in subsection 5.3. Outcomes (design variables) of three SOPSO problems are listed in Table 5. These Outcomes ensure that no plasticity is taking place through the disc based on the constraint priorly defined in Eq. 15c. This implies that the \(4.8\mathrm{\%}\) of the discs' area (Fig. 2b) which is plastically deformed based on the developed elastic solution disappeared. In other words, the failure probability can be reduced by applying the present analyses.

Table 5 Results of SOPSO (optimum values of the design variables)
Full size table

For \(\xi\) and \(\varphi\), and while reducing the value of \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\), similar values are obtained regardless of the number of \(L\). These values are also obtained while lessening \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) except at \(L=10\). On the other hand and while assigning \(\overline{W}\) as the aim of the optimization process, dissimilar values are obtained. These resulting \(\xi\) and \(\varphi\) are utilized to draw discs' profiles (Fig. 4). It can be remarked that the attained profiles are concave and so far congruous while minimizing \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) and \({\Delta \sigma }_{{\theta }_{\mathrm{max}}}\). Conversely, optimizing \(\overline{W}\) yielded concave profile only for \(L=3\), which turned to be convex for \(L=5\), \(8\) and \(10\). Therefore, this study is worthy from the viewpoint of obtaining light discs for sophisticated applications including aerospace ones.

Fig. 4
figure 4

Optimized disc profiles of single-objective optimization

Full size image

Regarding \({V}_{l}^{m}\) presented in Table 5, it can be noticed that while optimizing \(\overline{W}\), a value of \({V}^{m}=1\) is obtained for all the ILs since \({\rho }^{m}<{\rho }^{C}\). On the other hand, minimizing \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) for \(L=3\) revealed that the IL should have approximately \(72.2\mathrm{\%}\) of its composition as metal. This value drops by nearly \(36\mathrm{\%}\) as \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) becomes the solo goal of the PSO. Additionally, for \(L=5\), \(8\) and \(10\), it can be figured out that \({V}_{l}^{m}\) decreases steadily from \(l=2\) to the last IL, for the same objective (minimizing \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\)). This trend is logical, as the innermost layer is metal, whereas the outermost layer is completely ceramic. However, for the same three discs, different behaviors are observed as the target of the PSO becomes minimizing \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\).

For example, it is found that metal comprise almost \(48\mathrm{\%}\) of \(l=2\) for the five-layer disc. This value experienced slightly more than a doubling in the third layer, and then levelled off at \(100\mathrm{\%}\) through the fourth layer. Contrariwise, for the eight- and ten-layer discs, \({V}^{m}\) started at relatively high value (\(0.589\) and \(0.6441\), respectively), then went down for the next one and two layers, respectively. These values, afterwards, experienced qualitative leaps and hit their upper limit values, indicating that the following ILs of both discs should be completely made of metal.

Furthermore, these findings, listed in Table 5, are used to calculate and generate the distributions of \({\sigma }_{\theta }\) and compare them with the nonoptimized cases as shown in Fig. 5. Moreover, Table 6 presents some salient numbers of the attained \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\), \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) and \(\overline{W}\), at the instant of minimizing any of them, in comparison with the nonoptimized case.

Fig. 5
figure 5

Comparison between the distributions of \({\sigma }_{\theta }\) for nonoptimized and optimized discs: a \(L=3\), b \(L=5\), c \(L=8\), and d \(L=10\)

Full size image
Table 6 Comparison between the values of \(\left|{{\sigma}_{\theta}}_{\text{max}}\right|\), \({\Delta}{{\sigma}_{\theta}}_{\mathrm{max}}\), and \(\overline{W}\) at the instant of minimizing any of them with respect to the nonoptimized case
Full size table

Looking at Table 6, it can be concluded that \(\left|{\sigma }_{{\uptheta }_{\mathrm{max}}}\right|\) experienced a substantial decline ranging from nearly \(38 - 53.1\%\) for \(L=3-10\) as it is the PSO's goal if compared to the nonoptimized cases readings. However, the values of \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) substantially skyrocketed at that instant. On the other hand, \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) significantly declined by around \(38\mathrm{\%}\) while setting \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) as the target of the SOPSO. This occurred alongside the expected reduction in the values of \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\), which varied between almost \(26\mathrm{\%}\) (\(206.36\mathrm{ MPa}\) when \(L=3\)) and \(46\mathrm{\%}\) (\(46.07\mathrm{ MPa}\) when \(L=10\)) compared to the original values that were about \(278.1\mathrm{ MPa}\) and \(85.05\mathrm{ MPa}\), respectively.

Furthermore, it is obvious that \(\overline{W}\) lessens as a result of minimizing either \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) or \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\). For instance, \(\overline{W}=0.83\) for \(L=3\) if no optimization is conducted. This value went down moderately by nearly \(14.5\mathrm{\%}\) and \(8\mathrm{\%}\) while optimizing \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) and \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\), respectively. However, if minimizing \(\overline{W}\) becomes the target of the PSO, improved results are expected, as it decreases by about \(21\mathrm{\%}\) (\(\overline{W}=0.65\)) for the same disc. This percentage climbed close to \(36\mathrm{\%}\) (\(\overline{W}=0.512\)) for \(L=10\). Alongside this reduction, the values of \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) similarly witnessed a considerable drop. For example, it decreased by almost \(40\mathrm{\%}\) for \(L=8\) compared to \(773.4\mathrm{ MPa}\) for the corresponding nonoptimized case. On the contrary, \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) jumped as an inverse reaction. The nonoptimized cases have \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}=278.12\) and \(101.83\mathrm{ MPa}\) for \(L=3\) and \(8\), respectively. After optimization, these two numbers soared to around \(423.9\mathrm{ MPa}\) for the two discs. Eventually, the current proposed model helps designers for not only decreasing stresses but also for attaining lightweight discs.

5.5 Multi-objective optimization (MOPSO)

As seen from the preceding subsection, studying of any objective individually proportionately/inversely affects the other two objectives. Therefore, multi-objective optimization should be accomplished in order to help a decision-maker for his choice. Also, it is noticed that the range of variation of the parameters increases, and improved results are obtained with considering more \(L\). Additionally, the objectives for \(L=8\) and \(10\) are, as expected, improved than those of \(L=3\) or \(5\). Furthermore, it can be noticed from Fig. 2a that \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) decreases with the increase of the \(L\) due to the reduction of the property mismatch between successive layers. Therefore, increasing the structural safety can be attained by increasing the number of layers. Accordingly, the rest of this article would consider only discs with \(L=8\) and \(10\).

In this subsection, a combined case of the previously-stated three objectives is examined through a MOPSO problem to minimize them concurrently. The design variables for all calculations are likewise the ones in the SOPSO problem.

According to the MOPSO results, the optimal geometrical parameters are almost in line with those resulted from SOPSO. These values yielded convex, concave and linear disc profiles. In terms of \({V}_{l}^{m}\), there is such a great variation in its values. It can be mentioned that the more the desired decline in \(\overline{W}\) the more the increase in \({V}_{l}^{m}\), and this is practically logic as the density of the metal is lower than that of the ceramic (Table 4). Alternatively, seeking for decreasing \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) to its minimum feasible value entails a reduction in the metallic constituent percentage through the ILs. This percentage keeps dropping by moving towards the outermost layer. Between these two trends comes the behavior of lessening \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\). In general, it can be stated that there is a compromise between the shares of the metal and the ceramic through each IL. It cannot be stated explicitly that metal's percentage is surpassed by the ceramic amount or vice versa.

Numerically, some extreme points are presented in Fig. 6 and Table 7. It is seen that minimizing \(\overline{W}\) produces a significant rise for \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) and vice versa. For example, \(\overline{W}\) has its minutest value of \(0.526\) that corresponds to \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}=423.15\mathrm{ MPa}\) for the eight-layer disc (Fig. 6a and Table 7). On the other hand, if the configuration of the minimum value of \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) is chosen for design, which is marginally above \(59.01\mathrm{ MPa}\) for the same disc; \(\overline{W}\) would be equal to \(0.767\) that still outweighs the value of \(\overline{W}\) at the point of minimum \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) by about \(27\mathrm{\%}\). Furthermore, if the configuration yielding the least \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) is chosen for design, a reduction in the other two objectives would take place unlike nominating either their two corresponding minimum-value configurations. For instance, \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) has a minimum value of \(361.1\mathrm{ MPa}\) when \(L=10\), according to Fig. 6b and Table 7. With this value, \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) is slightly more than \(374\mathrm{ MPa}\). Such value is more than eightfold of the minimum reachable \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) (\(46.07\mathrm{ MPa}\)), and it is exceeded by about \(48\mathrm{ MPa}\) at the minimum point of \(\overline{W}\).

Fig. 6
figure 6

Multi-objective optimization (MOPSO) at \(\omega =500 \mathrm{rad}/\mathrm{s}\) for: a \(L=8\), and b \(L=10\)

Full size image
Table 7 Values of \(\overline{{{W}}}\), \(\left|{{\sigma}_{\theta}}_{\mathrm{max}}\right|\) and \({\Delta}{{\sigma}_{\theta}}_{\mathrm{max}}\) at their optimum positions according to MOPSO results for \({L}=8\) and \(10\) (Extracted from Fig. 6)
Full size table

As seen from all the previous set of results, the ceramic constituent for some objectives is rare or even absent in some ILs despite the presence of \({T}_{r}\), which is rather perplexing. This behavior depends on: (i) the centrifugal force (\({h}_{r}{\rho }_{r}{\omega }^{2}{r}^{2}\)), and (ii) the proposed \({T}_{r}\) values.

Although, the considered problems encompass both of \({T}_{r}\) and a centrifugal action; the impacts of the latter one are the dominant due to the great value of \(\omega\). Thus, the stresses stemming from the centrifugal force greatly outweigh those of the thermal load even if metal, which has smaller (greater) \(\rho\) (\(\alpha\)) than ceramic, is used. Therefore, the PSO nondominant particles would go for the small \(\rho\) constituent avoiding the substantial increase for the centrifugal force. Obviously, this is not always to be occurring. It relies on \(\omega\), \({T}_{r}\), \(\beta\), and some in-site conditions.

For that sake, another case of MOPSO, shown in Fig. 7 is provided for a ten-layer disc with \(\omega =200\mathrm{ rad}/\mathrm{s}\) in order to figure out whether there would be a great impact on the design variables or not. Results are compared with those displayed in Fig. 6b (\(\omega =500\mathrm{ rad}/\mathrm{s}\)). Some salient numbers are grouped in Table 8, where it is evident that the values of \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) and \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) decreased by the corresponding decline of \(\omega\). This is attributed to the significant drop of the centrifugal force. Additionally, larger applicable minimum \(\overline{W}\) is obtained. On the other hand, it is seen that there are no great variations for the thickness profile at the minimum applicable values of each objective. In other words, the same profile (concave or convex) is obtained, but with a small variation in its curvature.

Fig. 7
figure 7

Multi-objective optimization (MOPSO) at \(\omega =200 \mathrm{rad}/\mathrm{s}\) for a ten-layer disc

Full size image
Table 8 Comparison between the extreme values of TOPSO. For each objective, upper and lower values are for \(\omega =200 \mathrm{rad}/\mathrm{s}\) and \(\omega =500 \mathrm{rad}/\mathrm{s}\), respectively
Full size table

Regarding \({V}_{l}^{m}\), a great swing in the behaviors can be detected at the minimum \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) and \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) by the decline of \(\omega\). Generally, the percentage of metal increased by approximately \(6\) and \(24\mathrm{\%}\) for \(l=2\) and \(3\), respectively, at the minimum \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\). This percentage skyrocketed at \(l=4\) to be fully composed of metal. In contrast, this drop of \(\omega\) led to the presence of ceramic at the final two ILs, where it comprised nearly \(51\) and \(81\mathrm{\%}\), respectively, of their composition. This can be traced back to the strong effect of \({T}_{r}\) defined in Eq. 4, which increases towards the outer surface and requires smaller \(\alpha\), and hence smaller deformation. Similar readings can be observed through the same layers at the smallest \(\overline{W}\), but with lesser values. For example, the final IL that was fully metal at \(\omega =500\mathrm{ rad}/\mathrm{s}\) became composed of metal (\(79\mathrm{\%}\)) and ceramic (\(21\mathrm{\%}\)) at the new considered \(\omega\). In contrast, at minimum \(\Delta {\sigma }_{{\uptheta }_{\mathrm{max}}}\), one common behavior is observed. The share of metal through all the ILs declined by the considered drop of \(\omega\). This reduction ranged from around \(7{\text{ - }}41\%\).

Accordingly, no single configuration can be obtained for all discs at all working conditions. An optimum configuration depends on the geometrical, operating, and material parameters (disc radii, \({h}_{r}\), \(\omega\), \({T}_{r}\), \(\rho\) and \(\alpha\)). This is definitely alongside the desired objectives and prescribed constraints of the optimization problem.

6 Conclusion

In this article, a nonuniform thickness sandwich (multilayer) disc was considered. Its inner and outer layers (faces) were pure metal and ceramic, respectively. The disc's core was made of number of equal width layers with unique \(V\) for each one forming an FG structure. The considered rotating disc was exposed to a nonlinear thermal load and an external pressure. The numerical FDM was used to attain the thermoelastic behaviors that were enhanced through the notable PSO. Under prescribed constraints, there were three objectives considered: \(\overline{W}\), \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) and \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\). These objectives were minimized through having the optimal \({h}_{r}\) and \({V}_{l}^{m}\), i.e. \(l\in \{2, L-1\}\). Some salient conclusions can be abbreviated to the following points:

  • For SOPSO: \({V}_{l}^{m}\) witnessed a significant variation depending on the considered objective and \(L\). For example, all the ILs should be made of \(100\mathrm{\%}\) metal to have the minimum \(\overline{W}\), that is consistent with the constituent of low density. Regarding objectives, minimalizing \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) led to a significant jump (drawback) for the value of \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\), which, in contrast, resulted in reducing \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\). Additionally, a beneficial reduction for the values of \(\overline{W}\) occurred by setting either \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) or \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) as the PSO's target.

  • In terms of MOPSO: It was observed that the ceramic percentage through all the ILs exceeded (was surpassed by) the metal's share while targeting smaller values of \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) (\(\overline{W}\)). Alternatively, it could not be generalized that one constituent outweighed the other while considering lesser values of \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\).

  • There was a variety in the obtained profiles depending on \(L\) and the desired objectives. For \(L=5\), \(8\) and \(10\), convex (concave) profiles were the best to have least \(\overline{W}\) (\(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) and \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\)). However, concave profiles were always the optimal choice for the three-layer disc.

  • Increasing the disc's layers, which decreases the property mismatch at the interfaces, yielded better performance and reduced the stresses at a certain \(\overline{W}\), or a smaller \(\overline{W}\) was feasible if the same value of \(\left|{\sigma }_{{\theta }_{\mathrm{max}}}\right|\) or \(\Delta {\sigma }_{{\theta }_{\mathrm{max}}}\) to be chosen for design.

Eventually, these findings are confined to the considered disc, load, geometry, and materials in this study. Therefore, it is recommended to optimize the performance of any disc before fabrication to meet certain requirements, ensure efficient and stable working, and limit its failure probability.