Biomechanics of Swimming Microbes in Atherosclerotic Region with Infusion of Nanoparticles

Abstract

This study is focused to investigate the blood flow pattern with motion of motile gyrotactic microorganisms. Since nanoparticles play an essential factor for enhancing delivery efficiency in vascular flow therefore physiochemical properties of these particles are considered in this examination. Prandtl fluid characteristics are instigated to discuss the blood flow rheology. Moreover, considerations of gyrotactic microbes with nanoparticles will exaggerate the thermal features of considered base fluid. The governing model output containing coupled nonlinear systems is evaluated by HPM technique. The features of flow defining parameters in an anisotropic stenotic region with motile microbes are inspected and presented through different illustrations. It is concluded from the governing nanofluid model that with addition of gyrotactic microbe’s hemodynamics factors of stenotic lesion are enhanced. Heat transfer rate phenomena depict opposite trends for nanoparticles key parameters involved in a governing problem.

1 Introduction

Study of biological problems is an important class of bio-fluid mechanics. This study helps to understand normal features of blood flow through an organism and offers different methodologies to invent artificial organs. Principle of fluid mechanics suggests valuable outcomes for understanding complex features related with blood flow problems which are not very much cleared from experimental techniques. These mathematical models are useful for speculative study of recently developed treatment procedures like identification of arterial infections, drug delivery and designing several artificial organs. Different researchers conclude significant results of blood flow problems through mathematical models [1,2,3]. Arteriosclerosis is a major arterial disease which severely affects blood circulation. These arteriosclerotic lesions normally grow at certain positions, such as in carotid bifurcations, abdominal aorta and coronary arteries. It has been concluded from different investigations that the localization and initiation of these lesions are closely related with hemodynamic factors such as resistance in flow and stress on arterial walls. Several scientists demonstrated that the growth of arteriosclerosis is also associated strongly with features of blood flow in the arteries [4,5,6]. Stergiopulos et al. [7] discussed blood flow in flexible stenosis. Young and Tsai [8] considered an experiment on the arterial blood flow model with atherosclerosis and concluded that the hemodynamic feature shows an essential role in the expansion and development of the arterial diseases. Siegel et al. [9] considered different stress levels in vascular atherosclerotic arteries. Tian et al. [10] discussed pulsatile flow of non-Newtonian mathematical models through atherosclerosis with various types of severity. Rabby et al. [11] discussed the blood flow problem by treating it as Newtonian laminar fluid in an axis-symmetric stenotic artery.

Catheter is an effective technique in the modern era of medicine to treat different arterial diseases. In clinical experiments investigation of arterial blood flow, velocity and pressure rate catheter tool is effectively used. It can also be used as diagnostic technique tools like angiography, intravascular ultrasounds and for balloon angioplasty as well. In recent research catheters with different sizes have been used with the evolution of coronary balloon angioplasty. The consequence of catheterization with several physiological characteristics has been discussed by [5, 12]. Bjorno and Pettersson [13] discussed catheterization effects with and without atherosclerosis with different models. Srivastava and Rastogi discussed a two-phase macroscopic model with a narrow-catheterized artery [14]. Sankar and Hemlatha [15] considered Herschel–Bulkley fluid through catheterized blood vessels.

Nanoparticles-mediated blood flow is significantly contributing in the field of medicine to enhance the efficiency of delivering diagnostic and therapeutic agents [16, 17]. These new phenomena prevent conditions like cancer and combat human pathogens such as bacteria, which is investigated by many scientists [18, 19]. Fullstone et al. [20] formulated a nanoparticle agent-based model through capillaries under blood flow. Li et al. [21] presented the magnetic nanoparticles-based model for the development of advanced medical applications. Ijaz et al. [22] presented a heat transfer-based hybrid nanofluid model to demonstrate the hemodynamic features. For more references see [23,24,25,26,27,28,29,30,31,32,33,34].

Bioconvection is a microscopic convection in fluid that usually appears due to moments of microorganisms that are a little denser than fluid. This moment of microorganisms is distributed into different categories such as oxytactic, chemotaxis and negative gravitaxis. Gyrotactic organisms are used in several industrial products such as biodiesel, bio-fertilizers and biofuel and bio microsystems. Moreover, bioconvection phenomena play a key part in fuel cells, biological polymer mixture and environmental systems. Firstly, bioconvection phenomena with induction of nanoparticles are introduced by Kuznetsova and Avramenko [35]. Bhatti et al. [36] presented Jeffrey-based nanofluid formulation with movement of motile organisms. Akbar et al. [37] discussed the mechanism of bioconvection flow through the symmetric channel in the presence of nanoparticles. Later on, different researchers have presented various models to discuss the features of gyrotactic nanofluid features [38,39,40,41].

In this analysis non-Newtonian-based Prandtl nanofluid model is considered. The impact of the hemodynamic factor is evaluated under gyrotactic microorganism impact through the stenotic region. Inspiration of catheter with different degree is also considered in this analysis to attenuate the hemodynamics factors of arterial lesions. Flow pattern of blood in the presence of microorganism is plotted through streamline configuration.

2 Mathematical Model

The mass and momentum equations for an incompressible fluid are given by

$$\mathrm{div} \overline{\mathbf{V} }=0,$$

(1)

$$\rho \frac{d\overline{\mathbf{V}}}{dt }=\mathrm{div} \mathbf{T}+\uprho \mathbf{f} ,$$

(2)

where

$$\mathbf{T}=-p\mathbf{I}+\overline{\mathbf{S} }$$

(3)

where in above $\overline{\mathbf{S} }$ represents extra stress tensor of non-Newtonian Prandtl fluid model. The constitutive equation for the Prandtl fluid model is suggested by [44] and given as

$$\overline{\mathbf{S} }=\frac{A{\mathrm{sin}}^{-1} \left\{\frac{1}{C}{\left[{\left(\frac{\partial \overline{u} }{\partial \overline{z} }\right)}^{2}+{\left(\frac{\partial \overline{w} }{\partial \overline{r} }\right)}^{2}\right]}^{\frac{1}{2}}\right\}}{{\left[{\left(\frac{\partial \overline{u} }{\partial \overline{z} }\right)}^{2}+{\left(\frac{\partial \overline{w} }{\partial \overline{r} }\right)}^{2}\right]}^{\frac{1}{2}}}\frac{\partial \overline{w} }{\partial \overline{r} } ,$$

(4)

3 Mathematical Formulation

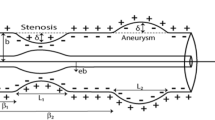
In this examination, we have considered a steady, laminar, incompressible viscous nanofluid flowing through a tube of length $L$ with insertion of catheter having radius $\kappa$. To address the theoretical model of a swimming motile gyrotactic microorganism with nanoparticles in non-Newtonian blood flow through anisotropic stenotic region with enclosure of catheter, cylindrical polar coordinates are assumed as ($r,\theta ,z$), in which $z$ represents the axial, $r$ represents the radial and $\theta$ represents the circumferential directions (as shown in Fig. 1$)$. Blood rheology is studied in this analysis by treating it as a Prandtl nano fluid. The anisotropic region with catheter insertion having time-variant features is described mathematically as [22]

Fig. 1

Geometry of catheter anisotropic region

$$\frac{R\left(z\right)}{{z}_{0}}=\left\{\begin{array}{ll}\tau \left(t\right)[\xi z+{e}_{0}-\frac{\delta \mathit{cos}\varphi }{{L}_{0}}(11-\frac{94}{3{L}_{0}}\left(z-d\right)+\frac{32}{{L}_{0}^{2}}{\left(z-d\right)}^{2}-\frac{32}{{L}_{0}^{3}}{\left(z-d\right)}^{3}))],&\quad d\le z\le \frac{3}{2}{L}_{0},\\ \tau \left(t\right)\left(1+\xi z\right), &\quad otherwise.\end{array}\right\} ,$$

(5)

in above, $\delta$ represents stenosis height, ${e}_{0}$ represents radius of non-stenotic area, $\Psi$ represents tapering angle, and is calculated from $\xi =\mathit{tan}\Psi ,$ which represents the tapered vessel's slope, defined as

$$\Psi =\left\{\begin{array}{lll}<0, &\quad converging &\quad region,\\ 0,& \quad non\; tappered &\quad region\\ >0, &\quad diverging&\quad region.\end{array}\right.,$$

(6)

in above $\tau (t)$ is a time-variant parameter that is given as

$$\tau \left(t\right)=1+\frac{{\alpha }_{o}(1-\mathit{cos}\omega t)}{{e}^{{\alpha }_{o}\omega t}},$$

(7)

in above $\upomega$ represents radial frequency of the forced oscillation and ${\alpha }_{o}$ as arbitrary constant.

The equations for the governing flow model are written as follows,

$$\frac{\partial \overline{u} }{\partial \overline{r} }+\frac{\overline{u} }{\overline{r} }+\frac{\partial \overline{w} }{\partial \overline{z} }=0,$$

(8)

$${\rho }_{f}\left(\frac{\partial \overline{u} }{\partial \overline{t} }+\overline{u }\frac{\partial \overline{u} }{\partial \overline{r} }+\overline{w }\frac{\partial \overline{u} }{\partial \overline{z} }\right)=-\frac{\partial \overline{p} }{\partial \overline{r} }+\left(\frac{1}{\overline{r}}\frac{\partial }{\partial \overline{r} }\left(\overline{r }{\overline{S} }_{\overline{r }\overline{r} }\right)\right)+\frac{\partial }{\partial \overline{z} }\left(\overline{r }{\overline{S} }_{\overline{rz} }\right)-\frac{{\overline{S} }_{\overline{\theta \theta }} }{\overline{r} },$$

(9)

$$\begin{aligned}& {\rho }_{f}\left(\frac{\partial \overline{v} }{\partial \overline{t} }+\overline{u }\frac{\partial \overline{v} }{\partial \overline{r} }+\overline{w }\frac{\partial \overline{v} }{\partial \overline{z} }\right)\\ &\quad=-\nabla .\overline{p }+{\nabla }^{2}.\overline{V }+\left[{\rho }_{f}{T}_{e}\left(1-{C}_{1}\right)\left(T-{T}_{1}\right)\right.\\ &\qquad-\left({\rho }_{p}-{\rho }_{f}\right){T}_{e}\left(C-{C}_{1}\right)\\ &\qquad\left.-\left(n-{n}_{1}\right)\vartheta \left({\rho }_{m}-{\rho }_{f}\right)\right]\end{aligned}$$

(10)

$$\begin{aligned}\left(\overline{u }\frac{\partial \overline{T} }{\partial \overline{r} }+\overline{w }\frac{\partial \overline{T} }{\partial \overline{z} }\right)&={\alpha }_{f}\left(\frac{{\partial }^{2}\overline{T} }{\partial {\overline{r} }^{2}}+\frac{1}{\overline{r} }\frac{\partial \overline{T} }{\partial \overline{r} }+\frac{{\partial }^{2}\overline{T} }{\partial {\overline{z} }^{2}}\right)\\ &\quad +\tau \left[{D}_{\overline{B} }\left(\frac{\partial \overline{C} }{\partial \overline{r} }\frac{\partial \overline{T} }{\partial \overline{r} }+\frac{\partial \overline{C} }{\partial \overline{z} }\frac{\partial \overline{T} }{\partial \overline{z} }\right)\right.\\ &\quad \left. +\frac{{D}_{\overline{T}} }{{\overline{T} }_{1}}\left\{{\left(\frac{\partial \overline{T} }{\partial \overline{r} }\right)}^{2}+{\left(\frac{\partial \overline{T} }{\partial \overline{z} }\right)}^{2}\right\}\right],\end{aligned}$$

(11)

$$\left(\overline{u }\frac{\partial \overline{C} }{\partial \overline{r} }+\overline{w }\frac{\partial \overline{C} }{\partial \overline{z} }\right)={D}_{\overline{B} }\left(\frac{{\partial }^{2}\overline{C} }{\partial {\overline{r} }^{2}}+\frac{1}{\overline{r} }\frac{\partial \overline{C} }{\partial \overline{r} }+\frac{{\partial }^{2}\overline{C} }{\partial {\overline{z} }^{2}}\right)+\frac{{\overline{D} }_{T}}{{\overline{T} }_{1}}\left(\frac{{\partial }^{2}\overline{T} }{\partial {\overline{r} }^{2}}+\frac{1}{\overline{r} }\frac{\partial \overline{T} }{\partial \overline{r} }+\frac{{\partial }^{2}\overline{T} }{\partial {\overline{z} }^{2}} \right),$$

(12)

in above p represents pressure, $\mathrm{\vartheta }$ as average volume of the microorganism, $n$ as concentration of the microorganism, ${\rho }_{f}$ as density of the base fluid, ${\rho }_{p}$ as density of the nanoparticles, ${\rho }_{m}$ as density of the microorganism, $g$ as gravity vector, ${T}_{e}$ as base fluid volumetric coefficient and $\mu$ as the suspension coefficient of the nanoparticle.

The temperature equation is written as follows:

$$\begin{aligned}\left(\overline{u }\frac{\partial \overline{T} }{\partial \overline{r} }+\overline{w }\frac{\partial \overline{T} }{\partial \overline{z} }\right)&={\overline{\alpha }}_{f}\left(\frac{{\partial }^{2}\overline{T} }{\partial {\overline{r} }^{2}}+\frac{1}{\overline{r} }\frac{\partial \overline{T} }{\partial \overline{r} }+\frac{{\partial }^{2}\overline{T} }{\partial {\overline{z} }^{2}}\right)\\ &\quad+\tau \left[\left(\frac{\partial \overline{C} }{\partial \overline{r} }\frac{\partial \overline{T} }{\partial \overline{r} }+\frac{\partial \overline{T} }{\partial \overline{z} }\frac{\partial \overline{C} }{\partial \overline{r} } \right)\right. \\ &\quad\left.+\frac{{\overline{D} }_{T}}{{\overline{T} }_{0}}\left\{{\left(\frac{\partial \overline{T} }{\partial \overline{r} }\right)}^{2}+{\left(\frac{\partial \overline{T} }{\partial \overline{z} }\right)}^{2}\right\}\right] , \end{aligned}$$

(13)

in above thermophoretic diffusion term is represented as ${\overline{D} }_{T}$,${\overline{D} }_{B}$ as Brownian diffusion term, $\tau$ as ratio of nanoparticle material heat capacity to fluid heat capacity, ${k}_{f}$ as coefficient of thermal conductivity, $(\rho c{)}_{f}$ and $(\rho c{)}_{p}$ as coefficients of volumetric heat capacity and nanoparticle.

Equation of concentration is designed as

$$\left(\overline{u }\frac{\partial \overline{C} }{\partial \overline{r} }+\overline{w }\frac{\partial \overline{C} }{\partial \overline{z} }\right)={D}_{\overline{B} }\left(\frac{{\partial }^{2}\overline{C} }{\partial {\overline{r} }^{2}}+\frac{1}{\overline{r} }\frac{\partial \overline{C} }{\partial \overline{r} }+\frac{{\partial }^{2}\overline{C} }{\partial {\overline{z} }^{2}}\right)+\frac{{\overline{D} }_{T}}{{\overline{T} }_{0}}\left(\frac{{\partial }^{2}\overline{T} }{\partial {\overline{r} }^{2}}+\frac{1}{\overline{r} }\frac{\partial \overline{T} }{\partial \overline{r} }+\frac{{\partial }^{2}\overline{T} }{\partial {\overline{z} }^{2}}\right),$$

(14)

Equation of gyrotactic microorganism is designed as

$$\begin{aligned}&\frac{\partial \overline{n} }{\partial \overline{t} }+\overline{u }\frac{\partial \overline{u} }{\partial \overline{r} }+\overline{w }\frac{\partial \overline{n} }{\partial \overline{z} }+\frac{\overline{b}{W }_{\overline{c}} }{{\overline{C} }_{0}-{\overline{C} }_{1}}\left[\frac{\partial }{\partial \overline{r} }\left(\overline{n }\frac{\partial \overline{C} }{\partial \overline{r} }\right)+\frac{\partial }{\partial \overline{z} }\left(\overline{n }\frac{\partial \overline{C} }{\partial \overline{z} }\right) \right]\\ &\quad =-{D}_{\overline{mo} }\left[\frac{{\partial }^{2}\overline{n} }{\partial {\overline{r} }^{2}}+\frac{1}{\overline{r} }\frac{\partial \overline{n} }{\partial \overline{r} }+\frac{{\partial }^{2}\overline{n} }{\partial {\overline{z} }^{2}}\right]\end{aligned}$$

(15)

in above Eq. (15) chemotaxis coefficient is represented by $\overline{b }$, ${W}_{\overline{c} }$ as coefficient of swimming speed and ${D}_{\overline{mo} }$ as coefficient of microorganisms diffusivity.

The boundary condition applied to the anisotropic stenotic geometry with catheter enclosure is defined as

$$\overline{w }=\overline{\gamma }, \overline{T }={\overline{T} }_{1},\overline{C }={\overline{C} }_{1},\overline{n }={\overline{n} }_{1},\quad \mathrm{ at }r=h,$$

(16)

$$\overline{w }=0,\overline{T }={\overline{T} }_{0},\overline{C }={\overline{C} }_{0},\overline{n }={\overline{n} }_{0},\quad \mathrm{ at }r=\epsilon .$$

(17)

in above $\gamma$ represents as constant slip condition on wall of anisotropic region. Dimensionless variables implemented in this study are

$$\begin{aligned}r&=\frac{\overline{r}}{{e }_{0}}, z=\frac{\overline{z}}{{s }_{1}}, w=\frac{\overline{w}}{{u }_{a}}, \gamma =\frac{\overline{\gamma }}{{u}_{a}}, \\ u&=\frac{{s}_{1}\overline{u}}{{u }_{a}\delta },p=\frac{{e}_{0}^{2}\overline{p}}{{u }_{a}{s}_{1}\mu } , h=\frac{\overline{h}}{{e }_{0}},\end{aligned}$$

$$\begin{aligned}{R}_{en}&=\frac{{s}_{1}{u}_{a}\rho }{\mu } , {S}_{rr}=\frac{{s}_{1}{\overline{S} }_{\dot{r}\dot{r}}}{{u}_{a}\mu } ,\\ {S}_{rz}&=\frac{{e}_{0}{\overline{S} }_{\dot{r}\dot{z}}}{{u}_{a}\mu } , {S}_{zz}=\frac{{s}_{1}{\overline{S} }_{\dot{z}\dot{z}}}{{u}_{a}\mu } , {S}_{\theta \theta }=\frac{{s}_{1}{\overline{S} }_{\dot{\theta }\dot{\theta }}}{{u}_{a}\mu },\end{aligned}$$

$$\theta =\frac{\overline{T }-{\overline{T} }_{1}}{{T}_{0}-{\overline{T} }_{1}} , \varphi =\frac{\overline{C }-{\overline{C} }_{1}}{{{\overline{C} }_{0}-\overline{C} }_{1}} , {\chi =\frac{\overline{n }-{\overline{n} }_{1}}{{\overline{n} }_{0}-{n}_{1}}}$$

(18)

${u}_{a}$ is the average velocity coefficient. The governing equation of mathematical model can be written as,

$$\frac{\partial p}{\partial r}=0 ,$$

(19)

$$-\frac{\partial p}{\partial z}+\frac{1}{r}\frac{\partial }{\partial r}\left[r{S}_{rz}\right]+{T}_{g}\theta +{N}_{g}\varphi -{R}_{b}\chi =0,$$

(20)

$$\left[{T}_{b}\left(\frac{\partial \varphi }{\partial r}\right)+{T}_{t}{\left(\frac{\partial \theta }{\partial r}\right)}^{2}\right]\left(\frac{\partial \theta }{\partial r}\right)+\frac{1}{r}\frac{\partial }{\partial r}\left(\frac{\partial \theta }{\partial r}r\right)=0 ,$$

(21)

$$\frac{1}{r}\frac{\partial }{\partial r}\left(\left(\frac{\partial \varphi }{\partial r}\right)r\right)+\frac{{T}_{t}}{{T}_{b}}\left(\frac{1}{r}\frac{\partial }{\partial r}\left(\frac{\partial \theta }{\partial r}r\right)\right)=0.$$

(22)

$$\frac{1}{r}\frac{\partial }{\partial r}\left(\frac{\partial \chi }{\partial r}r\right)-{P}_{t}\left[\left(\frac{\partial \chi }{\partial r}\right)\left(\frac{\partial \varphi }{\partial r}\right)+\left(\Theta +\chi \right)\frac{{\partial }^{2}\varphi }{\partial {r}^{2}}\right]=0 ,$$

(23)

where in above defined governing equation of flow model contains following variables,

$${T}_{b}=\frac{{D}_{B}({C}_{0}-{C}_{1})(\rho c{)}_{p}}{{k}_{f}(\rho c{)}_{f}} ,{T}_{t}=\frac{{D}_{B}({T}_{0}-{T}_{1})(\rho c{)}_{p}}{{k}_{f}{T}_{1}(\rho c{)}_{f}}, \alpha =\frac{A\mu }{C}, \beta =\frac{A{{u}_{a}}^{2}{{e}_{0}}^{2}}{6\mu {C}^{3}},$$

$${N}_{g}=-\frac{{T}_{e}g\left({\rho }_{p}-{\rho }_{f}\right){e}_{0}^{2}\left({T}_{0}-{T}_{1}\right)}{\mu {u}_{a}} , {P}_{t}=\frac{b{W}_{c}}{{D}_{mo}} , \Theta =\frac{{n}_{1}}{{n}_{0}-{n}_{1}} ,$$

$${T}_{g}=\frac{{T}_{e}g{\rho }_{f}{e}_{0}^{2}(1-{C}_{1})(T-{T}_{1})}{\mu {u}_{a}} ,{R}_{b}=\frac{({n}_{0}-{n}_{1})\Theta ({\rho }_{m}-{\rho }_{f})g{e}_{0}^{2}}{\mu {u}_{a}} ,$$

(24)

in above Eq. (24), ${T}_{g}$ represents local temperature Grashof number,${ N}_{g}$ represents local nanoparticle Grashof number, ${R}_{b}$ represents bioconvection Rayleigh number, ${T}_{b}$ represents Brownian motion variable, ${T}_{t}$ represents thermophoresis variable,${ P}_{t}$ represents Peclet number, $\Theta$ represents constant, $\alpha \mathrm{and} \beta$ represent as fluid features defining parameter.

Prandtl fluid shear stress after using (24) onto (4) is given as

$${S}_{rz}=\left[\alpha \left(\frac{\partial w}{\partial r}\right)+\beta {\left(\frac{\partial w}{\partial r}\right)}^{3}\right],$$

(25)

After using dimensional analysis, the geometry of the associated conditions is as follows,

$$w=0,\theta =1, \varphi =1,\chi =1 , at r=\epsilon ,$$

$$w=\gamma , \theta =0, \varphi =0 ,\chi =0 , at r=h.$$

(26)

4 Analytical Solution

To deal with nonlinear coupled differential equations, the HPM technique is used to solve the above governing model. Using the significant features of embedding parameter $q$, the above governing model can be written as

$$\begin{aligned}H\left(q,w\right)&=\left(1-q\right)\left[L\left(w\right)-L\left({w}_{10}\right)\right]\\ & \quad+q\left[ L\left(w\right)+\frac{1}{r}\frac{\partial }{\partial r}\left(r\left(\beta {\left(\frac{\partial w}{\partial r}\right)}^{3}\right)\right.\right.\\ &\quad\left. +{T}_{g}\theta +{N}_{g}\varphi -{R}_{b}\chi -\frac{\partial p}{\partial z}\right],\end{aligned}$$

(27)

$$H\left(q,\theta \right)=\left(1-q\right)\left[L\left(\theta \right)-L\left({\theta }_{10}\right)\right]+q\left[L\left(\theta \right)+{T}_{b}\left(\frac{\partial \varphi }{\partial r}\right)\left(\frac{\partial \theta }{\partial r}\right)+{T}_{b}{\left(\frac{\partial \theta }{\partial r}\right)}^{2}\right],\quad$$

(28)

$$H\left(q,\varphi \right)=\left(1-q\right)\left[L\left(\varphi \right)-L\left({\varphi }_{10}\right)\right]+q\left[L\left(\varphi \right)+\frac{{T}_{t}}{{T}_{b}}\left(\frac{1}{r}\frac{\partial }{\partial r}\left(\frac{\partial \theta }{\partial r}r\right)\right)\right],$$

(29)

$$H\left(q,\chi \right)=\left(1-q\right)\left[L\left(\chi \right)-L\left({\chi }_{10}\right)\right]+q\left[L\left(\chi \right)-\left(\left({P}_{t}\left(\frac{\partial \chi }{\partial r}\right)\left(\frac{\partial \varphi }{\partial r}\right)\right)+\left(\chi +\Theta \right)\frac{{\partial }^{2}\varphi }{\partial {r}^{2}}\right)\right],$$

(30)

The linear operators are written as,

$${L}_{r}\left(\theta \right)=\frac{1}{r}\left(\frac{\partial }{\partial r}\left(r\frac{\partial \theta }{\partial r}\right)\right), {L}_{r}\left(\varphi \right)=\frac{1}{r}\left(\frac{\partial }{\partial r}\left(r\frac{\partial \varphi }{\partial r}\right)\right),$$

$${L}_{r}\left(\chi \right)=\frac{1}{r}\left(\frac{\partial }{\partial r}\left(r\frac{\partial \chi }{\partial r}\right)\right),{L}_{r}\left(w\right)=\frac{1}{r}\left(\frac{\partial }{\partial r}\left(r\alpha \frac{\partial w}{\partial r}\right)\right),$$

(31)

The initial guesses are selected as,

$${\theta }_{10}=\left(\frac{\mathit{log}\left[h\right]-log[r]}{\mathit{log}\left[h\right]-log[\epsilon ]}\right),{ \varphi }_{10}=\left(\frac{\mathit{log}\left[h\right]-log[r]}{\mathit{log}\left[h\right]-log[\epsilon ]}\right),$$

$${\chi }_{10}=\left(\frac{\mathit{log}\left[h\right]-log[r]}{\mathit{log}\left[h\right]-log[\epsilon ]}\right), {w}_{10}=\left(\frac{1}{\alpha }\right)\left(\frac{\gamma Log[r]-\gamma Log[\epsilon ]}{Log[h]-Log[\epsilon ]}\right)$$

(32)

According to HPM, we obtain systems problems of the governing model by using the following series representation

$$\theta ={\theta }_{0}+q{\theta }_{1}+{q}^{2}{\theta }_{2}+O{\left(q\right)}^{3},$$

$$\varphi ={\varphi }_{0}+q{\varphi }_{1}+{q}^{2}{\varphi }_{2}+O{\left(q\right)}^{3},$$

$$\chi ={\chi }_{0}+q{\chi }_{1}+{q}^{2}{\chi }_{2}+O{\left(q\right)}^{3},$$

$$w={w}_{0}+q{w}_{1}+{q}^{2}{w}_{2}+O{\left(q\right)}^{3}.$$

(33)

Flow model defining equations from (27) to (30) are converted in component form by using above Eq. (33) as suggested by [42, 43]. Moreover, for desired solution embedding parameter is substituted as ${\varvec{q}}\to 1$ in the series expansion Eq. (33),

$$\varphi ={\varphi }_{0}+{\varphi }_{1}+{\varphi }_{2}+\dots ,$$

$$\theta ={\theta }_{0}+{\theta }_{1}+{\theta }_{2}+\dots ,$$

$$\chi ={\chi }_{0}+{\chi }_{1}+{\chi }_{2}+\dots ,$$

$$w={w}_{0}+{w}_{1}+{w}_{2}+\dots .$$

(34)

Obtained component form solution calculated from HPM technique is further solved by using Mathematica solver and HPM numerical code. Moreover, hemodynamics factors are evaluated further by using velocity solution.

5 Impedance Resistance

Pressure drop in anisotropic stenotic region can be obtained from

$$ \Delta p^{\prime} = \mathop \int \limits_{0}^{{\sigma ^{\prime}}} \left( { - \frac{{dp^{\prime}}}{{dz}}} \right){\text{d}}z, $$

(35)

above Eq. (35) helps to determine resistance to flow by using following relation between pressure drop and flow rate

$$ \lambda = \frac{{{\Delta} p^{\prime } }}{Q} = \left\{ {\mathop \int \limits_{0}^{{\sigma _{0} }} I\left( z \right)|_{{h = 1}} {\text{d}}z + \mathop \int \limits_{{\sigma _{0} = }}^{{\sigma _{0} + e_{1} }} I\left( z \right){\text{d}}z + \mathop \int \limits_{{\sigma _{0} + e_{1} }}^{{\mathop L\limits^{} }} I\left( z \right)\left| {_{{h = 1}} } \right.{\text{d}}z} \right\}. $$

(36)

where

$$Q={\int }_{0}^{h}rw\mathrm{d}r,$$

(37)

expression of pressure gradient in an anisotropic region is determine by using above equation and given as.

$$\frac{dp}{dz}=\frac{Q-{\eta }_{2}}{{\eta }_{3}}$$

(38)

where ${\eta }_{2}$ and ${\eta }_{3}$ are constants appearing in HPM solution and are determine from HPM Mathematica code.

6 Stress on Walls on Catheterized Stenosed Region

The shear stress expression of Prandtl nanofluid used to evaluate pressure on the walls is given as

$${S}_{rz}={\left.\left[\alpha \left(\frac{\partial w}{\partial r}\right)+\beta {\left(\frac{\partial w}{\partial r}\right)}^{3}\right]\right|}_{r=h} .$$

(39)

7 Discussion and Results

This section is design for the discussion of considered non-Newtonian nanofluid flow model through a catheterized stenotic region with swimming of gyrotactic organism. Table 1 is plotted to investigate the absolute error analysis while using HPM technique and noted that the accuracy of solution up to four decimal places. Furthermore, by addressing the hemodynamics factors of flow features through a stenotic area, this section is intended to have a major contribution with theoretical understanding of blood flow dynamics. Graphical outcomes are obtained by considering the pioneering parameters as ${R}_{b}=0.1-2$, ${P}_{t}=0.1-2$, $\alpha =0.1-2$, $\beta =2-9$ and ${T}_{t}={T}_{b}=2.0-6.0$.

7.1 Velocity Profile in Anisotropic Stenotic Region

The velocity profile portrays flow behavior in an anisotropic stenotic region, and in this unit is discussed for thermophoresis parameter ${T}_{t}$, Brownian motion parameter ${T}_{b}$, Peclet number ${P}_{t}$, bioconvection Rayleigh number ${R}_{b},$ fluid parameter $\beta$ and $\alpha .$ To understand the consequence of hemodynamics for some specific lesion, it is essential to understand blood velocity pattern in stenotic region. Substantial variations in velocity flow profile between different units in a stenotic region are due to the presence of force collision which plays an imperative role between the arterial walls and the flow. It is noted from all velocity configurations that flow velocity changes its behaviors for region $r\epsilon \left[0.65, 1.2\right].$ Flow velocity with enhancing Peclet and bioconvection Rayleigh numbers are analyzed through Figs. 2, 3. It is noted both parameters show opposite results. Figure 2 shows that in enhancing bioconvection Rayleigh number, buoyancy force effectively decreases near the right wall, which results as velocity decline. It is noted from Fig. 3 that the heat transfer rate by the motion of non-Newtonian fluid particles is maximum near the left wall of the atherosclerotic region as compared to the rest of the section. Fluid features defining parameters are visualized through (4)–(5) and concludes that by enhancing non-Newtonian fluid parameter $\alpha$ flow circulation reduces; however, the opposite trend is observed for the non-Newtonian fluid parameter $\beta$. Velocity profile analysis for the nanoparticles applications is designed through Figs. 6, 7. It is perceived from these flow analyses that random motion of nanoparticles results in velocity rises near the right wall as compared to the left wall of the atherosclerotic region. It is also concluded from Fig. 7, that due to the presence of a temperature gradient, flow velocity decreases near the right wall for different variations of the thermophoresis parameter.

Fig. 2

Velocity variation versus bioconvection Rayleigh number

Fig. 3

Velocity variation versus Peclet number

Fig. 4

Velocity variation versus α parameter

Fig. 5

Velocity variation versus β parameter

Fig. 6

Velocity variation versus thermophoresis parameter

Fig. 7

Velocity variation versus Brownian motion parameter

Fig. 8

Temperature variation versus thermophoresis parameter

Fig. 9

Temperature variation versus Brownian motion parameter

7.2 Temperature Significance Through Anisotropic Stenotic Region

Heat transfer significance in the presence of thermophoresis parameter ${T}_{t}$ and Brownian motion parameter ${T}_{b}$ is deliberated in this section. It is concluded from (8) to (9) that heat transfer rate enhances with increasing in values of ${T}_{t}$ and ${T}_{b}$. Heat transfer rate in anisotropic tapered region is enhanced due to random movement of nanoparticles and transport force phenomena that occurs due to the occurrence of a temperature gradient near atherosclerosis.

7.3 Concentration Significance Through Anisotropic Stenotic Region

Concentration profiles with significance of nanofluid parameters are elaborated in Figs. 10, 11. These concentration profiles depict opposite behavior for thermophoresis and Brownian motion parameters. This result is attained due to enhancement in random motion of nanoparticles.

Fig.10

Concentration variation versus thermophoresis parameter

Fig. 11

Concentration variation versus Brownian motion parameter

7.4 Stress on Wall of Anisotropic Stenotic Region

Pressure on the walls of the anisotropic stenotic region is planned and deliberate here through Figs. 12, 13, 14, 15, 16, 17) for different significant parameters which are involved in arterial height progression. From these configurations, we can see that the arterial wall pressure is directly proportional to the velocity gradient near the arterial wall. Graphical pattern of stress configurations (12) and (13) is designed for various values of Peclet and bioconvection Rayleigh numbers. It is perceived that the arterial pressure enhances with motile organism movement, which results in an increase in resistive force along constricted region. It is also concluded that Peclet number enhancement, creates more pressure along an atherosclerotic wall due heat transfer rate phenomena when compared to the influence of bioconvection Rayleigh number. Figures 14, 15, show that with increase in non-Newtonian fluid defining parameters pressure reduces from arterial wall segments. This result indicates that the Prandtl fluid model properties minimizes arterial stress from atherosclerotic walls. It has been observed from configurations (16)–(17) that arterial stress is enhanced due to the strong impact of the random motion of the nanoparticles and occurrence of temperature gradient phenomena near walls of the atherosclerotic region.

Fig. 12

Stress on wall in narrowed region versus bioconvection Rayleigh number

Fig. 13

Stress on wall in narrowed region versus Peclet number

Fig. 14

Stress on wall in narrowed region versus α parameter

Fig. 15

Stress on wall in narrowed region versus β parameter

Fig. 16

Stress on wall in narrowed region versus thermophoresis parameter

Fig. 17

Stress on wall in narrowed region versus Brownian motion parameter

7.5 Resistance to Flow

Resistance to flow is the main hemodynamic factor of stenotic lesion. To measure this key factor which causes lesions in an artery and creates hurdles in fluid circulation, configurations of resistance to flow are plotted versus various degrees of stenotic height $\delta$ through Figs. 18, 19, 20, 21, 22, 23. These configurations show that with an increase in the maximum height of stenosis resistance to blood flow also increases. The consequence of bioconvection Rayleigh and Peclet numbers is designed via (18)–(19) and it is perceived that due to motile organism movement resistive force enhances and creates more pressure in the pre-stenotic region. Prandtl fluid parameters show opposite behavior and make flow possible through the post stenotic region as depicted from Figs. 20, 21. It is noted that fluid flow enhances for the fluid parameter while reduces for fluid parameter. From Figs. 22, 23, it is noted that with the mediation of nanoparticles in base non-Newtonian fluid resistance to flow minimizes and makes flow easier to flow toward the post stenotic region.

Fig. 18

Resistance to flow due to narrowed region versus Peclet number

Fig. 19

Resistance to flow due to narrowed region versus bioconvection Rayleigh number

Fig. 20

Resistance to flow due to narrowed region versus thermophoresis parameter

Fig. 21

Resistance to flow due to narrowed region versus Brownian motion parameter

Fig. 22

Resistance to flow due to narrowed region versus α parameter

Fig. 23

Resistance to flow due to narrowed region versus β parameter

Fig. 24

Motile microbe’s movement variations in narrowed region versus Peclet number

7.6 Gyrotactic Microorganism in Anisotropic Stenotic Region

Gyrotactic microbe’s stimulation can be noted from (24) to (26) configurations. It is perceived after analyzing Fig. 24 that the motile microorganisms' motion is affected in the presence of nanoparticles defining parameters. Random motion of nanoparticles, in the presence of considered non-Newtonian fluid flow enhances motile organism movement, however, motile organism movement is noted to be slightly affected with enhancing the values of thermophoresis parameter as shown in the Fig. 25. Figure 26 shows that with enhancing Peclet number, advection transport is more progressive which disturbs motile microorganism movement and thus motile organism profile decreases.

Fig. 25

Motile microbe’s movement variations in narrowed region versus thermophoresis parameter

Fig. 26

Motile microbe’s movement variations in narrowed region versus Brownian motion parameter

Fig. 27

Blood flow pattern in anisotropic tapered region versus different values of Peclet number

Fig. 28

Blood flow pattern in anisotropic tapered region versus different values of bioconvection Rayleigh number

7.7 Flow pattern via Streamlines Configurations

Motile gyrotactic organism movement in blood though anisotropic stenotic segment is analyzed through (27)–(28). All formations are planned with three different sections to attain the proper consequence for theoretical knowledge of flow pattern in the microvascular stenotic artery. Flow pattern is designed here in multiple sections for various degrees of constricted arterial height. It is achieved from (27) that by enhancing Peclet number, flow pattern disturbs, due to rise in heat transfer rate by the motion of non-Newtonian fluid particles and results in signifying flow boluses. It is noted from (28) that for bioconvection Rayleigh number flow pattern changes. It is also noted that the number of flow boluses starts reducing, due to increase in resistive forces in a stenotic region.

8 Conclusion

The principal outputs obtained from this mathematical formulation of blood flow in the presence of motile gyrotactic microorganism are.

• Heat transfer rate enhances with the mediation of nanoparticles in anisotropic region.

• Non-Newtonian fluid parameters show opposite results for hemodynamics factors which are formed due enlargement of atherosclerotic lesions.

• Nanoparticle application shows lessening in resistance to blood flow.

• Arterial pressure reduces by enhancing random movement of nanoparticles.

• Motile gyrotactic microorganism movement enhances by increasing random motion of nanoparticles.

• Prandtl fluid properties show significant impact in minimizing the hemodynamics of the atherosclerotic region.

• Peclet number opposes motile gyrotactic microorganisms’ movement due to the presence of heat transfer rate phenomena.

Table 1 Absolute error analysis of HPM technique for velocity profile