Throughput and Detection Probability of Interweave Cognitive Radio Networks Using Intelligent Reflecting Surfaces

Abstract

In this paper, we derive a tight lower bound of the detection probability of the energy detector when intelligent reflecting surface (IRS) are used. The secondary source uses the energy detector to detect primary source activity. There is IRS between primary source and secondary source. The secondary sources compute the energy of the received signal from primary source and reflected on IRS. The proposed spectrum sensing algorithm using IRS offers 15, 21, 27, 33 dB gain with respect to conventional sensing without IRS for a number of reflectors $K=8,16,32,64$. We also used IRS for data communication between primary source and destination as well as the communication between secondary nodes. The proposed primary and secondary networks of cognitive radio network (CRN) using IRS offer 23, 29, 36, 43, 49 and 56 dB gain with respect to conventional CRN without IRS for a number of reflectors $K=8,16,32,64,128,256$. We show that the use of $N=20,10,5$ symbols in energy detection offers up to 8.5, 7.7 and 4.7 dB gain with respect to a single symbol. We plot the miss detection probability $P_\mathrm{md}$ versus the false alarm probability $P_f$. For $K=16$ reflectors, average SNR per bit $E_b/N_0=-10$ dB and $P_f=0.01$, $P_\mathrm{md}=2 10^{-3}, 7 10^{-3}, 2.5 10^{-2}$ when $N=20,10,5$ symbols are used in energy detection, whereas $P_\mathrm{md}=0.45$ when a single symbol is used.

1 Introduction

Cognitive radio networks (CRN) were suggested to improve the use of frequency bands [1]. There are three possible strategies: In interweave CRN, secondary source is allowed to transmit only when primary user is idle. In underlay cognitive radio networks, secondary source transmits over the same channel as primary source. Secondary source transmits with an adaptive power in order to not cause harmful interference to primary nodes. In overlay CRN, secondary and primary nodes transmit over the same channel and secondary nodes dedicate a part of their power to relay signal to primary nodes and ensure a good quality of service (QoS) in the primary network. The detection probability and throughput of CRN have been extensively studied in [1,2,3,4,5].

In this paper, we suggest a new spectrum sensing algorithm where the energy detector uses a signals obtained from reflections on intelligent reflecting surface (IRS) [6,7,8]. The phases of IRS are optimized so that all reflections have a null phase at the receiver [9,10,11,12,13,14]. IRS can be used in non-orthogonal multiple access (NOMA) systems as well as millimeter wave or free-space optical (FSO) communications [15,16,17,18]. A hardware and practical implementation of IRS was discussed in [19, 20]. The phase shifts of IRS reflectors can be continuous or quantized [21, 22]. To the best of our knowledge, the use of IRS in the spectrum sensing process with multiple symbols was not yet suggested to improve the detection probability.

2 Related Work

The false alarm and detection probabilities of the energy detector using a single symbol and intelligent reflecting surfaces were recently derived in [23]. The secondary throughput using IRS was derived in [23] as the product of the secondary user transmit probability and the transmission rate. The packet error probability was not studied in [23]. In [24], the transmitted power is minimized for CRN using IRS. The minimization has been performed under the constraint that the signal to interference plus noise ratio (SINR) is larger than a predetermined threshold for all users. The spectral and energy efficiencies of CRN using IRS were maximized in [25, 26]. The achievable weighted sum rate was maximized in [27]. The achievable rate of secondary users was maximized in [28] subject to a total transmit power constraint. Optimal resource allocation for CRN using IRS was proposed in [28]. Vertical and robust beamforming has been proposed to improve the performance of CRN using IRS [29, 30]. The physical layer security of CRN using IRS was studied in [31, 32] in order to maximize the secrecy rate.

The main innovation and contributions of the paper are:

- We suggest the use of IRS in the spectrum sensing process. The energy detector uses N symbols. The use of $N=20,10,5$ symbols in energy detection offers up to 8.5, 7.7 and 4.7 dB gain with respect to $N=1$ as considered in [23]. We derive the detection probability $P_d$ and the miss detection probability of the energy detector using intelligent reflecting surface (IRS). The proposed spectrum sensing algorithm using IRS offers 15, 21, 27, 33 dB gain with respect to conventional sensing without IRS [1-5] for a number of reflectors $K=8,16,32,64$.

- We derive the throughput of the primary and secondary networks of CRN using interweave transmission technique where secondary source is allowed to transmit only when primary source is idle. The proposed primary and secondary networks of CRN using IRS offer 23, 29, 36, 43, 49 and 56 dB gain with respect to conventional CRN without IRS [1-5] for a number of reflectors $K=8,16,32,64,128,256$.

- We plot the miss detection probability $P_\mathrm{md}=1-P_d$ versus the false alarm probability $P_f$. For $K=16$ reflectors, average SNR per bit $E_b/N_0=-10$ dB and $P_f=0.01$, $P_\mathrm{md}=2 10^{-3}, 7 10^{-3}, 2.5 10^{-2}$ when $N=20,10,5$ symbols are used in energy detection, whereas $P_\mathrm{md}=0.45$ when a single symbol is used ($N=1$) as studied in [23].

The paper contains eight sections. The system model is presented in Sect. 3. Section 4 derives a tight lower bound of detection probability of the energy detector using intelligent reflecting surfaces. Sections 5–6 derive the throughput in primary and secondary networks using IRS. Section 7 discusses the obtained results. Section 8 summarizes the obtained results. Section 9 concludes the paper.

3 System Model

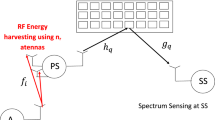
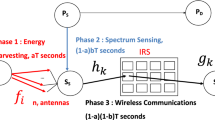
Figure 1 shows the system model with a primary source and destination ($P_S$ and $P_D$), a secondary source and destination ($S_S$ and $S_D$). We consider interweave cognitive radio networks (CRN) where $S_S$ performs spectrum sensing and is allowed to transmit only when $P_S$ is idle. We assume that $P_S$ is active with probability $p_a$. $S_S$ uses the energy detector (ED) to measure the energy of received signal and will detect $P_S$ is the measured energy E is larger than threshold T. Intelligent reflecting surfaces (IRSs) are placed between all nodes to improve the throughput and detection probability as all reflections have the same phase at the secondary and primary destination. Besides, IRSs are placed between $P_S$ and $S_S$ so that the spectrum sensing is based on received signals originating from all K reflections.

Fig. 1

System model: interweave CRN using intelligent reflecting surface (IRS)

Fig. 2

Detection probability when IRS is deployed as a reflector

Fig. 3

Detection probability when IRS is deployed as a reflector for different numbers of symbols N used in energy detection: $K=16$

Fig. 4

Miss detection probability versus false alarm probability

Fig. 5

Primary throughput for 64QAM modulation when IRS is deployed as a reflector

4 Spectrum Sensing Using Intelligent Reflecting Surface (IRS)

Spectrum sensing is performed at $S_S$ to detect $P_S$ activity. The energy detector is used at $S_S$ to detect if $P_S$ is active or idle. $S_S$ receives K reflected signals on IRS. Let $\sqrt{\lambda _1}a_k$ the channel coefficient between $P_S$ and k-th reflector of IRS, $\lambda _1=\frac{{\mathrm {PAL}}}{d_1^{\beta }}$ is the average power of channel gain, ${\mathrm {PAL}}=1$ is the path loss at reference distance $d_0$, $d_1=\frac{d_1^\mathrm{eff}}{d_0}$ is the normalized distance between $P_S$ and IRS, $d_0$ is a reference distance in meters, $d_1^\mathrm{eff}$ is the effective distance in meters between $P_S$ and IRS and $\beta$ is the path loss exponent. Therefore, $d_1$ is a normalized distance without unit. The same model is used for all other links with ${\mathrm {PAL}}=1$ and all other distances $d_i, i=1,\ldots ,6$ are also normalized. For Rayleigh channels, $a_k$ is a zero-mean complex Gaussian random variable (R.V.) with module $g_k=|a_k|$ and phase $\phi _k$: $a_k=g_ke^{-j\phi _k}$. $g_k$ is Rayleigh distributed with mean $\frac{\sqrt{\pi }}{2}$ and unit second order moment. Let $\sqrt{\lambda _2}b_k$ be the channel coefficient between k-th reflector of IRS and $S_S$. $\lambda _2=\frac{1}{d_2^{\beta }}$ where $d_2$ is the normalized distance between IRS and $S_S$. We denote by $b_k=h_ke^{-j\theta _k}$, $h_k=|b_k|$ is the absolute value of $b_k$ and $\theta _k$ is the phase. $h_k$ is Rayleigh distributed with mean $\frac{\sqrt{\pi }}{2}$ and unit second-order moment.

Let $\zeta _k$ be the phase shift induced by k-th IRS reflector. $\zeta _k$ is adjusted so that all K reflections have the same phase at $S_S$:

$$\begin{aligned} \zeta _k=\phi _k+ \theta _k. \end{aligned}$$

(1)

The received signal at $S_S$ is written as:

$$\begin{aligned} r_l^{S_S}=s_l^{P_S}\sqrt{2E_{P_S}\lambda _1\lambda _2}\sum _{k=1}^{K}a_kb_ke^{j\zeta _k}+n_l^{S_S}, \end{aligned}$$

(2)

where $s_l^{P_S}$ is the l-th transmitted symbol by $P_S$, $1\le l\le N$, N is the number of symbols used by the energy detector in the spectrum sensing process, $E_{P_S}$ is the transmitted energy per symbol of node $P_S$, $n_l^{S_S}$ is zero-mean Gaussian noise with variance $2N_0$.

Using (1) and (2), we obtain

$$\begin{aligned} r_l^{S_S}=s_l^{P_S}\sqrt{2E_{P_S}\lambda _1\lambda _2}A+n_l^{S_S}, \end{aligned}$$

(3)

where

$$\begin{aligned} A=\sum _{k=1}^{K}g_kh_k. \end{aligned}$$

(4)

Secondary source $S_S$ computes the energy E of received signal $r_l^{S_S}$ to detect $P_S$ activity:

$$\begin{aligned} E=\frac{\sum _{l=1}^N|r_l^{S_S}|^2}{N_0}=\frac{2N\lambda _1\lambda _2E_{P_S}}{N_0}A^2+\frac{\sum _{l=1}^N|n_l^{S_S}|^2}{N_0} \end{aligned}$$

(5)

For a fixed value of channel gains, i.e., fixed value of A, E is the sum of 2N Gaussian R.V. with unit variance and non-centrality parameter (NCP):

$$\begin{aligned} NCP=2N\Gamma _{P_SS_S}, \end{aligned}$$

(6)

where $\Gamma _{P_SS_S}$ is the signal-to-noise ratio (SNR) at $S_S$ defined as [33]:

$$\begin{aligned} \Gamma _{P_SS_S}=\frac{\lambda _1\lambda _2E_{P_S}A^2}{N_0}=ASNR \times A^2, \end{aligned}$$

(7)

where

$$\begin{aligned} ASNR=\frac{\lambda _1\lambda _2E_{P_S}}{N_0}. \end{aligned}$$

(8)

Using the central limit theorem (CLT), A is approximated by a Gaussian R.V. with mean $m_A=\frac{K\pi }{4}$ and variance $\sigma _A^2=K(1-\frac{\pi ^2}{16})$. The conditioned detection probability (DP) is equal to

$$\begin{aligned} P_d(\Gamma _{P_SS_S})=Q_N(\sqrt{NCP},\sqrt{T})=Q_N(\sqrt{2N\Gamma _{P_SS_S}},\sqrt{T}), \end{aligned}$$

(9)

where T is the ED threshold and $Q_N(.,.)$ is the generalized Macum Q-function.

The average detection probability (ADP) is computed as:

$$\begin{aligned} P_d=\int _0^{+\infty }P_d(x)f_{\Gamma _{P_SS_S}}(x){\mathrm {d}}x, \end{aligned}$$

(10)

where $f_{\Gamma _{P_SS_S}}(x)$ is the probability density function (PDF) of $\Gamma _{P_SS_S}$.

$\Gamma _{P_SS_S}$ is a non-central Chi-square R.V. with PDF: [33]

$$\begin{aligned} f_{\Gamma _{P_SS_S}}(x)=\frac{e^{-\frac{m_A^2}{2\sigma _A^2}}}{2 ASNR \sigma _A^2}(\frac{x}{m_A^2ASNR})^{-0.25}e^{-\frac{x}{2\sigma _A^2ASNR}}I_{-0.5}(\sqrt{\frac{m_A^2x}{\sigma _A^4ASNR}})\nonumber \\ \end{aligned}$$

(11)

The average miss detection probability is equal to

$$\begin{aligned} P_\mathrm{md}=\int _0^{+\infty }[1-P_d(x)]f_{\Gamma _{P_SS_S}}(x){\mathrm {d}}x, \end{aligned}$$

(12)

We use the tight upper bound derived in [34]

$$\begin{aligned} P_\mathrm{md}<F_{\Gamma _{P_SS_S}}(w_0), \end{aligned}$$

(13)

where $F_{\Gamma _{P_SS_S}}(w_0)$ is the cumulative distribution function (CDF) of SNR given by

$$\begin{aligned} F_{\Gamma _{P_SS_S}}(w_0)=1-Q_{0.5}\left( \frac{m_A}{\sigma _A},\sqrt{\frac{x}{ASNR \sigma _A^2}}\right) , \end{aligned}$$

(14)

and $w_0$ is water-fall threshold defined as [34]:

$$\begin{aligned} w_0=\int _0^{+\infty }[1-P_d(x)]{\mathrm {d}}x. \end{aligned}$$

(15)

We deduce a tight lower bound of detection probability

$$\begin{aligned} P_d>1-F_{\Gamma _{P_SS_S}}(w_0)=Q_{0.5}\left( \frac{m_A}{\sigma _A},\sqrt{\frac{xN_0}{E_{P_S}\lambda _1\lambda _2 \sigma _A^2}}\right) .\nonumber \\ \end{aligned}$$

(16)

5 IRS Deployed in the Primary Network

IRSs are deployed in the primary network between $P_S$ and $P_D$. Let $\sqrt{\lambda _3}c_k$ be the channel coefficient between $P_S$ and k-th reflector of IRS. $\lambda _3=\frac{1}{d_3^{\beta }}$ where $d_3$ is the normalized distance between $P_S$ and IRS. We can write $c_k=i_ke^{-j\eta _k}$ where $i_k=|c_k|$ is the absolute value of $c_k$ and $\eta _k$ is the phase of $c_k$. $i_k$ is Rayleigh distributed with mean $\frac{\sqrt{\pi }}{2}$ and unit second-order moment.

Let $\sqrt{\lambda _4}d_k$ be the channel coefficient between k-th reflector of IRS and $P_D$. $\lambda _4=\frac{1}{d_4^{\beta }}$ where $d_4$ is the normalized distance between IRS and $P_D$. We can write $d_k=j_ke^{-j\mu _k}$ where $j_k=|d_k|$ is the absolute value of $d_k$ and $\mu _k$ is the phase of $d_k$. $j_k$ is Rayleigh distributed with mean $\frac{\sqrt{\pi }}{2}$ and unit second-order moment.

The phase of k-th reflector of IRS is adjusted so that all reflections have the same phase at $P_D$:

$$\begin{aligned} v_k=\eta _k+\mu _k. \end{aligned}$$

(17)

The received signal at $P_D$ is equal to

$$\begin{aligned} r_l^{P_D}=s_l^{P_S}\sqrt{2E_{P_S}\lambda _3\lambda _4}\sum _{k=1}^Kc_kd_ke^{jv_k}+n_l^{P_D} \end{aligned}$$

(18)

where $n_l^{P_D}$ is a zero-mean Gaussian noise with variance $2N_0$.

Using (17), we obtain

$$\begin{aligned} r_l^{P_D}=s_l^{P_S}\sqrt{2E_{P_S}\lambda _3\lambda _4}B+n_l^{P_D} \end{aligned}$$

(19)

where

$$\begin{aligned} B=\sum _{k=1}^Ki_kj_k. \end{aligned}$$

(20)

Using the CLT, B is approximated by a Gaussian R.V. with mean $m_A=\frac{K\pi }{4}$ and variance $\sigma _A^2=K(1-\frac{\pi ^2}{16})$. Here, K is the number of IRS reflectors between $P_S$ and $P_D$ that can be different from the number of reflectors between $P_S$ and $S_S$.

The SNR at $P_D$ is equal to

$$\begin{aligned} \Gamma _{P_SP_D}=\frac{E_{P_S}\lambda _3\lambda _4}{N_0}B^2. \end{aligned}$$

(21)

Using the CLT, $\Gamma _{P_SP_D}$ is approximated by a non-central Chi-square distribution with one degree of freedom and CDF:

$$\begin{aligned} F_{\Gamma _{P_SP_D}}(x)=1-Q_{0.5}\left( \frac{m_B}{\sigma _B},\sqrt{\frac{xN_0}{\lambda _3\lambda _4E_{P_S}\sigma _A^2}}\right) . \end{aligned}$$

(22)

The packet error probability (PEP) at $P_D$ is tightly upper bounded using the CDF of SNR [35]

$$\begin{aligned} PEP^{P_D}<F_{\Gamma _{P_SP_D}}(T_0). \end{aligned}$$

(23)

where $T_0$ is a water-fall threshold defined as:

$$\begin{aligned} T_0=\int _0^{+\infty }1-[1-SEP(x)]^L{\mathrm {d}}x, \end{aligned}$$

(24)

where L is packet length and SEP(x) is the symbol error probability (SEP) of M-quadrature amplitude modulation (QAM) defined as [33]:

$$\begin{aligned} SEP(x)=2\left( 1-\frac{1}{\sqrt{M}}\right) erfc\left( \sqrt{x\frac{3\log _2(M)}{2(M-1)}}\right) , \end{aligned}$$

(25)

The throughput at $P_D$ is computed as:

$$\begin{aligned} Thr^{P_D}=p_alog_2(M)[1-PEP^{P_D}]. \end{aligned}$$

(26)

where $p_a$ is the probability that $P_S$ is active.

Fig. 6

Primary throughput for 64QAM modulation for different values of $p_a$; $K=16$

Fig. 7

Secondary throughput for 64QAM modulation when IRS is deployed as a reflector

Fig. 8

Secondary throughput for 16QAM modulation when IRS is deployed as a reflector

Fig. 9

Secondary throughput for 64QAM modulation for different values of $p_a$ and $P_f$: $K=16$

6 IRS Deployed in the Secondary Network

IRSs are deployed in the secondary network between $S_S$ and $S_D$. Let $\sqrt{\lambda _5}e_k$ be the channel coefficient between $S_S$ and k-th reflector of IRS. $\lambda _5=\frac{1}{d_5^{\beta }}$ where $d_5$ is the normalized distance between $S_S$ and IRS. We can write $e_k=l_ke^{-jm_k}$ where $l_k=|e_k|$ is the absolute value of $e_k$ and $m_k$ is the phase of $e_k$. $l_k$ is Rayleigh distributed with mean $\frac{\sqrt{\pi }}{2}$ and unit second-order moment.

Let $\sqrt{\lambda _6}f_k$ be the channel coefficient between k-th reflector of IRS and $S_D$. $\lambda _6=\frac{1}{d_6^{\beta }}$ where $d_6$ is the normalized distance between IRS and $S_D$. We can write $f_k=o_ke^{-jp_k}$ where $o_k=|f_k|$ is the absolute value of $f_k$ and $p_k$ is the phase of $f_k$. $o_k$ is Rayleigh distributed with mean $\frac{\sqrt{\pi }}{2}$ and unit second-order moment.

The phase of k-th reflector of IRS is adjusted so that all reflections arrive with the same phase at $S_D$:

$$\begin{aligned} w_k=m_k+p_k. \end{aligned}$$

(27)

The received signal at $S_D$ is equal to

$$\begin{aligned} r_l^{S_D}=s_l^{S_S}\sqrt{2E_{S_S}\lambda _5\lambda _6}\sum _{k=1}^Ke_kf_ke^{jw_k}+n_l^{S_D} \end{aligned}$$

(28)

where $s_l^{S_S}$ is the l-th transmitted symbol by $S_S$, $E_{S_S}$ is the transmitted energy per symbol of secondary source $S_S$ and $n_l^{P_D}$ is a zero-mean Gaussian noise with variance $2N_0$.

Using (27), we obtain

$$\begin{aligned} r_l^{S_D}=s_l^{S_S}\sqrt{2E_{S_S}\lambda _5\lambda _6}C+n_l^{S_D} \end{aligned}$$

(29)

where

$$\begin{aligned} C=\sum _{k=1}^Kl_ko_k. \end{aligned}$$

(30)

Using the CLT, C is approximated by a Gaussian R.V. with mean $m_C=\frac{K\pi }{4}$ and variance $\sigma _C^2=K(1-\frac{\pi ^2}{16})$.

The SNR at $S_D$ is equal to

$$\begin{aligned} \Gamma _{S_SS_D}=\frac{E_{S_S}\lambda _5\lambda _6}{N_0}C^2. \end{aligned}$$

(31)

Using the CLT, $\Gamma _{S_SS_D}$ is approximated by a non-central Chi-square distribution with one degree of freedom and CDF:

$$\begin{aligned} F_{\Gamma _{S_SS_D}}(x)=1-Q_{0.5}\left( \frac{m_C}{\sigma _C},\sqrt{\frac{xN_0}{\lambda _5\lambda _6E_{S_S}\sigma _C^2}}\right) . \end{aligned}$$

(32)

The packet error probability (PEP) at $S_D$ is tightly upper bounded using the CDF of SNR [35]

$$\begin{aligned} PEP^{S_D}<F_{\Gamma _{S_SS_D}}(T_0). \end{aligned}$$

(33)

where $T_0$ is defined in (24).

The throughput at $S_D$ is computed as:

$$\begin{aligned} Thr^{S_D}=[1-p_a][1-P_f]log_2(M)[1-PEP^{S_D}]. \end{aligned}$$

(34)

where $P_f$ is the false detection probability defined as:

$$\begin{aligned} P_f=\frac{\Gamma (N,\frac{T}{2})}{\Gamma (N)}, \end{aligned}$$

(35)

where $\Gamma (.,.)$ is the incomplete Gamma function, $\Gamma (.)$ is the Gamma function, N is the number of symbols used by the energy detector, and T is the detection threshold.

7 Theoretical and Simulation Results

We have made simulations using MATLAB software for a fixed false alarm probability $\overline{P_f}=0.05$ in Figs. 2, 3, 7 and 8 by setting the detection threshold as follows:

$$\begin{aligned} T=2\Gamma ^{-1}(N,\overline{P_f}\Gamma (N)) \end{aligned}$$

(36)

We used $N=10$ symbols for spectrum sensing using the energy detector in Fig. 2. The normalized distance between $P_S$ and IRS (placed between $P_S$ and $S_S$) is $d_1=1$. The normalized distance between IRS and $S_S$ is $d_2=1.1$. The normalized distance between $P_S$ and IRS of primary network is $d_3=1$. The normalized distance between IRS of primary network and $P_D$ is $d_4=1.3$. The normalized distance between $S_S$ and IRS of secondary network is $d_5=1.3$. The normalized distance between IRS of secondary network and $S_D$ is $d_6=1$. The path loss exponent is $\beta =3$.

Figure 2 compares the detection probability at $S_S$ when using IRS to conventional spectrum sensing algorithms [1-5]. To measure the detection probability, we did 10 000 Monte Carlo simulations. We plotted the detection probability versus $E_b/N_0$ where $E_b=\frac{E_s}{log_2(M)}$ is the transmitted energy per bit and M is the size of the constellation. $E_s=PT_s$ is the transmitted energy per symbol, $T_s$ is the symbol duration and P is the power of primary source $P_S$. We have fixed the value of $N_0$ and varied the transmitted power P to obtain different values of $E_b/N_0$. We observe the proposed spectrum sensing algorithm using IRS offers 15, 21, 27, 33 dB gain with respect to conventional sensing without IRS [1-5] for a number of reflectors $K=8,16,32,64$. The simulation results are close to the derived theoretical ones.

Figure 3 shows the detection probability versus the average SNR per bit for $K=16$ reflectors and the same parameters as Fig. 2. Figure 3 shows that the use of $N=20,10,5$ symbols in energy detection offers up to 8.5, 7.7 and 4.7 dB gain with respect to a single symbol, $N=1$, as considered in [23].

Figure 4 depicts the miss detection probability $P_\mathrm{md}=1-P_d$ versus the false alarm probability $P_f$ for average SNR per bit $E_b/N_0=-10$ dB. When there is no IRS, $P_\mathrm{md}=1$ as the average SNR per bit is very low. For $P_f=0.01$, $P_\mathrm{md}=2 10^{-3}, 7 10^{-3}, 2.5 10^{-2}$ when $N=20,10,5$ symbols are used in energy detection, whereas $P_\mathrm{md}=0.45$ when a single symbol is used $N=1$ as studied in [23].

Figure 5 compares the throughput at primary destination for 64QAM modulations when IRS are used to conventional CRN without IRS [1-5]. We have measured the packet error rate (PER) to deduce the throughput. Simulations have been performed until 500 packets are erroneously received. The primary user is active with probability $p_a=0.4$. The proposed primary network of CRN using IRS offers 23, 29, 36, 43, 49 and 56 dB gain with respect to conventional CRN without IRS [1-5] for a number of reflectors $K=8,16,32,64,128,256$.

Figure 6 depicts the primary throughput for 64QAM modulation, $K=16$ reflectors and the same parameters as Fig. 5. We have varied the value of the probability that primary user is active $p_a=0.6,0.4,0.2.$ Obviously, as $p_a$ increases, the primary throughput increases.

Figures 7, 8 show the throughput at the secondary destination for 64-QAM and 16-QAM modulation using IRS. The proposed secondary network of CRN using IRS offers 23, 29, 36, 43, 49 and 56 dB gain with respect to conventional CRN without IRS [1-5] for a number of reflectors $K=8,16,32,64,128,256$.

Figure 9 depicts the secondary throughput for 64QAM modulations and the same parameters as Fig. 7. We plotted the secondary throughput for $K=16$ reflectors and different values of the probability that primary user is active $p_a=0.6,0.4,0.2.$ We also varied the false alarm probability $P_f=0.05,0.2$. The secondary throughput decreases as the false alarm probability $P_f$ increases or the probability that primary user is active $p_a$ increases.

8 Discussion on the Obtained Results

In this paper, we have shown that the use of IRS allows to increase the detection probability of the energy detector. The proposed spectrum sensing algorithm using IRS offers 15, 21, 27, 33 dB gain with respect to conventional sensing without IRS [1-5]. We have also shown that the use of $N=20,10,5$ symbols during energy detection offers up to 8.5, 7.7 and 4.7 dB gain with respect to a single symbol, $N=1$, as considered in [23]. We also plotted the miss detection probability $P_\mathrm{md}$ versus the false alarm probability $P_f$. For $K=16$ reflectors, average SNR per bit $E_b/N_0=-10$ dB and $P_f=0.01$, $P_\mathrm{md}=2 10^{-3}, 7 10^{-3}, 2.5 10^{-2}$ when $N=20,10,5$ symbols are used in energy detection, whereas $P_\mathrm{md}=0.45$ when a single symbol is used. IRS allows also to increase the throughput of primary and secondary networks. The proposed primary and secondary networks of CRN using IRS offer 23, 29, 36, 43, 49 and 56 dB gain with respect to conventional CRN without IRS [1-5] for a number of reflectors $K=8,16,32,64,128,256$.

9 Conclusions and Perspectives

In this paper, we suggested a new spectrum sensing algorithm using intelligent reflecting surface (IRS). We derived a tight lower bound of detection probability of the energy detector using IRS. We observe the proposed spectrum sensing algorithm using IRS offers 15, 21, 27, 33 dB gain with respect to conventional sensing without IRS [1-5] for a number of reflectors $K=8,16,32,64$. We also used IRS for data communication between primary source and destination as well as the communication between secondary nodes. The proposed primary and secondary networks of CRN using IRS offer 23, 29, 36, 43, 49 and 56 dB gain with respect to conventional CRN without IRS [1-5] for a number of reflectors $K=8,16,32,64,128,256$. As a perspective, it will be interesting to derive the detection probability, primary and secondary throughput when the primary source and secondary source harvest energy using radio frequency signals, solar energy or wind.