Buckling Behavior of Nonlinear Elastic Cantilever Columns with an Elliptical Cross Section

Abstract

This study investigates the buckling behavior of nonlinear elastic cantilever columns, with emphasis on two aspects: the generalized moment of inertia (GMI) of the elliptical plane area, and the buckling behavior of cantilever columns fabricated using nonlinear elastic materials based on the Ludwick constitutive law. An explicit integration formula is developed to calculate the GMI of an elliptical cross section, and the geometric and material nonlinear differential equations that govern the elastica of the buckling columns are derived. To integrate the differential equations, the Runge–Kutta method is used, and an iterative method that improves upon the Regula–Falsi method is used to determine the unknown deflection of the free end of the column. As numerical examples, parametric studies of the GMIs and post-buckling behavior, including buckling loads, of nonlinear elastic cantilever columns with elliptical cross sections are extensively discussed.

1 Introduction

Several modern applications and engineering materials involve large strains, the deformations by which are inherently nonlinear, and the corresponding stresses depend on the underlying material properties [1]. In recent years, elastic materials have often been used to develop main structural members to support external loads sustainably in various engineering fields. These nonlinear materials include a Ludwick-type material whose load–strain relationship adheres to the constitutive law of $\sigma = E\varepsilon^{1/n}$. Here, ($\varepsilon ,\sigma$) are the strain and stress, respectively, $E$ is the Young’s modulus, and $n$ is the material constant [2].

For bending analysis, the Ludwick constitutive law of $\sigma = E\varepsilon^{1/n}$ should be converted to $M = EI_{g} \kappa^{1/n}$, where $M$ is the bending moment, $I_{g}$ the generalized moment of inertia (GMI) of the plane area, and $\kappa$ the curvature [3]. A primary objective of this study is the development of a method for calculating $I_{g}$ for bending analysis. In early studies, several researchers developed a method for calculating $I_{g}$ for several plane cross sections. One of the most important studies was that of Lee [3], where the $I_{g}$ for the rectangular cross section was expressed as $I_{g} = [0.5^{(1 + 1/n)} n/\left( {2n + 1} \right)]ab^{{\left( {2 + 1/n} \right)}}$; here, $a$ and $b$ are the width and height of the rectangle, respectively. Lee [4] and Brojan and Kosel [5] used the beta function to calculate the $I_{g}$ of a superellipsoidal cross section. Lee and Lee [6] computed the $I_{g}$ of a regular polygon cross section with circumradius $a$, where the equilateral triangle, square, pentagon, hexagon and circular cross sections were considered in a numerical example. Here, $I_{g}$ is expressed as an explicit integral formula that can be easily obtained by a direct integration method, such as the Runge–Kutta method.

The calculated $I_{g}$ should be applied to the bending analysis for the geometric nonlinear analysis of the structure. In previous studies, the GMI was applied to the analysis of large deflections of geometric nonlinear beams/columns, i.e., elastica analysis. The elastica problem was first investigated by Euler [7] in 1774, who managed the exact elastic deformation of long and slender rods for only linear materials. Since Euler, the elastica has expanded and evolved into nonlinear elastic materials as well as linear materials. Accordingly, a significant number of investigations pertaining to elastica have been conducted. Herein, representative studies related to the current one, including various topics pertaining to elastica, such as the basic theory for developing governing equations, are reviewed.

First, the geometric nonlinear elastica problem for linear elastic materials [8,9,10,11,12,13,14], a classical study such as that by Euler [7], is reviewed: Bisshopp and Drucker [8] developed a large deformation model for Euler beams using the Bernoulli–Euler beam theory; Oden and Childs [9] investigated finite deflections of an elastic rod based on large deformation theory, in which a moment–curvature relationship followed by a hyperbolic tangent law was adopted; Berkey and Freedman [10] investigated bifurcation elastica depicting a large deformed slender simple beam with pinned ends that was subjected to an axial thrust force at both ends; Lee et al. [11] numerically and experimentally solved the elastica of cantilevered beams with a variable cross section subjected combined with a linearly varying distributed load, a free end point load, and an end moment; Lee and Oh [12] computed the elastica and buckling load of simple tapered columns subjected to an axially compressive load at the end, whose column volume was maintained constant; Aristizabal–Ochoa [13] investigated the nonlinear behavior of post-buckled Timoshenko beam-columns with internal semi-rigid connections subjected to conservative and non-conservative end loads; Lee and Lee [14] reported the configurations of a shear-deformable column with the largest buckling load in the same column volume exhibiting a regular polygonal cross section based on large deformation theory.

Second, studies pertaining to elastica for nonlinear elastic materials have been investigated extensively [2,3,4,5, 15,16,17,18,19,20,21,22,23]. For example, for materials that adhere to the Ramberg–Osgood constitutive law, two typical studies have been conducted by Anatolyevich and Yokovlevna [15] and Giardina and Wei [16]. The nonlinear stress–strain relationship described by the Ramberg–Osgood law is specifically applicable to materials that are hardened by plastic deformation, as described in the two abovementioned papers [15, 16]. In particular, this study emphasizes Ludwick-type materials applicable to soft hardening, instead of Ramberg–Osgood-type materials applicable to plastic hardening, to analyze the elastica of large deformable structural systems. The most important studies [2,3,4,5, 17,18,19,20,21,22,23] pertaining to Ludwick-type materials relevant to this study are reviewed herein: Lewis and Monasa [2] investigated the elastica of cantilever beams subjected to an end moment where, in formulating the analysis, the Euler–Bernoulli law and the exact expression of the curvature was used; Lee [3] used the shear force formula instead of the bending moment formula to derive the governing differential equation to analyze the cantilever beam elastica; Lee [4] and Brojan and Kosel [5] explicitly determined the bending stress–strain relationship of superellipsoidal cross sections; Jung and Kang [17] investigated the nonlinear buckling of fiber materials with rectangular prismatic columns subjected to a combined load of horizontal and vertical point loads as well as distributed loads; Eren [18] calculated the cantilever elastica with a uniformly distributed load and one vertical concentrated load at the free end using the Euler–Bernoulli curvature–moment relationship, assuming different arc lengths; Brojan et al. [19] explained that the Euler column elastica typically exhibits the stability characteristics and buckling patterns observed individually in different structural systems; Saetiew and Chucheepsakul [20] established a set of highly nonlinear simultaneous first-order differential equations with boundary conditions to analyze the post-buckling behavior of linearly tapered columns; Eren [21] calculated the elastica of uniformly distributed loaded and simply supported beams followed by a curvature expression defined using two different arc length functions; Borboni and Santis [22] investigated the elastica of a nonlinear, asymmetric cantilever beam subjected to a horizontal force, vertical force and bending torque at the free end; Liu et al. [23] investigated the elastica of an axially extensible curved beam with a rectangular cross section, where the stress–strain relationship is formulated implicitly based on the Euler–Bernoulli postulation.

As discussed above, the topic of elastica analysis of nonlinear elastic materials remains one of the most important topics in mechanical and structural engineering. The cross-sectional properties of the second moment of inertia plane area $I$ of linear elastic materials are no longer available for the bending analysis of nonlinear elastic materials, including Ludwick-type materials. Therefore, cross-sectional properties other than $I$, which is the generalized moment of inertia (GMI) in the planar area $I_{g}$, must be derived for Ludwick-type materials. In addition, to apply GMIs to structural analysis, appropriate examples from various engineering problems must be selected. Hence, this study was conducted in two parts: the development of a GMI calculation method and the analysis of the elastica of nonlinear elastic materials.

First, a method to calculate the $I_{g}$ of the elliptical plane area and its solution is devised, and some numerical examples are presented. Subsequently, the calculated $I_{g}$ is applied to the buckling of a cantilever column. The derivation of governing differential equations for the nonlinear buckling elastica, numerical solution methods and numerical examples, including those of the buckled elastica and buckling load, are described. The calculated $I_{g}$, buckled elastica and buckling loads in the numerical examples presented herein are discussed extensively in the dimensionless and dimensional forms.

The following were assumed for the elastica analysis: the column axis is incompressible, the shear deformation effect is disregarded, the cross section remains plane even after deformation, and the load direction of the free end is considered to be vertical after buckling.

2 GMI of Elliptical Plane Area

2.1 Geometry of Elliptical Cross Section

Prior to the analysis of the buckling behavior of a nonlinear elastic column, Sect. 2 presents the mathematical formulation for calculating the GMI, denoted by $I_{g}$ as the representative nomenclature, of an elliptical cross section based on the Ludwick constitutive law.

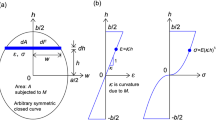
A closed elliptical curve with semi-axes $a$ and $b$ in Cartesian coordinates ($w,h$) is shown in Fig. 1a, and its equation is expressed arithmetically as

$$ \frac{{w^{2} }}{{a^{2} }} + \frac{{h^{2} }}{{b^{2} }} = 1 $$

(1)

where $w$ and $h$ represent the width and height axes, respectively, and the $w$-axis is the bending axis of the cross section that is applied to the bending moment after buckling.

Fig. 1

a Elliptical cross section subjected to bending moment $M$ and b its strain $\varepsilon$ and stress $\sigma$ distributions along cross section for nonlinear elastic material

The aspect ratio $\alpha$, defined as the ratio of $a$ to $b$, is expressed as

$$ \alpha = \frac{a}{b} $$

(2)

where it is noted that the bending axis, or $w$-axis, is the weak axis when $\alpha > 1$ and the strong axis when $\alpha < 1$.

Using Eqs. (1) and (2) yields the coordinate $w$ in terms of $\alpha$ and $b$ at any coordinate $h$, or

$$ w = \alpha \sqrt {b^{2} - h^{2} } $$

(3)

The area $A$ of an ellipse can be obtained using Eq. (4), and the semi-axis $b$ and coordinate $w$ are rearranged in the form of Eqs. (5) and (6), respectively, as follows:

$$ A = \pi ab = \alpha \pi b^{2} $$

(4)

$$ b = \sqrt {A/\alpha \pi } $$

(5)

$$ w = \alpha \sqrt {A/\alpha \pi - h^{2} } . $$

(6)

2.2 GMI of Elliptical Cross Section

Figure 1b shows the distributions of strain $\varepsilon$ and normal stress $\sigma$ along the coordinate $h$ that occur in the cross section owing to the bending moment $M$.

For nonlinear elastic materials adhering to the Ludwick constitutive law, the relationships between $(\varepsilon$,$\sigma )$ and curvature $\kappa$ are expressed as

$$ \varepsilon = \kappa h $$

(7)

$$ \sigma = E\varepsilon^{1/n} = E\left( {\kappa h} \right)^{1/n} $$

(8)

where $E$ is the Young’s modulus, and $n$ is the material constant of Ludwick-type materials. The typical values of $E$ and $n$ for the linear and soft hardening materials considered in this study are as follows:

• Linear elastic material: $E=207$ GPa and $n = 1$ for steel;

• Annealed copper: $E = 458.5$ MPa and $n = 2.16$; and.

• NP8 aluminum alloy: $E = 455.8$ MPa and $n = 4.785$,

where linear elastic materials $\left( {n = 1} \right)$ such as steel can be adopted for the GMI, as shown above.

Next, the equilibrium between the internal and external moments subjected to the cross section is considered. The infinite-element area $dA$ depicted in Fig. 1b is obtained using Eq. (6), or

$$ dA = 2wdh = 2\alpha \sqrt {A/\alpha \pi - h^{2} } dh. $$

(9)

The internal infinite force $dF$ exerting on $dA$ is expressed using Eqs. (8) and (9), as follows:

$$ dF = \sigma dA = 2\alpha E\left( {\kappa h} \right)^{1/n} \sqrt {A/\alpha \pi - h^{2} } dh $$

(10)

The internal infinite moment $dM$ due to $dF$ about the neutral axis is obtained as

$$ dM = \left( {dF} \right)h = 2\alpha \kappa^{1/n} E h^{{\left( {1 + 1/n} \right)}} \sqrt {A/\alpha \pi - h^{2} } dh $$

(11)

where the neutral axis is the $w$-axis because the ellipse is symmetric about the $w$-axis.

The total internal moment $M$ occurring in the cross section was obtained by integrating Eq. (11), or

$$ M = \int dM = = 4\alpha \kappa^{1/n} E\mathop \int \limits_{0}^{b} h^{(1 + 1/n)} \sqrt {A/\alpha \pi - h^{2} } dh. $$

(12)

The well-known relationship [3] between the external moment $M$ and curvature $\kappa$ is expressed in terms of $E$ and $I_{g}$, as follows:

$$ M = \kappa^{1/n} EI_{g} . $$

(13)

Finally, the $I_{g}$ of the elliptical cross section is obtained using Eqs. (12) and (13), as follows:

$$ I_{g} = 4\alpha \mathop \int \limits_{0}^{b} h^{(1 + 1/n)} \sqrt {A/\alpha \pi - h^{2} } dh. $$

(14)

By setting the normalized coordinate $\zeta$ as defined in Eq. (15.1), the corresponding coordinate $h$ is expressed by Eq. (15.2), as follows:

$$ \zeta = \frac{h}{b} $$

(15.1)

$$ h = b\zeta = \sqrt {A/\alpha \pi } \zeta . $$

(15.2)

Substituting Eq. (15.2) into Eq. (14) yields $I_{g}$ for the elliptical cross section with area $A$ and aspect ratio $\alpha$, or

$$ I_{g} = \frac{{4A^{{n_{2} }} }}{{\pi^{{n_{2} }} \alpha^{{n_{1} }} }}{ }\mathop \smallint \limits_{0}^{1} \zeta^{{2n_{1} }} \sqrt {1 - \zeta^{2} } d\zeta = C_{n} \frac{{A^{{n_{2} }} }}{{\alpha^{{n_{1} }} }} $$

(16.1)

$$ C_{n} = \frac{4}{{\pi^{{n_{2} }} }}{ }\mathop \smallint \limits_{0}^{1} \zeta^{{2n_{1} }} \sqrt {1 - \zeta^{2} } d\zeta $$

(16.2)

where $n_{1} = (1 + 1/n)/2$ and $n_{2} = (3 + 1/n)/2$. It is noteworthy that $I_{g}$ has a physical dimension of $I_{g} = \left[ A \right]^{{n_{2} }} = \left[ L \right]^{3 + 1/n}$, as shown in Eq. (16.1). For example, when $A$ is expressed in units of cm², the dimensional units for $I_{g}$ are as follows: cm⁴ for $n = 1$ of the linear elastic material; cm^3.463 for $n = 2.16$ of the annealed copper; and cm^3.209 for $n = 4.785$ of the NP8 aluminum alloy.

2.3 Numerical Examples of ${\varvec{I}}_{{\varvec{g}}}$

For a set of material constants $n$, an aspect ratio $\alpha$, and an area $A$ of an elliptical plane area, $I_{g}$ can be calculated using Eq. (16.1). For a specified value of $n$, $C_{n}$ in Eq. (16.2) can be numerically obtained using the directed integration method, such as the Runge–Kutta method [24] used in this study. After calculating $C_{n}$, the $I_{g}$ of the ellipse with $\alpha$ and $A$ was calculated using Eq. (16.1). In this study, a FORTRAN computer program was created to calculate $I_{g}$.

To verify the mathematical formulation for obtaining $I_{g}$ developed in this study, the $I_{g}$ values of this study and reference [4] were compared, as shown in Table 1. The GMI from reference [4] was formulated as $I_{g} = \left[ {2ab^{{\left( {n + 2} \right)}} /\left( {n + 3} \right)} \right]B\left( {0.5,\left( {n + 2} \right)/2} \right)$, where $B$ is a beta function. By varying $\alpha$, the two resulting $I_{g}$ values for three typical nonlinear elastic materials of $n = 1, 2.16$, and $4.785$ with $A = 20$ cm² were almost identical to each other within a 0.2% error, which implies the effectiveness of the calculation method presented herein.

Table 1 Comparison of $I_{g}$ between this study and reference [4] for $A = 20$ cm²

As one of the main cross sections of structural members, the elliptical and rectangular cross sections are often used in field engineering. It is beneficial to compare the $I_{g}$ of elliptical and rectangular cross sections as nonlinear elastic materials. Table 2 shows this comparison for the same aspect ratio $\alpha$ and cross-sectional area $A ( = 10$ cm²) for three different material constants $n$. The $C_{n}$ value for a rectangular area introduced in the Introduction was $C_{n} = 0.5^{{\left( {1 + 1/n} \right)}} /(2 + 1/n)$. It is clear that the $I_{g}$ values of the rectangular cross section were approximately 5% higher than that of the elliptical cross section, regardless of the values of $\alpha$ and $n$. It is noteworthy that the ratios 1.0472, 1.0495 and 1.0474 for $n = 1, 2.16$, and $4.785$, respectively, were similar, but not identical. In addition, even if omitted herein, the ratio of the rectangle to the ellipse is always the same regardless of $\alpha$.

Table 2 Comparison ^a of ${I}_{g}$ between elliptical and rectangular cross sections

The dimensionless value of $C_{n}$ expressed in Eq. (16.2) depends only on $n$. Once a $C_{n}$ vs. $n$ curve is plotted graphically, $I_{g}$ can be computed using Eq. (16.1), regardless of $\alpha$ and $A$. A graph showing the relationship between $C_{n}$ and $n$ is presented in Fig. 2. The $C_{n}$ values for $n = 1, 2.16$, and $4.785$ of steel, annealed copper and NP8 aluminum alloy (i.e., typical nonlinear elastic materials), respectively, are shown in this graph, as denoted by ●. As $n$ increased, $C_{n}$ increased, and the rate of increase in $C_{n}$ became more significant as $n$ decreased.

Fig. 2

Graph showing relationship between $C_{n}$ and $n$

The calculated results of ${I}_{g}$ for a specified $A(=20$ cm²) by changing the $\alpha$ of the abovementioned typical nonlinear materials, i.e., NP8 aluminum $(n=4.785)$, annealed copper ($n = 2.16$) and steel $\left( {n = 1} \right)$, are shown in Fig. 3. For example, the process to calculate $I_{g}$ expressed by Eq. (16.1) for $n = 2.16$ with $\alpha = 2$ is shown in this figure, and the result of $I_{g} = 15.13$ cm^3.463 is indicated by the symbol ■ of the coordinates (2,15.13). The value $C_{n} = 0.14034$ of $n = 2.16$ shown in Fig. 2 refers to this calculation. As $\alpha$ increased, the value of $I_{g}$ decreased, and the rate of decrease in $I_{g}$ became more dominant as $\alpha$ decreased. It is interesting that at $\alpha = 2.25$, all the $I_{g}$ values for three $n$ were the same as the magnitude of $I_{g} = 14.15$ and therefore, the order of the $I_{g}$ magnitude changed before and after $\alpha = 2.25$; the order of the magnitude of $I_{g}$ was from $n = 1$ to 2.16 to 4.785; however, the order was reversed beyond $\alpha = 2.25$.

Fig. 3

$I_{g}$(${\text{cm}}^{3 + 1/n}$) vs. α curves for A = 20 cm² for three typical values of $n$

3 Application of ${\varvec{I}}_{{\varvec{g}}}$ to Cantilever Column Buckling

In this section, to demonstrate the application of $I_{g}$ to structural analysis, cantilever column buckling is presented. The mathematical model of the buckled elastica is formulated, solution methods are developed, and finally, numerical examples and a discussion are presented.

3.1 Mathematical Modeling

Figure 4 presents a cantilever column of span length $l$, based on the Ludwick constitutive law under a compressive load $P$ at its free end. When $P$ is less than the critical buckling load $P_{cr}$, the column axis indicated by the dotted line remains straight. If $P$ exceeds $P_{cr}$, i.e., $P > P_{cr}$, the column buckles, and the column axis is deformed elastically. The shape of the buckled column, known as elastica, is represented by a solid line in Cartesian coordinates ($x,y$) starting at the clamped end $C$. The arc length at ($x,y$) measured from the clamped end $C$ along the deformed axis is denoted by $s$. Assuming incompressibility, the length of the deformed column axis retains its original length $l$. The angle of rotation at ($x,y$) is denoted by $\theta$; the horizontal and vertical deflections at the free end ($s = l$) are denoted by $\Delta_{h}$ and $\Delta_{v}$, respectively. In addition, in coordinates ($x,y$), the internal forces of the axial force $N$, shear force $Q$ and bending moment $M$ are applied owing to the deformation of the column axis.

Fig. 4

Geometry of cantilever column and its parameters

The internal forces of $\left( {N,Q,M} \right)$ at $\left( {x,y} \right)$ can be expressed using static equilibrium equations, as follows:

$$ N = P{\text{cos}}\theta $$

(17)

$$ Q = P{\text{sin}}\theta $$

(18)

$$ M = P\left( {{\Delta }_{h} - y} \right) $$

(19)

From the trigonometric relations of the elastica shown in Fig. 4, the following equations are obtained:

$$ \frac{dx}{{ds}} = {\text{cos}}\theta $$

(20)

$$ \frac{dy}{{ds}} = {\text{sin}}\theta $$

(21)

The bending moment $M$ is expressed using $\kappa = d\theta /ds$ and $I_{g} = \left( {C_{n} /\alpha^{{n_{1} }} } \right)A^{{n_{2} }}$ shown in Eq. (16.1), or

$$ M = EI_{g} \kappa^{1/n} = \frac{{C_{n} }}{{\alpha^{{n_{1} }} }}EA^{{n_{2} }} \left( {\frac{d\theta }{{ds}}} \right)^{1/n} $$

(22)

Combining Eqs. (19) and (22) and rewriting the results with respect to $d\theta /ds$ yields

$$ \frac{d\theta }{{ds}} = \left[ {\frac{{\alpha^{{n_{1} }} }}{{C_{n} }}\frac{{P\left| {{\Delta }_{h} - y} \right|}}{{EA^{{n_{2} }} }}} \right]^{n} $$

(23)

where the sign convention of $d\theta /ds$ follows that of $\left( {{\Delta }_{h} - y} \right)$.

To obtain the numerical results easily, the following dimensionless parameters are introduced:

$$ \lambda = \frac{s}{l} $$

(24)

$$ \xi = \frac{x}{l} $$

(25)

$$ \eta = \frac{y}{l} $$

(26)

$$ \delta_{h} = \frac{{{\Delta }_{h} }}{l} $$

(27)

$$ \delta_{v} = \frac{{{\Delta }_{v} }}{l}\left( { = 1 - \xi_{\lambda = 1} } \right) $$

(28)

$$ p = \frac{{Pl^{{2n_{1} }} }}{{EA^{{n_{2} }} }} $$

(29)

where $\left( {\lambda ,\xi ,\eta } \right)$ are the normalized coordinates; $\left( {\delta_{h} ,\delta_{v} } \right)$ are the normalized horizontal and vertical deflections at the free end, respectively; and $p$ is the load parameter.

By applying the dimensionless parameters above to Eqs. (20), (21), and (23), the nonlinear dimensionless differential equations that govern the elastica of the buckling column considered in this study are obtained:

$$ \frac{d\xi }{{d\lambda }} = {\text{cos}}\theta $$

(30)

$$ \frac{d\eta }{{d\lambda }} = {\text{sin}}\theta $$

(31)

$$ \frac{d\theta }{{d\lambda }} = \left[ {\frac{{\alpha^{{n_{1} }} }}{{C_{n} }}p\left| {\delta_{h} - \eta } \right|} \right]^{n} $$

(32)

where the unknown parameter $\delta_{h}$ in Eq. (32) is an eigenvalue that can be solved using an appropriate numerical solution method. In Eq. (32), the sign convention of $d\theta /d\lambda$ follows that of $\left( {\delta_{h} - \eta } \right)$.

Next, the boundary conditions for the differential equations above are considered. At the clamped end ($s = 0$), the coordinates ($x,y$) and rotation angle $\theta$ are zero, and the results in the dimensionless form are as follows:

$$ \xi = 0, \;\eta = 0, \;\theta = 0\;at\;\lambda = 0 $$

(33)

At the free end ($s = l)$, the coordinate $y$ becomes the horizontal deflection ${\Delta }_{h}$, and the result in the dimensionless form is

$$ \delta_{h} - \eta = 0\;at\;\lambda = 0 $$

(34)

The internal forces of $\left( {N,Q,M} \right)$ are normalized as follows:

$$ n = \frac{{Nl^{{2n_{1} }} }}{{EA^{{n_{2} }} }} = p{\text{cos}}\theta $$

(35)

$$ q = \frac{{Ql^{{2n_{1} }} }}{{EA^{{n_{2} }} }} = p{\text{sin}}\theta $$

(36)

$$ m = \frac{{Ml^{1/n} }}{{EA^{{n_{2} }} }} = p\left( {\delta_{h} - \eta } \right) $$

(37)

where $\left( {n,q,m} \right)$ are the normalized internal forces corresponding to $\left( {N,Q,M} \right)$.

3.2 Solution Methods and Validation

To solve the differential equations derived above, numerical methods for calculating the elastica and buckling loads were developed in this study. The input column parameters were the column length $l$, material properties of $E$ and $n$, semi-axes of $a$ and $b$, and axial load $P$. Using these parameters of dimensional units, the dimensionless parameters were obtained as $\alpha$ and $p$. To integrate the differential equations, the Runge–Kutta method [24] was used, and to obtain the eigenvalue $\delta_{h}$, i.e., the unknown horizontal deflection at the free end, a solution method of nonlinear equations such as the Regula–Falsi method [24] was used. These types of solution methods for the initial and boundary value problems with eigenvalues are often adopted [11, 14]. Specifically, the solution method for computing the elastica $\left( {\xi ,\eta ,\theta } \right)$ is as follows:

(1) Set column parameters $n$, $\alpha$ and $p$ (subsequently, calculate $C_{n}$ for a specified $n$.)

(2) Assume a trial eigenvalue $\delta_{h}$, i.e., an unknown horizontal deflection at the free end. The first trial is zero.

(3) Integrate differential Eqs. (30–32) subjected to the initial conditions presented in Eq. (33) using the Runge–Kutta method: After a complete integration in $0 \le \lambda \le 1$, the trial elastica $\left( {\xi ,\eta ,\theta } \right)$ is obtained along the entire arc length of the buckled column.

(4) Calculate the trial boundary condition of $D={\delta }_{h}-{\eta }_{\lambda =1}$ in Eq. (34). The first convergence criterion is

$$ \left\lfloor D \right\rfloor \le 1 \times 10^{ - 8} $$

(38)

If the first criterion is satisfied, then calculate the internal forces of $\left( {n,q,m} \right)$ and terminate the calculation. For example, the typical relationship between $D$ and $\delta_{h}$ is shown in Fig. 5, where the two solutions of $\delta_{h}$ with $D = 0$ are indicated by the symbol ● on the horizontal axis. The input column parameters are shown in Fig. 5.

Fig. 5

Typical relationship between $D$ and $\delta_{h}$

(5) If the criterion above is not satisfied, then perform an increment of ${\Delta }$ to the previous trial $\delta_{h}$, i.e., new trial $\delta_{h} \leftarrow \delta_{h} + {\Delta }$, and repeat steps 2–5.

(6) While repeating steps 2 through 5, monitor the sign of $D_{1} \times D_{2}$, where $D_{1}$ and $D_{2}$ are the corresponding values of $D$ in the previous and present trials, respectively. If the sign does not change until $\delta_{h}$ reaches 1, the specified $p$ is less than $p_{cr}$, and the column remains straight because $\delta_{h}$ cannot exceed 1, then terminate the calculation. Here, $p_{cr}$ is the buckling load parameter defined as

$$ p_{cr} = \frac{{P_{cr} l^{{2n_{1} }} }}{{EA^{{n_{2} }} }}. $$

(39)

(7) If the sign changes, then the solution of $\delta_{h}$ lies between $\delta_{{h_{1} }}$ and $\delta_{{h_{2} }}$. Here, $\delta_{{h_{1} }}$ and $\delta_{{h_{2} }}$ are the $\delta_{h}$ values corresponding to $D_{1}$ and $D_{2}$, respectively. The advanced trial $\delta_{{h_{3} }}$ is set using the Regula–Falsi method [24] as follows:

$$ \delta _{{h_{3} }} = \frac{{\delta _{{h_{1} }} \left| {D_{2} } \right| + \delta _{{h_{2} }} \left| {D_{1} } \right|}}{{\left| {D_{1} } \right| + \left| {D_{2} } \right|}}. $$

(40)

For example, in Fig. 5, $\delta_{{h_{3} }} = 0.181$ is obtained from Eq. (40) using the two coordinates of (0.1,0.0549) and (0.4,-0.148), where the sign of $D_{1} \times D_{2}$ changes. Comparing $\delta_{{h_{1} }} = 0.1$ and $\delta_{{h_{2} }} = 0.4$, the calculated $\delta_{{h_{3} }} = 0.181$ is much closer to the target value $\delta_{h} = 0.247$.

(8) Once the Regular–Falsi scheme is encountered, execute the steps above until the second criterion defined in Eq. (41) is satisfied:

$$ \frac{{\left| {\delta _{{h_{1} }} - \delta _{{h_{2} }} } \right|}}{{\delta _{{h_{2} }} }} \le 1 \times 10^{{ - 5}} $$

(41)

(9) If the second criterion is satisfied, then calculate the internal forces of $\left( {n,q,m} \right)$ and terminate the calculation. In the steps above, if the sign of $D_{1} \times D_{2}$ for a specified $p$ does not change until $\delta_{h} \left( { = \Delta_{h} /l} \right) = 1$, then the column remains straight, i.e., it does not buckle, because $\delta_{h}$ cannot exceed $1$; therefore, the specified $p$ is less than $p_{cr}$, i.e., $p < p_{cr} .$

The method for calculating the buckling load $p_{cr}$ is developed based on the fact that the buckling load is a jumped buckling load [6]. The column with load parameter $p < p_{cr}$ does not buckle, implying that the column axis is straight, i.e., $\delta_{h} = 0$, and the column with $p > p_{cr}$ buckles, implying $\delta_{h} \ne 0$. Therefore, $p$ becomes $p_{cr}$, which is the smallest $p$ at which $\delta_{h}$ occurs. For a column with a specified aspect ratio $\alpha$, $p_{cr}$ can be obtained using the solution method of elastica described above. Increase $p$ from $p = 0$ by increasing $\Delta p( = 0.2,$ randomly selected in this study) and execute steps 2–5. Subsequently, identify the first $p$ at which the sign of $D_{1} \times D_{2}$ changes and then, $p_{cr}$ lies between $p_{a}$ and $p_{b}$ (which are adjacent to each other), implying that $p_{b}$ is the first $p$ under which the sign of $D_{1} \times D_{2}$ changes. By repeating steps 2–5 from $p_{a}$ to $p_{b}$ with increasing smaller $\Delta p\left( { = \left( {p_{b} - p_{a} } \right)/10} \right)$ values until the following convergence criteria $E_{r}$ is satisfied, $p_{cr}$ is approximately equivalent to $p_{b}$, as follows:

$$ p_{cr} \approx p_{b} ,\;if\;E_{r} = \frac{{p_{b} - p_{a} }}{{p_{b} }} \le 1 \times 10^{ - 5} $$

(42)

A typical example of determining $p_{cr}$ for $n = 2.16$ and $\alpha = 1$ is shown in Fig. 6. For the first iteration $i = 1$, the first $p_{b}$ is $p_{b} =$ 0.4 with $E_{r} = \left( {0.4 - 0.2} \right)/0.4 = 0.5 > 1 \times 10^{ - 5}$, under which the sign of $D_{1} \times D_{2}$ changes, implying that the solution of $p_{cr}$ is bounded by $0.2\left( { = p_{a} } \right) < p_{cr} < 0.4\left( { = p_{b} } \right)$. Finally, for $i = 6$, $p_{cr}$ is approximated as $p_{cr} \left( { = p_{b} } \right) = 0.308$ with $E_{r} = 1.95 \times 10^{ - 6} < 1 \times 10^{ - 5}$.

Fig. 6

Convergence analysis for obtaining buckling load parameter $p_{cr}$

Two FORTRAN computer programs were self-coded based on the solution methods described above to calculate the elastica of $\left( {\xi ,\eta } \right)$ and the critical buckling load parameter, $p_{cr}$. In these computer programs, the calculation scheme of GMI described in the previous section was included as an internal function. For validation, the critical buckling loads $P_{cr}$ (kN) of this study and reference [25] were compared for a steel column ($n = 1$ and $E = 207$ GPa) with $l = 1$ m and $A = 20{ }$ cm². As shown by the results in Table 3, and the two numbers were similar. Although the $P_{cr}$ of this study is an approximate critical buckling load, it is similar to the exact solution $P_{cr}$ of reference [25], within a 0.29% error. This comparison validates the solution method developed in this study. Because the elastica of the buckling column considered herein was not reported in the literature, a direct comparison could not be realized. It is noteworthy that the solution method of $P_{cr}$ includes the solution methods of elastica; as such, the solution method of the elastica is verified.

Table 3 Comparisons ^a of buckling load $P_{cr}$ of this study and reference [25]

3.3 Numerical Examples

Based on the theories and numerical solution methods developed in this study, a parametric study involving the buckling load parameter $p_{cr}$ and post-buckled elastica $\left( {\xi ,\eta } \right)$ was conducted. As mentioned in Sect. 2.2, NP8 aluminum ($n = 4.785$), annealed copper ($n = 2.16$) and steel ($n = 1$), i.e., the most practical materials adhering to the Ludwick constitutive law in engineering, were considered in numerical examples.

First, the equilibrium path, i.e., the load parameter $p$ vs. deflection $\left( {\delta_{h} ,\delta_{v} } \right)$ curve, must be analyzed and discussed. The equilibrium paths against $\delta_{h}$ for $n = 2.16$ and $n = 1$ with $\alpha = 2$ are shown in Fig. 7a. For $n = 2.16$, if $p < 0.186\left( { = p_{cr} } \right)$, then $\delta_{h}$ does not occur, and the column remains straight. However, when $p$ reaches the buckling load parameter $p_{cr} = 0.186$,$\delta_{h}$ increases abruptly from $\delta_{h} = 0$ to $\delta_{h} = 0.774$, causing the catastrophic buckling of the column. After column buckling, two conjugate equilibrium paths exist: one is unstable, as indicated by a dotted line, whereas the other is stable, as indicated by the solid line. The unstable path is only the passing path to reach the final equilibrium state of the buckled column from the initial straight state (see Fig. 9b). An unstable and stable path convenes at $p_{cr} = 0.186$ with an abrupt increase in $\delta_{{h,p_{cr} }} = 0.774$. It is clear that this jump buckling phenomenon can be used for the solution method to calculate $p_{cr}$. After column buckling, the stable path passes through a strong nonlinear path with increasing $p$, reaching the peak coordinates $(\delta_{h,max} = 0.855$ at $p = 0.204$) and decreasing with increasing $p$. The maximum $\delta_{h,max}$ does not exceed 1 as expected because of incompressibility. The unstable path is highly nonlinear, and $\delta_{h}$ decreases as $p$ increases. For $n = 1$, $\delta_{h}$ does not occur until $p = 0.0983\left( { = p_{cr} } \right)$, and after buckling, the equilibrium path exhibits a clear nonlinear behavior. Here, only the stable path exists, i.e., the unstable path does not exist. This implies that after column buckling, $\delta_{h}$ does not increase abruptly, unlike the annealed copper column ($n = 2.16$), and post-buckling behavior is expected. This implies that for a steel column ($n = 1$), a catastrophic collapse due to buckling can be avoided because, unlike the annealed copper column, the bucking behavior should be detected immediately after column buckling. As $p$ increases, $\delta_{h}$ increases, reaches the peak coordinate ($\delta_{h,max} = 0.806$ at $p = 0.174$) and then decreases. It is clear that increasing $p$ indefinitely results in $\delta_{h}$ approaching zero. In Fig. 7b, the equilibrium paths of the vertical deflection $\delta_{v}$ for $n = 2.16$ and $n = 1$ with $\alpha = 2$ are shown. The path similarly passes through the nonlinear path of $\delta_{v}$ shown in Fig. 7a. However, the path does not correspond to the peak coordinates; therefore, $\delta_{v}$ consistently increases as $p$ increases. Unlike $\delta_{h}$ in Fig. 7a, $\delta_{v}$ can exceed 1; therefore, the free end of the buckled column can be located below the clamped end (for further details, see Fig. 9b). The value of $\delta_{v}$ approaches 2 if $p$ increases indefinitely.

Fig. 7

Equilibrium paths for $\alpha =2$ with $n=1$ and $n = 2.16$: a Horizontal deflection $\delta_{h}$. and b vertical deflection $\delta_{v}$

Next, the buckling load parameter $p_{cr}$ is discussed. Figure 8a shows the $p_{cr}$ vs. $\alpha$ curves for NP8 aluminum ($n = 4.785$), annealed copper ($n = 2.16$) and steel ($n = 1$) columns. As $\alpha$ increased, $p_{cr}$ decreased, as expected, because a cross section with a small $\alpha$ has a larger $I_{g}$. The decreasing slope of $p_{cr}$ was extremely steep at $\alpha < 1$; however, the slope was moderate at $\alpha > 1$. It is interesting that the magnitude order of $p_{cr}$ of the three different columns depended on $\alpha$. For example, at $\alpha = 3$ the order was from $n = 4.785$ to 2.16 to 1; however, at $\alpha = 0.2$, the order was reversed. To show an example of buckling load $P_{cr}$ (kN) in the dimensional units,$P_{cr}$ was calculated based on Fig. 8a for $l = 1$ m and $A = 20$ cm², and the results are shown in Fig. 8b. As $\alpha$ increased,$P_{cr}$ decreased, as shown in Fig. 8b. The decreasing slope of $P_{cr}$ was steeper for a smaller $\alpha$. The dimensionless $p_{cr}$ value shown in Fig. 8a did not indicate a significant difference among the three different columns; however, the buckling load $P_{cr}$ in the dimensional unit indicated a significant difference. This is because $P_{cr}$ is expressed in terms of $E$, as shown in Eq. (39). Consequently,$P_{cr}$ exhibited a significant difference based on the $E$ value of the column material.

Fig. 8

a $p_{cr}$ vs. $\alpha$ curves and b $P_{cr}$(kN) vs. $\alpha$ curves for $l = 1{ }$ m and $A = 20$ cm²

In field engineering, the buckling and post-buckling elastica must be understood for column analysis and design. First, in Fig. 9a, the buckling elastica $\left( {\xi ,\eta } \right)$ for NP8 aluminum ($n = 4.785$), annealed copper ($n = 2.16$), and steel ($n = 1$) columns with $\alpha = 2$ are shown. For $n = 1$, the buckling elastica with $p_{cr} = 0.0983$ remained straight, whereas for $n = 2.16$ and $4.785$, a significant deformed elastica occurred, as described by the equilibrium path shown in Fig. 7. For $n = 2.16$, significant deflections of the free end, i.e., $\delta_{h} = 0.774$ and $\delta_{v} = 0.493\left( { = 1 - 0.507} \right)$ under $p_{cr} = 0.186$, denoted by $\bullet$, occurred immediately after column buckling. Such sudden elastica cannot detect the cause of catastrophic collapse; therefore, $p_{cr}$ must be focused on in the column design of nonlinear elastic columns. As $n$ increases, the elastica becomes more severe. Second, the post-buckled elastica for $n = 2.16$ and $\alpha = 2$ is shown in Fig. 9b, where five elastica are presented, with $p = 0.25, 0.22, 0.204, 0.19$, and $0.186\left( { = p_{cr} } \right)$. In this figure, the dotted elastica is unstable, and the dashed elastica is stable. Therefore, the four dotted elastica with $p = 0.25, 0.22, 0.204$, and $0.19$ until the bucking elastica of $p_{cr} = 0.186$ with free end deflections $\delta_{h} = 0.774$ and $\delta_{v} = 0.493$ indicated by $\bullet$, as shown in Fig. 9a, were unstable. The trajectory of the free end where the coordinates of the free ends were continuously connected is presented. The unstable dotted elastica in the unstable dotted trajectory of the free end was only through a path that did not exist naturally. Therefore, the unstable elastica with $p > p_{cr}$ was located in the upper region from the buckling elastica with $p_{cr} = 0.186$, i.e., closer to the initial column, and all of the stable elastica with $p > p_{cr}$ must pass through this unstable region. As described above, the column head moved to the coordinates (0.507,0.774) indicated by $\bullet$ immediately after column buckling. After column buckling, the free end of the buckled column propagated along a stable dashed trajectory, i.e., lower region. In this stable trajectory, five post-buckled elastica with $p\left( { \ge p_{cr} } \right) = 0.186, 0.19, 0.204, 0.22$, and $0.25$ are presented. Here, an elastica with the maximum horizontal deflection $\delta_{h,max} = 0.855( < 1)$ at $p = 0.204$ denoted as ▲ was observed as well. An elastica can be placed under the clamped end, such as an elastica with $p = 0.25$.

Fig. 9

a Buckling elastica for $\alpha = 2$ by $n$ and b post-buckled elastica for $n = 2.16$ with $\alpha =$ $2$

The buckling behavior of the internal forces ($N,Q,M$) and the distributions of strain and stress ($\varepsilon ,\sigma$) were considered. In this numerical example, the internal forces of ($N,Q,M$) in dimensional form are discussed rather than those of ($n,q,m$) in nondimensional one. Figure 10 shows a diagram of the buckling internal forces ($N,Q,M$) for the NP8 aluminum alloy column ($n = 4.785$, $E = 455.8$ MPa) with $l = 1$ m, $a = 3.57$ cm and $b =$$1.78$ cm ($\alpha = 2, A = 20$ cm², and $I_{g} = 15.040$ cm^3.209). The buckling load $P_{cr} = 4.32$ kN, and its dimensional buckling elastica is shown in this figure, where its dimensionless elastica is presented in Fig. 9a. As expected, at the clamped end, $N_{c} \left( { = P_{cr} } \right) = 4.32$ kN and $Q_{c} = 0$ because $\theta_{c} = 0$ at the clamped end. At the free end, $N_{f}$ was approximately zero, i.e., $N_{f} \approx 0$, and $Q_{f} = P_{cr} = 4.32$ kN; this is because in this case, $\theta_{f} \approx \pi /2$, as shown in the buckling elastica in this figure. When $s > 0.55$ m, $N$ and $Q$ were almost vertically constant because the elastica was horizontally constant with $\theta \approx \pi /2$. As expected, at the free end, $M_{f}$ was zero, and at the clamped end, $M_{c}$ with $\Delta_{h,f} = 0.890$ m was the maximum as $M_{c} = P_{cr} \Delta_{h,f} = 3.85$ kNm.

Fig. 10

Buckling internal forces of $\left( {N, Q,M} \right)$ for $n = 4.785$ and $\alpha = 2$

Finally, the distributions of ($\varepsilon ,\sigma$) of the buckling elastic at the clamped end, where the maximum bending moment $M_{max} \left( { = M_{c} } \right)$ occurred, were obtained. Here, the column input parameters were the same as those shown in Fig. 10. The ($\varepsilon ,\sigma$) along the column depth in $- b \le h \le b$ can be obtained using the following equations for specified values of $N$ and $M$.

$$ \varepsilon = \varepsilon_{N} + \varepsilon_{M} = \left( {\frac{\left| N \right|}{{EA}}} \right)^{n} + \left( {\frac{\left| M \right|}{{EI_{g} }}} \right)^{n} h,\quad - b \le h \le b $$

(43)

$$ \sigma = E\varepsilon^{1/n} $$

(44)

For numerical values $N_{c} = 4.32$ kN and $M_{max} = 3.85$ kNm at the clamped end shown in Fig. 10, the corresponding ($\varepsilon_{N} ,\varepsilon_{M}$) can be obtained as $\varepsilon_{N} = + 7.72 \times 10^{ - 12}$ and $\varepsilon_{M,h = \pm b} = \pm 0.121$, respectively, from which $\varepsilon_{max} =$ 0.121 is obtained using Eq. (43). This results are shown in Fig. 11. Because $\varepsilon_{N}$ is approximately zero compared with $\varepsilon_{M,h = \pm b}$, the deviation of the neutral axis from the bending axis is negligible, i.e., the neutral axis is approximately remained at $h = 0$. Using $\varepsilon_{max} = \pm$ 0.121, the linear equation $\varepsilon = \kappa h$ along the column depth can be drawn in Fig. 11 where its slope $\kappa = 0.0678/{\text{cm}}$ is obtained from Eq. (22). Subsequently, the nonlinear equation of $\sigma = E\varepsilon^{1/n}$ in Eq. (44) is obtained, and its result is also shown in Fig. 11. The $\sigma_{max}$ is calculated as $\sigma_{max} = 293$ MPa at the two edge ends, and the nonlinear distribution shape is almost rectangular; therefore, the use of the cross-sectional area for $\sigma$ is effective compared with those of linear materials. The information provided in Fig. 11 is important for ensuring column safety when designing nonlinear material columns.

Fig. 11

Buckling strain $\varepsilon$ and stress $\sigma$ (MPa) at clamped end

4 Concluding Remarks

The GMI of the plane area of an ellipse for a nonlinear material adhering to the Ludwick constitutive law was investigated. The GMI of an elliptical plane was derived from an explicit integral formula based on the equilibrium of tensile and compressive forces applied internally to the elliptical cross section owing to the external bending moment. The GMI values calculated by varying the material constant in the nondimensional and dimensional forms were reported in tables and graphs. To demonstrate the practical use of the GMI in this study and in field engineering, its application to cantilever column buckling was considered. Numerical experiments of critical buckling loads and buckling behavior in dimensionless and dimensional forms were performed, and the results are presented in tables and figures. The contents of this study are beneficial to the analysis and design of cantilever columns fabricated using Ludwick-type materials.