1 Introduction

1.1 Background

Structural health monitoring (SHM) has received much attention as a rigorous tool in damage detection of engineering structures, particularly bridges and buildings. Structural damages such as cracks, corrosion, fatigue, and excessive stresses cause a change in modal parameters of the structure that consequently may affect their serviceability or dynamic performance [1, 2]. Vibration-based damage detection methods are extensively used in SHM, due to their efficiency in instrument deployment. Acoustic, ultrasonic, and radiography inspection methods are not applicable to unreachable parts of structures, and visual methods significantly depend on technical experience and engineering judgment. However, vibration-based methods are not error proof. This is because extracted modal parameters of the structure are affected by uncertainties emanated from limited number of installed sensors, uncontrolled excitations, environmental conditions, and noisy measured vibration data.

Vibration-based methods [3] track variations in dynamic properties of structures within time or frequency domain. However, natural frequency and modal damping are not reliable for damage detection of complex structures and simple structures with low-level damage [4,5,6,7]. Modal-based damage detection methods such as mode shape, modal curvatures, modal damping, and strain energy are not able to capture desirable low-level damages. Modal characteristics are extracted indirectly from the measured frequency response functions (FRFs) data at the excitation frequencies around resonances. In modal characteristics-based model updating, measured data are less than unknown parameters. In contrast, FRF-based model updating reduces loss of information as it includes vibration data over a broad range of frequency [8, 9]. Hence, FRFs give more reliable damage detection results. This is because FRF estimation reduces modal analysis errors during modal extraction and curve fitting processes [10,11,12,13]. Signal processing is an essential part of the vibration-based methods. In this regard, the complete ensemble empirical mode decomposition with adaptive noise technique and multiple signal classification was used to identify the presence, location, and severity of damages in a steel truss bridge model [14, 15].

1.2 Fourier transform-based methods

Fourier transform (FT) analysis method describes a vibration data over its frequency content. However, it does not account for discontinuities, local changes, and transitory properties of time-varying data [16]. Thus, extracted data from FT may not completely reflect the characteristics of a vibration data. To overcome non-stationary and local discontinuity properties of FT, short time Fourier transform (STFT) is used in a time–frequency domain analysis [17]. However, for a short time interval, a stationary signal is needed, and an extended time interval requires an increase in frequency resolution. Consequently, spectral components of a large interval are smeared and result in a decreased resolution within the time domain [18]. To address this shortcoming, an autoregressive (AR) model was developed [19]. For the AR model, there are two main shortcomings: (1) length of the stationary interval controls time and frequency resolution of the time–frequency representation, and (2) reduction of the time interval gives lower-order models and reduces assessment accuracy [19]. Further, fractal dimension analysis was developed to detect cracks in structural elements. In fractal dimension analysis, damage index is extracted by a constant moving window across the fundamental mode shape of the structure. However, inclusion of higher modes may lead to a false damage localization [20]. Instead of using traditional modal-based techniques such as FT, Mosavi et al. used several time-domain statistical features including root mean square (RMS), shape factor, kurtosis, and entropy to study damage detections of bridges [21].

1.3 Wavelet transform-based methods

Unlike FTs, wavelet transforms (WTs) represent a vibration data in time–frequency domain with localization [22,23,24,25,26,27,28]. The advantages of utilizing wavelets are to improve the frequency resolution limitations of data associated with the previous techniques and efficiently separate the components of a signal. The WT is a decomposition algorithm that has an ability to analyze non-linear and non-stationary signals. WTs are categorized into discrete wavelet transform (DWT) and continuous wavelet transform (CWT). Using CWT and stationary wavelet transform (SWT), Cao and Qiao developed a two-step progressive wavelet analysis, and improved abnormality analysis of mode shapes in damage detection [29]. In a different work, Wu and Wang conducted experimental studies adopting SWT and identified crack location and depth in a beam subject to a static displacement [30]. Okafor and Dutta used a small set of wavelet coefficients with uniformly spread white noise to represent a spatially localized abnormality in mode shape [31]. Montanari et al. reported an optimal number of sampling intervals based on spatial CWT damage detection methods in beam structures [32]. It was found that the optimal number of sampling intervals is correlated with deflection shape and damage location [32]. Solis et al. used a CWT to study variations in mode shapes for damage localization [23]. It was reported that damage location may be found using a small number of sensors and mode shapes [23]. Pnevmatikos and Hatzigeorgiou proposed a damage detection method using DWTs for a frame structure subject to ground motion excitations [27]. In this work, a high-accuracy damage detection was achieved by increasing the level and order of the DWTs, even in the presence of noisy signals [27].

1.4 Artificial intelligence-based methods

Although several studies on WT-based damage detection methods showed their efficiency in capturing even small damages, these methods may suffer from poor accuracy if used in complex structures or in the presence of multiple damages and uncertainties such as noise, temperature, and limited number of sensors. Pattern recognition is an artificial intelligence (AI)-based method and has become popular in structural damage detection due to its excellent self-organization, self-learning, auto-association, and non-linear modeling capability [33,34,35]. Artificial neural network (ANN) methods are often used on finite element (FE) models of structures or on real measured vibration data to identify damages of tested structures [33,34,35,36]. Padil et al. demonstrated that ANNs give inaccurate damage detection results if used with highly noisy data [37]. Application of ANNs for damage detection is limited to structures with a small number of degrees of freedom (DOFs) as ANNs require extensive computational efforts for structures with high DOFs [8, 38, 39]. Bakhary et al. developed a progressive method for noise-free and low-level damaged structures using ANNs [40]. Substructure technique with a two-stage ANN was implemented to identify damage location and severity in simple structures [40]. Mehrjoo et al. proposed a method for damage severity assessment of joints in truss bridge structures using an ANN classifier. However, their method was not able to capture very small damages in the presence of low-level noises [8].

Deep neural networks (DNNs) were shown to be more effective compared to conventional ANNs [41]. DNNs represent deep learned features of original vibration data much better, and hence make them more desirable for classification. In addition to DNNs, couple sparse coding (CSC) was also adopted as a second classification method and spectral tool to represent and compress high-dimensional signals [42]. The idea of collating several classifier systems or an ensemble of classifiers to overcome limitations of a single classifier was first proposed by Wolpert [43]. Fallahian et al. proposed a new damage detection method in the presence of uncertainties such as high-level noise and temperature effects using DNNs and CSCs [44].

In recent years, convolutional neural networks (CNNs)-based models have been significantly utilized to extract spatial features of images, which are usually 2D data. This has led to promising results in image classification [45], image segmentation, and object detection. Due to two fundamental properties, including spatially shared weights and spatial pooling, CNNs-based models can extract features with high precision. Additionally, recurrent neural network (RNNs)-based methods can generate and address memories of arbitrary-length sequences of input patterns [46]. The most application of RNNs-based models is in supervised learning tasks with sequential input data, such as sentiment classification and target outputs [47]. Yang et al. proposed a novel hierarchical deep CNN to identify damage in structures [48].

1.5 Contribution

As the above survey demonstrates, although each damage detection method has its own advantage/advantages, a general method, able to cover all aspects of structural damage detection, is yet to remain a research topic of interest. Hence, in this work, we overcome the shortcomings of previously developed damage detection methods, mainly (1) identification of low-level damages in the presence of uncertainties like noise and temperature for structures with large DOFs, and (2) reduction of false detections. To achieve this aim, we combine several methods and use capabilities of each method to develop a more general and comprehensive damage detection algorithm. The proposed algorithm is composed of four primary steps: (1) vibration data are decomposed by DWT, (2) the decomposed data are then reduced by principal component analysis (PCA), (3) DNN and CSC are used to train individual damage models of the structure using the compressed decomposed vibration data and damage data (including damage locations and severity) as input parameters, and (4) the individual damage models are combined by majority voting to predict damage of the structure. This proposed four-step algorithm considers vibration data such as FRF and structural response signals as input parameters for training two DNN and two CSC damage models. To account for uncertainty effects, a white Gaussian noise pollution with up to 20% noise-to-data ratio is added to the vibration data, and a uniformly distributed temperature gradient is introduced to the numerical model of the structure. To demonstrate the efficiency and accuracy of the proposed algorithm in the detection of low-level damages, simulated vibration data of a one-bay three-story frame is considered and assessed. Additionally, measured vibration data of a large-scale bridge structure with many DOFs is used for validation of the proposed algorithm and comparison of the proposed method with the methods previously developed.

2 Damage detection algorithm

In this section, the proposed damage detection algorithm is described in detail. The proposed algorithm is schematically illustrated in Fig. 1. The vibration data set is taken from a tested structure or a numerical model of the structure, respectively (Fig. 1a), and is composed of two different subsets: (1) training vibration subset, which is used to train damage models of the structure (Fig. 1b), and (2) test vibration subset, which is used to test the robustness of the algorithm (Fig. 1g). The input vibration data set could be a set of displacement response signals, acceleration response signals, or frequency response functions (FRFs). Both vibration subsets are decomposed by DWT (Fig. 1c), and subsequently, are reduced and compressed by PCA [49] (Fig. 1d). The decomposed and compressed training vibration subset along with the corresponding training damage subset (Fig. 1e) are then used to train four individual damage models for the structure: (1) two CSC-based damage models for FRFs and displacement signals, and (2) two DNN-based damage models for FRFs and displacement signals (Fig. 1f). Afterward, a final damage model is created by collating the four trained individual damage models (Fig. 1h). To evaluate the performance of the algorithm, the test vibration subset is inputted to the final damage model of the structure (Fig. 1g), and the output is compared with the test damage subset to assess the accuracy of the algorithm (Fig. 1i). The detailed information on each step of the proposed algorithm is given in the following sections. So, for damage detection, any new vibration data (Fig. 1g) can be inputted to the trained damage model (Fig. 1h) to predict the location and severity of any possible damage (Fig. 1i), as collectively shown by a red dashed rectangle in Fig. 1.

Fig. 1
figure 1

The proposed damage detection algorithm

Full size image

2.1 Vibration data decomposition by DWT

As shown in Fig. 1, the first primary step of the proposed algorithm is to decompose the training vibration subset by wavelet analysis, as a powerful tool in characterization of local features (Fig. 1c). Let us consider a training vibration subset, X, composed of P vibration vectors of size N, which forms a matrix of size \(N \times P\):

$$X = \left[ {\begin{array}{*{20}c} {X_{1} } & {X_{2} } & \ldots & {X_{j} } & \ldots & {X_{P} } \\ \end{array} } \right],$$
(1)

where Xj is the jth training vibration vector:

$$X_{j} = \left[ {\begin{array}{*{20}c} {x_{1j} } & {x_{2j} } & \ldots & {x_{ij} } & \ldots & {x_{NP} } \\ \end{array} } \right]^{T} ,$$
(2)

in which T is the transpose of the vector and xij is the ith element of the jth vibration vector. The CWT of the jth vibration vector, Xj(t), is given by:

$$X_{j} \left( {a,b} \right) = \frac{1}{{\sqrt {\left| a \right|} }}\int\limits_{ - \infty }^{ + \infty } {X_{j} \left( t \right)\overline{\psi }\left( {\frac{t - b}{a}} \right)} \quad a \ne 0 \in R,\;b \in R,$$
(3)

where a and b are scale and transition parameters; \(\overline{\psi }\left( t \right)\) is the complex conjugate form of the mother wavelet function, \(\psi \left( t \right)\); R is the set of real numbers; and ‖ is the absolute value operator. Herein, the Haar wavelet is used in the damage detection process. To perform discrete wavelet analysis of the jth vibration vector, Xj(t), the parameters a and b need to be discretized. A common choice for discretizing parameters a and b are 2n and 2nm, respectively, where n and m are sets of positive integers [50]. So, the discretized wavelets, \(\psi_{n,m}\), are given by:

$$\psi_{n,m} \left( t \right) = \frac{1}{{\sqrt {2^{n} } }}\psi \left( {\frac{t}{{2^{n} }} - m} \right),$$
(4)

where \(\psi_{n,m}\) creates an orthonormal subspace. The DWT decomposes a vibration vector to its approximate and detail components, as shown in Fig. 2. The vibration vector is passed through a series of low-pass filters to analyze low-frequency contents (approximate components), and a series of high-pass filters is used to analyze high-frequency contents of the data (detail components) [27]. The detail component at level n is given by:

$$D_{n} = \sum\nolimits_{m} {a_{n,m} } \psi_{n,m} ,$$
(5a)

where

$$a_{n,m} = \int_{ - \infty }^{ + \infty } {X_{j} \left( t \right)} \,\psi_{n,m} \left( t \right)\,dt,$$
(5b)

and the approximate component at level n is given by:

$$A_{n} = \sum\limits_{{J > n}} {D_{J} } ,$$
(6)

Finally, the jth vibration vector, Xj(t), at level n is reconstructed by:

$$X_{j} \left( t \right) \approx A_{n} + \sum\limits_{J \le n} {D_{J} } ,$$
(7)
Fig. 2
figure 2

A four-level discrete wavelet decomposition

Full size image

It should be noted that the term, \(\sum\limits_{J \le n} {D_{J} }\) (i.e., the detail components) provides useful information on detecting low-level damages, which contain high frequencies of vibration.

2.2 Vibration data compression by PCA

The training vibration subset, decomposed by DWT in Sect. 2.1, is compressed in this section by PCA [49, 51,52,53] (Fig. 1d) to avoid high computational efforts, particularly in structures with large number of DOFs. Throughout PCA, the decomposed training vibration subset, \(X\), composed of P vibration vectors of size N, \(X_{j} \left( t \right)\) (see Eq. 7), is transformed into a new subset of P vibration vectors of size Q (Q < N). This is an eigenvalue problem, and eigenvalue decomposition of the covariance matrix is used in the transformation process. Hence, mean vector, \(\mu_{X}\), and covariance matrix, CX, of the decomposed vibration data set are first determined as:

$$\mu_{X} = \frac{1}{P}\sum\limits_{j = 1}^{P} {X_{j} } ,$$
(8)
$$C_{X} = \frac{1}{P}\sum\limits_{j = 1}^{P} {\overline{X}_{j} } \overline{X}_{j}^{T} ,$$
(9a)

where

$$\overline{X}_{j} \left( i \right) = X_{j} \left( i \right) - \mu_{X} \left( i \right),$$
(9b)

Then, the eigenvalue problem is defined as:

$$C_{X} \phi = \lambda \phi ,$$
(10)

Solving this eigenvalue problem, eigenvalues, \(\lambda_{i}\), and their corresponding eigenvectors, \(\phi_{i}\), are determined, and the eigenvalues are sorted in descending order:

$$\begin{gathered} \phi = \left[ {\begin{array}{*{20}c} {\phi_{1} } & {\phi_{2} } & \ldots & {\phi_{i} } & \ldots & {\phi_{N} } \\ \end{array} } \right] \hfill \\ \lambda = \left[ {\begin{array}{*{20}c} {\lambda_{1} } & {\lambda_{2} } & \ldots & {\lambda_{i} } & \ldots & {\lambda_{N} } \\ \end{array} } \right]\quad \lambda_{1} \ge \lambda_{2} \ge \ldots \ge \lambda_{i} \ge \ldots \lambda_{N} , \hfill \\ \end{gathered}$$
(11)

Hereafter, the decomposed \(N \times P\) subset is transformed to a reduced \(Q \times P\) subset according to proportion of total variance:

$$\pi_{Q} = \sum\limits_{k = 1}^{Q} {\frac{{\lambda_{k} }}{{\sum\limits_{i = 1}^{N} {\lambda_{i} } }}} ,$$
(12)

Thus, the proportion of total variance shows the quality of the reduced \(Q \times P\) subset. Finally, the vibration vectors of the reduced \(Q \times P\) subset is determined:

$$\tilde{X}_{j} = \beta X_{j} ,$$
(13a)

in which β is the transformation matrix:

$$\beta = \left[ {\begin{array}{*{20}c} {\phi_{1} } & {\phi_{2} } & \ldots & {\phi_{i} } & \ldots & {\phi_{Q} } \\ \end{array} } \right]^{T} ,$$
(13b)

2.3 Training damage models

In this section, the decomposed and compressed training vibration subset (Fig. 1d) as well as the corresponding training damage subset (Fig. 1e) is used to train four individual damage models of the structure using deep learning methods of DNN and CSC (Fig. 1f).

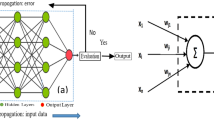
As shown in Fig. 3, DNN creates a hierarchy structure including an input layer, an output layer, and a number of hidden layers. The method generally learns features of higher layers of the hierarchy structure from features of lower layers [54,55,56]. For developing a damage model, the input layers are the training vibration and corresponding damage subsets. For the trained damage model, the input layer is the test vibration subset, and the output layer is the predicted damage subset. This training generates a robust pattern recognition model of the structural damage, generalizes normal conditions of the vibration and damage subsets, and characterizes environmental and operational variations such as temperature and noise through its low-level features [44]. Thus, in this work, DNN is trained on the vibration subset, \(\tilde{X}\), and corresponding damage subset, \(Y\), to learn correlations between vibration data and structural damage, and develop a damage model of the structure. Afterward, the test vibration subset, \(\tilde{X}^{\prime }\), is inputted to the DNN-trained damage model, and then, the residual matrix, r, as a training quality index, is determined:

$$r = Y - Y^{\prime } ,$$
(14)

where \(Y^{\prime }\) is the matrix of the predicted damage and is the output of the DNN-trained damage model.

Fig. 3
figure 3

An example of the DNN layout used for training the structural damage model

Full size image

In the proposed algorithm, to capture any damage information and features ignored by DNN, CSC-trained damage models are also developed [49]. Hence, the training vibration and damage subsets are fed into CSC. Let us consider a training damage subset, Y, composed of P vectors of size M, which forms a matrix of size \(M \times P\):

$$Y = \left[ {\begin{array}{*{20}c} {Y_{1} } & {Y_{2} } & \ldots & {Y_{j} } & \ldots & {Y_{P} } \\ \end{array} } \right],$$
(15)

where Yj is the jth training damage vector:

$$Y_{j} = \left[ {\begin{array}{*{20}c} {y_{1j} } & {y_{2j} } & \ldots & {y_{ij} } & \ldots & {y_{MP} } \\ \end{array} } \right]^{T} ,$$
(16)

CSC represents the training vibration vector, \(\tilde{X}_{j}\), and the training damage vector, \(Y_{j}\), as sparse linear combinations:

$$\begin{gathered} \tilde{X}_{j} \approx D_{X} \alpha , \hfill \\ \alpha = \left[ {\begin{array}{*{20}c} {\alpha_{1} } & {\alpha_{2} } & \ldots & {\alpha_{i} } & \ldots & {\alpha_{K} } \\ \end{array} } \right]^{T} , \hfill \\ \end{gathered}$$
(17)

in which the vector α is the sparse code of the vibration vector, \(\tilde{X}_{j}\), and has K elements; \(D_{X}\) is a transformation matrix of size \(Q \times K\), and is called dictionary of the vibration vector. Similarly, the damage vector is represented by:

$$Y_{j} \approx D_{Y} \alpha ,$$
(18)

where \(D_{Y}\) is a transformation matrix of size \(M \times K\), and is called dictionary of the damage vector. Generally, CSC uses \(\tilde{X}_{j}\) and \(Y_{j}\) as inputs, and solves the following optimization problem to train a damage model for the structure:

$$\min_{{\alpha \in R^{K} }} :\left\| {\tilde{X}_{j} - D_{X} \alpha } \right\|_{2}^{2} + \kappa_{1} \left\| \alpha \right\|_{1} + \kappa_{2} \left\| {Y_{j} - D_{Y} \alpha } \right\|_{2}^{2},$$
(19)

where κ1 and κ2 are the regularization parameters; \(\left\| {} \right\|_{1}\) and \(\left\| {} \right\|_{2}\) are the first and second norm operators, respectively. From the optimization problem in Eq. (19), all variables are determined. The sparse vector, α, reconstructs the input vibration vector, \(\tilde{X}_{j}\), from both the dictionary, \(D_{X}\), with minimum error, \(\left\| {\tilde{X}_{j} - D_{X} \alpha } \right\|_{2}^{2}\), and the dictionary, \(D_{y}\), with minimum distance from \(Y_{j}\), \(\left\| {Y_{j} - D_{Y} \alpha } \right\|_{2}^{2}\).

The test vibration vector, \(\tilde{X}^{\prime }_{j}\), is then used in the CSC-trained model (see Eq. 19), to predict the damage, \(Y_{j}^{\prime }\), by solving this minimization problem:

$$\min_{{Y_{j}^{{^{\prime } }} \in R^{M \times P} }} :\left\| {\tilde{X}^{\prime }_{j} - D_{X} \alpha } \right\|_{2}^{2} + \kappa_{1} \left\| \alpha \right\|_{1} + \kappa_{2} \left\| {Y^{\prime }_{j} - D_{Y} \alpha } \right\|_{2}^{2} ,$$
(20)

To solve the optimization problems in Eqs. (19) and (20), the feature-sign search algorithm is used [57]. It should be noted that in the proposed algorithm, both FRFs and displacement signals are separately used in DNN and CSC as input vibration data, and thus four individual damage models, including two DNN-trained and two CSC-trained damage models, are created. Collating these four damage models, a more general and thorough trained damage model of the structure, which considers various features of the structure, is developed.

2.4 Final damage model of structure

The four individual damage models, two DNN- and two CSC-trained damage models, developed in Sect. 2.3, are combined together in this section to reach a final damage model (Fig. 1h). This is because the ensemble learning increases damage detection accuracy, and reduces selection probability of a poor single classifier [58]. Each of the damage models is trained on a re-weighted version of the original output to generate a sequence of new models [59]. The weights are then modified to address any pattern misclassification. Afterward, an ensemble classifier is created by forward iteration. In each iteration, the first decision stump, is trained with a random subset of the weighted output. For the second decision stump, half of the weighted output, classified correctly by first decision stump, is selected as the training subset. The third decision stump is then trained with a higher weight of misclassified observations on the first and second decision stumps. Finally, the three decision stumps are combined through a majority voting, where the final decision is the one that correctly classifies more than half of the output [60].

3 Validation of damage detection algorithm

In this section, the accuracy of the damage detection algorithm proposed in Sect. 2 is evaluated using two case studies: (1) numerical model of a one-bay three-story frame, which is modeled in SAP2000 program, and (2) experimental data of a large-scale bridge, which is modeled in MATLAB. For both case studies, during the training phase of the algorithm, 70% of the input data is used to train DNN and CSC damage models. For the test phase of the algorithm, the remaining 30% of the input data is used to evaluate the accuracy of the algorithm. In this study, for DNN, the number of layers is taken 5, where the number of neurons is 100, 350, 150, and 50, respectively, for the 1st–4th layers. The neurons number for the last layer is based on the number of the elements of the structure.

3.1 Numerical model case

Supports and connections play an important role in the stability of structures, particularly during seismic events. Hence, in this section, the performance of the proposed algorithm in capturing low-level damages, localized near a support or a point of geometric discontinuity such as a corner connection, is evaluated in a frame structure. The numerical model is a 2D one-bay three-story frame shown in Fig. 4. The story height and the bay length are 3 m and 2.5 m, respectively. Table 1 summarizes material properties of the frame elements. The 2D FE model of the frame is composed of 32 nodes. Each node has three DOFs including two translational and one rotational DOFs. Given fixed supports at nodes 31 and 32, the numerical model has 90 DOFs. The beam–column connections (elements 28–33) are considered semi-rigid, and thus are modeled with very short beam elements of very high relative rigidity. The frame is excited by a dynamic half-sine impulse load or a concentrated static load at vertical DOFs of nodes 21, 25, 28 and horizontal DOFs of nodes 2, 14, 8 and 5. The acceleration and displacement responses are measured at vertical DOFs of nodes 20, 24, 29, and horizontal DOFs of nodes 1, 4, 7, 13, and 16. To consider measurement errors and uncertainties, a white Gaussian noise pollution with up to 20% noise-to-signal ratio is added to the response signals.

Fig. 4
figure 4

Numerical case study: a 2D one-bay three-story frame structure; a geometry of the frame and element numbers, and b node numbers

Full size image
Table 1 Geometry and material properties of the three-story frame structure
Full size table

For this numerical case study, stiffness reduction of an element or elements of the frame is taken as the damage indicator, and accordingly, five damage cases are introduced, as shown in Fig. 5. Case 1 (Fig. 5a) considers a single damage case, where the middle element of the left column (element no. 2) is the only damaged member with 30% stiffness reduction. In this damage case, since the excitation location (node 2) and the response measurement location (node 1) are very close, high levels of noise may pollute the measured response signal, and hence the test data is polluted with up to 20% noise. Case 2 (Fig. 5b) also includes a single damage, in which the damage is adjacent to the beam–column connection element no. 28. This damage case investigates the efficiency of the proposed algorithm in damage detection of connections with low-level damages. The damage considered is 6% for this scenario. Case 3 (Fig. 5c) is a double-damage scenario. Elements no. 8 and 23 suffer from 15 and 40% stiffness reduction, respectively. This damage case verifies the proposed algorithm for simultaneous damage detection in beams and columns. Case 4 (Fig. 5d) comprises two beam–column connections, no. 29 and 30, which experience 10% and 15% stiffness reduction, respectively. Case 5 (Fig. 5e) is a multi-damage case to validate the proposed algorithm for simultaneous damage detection in connections, beams, and columns. Connection no. 28 and elements no. 8 and 24 are damaged by 10%, 20%, and 15%, respectively.

Fig. 5
figure 5

Damage cases (rectangular hatches) for the frame structure: a case 1, b case 2, c case 3, d case 4, e case 5

Full size image

Vibration data and damage data are inputted to the algorithm (see Fig. 1). In this study, the FRF data and displacement response of the frame are used as input vibration data in the algorithm. For each damage case, the vibration data comprises: (1) FRFs between the excitation DOFs and the measurement DOFs, and (2) the displacement response signals at the DOFs. The input damage data is composed of both the damage location (element number) and damage severity (stiffness reduction of the corresponding element).

As shown in Figs. 6 and 7, DWT (see Sect. 2.1) decomposes the FRF data (excitation at node 4 and response measurement at node 25) into its approximation and detail components at level 5 for the undamaged structure. In Fig. 6, the FRF data includes no noise, while in Fig. 7 10% noise is added to the data. One level of approximate component (A5) and four levels of detail component (D2–D5) are used to train the data for the damage detection process. As seen in Fig. 7, the noise affects the level 1 detail component (D1), particularly at very high frequencies, compared to the other components. Thus, D1 can be ignored in the damage detection process. The same decision is made about the displacement response signals.

Fig. 6
figure 6

The approximation component, A5, and the detail components D1–D5 of the FRF of the undamaged frame with 0% noise

Full size image
Fig. 7
figure 7

The approximation component, A5, and the detail components D1–D5 of the FRF of the undamaged frame with 10% noise

Full size image

Table 2 compares the actual damage and the predicted damage by the algorithm for the five damage cases. For case 1, the predicted damage (32%) is very close to the actual damage (30%). For case 2, the algorithm detects the low-level damage (8%) with a slight error. For multiple damage cases (damage cases 3, 4, and 5), the severity of the predicted damages is close to the actual damages.

Table 2 Actual and predicted damages for the frame structure and different damage cases
Full size table

The coefficient of determination (R2) is also determined to evaluate the performance of the algorithm:

$$R^{2} = \left( {\frac{{\sum {y \cdot y^{\prime } - \left( {\sum y } \right)\left( {\sum {y^{\prime } } } \right)} }}{{\sqrt {\left( {\sum {y^{2} } } \right) - \left( {\sum y } \right)^{2} } \sqrt {\left( {\sum {y^{\prime 2} } } \right) - \left( {\sum {y^{\prime } } } \right)^{2} } }}} \right),$$
(21)

where \(y\) is the actual value, \(y^{\prime }\) is the predicted value, and r is the number of damage scenarios. The mean R2 for the frame structure is 0.96 for 100 damage scenarios.

A robust damage detection method not only minimizes damage detection errors for safety reasons, but also reduces the number of false damage predictions for economic considerations. Figure 8 shows the distribution of the damages between all elements of the frame structure for damage cases of 3 and 5. As seen in Fig. 8, the proposed method minimizes false detections for damage cases 3 and 5, as the value of the predicted damage for most of the undamaged elements is close to zero. Figure 9 shows the distribution of the damages between all elements of the frame structure for damage cases of 3 and 5 using the DNN model only. Unlike the proposed method, which ensembles DNN and CSC models, the DNN model only gives a poor prediction at false detections. It should be mentioned that a similar pattern is seen for other damage cases 1, 2, and 4 not shown here.

Fig. 8
figure 8

Actual and predicted damage values for elements of the frame structure for: a damage case 3, and b damage case 5

Full size image
Fig. 9
figure 9

Actual and predicted damage values for elements of the frame structure using the DNN model only for: a damage case 3, and b damage case 5

Full size image

3.2 Experimental test case

The previously published experimental data for I-40 bridge over the Rio Grande in New Mexico is used to validate the efficiency of the proposed algorithm in detection of low-level damages in complex structures. Detailed information on I-40 bridge, such as geometric properties, experimental data, and damage detections can be found in [61,62,63]. The elevation view and cross section of the bridge is shown in Figs. 10 and 11, respectively [61]. Forced vibration and ambient vibration tests were performed on I-40 bridge. The forced vibration excitations were applied by a hydraulic shaker using a uniform random signal between 2 and 12 Hz. The response of the bridge was measured using 26 equally spaced accelerometers installed on both sides of the bridge deck (see Fig. 12). Four levels of damage were introduced in the vicinity of N7 using torch cuts in the web and flange of the bridge girder. These cuts resulted in approximate stiffness reductions of 5% (damage case 1), 10% (damage case 2), 32% (damage case 3) and 92% (damage case 4) [63].

Fig. 10
figure 10

Elevation view of I-40 bridge [61]

Full size image
Fig. 11
figure 11

Cross section of I-40 bridge [61]

Full size image
Fig. 12
figure 12

Sensor arrangement for the experimental test on I-40 bridge [61]

Full size image

The 3D FE model of the bridge consists of 144 elements for the concrete deck and 12 elements for each plate of the web. The numerical model was updated using experimental data from the undamaged structure. Table 3 summarizes the correlation between the numerical and experimental undamaged modes: ωe and ωn are the experimental and numerical natural circular frequencies. The modal assurance correlation (MAC) values demonstrate the accurate correlation between the dynamic behavior of the undamaged real bridge with the updated numerical model.

Table 3 Correlation between numerical and experimental modes of the undamaged bridge
Full size table

Details on numerical modeling and modal analysis of the bridge can be found in [44]. To account for uncertainty effects of temperature, a uniformly distributed temperature gradient is introduced to all elements of the FE model. The four DNN- and CSC-trained damage models are developed using FRFs and displacement signals data generated by the FE model. After the training phase, experimental FRFs of the bridge are fed to the trained damage model, and the damage in each element of the bridge is determined. The results are given for two different cases: (1) when the FRFs and displacement signals are decomposed by DWT (DWT DNN-CSC, DDC), and (2) when the original FRFs and displacement signals are used without any decomposition (DNN-CSC, DC).

Table 4 summarizes damage detection results of the bridge for the four damage cases. For the case of the extremely large damage (damage case 4, 92%), slight errors are seen for both approaches. The accuracy of the DDC approach increases compared to the DC, as the damage severity reduces. In particular, for 5% and 10% damages, DDC gives 4.5% and 14% damages for element 24, respectively. Figure 13 shows the damage detection results for the low-level damage case (5%) using both DDC and DC approaches. Using DC, the number of false detections is high, particularly in elements 2, 10, 26, and 48 (Fig. 13a). These false detections are due to the temperature variation introduced in the FE model. In contrast, DDC precisely detects the location of the damage in element 24, and reduces the number of false detections (Fig. 13b). Thus, the proposed algorithm detects damage location and severity, even for low-level damages, in the presence of temperature gradient introduced in the FE model.

Table 4 Actual and predicted damages for the elements of the bridge structure
Full size table
Fig. 13
figure 13

Actual and predicted damage values for elements of the bridge structure and low-level damage case (5%): a DC, and b DDC

Full size image

The false damage detections, particularly at the supports, could be due to the uniformity of the temperature used here, while there may be non-uniform gradients of temperature in reality. Thus, having temperature sensors placed along the bridge structure, the results are improved. Moreover, temperature variations can lead the supports to move or boundary conditions to change, both not considered in the numerical model of the bridge.

4 Conclusions

In this work, a new damage detection algorithm is developed based on an ensemble system of deep neural network and couple spare coding. The vibration data of the structure is decomposed by discrete wavelet analysis before training the ensemble system. Majority voting is used to combine the output of the deep neural network and couple spare coding classifiers.

The numerical study of the frame structure, subject to single- and multi-damage cases, demonstrates that the algorithm detects low-level damages with a very high level of accuracy, particularly in beam–column connections in the presence of noise. From the study of the large-scale bridge structure, it was found that the algorithm: (i) locates low-level damages and predicts their severity with high precision in the presence of temperature, and (ii) gives lower false damage detections. This study generally shows that the combination of ensemble pattern recognition models and wavelet analysis techniques is promising, and gives better prediction of damage location and severity.