Abstract
Spatial models based on the Gaussian distribution have been widely used in environmental sciences. However, real data could be highly non-Gaussian and may show heavy tails features. Moreover, as in any type of statistical models, in spatial statistical models, it is commonly assumed that the covariates are observed without errors. Nonetheless, for various reasons such as measurement techniques or instruments used, measurement error (ME) can be present in the covariates of interest. This article concentrates on modeling heavy-tailed geostatistical data using a more flexible class of ME models. One novelty of this article is to allow the spatial covariance structure to depend on ME. For this purpose, we adopt a Bayesian modeling approach and utilize Markov chain Monte Carlo techniques and data augmentations to carry out the inference. However, when the number of observations is large, statistical inference is computationally burdensome, since the covariance matrix needs to be inverted at each iteration. As another novelty, we use a prediction-oriented Bayesian site selection scheme to tackle this difficulty. The proposed approach is illustrated with a simulation study and an application to nitrate concentration data. Supplementary materials accompanying this paper appear online.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A popular approach for modeling continuous spatial data is often based on the Gaussian process. However, in many applications, including those in environmental sciences, datasets often present asymmetry. This may manifest itself in the exploratory data analysis by demonstrating heavier tails than in a Gaussian process or spatial heteroscedasticity caused by outliers (Tadayon 2017). In other words, the observed data may contain special cases which have extreme values compared to their neighboring observations. All this calls for statistical models to address these non-Gaussianity features. A widely used approach is to find some nonlinear transformations so that the assumption of normality for the transformed data holds. However, an appropriate transformation may not exist or may be difficult to find or even to interpret (Kim and Mallick 2004). Evidently, the situation is exacerbated in multivariate settings with several spatial response variables. Recently, more suitable theoretical strategies have been developed to handle some of the potential weaknesses associated with the transformation methods (Palacios and Steel 2006; Fonseca and Steel 2011). Here, we focus on the Gaussian log-Gaussian (GLG, hereafter) model defined by Palacios and Steel (2006) as a scale mixing of a Gaussian process to accommodate heavier tails than the common Gaussian process. In this model, the Gaussian stochastic process \(\varepsilon \left( s\right) \) is replaced by a ratio of two independent stochastic processes, as \(\varepsilon \left( s\right) /\sqrt{\lambda \left( s\right) }\), where the mixing term \(\lambda \left( s\right) \) is a log-Gaussian stochastic process. Previous works on this model include Steel and Fuentes (2010), Fonseca and Steel (2011) and Bueno et al. (2017).
In practice, many environmental phenomena act on a very large scale and occasionally within areas with rough terrain and poor infrastructure. This makes maintaining gauges challenging, expensive and naturally with ME. For example, pollution level, e.g., ammonium (\(\mathrm {NH_{4}^+}\)) or nitrite (\(\mathrm {NO_{2}^-}\)) concentration (as explanatory variables in modeling groundwater nitrate concentration, see Nolan and Stoner, 2000), is difficult to measure and is often approximated by using the distance from a polluted site or by using the measures at a few monitoring sites. In the last decade, the impact of covariate ME on spatial regression modeling has been received increasing attention. Li et al. (2009) showed that ignoring ME results in attenuated regression coefficient (naive) estimates and inflated variance components. Some other works in this area include Huque et al. (2014), Huque et al. (2016) and Alexeeff et al. (2016). On the other hand, it is clear and expected that ME in the covariates can affect the covariance function. More precisely, covariate ME (when the covariates are included in the covariance function,) presents a new spatial correlation structure based on including covariates information, i.e., ME variance (Bueno et al. 2017). Including covariates information in the covariance structure of the process under study has recently become popular in the context of spatial models (Schmidt et al. 2011; Reich et al. 2011; Ingebrigtsen et al. 2014; Neto et al. 2014; Bueno et al. 2017). The common goal of these investigations is to consider more flexible models to accommodate non-stationarity, non-isotropicity or heteroscedasticity. However, none of these works considered covariate ME which is evidently one of the potential contributors to environmental exposures.
On the other hand, nowadays, with the advancement of remote sensors, wide usage of GPS devices in vehicles and cell phones, popularity of mobile applications and geographic information systems, as well as cheap data storage and computational devices, enormous geo-referenced data are being collected from broader disciplines and are called big spatial data (BSD). A core difficulty of analyzing BSD using both Bayesian or likelihood-based approaches is in inverting an \(n\times n\) covariance matrix, where n indicates the sample size. In Bayesian inference (as in a frequentist framework), the inverse of covariance matrix needs to be calculated at each iteration which makes it infeasible for large n. An introductory overview of several methods for analyzing BSD can be found in Heaton et al. (2017), wherein all of the suggested strategies were conducted based on a Gaussian spatial process. The prediction-oriented Bayesian site selection (BSS) approach proposed by Park and Liang (2015) is another strategy to overcome this problem. This method first splits the observations into two parts: the observations near the target prediction sites (part I) and the remaining (part II). Then, by treating the observations in part I as response variable and those in part II as explanatory variables, BSS forms a regression model which relates all observations through a conditional likelihood derived from the original model. The dimension of the data can then be reduced by applying a stochastic variable selection procedure to the regression model, which selects only a subset of the part II as explanatory data. BSS is able to catch the long range dependence through selection of appropriate explanatory variables.
1.1 Motivational Example: Nitrate in Drinking Water
The presence of nitrates (\(\mathrm {NO_{3}^-}\), with the maximum tolerable concentration 50 mg/L) in drinking water is perceived as a pollution problem. Elevated levels of \(\mathrm {NO_{3}^-}\) in drinking water (much more than the regulatory limit 10 mg/L) presents a serious threat to infants and livestock as attested by conditions such as infant methemoglobinemia, nitrate poisoning of livestock and digestive system cancers (Bastian and Murray 2012). Therefore, the detection of areas with high nitrate concentration in drinking water has gathered much attention from researchers. As a demonstrative example, we describe the means concentrations of \(\mathrm {NO_{3}^-}\), \(\mathrm {NO_{2}^-}\) and \(\mathrm {NH_{4}^+}\) in drinking water over the USA as motivation for our proposed model (presented in Sect. 2). At each location, we derive means concentrations as the average of the measured concentrations from measurements (per site) around days 9, 18 and 27 of each month within year 2003. The dataset (downloadable from the EPA website) has been collected from a monitoring network composed of 36, 760 stations and contains the means concentrations of \(\mathrm {NO_{3}^-}\), \(\mathrm {NO_{2}^-}\) and \(\mathrm {NH_{4}^+}\) and monitors geographic coordinates given as latitude and longitude. The regulatory limits and maximum permissible levels of \(\mathrm {NO_{2}^-}\) and \(\mathrm {NH_{4}^+}\) are, respectively, 0.003 mg/L and 0.04 mg/L, and 1 mg/L and 0.5 mg/L. Due to measurement methods, e.g., the sulfanilamide and the phenate methods, \(\mathrm {NO_{2}^-}\) and \(\mathrm {NH_{4}^+}\) are often affected by ME (see Sathasivan et al. 2008; Jarvis et al. 2009; Choi and Kim 2010; Opsahl et al. 2017).
Panels (a) and (b) of Fig. 1 show a schematic description of the region and a histogram of the nitrate concentration, respectively. As a result of simple exploratory data analysis, the histogram shows a non-Gaussian feature, but to explore more precisely, further investigation is needed. To that end, a simple regression model was fitted and other exploratory data analyses were pursued: normal QQ-plots as well as the Kolmogorov–Smirnov test for the normality of both the response and the residuals. The p-values obtained from two-sided Kolmogorov–Smirnov normality tests for both the response and the residuals are approximately \(2 \times {10^{ - 16}}\). The QQ-plot of the response variable in Panel (c) reveals significant deviation from normal behavior which was also confirmed by the QQ-plot of the residuals (not shown here). However, non-Gaussianity in purely spatial problems is, in general, very hard to assess because of having only one observation to work from. That is, in spatial problems we observe one observation \({\mathbf{Y}} \sim {N_n}\left( {{\varvec{\mu }},\Upsilon } \right) \) rather than independent observations from a Gaussian distribution. For more exploration, one way of assessing normality is to decorrelate the observations, e.g., to \({\mathbf{Y}}^*\), such that \({\mathbf{Y}}^* \sim {N_n}\left( {{\varvec{\mu }}^* ,I_n } \right) \), and then normality will be proven if the QQ-plot of the new residuals is normal (see “Appendix A”). Panel (d) confirms our previous result. Finally, we performed another initial exploratory analysis based on Haining’s method for outlier detection (Haining 1993). The last panel of Fig. 1 which indicates the upper and lower outlier bounds confirms the existence of (at least) one region in the space with larger observational variance relative to the rest.
Panel a shows the spatial locations of the water quality monitoring stations in the USA; the coordinates (latitude and longitude) are in decimal degrees. Panel b displays the histogram of the nitrate concentration and its kernel density estimate. Panels c and d show the normal QQ-plots of the nitrate concentration and the residuals of a simple regression based on the decorrelated data, respectively. Panel e displays the upper and lower outlier bounds based on Haining’s method.
We will propose a GLG spatial model which relax the assumption that covariates are observed without ME and also allow us to accommodate and identify observations that have extreme values compared to their neighboring observation under a Gaussian process. Our approach leads to a non-Gaussian covariate-dependent spatial ME model for analyzing BSD. Specifically, we accommodate covariate ME in a non-Gaussian spatial model and incorporate covariate information (ME variance) into the spatial covariance structure. We also address computational issues related to non-Gaussian BSD (which is also not addressed in the literature, as far as we are aware) by modifying the BSS method. The organization of the paper is as follows: After describing our proposed model and its properties (Sect. 2), in Sect. 3, we describe the inference procedure and discuss prior specification for the proposed model parameters. An analysis of synthetic data is presented in Sect. 4. Section 5 illustrates the implementation of our model to analyze the nitrate concentration presented in Sect. 1.1. The article ends with a conclusion section.
2 An Overview of the GLG Covariate-Dependent Spatial ME Model
The considered model is set up by the following components: Let \(\left\{ {Y\left( {s} \right) } :{s \in \mathscr {D}\subset \mathfrak {R}^d} \right\} \) denote a spatial random field, where s represents a site in d-dimensional space and \({Y\left( {{s_i}} \right) }\) be the observations of the process in locations \(s_i\) (\(i = 1,\ldots , n\)). Our starting model for the ith location given covariates \({\mathbf{x}}\left( {{s_i}} \right) = \left( {{x_1}\left( {{s_i}} \right) , \ldots ,{x_k}\left( {{s_i}} \right) } \right) '\) is
where the mean surface \(\beta _0+\mathbf{x}'{\left( \cdot \right) }{{\varvec{\beta }}_x}\) with unknown coefficient vector \({\varvec{\beta }}\)\(={\left( {{\beta _0},{{{\varvec{\beta }}}_x'}} \right) ^\prime }\)\(=\left( {\beta _0,{\beta _1},{\beta _2},\ldots ,{\beta _k}}\right) '\) is often termed trend or drift. The scale parameters \(\sigma \) and \(\tau \) are defined in \(\mathfrak {R}_+\), and the process \(\varepsilon {\left( \cdot \right) }\) is a zero-mean and unit-variance Gaussian random field with a valid correlation function \(C\left( \mathscr {H} \right) \) in \(\mathfrak {R}^d\), which captures spatial correlation based on the Euclidean distance \( \mathscr {H}\) between sites i and j, i.e., \(\mathscr {H}= \left\| {{s_i} - {s_{j}}} \right\| \). The latent process \(\lambda \left( \cdot \right) \) also affects the spatially dependent process and is responsible for capturing the variance inflation in the process \(\varepsilon {\left( \cdot \right) }\) across different locations. Finally, \(\rho \left( \cdot \right) \) denotes an uncorrelated Gaussian process with zero mean and unitary variance, modeling a nugget effect. To make our results comparable with the previous works, we focus on modeling the latent variable \(\left\{ {\lambda \left( s \right) }: {s \in \mathscr {D}} \right\} \) as a stationary log-Gaussian process such that \(\ln \lambda \left( \cdot \right) \) is a Gaussian process with mean function \(-{\nu }/{2}\) (\(\nu >0\)) and covariance function \(\nu C\left( \mathscr {H} \right) \). Thus, \({{\varvec{\psi }}}{\left( \cdot \right) } = \ln {{\varvec{\lambda }}{\left( \cdot \right) }} \sim {N_n}\left( { - {(\nu /2)}{} \mathbf{1}_n ,\nu {\Sigma }} \right) \), where \({\varvec{\lambda }}= {\left( {{\lambda \left( {{s_1}} \right) }, \ldots ,{\lambda \left( {{s_n}} \right) }} \right) ^\prime }\), \(\mathbf{1}_{n}\) is an \(n\times 1\) vector of 1’s and \({\Sigma }\) is an \(n\times n\) correlation matrix with \({C}\left( \mathscr {H}\right) \) as its \(\left( i,j\right) \)th element. \(\varepsilon {\left( \cdot \right) }\), \(\ln \lambda \left( \cdot \right) \) and \(\rho \left( \cdot \right) \) are considered independent of each other.
Clearly, observations with relatively small values of the scale mixing process will tend to be away from the mean surface. We interpret these observations in terms of spatial heteroscedasticity or following Palacios and Steel (2006) call them outliers, even though we really mean that they belong to a region with larger observational variance relative to the rest of the space. Obviously, \(\lambda \left( \cdot \right) \) is a unit-mean process with variance \(\exp \left( \nu \right) - 1\). Hence, \( \nu \) governs the behavior of \(\lambda \left( \cdot \right) \); small values of \(\nu \) minimize the variance of \(\lambda \left( \cdot \right) \), which leads to contracting its distribution around one, and so the proposed model tends to be a Gaussian model, while larger values of \(\nu \) drive the distribution of \(\lambda \left( \cdot \right) \) toward zero, justifying the existence of some regions in the space with larger observational variances. It is noteworthy that although different correlation functions for \(\varepsilon {\left( \cdot \right) }\) and \(\lambda {\left( \cdot \right) }\) can be chosen, for the purpose of model complexity reduction, it is assumed that the elements of \(\lambda {\left( \cdot \right) }\) are correlated through the same correlation function as that of \(\varepsilon {\left( \cdot \right) }\). Further, this approach prevents identifiability problems (which have already been addressed by Palacios and Steel, 2006). Therefore, for \(\mathbf{Y}=\left( {{Y}\left( s_1\right) , \ldots ,{Y}\left( s_n\right) } \right) '\), \(\Lambda = diag\left( {{{\varvec{\lambda }}}} \right) \), \(\mathbf{X}=\left( {\mathbf{x}_1, \ldots ,\mathbf{x}_n} \right) \) and fixed parameters, we have \(\mathbf{Y}\left| {{\varvec{\lambda }}} \right. \sim {N_{n}}\left( {{\beta _0}{} \mathbf{1}_n + \mathbf{X} {{\varvec{\beta }}_x},{{\sigma ^2}{\Lambda ^{ - {1}/{2}}}{\Sigma } {\Lambda ^{ - {1}/{2}}}}}{+\tau ^2 I_n} \right) \).
In the presence of ME, the covariate \(\mathbf{x}\left( \cdot \right) \) can be observed only through \(\mathbf{w}\left( \cdot \right) =\left( {{w_1}, \ldots ,{w_k}} \right) '\) such that \(\mathbf{w}{\left( \cdot \right) }=\mathbf{x}{\left( \cdot \right) }+\mathbf{u}{\left( \cdot \right) }\), where \(\mathbf{u}\left( \cdot \right) \sim {N_k}\left( {\mathbf{0}_{k},{\sigma _u^2}{I_k}} \right) \) is an uncorrelated white noise process. Here, \(\mathbf{w}\left( \cdot \right) \sim {N_k}\left( {\mathbf{x}{\left( \cdot \right) },{\sigma _u^2}{I_k}} \right) \) and a functional ME model will be used. A review of the literature of ME reveals that the variance of the ME has been determined, perhaps by making a large number of independent repeated measurements (Fuller 2009). Considering ME, we rewrite model (1) as
In this model, we assume that the random field \(\mathbf{u}{\left( \cdot \right) }\) is independent of \(\varepsilon {\left( \cdot \right) }\), \(\lambda {\left( \cdot \right) }\) and \(\rho {\left( \cdot \right) }\). The main reason behind this assumption is that the source of response error (in the motivational example) is independent of the source of ME in covariates (due to different techniques employed to collect the data). Note that the term nugget effect is responsible for capturing microscale variability at fine scales that cannot be distinguished from observational data since it occurs at a scale that is much smaller than the inter-distance between observations sites. However, the term \(\mathbf{u}'{\left( \cdot \right) }{{\varvec{\beta }}_x}\) (i.e., the ME effect) is commonly due to instrument or laboratory analysis error. Assuming isotropy, we also consider a Cauchy correlation function, as \({C}\left( \mathscr {H} \right) = {\left[ {1 + {{\left( { {\mathscr {H}}/ {{{\theta _1}}}} \right) }^{{\theta _2}}}} \right] ^{ - 1}}\), \({\theta _1}>0\), \(0 < {\theta _2} \le 2\), at spatial distance \(\mathscr {H}\). This class of correlation functions, which allows for smoother processes than induced by the exponential function, also provides the simultaneous fitting of both the long-term and the short-term correlation structure within a simple analytical model. The parameters \(\theta _1\) and \(\theta _2\) are the range and the smoothness parameters, respectively. We collect all the model parameters as \({{\varvec{\eta }}}=\left( {{\varvec{\beta }}},{\sigma ^2},\theta _1,\theta _2,{\sigma _u^2},\nu {,\tau ^2}\right) '\). Thus, for \(\mathbf{W}=\left( {\mathbf{w}_1, \ldots ,\mathbf{w}_n } \right) \), we have
Next, we briefly outline some preliminary properties of the proposed model (2).
2.1 Properties
The covariance between any two points of the process, the marginal kurtosis at location s and the marginal moments of \(Y\left( s \right) \) given \({{\mathbf{w}}\left( {{s}} \right) }\) around its mean are of special interests here. The proofs are presented in “Appendix B.”
-
Covariance: For the marginal distribution of \({Y\left( {{s}} \right) }\) after integrating out \(\lambda \left( s\right) \), we have
$$\begin{aligned} Cov\left[ {Y\left( {{s_i}} \right) \left| {{\mathbf{w}}\left( {{s_i}} \right) } \right. ,Y\left( {{s_j}} \right) \left| {{\mathbf{w}}\left( {{s_j}} \right) } \right. } \right] ={\sigma ^2}C\left( \mathscr {H}\right) \exp \left\{ {\frac{\nu }{4}\left[ {3 + C\left( \mathscr {H} \right) } \right] } \right\} , \end{aligned}$$(4)where \({s_i},{s_j} \in \mathscr {D}\), \(i,j=1,\ldots ,n\) and \(i \ne j\) (see 10). Firstly, this term will always be positive. Secondly, it is obvious that for fixed values of \({\sigma ^2}\) and \(\nu \), Eq. (4) depends only on the distance \(\mathscr {H}\) which means model (2) has a stationary spatial covariance structure. Thirdly, for constant values of \({\sigma ^2}\) and \(\mathscr {H}\), this covariance is a monotonically increasing function of \(\nu \), that is, in the same distances, this covariance would be maximum within the regions with extreme values of the response. Moreover, \(\mathrm{Var}\left[ {Y\left( {{s_i}} \right) \left| {{\mathbf{w}}\left( {{s_i}} \right) } \right. } \right] = {\sigma ^2}\exp \left\{ {\nu } \right\} +{\sigma _u^2{{\varvec{\beta }}_x'} {{\varvec{\beta }}_x}}{+\tau ^2 }\) (see 11) means that large values of \(\nu \) are associated with a greater variance in the spatial process \( {Y\left( \cdot \right) }\) and this is true for any location. As a result of (4), it is easy to see that
$$\begin{aligned} Corr\left[ {Y\left( {{s_i}} \right) \left| {{\mathbf{w}}\left( {{s_i}} \right) } \right. ,Y\left( {{s_j}} \right) \left| {{\mathbf{w}}\left( {{s_j}} \right) } \right. } \right] =\frac{{{\sigma ^2}C\left( {\mathscr {H}} \right) \exp \left\{ {\frac{\nu }{4}\left[ {3 + C\left( {\mathscr {H}} \right) } \right] } \right\} }}{{{\sigma ^2}\exp \left\{ \nu \right\} + \sigma _u^2{{\varvec{\beta }}_x'}{{\varvec{\beta }}_x}{+\tau ^2 }}}. \end{aligned}$$(5)Roughly speaking, if the distance between \(s_i\) and \(s_{j}\) tends to 0, the correlation between \(Y\left( {{s_i}} \right) \left| {{\mathbf{w}}\left( {{s_i}} \right) } \right. \) and \(Y\left( {{s_j}} \right) \left| {{\mathbf{w}}\left( {{s_j}} \right) } \right. \) tends to one for enough small values of \(\sigma _u^2\) and \(\tau ^2\). Therefore, interlocking the model with ME does not induce a discontinuity at 0.
-
Kurtosis: In order to evaluate the tail behavior of the finite-dimensional distribution of the proposed process, we consider the kurtosis of the process \(Y\left( {{s}} \right) \) given \({{\mathbf{w}}\left( {{s}} \right) }\). The marginal kurtosis with respect to \(\lambda \left( s\right) \) is given by:
 (6)
(6)(see 12). This term is always positive and tends to \(3e^\nu \) as \(\sigma _u\) tends to 0. Although we cannot say anything about whether (6) is an increasing or decreasing function of \(\nu \), we can say, with certainty, that large values of kurtosis will be accrued for enough large values of \(\nu \), where the distribution of \({Y\left( {s} \right) }\) given \({{\mathbf{w}}\left( {{s}} \right) }\) is peaked.
-
Marginal Moments: Evaluating the effect of log-normal scale mixing on the tail behavior of the finite-dimensional distributions can be achieved through the marginal central moments. In the absence of a nugget effect,
$$\begin{aligned} E\left\{ {\left. {{{\left[ {Y\left( s \right) - E\left( {Y\left( s \right) } \right) } \right] }^n}} \right| {\mathbf{w}}\left( s \right) } \right\} = \sum \limits _{\begin{array}{c} i = 2m\\ m = 0, \ldots ,{n}/{2} \end{array}} ^n {\left( \begin{array}{l} n\\ i \end{array} \right) } f\left( {n,i} \right) g\left( {n,i} \right) , \end{aligned}$$(7)for even n, and
 for odd n, where \({c_n} = \prod \nolimits _{m = 1}^{n/2} [ n - 2m + 1 ]\),
for odd n, where \({c_n} = \prod \nolimits _{m = 1}^{n/2} [ n - 2m + 1 ]\),  and \( g\left( {n,i} \right) = \left[ {{{{{\sigma _u^2{{\varvec{\beta }}_x'}{{\varvec{\beta }}_x}} }}}}/{{{2}}}\right] ^{{i}/{2}} \left[ {{i!}}/{{\left( {\frac{i}{2}} \right) !}}\right] \) (see 13). Equation (6) immediately results from (7) for \(\tau =0\).
and \( g\left( {n,i} \right) = \left[ {{{{{\sigma _u^2{{\varvec{\beta }}_x'}{{\varvec{\beta }}_x}} }}}}/{{{2}}}\right] ^{{i}/{2}} \left[ {{i!}}/{{\left( {\frac{i}{2}} \right) !}}\right] \) (see 13). Equation (6) immediately results from (7) for \(\tau =0\).
2.2 The Prediction-Oriented Selection Scheme
Here, we only modify the BSS procedure such that it can be used in our non-Gaussian ME model. With a slight abuse of notations, let \({{\varvec{D}}}\) denote a realization of model (2) at \(n_d\) distinct locations \({\mathbf{s}} = \left\{ {{s_1}, \ldots ,{s_{n_d}}} \right\} \) and \({{\mathbf{s}}^p} = \left\{ {s_1^p, \ldots ,s_{n_p}^p} \right\} \) indicate \(n_p\) distinct locations of interest for prediction. Suppose that \({{\varvec{D}}}\) has been partitioned into two distinct subsets: \({{{\varvec{D}}}_\pi } = \left\{ {y\left( {{s_i}} \right) ;{s_i} \in {{\mathbf{s}}^\pi }} \right\} \), which includes all observations that are near the prediction sites \({{\mathbf{s}}^p}\), i.e., \({{\mathbf{s}}^\pi } = \left\{ {s_1^\pi , \ldots ,s_{{n_\pi }}^\pi } \right\} \) (see “Appendix C” for selection procedure), and \({{{\varvec{D}}}_{ - \pi }} = {{\varvec{D}}}\backslash {{{\varvec{D}}}_{ \pi }}\), where \(\backslash \) is the relative complement symbol. Moreover, we consider \({\mathbf{Y}}^\pi ={\mathbf{Y}}\left( {{{\mathbf{s}}^\pi }} \right) \) as a vector of observations contained in \({{\varvec{D}}}_\pi \) and likewise \({\mathbf{Y}}\left( {{{\mathbf{s}}^{-\pi }}} \right) \) as a vector of observations contained in \({{\varvec{D}}}_{-\pi }\). We aim to use \({\mathbf{Y}}\left( {{{\mathbf{s}}^{-\pi }}} \right) \) as explanatory variable in a regression model for the response, but since the variables in \({\mathbf{Y}}\left( {{{\mathbf{s}}^{-\pi }}} \right) \) can be highly correlated, we select a subset of \({\mathbf{Y}}\left( {{{\mathbf{s}}^{-\pi }}} \right) \), say \({{\mathbf{Y}}^\delta } ={{\mathbf{Y}}\left( {{{\mathbf{s}}^\delta }} \right) }\), of size \({n_\delta }\) as the explanatory variables for \({\mathbf{Y}}^\pi \) (see “Appendix C” for selection procedure). Therefore, the conditional distribution \(\left. {\mathbf{Y}}^\pi \right| {{\mathbf{y}}^\delta },{\varvec{\lambda }},{\mathbf{W}},{{\varvec{\eta }}}\) can be easily obtained through the properties of the multivariate normal distribution as
where \({{\varvec{\mu }}_\pi }\) and \({\Omega _\pi }\) are, respectively, the mean and the variance of \(\left. {\mathbf{Y}}^\pi \right| {\varvec{\lambda }},{\mathbf{W}},{{\varvec{\eta }}}\); likewise, \({{\varvec{\mu }}_\delta }\) and \({\Omega _\delta }\) are, respectively, the mean and the variance of \({{{\mathbf{Y}}^\delta }\left| {{\varvec{\lambda }},{\mathbf{W}},{{\varvec{\eta }}}} \right. }\) and \(\Omega _{\pi \delta }\)\(= Cov\left[ \left( {\left. {\mathbf{Y}}^\pi \right| {\varvec{\lambda }},{\mathbf{W}},{{\varvec{\eta }}}} \right) ,\right. \)\(\left. \left( {{{\mathbf{Y}}^\delta }\left| {{\varvec{\lambda }},\mathbf{W},{{\varvec{\eta }}}} \right. } \right) \right] \). Clearly, \({\Omega _\pi }\), \({\Omega _\delta }\) and \({\Omega _{\pi \delta }}\) are all readily obtained as appropriate sub-matrices of \(\Omega \) in (3). Then, by marginalizing out the nuisance parameters \({\varvec{\lambda }}, \mathbf{W}\) and \({{\mathbf{Y}}^\delta }\), the likelihood function can be written as:

Due to high-dimensional intractable integrals which have no analytic closed form, the computation of likelihood function is actually challenging. We present below a Bayesian framework which relies on the prediction-oriented selection scheme to facilitate calculations. Further, the Bayesian paradigm allows for taking into account uncertainties in the parameters.
3 Prior Designation and Bayesian Prediction
In this section, we outline our inferential approach based on the Bayesian paradigm. A convenient strategy of avoiding improper posterior distribution in the absence of prior information is to utilize proper (but diffuse) priors. As a feasible but not necessary optimal scheme, the prior distributions are supposed to be mutually independent a priori. The hyper-parameters of the adopted priors including \({c_1},{c_2},\ldots ,{c_8}\) are chosen to reflect vague prior information. Customarily, it is assumed that the coefficients \({\varvec{\beta }}\) have been drawn, independently, from the common prior distribution \({N_{k+1}}\left( {\mathbf{0}_{k+1},{c_1}{I_{k+1}}} \right) \) with some large fixed variance \(c_1\) which results in vague prior information. Hence, we are able to compare models with different trends if we allow \(c_1\) to vary. Ideally, it is often expected that the prior of the (inverted) variance parameter would be invariant to rescaling the observations. Consequently, the inverse-gamma family of non-informative prior distributions with small values for its hyper-parameters can be chosen for \(\sigma ^{-2}\). However, Palacios and Steel (2006) suggested the generalized inverse-Gaussian (GIG) prior which is a flexible family of distributions that includes both the gamma and the inverse-gamma distributions as special cases. We consider the GIG prior class for \(\sigma ^{2}\) as
where \({\kappa _\gamma }\) is the modified Bessel function of the third kind and order \(\gamma \). Regarding the flexibility of the proposed class for the case \(\gamma =0\), we assume \({\sigma ^2} \sim GIG\left( 0, {{c_2},{c_3}} \right) \), \({\tau ^2} \sim GIG\left( 0, {{c_4},{c_5}} \right) \) and \({\nu } \sim GIG\left( 0, {{c_6},{c_7}} \right) \). Since the range parameter \({\theta _1}\) has an inverse relationship with the Euclidean distance \({\mathscr {H}}\), we consider \({\theta _1} \sim Exp\left[ {c_8}/med\left( {{\mathscr {H}}^*} \right) \right] \), where \({med\left( {\mathscr {H}}^* \right) }\) is the median value of all distances in the space. Ultimately, we assume a uniform prior for the smoothness parameter as \({\theta _2} \sim U\left( {0,2} \right) \). By combining the likelihood function (9) with the joint prior density, the posterior distribution can be obtained. However, the existence of multiple integrals makes it analytically intractable. Consequently, we first augment the observed data with latent variables \({\varvec{\lambda }}\), \(\mathbf W\) and \({{\varvec{\varepsilon }}}\) so that both the augmented posterior \(\pi \left( {{{\varvec{\eta }}}\left| {{\mathbf{y}}^\pi , {\mathbf{y}^\delta },{\varvec{\lambda }},\mathbf{W},{{\varvec{\varepsilon }}}} \right. } \right) \) and the conditional predictive distribution \(P\left( {{\mathbf{Y}}\left( {{{\mathbf{s}}^p}} \right) \left| {{{\mathbf{y}}^\pi }, {\mathbf{y}^\delta },{\varvec{\lambda }},{\mathbf{W}},{{\varvec{\varepsilon }}}} \right. } \right) \) are available. Details of the posterior sampling framework are given in “Appendix D.” The posterior predictive distribution of \({\mathbf{Y}}\left( {{{\mathbf{s}}^p}} \right) \) can be easily obtained as

Thus, \({\widehat{\mathbf{Y}\left( {{\mathbf{s}^p}} \right) }}\) is the sample mean of draws \({{\mathbf{Y}}^{\left( i \right) }}\left( {{{\mathbf{s}}^p}} \right) \) from an \(n_p\)-variate normal distribution with mean \({\varvec{\mu }}_{{{\mathbf{s}}^p}}^{\left( i \right) } + {\Omega _{p,\pi {\delta _i}}}\Omega _{\pi {\delta _i}}^{ - 1}\left[ {{{\mathbf{Y}}_i^{\pi \delta }} - {{\varvec{\mu }}_{\pi \delta }^{\left( i \right) }}} \right] \) and variance \({\Omega _p} - {\Omega _{p,\pi {\delta _i}}}\Omega _{\pi {\delta _i}}^{ - 1}{{\Omega '}_{p,\pi {\delta _i}}}\), where \({\varvec{\mu }}_{{{\mathbf{s}}^p}}^{\left( i \right) }\) denotes the mean of \({\mathbf{Y}}\left( {{{\mathbf{s}}^p}} \right) \) based on the sample \({\left\{ {{{\varvec{\lambda }}^{\left( i \right) }},{{\mathbf{W}}^{\left( i \right) }},{{{\varvec{\varepsilon }}}^{\left( i \right) }},{{y^\delta }^{\left( i \right) }},{{{\varvec{\eta }}}^{\left( i \right) }}} \right\} _{i = 1}^m}\), \({\mathbf{Y}}_i^{\pi {\delta }} = {\left( {{{\mathbf{Y}}^{\pi '}},{ {\mathbf{Y}^\delta }^{{{\left( i \right) }^\prime }}}} \right) ^\prime }\) is the joint vector formed by \({{{\mathbf{Y}}^\pi }}\) and \({\mathbf{Y}^\delta }^{\left( i \right) }\), \({\Omega _{p,\pi {{\delta }_i}}}\) is the covariance matrix of \({\mathbf{Y}}\left( {{{\mathbf{s}}^p}} \right) \) and \({\mathbf{Y}}_i^{\pi {\delta }}\), \({{\varvec{\mu }}_{\pi {\delta }}^{\left( i \right) }}\) and \(\Omega _{\pi {{\delta }_i}}\) are the mean and the covariance matrix of \({\mathbf{Y}}_i^{\pi {\delta }}\), respectively. Obviously, the prediction variance is given as \({\widehat{\mathrm{Var}\left( {\left. {{Y\left( s^p\right) }} \right| \cdot } \right) } }= {m^{-1}}\sum \limits _{i = 1}^m {{{\left( {{y^{\left( i \right) }}\left( {{s^p}} \right) - {{\widehat{ y\left( {{s^p}} \right) }}}} \right) }^2}}\).
4 Simulation Study
We now evaluate the performance of BSS in model (2) using a simulation study along with comparison to the standard Bayesian method. In this study, our goal is to assess the performance of the proposed model compared to its competitors: naive Gaussian, Gaussian ME and naive GLG. To that end, we have the following settings: We simulated \(\mathscr {R}=\) 35 independent datasets from the Gaussian model (resulted from letting \(\lambda \left( s_i\right) =1\) in Eq. (2)), with \(k=2\) and the following presumed parameters: \(\beta _0=3\), \(\beta _1=-2\), \(\beta _2=1.5\), \(\sigma ^2=1\), \(\sigma _u^2=0.4\), \(\theta _1=10\), \(\theta _2=1\) and \(\tau ^2=0.3\). Each dataset contains \(7\times 10^4\) observations with locations drawn uniformly from the square region \(\left[ {0,500} \right] \times \left[ {0,500} \right] \). Thus, e.g., for a small and a large distance, say \(\mathscr {H}_s=1\) and \(\mathscr {H}_l=700\), respectively, we have \(C\left( \mathscr {H}_s\right) \approx 0.9\) and \(C\left( \mathscr {H}_l\right) \approx 0.01\). For simplicity, in each \(\mathscr {R}\) simulation, we considered the simple linear regression \({\beta _0} + {\beta _1}x_{{1}}^{\left( r \right) }+ {\beta _2}x_{{2}}^{\left( r \right) }\), \(r=1,\ldots ,\mathscr {R}\). In fact, we drew two distinct samples each of size \(7\times 10^4\) from the normal distributions with means 3 and 5, and variances 3 and 3.5, and saved these values into two distinct vectors named \(x_1\) and \(x_2\), respectively. Henceforth, we look at these data as fixed (not random) and true (unobserved) values of two covariates \(x_1\) and \(x_2\). In other words, we suppose that \(x_i^{\left( r\right) }\) for \(i=1,2\) is not directly observed, but we observed instead \(w_i^{\left( r \right) } = x_i^{\left( r \right) } + u_i^{\left( r \right) }\), where \(u_i^{\left( r \right) } \sim N\left( {0,\sigma _u^2 = 0.4} \right) \). It is worth remembering that we were interested in investigating the potential of the proposed model for accommodating outlier regions. To that end, after obtaining the responses in each \(\mathscr {R}\) simulations, a region in the central part of the under study space (with about 3500 sites) is selected and contaminated to give rise to a heavy-tailed data such that favorable outlier regions are achieved. To fit our model to the data, we use the publicly available statistical software R.
The hyper-parameters \(c_1, c_2,\ldots , {c_8}\) are as follows: As a benchmark value for \(c_1\), we choose \(10^4\). For posterior and predictive inference, this is not a critical prior, and any suitably large value of \(c_1\) will lead to very similar results. The hyper-parameters \(c_2, c_3,\ldots , c_7\) are chosen smaller than unity to reflect prior means and standard deviations around 1. A rough idea of \(c_8\) could be around the mean value of all distances in each dataset. Since we would expect inference to be the most challenging for the hyper-parameter \({c_0}\), different values of \({c_0}\) are considered and the results will be compared. For each dataset, BSS was run until convergence conditions of the MCMC were satisfied through the Gelman–Rubin convergence diagnostics (Gelman and Rubin 1992). Moreover, the performance of the MCMC algorithm was assessed by the examination of trace plots, burn-in, thinning and a measure of effective sample size (ESS), some of which are shown in Fig. 2. Results are based on \(10^4\) iterations after the burn-in period, in which a thinning factor 10 was taken to reduce the autocorrelation in the generated chains. In each dataset, two subsets of sizes 50 and 150 were randomly selected from the contaminated and uncontaminated sites, respectively, and used for prediction, i.e., \(n_p=200\), and the remaining samples (i.e., \(n_d=69,800\)) were used for model training. To assess the sensitivity of BSS to the choice of \(n_\pi \), BSS was first applied to this example with \({c_0}=5\) and three different choices of \(n_\pi ={500, 650}\) and 800. To compare the four mentioned models, we computed the square root of the mean squared prediction errors (RPE) and the deviance information criterion (DIC) which is a popular criterion for model assessment in the literature. Moreover, to evaluate the performance of BSS in each procedure, we also carried out a Bayesian inference for the full data (BFD).
Owing to extremely high computation times, we divided our \(\mathscr {R}\) simulations into 140 different jobs (appropriately) and submitted them separately to the facilities of the Western Canada Research Grid (https://www.westgrid.ca/), to speed up the process. The results (Table 1) indicate that BSS presents more accurate prediction as \(n_\pi \) increases and further, the GLG ME model presents a better fit and prediction than the others. Furthermore, for a fixed value of \({c_0}\), as \(n_\pi \) increases, \(n_\delta \) tends to decrease, whereas the contribution of the prediction-oriented selection scheme (Prop) increases. This table also reports the square root of the mean squared fitting errors for the first-tier neighboring observations (RFE\(_{t_1}\), see “Appendix C”) as a possible tool for ascertaining the size of \(n_\pi \), which evidently provides the same ordering of model accuracies as that for RPE. Obviously, BSS acts as good as BFD, however, in shorter time periods. The CPU times, in hours, were recorded for a single run of the algorithm on an iMac with Intel Core i7 2.93GHz processor and 8GB RAM. It is worth pointing out that for this example, even with only less than \(2\%\) (on average) of samples being used at each iteration, BSS still performs reasonably well in both fitting and prediction. Overall, the smallest DIC (best fit) was for the GLG ME model with \(n_\pi ={800}\); nonetheless, one may prefer to choose \(n_\pi ={650}\) based on this model, since, firstly, it takes less time and secondly (not shown here), large values of \(n_\pi \) lead to decrease in the covariates’ contribution to the regression model (i.e., the modulus of the regression coefficients tends to decrease). A suggested strategy will be discussed in Conclusion section. However, these concerns are ignorable in our example because the prediction sites are randomly selected from the full dataset and the number of covariates included in each model is relatively small.
With the aim of evaluating the sensitivity of BSS to the choice of \({c_0}\), we again carried out the inference based on the GLG ME model, but this time we fixed \(n_\pi ={650}\) and instead considered different values for \({c_0}\) as \({c_0}=1,3,5,7\) and 9. Table 2 summarizes the results, with the results for \({c_0} =5\) taken from Table 1. This table shows that \(n_\delta \) tends to increase while \({c_0}\) increases, and again the contribution of covariates to the regression model tends to decrease. Apparently, the results suggest relatively small values for \({c_0}\), which will lead to a parsimonious regression model. Thus, for this example if we let \(n_\pi ={650}\), BSS with \({c_0}=3\) presents better results. However, if we can afford relatively more computations, BSS with \(n_\pi ={800}\) and \({c_0}=5\) is a better choice (based on the results of BSS with \(n_\pi ={800}\) and three different values \({c_0}=2,3\) and 4, which are not shown here).
In a nutshell, within the limit of our computational resources, a reasonably large value of \(n_\pi \) is actually recommended; however, when one goes for prediction, an overly large value of \(n_\pi \) is not essential as the prediction accuracy depends mainly on the neighbors of the prediction site. In practice, the value of \(n_\pi \) can be determined according to the value of RFE\(_{t_1}\). Briefly, BSS suggests a trade-off between \({c_0}\) and \(n_\pi \).
Finally, since the inference may be challenging in identifying the model’s variance components (i.e., \(\sigma ^2, \tau ^2, \nu , \sigma _u^2, \theta _1\) and \(\theta _2\)), here, we discuss to what extent information about these parameters can be recovered from data. To assess identifiability of each of these parameters, say \(\sigma ^2\), three datasets (of size \(10^4\)) were generated from the proposed model with different values of \(\sigma ^2\) (and fixed values for the others, as described above and with \(\nu =1.5\)). Then, the Bayesian estimations were obtained (Table 3). The same applies for inference on the others. Table 3 indicates that the data allow for meaningful inference on the model’s variance components.
5 Application: Nitrate in Drinking Water
In order to demonstrate the performance of the BSS scheme for real problems, we fit our proposed models to the nitrate concentration data presented in Sect. 1.1. In the continuation of the exploratory data analysis, we looked for the nearest and farthest standard Euclidean distances. They were about 0.03 and 58, respectively, and also the median of these distances was 18.14. Moreover, we use the H-scatter plot (panel (a) of Fig. (3)) as a tool for outlier detection and to show the spatial variability and dependence in the data. An H-scatter plot shows all possible pairs of data values whose locations are separated by a certain distance \(\mathscr {H}\) in a particular direction. When the spatial correlations are strong with closer distance of the sampling sites or the data are highly homogenous, the monitoring sites tend to become a straight line with the angle of \(45^\circ \). If the spatial correlation between two samples decreases or the relationship between two variables weakens, the shape of the cloud of points will spread out displaying a characteristic butterfly-wing shape. The points are located far from the cross-line for small \(\mathscr {H}\) and have a strong variability, can be supposed as outliers in the dataset. Clearly, the spatial correlation tends to decrease with increasing point separation. A geostatistical description of the response variability was revealed by the omnidirectional experimental semi-variogram map as shown in panel (b) of Fig. 3. In this map, a class of distance and a direction are aligned. This class can be converted into a grid cell representing the vertex of the vector whose origin is at the center of the grid and whose norm equals the distance between the two points and direction equals the direction along which the two points. From this plot, the isotropic nature of the spatial dependence is clearly visible. Finally, the empirical semi-variogram of the data is plotted in panel (c).
Now, a randomly selected subset of size 60 is left out of the analysis for predictive performance assessment and the remaining samples used for model fitting. In addition, we considered three different values of \({c_0}=2,3\) and 4, and three different values of \(n_\pi = {200},350\) and 500. To make our results more interpretable, for each value of \(n_\pi \), BSS was run 10 times independently, where the hyper-parameter values are chosen the same as those in Sect. 4. Again, the convergence of the MCMC was verified through the Gelman–Rubin convergence diagnostics and the results are based on the last \(10^4\) iterations of each chain with the thinning factor 10. Knowledge of the ME variance was empirically determined for both explanatory variables in our study by the data center as \(\sigma _u^2 \approx 0.01\). The results are summarized in Table 4. A simple comparison of the calculated DICs reveals the better performance of BSS with \({c_0}=3\) and \(n_\pi ={500}\). Finally, Fig. 4 shows a map of the predicted nitrate concentration under BFD (left panel) and also based on the BSS scheme on GLG ME model with \({c_0}=3\) and \(n_\pi ={500}\) (right panel).
6 Conclusion
In this paper, we have developed a modeling approach to account for covariate ME in non-Gaussian BSD. In particular, we focused on a GLG spatial model which is a more flexible class of sampling models for modeling of geostatistical data with heavy tails. One important aspect of our proposed framework is that the process variance is allowed to depend on covariate ME variance, accounting for covariate uncertainty. Moreover, we equated heavy tails with outliers/large values and explained that the large values may be due to the large variance. Although this could be a property of a non-stationary Gaussian process, and not necessarily indicate non-Gaussian distribution, the exploratory data analysis of the studied real data implied that the response is stationary. In continuing, we have developed a prediction-oriented BSS approach to overcoming the large matrix inverse problem which is an obstacle encountered by BSD. The analysis of our artificial dataset showed that by choosing appropriate values for \(n_\pi \) and \({c_0}\), we can expect both parameter estimations and predictions based on the BSS approach are nearly as good as those produced by BFD, however, with a small subset of the data. It should be noted that, if the response variables are not uniformly selected from the set of observations and the number of explanatory variables included in the regression is too large (none of them satisfied in our study), the resulting parameter estimates from BSS may be biased. To address this issue, Park and Liang (2015) proposed an ensemble BSS approach, which works in a style of bootstrap sampling.
Obviously, the conclusions and the final suggestion in our case study do not constitute the general answer to the question about the best choice of computational methods. In other words, owing to the introduction of many latent variables with strongly dependent components in the model, the described MCMC method may converge slowly and thus fails to offer valid results. A potential strategy would be to use an inverse Bayes’ formula for producing approximately independent samples from the posterior density of the latent variables which reduces the correlation in the Gibbs sampler and accelerates the convergence. The variational Bayes method is one of the other applicable strategies. Although this method requires more complex theoretical calculations, it could increase the speed of calculations. One of the additional assumptions required by our approach is that \({{\varvec{\varepsilon }}}\left( \cdot \right) \) and \({\varvec{\lambda }}\left( \cdot \right) \) have the same correlation structure, but one can choose different spatial correlation structures and solve the identifiability issue. In addition, the focus of this work was on the functional ME. Extending the proposed model to the structural ME is another interesting direction for future work.
References
S.E. Alexeeff, R.J. Carroll, and B. Coull. Spatial measurement error and correction by spatial SIMEX in linear regression models when using predicted air pollution exposures. Biostatistics, 17(2):377–389, 2016.
R. Bastian and D. Murray. Guidelines for water reuse. US EPA Office of Research and Development, Washington, DC, EPA/600/R-12/618, 2012.
R.S. Bueno, T.C.O. Fonseca, and A.M. Schmidt. Accounting for covariate information in the scale component of spatio-temporal mixing models. Spatial Statistics, 22:196–218, 2017.
E.K. Choi and Y.P. Kim. Effects of aerosol hygroscopicity on fine particle mass concentration and light extinction coefficient at Seoul and Gosan in Korea. Asian Journal of Atmospheric Environment, 4(1):55–61, 2010.
T.C.O Fonseca and M.F.J. Steel. Non-Gaussian spatio-temporal modelling through scale mixing. Biometrika, 98(4):761–774, 2011.
W.A. Fuller. Measurement Error Models. John Wiley & Sons, 2009.
A. Gelman and D.B. Rubin. Inference from iterative simulation using multiple sequences. Statistical Science, pages 457–472, 1992.
P.J. Green. Reversible jump markov chain monte carlo computation and Bayesian model determination. Biometrika, 82(4):711–732, 1995.
R. Haining. Spatial Data Analysis in the Social and Environmental Sciences. Cambridge University Press, 1993.
M.J. Heaton, A. Datta, A. Finley, R. Furrer, R. Guhaniyogi, F. Gerber, R.B. Gramacy, D. Hammerling, M. Katzfuss, F. Lindgren, et al. Methods for analyzing large spatial data: A review and comparison. arXiv preprint arXiv:1710.05013, 2017.
M.H. Huque, H.D. Bondell, and L. Ryan. On the impact of covariate measurement error on spatial regression modelling. Environmetrics, 25(8):560–570, 2014.
M.H. Huque, H.D. Bondell, R.J. Carroll, and L.M. Ryan. Spatial regression with covariate measurement error: A semiparametric approach. Biometrics, 72(3):678–686, 2016.
R. Ingebrigtsen, F. Lindgren, and I. Steinsland. Spatial models with explanatory variables in the dependence structure. Spatial Statistics, 8:20–38, 2014.
J.C. Jarvis, M.G. Hastings, E.J. Steig, and S.A. Kunasek. Isotopic ratios in gas-phase HNO\(_3\) and snow nitrate at Summit, Greenland. Journal of Geophysical Research: Atmospheres, 114(D17):1–14, 2009.
H.M. Kim and B.K. Mallick. A Bayesian prediction using the skew Gaussian distribution. Journal of Statistical Planning and Inference, 120(1-2):85–101, 2004.
Y. Li, H. Tang, and X. Lin. Spatial linear mixed models with covariate measurement errors. Statistica Sinica, 19(3):1077, 2009.
J.H. V. Neto, A.M. Schmidt, and P. Guttorp. Accounting for spatially varying directional effects in spatial covariance structures. Journal of the Royal Statistical Society: Series C (Applied Statistics), 63(1):103–122, 2014.
B.T. Nolan and J.D. Stoner. Nutrients in groundwaters of the conterminous United States, 1992- 1995. Environmental Science & Technology, 34(7):1156–1165, 2000.
S.P. Opsahl, M. Musgrove, and R.N. Slattery. New insights into nitrate dynamics in a karst groundwater system gained from in situ high-frequency optical sensor measurements. Journal of hydrology, 546:179–188, 2017.
M.B. Palacios and M.F.J. Steel. Non-Gaussian Bayesian geostatistical modeling. Journal of the American Statistical Association, 101(474):604–618, 2006.
J. Park and F. Liang. A prediction-oriented Bayesian site selection approach for large spatial data. Journal of Statistical Research, 47(1):11–30, 2015.
B.J. Reich, J. Eidsvik, M. Guindani, A.J. Nail, and A.M. Schmidt. A class of covariate-dependent spatio-temporal covariance functions for the analysis of daily ozone concentration. The Annals of Applied Statistics, 5(4):2265, 2011.
A. Sathasivan, I. Fisher, and T. Tam. Onset of severe nitrification in mildly nitrifying chloraminated bulk waters and its relation to biostability. Water research, 42(14):3623–3632, 2008.
A.M. Schmidt, P. Guttorp, and A. O’Hagan. Considering covariates in the covariance structure of spatial processes. Environmetrics, 22(4):487–500, 2011.
M.F.J Steel and M. Fuentes. Non-Gaussian and non-parametric models for continuous spatial data. Handbook of Spatial Statistics, pages 149–167, 2010.
V. Tadayon. Bayesian analysis of censored spatial data based on a non-gaussian model. Journal of Statistical Research of Iran, 13(2):155–180, 2017.
Acknowledgements
The Associate Editor and two referees are gratefully acknowledged. Their precise comments and constructive suggestions have clearly improved the manuscript.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Supplementary Materials
The supplementary materials contain R codes and corresponding “ReadMe” files for the simulation and real data application conducted in this paper. (zip 69 KB)
Appendices
Appendix
A Spatial Data Decorrelation
Let  , and assume the parameters \({\varvec{\mu }},\theta \) and \(\delta ^2\) are known. Then,
, and assume the parameters \({\varvec{\mu }},\theta \) and \(\delta ^2\) are known. Then,  . This decorrelated vector can now be used for assessing normality. However, in practice, as the parameters are unknown, they are replaced by some appropriate estimates. The details are as follows: (I) Estimate \({\varvec{\mu }}\) using ordinary least squares; (II) estimate the covariance parameters \(\theta \) and \(\delta ^2\) based on the variogram of
. This decorrelated vector can now be used for assessing normality. However, in practice, as the parameters are unknown, they are replaced by some appropriate estimates. The details are as follows: (I) Estimate \({\varvec{\mu }}\) using ordinary least squares; (II) estimate the covariance parameters \(\theta \) and \(\delta ^2\) based on the variogram of  ; (III) calculate the Cholesky decomposition \(LL'\) of
; (III) calculate the Cholesky decomposition \(LL'\) of  , and (IV) decorrelate the data as
, and (IV) decorrelate the data as  .
.
B Proofs
This section presents some detailed proofs of the results shown in Sect. 2.1. To prove Eq. (4), let \(Y_\mathbf{w}\left( {s} \right) ={Y\left( {s} \right) } \left| {{\mathbf{w}}\left( {s} \right) } \right. \) and follow the definition and simple properties of the covariance (and variance) as:


Let  . The proof of Eq. (6) requires calculating the following terms:
. The proof of Eq. (6) requires calculating the following terms:
In what follows, we compute each of the expected values in the above equation separately (details not presented here).

Thus, substituting these expectations in (12), the marginal kurtosis is reduced to (6). Ultimately, we focus on Eq. (7).

Palacios and Steel (2006) showed that in the absence of a nugget effect,
and on the other hand,
hence, Eq. (7) can be easily obtained by substituting (14) and (15) into (13).
C Prediction-Oriented Site Selection
Determining\({\mathbf{s}}^\pi \): We choose the nearest sites to the prediction sites \({{{\mathbf{s}}^p}}\) in q-tier, where q determines \({n_\pi }\) as \({n_\pi } = q{n_p}\) and can be derived through an examination of the fitting to \({{\mathbf{Y}}\left( {{{\mathbf{s}}^\pi }} \right) }\) or its subset (e.g., one can choose the value of \({n_\pi }\) such that the mean squared fitting errors for the first-tier neighboring sites are minimized among a few values of \({n_\pi }\) under consideration). The selection scheme entails the following steps:
- 1.:
-
For \(i = 1, \ldots , n_p\), do the following sub-steps to identify the first tier of the nearest sites to \({{{\mathbf{s}}^p}}\):
- (a):
-
Draw a site \(s_i^p\) from the set \({{{\mathbf{s}}^p}}\) at random and without replacement.
- (b):
-
Identify the nearest neighbor of \(s_i^p\) by setting \(s_{1,i}^\pi = \mathop {arg\min }\limits _{s \in {\mathbf{s}}\backslash \left\{ {s_{1,1}^\pi , \ldots ,s_{1,i - 1}^\pi } \right\} } \left\| {s - s_i^p} \right\| \) and finally, set \({\mathbf{s}}_1^\pi = \left\{ {s_{1,1}^\pi , \ldots ,s_{1,{n_p}}^\pi } \right\} \).
- 2.:
-
Set \({\mathbf{s}} \leftarrow {\mathbf{s}}\backslash {\mathbf{s}}_1^\pi \) and repeat the sub-steps in step 1 to identify the second tier of the nearest sites to \({{{\mathbf{s}}^p}}\). Denote the second-tier neighboring set by \({\mathbf{s}}_2^\pi \).
\(\vdots \)
- q.:
-
Set \({\mathbf{s}} \leftarrow {\mathbf{s}}\backslash {\mathbf{s}}_{q-1}^\pi \) and repeat the sub-steps in step 1 to identify the qth tier of the nearest sites to \({{{\mathbf{s}}^p}}\). Denote the qth tier neighboring set by \({\mathbf{s}}_q^\pi \).
This procedure provides \({{\mathbf{s}}^\pi } = \bigcup \nolimits _{r = 1}^q {{\mathbf{s}}_r^\pi }\) as the set of response variables.
Determining\({\mathbf{s}}^{\delta }\): We aim to draw \({n_\delta }\) sites from the set \({\mathbf{s}}\backslash {{\mathbf{s}}^\pi }\). To minimize the loss of data information caused by site selection, \({\mathbf{s}}^\delta \) should be selected uniformly from the observation region of \({\left\{ {Y\left( {{s_i}} \right) } \right\} }\) and thus, following the theory of Poisson process, the number of selected sites can be modeled as a Poisson random variable. Therefore, to enhance our selection pattern, we impose a truncated Poisson prior distribution as \(\pi \left( {n_\delta } \right) \propto \left( {{{c_0}^{n_\delta }}}/{{{n_\delta }!}}\right) \exp \left\{ { - {{c_0}}} \right\} \), \({n_\delta } = 0,1, \ldots ,{n_d} - {n_\pi }\), where \({c_0}\) is a hyper-parameter which have to be specified by the user. Alternatively, one can specify a prior distribution that incorporates the spatial information of \({\mathbf{Y}}\left( {{{\mathbf{s}}^{-\pi }}} \right) \), but this will complicate the simulation of the posterior distribution.
D Bayesian Posterior Sampling
In this section, we summarize the Gibbs sampling iterates for drawing samples from the posterior \(P\left( {{\varvec{\lambda }},{\mathbf{W}},{{\varvec{\varepsilon }}},{{\varvec{\eta }}},{{\mathbf{Y}^\delta }}\left| {{{\mathbf{y}}^\pi }} \right. } \right) \). So, we need to specify all full conditional distributions (which are presented in Sect. D.1). However, the difficulty associated with drawing samples from the full conditional distribution of \( {{\mathbf{Y}^\delta }}\) is that a direct application of MCMC fails as it requires the state space of the Markov chain to be of a fixed dimension, but the dimension of \({{\mathbf{Y}^\delta }}\) may actually vary. To overcome this issue, we can use a reversible-jump MCMC (RJMCMC) algorithm (Green 1995), which allows the dimension of the state space of the Markov chain to vary. The underlying idea is that RJMCMC introduces three types of moves: exchange, birth and death. Exchange means that the chain remains in the space with the same dimension, but moves into a new state. Birth and death are the moves that change the dimension of the state space. Intuitively, a birth step augments the state space by adding new states, whereas a death step reduces the dimension of the state space. At each iteration, the type of move, whether an exchange, birth, or death, is randomly chosen with the respective proposal probabilities denoted by \(q_e\), \(q_b\) and \(q_d\), and one accepts the new state using a Metropolis–Hastings rule.
Let \({\left\{ {{{\varvec{\lambda }}^{\left( t \right) }},{{\mathbf{W}}^{\left( t \right) }},{{{\varvec{\varepsilon }}}^{\left( t \right) }},{{{\varvec{\eta }}}^{\left( t \right) }},{ {{\mathbf{y}^\delta }}^{\left( t \right) }}} \right\} }\) denote the sample generated at the iteration t. Obviously, \(min\left( {n_\delta }\right) =0\) and \(max\left( {n_\delta }\right) =n_d - n_\pi \). To update \( {{\mathbf{y}^\delta }}^{\left( t \right) }\), we use a RJMCMC move. For \({n_\delta }=0\), we consider \(q_e={1}/{3}\) and \(q_b={2}/{3}\); for \({n_\delta }=n_d - n_\pi \), we set \(q_e={1}/{3}\) and \(q_d={2}/{3}\); and finally for \({n_\delta }= 1, \ldots ,{n_d} - {n_\pi } - 1\), we suppose \(q_b = q_d = q_e ={1}/{3}\). Given \({{{\varvec{\lambda }}^{\left( t \right) }},{{\mathbf{W}}^{\left( t \right) }},{{{\varvec{\varepsilon }}}^{\left( t \right) }},{{{\varvec{\eta }}}^{\left( t \right) }},{ {{\mathbf{y}^\delta }}^{\left( t \right) }}}\), the next iteration of the Gibbs sampler consists of the following steps: (I) Generate \({{\varvec{\lambda }}^{\left( t+1 \right) }},{{\mathbf{W}}^{\left( t+1 \right) }},{{{\varvec{\varepsilon }}}^{\left( t+1 \right) }}\) and \({{{\varvec{\eta }}}^{\left( t+1 \right) }}\) from their corresponding full conditional distributions. (II) Draw \({ {{\mathbf{y}^\delta }}^{\left( t+1 \right) }}\):
-
(Birth) Uniformly randomly choose a point from \({{\varvec{D}}}_{-\pi }\backslash { {{\mathbf{y}^\delta }}^{\left( t \right) }}\), say \( {y}^*\), and add it to the current site set \( {{\mathbf{y}^\delta }}^{\left( t \right) }\) (i.e., \({{{\mathbf{y}^\delta }}^{\left( {t + 1} \right) }} = {{{\mathbf{y}^\delta }}^{\left( t \right) }} \cup { {y}^*}\)) with probability
$$\begin{aligned} \min \left\{ {1,\frac{{P\left( {{{\varvec{\lambda }}^{\left( {t + 1} \right) }},{{\mathbf{W}}^{\left( {t + 1} \right) }},{{{\varvec{\varepsilon }}}^{\left( {t + 1} \right) }},{{{\varvec{\eta }}}^{\left( {t + 1} \right) }}\left| {{{\mathbf{y}}^\pi },{{ {y}}^*}} \right. } \right) P \left( {{{{ {y}}}^*}} \right) }}{{P\left( {{{\varvec{\lambda }}^{\left( t \right) }},{{\mathbf{W}}^{\left( t \right) }},{{{\varvec{\varepsilon }}}^{\left( t \right) }},{{{\varvec{\eta }}}^{\left( t \right) }}\left| {{{\mathbf{y}}^\pi },{ {{\mathbf{y}^\delta }}^{\left( t \right) }}} \right. } \right) P \left( {{ {{\mathbf{y}^\delta }}^{\left( t \right) }}} \right) }}\frac{{{n_d} - {n_\pi } - {n_\delta } }}{{{n_\delta } + 1}}\frac{{{q_d}}}{{{q_b}}}} \right\} . \end{aligned}$$ -
(Death) Uniformly randomly select \( {y}^*\) out of \({ {{\mathbf{y}^\delta }}^{\left( {t } \right) }}\) and remove it from the current site set \({ {{\mathbf{y}^\delta }}^{\left( t \right) }}\) (i.e., \({{{\mathbf{y}^\delta }}^{\left( {t + 1} \right) }} = {{{\mathbf{y}^\delta }}^{\left( t \right) }}\backslash { {y}^*}\)) with probability
$$\begin{aligned} \min \left\{ {1,\frac{{P\left( {{{\varvec{\lambda }}^{\left( {t + 1} \right) }},{{\mathbf{W}}^{\left( {t + 1} \right) }},{{{\varvec{\varepsilon }}}^{\left( {t + 1} \right) }},{{{\varvec{\eta }}}^{\left( {t + 1} \right) }}\left| {{{\mathbf{y}}^\pi },{{ {y}}^*}} \right. } \right) P \left( {{{ {y}}^*}} \right) }}{{P\left( {{{\varvec{\lambda }}^{\left( t \right) }},{{\mathbf{W}}^{\left( t \right) }},{{{\varvec{\varepsilon }}}^{\left( t \right) }},{{{\varvec{\eta }}}^{\left( t \right) }}\left| {{{\mathbf{y}}^\pi },{{{\mathbf{y}^\delta }}^{\left( t \right) }}} \right. } \right) P\left( {{{{\mathbf{y}^\delta }}^{\left( t \right) }}} \right) }}\frac{{{n_\delta }}}{{{{n_d}-{n_\pi }-{n_\delta } } + 1}}\frac{{{q_b}}}{{{q_d}}}} \right\} . \end{aligned}$$ -
(Exchange) Uniformly randomly choose \( {y}^*\) from \({{\varvec{D}}}_{-\pi }\backslash {{{\mathbf{y}^\delta }}^{\left( t \right) }}\) and also \( {y}^{**}\) from \({{{\mathbf{y}^\delta }}^{\left( {t} \right) }}\). Then, exchange \( {y}^*\) and \( {y}^{**}\) (i.e., \({{{\mathbf{y}^\delta }}^{\left( {t + 1} \right) }} = {{{\mathbf{y}^\delta }}^{\left( t \right) }} \cup \left\{ {{ {y}^*}} \right\} \backslash \left\{ {{ {y}^{**}}} \right\} \)) with probability
$$\begin{aligned} \min \left\{ {1,\frac{{P\left( {{{\varvec{\lambda }}^{\left( {t + 1} \right) }},{{\mathbf{W}}^{\left( {t + 1} \right) }},{{{\varvec{\varepsilon }}}^{\left( {t + 1} \right) }},{{{\varvec{\eta }}}^{\left( {t + 1} \right) }}\left| {{{\mathbf{y}}^\pi },{{ {y}}^*}} \right. } \right) }}{{P\left( {{{\varvec{\lambda }}^{\left( t \right) }},{{\mathbf{W}}^{\left( t \right) }},{{{\varvec{\varepsilon }}}^{\left( t \right) }},{{{\varvec{\eta }}}^{\left( t \right) }}\left| {{{\mathbf{y}}^\pi },{ {\mathbf{y}^\delta }^{\left( t \right) }}} \right. } \right) }}} \right\} . \end{aligned}$$
1.1 D.1 The Full Conditional Distributions
Below, we describe the full conditional distributions of all unobservable quantities through a Gibbs sampler framework to draw samples from \(P\left( {{\varvec{\lambda }},{\mathbf{W}},{{\varvec{\varepsilon }}},{{\varvec{\eta }}}\left| {{{\mathbf{y}}^\pi }, {{\mathbf{y}^\delta }}} \right. } \right) \). In what follows, we use the notation \({{ \textit{g} _{ - \vartheta }}}\) to show the vector \( \textit{g} \) without \(\vartheta \). Moreover, we partition the latent variables into two parts as follows: \({\varvec{\lambda }}= \left( {{{\varvec{\lambda }}^\pi }',{{\varvec{\lambda }}^\delta }'} \right) '\), \({{\varvec{\varepsilon }}}= \left( {{{{\varvec{\varepsilon }}}^\pi }',{{{\varvec{\varepsilon }}}^\delta }'} \right) '\), \({\mathbf{W}} = \left( {{{\mathbf{W}}^\pi },{{\mathbf{W}}^\delta }} \right) \) and \(\Lambda = \left( {{\Lambda ^\pi },{\Lambda ^\delta }} \right) \), respective to the location sets \({\mathbf{s}}^\pi \) and \({{{\mathbf{s}}^\delta }}\). Regardless of the details, the full conditional distributions are as follows:
-
Latent variable\({{\varvec{\psi }}}\): For each of the components of \({{\varvec{\psi }}}^\pi \) (i.e., \({\psi _i}\)), we can write
 (16)
(16)
where the first term in the right-hand side of (16), i.e., the likelihood contribution, is proportional to a product of normal density functions truncated on \(\left[ 0,\infty \right) \). To construct a suitable candidate generator, we approximate this distribution by log-normal distributions on \(\lambda _i\)s. By matching the first two moments of \(\lambda _i\), we obtain an approximating distribution of the likelihood contribution to \(\psi _i\) as
such that \({h_i} = {{{\sigma }{{{t}}_{{1_i}}}sign\left( {{\varepsilon _i}} \right) }}/{\sqrt{\sigma _u^2{{\varvec{\beta }}_x'} {{\varvec{\beta }}_x}{+\tau ^2}} }\), \({{\mathbf{t}}_1} = \sigma ^{-1}\left( {{{\mathbf{y}}^\pi } - {\beta _0}{{\mathbf{1}}_{{n_\pi }}} - {{\mathbf{W}}^\pi }{{\varvec{\beta }}_x}} \right) \), \({sign\left( {\cdot } \right) }\) denotes the sign function and \({\ell \left( \cdot \right) } = {{\phi \left( \cdot \right) }}/{{\Phi \left( \cdot \right) }}\) where \(\phi \) and \(\Phi \) denote the standard normal density and cumulative distribution function, respectively. On the other hand, the second term in the right-hand side of (16) can be easily obtained as

where \({\Sigma {{ ^{\left( i \right) }}^\prime }}\) shows the ith row of \({{\Sigma }}\) and \({\Sigma ^{\left( { - i, - i} \right) }}\) is \({{\Sigma }}\) in which the ith row and the ith column have been omitted. Combining (18) and (17), we propose a candidate value for \(\psi _i\), say \(\psi _i^{cand}\) from \({\psi _i}\left| {{{\mathbf{y}}^\pi }, {{\mathbf{y}^\delta }},{{{\varvec{\psi }}}_{ - i}^\pi },{{{\varvec{\psi }}}^\delta },{\mathbf{W}},{{\varvec{\varepsilon }}},{{\varvec{\eta }}}} \right. \sim N\left( {\frac{{b_i^2a_i^* + b_i^{{*^2}}{a_i}}}{{b_i^2 + b_i^{{*^2}}}},\frac{{b_i^2b_i^{{*^2}}}}{{b_i^2 + b_i^{{*^2}}}}} \right) \) where \(a_i^* \) and \(b_i^{{*^2}}\) are the mean and the variance of the normal distribution in (18), respectively.
-
Latent variable\(\mathbf W\): Suppose that \({{\mathbf{t}}_2} = \left( {{{\mathbf{y}}^\pi } - {\beta _0}{{\mathbf{1}}_{{n_\pi }}} - \sigma {{{{{\varvec{\varepsilon }}}^\pi }}}/{{\sqrt{{{\varvec{\lambda }}^\pi }} }}} \right) \). Then,
 (19)
(19)
At iteration t, the coefficient vector \({\varvec{\beta }}\) is known and so a sample from \({{\mathbf{W}}^\pi }\left| {{{\mathbf{y}}^\pi },{{\mathbf{y}^\delta }},{\varvec{\lambda }},{{\mathbf{W}}^\delta },{{\varvec{\varepsilon }}},{{\varvec{\eta }}}} \right. \) can be easily obtained as a solution of the under-determined systems of linear equations \(\mathbf{W}^\pi {\varvec{\beta }}_x=\mathscr {C}\), where \(\mathscr {C}\) is a sample of (19). If the under-determined linear system has no solution, \(\mathscr {C}\) is substituted with another sample of (19).
-
Latent variable\({{\varvec{\varepsilon }}}\): Let \({{t}_{{1_i}}^*}={t_{{1_i}}}\sqrt{{\lambda _i^\pi }}\) for \( i=1,2,\ldots ,n_\pi \), \( \textit{g} _\varepsilon = {\Sigma _{\pi \delta }}\Sigma _\delta ^{ - 1}{{{\varvec{\varepsilon }}}^\delta }\) and \(\mathcal {G}_\varepsilon ={\Sigma _\pi } - {\Sigma _{\pi \delta }}\Sigma _\delta ^{ - 1}{\Sigma _{\delta \pi }}\). Thus, for \(A_1{ = [{{{\sigma ^2}}}/\left( {\sigma _u^2{{\varvec{\beta }}_x'} {{\varvec{\beta }}_x}}{+\tau ^2}\right) ]{\Lambda ^{{\pi ^{ - 1}}}} + \mathcal{G}_\varepsilon ^{ - 1}}\),
$$\begin{aligned} {{{{\varvec{\varepsilon }}}^\pi }\left| {{{\mathbf{y}}^\pi }, {\mathbf{y}^\delta },{\varvec{\lambda }},{\mathbf{W}},{{{\varvec{\varepsilon }}}^\delta },{{\varvec{\eta }}}} \right. }\sim {N_{n_\pi }}\left( {{A_1^{ - 1}\left[ {{\Lambda ^{{\pi ^{ - 1}}}}{\mathbf{t}}_1^* + \mathcal{G}_\varepsilon ^{ - 1}{g_\varepsilon }} \right] },A_1^{ - 1}} \right) . \end{aligned}$$
-
The intercept: By setting \({{\mathbf{t}}_3} = {{\mathbf{y}}^\pi } - {\mathrm{{W}}^\pi }{{\varvec{\beta }}_x} - \sigma {{{{{\varvec{\varepsilon }}}^\pi }}}/{\sqrt{{{\varvec{\lambda }}^\pi }} }\), the conditional distribution of the intercept parameter is obtained as
$$\begin{aligned} N\left( {\left[ {{\frac{{{n_\pi }}}{{ {\sigma _u^2{{\varvec{\beta }}_x'} {{\varvec{\beta }}_x}{+\tau ^2}}}} + \frac{1}{{{c_1}}}}}\right] ^{-1}{{\sum \limits _{i = 1}^{{n_\pi }} {{t_{{3_i}}}} }}/{{ \left( {\sigma _u^2{{\varvec{\beta }}_x'} {{\varvec{\beta }}_x}{+\tau ^2}}\right) }},\left[ {{\frac{{{n_\pi }}}{{{\sigma _u^2{{\varvec{\beta }}_x'} {{\varvec{\beta }}_x}{+\tau ^2}} }} + \frac{1}{{{c_1}}}}}\right] ^{-1}} \right) . \end{aligned}$$
In the six last items, the full conditional distribution of parameters \({\varvec{\beta }}_x\), \(\sigma ^2\), \(\tau ^2\), \(\nu \), \(\theta _1\) and \(\theta _2\) are of nonstandard forms, so a Metropolis–Hastings step or a sampling importance resampling (SIR) algorithm can be used. Choosing the first approach to draw samples from an unknown quantity, say \(\vartheta \), consists of accepting the produced value \(\vartheta ^*\) from the candidate generator \(q\left( {\vartheta ^*} \right) \) at the kth iteration with probability \(min\left\{ 1,r_k\right\} \), where \({r_k} = {{f\left( {{\vartheta ^*}\left| {data} \right. } \right) q\left( \vartheta ^{\left( k \right) } \right) }}/{{f\left( {{\vartheta ^{\left( k \right) }}\left| {data} \right. } \right) q\left( {{\vartheta ^*}} \right) }}\) and \(f\left( {{\cdot }\left| data \right. } \right) \) is proportional to the posterior distribution of \(\vartheta \). By choosing the SIR algorithm, we may generate (say m) approximate samples from the posterior distribution of \(\vartheta \) as follows:
-
Draw samples \(\left\{ {{\vartheta ^{\left( i \right) }}} \right\} _{i = 1}^m\) from the proposal distribution \(q\left( \vartheta \right) \),
-
Calculate importance weights \({\omega _i} = {f\left( {{\vartheta ^{\left( i \right) }}\left| data \right. }\right) /{q\left( {{\vartheta ^{\left( i \right) }}} \right) }}\),
-
Normalize the importance weights as \({p_i} = {{{\omega _i}}/ {\sum \nolimits _i {{\omega _i}} }}\),
-
Resample with replacement from \(\left\{ {{\vartheta ^{\left( i \right) }}} \right\} _{i = 1}^L\) with sample probabilities \(p_i\).
A conservative candidate distribution for applying the SIR algorithm is the pre-specified prior on \(\vartheta \).
-
Parameter\({\varvec{\beta }}_x\): It is easy to see that \(\pi \left( {{{\varvec{\beta }}_x}\left| {{{\mathbf{y}}^\pi }, {\mathbf{y}^\delta },{\varvec{\lambda }},{\mathbf{W}},{{\varvec{\varepsilon }}},{{{\varvec{\eta }}}_{ - {{\varvec{\beta }}_x}}}} \right. } \right) \) is proportional to
$$\begin{aligned} {\left( {\frac{1}{{{{{\varvec{\beta }}}_x'}{{\varvec{\beta }}_x}}}} \right) ^{\frac{n_\pi }{2}}}\exp \left\{ { - \frac{1}{{2{c_1}}}{{{\varvec{\beta }}}_x'}{{\varvec{\beta }}_x}} \right\} \exp \left\{ { - \frac{1}{2\left( {\sigma _u^2}{{\varvec{\beta }}_x'}{{\varvec{\beta }}_x}{+\tau ^2}\right) }{{\left( {{\mathbf{t}_2} - {\mathbf{W} ^\pi }{{\varvec{\beta }}_x}} \right) }^\prime }\left( {{\mathbf{t}_2} - {\mathbf{W} ^\pi }{{\varvec{\beta }}_x}} \right) } \right\} , \end{aligned}$$
and the proposal distribution \({N_k}\left( {{{\mathbf{W}}^\pi }^\prime {{\mathbf{t}}_2},\left[ {{c_1} + \sigma _u^2} {+\tau ^2}\right] {I_k}} \right) \) is of interest.
-
Parameter\(\sigma ^2\): Similarly, for \({{\mathbf{t}}_4} = {{\mathbf{y}}^\pi } - {\beta _0}{{\mathbf{1}}_{{n_\pi }}} - {{\mathbf{W}}^\pi }{{\varvec{\beta }}_x}\), \(\pi \left( {{\sigma ^2}\left| {{{\mathbf{y}}^\pi },{\mathbf{y}^\delta },{\varvec{\lambda }},{\mathbf{W}},{{\varvec{\varepsilon }}},{{{\varvec{\eta }}}_{ - {\sigma ^2}}}} \right. } \right) \) is proportional to
$$\begin{aligned} {\left( {\sigma ^2} \right) ^{ - \frac{n_\pi }{2} - 1}}\exp \left\{ { - \frac{1}{2}\left[ {\frac{{c_2^2}}{{\sigma ^2}} + c_3^2{\sigma ^2}} \right] } \right\} \exp \left\{ { - \frac{1}{{2\left( {\sigma _u^2}{{\varvec{\beta }}_x'}{{\varvec{\beta }}_x}{+\tau ^2}\right) }}\sum \limits _{i = 1}^{n_\pi } {{{\left( {{t_{{4_i}}} - \sigma \frac{{{\varepsilon _i^\pi }}}{{\sqrt{{\lambda _i^\pi }} }}} \right) }^2}} } \right\} , \end{aligned}$$
and our suggested proposal distribution is \(GIG\left( {{{{n_\pi }}}/{2},{c_2},\sqrt{c_3^2 + \sum \nolimits _{i = 1}^{{n_\pi }} {{{\varepsilon _i^\pi }}/{{\sqrt{\lambda _i^\pi } }}} } } \right) \).
-
Parameter\(\tau ^2\): \(\pi \left( {\tau ^2\left| {{{\mathbf{y}}^\pi },{{\mathbf{y}}^\delta },{\varvec{\lambda }},{\mathbf{W}},{{\varvec{\varepsilon }}},{{{\varvec{\eta }}}_{ - \tau ^2}}} \right. } \right) \) is a proportion of
where \({{\mathbf{t}}_5} = {{\mathbf{y}}^\pi } - {\beta _0}{{\mathbf{1}}_{{n_\pi }}} - {{\mathbf{W}}^\pi }{{\varvec{\beta }}_x} - \sigma {{{{{\varvec{\varepsilon }}}^\pi }}}/{{\sqrt{{{\varvec{\lambda }}^\pi }} }}\).
-
Parameter\(\nu \): Consider \({ \textit{g} _\lambda } = - \left( {\nu }/{2}\right) {{\mathbf{1}}_{{n_\pi }}} + {\Sigma _{\pi \delta }}\Sigma _\delta ^{ - 1}\left( {{\ln {\varvec{\lambda }}^\delta } + \left( {\nu }/{2}\right) {{\mathbf{1}}_{{n_d} - {n_\pi }}}} \right) \) and \({\mathcal {G}_\lambda } = {\Sigma _\pi } - {\Sigma _{\pi \delta }}\Sigma _\delta ^{ - 1}{\Sigma _{\delta \pi }}\). Then, \({\nu \left| {{{\mathbf{y}}^\pi },{\mathbf{y}^\delta },{\varvec{\lambda }},{\mathbf{W}},{{\varvec{\varepsilon }}},{{{\varvec{\eta }}}_{-\nu } }} \right. } \) is a proportion of
and so a candidate distribution can be chosen as
-
Parameter\(\theta _1\): Similarly, \(\pi \left( {{\theta _1}\left| {{{\mathbf{y}}^\pi }, {\mathbf{y}^\delta },{\varvec{\lambda }},{\mathbf{W}},{{\varvec{\varepsilon }}},{{{\varvec{\eta }}}_{ - {\theta _1}}}} \right. } \right) \) is proportional to
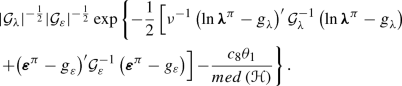
A conservative candidate distribution is the pre-specified prior on \(\theta _1\).
-
Parameter\(\theta _2\): Finally, \(\pi \left( {{\theta _2}\left| {{{\mathbf{y}}^\pi }, {\mathbf{y}^\delta },{\varvec{\lambda }},{\mathbf{W}},{{\varvec{\varepsilon }}},{{{\varvec{\eta }}}_{ - {\theta _2}}}} \right. } \right) \) is a proportion of
$$\begin{aligned} {\left| {\mathcal {G}_\lambda } \right| ^{ - \frac{1}{2}}}{\left| {\mathcal {G}_\varepsilon } \right| ^{ - \frac{1}{2}}}\exp \left\{ - \frac{1}{{2 }}\left[ \nu ^{-1}\left( {\ln {\varvec{\lambda }}^\pi -{ \textit{g} _\lambda }} \right) ^\prime {\mathcal {G}_\lambda ^{- 1}}\left( {\ln {\varvec{\lambda }}^\pi - { \textit{g} _\lambda }} \right) { + {{\left( {{{{\varvec{\varepsilon }}}^\pi } - { \textit{g} _\varepsilon }} \right) }^\prime }\mathcal{G}_\varepsilon ^{ - 1}\left( {{{{\varvec{\varepsilon }}}^\pi } - {g_\varepsilon }} \right) } \right] \right\} , \end{aligned}$$and again we choose the pre-specified prior on \(\theta _2\) as the proposal distribution.
Rights and permissions
About this article
Cite this article
Tadayon, V., Rasekh, A. Non-Gaussian Covariate-Dependent Spatial Measurement Error Model for Analyzing Big Spatial Data. JABES 24, 49–72 (2019). https://doi.org/10.1007/s13253-018-00341-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13253-018-00341-3







 for odd n, where
for odd n, where  and
and