Fluid–Structure Interaction Study of Transcatheter Aortic Valve Dynamics Using Smoothed Particle Hydrodynamics

Abstract

Computational modeling of heart valve dynamics incorporating both fluid dynamics and valve structural responses has been challenging. In this study, we developed a novel fully-coupled fluid–structure interaction (FSI) model using smoothed particle hydrodynamics (SPH). A previously developed nonlinear finite element (FE) model of transcatheter aortic valves (TAV) was utilized to couple with SPH to simulate valve leaflet dynamics throughout the entire cardiac cycle. Comparative simulations were performed to investigate the impact of using FE-only models vs. FSI models, as well as an isotropic vs. an anisotropic leaflet material model in TAV simulations. From the results, substantial differences in leaflet kinematics between FE-only and FSI models were observed, and the FSI model could capture the realistic leaflet dynamic deformation due to its more accurate spatial and temporal loading conditions imposed on the leaflets. The stress and the strain distributions were similar between the FE and FSI simulations. However, the peak stresses were different due to the water hammer effect induced by the fluid inertia in the FSI model during the closing phase, which led to 13–28% lower peak stresses in the FE-only model compared to that of the FSI model. The simulation results also indicated that tissue anisotropy had a minor impact on hemodynamics of the valve. However, a lower tissue stiffness in the radial direction of the leaflets could reduce the leaflet peak stress caused by the water hammer effect. It is hoped that the developed FSI models can serve as an effective tool to better assess valve dynamics and optimize next generation TAV designs.

Introduction

Computational analysis of bio-prosthetic heart valve (BHV) dynamics under pulsatile loading conditions has been challenging primarily due to technical difficulties involved in the modeling of nonlinear large deformation of the leaflets, unsteady flow transition to turbulence, and nonlinear interactions between the leaflets and the surrounding fluid. Many decoupled finite element (FE) and computational fluid dynamics (CFD) simulations have been performed to investigate valve leaflet dynamics,15,16,18,20,24,26,31,41 however, structural responses and hemodynamics of a BHV cannot be accurately evaluated using either FE models or CFD models alone due to strong coupling effects between the blood flow and very flexible and stretchable leaflets. In recent years, FSI simulations of BHV opening and closing dynamics have been actively pursued.22 Most of these FSI models adopted mesh-based methods, which can be broadly classified into two categories: (a) boundary conforming methods, in which the grid moves with the boundary; and (b) non-boundary conforming methods, in which the structure is immersed in the fixed background fluid grid. In boundary conforming methods, the arbitrary Lagrangian–Eulerian (ALE) approach is probably the most popular one reported in the literature.14 A major limitation of the ALE approach lies in its time-consuming re-meshing process, which is usually required to maintain a high quality mesh throughout the simulation (large deformation of valve leaflets can severely distort the fluid mesh, leading to bad quality meshes and convergence issues). The immersed boundary method (IBM)28 is one of the most popular non-boundary conforming methods. The IBM method has been extended to second-order accurate, adaptive grids, and sharp interface.3,5,7,8,12,13 Other methods, such as the fictitious domain method,1,32 and the operator splitting method used by LS-Dyna30,37,43,48 have been used to simulate FSI of BHVs. These approaches are clearly promising in simulating flow through BHVs, facilitating device design and providing clinical implications. However, there are several limitations associated with these methods, including time-consuming re-meshing, numerical instabilities, high computational cost, and challenges dealing with valve closing, which remain to be addressed.22

Recently, there has been a trend toward mesh-free methods that have the potential to overcome the challenges in mesh-based methods.22 An example of a mesh-free method is the smoothed particle hydrodynamics (SPH) method.19,25 SPH is a meshless, Lagrangian particle-based method, in which a continuum medium, such as fluid, is discretized as a set of particles distributed over the solution domain without the need of a spatial mesh.35 The method’s Lagrangian nature, associated with the absence of a fixed mesh, is its main strength. Difficulties associated with fluid flow and structural problems involving large deformations and free surfaces can be resolved by SPH in a relatively natural way. Therefore, it has emerged as a new FSI method to assess the hemodynamic responses of BHVs and blood flow in the left ventricle.33,34,44,45,50

In this study, we developed a novel, fully-coupled FSI model using SPH that could capture the hemodynamics and structural responses of a BHV during the full cardiac cycle. A previously developed FE model of transcatheter aortic valves (TAV)18,41 was utilized and coupled with SPH in ABAQUS/Explicit 6.13 (Dassault Systèmes SIMULIA Corp., Johnston, RI).35 With the developed FSI TAV model, we further investigated the differences in simulation results between a structural FE-only model and a full-coupled FSI model. For instance, the “water-hammer” effect, which is a pressure surge when the blood is forced to stop suddenly at the valve closure, can be naturally evaluated in a FSI study, but not in a FE study. In addition, we utilized the developed computational models to study the impact of leaflet material anisotropy on the TAV leaflet dynamics.

Methods

Smoothed Particle Hydrodynamics Formulation

In this study, the SPH method was used to model the blood flow passing through a TAV. The SPH methodology is thus briefly introduced as follows. As illustrated by a 2D example in Fig. 1, each SPH particle has its own physical properties, A, which are interpolated by a kernel function, W, using the properties of its neighboring particles.

Figure 1

A 2D illustration of the basic principle of the smoothed particle hydrodynamics methodology. The property A of particle ‘a’ is determined by the properties of its neighboring particles, for example, ‘b’, based on an interpolating kernel function (W) which is a function of the smoothing length, h, and the distance between particle ‘a’ and its neighboring particle ‘b’.

This concept is interpreted numerically using a summation25:

$$A({\mathbf{r}}_{\text{a}} ) = \mathop \sum \limits_{\text{b}} m_{\text{b}} \frac{{A_{\text{b}} }}{{\rho_{\text{b}} }} W\left( {{\mathbf{r}}_{\text{a}} - {\mathbf{r}}_{\text{b}} , h} \right)$$

(1)

where $A_{\text{b}}$ denotes any physical property at particle ‘b’ within the neighboring domain (limited by the influence length h of the kernel) of particle ‘a’ at position ${\mathbf{r}}_{\text{a}}$. Particle ‘b’ has mass $m_{\text{b}}$, position ${\mathbf{r}}_{\text{b}}$, and density $\rho_{\text{b}}$. In this study, a cubic spline kernel function was adopted. Using this equation and its derivatives, the governing equations of fluid flow (conservation of mass, momentum and energy) can be rewritten under the form of SPH formulation.

The time derivative form of the conservation of mass gives

$$\frac{{d\rho_{\text{a}} }}{dt} = \mathop \sum \limits_{\text{b}} m_{\text{b}} {\mathbf{V}}_{\text{ab}} \cdot \nabla_{\text{a}} W_{\text{ab}} .$$

(2)

Here $\nabla_{\text{a}} W_{\text{ab}}$ is the gradient of the kernel function regarding the coordinates of given particle ‘a’ and ${\mathbf{V}}_{\text{ab}} = {\mathbf{V}}_{\text{a}} - {\mathbf{V}}_{\text{b}}$ denotes the relative velocity vector between particles ‘a’ and ‘b’.

Similarly, the conservation of momentum under the SPH scheme can be written as

$$\frac{{d{\mathbf{V}}_{\text{a}} }}{dt} = - \mathop \sum \limits_{\text{b}} m_{\text{b}} \left( {\frac{{P_{\text{a}} + P_{\text{b}} }}{{\rho_{\text{a}} \rho_{\text{b}} }}} \right)\nabla_{\text{a}} W_{\text{ab}} + \mathop \sum \limits_{\text{b}} m_{\text{b}} \frac{{\left( {\mu_{\text{a}} + \mu_{\text{b}} } \right){\mathbf{V}}_{\text{ab}} }}{{\rho_{\text{a}} \rho_{\text{b}} {\mathbf{r}}_{\text{ab}}^{2} }}{\mathbf{r}}_{\text{ab}} \cdot \nabla_{\text{a}} W_{\text{ab}}$$

(3)

where $P$ is pressure and $\mu$ is the dynamic viscosity of the fluid. The movement of the particles is governed by

$$\frac{{d{\mathbf{r}}_{\text{a}} }}{dt} = {\mathbf{V}}_{\text{a}}$$

(4)

In ABAQUS, the pressure is related to the density by the Mie–Grüneisen equation of state.35 In this work, the linear $U_{\text{s}} - U_{\text{p}}$ Hugoniot form is used, given by

$$p = \frac{{\rho_{0} c_{0}^{2} \eta }}{{(1 - s\eta )^{2} }}\left( {1 - \frac{{\varGamma_{0} \eta }}{2}} \right) + \varGamma_{0} \rho_{0} E_{\text{m}}$$

(5)

where $\varGamma_{0}$ is a material constant, $c_{0}$ is the artificial speed of sound, $\eta = 1 - \rho_{0} /\rho$ is the nominal volumetric compressive strain, $\rho$ is the current density, and $E_{\text{m}}$ is internal energy per unit mass. It is commonly assumed that blood is isothermal, incompressible and Newtonian.22 Thus, in this study, we set a reference density of $\rho_{0} =$ 1056 kg/m³, and a dynamic viscosity of $\mu = 0.0035\; {\text{Pa s}}.$ For the blood flow in the aorta, the speed of sound is high compared to the bulk velocity of the blood, therefore an artificial sound speed of $c_{0} = 145 \;{\text{m}}/{\text{s}}$ was employed to avoid very small computational time steps while keeping density fluctuations within a small range to maintain incompressible flow behavior. Other material parameters were chosen as s = 0 and $\varGamma_{0} = 0$.

Finite Element Modeling of TAV

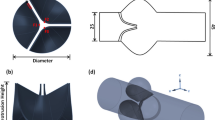
TAV leaflets are generally fabricated from either thin (~0.25 mm) glutaraldehyde-treated bovine pericardium (GLBP) or porcine pericardium.51 In this study, GLBP was selected as a representative valve leaflet material. GLBP was assumed to be an incompressible, anisotropic, nonlinear, hyperelastic material;42 thus the strain energy function, W, can be expressed by a fiber-reinforced hyperelastic material model (MHGO) based on the work of Holzapfel and coauthors,6,10

$$W = C_{10} \left\{ {{ \exp }\left[ {C_{01} \left( {\bar{I}_{1 } - 3} \right)} \right] - 1} \right\} + \frac{{k_{1} }}{{2k_{2} }}\mathop \sum \limits_{i = 1}^{2} \left\{ {{ \exp }\left[ {k_{2} \left( {\bar{I}_{4i} - 1} \right)^{2} } \right] - 1} \right\} + \frac{1}{D}\left( {J - 1} \right)^{2} ,$$

(6)

where $C_{10}$, $C_{01}$, $k_{1}$, $k_{2}$ and $D$ are material constants, $\bar{I}_{1 }$ and $\bar{I}_{4i}$ are the deviatoric strain invariants. $C_{10}$ and $C_{01}$ are used to describe the matrix material. $D$ is a material constant to impose incompressibility, and $J$ is the determinant of the deformation gradient. $k_{1}$ is a positive constant with the dimension of stress to describe the fiber material and $k_{2}$ is a dimensionless parameter. The fiber orientations is defined by $\theta$, which is the angle between the fiber orientation and the circumferential direction (Fig. 2b).

Figure 2

(a) GLBP equi-biaxial response from Sun’s thesis39 (open circles), with anisotropic MHGO model fit (black lines), and the averaged response (red squares) with isotropic Ogden model fit (red line). (b) Diagram of the leaflet material orientations and the fiber orientations, m ₀₁ and m ₀₂, drawn on the 2D leaflet schematic.

In the heart valve industry, it is well known that leaflets made of pericardial tissues can have various degrees of anisotropy, however, the impact of leaflet material anisotropy on the valve stress distribution and hemodynamics has not been investigated using a fully-coupled FSI model. Thus, in this study, an incompressible, isotropic, hyperelastic Ogden model27 was used for comparison to the anisotropic MHGO model. The Ogden strain energy function is given by

$$W = \mathop \sum \limits_{i = 1}^{N} \frac{{2\mu_{i} }}{{a_{i}^{2} }}\left( {\bar{\lambda }_{1}^{{a_{i} }} + \bar{\lambda }_{2}^{{a_{i} }} + \bar{\lambda }_{3}^{{a_{i} }} - 3} \right)$$

(7)

where $\mu_{i}$ and $a_{i}$ are material constants, and $\bar{\lambda }_{i}$ are the modified principal stretches.

The FE model of a generic size 23 TAV developed previously18 was used in this study. The TAV leaflets were discretized using 7896 large-strain brick (C3D8R) elements with a thickness of 0.25 mm. For an anisotropic MGHO model, local material orientations were defined for the leaflets at each element. The material properties defined by the constitutive law of Eq. (6) were incorporated into ABAQUS via a user subroutine UMAT.40 The contact between each leaflet was modeled using a general contact algorithm in ABAQUS. The TAV stent was not included in the simulations because the deformation of the metallic stent is assumed to be minimal. Thus, the stent-attachment nodes were fixed in space to mimic attachment to the non-deformable stent. The GLBP leaflet material parameters were determined by fitting the biaxial testing data of GLBP leaflets presented by Sun.39 The constitutive model was able to capture the response very well (Fig. 2a). The two fiber families were assigned identical material properties and oriented symmetrically about the leaflet material axis in the radial direction illustrated in Fig. 2b. The averaged material response from the biaxial testing data was fitted using a four-parameter isotropic Ogden model. The material parameters of both models are given in Table 1. The mass density of the leaflets was defined as 1100 kg/m³.

Table 1 GLBP material properties.

FE-SPH Model Setup and Boundary Conditions

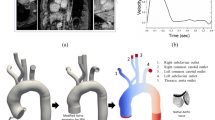
The aortic valve flow condition was modeled following the ISO 5840-3:2013 testing conditions by adopting a 36.8 mm diameter tubular structure, as illustrated in Fig. 3. The tubes upstream and downstream from the valve were long enough to eliminate the boundary effect on the region of interest. The length of downstream SPH particles was chosen as 110 mm, which corresponds to a typical, normal human ascending aorta length.38 (Note that the downstream length in our study includes sinus height). To accommodate a size 23 TAV, rigid gaskets and skirts were introduced to the model (Fig. 3). The tube, gaskets, and skirts were all fixed in space. The mesh sensitivity of SPH particles was checked on the FSI-Ogden model. Three different mesh densities were used with spatial resolutions of 0.9, 0.7, and 0.5 mm, respectively. This leads to approximately 370,300 one-node PC3D elements, 790,200 elements, and 2,171,800 elements in the fluid domain, respectively. The relative error of the peak velocity through the valve was 16.5% between the coarse and fine meshes, and 4.1% between the medium and fine meshes. A reasonable grid convergence was obtained on the medium mesh density (for further details refer to Appendix A.1). Therefore, the results presented in this study employed the medium mesh density. Two rigid plates were used to apply pressure boundary conditions on the blood volume. This setting implicitly assumes that the inlet and outlet velocities have flat profiles as the particles adjacent to the plates are driven by the flat plates, which is commonly adopted for FSI simulations.22,37 A nearly-closed configuration of the leaflets (see the inset in Fig. 6) was chosen as the stress-free initial configuration. Physiological pressure waveforms at a heart rate of 75 bpm (Fig. 4a) were used to obtain the pressure gradient between the left ventricle and aorta (Fig. 4b), which was applied in the simulation. The beginning of the ejection phase was selected as the starting point of the simulation. Two cardiac cycles were conducted and the results from the second cycle were analyzed. We found that the difference between the first and second cycle was within 10% error. Simulations were performed on an Intel Xeon E5-2670 cluster with 64 cores and required 155 h for the FSI model using the medium mesh in one cardiac cycle. In the FE-only simulations, three leaflets were simulated with the stent-attachment nodes fixed in space. The same pressure gradient waveform was uniformly applied to the surface of the leaflets to deform the leaflets.

Figure 3

Three-dimensional FE-SPH model for TAV opening and closing simulations. The model consists of a 36.8 mm diameter rigid tubular structure, a rigid gasket and skirt to seal the gap between the tube and valve, two rigid plates at the aortic and ventricular sides respectively, blood particles (half SPH particles are shown in the fluid domain for clarity), and three flexible TAV leaflets.

Figure 4

(a) Wiggers diagram representing physiological pressure waveforms at a heart rate of 75 bpm.47 (b) Pressure boundary conditions applied to the plates.

Results

TAV Leaflet Kinematics

Leaflet kinematics were evaluated during the TAV opening and closing phases. Leaflet motion was monitored through the time-dependent radial position of the midpoint of the leaflet free edge (see red dot in Fig. 2b). Since the three leaflets move similarly during the opening and closing phases, the averaged radial motion of the midpoints is shown in Fig. 5a. Several qualitative differences in the leaflet motion between the FE-only and FSI simulations were observed. Firstly, the opening process in the FE-only models began immediately once the pressure load was applied; while in the FSI models, there was approximately 20 ms delay before the free edges of the leaflets began to open. The total valve opening time in the FE models was short, about 5 ms, compared to about 40 ms in the FSI models. A larger radial excursion of the free edge was observed for the FE models than that of the FSI models.

Figure 5

(a) Time-dependent radial position of the midpoint of leaflet free edge during a cardiac cycle. (b) Time-dependent GOA of TAV during a cardiac cycle. Note for the sake of clarity, a full cardiac cycle was truncated to show the variation from 0 to 0.4 s.

The geometric orifice area (GOA) of each TAV was calculated during a cardiac cycle from our simulations. An in-house MATLAB (The MathWorks, Inc., Natick, MA) code was implemented to obtain the GOA based on images of the deformed valve from the top-view. The time-dependent GOA curves in Fig. 5b showed a similar behavior. The results from the FSI models had smaller GOAs than those from the FE models. The closing process in the FE models was faster than that in the FSI models. The FE results had higher frequency fluctuations in the leaflet motion during the opening and ejection phases.

A series of the time-dependent leaflet deformed shape, represented by a middle-line at the perpendicular bisection plane of the leaflet, was shown in Fig. 6. The red curves represent the opening profiles, and the blue curves are the closing profiles. As shown in Fig. 6, at t = 0 ms, all models started from the same initial configurations. For the FSI models, at the beginning of the opening process, the leaflet deformation was initiated at the bottom of the valve near the attachment edge and the belly region of the leaflets (see leaflet profiles at 20 ms in Figs. 6a and 6b), then expanded towards the free edge region as the fluid pushed through the valve. However, for the FE model, at t = 5 ms, the valves almost reached the maximum opening orifice area. During the closing phase, the coaptation of the free edges occurred earlier in the FE models (at approximately t = 240 ms) than in the FSI models (at approximately t = 270 ms). The coaptation of the leaflets was achieved in all models before the maximum transvalvular pressure gradient was reached. The fully-closed leaflet shapes were almost the same in both FE and FSI models. At other phases, however, relatively larger discrepancies in leaflet deformed curvature were observed between the FE-only and FSI simulations.

Figure 6

A series of the time-dependent leaflet deformed shape (the red curve in the center inset) is depicted with respect to the perpendicular bisection plane of the leaflet. The red curves represent the opening profiles, and the blue curves represent the closing profiles. (a) FSI-Ogden model. (b) FSI-MHGO model. (c) FE-Ogden model. (d) FE-MHGO model.

The material models also had a noticeable impact on the leaflet kinematics. The isotropic Ogden model showed a slightly stiffer leaflet behavior compared to the anisotropic MHGO model in the radial direction, since the radial position of free edge midpoint was lower during the ejection phase for both the FE and FSI models. In the FSI-MHGO model, large magnitude and low frequency fluctuations of the leaflets during the ejection phase were observed. Similarly, the fully-closed configuration in the MHGO models (see Fig. 6) was more concave than that of the Ogden models.

Structural Stress and Strain Responses

Maximum principal true strain (LE) contour plots of the deformed leaflets are shown in Figs. 7, 8, and 9 for the FE-MHGO, FSI-MHGO, and FSI-Ogden models, respectively. In the FE-MHGO model (Fig. 7), during the ejection phases at t = 5 ms, the peak strain was observed below the commissure region along the leaflet-stent attachment line with a peak value about 0.22. During the valve closing phase, large strain was concentrated in the commissure and belly regions. A peak value of 0.185 was found at the stent-leaflet attachment hinge regions in the fully-closed configuration. Compared to the results of the FE-MHGO model, in the FSI-MHGO model (Fig. 8), the peak value of strain was much smaller (i.e., about 0.112 at t = 40 ms) during the opening phase and mainly concentrated below the commissure region along the leaflet-stent attachment line. In the fully-closed configuration, a similar strain pattern was observed with a peak strain of 0.185.

Figure 7

Opening and closing of TAV leaflets colored by the maximum principal strain from the FE-MHGO model. Note the different scale for each time instance.

Figure 8

Opening and closing of TAV leaflets colored by the maximum principal strain from the FSI-MHGO model. Note the different scale for each time instance.

Figure 9

Opening and closing of TAV leaflets colored by the maximum principal strain from the FSI-Ogden model. Note the different scale for each time instance.

Comparing the FSI-Ogden and FSI-MHGO models, a similar pattern of strain distribution was found during the opening phase, see Figs. 8 and 9. However, the strain distribution was different in the fully-closed configuration. A peak strain value of 0.144 was observed in the FSI-Ogden model and concentrated in the commissure regions.

The maximum principal stress distribution on the leaflets in the fully open and closed configurations are depicted in Fig. 10. The stress distribution and peak value were very similar in the fully-closed phase between the FE-only and FSI models. However, in the full open phase, the peak stress value was much smaller in the FSI models compared to the FE models. Differences between the isotropic and anisotropic models were observed. The peak stress value at the commissure in the fully-closed configuration reached 1.13 MPa in the FSI-MHGO model compared to the value of 1.42 MPa in the FSI-Ogden model. The peak stress in the belly region was 0.74 and 0.59 MPa for the FSI-MHGO and FSI-Ogden models, respectively. Meanwhile, the high stress regions in the MHGO models shifted downwards from the commissure region and distributed along the attachment line.

Figure 10

Contour plots of the maximum principal stress (in MPa) for each valve in the fully-open (t = 40 ms) and fully-closed (t = 300 ms) configurations. (a) FE-Ogden model. (b) FSI-Ogden model. (c) FE-MHGO model. (d) FSI-MHGO model.

Hemodynamics

The TAV hemodynamics were evaluated based on the FSI-MHGO and FSI-Ogden models. The waveforms of the transvalvular pressure drop are plotted in Fig. 11a. The transvalvular pressure was recorded one diameter upstream and three diameters downstream from the annulus of the valve following the ISO-5840 guideline. The two pressure curves were very similar during systole. The FSI-MHGO model had a slightly lower peak pressure drop (11.7 mmHg at t = 25 ms) compared to the FSI-Ogden model (14.5 mmHg at t = 25 ms). Note that the transvalvular pressure was not the same as the pressure boundary conditions applied on the plates. Especially during the valve closing phase, large oscillations can be seen due to the strong effect of water inertia. The axial hydrodynamic force acting on the leaflets in a cardiac cycle is shown in Fig. 11b. In systole, this force is equal to the pull-out force on the TAV that may cause device migration under the forward blood flow. The peak values of pull-out force are 0.26 and 0.20 N for the FSI-Ogden and FSI-MHGO models, respectively. In the diastole, the peak hydrodynamic forces reach up to −6.9 and −6.1 N at t = 270 ms for the FSI-Ogden and FSI-MHGO models, respectively. The maximum static pressure force of −5.4 N on the valve in diastole, represented as the dotted line in Fig. 11b.

Figure 11

Comparison of (a) transvalvular pressure gradient, (b) hydrodynamic force acting on the leaflets (the dotted line represent the maximum hydrostatic pressure force in diastole), (c) maximum velocity at 15 mm downstream the TAV annulus (basal ring), (d) flow rate through the TAV in a cardiac cycle between the FSI-Ogden and FSI-MHGO models. For the sake of clarity, only a partial cardiac cycle from 0 to 0.4 s is shown.

The maximum flow velocity at an axial distance of 15 mm downstream of the TAV annulus was monitored throughout the cardiac cycle (see Fig. 11c). The velocity reached a peak value of 1.40 and 1.36 m/s for the FSI-Ogden and FSI-MHGO models at t = 80 ms, respectively. The time-dependent flow rate, which was averaged among several cross-sectional planes starting from the upstream to the downstream of the valve, is depicted in Fig. 11d. The peak flow rates in the FSI-Ogden and FSI-MGHO models were 13.1 and 14.7 L/min, respectively. Other hemodynamic parameters, such as mean systolic pressure difference (MSPD), peak systolic pressure difference (PSPD), effective orifice area (EOA), regurgitant volume (RV) are listed in Table 2. The EOA was calculated according to the formula defined as49: ${\text{EOA}}\left( {{\text{cm}}^{2} } \right) = \frac{{Q_{\text{rms}} }}{{51.6\sqrt {\Delta P} }}$, where $Q_{\text{rms}}$ is the root mean square systolic flow rate (${\text{cm}}^{3} /{\text{s}}$), and $\Delta P$ is the mean systolic pressure drop (mmHg).

Table 2 Hemodynamic parameters calculated from the results of FSI simulations.

Flow velocity vector field were assessed on a cross-section through the symmetry plane of the valve at six time instances throughout the cardiac cycle (Fig. 12). During the opening phase (t = 25 ms and 40 ms), the forward flow developed along the axial direction with an almost circular jet profile. At t = 100 ms, a wide central jet with a maximum velocity of 1.40 m/s was observed immediately downstream of the valve. Vortices were identified beside the central jet downstream the tube expansion. These vortices developed progressively downstream throughout the ejection phase (t = 230 ms). During the closing phase (t = 270 ms), due to the closing of the leaflets and the reverse pressure gradient, a large reverse flow was generated through the central gap between the leaflets. The regurgitant jet only existed for a very short time due to the rapid closing, thus did not result in large RVs (see Table 2). After valve closure, the flow was nearly hydrostatic with negligible velocities at t = 300 ms.

Figure 12

Blood velocity vector fields at different time instances for the FSI-Ogden (the left hand side) and FSI-MHGO (the right hand side) models. Note the color legend on the top applies to the first four time instances, while the bottom legend corresponds to the last two instances.

Additionally, we calculated the rapid valve opening and closing times and ejection time defined as the time from the initial opening to complete closure of the valve. According to Refs. 17, 37, and 48 rapid valve opening times can be calculated when the radial displacement curves of the nodes have a high positive and high negative slope, respectively. All numerical predictions for these quantities are listed in Table 3.

Table 3 RVOT, RVCT, and ET calculated from our models and measured in vivo.17

Discussion

In this study, we developed, to our knowledge, the first SPH-based FSI model to investigate TAV leaflet dynamics throughout the whole cardiac cycle. In the simulations, we also utilized nonlinear hyperelastic material models to describe the experimentally derived leaflet material properties. Comparative simulations were performed to study the effects of using FE-only models vs. FSI models, as well as the isotropic Ogden material model vs. the anisotropic MHGO material model.

Valve leaflet dynamics were only recently evaluated in vivo using 4-dimensional (4D), volume-rendered CT scans.9,21 Notably, a report by Makkar et al.21 demonstrated that by using 4D CT scans, reduced TAV leaflet motion was observed in patients who had a stroke after TAV implantation. However, such 4D CT scans are not commonly available yet, and post-procedural CT scans are not part of the standard of care in TAV patients. To date, ex vivo bench testing probably remains to be the best approach to quantify BHV leaflet dynamics for the device design evaluation and optimization. However, the experimental studies of valve deformation are relatively expensive and difficult to perform because of practical limitations in measurements very close to the leaflets and valve housing. FE-only models, due to an inaccurate pressure field applied to the leaflets and the lack of fluid damping as illustrated in this study, led to inaccurate simulations of leaflet dynamics; consequently, a match between FE result and experiment data is usually hard to achieve.15,31

From the results of this study, it can be seen that FE-only models tend to overestimate the pressure force exerted on the leaflets in systole, leading to abnormally fast opening of the valve, whereas the results from the FSI models were comparable with in vivo measurement,17 as demonstrated in other FSI results as well.29,37 Some FE-only studies used a numerical damping force to account for the effect of surrounding fluid.15,23,31 Since the damping coefficient is not known a priori, it can only be chosen by a trial-and-error process.12 Moreover, the valve orifice area was larger in the FE models in the fully open configuration than the FSI models, as observed in Ref. 37 which is consistent with our findings.

In the closing phase, by comparison of the hydrostatic pressure force with the hydrodynamic force on the leaflet in Fig. 11b, it can be seen that the large fluctuation in the closing phase was not captured by the hydrostatic force. The peak hydrodynamic forces reach up to −6.9 and −6.1 N at t = 270 ms for the FSI-Ogden and FSI-MHGO models, respectively. These forces would exceed the maximum hydrostatic force on the valve ($F_{\text{p}} = \Delta P_{ \hbox{max} } \cdot A = 5.4 \;{\text{N}}$) in the closed configuration by about 13–28%. Thus, when considering the dynamic pull-out force on TAVs, the fluid inertial force due to the water hammer effect in the closing phase should be considered. Moreover, the larger peak hydrodynamic force obtained in the FSI-Ogden model may be attributed to the relatively stiffer material response in the radial direction than that of the FSI-MHGO model.

Our FSI simulations replicated similar leaflet dynamics during the cardiac cycle as observed in the experiments.4,46 Noticeably, the leaflets were pushed open by the fluid flow from the belly of the valve first and progressively to the free edge of the leaflets. Thus, the fully-opened leaflets appears to be convex in the FSI simulations, whereas in the FE-only simulations, the free edge of the leaflets were deformed instantaneously once the uniform pressure loading is applied, resulting in a concave shape of the fully-opened leaflets.

The peak flow rates obtained from the FSI-Ogden and FSI-MGHO models were 13.1 and 14.7 L/min, respectively. These values agree with the findings in Ref. 37 (with a peak flow rate of 15.7 L/min) using a similar pressure drop waveform as the boundary condition. Other FSI studies12,29 obtained higher peak flow rates possibly due to the larger transvalvular pressure drop used in their simulations. The cardiac output from our simulations is smaller than the physiological measurement. This may be related to two simplifications of our FSI model setups. Firstly, the straight tube geometry with sudden contraction and expansion used in our models would cause a larger pressure drop compared to the anatomical aortic root geometry with sinuses. Secondly, rigid aortic wall used in our models is not physiological, which may cause additional errors. Nonetheless, other hemodynamic parameters, such as EOA, were comparable to the published clinical data.2,36

There are several limitations of the study, which should be considered when interpreting our results. Firstly, we used a straight and rigid tube connection downstream from the aortic annulus, neglecting the anatomic geometry of the sinuses and the compliant tissue behavior of the aortic root. This simplification of a straight tube may affect the kinematics of the leaflets and associated stress distribution.14,17 The influence of arterial wall elasticity in heart valve simulations was studied by Hsu et al.11 They found that the major difference between rigid and elastic models occurred immediately following valve closure. The rigid wall model results had larger and longer oscillations in the flow rate and the valve movement compared to those of the compliant arterial wall model. Therefore, the water hammer impact in our model may be overestimated due to the absence of aortic compliance. Secondly, the SPH solver in ABAQUS has no turbulence model, and the no-slip wall boundary condition is not fully constrained. This omission is likely to affect the blood flow in the boundary layers region. Thirdly, the stent of TAV was ignored in our model. It may affect the hemodynamics of the valve. However, it is unlikely to deteriorate our conclusions due to the side-by-side comparison between the FSI and FE models.

In conclusion, the major novelty of the present study is the development of a SPH-FE coupled FSI model that is capable of modeling the overall structural and hemodynamic characteristics of TAVs throughout the whole cardiac cycle. Through a comparative study using FE-only models, the FSI models were able to capture the leaflet kinematics during the valve opening and closing phases due to more realistic spatial and temporal loading conditions. The stress and the strain distributions were similar between the FE and FSI simulations. However, the peak stresses were different due to the water hammer effect induced by the fluid inertia in the FSI model during the closing phase, which led to 13–28% lower peak stresses in the FE-only model compared to that of the FSI model. The simulation results also indicated that tissue anisotropy had a minor impact on hemodynamics of the valve. However, a lower tissue stiffness in the radial direction of the leaflets could reduce the leaflet peak stress caused by the water hammer effect. It is hoped that the developed FSI models can serve as an effective tool to better assess valve dynamics and optimize next generation TAV designs.

Appendix

A.1: Mesh Sensitivity of Fluid Domain

The mesh sensitivity of SPH particles was analyzed by using the FSI-Ogden model. Three different mesh densities were used with spatial resolutions of 0.9 mm (coarse mesh), 0.7 mm (medium mesh), and 0.5 mm (fine mesh) respectively. This leads to approximately 370,300 one-node PC3D elements, 790,200 elements, and 2,171,800 elements in the fluid domain, respectively. The relative error of the peak velocity through the valve was 16.5% between the coarse and fine meshes, and 4.1% between the medium and fine meshes. A reasonable grid convergence was obtained on the medium mesh density. Therefore, the results presented in this study employed the medium mesh density.

The results of the corresponding FSI analyses were compared in terms of (a) transvalvular pressure gradient, (b) hydrodynamic force acting on the leaflets, (c) maximum velocity at 15 mm downstream the TAV annulus, (d) flow rate through the TAV, as shown in Fig. A1. The comparison of the respective results showed differences in peak values within 5% between the medium and the fine mesh, resulting in acceptable level of grid convergence.

Figure A1

Comparison of (a) transvalvular pressure gradient, (b) hydrodynamic force acting on the leaflets, (c) maximum velocity at 15 mm downstream the TAV annulus, (d) flow rate through the TAV, for different mesh densities of SPH particles using the FSI-Ogden model.

A.2: Fiber Orientation on the Leaflet

Two families of fibers with orientations m ₀₁ and m ₀₂ for the FSI-MHGO model in the open (t = 100 ms) and closed (t = 300 ms) configurations are shown in Fig. A2.

For ease in visualization, the fiber directions are projected onto the undeformed leaflet configuration. The m ₀₁ and m ₀₂ fibers in the belly region, where the leaflets subject to high strain and stress, undergo significant rotation in closed configuration compared to the open configuration. The differences in fiber orientations signify the presence of anisotropy in BAV tissues.

Figure A2

The fiber orientations for the FSI-MHGO model in open (t = 100 ms) and closed (t = 300 ms) configurations: m ₀₁ in (a) and m ₀₂ in (c) at t = 100 ms; m ₀₁ and m ₀₂ in (b) and (d), respectively, at t = 300 ms.