1 Introduction

In recent years, evolutionary game theory has become a powerful tool for predicting and even designing evolution in many fields [27, 35, 40]. Its origin comes from biology where it was introduced by [22] to model competitions among animals. It differs from classical game theory by: (i) its focusing on the evolution dynamics of the fraction of members of the population that uses a given strategy and (ii) in the notion of evolutionarily stable strategy [35] which includes robustness against a deviation of a whole small fraction of the population; this is in contrast to the standard Nash equilibrium that only incorporates robustness against deviation of a single player. Recently, however, evolutionary game theory has become of increased interest to social scientists [9, 27]. In computer science, evolutionary game theory is appearing; some examples of applications can be found in multiple access protocols [14, 39, 40], multi-homing [34] and resources competition in the Internet [45].

The ESS is a static concept that abstracts how the equilibrium is reached; it relies on a criterion of immunity against the penetration of mutant into population but does not rely on a dynamic process that describe the evolution of strategies into the population. Many and various dynamics are proposed in the literature to model the evolution of the population composition over time. Formally, this is accomplished by means of mechanisms called revision protocols. These dynamics describe when and how an individual decides to switch strategies, and they implicitly specify what information agents use to make these decisions. The central concept in the evolutionary games is the replicator dynamics [38, 42], which is the most studied one. In this dynamic, the percentage growth rate of a strategy currently used is equal to the difference between that strategy’s payoff and the expected payoff obtained by all individuals in the population. Thus, strategies leading to a payoff that is higher than the average become more abundant.

Initially, evolutionary game framework and replicator dynamics concept have been used to study biological systems and economic problems. Recently, this rich framework offers good capabilities to study large interaction networks of decision makers. In evolutionary game theory (EGT), the success of a given strategy depends on the frequency of all strategies represented in the population, and successful strategies spread over the population. Unfortunately, the theory developed in this field has mostly focused on the homogeneous population in which a given individual equally likely interacts with any other member of the population. Then, the success of any individual depends on the frequency of all other strategies represented in the population. In many examples such that social networks, however, the population is composed of several communities or groups that can be seen as clusters [2, 21, 33]. Therefore, community strategies are influenced by interactions inside the community and also with other communities [7]. Besides, the interactions among individuals are inherently nonuniform, and individuals are more likely to interact with some agents than others because of spatial barriers, language or cultural differences [44]. In biology, some animal species are strongly territorial [8], and territories vary in quality [11]. Hence, an animal may fight against animals from different species and the payoff depends on the species. For example, the probability that an animal being hurt or killed is higher if it meets a larger animal than smaller animal.

The major question posed in the EGT literature is related to the stability of a steady state which leads to a refinement of the Nash equilibrium. Much of work on evolution has studied the relationship between the steady state of the replicator dynamics and the ESS concept. Taylor and Jonker [38] established conditions under which one may infer the existence of a stable state under the replicator dynamics given an evolutionarily stable strategy. However, this can fail to be true for multi-populations or more than two strategies [28, 30]. In the last two decades, there have been several attempts to relax the assumption derived by Taylor and Jonker [38] in order to explore games in which agents only interact with their neighbors on a lattice [13, 17, 23] or on a random graph [24–26, 31, 36]. These modifications on the replicators dynamics lead to lose the connection between the stable equilibrium of the replicator and ESS. Indeed, under some payoffs, stable states have no corresponding analogue neither in the replicator dynamics nor in the analysis of ESS. In this paper, we aim to connect the analysis of the stability in a static concept and the steady state of the replicator dynamics. Instead of considering well-mixed population, we explore games in which the population is composed of several communities or groups. Each group has its own set of strategies, payoff matrix and resulting outcomes. In addition, each group may interact with any other group with different interacting probabilities. Our work focuses on different types of individuals, such that any pairwise interaction does not lead to the same fitness, depending on the type of individuals that are competing, and not only the strategy used. We study the existence of ESSs with different levels of stability defined as follows:

  • Strong ESS The stability condition guarantees that no alternative strategy can invade the population. This condition states that all groups or communities have an incentive to remain at the ESS when a rare alternative strategy is used by mutants in all groups that form the population.

  • Weak ESS The stability condition guarantees the stability against a fraction of mutants in a single group.

  • Intermediate ESS This equilibrium focuses on the global fitness of the whole population instead of a single group. It guarantees that all the population cannot earn a higher total payoff when deviating from the ESS.

We show that any fully mixed Nash equilibrium is not a strong ESS wherein all communities using this equilibrium cannot be invaded by a small group from all communities with a mutant strategy. But under some assumptions on the payoff and interaction probabilities, this mixed equilibrium is an ESS when we consider the global fitness of all the population instead of the fitness of each community. Furthermore, we analyze one of the most studied examples in evolutionary games, that of the Hawk and the Dove, a model for determining the degree of aggressiveness in the population. Our new model allows to study the evolution of aggressiveness within different species of animals.

For the evolutionary dynamics, we introduce the replicator dynamics in structured populations and under nonuniform interactions in communities. We study the relationship between the steady state of the replicator dynamics and the ESSs with different levels of stability. In particular, we show that the fullymixed intermediate ESS is asymptotically stable in the replicator dynamics. In contrast, the condition of weak stability does not ensure the stability condition of the replicator dynamics.

The majority of works in evolutionary dynamics have studied the replicator dynamics without taking into account the delay effect. Many examples in biology and economics show that the impact of actions is not immediate and their effects only appear at some point in the future. Therefore, a more realistic model of the replicator dynamics would take into consideration some time delay. The authors in [43] studied the effect of symmetric time delays in the replicator dynamics in a population model with two strategies. They assumed that an individual’s fitness at the current time is equal to the expected payoff value of the strategy used by this individual at some previous time. The authors proved that the unique interior steady point becomes unstable for sufficiently large values of the delay. A similar result was proved by the authors in [1] in their social-type model. In the reference [41], the authors studied the replicator dynamics with asymmetric delays across the strategies and showed that for large delays the instability occurs. On the other hand, the author in [20] examined the effect of heterogeneously distributed delays among the individuals, and he derived conditions under which the mixed ESS is asymptotically stable in the replicator dynamics for any delay distribution.

In this work, we study the effect of time delays on the stability of the replicator dynamics in a population composed of communities. Two types of time delays can be distinguished: strategic delay which is the delay associated with the strategies of players and spatial delay which is the delay associated with the communities of the competing players. As in one population scenario, we show that for large strategic delays, the mixed intermediate ESS may become an unstable state for the replicator dynamics. In contrast, the replicator dynamics converge to the intermediate ESS for any value of the spatial delay. Spatial delays come from the latency induced by the individuals type when they interact. In fact, we can assume that in some situations, the delay of a pairwise interaction between individuals from the same community can be lower than when individuals from different communities are interacting. For example, in a social network, individuals from the same community will share faster same content/information as there is some kind of confidence between them, whereas a content coming from an individual from another community may yield to a careful behavior and then increases the outcome delay of the interaction.

The paper is structured as follows. First in Sect. 2, we present new ESS definitions with different levels of stability in multi-community settings. Section 3 is devoted to the study of nonuniform interactions between two communities. In Sect. 4, we study the replicator dynamics, both in its classical form and with strategic and spatial delays. We apply our model to the Hawk–Dove game in Sect. 5. Finally, we conclude the paper in Sect. 6.

2 Evolutionarily Stable Strategies

We consider a large population of players or individuals divided into N communities and each community has its own set of strategies, payoff matrices and interacting probabilities. Random matching occurs through pairwise interactions and may engage individuals from the same community or from different communities. Let \(p=(p_1,\ldots ,p_N)\) where \(p_i=(p_{i1},\ldots ,p_{iN})\) is the vector describing the interaction probabilities of community i with other communities. Here \(p_{ij}\) denotes the probability that an individual in community i involved in an interaction, interacts with an individual in community j and \(\sum _j p_{ij}=1\) (Fig. 1). We assume there are \(n_i\) pure strategies for each community i and a strategy of an individual is a probability distribution over the pure strategies. We denote by \(A^{ij} =(a^{ij}_{kl})_{k=1\ldots n_i, l=1\ldots n_j}\) the payoff matrix. If a player of community i using pure strategy k interacts with a player of community j using pure strategy l, its payoff is \(a^{ij}_{kl}\). Let \(\mathbf{{s}}=(s_1,\ldots ,s_N)\) be the population profile where \(s_i\) is the column vector describing the distribution of pure strategies in community i (\(s_{ik}\) is the frequency of the pure strategy k in community i). We denote by \(U_i(k,\mathbf{s},p)\) the expected payoff of pure strategy k in community i, which depends on the frequency of strategies in community i and in the other communities. The payoff function \(U_i\) is given by:

$$\begin{aligned} U_i(k,\mathbf{s},p)= \sum _{j=1}^{N} p_{ij} e_k A^{ij} s_j, \end{aligned}$$
(1)

where \(e_k\) is a row vector corresponding to the kth element of the canonical basis of \(\mathbb {R}^{n_i}\). The expected payoff of a player from community i using a mixed strategy z, when the profile of the population is \(\mathbf{s}\), is given by:

$$\begin{aligned} \bar{U}_i(z,\mathbf{s},p)=\sum _{k=1}^{n_i}{z_{k}U_i(k,\mathbf{s},p)}. \end{aligned}$$
(2)

Our model covers the many situations as:

  • The probabilities of interactions may depend on the size of the communities. An individual is more likely to meet and interact with an opponent from the larger community. For example, if \(\alpha _1\) and \(\alpha _2\) are the size of groups 1 and 2, respectively, then the probability for an individual from group 1 interacts with an opponent, uniformly randomly picked, from the same group is \(p_{11}=\frac{\alpha _1}{\alpha _1+\alpha _2}\) while the probability to interact with an individual from the other group is \(p_{12}=\frac{\alpha _2}{\alpha _1+\alpha _2}\) . Similarly, the probability for an individual from group 2 interacting with an individual from group 2 is \(p_{22}=\frac{\alpha _2}{\alpha _1+\alpha _2}\) and the probability to interact with a player from group 1 is \(p_{22}=\frac{\alpha _1}{\alpha _1+\alpha _2}\).

  • The probabilities of interactions may also depend on spatial aspects, in which an individual is more likely to interact with individuals in his neighborhood. If we consider that the rate of interaction is uniform, denoted by \(\gamma \), then the total rate of inter-group interactions in group 1 and 2 are given by \(\alpha _1 \gamma p_{12}\) and \(\alpha _2 \gamma p_{21}\), respectively. Since the total rate of inter-group interactions should be the same, we have \(p_{12}= p_{21} \frac{\alpha _2}{\alpha _1}\). This gives us the relationship between the probabilities of inter-group interactions in both groups.

Fig. 1
figure 1

Spatial interactions between two communities

Full size image

In the following, we present different ESS characterizations that differ in the stability level.

2.1 Strong ESS

A strong ESS is a strategy that, when adopted by the entire population, cannot be invaded by a sufficiently small group composed from all communities and using an alternative strategy. The incumbent players following the strong ESS will get a strictly higher expected payoff when playing against the population composed of incumbents and mutants, than the mutants will get. The following definition can be stated:

Definition 1

A strategy \(\mathbf{s}^*\) is a strong ESS, if for all \(\mathbf{s}\not =\mathbf{s}^*\), there exists an \(\epsilon (\mathbf{s})>0\) such that for all \(i=1,\ldots ,N\) and \(\epsilon \le \epsilon (\mathbf{s})\),

$$\begin{aligned} \bar{U}_i(s_i,\mathbf{\epsilon }{} \mathbf{s}+(1-\epsilon ) \mathbf{s}^*,p) < \bar{U}_i(s_i^*,\epsilon \mathbf{s}+(1-\epsilon ) \mathbf{s}^*,p). \end{aligned}$$
(3)

This strong ESS must in fact have a uniform invasion barrier [42] or threshold where any proportion of invaders using an alternative strategy is repelled. An alternative definition can be established as follows:

Definition 2

A strategy \(\mathbf{s}^*\) is a strong ESS if it meets two conditions for all i and for all \(\mathbf{s} \not = \mathbf{s}^*\),

$$\begin{aligned}&\circ \;\bar{U}_i(s_i, \mathbf{s}^*,p) \le \bar{U}_i(s_i^* , \mathbf{s}^*,p), \end{aligned}$$
(4)
$$\begin{aligned}&\circ \; \text{ if } \bar{U}_i(s_i,\mathbf{s}^*,p)=\bar{U}_i(s_i^*,\mathbf{s}^*,p),\text{ then } \bar{U}_i(s_i,\mathbf{s},p) < \bar{U}_i(s_i^*,\mathbf{s},p) {{ \text{ where } \mathbf{s}\;\text{ is } \text{ the }}}\nonumber \\&{{ \text{ vector } \text{ composed, } \text{ for } \text{ each } \text{ community, } \text{ of } \text{ the } \text{ strict } \text{ equilibrium } \text{ if } \text{ exists } }}\nonumber \\&{{ \text{ or } \text{ of } \text{ the } \text{ alternative } \text{ best } \text{ reply } \text{ otherwise. } }} \end{aligned}$$
(5)

Proposition 1

The Definitions 1 and 2 are equivalent.

Proof

See Appendix “Proof of Proposition 1”. \(\square \)

A strong ESS yields a higher expected payoff than any alternative strategy when played against itself [condition (4)]. If there is a strategy that yields the same payoff as the strong ESS when played against the ESS, then this strategy will yield a strictly lower expected payoff when played against itself than the ESS, and cannot spread in the population [condition (5)].

2.2 Weak ESS

In this subsection, we assume that mutants arise in one community and we introduce an alternative ESS version with a weaker stability condition. A weak ESS is a strategy that, when adopted by the entire population, each community resists invasion by a sufficiently small group of mutants using an alternative strategy in that community. The definition of the weak ESS is given by:

Definition 3

A strategy \(\mathbf{s}^*\) is a weak ESS if for all \(\mathbf{s} \not = \mathbf{s}^*\) and for all \(i =1,\ldots ,N\), there exists \(\epsilon _i(\mathbf{s})>0\) such that for all \(\epsilon _i \le \epsilon _i(\mathbf{s})\),

$$\begin{aligned} \bar{U}_i(s_i,(\epsilon _is_i+(1-\epsilon _i)s_i^*, \mathbf{s}^*_{-i}),p)<\bar{U}_i(s_i^*, (\epsilon _is_i+(1-\epsilon _i)s_i^*, \mathbf{s}^*_{-i}),p) , \end{aligned}$$
(6)

where \((\epsilon _is_i+(1-\epsilon _i)s_i^*, \mathbf{s}^*_{-i})\) is the profile of the population where the ith community is composed of the fraction \(\epsilon _i\) of mutants using an alternative strategy \(s_i\) and the fraction \(1-\epsilon _i\) of incumbent players using \(s_i^*\), and the remaining of the population follows the ESS \(\mathbf{s}^*_{-i}\).

An equivalent definition of the weak ESS can be stated as follows:

Definition 4

A strategy \(\mathbf{s}^*\) is a weak ESS if, for all i and for all \(\mathbf{s} \not = \mathbf{s}^*\),

$$\begin{aligned}&{} \circ \, \bar{U}_i(s_i, \mathbf{s}^*,p) \le \bar{U}_i(s_i^*, \mathbf{s}^*,p), \end{aligned}$$
(7)
$$\begin{aligned}&{} \circ \, {\text{ if } } \;\bar{U}_i(s_i, \mathbf{s}^*,p)=\bar{U}_i(s_i^*, \mathbf{s}^*,p), {\text{ then }}\; \bar{U}_i(s_i,(s_i,\mathbf{s}^*_{-i}),p)<\bar{U}_i(s_i^*,(s_i,\mathbf{s}^*_{-i}),p), \;\; \end{aligned}$$
(8)

where \(\bar{U}_i(s_i,\mathbf{s}^*,p)\) is the expected payoff of a mutant in community i using \(s_i\), and \(\bar{U}_i(s_i^*,\mathbf{s}^*,p)\) is the expected payoff of an incumbent player in community i using \(s_i^*\) when the profile of the population is \(\mathbf{s}^*\).

Proposition 2

The Definitions 3 and 4 are equivalent.

Proof

See Appendix “Proof of Proposition 2”. \(\square \)

This ESS definition is different from that of Cressman, referred to as Cressman ESS in the literature [12, 29], which considers invasion of the communities by a fraction of mutants from all communities. For a state to be a Cressman ESS, it is enough that one community resist invasion from a mutant strategy. In our definition, we consider invasion of a single community by a small local group of mutants. In Sect. 3, we introduce a particular example with two communities and we show that a weak ESS cannot be a Cressman ESS in this case.

2.3 Intermediate ESS

In the intermediate ESS version [37, 42], the focus is the total payoff of the whole population instead of the fitness of each community. An intermediate ESS is a strategy that, when adopted by the entire population, for any small group using a mutant strategy, the total expected payoff of the incumbent strategies in all the communities is strictly higher than that of the mutant strategy. The formal definition of an intermediate ESS is given by:

Definition 5

A strategy \(\mathbf{s}^*\) is an intermediate ESS if for all \(\mathbf{s} \not = \mathbf{s}^*\), there exists an \(\epsilon (\mathbf{s})>0\) such that for all \(\epsilon \le \epsilon (\mathbf{s})\),

$$\begin{aligned} \displaystyle \sum _{i=1}^{N} {\bar{U}_i\left( s_i,\epsilon \mathbf{s}+(1-\epsilon ) \mathbf{s}^*,p\right) } < \sum _{i=1}^{N} {\bar{U}_i\left( s_i^*,\epsilon \mathbf{s}+(1-\epsilon ) \mathbf{s}^*,p\right) }. \end{aligned}$$
(9)

Equivalently, we have the following definition:

Definition 6

A strategy \(\mathbf{s}^*\) is an intermediate ESS if for all \(\mathbf{s} \not = \mathbf{s}^*\),

$$\begin{aligned}&{} \circ \, \displaystyle \sum _{i=1}^{N}{\bar{U}_i\left( s_i,\mathbf{s}^*,p\right) } \le \sum _{i=1}^{N} {\bar{U}_i\left( s_i^*,\mathbf{s}^*,p\right) }, \end{aligned}$$
(10)
$$\begin{aligned}&{} \circ \, {\text{ if }} \displaystyle \sum _{i=1}^{N}{\bar{U}_i\left( s_i,\mathbf{s}^*,p\right) } = \sum _{i=1}^{N}{\bar{U}_i\left( s_i^*,\mathbf{s}^*,p\right) },\quad {\text{ then }} \displaystyle \sum _{i=1}^{N} {\bar{U}_i\left( s_i,\mathbf{s},p\right) } {<} \displaystyle \sum _{i=1}^{N}{\bar{U}_i\left( s_i^*,\mathbf{s},p\right) }.\; \end{aligned}$$
(11)

The condition (10) defines the best reply requirement according to which a mutant strategy cannot yield a better total payoff than the ESS. When the comparison in this condition is an equality, i.e., in case of an alternative best reply, the condition (11) guarantees that the population profile does not shift away from the ESS. It means that all the population have a positive incentive to remain at the ESS when there is a mutant strategy.

Proposition 3

The Definitions 5 and 6 are equivalent.

Proof

The proof follows by carrying out exactly the same procedure as done in Proposition 2. \(\square \)

2.4 Relationship Between the ESS Concepts

In this section, we discuss the relationship between different concepts of ESS introduced earlier. We explain how these ESS concepts are overlapped one into another. Note that every ESS from strong to weak stability is a Nash equilibrium. However, a strict Nash equilibrium must be a strong ESS, and therefore, the strict Nash equilibrium is an intermediate and weak ESS. We note that the second condition of the ESS (stability) comes into play only in the case of alternative best replies. Hence, with strict Nash equilibrium, there is no alternative to play another strategy that get the same payoff.

Now, let us discuss the relationship between different ESSs based on their stabilities. The definition of the strong ESS makes it clear that strong ESS is an intermediate and also a weak ESS. Indeed, if we suppose there is a small fraction of mutants from all the communities using an alternative strategy, the strong ESS, when adopted by all the population, would resist this invasion because incumbent players would get a strictly higher expected payoff than mutants. The total expected payoff of the strong ESS in all the communities would also be strictly higher than that of the mutant strategy, and therefore, the strong ESS is an intermediate ESS.

A similar argument explains why an intermediate ESS is also a weak ESS. In fact, if we suppose there is a small fraction of mutants in a single community, an intermediate ESS would resist this invasion by definition and also a weak ESS; therefore, an intermediate ESS is a weak ESS. In the next section, we will show through the study of two communities that (i) an intermediate ESS is not always a strong ESS and (ii) a weak ESS is not always an intermediate ESS. We then have the following relationships between the different concepts of ESS considering interacting communities:

$$\begin{aligned} \text{ Strong } \text{ ESS } \quad \Rightarrow \quad \text{ Intermediate } \text{ ESS } \quad \Rightarrow \quad \text{ Weak } \text{ ESS. } \end{aligned}$$

We note that all these definitions are obviously identical when there is a single community.

3 Two-Community Two-Strategy Model

For the sake of clarity, we focus only on the case where there are two communities that interact in a nonuniform manner. All results obtained with two communities are still valid for more than two communities.

We consider two communities in which each individual from community \(i=1,2\) involved in an interaction may interact with an individual from the same community with probability \(p_i\) or with an individual from the other community with probability \(1-p_i\). In addition, we consider that each community i has two strategies \(\{G_i,H_i\}\). Since there are two possible strategies in each community, the population profile can be defined by \(\mathbf{{s}}=(s_1,s_2)\) where \(s_i\) is the frequency of strategy \(G_i\) in community i (so \(1-s_i\) is the frequency of strategy \(H_i\)). In fact, in the two-strategy setting, we have \(s_{12}=1-s_{11}\) and \(s_{22}=1-s_{21}\) and the population state can then be completely defined by the vector \(\mathbf s =(s_1,s_2)\) where \(s_1\) and \(s_2\) are scalars. The pairwise interactions inside the communities are described by the matrices A and D:

The interactions between individuals from different communities are described by the following matrices:

Using Eqs. (1) and (2), we can derive the expected payoffs of players from either community.

Table 1 Parameters of the model
Full size table

In addition, we define in Table 1 the parameters which will be used to analyze the model. The parameters \(L_1\), \(L_2\), \(L_{12}\) and \(L_{21}\) depend on the payoffs. The parameters \(K_1\), \(K_2\), \({\varDelta }\) and \({\varDelta }_1\) depend on the payoffs and the interaction probabilities.

3.1 Fully Mixed Nash Equilibrium and ESS

In this subsection, we characterize the existence of fully mixed ESSs under different levels of stability. At the fully mixed ESS, all strategies in both communities coexist, that is, \(0<s_i^*<1\) for \(i=1,2\). The following theorem summarizes results on the existence of fully mixed ESSs.

Theorem 1

Let \(\mathbf{{s}^*}=(s_1^*,s_2^*)\) with

$$\begin{aligned} s_1^*=\frac{(1-p_1)L_{12}K_2-p_2L_2K_1}{{\varDelta }} \quad and \quad s_2^*=\frac{(1-p_2)L_{21}K_1-p_1L_1K_2}{{\varDelta }}. \end{aligned}$$

We have the following results on \(\mathbf{s}^*\):

  • \(\mathbf{{s}^*}\) is a unique fully mixed Nash equilibrium, i.e., \(0<s^*_1<1\) and \(0<s^*_2<1\), if

    • \(0<{\varDelta }\), \( 0<(1-p_1)L_{12}K_2-p_2L_2K_1\), \((1-p_1)L_{12}K_2-p_2L_2K_1<{\varDelta }\), \(0<(1-p_2)L_{21}K_1-p_1L_1K_2\), and \((1-p_2)L_{21}K_1-p_1L_1K_2<{\varDelta }\), or

    • \({\varDelta }<0\) , \((1-p_1)L_{12}K_2-p_2L_2K_1<0\), \({\varDelta }<(1-p_1)L_{12}K_2-p_2L_2K_1\), \(0<(1-p_2)L_{21}K_1-p_1L_1K_2<0\), and \({\varDelta }<(1-p_2)L_{21}K_1-p_1L_1K_2\).

  • \(\mathbf{s}^*\) cannot be a strong ESS.

  • \(\mathbf{{s}^*}\) is a weak ESS if \(L_1<0\) and \(L_2<0\).

  • \(\mathbf{{s}^*}\) is an intermediate ESS if \(L_1<0\), \(L_2<0\) and \({\varDelta }_1>0\).

Proof

See Appendix “Proof of Theorem 1”. \(\square \)

Theorem 1 establishes that any fully mixed strong ESS does not exist. Indeed, the stability condition (5) in Definition 2 cannot be satisfied for a fully mixed equilibrium. In contrast, the fully mixed equilibrium can be an intermediate or a weak ESS under some conditions on the payoffs and the interaction probabilities. We also note that for a weak ESS to be an intermediate ESS, it is required that the condition \({\varDelta }_1>0\) be satisfied. This condition cannot be always satisfied. As an example, we consider the following payoffs:

$$\begin{aligned} A=\left( \begin{array}{cc} -1 &{} 8 \\ 0 &{} 4 \; \end{array} \right) ,\quad D=\left( \begin{array} {cc} -1 &{} 8\\ 0 &{} 4 \end{array} \right) ,\quad B=\left( \begin{array} {cc} \frac{1}{2}&{} 8 \\ 0 &{} \frac{16}{3} \end{array} \right) ,\quad C=\left( \begin{array} {cc} -3 &{} 8\\ 0 &{} \frac{8}{3} \end{array} \right) . \end{aligned}$$

When \(p_1=0.9\) and \(p_2=0.35\), there exists a unique fully mixed equilibrium given by \(s_1^*=0.85\) and \(s_2^*=0.14\). The conditions \(L_1<0\) and \(L_2<0\) are satisfied; therefore, \(\mathbf{s}^*=(s_1^*,s_2^*)\) is a weak ESS. However, \({\varDelta }_1\) is strictly negative and consequently \(\mathbf{s}^*\) is not an intermediate ESS. When \(p_1=0.75\) and \(p_2=0.6\), then for the same values of payoffs we have \(\mathbf{s}^*=(0.9,0.51)\) and \({\varDelta }_1>0\). Therefore, \(\mathbf{s}^*\) is a weak and intermediate ESS. In addition, \(\mathbf{s}^*\) cannot be a Cressman ESS because neither community would resist invasion from a small fraction of mutants composed of all the communities.

When \(p_1=p_2=1\), the two communities are fully independent, and \(s^*_1=-\frac{b_1-d_1}{L_1}\), \(s^*_2=-\frac{b_2-d_2}{L_2}\) and \({\varDelta }_1=4L_1L_2\). We find the classical case of a single community: If \(L_1<0\) and \(L_2<0\), then \(\mathbf{s}^*=(s_1^*,s_2^*)\) is an evolutionarily stable strategy. When \(p_1=p_2=0\), the evolutionary game is fully asymmetric and \(s^*_1=-\frac{b_{21}-d_{21}}{L_{21}}\), \(s^*_2=-\frac{b_{12}-d_{12}}{L_{12}}\) and \({\varDelta }_1=-(L_{12}+L_{21})^2\) which is strictly negative. Therefore, \(\mathbf{s}^*=(s_1^*,s_2^*)\) is neither an intermediate nor a weak ESS. In [18, 32], the authors show that no mixed evolutionarily stable strategy can exist in asymmetric games. In [18], the authors introduced the notion of Nash–Pareto pairs in asymmetric games, which is an equilibrium characterized by the concept of Pareto optimality: It is not possible for players from both groups to simultaneously profit from a deviation from the equilibrium. The mixed equilibrium \(\mathbf{s}^*\) is a Nash–Pareto pair if \(L_{12}L_{21}<0\) [18].

We note that an ESS \(\mathbf{s}^*=(s_1,s_2)\) may also be completely pure if \(s_i \in \{0 ,1\}\) for \(i=1,2\), or partially mixed when \(s_1^*=0\) or \(s_1^*=1\) and \(0<s_{2}^*<1\) (or the inverse). In Appendices “Completely Pure ESSs” and “Partially mixed ESSs”, we study the conditions of existence of completely pure and partially mixed ESS, respectively.

Having studied the existence of the ESS with different levels of stability in the two-community model, we are now interested in examining the relation of this static notion with the replicator dynamics. Indeed, the concept of evolutionarily stable strategy is deeply connected to the replicator dynamics. In the next section, we study the stability of the ESSs in the replicator dynamics.

4 Replicator Dynamics in Two-Community Two-Strategy Model

We introduce the replicator dynamics which describe the evolution of the various strategies in the communities. Replicator dynamics is one of the most studied dynamics in evolutionary game theory [18, 38, 42]. In this dynamics, the proportion of a given strategy in the population grows at a rate equal to the difference between the expected payoff of that strategy and the average payoff in the population [19, 42]. Thus, successful strategies increase in frequency in the population.

4.1 Replicator Dynamics Without delay

The replicator dynamics equation writes, for \(i=1,2\):

$$\begin{aligned} \dot{s_i}(t)= & {} s_i(t)\big [U_i(G_i,\mathbf{s}(t),p)-\bar{U_i}(s_i(t),\mathbf{s}(t),p)\big ],\\= & {} s_i(t)(1-s_i(t))\big [U_i(G_i,\mathbf{s}(t),p)-U_i(H_i,\mathbf{s}(t),p)], \end{aligned}$$

with \(\mathbf{s}(t)=(s_1(t),s_2(t))\), which yields the following pair of nonlinear ordinary differential equations:

$$\begin{aligned} \dot{s}_1(t)= & {} s_1(t)(1-s_1(t))\big [p_1s_1(t)L_1+(1-p_1)s_2(t)L_{12}+K_1\big ],\nonumber \\ \dot{s}_2(t)= & {} s_2(t)(1-s_2(t))\big [p_2s_2(t)L_2+(1-p_2)s_1(t)L_{21}+K_2\big ]. \end{aligned}$$
(12)

There are nine stationary points at which both \(\dot{s}_1=0\) and \(\dot{s}_2=0\), which are: (0, 0), (1, 1), (0, 1), (1, 0), \((0,-\frac{K_2}{p_2L_2})\), \((- \frac{K_1}{p_1L_1},0)\), \((1,-\frac{(1-p_2)L_{21}+K_2}{p_2L_2})\), \(( -\frac{(1-p_1)L_{12}+K_1}{p_1L_1} , 1 )\) and the interior point \(\mathbf{s}^*\) defined in Theorem 1. Recall that the strict Nash equilibrium is locally asymptotically stable in the replicator dynamics and the stationary points are a Nash equilibria. The dynamic property of \(\mathbf{s}^*\) is brought out in the next theorem.

Theorem 2

The interior stationary point \(\mathbf{s}^*\) is asymptotically stable in the replicator dynamics if \(L_1<0\), \(L_2<0\), and \({\varDelta }>0\).

Proof

See Appendix “Proof of Theorem 2”. \(\square \)

The next corollary about the asymptotic stability of the fully mixed intermediate ESS follows.

Corollary 1

The fully mixed intermediate ESS is asymptotically stable in the replicator dynamics.

Proof

See Appendix “Proof of Corollary 1”. \(\square \)

This result confirms that the ESS with the intermediate level of stability is asymptotically stable in the replicator dynamics. In contrast, for the weak ESS to be asymptotically stable, it is required that the condition \({\varDelta }>0\), which depends on the payoff matrices and the interacting probabilities be satisfied.

Remark 1

We consider the numerical example in Sect. 3.1. For \(p_1=0.9\) and \(p_2=0.35\), there exists a unique fully mixed equilibrium given by \(\mathbf{{s}}^*=(0.85,0.14)\) and it is not an intermediate ESS because we have \({\varDelta }_1<0\) (Theorem 1). However, \(\mathbf{{s}}^*\) is asymptotically stable in the replicator dynamics (conditions in Theorem 2 are satisfied). Therefore, an asymptotically stable point in the replicator dynamics is not necessarily an intermediate ESS.

In the next theorem, we study the asymptotic stability of strong ESSs.

Theorem 3

  • The partially mixed strong ESSs are asymptotically stable in the replicator dynamics.

  • The completely pure strong ESSs are asymptotically stable in the replicator dynamics.

Proof

See Appendix “Proof of Theorem 3”. \(\square \)

This theorem establishes that all strong ESSs are asymptotically stable in the replicator dynamics. In the next section, we study the stability of the fully mixed intermediate ESS in the replicator dynamics with delays.

4.2 Replicator Dynamics with Strategic Delay

In this section, we examine the impact of time delays of strategies on the dynamics. An action taken today will have some effect after some time [6, 40]. We assume the strategies take a delay \(\tau _{st}\). The replicator dynamics for the first community is then given by:

$$\begin{aligned} {} \dot{s}_1(t)= s_1(t)(1-s_1(t))\big [U_1(G_1,\mathbf{s}(t-\tau _{st}),p)-U_1(H_1,\mathbf{s}(t-\tau _{st}),p)\big ]. \end{aligned}$$

Then we get:

$$\begin{aligned} {} \dot{s}_1(t)=s_1(t)(1-s_1(t)) \big [p_1L_1 s_1(t-\tau _{st})+(1-p_1)L_{12} s_2(t-\tau _{st})+K_1 \big ]. \end{aligned}$$

Doing the same with the second group, we get:

$$\begin{aligned} {} \dot{s}_2(t)=s_2(t) (1-s_2(t)) \big [p_2L_2s_2(t-\tau _{st})+(1-p_2)L_{21} s_1(t-\tau _{st})+ K_2 \big ]. \end{aligned}$$

We introduce a small perturbation around \(\mathbf{{s}^*}\) defined by \(x_1(t)=s_1(t)-s_1^*\) and \(x_2(t)=s_2(t)-s_2^*\). We then make a linearization of the two above equations around the interior equilibrium point \(\mathbf{s}^*=(s_1^*,s_2^*)\), and we study the linearized system. We get the following system:

$$\begin{aligned} {} \dot{x}_1(t)= & {} \gamma _1\big (p_1L_1 x_1(t-\tau _{st})+(1-p_1)L_{12} x_2(t -\tau _{st})\big ),\nonumber \\ {} \dot{x}_2(t)= & {} \gamma _2\big (p_2L_2 x_2(t-\tau _{st})+(1-p_2)L_{21} x_1(t-\tau _{st})\big ), \end{aligned}$$

with \(\gamma _1=s_1^*(1-s_1^*) \) and \(\gamma _{2}=s_2^*(1-s_2^*) \). Taking the Laplace transform of the system above, we obtain the following characteristic equation:

$$\begin{aligned} {} \lambda ^2-\lambda \big [p_1\gamma _1 L_1+p_2\gamma _{2} L_2 \big ] e^{-\lambda \tau _{st}} + \gamma _1\gamma _{2}\big [ p_1p_2 L_1 L_2-(1-p_1)(1-p_2)L_{12}L_{21} \big ]e^{-2\lambda \tau _{st} }=0.\;\;\;\;\; \end{aligned}$$
(13)

The zero solution is asymptotically stable if all solutions of (13) have negative real parts [4]. Equation (13) is typical for a linear system of two equations of the form \(\dot{x}(t)=Ax(t-\tau _{st})\) which was studied by the authors in [10, 16]. Based on their results, we establish the following theorem on the asymptotic stability of the intermediate ESS in the presence of symmetric strategic delays.

Theorem 4

The fully mixed intermediate ESS is asymptotically stable in the delayed replicator dynamics if \(\tau _{st} < \bar{\tau }_{st}=\text{ min }(\frac{\pi }{2|\lambda _+|},\frac{\pi }{2|\lambda _-|})\), with \(\lambda _\pm =\frac{p_1\gamma _1L_1+p_2\gamma _{2}L_2\pm \sqrt{D}}{2},\, \text{ and } \, \, D=\big [p_1\gamma _1L_1+p_2\gamma _{2}L_2\big ]^2-4\gamma _1\gamma _{2}\big [ p_1p_2 L_1 L_2-(1-p_1)(1-p_2)L_{12}L_{21} \big ]\).

Proof

See Appendix “Proof of Theorem 4”. \(\square \)

Theorem 4 gives an upper bound on strategic delays for which the intermediate ESS remains asymptotically stable in the population. Beyond this delay bound, the stability is lost and persistent oscillations around the ESS occur.

4.3 Replicator Dynamics with Spatial Delay

In this section, we assume the delays are not associated with the strategy used by an individual, but rather with the opponent with which an individual interacts [5]. Spatial delays arise when two individuals from different communities get involved in an interaction and are denoted by \(\tau _{sp}\). The replicator dynamics with spatial delays is given by:

$$\begin{aligned}&\dot{s}_1(t)=s_1(t)(1{-}s_1(t))\big [U_1(G_1,(s_1(t),s_2(t{-}\tau _{sp})),p) - U_1(H_1,(s_1(t),s_2(t-\tau _{sp})),p)\big ], \nonumber \\&\dot{s}_2(t)=s_2(t)(1{-}s_2(t))\big [U_2(G_2,(s_1(t{-}\tau _{sp}),s_2(t)),p) - U_2(H_2,(s_1(t-\tau _{sp}),s_2(t)),p)\big ]. \end{aligned}$$

Following the same procedure as in the previous sections, we get the following characteristic equation:

$$\begin{aligned} \lambda ^2-(p_1\gamma _1L_1+p_2\gamma _{2}L_2)\lambda + \gamma _1 \gamma _{2} p_1p_2L_1L_2-\gamma _1 \gamma _2 (1-p_1)(1-p_2)L_{12}L_{21} e^{-2\lambda \tau _{sp}}=0. \end{aligned}$$

Or equivalently:

$$\begin{aligned} {} \lambda ^2+\alpha \lambda +\beta + \delta e^{-\lambda \tau }=0, \end{aligned}$$
(14)

where \(\tau =2\tau _{sp}\), \(\alpha =-(p_1\gamma _1L_1+p_2\gamma _{2}L_2)\), \(\beta =\gamma _1\gamma _{2}p_1p_2L_1L_2\), \(\delta =-\gamma _1\gamma _{2}(1-p_1)(1-p_2)L_{12}L_{21}\). Now, we summarize the stability property of the mixed ESS for the delayed replicator dynamics in the following theorem which is based on the results of the authors in [15] related to the location of the roots of the characteristic equation (14) .

Theorem 5

The fully mixed intermediate ESS is asymptotically stable in the replicator dynamics with spatial delays for any \(\tau _{sp} \ge 0\).

Proof

See Appendix “Proof of Theorem 5”. \(\square \)

Spatial delays do not affect the stability of the mixed ESS. Indeed, for any value of the delay \(\tau _{sp}\), the frequency of strategies in the population converges to the mixed intermediate ESS after some possible damped oscillations.

4.4 Replicator Dynamics with Spatial Strategic Delays

In this section, we study the stability of the replicator dynamics with both strategic and spatial delays. In particular, we aim to study whether the spatial delay has a stabilizing effect on the replicator dynamics with strategic delay. We define the delays as follows:

  • \(\tau _{st}\) is the strategic delay, that is, the delay associated with the strategies;

  • \(\tau _{sp}\) is the spatial delay associated with the inter-community interactions.

The expected payoffs of strategies \(G_1\) and \(H_1\) in community 1 then write:

$$\begin{aligned}&{} U_1(G_1,(s_1(t-\tau _{st}),s_2(t-\tau _{st}-\tau _{sp})),p)=p_1\big [s_1(t-\tau _{st})a_1+(1- s_1(t-\tau _{st}))\times b_1\big ] \\&{} \quad +(1-p_1)\big [s_2(t-{\tau }_{st}-\tau _{sp})a_{12}+(1-s_2(t-{\tau }_{st}-\tau _{sp}))b_{12}\big ]. \end{aligned}$$

and

$$\begin{aligned}&{} U_1(H_1,(s_1(t-\tau _{st}),s_2(t-{\tau }_{st}-\tau _{sp})),p)=p_1\big [s_1(t-\tau _{st})c_1+(1- s_1(t-\tau _{st}))\times d_1\big ] \\&{} \quad +(1-p_1)\big [s_2(t-{\tau }_{st}-\tau _{sp})c_{12}+(1-s_2(t-{\tau }_{st}-\tau _{sp}))d_{12}\big ]. \quad \end{aligned}$$

Hence, the equation governing the evolution of the proportion of players using strategy \(G_1\) in the first community is given by:

$$\begin{aligned} \dot{s}_1(t)=s_1(t)(1-s_1(t))\big [p_1L_1s_1(t-\tau _{st})+(1-p_1) L_{12} s_2(t-{\tau }_{st}-\tau _{sp})+K_1\big ]. \end{aligned}$$

Doing the same with the second community, we obtain:

$$\begin{aligned} \dot{s}_2(t)=s_2(t)(1-s_2(t))\big [p_2 L_2 s_2(t-\tau _{st})+(1-p_2)L_{21} s_1(t-{\tau }_{st}-\tau _{sp}) +K_2\big ]. \end{aligned}$$

Following the same procedure in the previous sections, we get the following characteristic equation with mixed delays:

$$\begin{aligned}&\lambda ^2-\lambda [p_1\gamma _1 L_1+p_2\gamma _{2}L_2]e^{-\tau _{st} \lambda }+p_1p_2 \gamma _1 \gamma _2 L_1 L_2 e^{-2 \tau _{st} \lambda }\nonumber \\&\quad -(1-p_1)(1-p_2)\gamma _1 \times \gamma _2 L_{12}L_{21} e^{-2 (\tau _{st}+\tau _{sp})\lambda }=0. \end{aligned}$$
(15)

When \(\tau _{sp}=0\), we find the characteristic equation (13) obtained when there is only a strategic delay. Equation (15) can be solved numerically.

Equation (15) can be simplified by making the assumption of small time delays. By substituting the exponential term with a Taylor series expansion and keeping only linear terms in \(\tau _{st}\) and \(\tau _{sp}\) in the above equation, we obtain the following second-order equation:

$$\begin{aligned} (1+A \tau _{st})\lambda ^2+ \lambda (-A-2B \tau _{st}+2C(\tau _{st}+\tau _{sp}))+B-C=0, \end{aligned}$$

where \(A=p_1\gamma _1L_1+p_2\gamma _2L_2\), \(B=p_1p_2\gamma _1\gamma _2L_1L_2\), and \(C=(1-p_1)(1-p_2)\gamma _1\gamma _2 L_{12}L_{21}\). We can establish the following proposition:

Proposition 4

If \(\tau _{st}<-\frac{1}{p_1\gamma _1L_1+p_2\gamma _2L_2}\) and \({\varDelta }\tau _{st}-C \tau _{sp}< -\frac{p_1\gamma _1L_1+p_2\gamma _2L_2}{2}\), then the fully mixed intermediate ESS is asymptotically stable.

Proof

The fully mixed intermediate ESS is asymptotically stable if all the roots of the characteristic equation have negative real parts. Since we have a second-order equation, the roots have negative real parts if their product is positive and their sum is negative, that is, if (i) \(\frac{B-C}{1+A\tau _{st}}=\frac{{\varDelta }}{1+A\tau _{st}}>0\) and (ii) \(\frac{A+2B \tau _{st}-2C(\tau _{st}+\tau _{sp})}{1+A\tau _{st}}<0\). By virtue of Corollary 1, we have \({\varDelta }>0\) and then condition (i) yields \(\tau _{st}<-\frac{1}{p_1\gamma _1L_1+p_2\gamma _2L_2}\) and condition (ii) yields \({\varDelta }\tau _{st}-C \tau _{sp}< -\frac{p_1\gamma _1L_1+p_2\gamma _2L_2}{2}\). \(\square \)

5 Application to Hawk–Dove Game

In the classical Hawk–Dove game [3, 35], two individuals compete for a scarce resource. A player may use a Hawk strategy (H) or a Dove strategy (D). The strategy H stands for an aggressive behavior that fights for the resource while the strategy D represents a peaceful behavior which never fights. The matrix that gives the outcome for such competition is given as follows:

where \(C>0\) and \(V>0\). V represents the value of the resource for which the players compete, and C represents the cost incurred by a hawk when fighting for the resource against a hawk. The coefficients of the payoff matrix can be interpreted as follows: If two doves meet, they share equally the resource and each one obtains as a payoff \(\frac{V}{2}\). If two hawks meet, they fight until one of them gets injured and the other takes the whole resource. When a hawk and a dove meet, the dove withdraws and the hawk takes the whole resource. If \(C<V\), then the strategy H is dominant and the entire population will adopt the aggressive behavior. If \(C>V\), there exists a mixed ESS given by \((\frac{V}{C},1-\frac{V}{C})\), at which both behaviors coexist.

We apply our model to the Hawk–Dove game played in a population composed of two communities of hawks and doves with different levels of aggressiveness and which interact in a nonuniform fashion. Let:

  • \(p_1\) (resp. \(p_2\)) be the probability that an individual from Community 1 (resp. 2), involved in an interaction, competes with an individual from the same community;

  • \(1-p_1\) (resp. \(1-p_2\)) be the probability that an individual from Community 1 (resp. 2) competes with an inter-community opponent.

Furthermore, the interactions inside the communities 1 and 2 are described by the matrices A and D:

The inter-community interactions are described by the following matrices:

We introduce the parameters \(C_{SW}\), \(C_{WS}\) and \(\alpha \) into the payoff matrices to incorporate the disparity in the levels of aggressiveness of the two communities. These parameters can be defined as follows:

  • C is the fighting cost incurred by a hawk when fighting against a hawk from the same community;

  • \(C_{SW}\) is the fighting cost incurred by a hawk from the more aggressive community when fighting against a hawk from the other community;

  • \(C_{WS}\) is the fighting cost incurred by a hawk from the less aggressive community when fighting against a hawk from the other community;

  • \(\alpha \) is the resource part that takes a dove from the more aggressive community when competing with a dove from the other community.

The parameters satisfy: \(0<C_{SW}<C<C_{WS}\) and \(0.5\le \alpha < 1\). When two hawks from different communities compete for a resource, they do not incur the same cost as when fighting against an intra-community hawk. Also, when two doves from different communities meet, they share the resource unevenly. In particular, with these parameters, the first community is more aggressive than the second community: Hawks in community 1 provoke more injuries than hawks in the other community, and doves in community 1 take more resource than those in community 2. When \(C_{SW}=C_{WS}\) and \(\alpha =0.5\), the two communities have the same degree of aggressiveness. We aim to illustrate with numerical examples (i) the effect of the interaction probabilities and the parameters of the game on the existence of ESSs and (ii) the impact of these parameters and delays on the convergence to the fully mixed intermediate ESS in the replicator dynamics.

5.1 ESSs in the Hawk–Dove Game

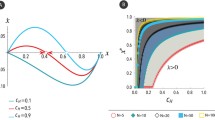
In Fig. 2, we plot the region of ESSs in function of the interaction probabilities \(p_1\) and \(p_2\) for the parameter values \(C=6\), \(C_{SW}=5\), \(C_{WS}=9\), \(\alpha =0.7\) and for two different values of the resource: \(V=2\) in the left subfigure and \(V=4\) in the right subfigure. We observe that in both subfigures, the fully mixed intermediate ESS exists for the higher values of \(p_1\) and \(p_2\), that is, when the intra-group interactions are more probable than inter-group interactions in both communities. This region allows all strategies in both communities to coexist. For the lower values of \(p_1\) and \(p_2\), we observe in both subfigures, the existence of completely pure strong ESS. The area between these two regions is characterized by the existence of partially mixed strong ESS, that is, an ESS which is pure in one community and mixed in the other. We also note the existence of fully mixed weak ESS in a small region in both figures.

Furthermore, we plot in Fig. 3 the region of ESSs in function of \(p_1\) and \(\alpha \) for two values of \(p_2\): \(p_2=0.2\) in the left subfigure and \(p_2=0.6\) in the right subfigure. When \(p_2=0.2\), we note that any fully mixed intermediate ESS does not exist. We observe that fully mixed weak ESSs exist for a small range of higher values of \(p_1\) and \(\alpha \). The completely pure and partially mixed strong ESS exist for a large range of values of \(p_1\) and \(\alpha \). In the right subfigure, when \(p_2=0.6\), we note the appearance of fully mixed intermediate ESSs for the higher values of \(p_1\).

Fig. 2
figure 2

Regions of ESSs in the interaction probabilities plane \((p_1, \, p_2)\) for the parameter values \(C=6\), \(C_{SW}=5\), \(C_{WS}=9\), \(\alpha =0.7\). The plus signs represent fully mixed intermediate ESS, the squares represent fully mixed weak ESSs, the circles represent partially mixed strong ESS, and the diamonds represent completely pure strong ESS

Full size image
Fig. 3
figure 3

Regions of ESSs in the plane \((p_1,\,\alpha )\) for the parameter values \(C=6\), \(C_{SW}=5\), \(C_{WS}=9\), and \(V=4\). The plus signs represent fully mixed intermediate ESS, the squares represent fully mixed weak ESSs, the circles represent partially mixed strong ESS, and the diamonds represent completely pure strong ESS

Full size image

5.2 Replicator Dynamics in the Hawk–Dove Game

In this subsection, we study the effects of delays and the game parameters on the convergence of the replicator dynamics to the fully mixed intermediate ESS. For the parameter values \(C=6\), \(C_{SW}=5\), \(C_{WS}=9\), \(\alpha =0.7\), \(V=4\), \(p_1=0.7\), \(p_2=0.6\), we conclude from Fig. 2b that there exists a fully mixed intermediate ESS which is given by \(\mathbf{{s}}^*=(0.73,0.42)\). Furthermore, \(\mathbf{{s}}^*\) is asymptotically stable in the replicator dynamics (Corollary 1). We plot in Fig. 4, the evolution of the proportion of hawks in both communities over time according to the replicator dynamics with strategic delays where the initial (arbitrary) population profile is given by (0.6, 0.2). Each strategy has a delay of \(\tau _{st}\). We observe in the left subfigure the convergence to the ESS for \(\tau _{st}=1.6\) time units after some damped oscillations, whereas we observe permanent oscillations around the ESS in the right subfigure for \(\tau _{st}=2.5\) time units. From Theorem 4, the maximum value of the strategic delay for which the fully mixed intermediate ESS is asymptotically stable is \(\bar{\tau }_{st}=2.4\) time units. Therefore, the asymptotic stability of the ESS is lost for \(\tau _{st}=2.5\) time units.

Furthermore, we study the effect of spatial delays on the convergence to the ESS in the replicator dynamics. Spatial delays appear in inter-community interactions only. In Fig. 5a, we observe a convergence to the intermediate ESS. Indeed, from Theorem 5, the replicator dynamics converges to the fully mixed intermediate ESS for any value of \(\tau _{sp}\). When both delays exist, spatial delay (\(\tau _{sp}=1.4\) time units) and strategic delay (\(\tau _{st}=2.5\)), we observe in Fig. 5b persistent oscillations (Fig. 5).

Fig. 4
figure 4

Replicator dynamics with strategic delays \(\bar{\tau }_{st}=2.4\) time units, \(C=6\), \(C_{SW}=5\), \(C_{WS}=9\), \(\alpha =0.7\), \(V=4\), \(p_1=0.7\), \(p_2=0.6\)

Full size image
Fig. 5
figure 5

Replicator dynamics with purely spatial delays (left) and spatial strategic delays (right). \(C=6\), \(C_{SW}=5\), \(C_{WS}=9\), \(\alpha =0.7\), \(V=4\), \(p_1=0.7\), \(p_2=0.6\)

Full size image

In addition, we study the effect of the resource value on the convergence to the ESS. For a fixed strategic delay value of \(\tau _{st}=2.2\) time units, we observe in Fig. 6a oscillations around the fully mixed intermediate ESS when \(V=3\). For the same value of the strategic delay and when \(V=4\), we observe the convergence to the ESS (Fig. 6b). We note that increasing the resource value had a stabilizing effect. Furthermore, we illustrate in Fig. 7 the effect of the intra-community fighting cost C on the convergence to the fully mixed ESS in the replicator dynamics. In the left subfigure, for \(C=6\), we observe the convergence to the mixed ESS whereas in the right subfigure, for \(C=8\), we note persistent oscillations around the ESS and the loss of stability. Therefore, increasing the intra-community fighting cost had a destabilizing effect.

Fig. 6
figure 6

Effect of the resource value on the convergence to the ESS for the same strategic delay value \(\tau _{st}=2.2\) time units. \(C=6\), \(C_{SW}=5\), \(C_{WS}=9\), \(\alpha =0.7\), \(p_1=0.7\), \(p_2=0.6\)

Full size image
Fig. 7
figure 7

Effect of the intra-community fighting cost on the convergence to the ESS for the same strategic delay value \(\tau _{st}=2.2\) time units. \(V=4\), \(C_{SW}=5\), \(C_{WS}=10\), \(\alpha =0.7\), \(p_1=0.7\), \(p_2=0.6\)

Full size image

6 Conclusion

In this paper, we developed a novel mathematical tool to model the evolution of a population composed of several communities that interact in a nonuniform manner. We defined three ESSs with different levels of stability against mutations: strong, weak and intermediate ESS. Through the analysis of two-community two-strategy model, we show that any fully mixed strong ESS cannot exist; fully mixed intermediate and weak ESS may exist under some conditions on the payoffs and the interaction probabilities. In addition, we studied the replicator dynamics in its classic form and with delays. We defined strategic delays, spatial delays and spatial strategic delays. For the Hawk–Dove game played between two communities with an asymmetric level of aggressiveness, we characterized the regions of ESS in function of the interaction probabilities and the game parameters. We illustrated through numerical examples how the value of delays and the game parameters affect the convergence to the ESS in the replicator dynamics.