Entropy generation and temperature-dependent viscosity in the study of SWCNT–MWCNT hybrid nanofluid

Abstract

Nanofluids are of excellent significance to scientists, because, due to their elevated heat transfer rates, they have important industrial uses. A new class of nanofluid, “hybrid nanofluid,” has recently been used to further improve the rate of heat transfer. The current phenomenon particularly concerns the analysis of the flow and heat transfer of SWCNT–MWCNT/water hybrid nanofluid with activation energy through a moving wedge. The Darcy–Forchheimer relationship specifies the nature of the flow in the porous medium. Further the impact of variable viscosity, velocity and thermal slip, thermal radiation and heat generation are also discussed in detail. The second law of thermodynamics is utilized to measure the irreversibility factor. The numerical technique bvp4c is integrated to solve the highly nonlinear differential equation. For axial velocity, temperature profile, and entropy generation, a comparison was made between nanofluid and hybrid nanofluid. The variable viscosity parameter enhances the axial velocity and diminishes the temperature distribution for both nanofluid and hybrid nanofluid. Furthermore, the solid volume fraction diminishes the velocity and concentration profile while enhancing the temperature distribution.

Introduction

Nanofluid has many applications in several crucial areas such as transportation, microfluidics, microelectronics, medical, manufacturing, and power saving; all these elements reduce process time and increase heat ratings as well as extend the life span of machinery and so on. Nanofluids are used as coolants in the automobile and nuclear reactor thermal exchange system. In essence, the suspension of nanoparticles into the base fluid is nanofluid. The size of nanoparticles is commonly 1–100 nm, but it can contrast slightly as demonstrated by their size and shape. Choi and Eastman (1995) postulate the idea of nanofluid to upgrade the properties of certain important fluids; for example, ethylene glycol, water, oil, etc. A homogeneous mixture of nanometer-sized solid metal particles and a low thermal conductivity base fluid results in a nanofluid with improved thermal conductivity. In numerous medium, the experimental and theoretical literature about the synthetization, properties, and conduct of nanofluids are noticed in (Buongiorno 2006; Nadeem et al. 2018; Ahmed et al. 2019; Ellahi et al. 2016).

Mono-nanofluids have a better thermal network and strong rheological properties, but they do not have all the desirable characteristics required for a specific application. Several real-time applications require trade-off among various nanofluid properties/characteristics; for example, metal oxides such as ${\text{Al}}_{2} {\text{O}}_{3}$ represent useful chemical inertia and consistency, which, however, show lower thermal conductivity, while metallic nanoparticles such as copper, aluminum, and silver have higher thermal conductivity, but are chemically reactive and unstable. Through hybridizing these metallic nanoparticles with metal oxides, the resulting fluid called hybrid nanofluid has improved thermophysical properties and rheological behavior, together with enhanced heat transfer properties. Hybrid nanofluids are developed by adding two or more distinct nanoparticles to the base fluid that have a higher thermal conductivity comparable to mono-nanofluids due to the synergistic effect. The amounts of the volume fraction of nanoparticles can be varied to obtain the desired heat flow rate. Hybrid nanofluids have potential use in the fields of heat transport such as naval structures, microfluidics, defense, medical, acoustics, transportation, etc. There are plenty of theoretical and experimental data available that address hybrid nanofluid behavior in various flow frameworks. Through an experimental study, Zadkhast et al. (2017) develop a new comparison to estimate MWCNT–CuO/water hybrid nanofluid thermal conductivity. Nadeem et al. (2019) numerically investigate the feature of heat transfer in the existence of SWCNT–MWCNT/water hybrid nanofluid. Esfe et al. (2017) computed a hybrid nanofluid’s thermal conductivity namely SWCNT–MgO/EG and demonstrated the experimental values using artificial neural networks. Alarifi et al. (2019) experimentally examine the impact of temperature, shear rate, and solid concentration of nanoparticle on the rheological properties of TiO₂–MWCNT/oil hybrid nanofluid. It is seen that enhancing the solid concentration dynamic viscosity of nanofluid increases. Experimental investigation of the flow behavior of hybrid nanofluids has been done by Esfe et al. (2019), Amini et al. (2019) and Goodarzi et al. (2019).

It is known that during every thermal process, the entropy age estimates the amount of irreversibility. Cooling and heating are an important event in many industrial sectors and in the engineering process, particularly in energy and electronic devices. Therefore, to avoid any irreversibility losses that may influence system efficiency, it is essential to maximize entropy production. To control entropy optimization, Bejan (1979) and Bejan and Kestin (1983) first concluded an excellent number as the proportion between thermal irreversibility and total heat loss because of liquid frictional factors, that is called Bejan number (Be). Bhatti et al. (2019) analyzed the entropy age (or generation) on the interaction of nanoparticle over a stretching sheet saturated in porous medium. Successive linearization technique and Chebyshev spectral collocation scheme are employed to describe the numerical solution for Bejan number and entropy profile. Feroz et al. (2019) demonstrate the magnetohydrodynamics (MHD) nanofluid flow of CNTs along with two parallel rotating plates under the influence of ion-slip effect and Hall current. Shahsavar et al. (2019) numerically investigated the entropy generation characteristic of water–Fe₃O₄/CNT hybrid nanofluid flow inside a concentric horizontal annulus. Massive improvements in nanofluid thermophysical properties over the conventional fluids have led to the rapid evolution of utilizing ${\text{MWCNT}}/{\text{GNPs}}$ hybrid nanofluids in the field of heat transfer discussed by Hussien et al. (2019). Ellahi et al. (2018) scrutinized the influence of magnetohydrodynamics (MHD) heat transfer flow under the impact of slip past a moving flat plate with entropy generation. Lu et al. (2018) examined the entropy optimization and nonlinear thermal radiation in the flow of hybrid nanoliquid over a curved sheet. The finite-difference technique bvp4c function is used to solve the numerical solution. Recently, the application of entropy generation is found in Khan et al. (2019), Sheikholeslami et al. (2019), Zeeshan et al. (2019), and Javed et al. (2019).

It has been seen that a lot of thought is busy in literature with no-slip condition to flow. No-slip phenomenon emerges in many assembling progresses at the walls, pipe’s boundary, and curved channel. The liquids indicating boundary slip deserve deliberation in mechanical issues like internal cavities, transmission lines, and polishing of artificial heart valves. Because of the broad application of partial slip, analysts take the slip condition instead of the no-slip condition. The feature of mass and heat transfer in copper–water nanofluid with partial slip past a shrinking sheet is examined by Dzulkifli et al. (2019). He found that the Soret effect at the surface enhances the heat transfer and reduces the mass transfer. Ellahi et al. (2019) examined the peristaltic transport of Jeffrey fluid across the rectangular duct in the presence of partial slip. Alamri et al. (2019) studied the influence of second-order slip on plane Poiseuille nanofluid with Stefan blowing. The exact solution of Jeffery fluid incorporated in a porous medium through a rectangular duct with partial slip is discussed by Ellahi et al. (2019). Zaib et al. (2019) studied the aspect of micropolar nanofluid flow via a vertical Riga surface in the result of partial slip. Recently, more study about partial slip, nanofluid, and entropy generation are found in Sarafraz et al. (2020), Zeeshan et al. (2019), Riaz et al. (2020), Ahmad et al. (2020), Ellahi et al. (2019), Alamri et al. (2019), and Noreen et al. (2017).

Objective of this communication is to examine entropy generation in stagnation point SWCNT–MWCNT/water hybrid nanofluid flow due to moving wedge with heat generation and activation energy. To the best of our knowledge, no one study to investigate the entropy optimization for two phase fluid model along with variable viscosity, Darcy–Forchheimer, and thermal and velocity slip effect. Concluded suitable transformation nonlinear flow expression is changed to ordinary ones and solved by numerical technique bvp4c (Ahmad et al. 2019; Nadeem et al. 2019; Suleman et al. 2019). The property of immersed parameter on axial velocity, temperature distribution, concentration profile, entropy generation, and Bejan number are explored graphically.

Mathematical modeling

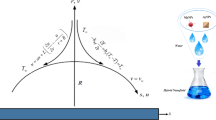
Figure 1 demonstrates the geometric configuration and the considered problem’s schematic physical model. In the present analysis, we assume the steady, incompressible two-dimensional SWCNT–MWCNT/water hybrid nanofluid flow in the presence of activation energy and thermal slip past a permeable wedge. We find a Cartesian coordinate scheme (x, y), where y and x are the coordinates measured normal and along to the permeable wedge. The velocity of the free stream (inviscid flow) is also thought to be $\hat{u}_{\infty } (x)$ and the velocity of the moving wedge is $\hat{u}_{\text{w}} (x)$. Liquid and ambient fluid temperature is $\hat{T}_{\text{w}}$ and $\hat{T}_{\infty }$, where $\hat{T}_{\text{w}} > \hat{T}_{\infty }$ is used for wedge heating (assisting flow) and $\hat{T}_{\text{w}} < \hat{T}_{\infty }$ is used for wedge cooling (opposite flow).

Fig. 1

Physical representation of flowchart

Considering the combination of SWCNT into MWCNT/water, hybrid nanofluid is acquired in the current research. First, MWCNT ($\phi_{1}$) nanoparticles are inserted in water to create a MWCNT/water nanofluid, and then, SWCNT nanoparticles of various fractions ($\phi_{2}$) are added to the nanofluid blend to obtain the homogeneous mixture of hybrid nanofluid SWCNT–MWCNT/water.

Imposing the approximation of the boundary layer and assuming that we have a system of equations:

$$ \frac{{\partial \hat{u}}}{\partial x} + \frac{{\partial \hat{v}}}{\partial y} = 0,\, $$

(1)

$$ \begin{aligned} & \hat{u}\frac{{\partial \hat{u}}}{\partial x} + \hat{v}\frac{{\partial \hat{u}}}{\partial y} - \hat{u}_{\infty } \frac{{{\text{d}}\hat{u}_{\infty } }}{{{\text{d}}x}} = \frac{1}{{\rho_{\text{hnf}} }}\frac{\partial }{\partial y}\left( {\mu_{\text{hnf}} (\hat{T})\,\frac{{\partial \hat{u}}}{\partial y}} \right) \\ &\quad- \frac{1}{{\rho_{\text{hnf}} }}\frac{{\mu_{\text{hnf}} (\hat{T})}}{{K^{**} }}(\hat{u} - \hat{u}_{\infty } ) - F^{**} (\hat{u}^{2} - \hat{u}^{2}_{\infty } ),\, \end{aligned} $$

(2)

$$ \begin{aligned} & \hat{u}\frac{{\partial \hat{T}}}{\partial x} + \hat{v}\frac{{\partial \hat{T}}}{\partial y} = \alpha_{\text{hnf}} \frac{{\partial^{2} \hat{T}}}{{\partial y^{2} }} + \frac{{\mu_{\text{hnf}} (\hat{T})}}{{(\rho C_{\text{p}} )_{\text{hnf}} }}\left( {\frac{{\partial \hat{u}}}{\partial y}} \right)^{2} \\ &\quad+ \frac{{16\sigma^{*} \hat{T}_{\infty }^{3} }}{{3k^{*} (\rho C_{\text{p}} )_{\text{hnf}} }}\frac{{\partial^{2} \hat{T}}}{{\partial y^{2} }} + \frac{Q(x)}{{(\rho C_{\text{p}} )_{\text{hnf}} }}(\hat{T} - \hat{T}_{\infty } ).\, \end{aligned} $$

(3)

$$ \hat{u}\frac{{\partial \hat{C}}}{\partial x} + \hat{v}\frac{{\partial \hat{C}}}{\partial y} = D_{\text{hnf}} \frac{{\partial^{2} \hat{C}}}{{\partial y^{2} }} - k_{\text{r}}^{2} \left( {\frac{{\hat{T}}}{{\hat{T}_{\infty } }}} \right)^{n} \exp \left( {\frac{{ - E_{\text{a}} }}{{k\hat{T}}}} \right)(\hat{C} - \hat{C}_{\infty } ).\, $$

(4)

The interrelated conditions are:

$$ \begin{aligned} & \hat{u} = \hat{u}_{\text{w}} (x) + N_{1} (x)\upsilon_{\text{f}} \frac{{\partial \hat{u}}}{\partial y},\, \, \\&\hat{v} = 0,\,\,\hat{T} = \hat{T}_{\text{w}} + D_{1} (x)\frac{{\partial \hat{T}}}{\partial y},\,\hat{C} = \hat{C}_{\text{w}} ,\,{\text{when }}y \to 0,\, \\ & \hat{u} \to \hat{u}_{\infty } (x),\,\hat{T} \to \hat{T}_{\infty } ,\,\hat{C} \to \hat{C}_{\infty } ,\,{\text{when }}y \to \infty .\, \\ \end{aligned} $$

(5)

Table 1 quantifies the thermophysical properties of the base fluid, i.e., water and for nanoparticles like MWCNTs and SWCNTs. The variable viscosity which is varying inversely to temperature is defined as (Nadeem et al. 2016):

$$ \mu_{\text{f}} = \frac{1}{{a(T - T_{\text{r}} )}}, $$

(6)

where $a = \tfrac{\delta }{{\mu_{{{\text{f}}\infty }} }}\,{\text{and}}\,T_{\text{r}} = T_{\infty } - \tfrac{1}{\delta },$ $\delta$, and a are constant.

Table 1 Thermophysical properties of the base fluid and the nanoparticles

The values of $\mu_{\text{nf}}$, $\rho_{\text{nf}}$, and $\alpha_{\text{nf}}$ for nanofluid (SWCNT/water) are defined as:

$$ \begin{aligned} \mu_{\text{nf}} & = \frac{{\mu_{\text{f}} }}{{(1 - \phi )^{2.5} }},\,\,\rho_{\text{nf}} = (1 - \phi )\rho_{\text{f}} + \phi \rho_{\text{SWCNT}} , \\ \alpha_{\text{nf}} & = \frac{{k_{\text{nf}} }}{{(\rho C_{\text{p}} )_{\text{nf}} }},\, \, \frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = \frac{{(1 - \phi ) + 2\phi (\tfrac{{k_{\text{SWCNT}} }}{{k_{\text{SWCNT}} - k_{\text{f}} }})\ln (\tfrac{{k_{\text{SWCNT}} + k_{\text{f}} }}{{k_{\text{f}} }})}}{{(1 - \phi ) + 2\phi (\tfrac{{k_{\text{f}} }}{{k_{\text{SWCNT}} - k_{\text{f}} }})\ln (\tfrac{{k_{\text{SWCNT}} + k_{\text{f}} }}{{k_{\text{f}} }})}},\, \, \\ & \quad (\rho C_{\text{p}} )_{\text{nf}} = (\rho C_{\text{p}} )_{\text{f}} (1 - \phi ) + (\rho C_{\text{p}} )_{\text{SWCNT}} \phi . \\ \end{aligned} $$

(7)

The values of $\mu_{\text{hnf}}$, $\rho_{\text{hnf}}$, and $\alpha_{\text{hnf}}$ for hybrid nanofluid (SWCNT–MWCNT/water) are defined as:

$$ \begin{aligned} \mu_{\text{hnf}} & = \frac{{\mu_{\text{f}} (1 - \phi_{1} )^{ - 2.5} (1 - \phi_{2} )^{ - 2.5} }}{{\left( {1 - {\raise0.5ex\hbox{$\scriptstyle \theta $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\theta_{\text{r}} }$}}} \right)}},\, \, \rho_{\text{hnf}} = (1 - \phi_{2} )\left\{ {(1 - \phi_{1} )\rho_{\text{f}} + \phi_{1} \rho_{\text{MWCNT}} } \right\} + \phi_{2} \rho_{\text{SWCNT}} , \\ \alpha_{\text{hnf}} & = \frac{{k_{\text{hnf}} }}{{(\rho C_{\text{p}} )_{\text{hnf}} }},\, \, (\rho C_{\text{p}} )_{\text{hnf}} = (1 - \phi_{2} )\left\{ {(1 - \phi_{1} )(\rho C_{\text{p}} )_{\text{f}} + \phi_{1} (\rho C_{\text{p}} )_{\text{MWCNT}} } \right\} + \phi_{2} (\rho C_{\text{p}} )_{\text{SWCNT}} , \\ \frac{{k_{\text{hnf}} }}{{k_{\text{bf}} }} & = \frac{{(1 - \phi_{2} ) + 2\phi_{2} (\tfrac{{k_{\text{SWCNT}} }}{{k_{\text{SWCNT}} - k_{\text{bf}} }})\ln (\tfrac{{k_{\text{SWCNT}} + k_{\text{bf}} }}{{k_{\text{bf}} }})}}{{(1 - \phi_{2} ) + 2\phi_{2} (\tfrac{{k_{\text{bf}} }}{{k_{\text{SWCNT}} - k_{\text{bf}} }})\ln (\tfrac{{k_{\text{SWCNT}} + k_{\text{bf}} }}{{k_{\text{bf}} }})}}, \\ \frac{{k_{\text{bf}} }}{{k_{\text{f}} }} & = \frac{{(1 - \phi_{1} ) + 2\phi_{1} (\tfrac{{k_{\text{MWCNT}} }}{{k_{\text{MWCNT}} - k_{\text{f}} }})\ln (\tfrac{{k_{\text{MWCNT}} + k_{\text{f}} }}{{k_{\text{f}} }})}}{{(1 - \phi_{1} ) + 2\phi_{1} (\tfrac{{k_{\text{f}} }}{{k_{\text{MWCNT}} - k_{\text{f}} }})\ln (\tfrac{{k_{\text{MWCNT}} + k_{\text{f}} }}{{k_{\text{f}} }})}}. \\ \end{aligned} $$

(8)

where $\phi_{1} , \, \phi_{2}$ are the solid volume friction of MWCNT and SWCNT, respectively, is volume fraction of nanoliquid, $k_{\text{f}}$ are the thermal conductivity of regular liquid, and $C_{\text{p}} \;$ is specific heat.

To achieve true similarity solution, we defined variable velocity and thermal slip as:

$$ \begin{aligned} & u_{\infty } (x) = cx^{m} ,\, \, T_{\text{w}} = T_{\infty } + bx^{{\tfrac{5m - 1}{2}}} , \\ & D_{1} (x) = D_{1}^{*} x^{{\tfrac{1 - m}{2}}} ,N_{1} (x) = N_{1}^{*} x^{{\tfrac{1 - m}{2}}} , \\ \end{aligned} $$

(9)

where $b$, $c$ are the constants and $m = \beta /(2 - \beta )$ with $\beta$ is Hartree parameter of pressure gradient.

Similarity transformation

The similarity variables are accepted by:

$$ \begin{aligned} & \hat{u} = cx^{m} f^{\prime}(\eta ),\, \, \hat{v} = - \tfrac{1}{2}\sqrt {c\nu_{\text{f}} } x^{{\tfrac{m - 1}{2}}} \left[ {(m - 1)\eta f^{\prime}(\eta ) + (m + 1)f(\eta )} \right],\,\, \\ & \eta = \sqrt {(\tfrac{c}{{\nu_{\text{f}} }})} yx^{{\tfrac{m - 1}{2}}} ,\, \, \theta (\eta ) = \frac{{\hat{T} - \hat{T}_{\infty } }}{{\hat{T}_{\text{w}} - \hat{T}_{\infty } }},g(\eta ) = \frac{{\hat{C} - \hat{C}_{\infty } }}{{\hat{C}_{\text{w}} - \hat{C}_{\infty } }}. \\ \end{aligned} $$

(10)

Now, $\eta$ is the similarity variable, and $f(\eta )$, $g(\eta )$, and $\theta (\eta )$ are the linear velocity, concentration, and temperature dimensional coordinates, respectively.

Using similarity transformation, Eqs. (1–4) give:

$$ \begin{aligned} & \frac{1}{{1 - {\raise0.5ex\hbox{$\scriptstyle \theta $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\theta_{\text{r}} }$}}}}\,f^{\prime\prime\prime} + \frac{{\left( {(1 - \phi_{2} )\left\{ {(1 - \phi_{1} ) + \phi_{1} \tfrac{{\rho_{\text{MWCNT}} }}{{\rho_{\text{f}} }}} \right\} + \phi_{2} \tfrac{{\rho_{\text{SWCNT}} }}{{\rho_{\text{f}} }}} \right)}}{{(1 - \phi_{1} )^{ - 25/10} (1 - \phi_{2} )^{ - 25/10} \,}}\\ &\quad\left( {\tfrac{m + 1}{2}ff^{\prime\prime} + m(1 - f^{\prime 2} ) + F_{\text{r}} (1 - f^{\prime 2} )} \right) \\ & \quad + \frac{{\theta \prime f^{\prime\prime}}}{{\theta_{\text{r}} \left( {1 - {\raise0.5ex\hbox{$\scriptstyle \theta $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\theta_{\text{r}} }$}}} \right)^{2} }} + \frac{{P_{m} }}{{1 - {\raise0.5ex\hbox{$\scriptstyle \theta $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\theta_{\text{r}} }$}}}}\,(1 - f\prime ),\, \\ \end{aligned} $$

(11)

$$ \begin{aligned} & \left( {\frac{{k_{\text{hnf}} }}{{k_{\text{f}} }} + R_{\text{d}} } \right)\theta^{\prime\prime} + \Pr \left( {\gamma \theta + \frac{{E_{\text{c}} }}{{(1 - {\raise0.5ex\hbox{$\scriptstyle \theta $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\theta_{\text{r}} }$}})(1 - \phi_{1} )^{25/10} (1 - \phi_{2} )^{25/10} }}f^{{{\prime \prime }2}} } \right)\, \\ & \quad + \frac{m + 1}{2}\Pr \left( {(1 - \phi_{2} )\left\{ {(1 - \phi_{1} ) + \phi_{1} \tfrac{{\left( {\rho C_{\text{p}} } \right)_{\text{MWCNT}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{f}} }}} \right\} + \phi_{2} \tfrac{{\left( {\rho C_{\text{p}} } \right)_{\text{SWCNT}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{f}} }}} \right)f\theta^{\prime} = 0, \\ \end{aligned} $$

(12)

$$ \left( {\frac{{(1 - \phi_{1} )^{25/10} (1 - \phi_{2} )^{25/10} }}{{S_{\text{c}} }}} \right)g^{\prime\prime} + \left( {\frac{m + 1}{2}} \right)fg^{\prime} - R_{\text{c}} (1 + \alpha_{1} \theta )^{n} g\exp \left( {\frac{ - E}{{1 + \alpha_{1} \theta }}} \right) = 0.\, $$

(13)

The appropriate conditions are:

$$ \begin{aligned} & f^{\prime}(\eta ) = \lambda + Af^{\prime\prime}(\eta ),\,\, \, f(\eta ) = 0,\, \, \theta (\eta ) = 1 + B\theta^{\prime}(\eta ),\,\,g(\eta ) = 1,\,{\text{when }}\eta \to 0, \\ & f^{\prime}(\eta ) = 1,\,\,g(\eta ) = 0,\,\,\theta (\eta ) = 0,\,\,{\text{when }}\eta \to \infty .\, \\ \end{aligned} $$

(14)

Here, primes stands for differentiation with respect to $\eta$ and $m = \beta /(2 - \beta )$ where $\beta$ is Hartree parameter, and some other parameter used in above equations is defined as:

$$ \begin{aligned} & \Pr = (c_{\text{p}} \rho_{\text{f}} )/k_{\text{f}} ,\,B = D_{1}^{*} \sqrt {\tfrac{(m + 1)c}{{2\nu_{\text{f}} }}} ,\,A = N_{1}^{*} \upsilon_{\text{f}} \sqrt {\tfrac{(m + 1)c}{{2\nu_{\text{f}} }}} ,\,F_{\text{r}} = \frac{{C_{\text{b}} }}{{\sqrt {K^{**} } \rho_{\text{f}} }},\,P_{\text{m}} = \frac{{\upsilon_{\text{f}} }}{{cK^{**} }}, \\ & E_{\text{c}} = \frac{{u_{\infty }^{2} }}{{\Delta TC_{\text{pf}} }},\,\gamma = \frac{{Q_{0} }}{{c(\rho C_{\text{p}} )_{\text{f}} }},\,\theta_{\text{r}} = \frac{1}{{\delta (T_{\text{w}} - T_{\infty } )}},\,R_{\text{d}} = \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k_{\text{f}} k^{*} }},\,R_{\text{c}} = \frac{{k_{\text{r}}^{2} }}{c},\,E = \frac{{E_{\text{a}} }}{{kT_{\infty } }}. \\ \end{aligned} $$

Physical quantities

From an engineering point of perspective, physical quantities are very useful. The flow conduct characterized by skin friction, Nusselt number, and Sherwood number was recorded in these quantities as:

$$ \begin{aligned} & C_{\text{f}} = \tfrac{{\tau_{\text{w}} }}{{\rho_{\text{hnf}} \hat{u}_{\infty }^{2} }},\,{\text{Nu}}_{x} = \frac{{ - xk_{\text{hnf}} }}{{k_{\text{f}} (\hat{T}_{\text{w}} - \hat{T}_{\infty } )}}\left. {\tfrac{{\partial \hat{T}}}{\partial y}} \right|_{y = 0} ,\,{\text{Sh}}_{x} = \frac{{q_{m} }}{{D_{\text{hnf}} (\hat{C}_{\text{w}} - \hat{C}_{\infty } )}} \\ & \tau_{\text{w}} = \left[ {\mu_{\text{hnf}} (\hat{T})\tfrac{{\partial \hat{u}}}{\partial y}} \right]_{y = 0} ,q_{m} = - D_{\text{hnf}} \left. {\tfrac{{\partial \hat{C}}}{\partial y}} \right|_{y = 0} . \\ \end{aligned} $$

(15)

Using Eq. (10) in Eq. (15), we get:

$$ \begin{aligned} & Re_{x}^{1/2} C_{{{\text{f}}x}} = \frac{1}{{(1 - \phi_{1} )^{2.5} (1 - \phi_{2} )^{2.5} \,\left( {(1 - \phi_{2} )\left\{ {(1 - \phi_{1} ) + \phi_{1} \tfrac{{\rho_{\text{MWCNT}} }}{{\rho_{\text{f}} }}} \right\} + \phi_{2} \tfrac{{\rho_{\text{SWCNT}} }}{{\rho_{\text{f}} }}} \right)}}\left( {1 - \frac{\theta (0)}{{\theta_{\text{r}} }}} \right)f^{\prime\prime}(0), \\ & Re_{x}^{ - 1/2} {\text{Nu}}_{x} = \frac{{ - k_{\text{hnf}} }}{{k_{\text{f}} }}\theta^{\prime}(0),Re_{x}^{ - 1/2} {\text{Sh}}_{x} = - g^{\prime}(0). \\ \end{aligned} $$

(16)

Here, Reynolds number is denoted by $Re_{x} = \tfrac{{xu_{\infty } }}{{\nu_{\text{f}} }}$.

Entropy generation analysis

Entropy generation (or production) abrogates the available energy in the framework of few industrial and engineering processes. It is, therefore, worthwhile to discover in a framework the rate of entropy production.

The volumetric rate of local entropy generation of viscous fluid is defined as (Bejan 1979; Bejan and Kestin 1983; Bhatti et al. 2019):

$$ \begin{aligned} & S_{\text{G}} = \frac{{k_{\text{f}} }}{{\hat{T}_{\infty }^{2} }}\left[ {\frac{{k_{\text{hnf}} }}{{k_{\text{f}} }} + \frac{{16\sigma^{*} \hat{T}_{\infty }^{3} }}{{3k^{*} k_{\text{f}} }}} \right]\left( {\frac{{\partial \hat{T}}}{\partial y}} \right)^{2} + \left( {\frac{{\mu_{\text{hnf}} (\hat{T})}}{{\hat{T}_{\infty } }}} \right)\left( {\frac{{\partial \hat{u}}}{\partial y}} \right)^{2} + \frac{{\hat{u}^{2} }}{{\hat{T}_{\infty } }}\left( {\frac{{\mu_{\text{hnf}} (\hat{T})}}{{K^{**} }} + F^{**} \left| {\hat{u}} \right|} \right) \\ & \quad + \frac{RD}{{\hat{C}_{\infty } }}\left( {\frac{{\partial \hat{C}}}{\partial y}} \right)^{2} + \frac{RD}{{\hat{T}_{\infty } }}\left( {\frac{{\partial \hat{T}}}{\partial y}\frac{{\partial \hat{C}}}{\partial y}} \right). \\ \end{aligned} $$

(17)

The associated relationship can structure the dimensionless entropy generation:

$$ N_{\text{s}} = \frac{{T_{\infty } (y/\eta )^{2} }}{{k_{\text{f}} (T_{\text{w}} - T_{\infty } )}}S_{\text{G}} . $$

(18)

After using the similarity transformation (10), the dimensionless form of entropy generation become:

$$ \begin{aligned} N_{\text{s}} (\eta ) & = \left( {\frac{{k_{\text{hnf}} }}{{k_{\text{f}} }} + R_{\text{d}} } \right)\alpha_{1} \theta^{{{\prime }2}} + \frac{{{\text{Br}}\left( {1 - {\raise0.5ex\hbox{$\scriptstyle \theta $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\theta_{\text{r}} }$}}} \right)^{ - 1} }}{{(1 - \phi_{1} )^{2.5} (1 - \phi_{2} )^{2.5} }}f^{{{\prime \prime }2}} + \frac{{{\text{BrPm}}\left( {1 - {\raise0.5ex\hbox{$\scriptstyle \theta $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\theta_{\text{r}} }$}}} \right)^{ - 1} }}{{(1 - \phi_{1} )^{2.5} (1 - \phi_{2} )^{2.5} }}f^{{{\prime }2}} \\ & \quad + F_{\text{r}} {\text{Br}}f^{{{\prime }3}} + L\frac{{\alpha_{2} }}{{\alpha_{1} }}g^{{{\prime }2}} + Lg{\prime }\theta {\prime }\text{.} \\ \end{aligned} $$

(19)

Parameters used in the above equation are defined as:

$$ \alpha_{1} = \frac{\Delta T}{{T_{\infty } }},\,\alpha_{2} = \frac{\Delta C}{{C_{\infty } }},\,{\text{Br}} = \frac{{\mu_{\text{f}} u_{\infty }^{2} }}{{k_{\text{f}} \Delta T}},\,L = \frac{{RD(C_{\text{w}} - C_{\infty } )}}{{k_{\text{f}} }}. $$

(20)

Bejan number is described as the proportional of the entropy minimization due to thermal irreversibility to the total entropy optimization, that is:

$$ {\text{Be}} = \frac{{{\text{entropy}}\,{\text{production}}\,{\text{due}}\,{\text{to}}\,{\text{thermal}}\,{\text{irreversibility}}}}{{{\text{total}}\,{\text{entropy}}\,{\text{generation}}}}. $$

(21)

In mathematical form, it expresses as:

$$ {\text{Be}} = \frac{{\left( {\frac{{k_{\text{hnf}} }}{{k_{\text{f}} }} + R_{\text{d}} } \right)\alpha_{1} \theta^{{{\prime }2}} }}{{\left( {\frac{{k_{\text{hnf}} }}{{k_{\text{f}} }} + R_{\text{d}} } \right)\alpha_{1} \theta^{{{\prime }2}} + \frac{{{\text{Br}}\left( {1 - {\raise0.5ex\hbox{$\scriptstyle \theta $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\theta_{\text{r}} }$}}} \right)^{ - 1} }}{{(1 - \phi_{1} )^{2.5} (1 - \phi_{2} )^{2.5} }}f^{{{\prime \prime }2}} + \frac{{{\text{BrPm}}\left( {1 - {\raise0.5ex\hbox{$\scriptstyle \theta $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\theta_{\text{r}} }$}}} \right)^{ - 1} }}{{(1 - \phi_{1} )^{2.5} (1 - \phi_{2} )^{2.5} }}f^{{{\prime }2}} + F_{\text{r}} {\text{Br}}f^{{{\prime }3}} + L\frac{{\alpha_{2} }}{{\alpha_{1} }}g^{{{\prime }2}} + Lg{\prime }\theta {\prime }}}. $$

Bejan number requirement lies among $0 < {\text{Be}} < 1$. ${\text{Be}} = 0$ means that there is no entropy generation because of heat transfer. Similarly, the entropy minimization is less due to heat transfer than fluid friction when ${\text{Be}} < 0.5$.

Results and discussion

Numerical solutions

The numerical solution is achieved with the help of finite-difference method bvp4c from MATLAB. For manipulating this technique first, we transform the given nonlinear third-order differential equation to the first-order ODEs by presented substitution. The convergence criteria were allotted as $10^{ - 5}$:

$$ f = y_{1} ,\, \, f^{\prime} = y_{2} ,\, \, f^{\prime\prime} = y_{3} , $$

(22)

$$ \,yy1 = f^{\prime\prime\prime} = - \left( {1 - {\raise0.5ex\hbox{$\scriptstyle \theta $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\theta_{\text{r}} }$}}} \right)\left\{ \begin{aligned} \frac{{\left( {(1 - \phi_{2} )\left\{ {(1 - \phi_{1} ) + \phi_{1} \tfrac{{\rho_{\text{MWCNT}} }}{{\rho_{\text{f}} }}} \right\} + \phi_{2} \tfrac{{\rho_{\text{SWCNT}} }}{{\rho_{\text{f}} }}} \right)}}{{(1 - \phi_{1} )^{ - 25/10} (1 - \phi_{2} )^{ - 25/10} \,}}\left( {\tfrac{m + 1}{2}fy_{3} + m(1 - y_{2}^{2} ) + F_{\text{r}} (1 - y_{2}^{2} )} \right) \hfill \\ \, + \frac{{y_{3} y_{5} }}{{\theta_{\text{r}} \left( {1 - {\raise0.5ex\hbox{$\scriptstyle {y_{4} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\theta_{\text{r}} }$}}} \right)^{2} }} + \frac{{P_{m} }}{{1 - {\raise0.5ex\hbox{$\scriptstyle {y_{4} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\theta_{\text{r}} }$}}}}\,(1 - y_{2} ) \hfill \\ \end{aligned} \right\},\, $$

(23)

$$ \theta = y_{4} ,\,\theta {\prime } = y_{5} , $$

(24)

$$ yy2 = \theta^{\prime\prime} = \left( {\frac{{k_{\text{hnf}} }}{{k_{\text{f}} }} + R_{\text{d}} } \right)^{ - 1} \left\{ \begin{aligned} - \Pr \left( {\gamma y_{4} + \frac{{E_{\text{c}} }}{{(1 - {\raise0.5ex\hbox{$\scriptstyle \theta $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\theta_{\text{r}} }$}})(1 - \phi_{1} )^{25/10} (1 - \phi_{2} )^{25/10} }}y_{3}^{2} } \right) \hfill \\ - \frac{m + 1}{2}\Pr \left( {(1 - \phi_{2} )\left\{ {(1 - \phi_{1} ) + \phi_{1} \tfrac{{\rho_{\text{MWCNT}} }}{{\rho_{\text{f}} }}} \right\} + \phi_{2} \tfrac{{\rho_{\text{SWCNT}} }}{{\rho_{\text{f}} }}} \right)y_{1} y_{5} \hfill \\ \end{aligned} \right\}\,, $$

(25)

$$ g = y_{6} ,\, \, g{\prime } = y_{7} , $$

(26)

$$ yy3 = g^{\prime\prime} = \left( {\frac{{S_{\text{c}} }}{{(1 - \phi_{1} )^{25/10} (1 - \phi_{2} )^{25/10} }}} \right)\left\{ { - \left( {\frac{m + 1}{2}} \right)y_{1} y_{7} + R_{\text{c}} (1 + \alpha_{1} y_{4} )^{n} y_{6} \exp \left( {\frac{ - E}{{1 + \alpha_{1} y_{4} }}} \right)} \right\}. $$

(27)

The relevant boundary conditions are:

$$ \begin{aligned} & y_{0} (2) = \lambda + Ay_{0} (3),\,y_{0} (1) = 0,\,\,y_{0} (4) = 1 + By_{0} (5),\,y_{0} (6) = 1, \\ & y_{\inf } (2) \to 1,\,y_{\inf } (4) \to 0,\,y_{\inf } (6) \to 0. \\ \end{aligned} $$

(28)

$$ y_{\inf } (2) \to 1,\,y_{\inf } (4) \to 0,\,y_{\inf } (6) \to 0. $$

To warranty of every numerical solution approach asymptotic value accurately, we take $\eta_{\infty } = 5$ (Table 2).

Table 2 Comparison of $f^{\prime\prime}(0)$ with previous published results when $P_{\text{m}} = F_{\text{r}} = \lambda = 0 = A = \theta_{\text{r}} = \phi_{i}$

Velocity, micropolar, and temperature profile

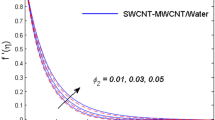
By deploying the shooting method/bvp4c, the solution to the present problem is gained numerically. Due to fluid friction, heat transfer and concentration gradient entropy production are formulated. The influences of solid volume fraction $0.01 < \phi_{2} < 0.05$, inertia coefficient $0.1 \le F_{\text{r}} \le 1.0$, porous parameter $0.1 \le \phi_{2} \le 0.5$, variable viscosity parameter $0.4 \le \phi_{2} \le 1.0$, wedge parameter $0.1 \le \lambda \le 0.3$, heat generation parameter $0.01 \le \gamma \le 0.15$, radiation parameter $0.5 \le R_{\text{d}} \le 1.5$, and Schmidt number $1.5 \le S_{\text{c}} \le 3.0$ on velocity profile, temperature distribution, concentration field, entropy generation number, and Bejan number are studied graphically. The accuracy of our problem, the present result in the absence of slip condition, hybrid nanofluid, and porosity parameter have been related with the earlier available result of Zaib and Haq. (2019) and Yih (1999). This result show good agreement with the above published articles. Figures 2, 3, 4, and 5 manipulate the influence of SWCNT solid volume friction ($\phi_{2}$) on axial velocity, temperature profile, concentration field, and entropy generation. These profiles are sketched for both hybrid nanofluid (SWCNT–MWCNT/water) and nanofluid (SWCNT–water). It is observed from Fig. 2 that the velocity field diminishes for both hybrid nanofluid and SWCNT–water nanofluid. This is because of more collision with suspended nanoparticles. Nanoparticles scatter energy in the form of heat. Therefore, the temperature profile enhances which is clarifying in Fig. 3. Figures 4, 5 reveal the impact of $\phi_{2}$ on concentration profile and entropy generation. Both the profiles decelerate with larger $\phi_{2}$. The upshot of inertia coefficient $F_{\text{r}}$ and porous parameter $P_{m}$ on axial velocity are discussed in Figs. 6 and 7. The velocity distribution enhances with boosting the $F_{\text{r}}$ and $P_{m}$. Furthermore, the momentum boundary-layer thickness decreases with larger $F_{\text{r}}$ and $P_{m}$. Figures 8, 9 highlight the upshot of variable viscosity parameter on axial velocity and temperature field. Velocity filed upgrades, while temperature diminishes with larger variable viscosity. Physically by increasing the parameter of variable viscosity, momentum transfer dominates due to low fluid viscosity, which improves the distribution of velocity (see in Fig. 8).

Fig. 2

Influence of $\phi_{2}$ on velocity field

Fig. 3

Influence of $\phi_{2}$ on temperature field

Fig. 4

Impact of $\phi_{2}$ on temperature field

Fig. 5

Result of $\phi_{2}$ on entropy generation

Fig. 6

Upshot of $F_{\text{r}}$ on $f^{\prime}(\eta )$

Fig. 7

Upshot of $P_{\text{m}}$ on $f^{\prime}(\eta )$

Fig. 8

Conclusion of $\theta_{\text{r}}$ on $f^{\prime}(\eta )$

Fig. 9

Conclusion of $\theta_{\text{r}}$ on $\theta (\eta )$

The conclusion of velocity and thermal slip is carried out for axial velocity and temperature field separately in Figs. 10 and 11. The velocity profile improves for improving the velocity slip parameter, while their consistent momentum boundary-layer thickness reduces, which is proven in Fig. 10. In the incidence of thermal slip, a smaller amount of heat transfer from the surface to fluid, as a result temperature distribution, diminishes which is illuminated in Fig. 11. Figure 12 discloses the influence of velocity through moving wedge parameter $\lambda$. Here, velocity is an enhancing function of $\lambda$ for both nanofluid and hybrid nanofluid. In Figs. 13 and 14, temperature profile is display to measure the effect of Eckert number $E_{\text{c}}$ and heat generation parameter $\gamma$ separately. Mechanical energy is converted to thermal energy due to higher Eckert number which produced friction inside the fluid; as a result, temperature field enhances (see Fig. 13). For larger $\gamma$, the internal source of energy of fluid enhances which enhance the temperature field (see Fig. 14). From Fig. 15, it is gotten that $\theta (\eta )$ is an increasing function of radiation parameter $R_{\text{d}}$ for both nanofluid and hybrid nanofluid. Physically increase values of $R_{\text{d}}$ give the additional heat to the fluid in the radiation cycle as the impact temperature distribution improves. Figures 16, 17, 18 are delineated to evaluate the concentration profile for higher value of involved parameter like reaction rate constant $R_{\text{c}}$, Schmidt number $S_{\text{c}}$, and activation energy parameter $E$. Concentration profile reduces for larger value of reaction rate constant (see Fig. 16). It is due to fact that the destructive rate of chemical reaction enhances with enhancing $R_{\text{c}}$. It is used to terminate or dissolve the liquid specie more effectively. From Fig. 17, $g(\eta )$ is a decreasing function of Schmidt number. Because higher the Schmidt number, reduce the mass diffusivity. The concentration profile enhances with enhancing activation energy parameter, which is demonstrated in Fig. 18. Figures 19, 20, 21, 22 manifest the upshot of Brinkman number, radiation parameter, temperature difference and concentration difference on entropy generation, and Bejan number. Entropy generation enhances with upgrade the Brinkman number, while it reduces with radiation parameter for both nanofluid and hybrid nanofluid, which is validating in Figs. 19 and 20. Furthermore, the Bejan number increases for increasing the temperature difference and concentration difference (see in Figs. 21 and 22). Tables 3, 4, 5 scrutinize the numerical value of skin friction, Nusselt number, and Sherwood number.

Fig. 10

Conclusion of $A$ on $f^{\prime}(\eta )$

Fig. 11

Outcome of $B$ on $\theta (\eta )$

Fig. 12

Outcome of $\lambda$ on $f^{\prime}(\eta )$

Fig. 13

Influence of $E_{\text{c}}$ on $\theta (\eta )$

Fig. 14

Influence of $\gamma$ on $\theta (\eta )$

Fig. 15

Influence of $R_{\text{d}}$ on $\theta (\eta )$

Fig. 16

Impact of $R_{\text{c}}$ on $g(\eta )$

Fig. 17

Influence of $S_{\text{c}}$ on $g(\eta )$

Fig. 18

Influence of $E$ on $g(\eta )$

Fig. 19

Effect of $B_{\text{r}}$ on entropy generation

Fig. 20

Action of $R_{\text{d}}$ on entropy generation

Fig. 21

Action of $\alpha_{1}$ on Bejan number

Fig. 22

Action of $\alpha_{2}$ on Bejan number

Table 3 Numerical value of skin friction (White 2015) when $\Pr = 6.2,\,m = 0.5,\,\phi_{1} { = 0} . 0 3 ,\,{\text{and}}\,A = 0.1$

Table 4 Numerical value of Nusselt number (White 2015) when $\Pr = 6.2,\,m = 0.5,\,{\text{and}}\,\phi_{1} = 0.03$

Table 5 Numerical value of Sherwood number (White 2015) when $\Pr = 6.2,\,m = 0.5,\,E = 1.0,\,{\text{and}}\,\phi_{1} = 0.03$

Concluding remarks

In the current study, two-dimensional, steady, incompressible hybrid nanofluid embedded in porous medium is scrutinized. Entropy generation is found using the second law of thermodynamics. By means of transformation, the governing nonlinear partial differential equations (PDEs) are transformed into ordinary differential equations (ODEs) and tackled these equations numerically by applying the finite-difference technique bvp4c. The main perceiving point of existing analysis is itemized beneath:

• Higher inertia coefficient $F_{\text{r}}$, porous $P_{m}$, and variable viscosity parameter $\theta_{\text{r}}$ reduce the momentum boundary-layer thickness.

• Thermal field shows boosting impact via larger $E_{\text{c}}$, $\gamma$, and $R_{\text{d}}$ for both nanofluid and hybrid nanofluid.

• ($g(\eta )$) reduces for larger value of ($R_{\text{c}}$) and ($S_{\text{c}}$) while boosting for higher ($E$).

• Nusselt number reduces for enlarging the value of thermal slip $B$ and radiation parameter $R_{\text{d}}$.

• The solid volume fraction enhances the temperature distribution.

• Rise the $\alpha_{1}$, $R_{\text{c}} ,\,S_{\text{c}}$, and $\phi_{2}$ Sherwood number upgrades.

• Entropy generation is an enhancing function of Brinkman number, while it is a lessening function of $\phi_{2}$ and $R_{\text{d}}$.

• The temperature and concentration difference parameter upgrade the Bejan number.