1 Introduction

Rotating surfaces, often referred to as rotary components, play crucial role in various engineering applications due to their unique characteristics and functionalities. These components have circular or rotational motion and are employed in many industries, including aerospace, automotive, manufacturing, energy, etc. Asghar et al [1] investigated the consequence of viscous dissipation together with thermal radiation, under convective heat transfer on the flow of a hybridised nanofluid, particularly on rotating heated stretching\(/\)shrinking surfaces. Ahmed et al [2] thoroughly studied the bioconvection flow of Casson nanofluid caused by a spinning disc, taking into account the influence of Joule heating along heated convective circumstances (i.e., the thermal convective boundary conditions) with gyrotactic micro-organisms. A significant heat transportation study of a hybridised nanofluid flowing among two rotating plates in a vertical plane was done by Hussain et al [3]. Rafique et al [4] examined the complicated interplay of numerous elements affecting the behaviour of nanofluids in unsteady bidirectional rotating stagnation point flows in their extensive investigation. Three important components of the experiment, such as thermal radiation, nanoparticle aggregation and altering viscosity, have been discussed. Pandey and Das [5] investigated the thermophysical properties of hybrid nanofluids and examined the stabilising influence of surface stretching. They expanded the scope of their analysis from the conventional case of rotationally symmetric flow and heat transmission towards a rotating disk to the more complex scenario involving a stretchable disk.

The level of porosity has a big impact on how heat transmits and convenes within the medium. The effective thermal conductivity and convective heat transportation coefficients of the porous medium are strongly influenced by the porosity parameter. In a variety of technical applications, including geothermal systems, packed beds, porous heat exchangers and porous construction materials, it is used to predict and analyse heat transfer phenomena. Considering porous media in hybrid nanoparticles and using different shapes of nanoparticles can have significant advantages in various applications. These are: (i) Porous media provide a larger surface area for nanoparticles to interact with the surrounding fluid. This can lead to increased heat transfer and mass transport, making porous media useful in applications like heat exchangers and filtration systems, (ii) porous media can enhance the convective heat transfer characteristics of nanofluids. This is particularly useful in applications, such as heat exchangers, where efficient heat transfer is crucial, (iii) porous media can help regulate fluid flow patterns, (iv) porous media can provide structural support to nanoparticles, preventing agglomeration or sedimentation. Further, different shapes of nanoparticles have unique properties. For example, nanorods may have different thermal conductivity characteristics compared to spherical nanoparticles. Different shapes can have variations in surface chemistry, which can be crucial in applications like catalysis or drug delivery. For example, rod-shaped nanoparticles may have different catalytic activities compared to spherical ones. Different-shaped nanoparticles can exhibit unique optical properties. This is important in applications like sensors, displays and photovoltaics. Mahesh et al [6] thoroughly examined, while taking into account the important role of viscous dissipation together with the influence of radiation on the flow features of a magnetohydrodynamic (MHD). The authors have considered in their study pair stress hybridised nanofluid across a porous sheet. Sadighi et al [7] scrutinised the thermodynamic first law application to magnetised nano-structured fluid movement with multiple factors, including inclined magnetised field and radiation, on a porous widening interface in a permeable Darcian medium. Maheswari et al [8] inspected the MHD Forchheimer flow of nanofluids over a permeable stretching sheet with the inclusion of radiation effects. Khan et al [9] examined the movement of a Maxwell fluid across a steadily extending surface using the MHD Cattaneo–Christov thermal flux framework. The consequences of thermal generation in a porous media were taken into account in the investigation. Pattnaik et al [10] presented a hybridised approach for thoroughly examining the computational performance of thermal radiation as well as the impact of chemical reaction on viscoelastic nanofluid flow. Mandal and Shit [11] looked at convective heat transfer on a permeable radiative stretchable rotating disc as well as entropy in an unsteady MHD flow involving a viscosity nanofluid. Mandal et al [12] investigated entropy in a nanofluid flow containing gyrotactic micro-organisms in the presence of thermo-solutal stratification. The entire procedure took place across an inclined radiative stretching cylinder. Mandal and Shit [13] focussed on the entropy within an erratic three-dimensional Williamson nanofluid MHD flow across a stretching sheet experiencing convective heating. Mandal and Shit [14] studied entropy in a thin liquid layer including Maxwell nanofluids in an unstable MHD flow where the fluid characteristics are variable. Mukherjee et al [15] developed a mathematical model of how a graphene and PDMS-containing Maxwell nanofluid would move across a stretching surface.

Thermal radiation is the key factor in determining the temperature distribution and energy exchange between surfaces and their surroundings during heat transfer processes. Mishra et al [16] mainly investigated the behaviour of microstructured fluid flow along an extending vertical interface under the combined influence of heat flux, viscosity and Lorentz force. Pattnaik et al [17] analysed the flow behaviour of an axisymmetric radiative titanium dioxide magnetised nanofluid over an elongated cylindrical surface. The investigation considered the impact of both homogeneous and heterogeneous reactions within a Darcy–Forchheimer porous medium. Mathur et al [18] inspected the flow of a magneto-microstructure nanofluid towards an elastic surface while taking into account the TiO\(_2\) nanoparticles in water and kerosene. The mechanism of heat and mass transportation in a viscoelastic fluid moving across an enlarging sheet are explored by Mishra et al [19]. The goal of the study is to comprehend how the combined impacts of MHD and chemical reaction effects affect the fluid’s dynamic behaviour. The interplay of an inclined magnetic field with non-uniform heat sources results in significant improvements in the heat transportation properties of nanofluids, which are thoroughly explored by Jena et al [20]. Kumar and Mondal [21] performed a study, accounting for the effects of both thermal radiation and magnetic field, to determine the irreversibility in the flow of a hybrid nanofluid across a rotating disc. Kumar and Mondal [22] studied the magneto-convective transport of immiscible binary fluids in an inclined channel. Tyagi et al [23] investigated the most recent developments in nanofluid spray and jet impingement cooling. Sarma et al [24] focussed on the optimisation of entropy and explored how conjugate heat transport affects the thermo-electro-hydrodynamics of nanofluids. Mondal and Wongwises [25] described an MHD micropump for nanofluids in a revolving microchannel while considering the electrical double-layer effect.

In heat transfer, the dissipation effect involves the transformation of mechanical energy into heat within a fluid or a solid. Friction and internal resistance cause mechanical energy to be lost as heat moves through a medium, which raises the medium’s internal energy and temperature. The association of viscous dissipation on the MHD free convection flow towards a semi-infinite moving vertical porous plate was studied by Matta et al [26], taking into account the influence of heat sink and chemical reactions. Pordanjani et al [27] focussed on investigating slippage and non-slip flows of MHD nanofluids in a microchannel, with a specific focus on cooling discrete heat sources. Wahid et al [28] examined the MHD stagnation-point flow of a nanofluid across a contracting sheet in their work. The analysis takes into account important physical processes, such as Joule heating, viscous dissipation and melting effects. A numerical simulation was done by Gopal et al [29] to analyse the effects of first-order chemical reaction along with Ohmic effects on the MHD nanofluid flow over an exponentially widening surface. Chiranjeevi et al [30] studied the combined influence of radiation absorption, a transverse magnetised field and viscous dissipation on the MHD-free convective laminar flow over a moving vertical permeable plate. Panda et al [31] explored the hybrid nanofluid that is propelled by buoyancy and dissipation in the Falkner–Skan flow was the subject of their investigation, which concentrated on the effects of shape factor.

1.1 Objective of the current investigation

The objective of the study is to investigate the three-dimensional convective rotating hybridised nanofluid flow across a linear stretching/shrinking plate while considering the influence of dissipative heat. The study aims to recognise the combined effects of nano-fluids (fluids containing suspended nanoparticles) with convective motion, rotation and heat dissipation on the flow characteristics and heat transmission near the stretching/shrinking sheet.

1.2 Novelty of the proposed investigation

The study is novel due to the following reasons:

  • This study departs from the conventional focus on two-dimensional flows by introducing a comprehensive three-dimensional analysis. This inclusion enhances the model’s realism and complexity, rendering it more applicable to real-world situations.

  • The investigation delves into hybrid nanofluids, signifying a fusion of diverse nanoparticle types. The unexplored territory of the combined impacts and interactions among these nanoparticles on flow dynamics and heat transfer introduces a fresh dimension of novelty to this research.

  • The infusion of convective motion and rotation into the flow analysis injects an added layer of authenticity. The relatively uncharted territory of how these supplementary forces influence flow patterns and heat transfer coefficients contributes distinct novelty to the study.

  • The inclusion of a stretching/shrinking sheet in the flow introduces boundary conditions that vary across the surface. Exploring the flow and heat transmission features within such conditions offers significant applications to a range of industrial and natural processes.

  • This study takes into account dissipative heat, a phenomenon in which mechanical energy transforms into thermal energy due to fluid viscosity. Although simplified models often disregard this effect, it can substantially impact flow patterns and heat transfer rates. However, the outcomes hold relevance for diverse engineering applications, including materials processing, cooling systems and environmental processes. In these scenarios, the intricate interplay of nanofluids, convective motion, rotation and heat dissipation assumes a pivotal role.

Fig. 1
figure 1

Flow geometry of the current problem.

Full size image

2 Mathematical formulation

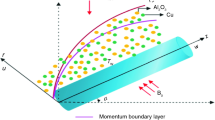
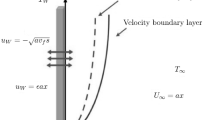
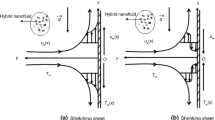
A steady three-dimensional flow of hybrid nanofluid comprising Ag and MoS\(_4\) nanoparticles in water past an expanding\(/\)contracting surface embedded within a permeable medium is analysed in the current discussion. The proposed sheet is along the xy-plane, i.e., \(z=0\) (figure 1). When \(z\ge 0\), half of the area is taken up by this fluid. A uniform magnetisation of particular strength \(B_0\) is proposed along the normal direction of the flow. The mathematical governing equations capture the physical model, incorporating the principles of laminar, Newtonian and incompressible flow. However, the assumptions made near the interface \(z=0\) are

  1. (i)

    The stretching/shrinking sheet velocity towards the x direction is linearly presented as \({{U}_{w}}=ax\).

  2. (ii)

    At a constant velocity, the system rotates normal to the interface of the z-axis.

  3. (iii)

    The radiating heat flux along the z-axis is denoted as \({{q}_{r}}\) (Rosseland approximation).

  4. (iv)

    The external heat source/sink applied in the heat transport phenomena is q.

Additionally, a uniform temperature \({{T}_{f}}\) is assumed for the hot fluid at the bottom and the heat transfer coefficient is presented as \({{h}_{f}}\). Here, the fluid phase and the nanoparticles are considered to be in thermal equilibrium condition. The slip velocity within the phases is neglected due to their size, i.e., they are exceptionally small. The flow phenomena for the hybrid nanofluid are described as [1]

$$\begin{aligned}{} & {} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0, \end{aligned}$$
(1)
$$\begin{aligned}{} & {} u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}-2\Omega v \nonumber \\{} & {} \quad =\frac{{{\mu }_{hnf}}}{{{\rho }_{hnf}}}\frac{{{\partial }^{2}}u}{\partial {{z}^{2}}}-\frac{{{\sigma }_{hnf}}}{{{\rho }_{hnf}}}B_{0}^{2}u-\frac{{{\mu }_{hnf}}}{{{\rho }_{hnf}}}\frac{u}{{{K}^{*}}}, \end{aligned}$$
(2)
$$\begin{aligned}{} & {} u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}+2\Omega u \nonumber \\{} & {} \quad =\frac{{{\mu }_{hnf}}}{{{\rho }_{hnf}}}\frac{{{\partial }^{2}}v}{\partial {{z}^{2}}}-\frac{{{\sigma }_{hnf}}}{{{\rho }_{hnf}}}B_{0}^{2}v-\frac{{{\mu }_{hnf}}}{{{\rho }_{hnf}}}\frac{v}{{{K}^{*}}}, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z}\nonumber \\{} & {} \quad =\frac{{{k}_{hnf}}}{{{\left( \rho {{C}_{P}} \right) }_{hnf}}}\frac{{{\partial }^{2}}T}{\partial {{z}^{2}}}-\frac{1}{{{\left( \rho {{C}_{P}} \right) }_{hnf}}}\frac{\partial {{q}_{r}}}{\partial z}\nonumber \\{} & {} \qquad +\frac{{{\mu }_{hnf}}}{{{\left( \rho {{C}_{P}} \right) }_{hnf}}}\left\{ {{\left( \frac{\partial u}{\partial z} \right) }^{2}}+{{\left( \frac{\partial v}{\partial z} \right) }^{2}} \right\} \nonumber \\{} & {} \qquad +\frac{{{\sigma }_{hnf}}}{{{( \rho {{C}_{p}} )}_{hnf}}}B_{0}^{2}( {{u}^{2}}+{{v}^{2}} )+\frac{q(T-{{T}_{\infty }})}{{{\left( \rho {{C}_{P}} \right) }_{hnf}}}, \end{aligned}$$
(4)

with proposed boundary conditions [1]

$$\begin{aligned}{} & {} u=\lambda {{U}_{w}},\quad v=0,\quad w={{w}_{w}},\quad \nonumber \\{} & {} -{{k}_{hnf}}\frac{\partial T}{\partial z}={{h}_{f}}({{T}_{f}}-T),\,\,\text {as}\,\,z=0, \end{aligned}$$
(5)
$$\begin{aligned}{} & {} u\rightarrow 0,\quad v\rightarrow 0,\quad T\rightarrow {{T}_{\infty }}\,\,\,\,\textrm{as}\,\,z\rightarrow \infty \end{aligned}$$
(6)

The stretching/shrinking constant is denoted as \(\lambda \), besides that \(\lambda =0,\lambda >0\) and is depicted as static, stretching and shrinking of the sheet. Further, the ambient temperature is denoted as \({{T}_{\infty }}\) and the fluid temperature is T. The expression for the radiative heat flux \({{q}_{r}}\) is

$$\begin{aligned}{} & {} {{q}_{r}}=-\frac{4{{\sigma }^{*}}}{3{{k}^{*}}}\frac{\partial {{T}^{4}}}{\partial y}. \end{aligned}$$
(7)

Here, \({{\sigma }^{*}},{{k}^{*}}\) correspond to Boltzmann constant and mean absorption coefficient, respectively. By neglecting the higher-order terms from the expansion of about \({{T}_{\infty }}\), the linear transformation is \({{T}^{4}}\cong 4T_{\infty }^{3}T-3T_{\infty }^{4}\). Therefore, eq. (4) can be rewritten as

$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z}\nonumber \\&\quad =\left[ \frac{{{k}_{hnf}}}{{{\left( \rho {{C}_{P}} \right) }_{hnf}}}+\frac{16{{\sigma }^{*}}T_{\infty }^{3}}{3{{k}^{*}}{{\left( \rho {{C}_{P}} \right) }_{hnf}}} \right] \frac{{{\partial }^{2}}T}{\partial {{z}^{2}}}\nonumber \\&\qquad +\frac{{{\sigma }_{hnf}}B_{0}^{2}}{{{\left( \rho {{C}_{P}} \right) }_{hnf}}}({{u}^{2}}+{{v}^{2}}) +\frac{{{\mu }_{hnf}}}{{{\left( \rho {{C}_{P}} \right) }_{hnf}}}\nonumber \\&\qquad \times \left[ {{\left( \frac{\partial u}{\partial z} \right) }^{2}}+{{\left( \frac{\partial v}{\partial z} \right) }^{2}} \right] \nonumber \\&\qquad +\frac{q}{{{\left( \rho {{C}_{P}} \right) }_{hnf}}}(T-{{T}_{\infty }}). \end{aligned}$$
(8)

The effective models for various thermophysical attributes considered in the above-mentioned flow phenomena are described briefly.

2.1 Model analysis for the hybrid nanofluid

  • Effective viscosity model

    $$\begin{aligned} \frac{{{\mu }_{hnf}}}{{{\mu }_{f}}}=\frac{1}{{{(1-{{\phi }_{\textrm{Ag}}})}^{2.5}}{{(1-{{\phi }_{\mathrm {Mo{{S}}_{4}}}})}^{2.5}}}. \end{aligned}$$

  • Density model

    $$\begin{aligned}&\frac{{{\rho }_{hnf}}}{{{\rho }_{f}}}=(1-{{\phi }_{\mathrm {Mo{{S}}_{4}}}})\left[ 1-{{\phi }_{\textrm{Ag}}}+{{\phi }_{\textrm{Ag}}}\left( \frac{{{\rho }_{\textrm{Ag}}}}{{{\rho }_{f}}} \right) \right] \\&\qquad \qquad +{{\phi }_{\mathrm {Mo{{S}}_{4}}}}\left( \frac{{{\rho }_{\mathrm {Mo{{S}}_{4}}}}}{{{\rho }_{f}}} \right) . \end{aligned}$$

  • Heat capacity model

    $$\begin{aligned}&\frac{{{(\rho {{C}_{p}})}_{hnf}}}{{{(\rho {{C}_{p}})}_{f}}}\\&\quad =(1-{{\phi }_{\mathrm {Mo{{S}}_{4}}}})\left[ 1-{{\phi }_{\textrm{Ag}}}+{{\phi }_{\textrm{Ag}}}\left( \frac{{{\left( \rho {{C}_{p}} \right) }_{\textrm{Ag}}}}{{{\left( \rho {{C}_{p}} \right) }_{f}}} \right) \right] \\&\qquad +{{\phi }_{\mathrm {Mo{{S}}_{4}}}}\left( \frac{{{\left( \rho {{C}_{p}} \right) }_{\mathrm {Mo{{S}}_{4}}}}}{{{\left( \rho {{C}_{p}} \right) }_{f}}} \right) . \end{aligned}$$

  • Effective thermal conductivity model

    $$\begin{aligned} \frac{{{k}_{hnf}}}{{{k}_{nf}}}=\left[ \frac{{{k}_{\mathrm {Mo{{S}}_{4}}}}+(n-1){{k}_{nf}}-(n-1){{\phi }_{\mathrm {Mo{{S}}_{4}}}}({{k}_{nf}}-{{k}_{\mathrm {Mo{{S}}_{4}}}})}{{{k}_{\mathrm {Mo{{S}}_{4}}}}+(n-1){{k}_{nf}}-{{\phi }_{\mathrm {Mo{{S}}_{4}}}}({{k}_{nf}}-{{k}_{\mathrm {Mo{{S}}_{4}}}})} \right] , \end{aligned}$$

    where

    $$\begin{aligned} \frac{{{k}_{nf}}}{{{k}_{f}}}{=}\left[ \frac{{{k}_{\textrm{Ag}}}{+}(n{-}1){{k}_{f}}{-}(n{-}1){{\phi }_{\textrm{Ag}}}({{k}_{f}}{-}{{k}_{\textrm{Ag}}})}{{{k}_{\textrm{Ag}}}{+}(n{-}1){{k}_{f}}{-}{{\phi }_{\textrm{Ag}}}({{k}_{f}}{-}{{k}_{\textrm{Ag}}})}\right] . \end{aligned}$$

  • Electrical conductivity model

    $$\begin{aligned} \frac{{{\sigma }_{hnf}}}{{{\sigma }_{f}}}=\frac{{{\sigma }_{\mathrm {Mo{{S}}_{4}}}}(1+2{{\phi }_{\mathrm {Mo{{S}}_{4}}}})+2{{\sigma }_{nf}}(1-{{\phi }_{\mathrm {Mo{{S}}_{4}}}})}{{{\sigma }_{\mathrm {Mo{{S}}_{4}}}}(1-{{\phi }_{\mathrm {Mo{{S}}_{4}}}})+{{\sigma }_{nf}}(2+{{\phi }_{\mathrm {Mo{{S}}_{4}}}})}, \end{aligned}$$

    where

    $$\begin{aligned} \frac{{{\sigma }_{nf}}}{{{\sigma }_{f}}}=\frac{{{\sigma }_{\textrm{Ag}}}(1+2{{\phi }_{\textrm{Ag}}})+2{{\sigma }_{f}}(1-{{\phi }_{\textrm{Ag}}})}{{{\sigma }_{\textrm{Ag}}}(1-{{\phi }_{\textrm{Ag}}})+{{\sigma }_{f}}(2+{{\phi }_{\textrm{Ag}}})}. \end{aligned}$$

It is clear from the above expression that the silver (Ag) and molybdenum tetrasulphide volume fractions are signified by \({{\phi }_{1}}\approx {{\phi }_{\textrm{Ag}}}\) and \({{\phi }_{2}}\approx {{\phi }_{\text {Mo}{{\text {S}}_{4}}}}\). In this particular scenario, the similarity variables are outlined as follows:

$$\begin{aligned}&u=ax{f}'(\eta ),\quad v=axg(\eta ),\quad w=-\sqrt{a{{v}_{f}}}f(\eta ),\nonumber \\&\theta (\eta ) =\frac{T-{{T}_{\infty }}}{{{T}_{f}}-{{T}_{\infty }}},\quad \eta =z\sqrt{\frac{a}{{{v}_{f}}}}. \end{aligned}$$
(9)

In general, the kinematic viscosity, \({{v}_{f}}\) and a, are termed as positive constants. \({{w}_{w}}=-\sqrt{a{{v}_{f}}}S, \) where S signifies the injection/suction factor. In particular \(S>0\) stands for suction and \(S<0\) stands for injection. The assumption of eq. (8) obviously fulfilled eq. (1) and further, substituting into eqs (2)–(4) the transformed non-dimensional ODEs are presented as

$$\begin{aligned}&\frac{{{\xi }_{1}}}{{{\xi }_{2}}}{f}'''(\eta )+{f}''(\eta )f(\eta )-{f}'{{(\eta )}^{2}}\nonumber \\&\quad +2\omega g(\eta )-\frac{{{\xi }_{5}}}{{{\xi }_{2}}}M{f}'(\eta )-\frac{{{\xi }_{1}}}{{{\xi }_{2}}}Da{f}'(\eta )=0, \end{aligned}$$
(10)
$$\begin{aligned}&\frac{{{\xi }_{1}}}{{{\xi }_{2}}}{g}''(\eta )+{g}'(\eta )f(\eta )-g(\eta ){f}'(\eta )\nonumber \\&\quad -2\omega {f}'(\eta )-\frac{{{\xi }_{5}}}{{{\xi }_{2}}}Mg(\eta )-\frac{{{\xi }_{1}}}{{{\xi }_{2}}}Dag(\eta )=0, \end{aligned}$$
(11)
$$\begin{aligned}&\frac{1}{\Pr {{\xi }_{3}}}\left\{ {{\xi }_{4}}+\frac{4Rd}{3} \right\} {\theta }''(\eta )+{\theta }'(\eta )f(\eta )-2\theta (\eta ){f}'(\eta )\nonumber \\&\qquad +\frac{{{\xi }_{5}}}{{{\xi }_{3}}}MEc({f}'{{(\eta )}^{2}}+g{{(\eta )}^{2}}) \nonumber \\&\qquad +\frac{{{\xi }_{1}}}{{{\xi }_{3}}}Ec({f}''{{(\eta )}^{2}}+{g}'{{(\eta )}^{2}})+\frac{1}{{{\xi }_{3}}}Q\theta (\eta )=0, \end{aligned}$$
(12)

where

$$\begin{aligned}&\frac{{{\mu }_{hnf}}}{{{\mu }_{f}}}={{\xi }_{1}},\quad \frac{{{\rho }_{hnf}}}{{{\rho }_{f}}}={{\xi }_{2}},\quad \frac{{{\left( \rho {{C}_{P}} \right) }_{hnf}}}{{{\left( \rho {{C}_{P}} \right) }_{f}}}={{\xi }_{3}},\\&\frac{{{k}_{hnf}}}{{{k}_{f}}}={{\xi }_{4}}, \quad \frac{{{\sigma }_{hnf}}}{{{\sigma }_{f}}}={{\xi }_{5}}. \end{aligned}$$

Depending on the boundary conditions:

$$\begin{aligned}&f(0)=S,\quad g(0)=0,{f}'(0)=\lambda ,\nonumber \\&-{{\xi }_{4}}{\theta }'(0)=Bi\left[ 1-\theta (0) \right] \end{aligned}$$
(13)
$$\begin{aligned}&{f}'(\eta )\rightarrow 0,\quad \theta (\eta )\rightarrow 0,\quad g(\eta )\rightarrow 0\,\,\text {as}\,\,\eta \rightarrow \infty \end{aligned}$$
(14)
$$\begin{aligned}&\omega =\frac{\Omega }{a},\quad Q=\frac{q}{a{{\left( \rho {{C}_{P}} \right) }_{f}}},\quad Ec=\frac{{{a}^{2}}{{x}^{2}}}{({{T}_{w}}-{{T}_{\infty }}){{\left( {{C}_{P}} \right) }_{f}}},\nonumber \\&M=\frac{{{\sigma }_{f}}B_{0}^{2}}{a{{\rho }_{f}}},\quad \Pr =\frac{{{\left( \mu {{C}_{P}} \right) }_{f}}}{{{k}_{f}}},\quad Rd=\frac{16{{\sigma }^{*}}T_{\infty }^{3}}{3{{k}^{*}}{{k}_{f}}},\nonumber \\&Bi= \frac{{{h}_{f}}}{{{k}_{f}}}\sqrt{\frac{{{v}_{f}}}{a}},\quad Da=\frac{{{\upsilon }_{f}}}{{{K}^{*}}}. \end{aligned}$$
(15)

Here, \(\omega \) is the rotation parameter, Ec denotes Eckert number, \(\Pr \) denotes Prandtl number, \({{B}_{0}}\) denotes magnetic field strength, Bi is the Biot number, M is the magnetic parameter, Da is the porosity parameter, Q is the heat source/sink parameter and Rd is thermal radiation. The skin friction (drag force) coefficients \({{C}_{fx}}\) and \({{ C}_{fy}}\) in x- and y-axes, respectively and local Nusselt number \(N{{u}_{x}}\), are given as

$$\begin{aligned}&{{C}_{fx}}=\frac{{{\mu }_{hnf}}}{U_{w}^{2}}{{\left( \frac{\partial u}{\partial z} \right) }_{z=0}},\quad {{C}_{fy}}=\frac{{{\mu }_{hnf}}}{U_{w}^{2}}{{\left( \frac{\partial v}{\partial z} \right) }_{z=0}}\nonumber \\&N{{u}_{x}}=\frac{x}{{{k}_{f}}({{T}_{f}}-{{T}_{\infty }})}\left[ -{{k}_{hnf}}{{\left( \frac{\partial T}{\partial z} \right) }_{z=0}}+{{\left. {{q}_{r}} \right| }_{z=0}} \right] . \end{aligned}$$
(16)

From eqs (9) and (16), one can obtain

$$\begin{aligned}&\sqrt{{{{\text {Re}}}_{x}}}{{C}_{fx}}={{\xi }_{1}}{f}''(0),\quad \sqrt{{{{\text {Re}}}_{x}}}{{C}_{fy}}={{\xi }_{1}}{g}'(0),\nonumber \\&\frac{N{{u}_{x}}}{\sqrt{{{{\text {Re}}}_{x}}}}=-\left[ {{\xi }_{4}}+\frac{4}{3}Rd \right] {\theta }'(0). \end{aligned}$$
(17)

Here \({{{\text {Re}}}_{x}}={{{U}_{w}}x}/{{{v}_{f}}}\) is the local Reynolds number.

3 Methodology

Numerical approaches are used to address the model, which is described by a collection of equations, rather than an analytical strategy. The complex system of nonlinear partial differential equations using the boundary layer flow is converted into a set of ordinary differential equations (ODEs) and then solved using the bvp5c tool in MATLAB. The outcome is a collection of first-order ODEs that have been modified, which are presented as follows:

$$\begin{aligned}&f={{y}_{1}},\quad {f}'={{y}_{2}},\quad {f}''={{y}_{3}}, \\&{f}'''(\eta )=\bigg [ -{{y}_{3}}{{y}_{1}}+{{y}_{2}}^{2}-2\omega {{y}_{4}}+\frac{{{\xi }_{5}}}{{{\xi }_{2}}}M{{y}_{2}}\\&\qquad \quad \quad +\frac{{{\xi }_{1}}}{{{\xi }_{2}}}Da{{y}_{2}}/{\frac{{{\xi }_{1}}}{{{\xi }_{2}}}}\; \bigg ]\\&g={{y}_{4}},\quad {g}'={{y}_{5}}, \\&{g}''(\eta )=\bigg [ -{{y}_{5}}{{y}_{1}}+{{y}_{4}}{{y}_{2}}+2\omega {{y}_{2}}+\frac{{{\xi }_{5}}}{{{\xi }_{2}}}M{{y}_{4}}\\&\qquad \qquad +\frac{{{\xi }_{1}}}{{{\xi }_{2}}}Da{{y}_{4}}/{\frac{{{\xi }_{1}}}{{{\xi }_{2}}}}\; \bigg ]\\&\theta ={{y}_{6}},\quad {\theta }'={{y}_{7}},\\&{\theta }''(\eta ) = \bigg [-{{y}_{7}}{{y}_{1}}+2{{y}_{6}}{{y}_{2}}-\frac{{{\xi }_{5}}}{{{\xi }_{3}}}MEc({{y}_{2}}^{2}+{{y}_{4}}^{2})\\&\qquad \qquad -\frac{{{\xi }_{1}}}{{{\xi }_{3}}}Ec({{y}_{3}}^{2}+{{y}_{5}}^{2})\\&\qquad \qquad -\frac{1}{{{\xi }_{3}}}Q{{y}_{6}}/{\frac{1}{\Pr {{\xi }_{3}}}\left\{ {{\xi }_{4}}+\frac{4Rd}{3} \right\} } \bigg ]. \end{aligned}$$
Table 1 Shapes of nanoparticles [31].
Full size table
Table 2 Thermophysical characteristics of the base fluid and the nanoparticles.
Full size table
Table 3 Numerical validation with previous study in particular case where \(S=Q={{\phi }_{1}}={{\phi }_{2}}=Rd=Da=Ec=Bi=M=0,\lambda =1,\Pr =6.2.\)
Full size table
Table 4 Computational data of skin friction for effective parameters.
Full size table
Table 5 Computational data of Nusselt number for effective parameters.
Full size table

The renovated boundary circumstances are

$$\begin{aligned}&{{y}_{a}}(1)-S,{{y}_{a}}(4),{{y}_{a}}(2)-\lambda ,\\&-{{\xi }_{4}}{{y}_{a}}(7)-Bi\left[ 1-{{y}_{a}}(6) \right] , {{y}_{b}}(2),{{y}_{b}}(6),{{y}_{b}}(4) \end{aligned}$$

First of all, the unknown initial conditions are obtained using the shooting technique and further the Runge–Kutta technique is useful for the computation. The iteration is continued to get the result of each profile up to a desired accuracy.

4 Results and discussion

The proposed study investigates the three-dimensional convective rotating hybrid nanofluid flow over a linear stretching/shrinking sheet under the influence of dissipative heat. The impact of dissipative heat, such as viscous and Joule heating effects, is considered to enrich the flow profiles. In addition to that, Hamilton–Crosser conductivity model is taken into account to study the behaviour of different shapes of the nano-particles. Table 1 shows the numerical range of different shapes of the particles. The hybrid nanofluid has unique properties and these are considered in the analysis, along with the influence of convective and Coriolis forces due to rotation. Table 2 depicts the thermal properties of the nanoparticles Ag and MoS\(_4\) as well as water, the base fluid. The mathematical formulation of the problem is presented and a set of partial differential equations is derived to model the fluid flow, heat transfer and nanoparticle distribution. These equations are then transformed into a non-dimensional form to facilitate numerical solutions. Runge–Kutta’s fourth-order shooting technique is used to simulate the various profiles of flow and heat transfer characteristics. The influences of various factors, such as rotation, convective heat, nanoparticle volume fraction and stretching/shrinking rate, are systematically analysed. Further, the validation of the present result is presented with the earlier work of Asghar et al [1] in the particular case and the numerical results are shown in table 3. The computation of each of the profiles is obtained by considering various factors within their proper range defined as \(M=1,\) \(Da=0.5,\) \(\omega =0.1,\) \(\lambda =0.5,\) \(\Pr =6.2,\) \(Q=0.1\), \(Ec=0.1,\) \(Rd=0.3,\) \(Bi=0.1,\) \({{\phi }_{1}}=0.01,\) \({{\phi }_{2}}=0.01,\) \(n=3\) except for the variation of the parameters which are displayed in the corresponding figure. Figure 2a depicts the influence of magnetic parameter (M) on the velocity profile for both cases of stretching/shrinking sheets. The application of a magnetic field to a conducting fluid gives rise to Lorentz force which acts perpendicular to the direction of the magnetic field as well as to the flow direction in the case of stretching \((\lambda >0)/\)shrinking sheet \((\lambda <0)\) and this force opposes the fluid flow which results in a decrease in the fluid velocity. When a fluid flows through a magnetic field, it can experience various effects due to the interaction between the magnetic field and the charged particles. In the presence of a strong magnetic field, the motion of charged particles (and hence the fluid) can be impeded. This can result in a reduction in fluid velocity, especially in conductive fluids. In the presence of a magnetic field, the fluid can experience a magnetic drag force, which is proportional to the magnetic field strength and the fluid velocity. This can affect the overall flow dynamics. A decrease in the velocity profile with an increase in porosity parameter (Da) in the case of stretching/shrinking medium is observed in figure 2b. It is because of the resistance offered by the porous medium. The porosity parameter also represents the void fraction within the medium. This also results in higher resistance to the fluid flow and a reduction in the velocity profile. Higher porosity typically leads to slower fluid velocities. This is because a higher porosity means there are more void spaces for the fluid to occupy, resulting in a lower flow rate. The influence of the rotational parameter \((\omega )\) on the velocity profile for both stretching/shrinking parameters is given in figure 3a. It is revealed that an increase in \(\omega \ \)decreases the velocity profile for \(\lambda >0\) and increases for \(\lambda <0\). The system is considered to be rotating with uniform velocity in a direction perpendicular to the z-axis. The rotational parameter gives the rate at which the fluid is rotating, an increase in \(\omega \) means the fluid is rotating at a high speed. This will cause a stronger centrifugal force that will act in a direction opposite to the fluid direction and hence the velocity of the fluid near the stretching sheet decreases. The nanoparticles also be affected by to increase in \(\omega \). The centrifugal force will make the particles move away from the sheet causing a reduction in the fluid velocity. Figure 3b represents the variation in velocity due to changes in solid volume fractions \(({{\phi }_{{{1}_{{}}}}}\) and \({{\phi }_{2}})\). Here, \({{\phi }_{1}}\) represents the solid volume fraction for Ag nanoparticle and \({{\phi }_{2}}\) represents the solid volume fraction for MoS\(_4\) nanoparticle. The range of these particles is presented as \({{\phi }_{{{1}_{{}}}}},{{\phi }_{2}}\in [0,0.09]\). The considered zero values of the particle concentration suggest the profile behaviour in the situation of pure fluid. However, the variation of stretching/shrinking is shown significantly. The study clarifies that for the enhanced particle concentration the fluid velocity is enhanced in magnitude in either of the case. This significant nature is attributed to the clogging of the particles near the surface of the sheet. The effect of the magnetic field on the transverse velocity profile is shown in figure 4a for both scenarios of stretching/shrinking cases. It is detected that there is a reduction in the velocity profile with an increase in the magnetic parameter. This is due to the Lorentz force which is developed due to the application of magnetised field to the conducting nanofluid and this force opposes the transverse velocity of the fluid particles. The rotational parameter \((\omega )\) also shows an effect on the transverse velocity.

Fig. 2
figure 2

(a) Magnetic parameter (M) vs. \({f}'(\eta )\) and (b) porosity parameter (Da) vs. \({f}'(\eta ).\)

Full size image
Fig. 3
figure 3

(a) Rotation parameter \((\omega )\) vs. \({f}'(\eta )\) and (b) volume fraction \(({{\phi }_{1}}\) and \({{\phi }_{2}})\) vs. \({f}'(\eta ).\)

Full size image
Fig. 4
figure 4

(a) Magnetic parameter (M) vs. \(g(\eta )\) and (b) rotation parameter \((\omega )\) vs. \({f}'(\eta ).\)

Full size image
Fig. 5
figure 5

(a) Porosity parameter (Da) vs. \(g(\eta )\) and (b) volume fraction \(({{\phi }_{1}}\) and \({{\phi }_{2}})\) vs. \(g(\eta ).\)

Full size image
Fig. 6
figure 6

(a) Magnetic parameter (M) vs. \(\theta (\eta )\) and (b) Eckert number (Ec) vs. \(\theta (\eta )\).

Full size image
Fig. 7
figure 7

(a) Radiation parameter (Rd) vs. \(\theta (\eta )\) and (b) Biot number (Bi) vs. \(\theta (\eta )\).

Full size image
Fig. 8
figure 8

(a) Volume fraction \(({{\phi }_{1}}\) and \({{\phi }_{2}}) \) vs. \(\theta (\eta )\) and (b) heat source/sink parameter vs. \(\theta (\eta ).\)

Full size image
Fig. 9
figure 9

(a) Shape of the nanoparticles vs. thermal conductivity ratio and (b) streamline pattern when \(\lambda <0.\)

Full size image
Fig. 10
figure 10

(a) Streamlines pattern when \(\lambda >0\) and (b) comparison with the previous study.

Full size image

In figure 4b, it is detected that the upsurge in \(\omega \) increases the transverse velocity profile for the stretching sheet as well as for the shrinking sheet. The Gaussian effect in the velocity profile is due to the rotational parameter, and in the absence of \(\omega \) we can see in the figure that the velocity profile is streamlined along the x-axis. In the presence of \(\omega \) the velocity profile shows a Gaussian-like effect. In figure 5a, the consequence of porosity parameter (Da) on transverse velocity profile is studied. It is observed here that an increase in Da decreases the transverse velocity profile which means higher porosity reduces the fluid flow in a direction perpendicular to the main flow. An increase in the number of void spaces in the porous medium will create more resistance to the fluid flow and hence there is a reduction in the velocity profile. Figure 5b depicts the role of the particle concentration of both the nanoparticles on the transverse velocity distribution. Similar to the behaviour described in figure 3b, for the velocity distribution it is observed that the transverse velocity also produces a significant hike in magnitude with increasing particle concentration. Figures 6–8 show the consequence of different parameters on the temperature profile for both stretching as well as shrinking sheets. It is observed in figure 6a that the consequence of the magnetic parameter (M) is the increase in the temperature profile for both \(\lambda >0\) and \(\lambda <0\). Presence of a magnetic field enhances the heat transportation within the nanofluid. The interaction between the nanoparticles and the magnetic field leads to an additional convection which is the reason for more efficient heat transmission. Eckert number (Ec) relates the kinetic energy of the fluid flow to the enthalpy change of the fluid due to heating. Figure 6b shows that the upsurge in Ec increases the temperature profile for both stretching/shrinking sheets. Higher Ec means higher kinetic energy compared to the enthalpy change and hence higher temperature profile. This means that the fluid has a higher velocity and the motion of the fluid molecules is more significant in terms of its energy content. The high kinetic energy leads to increased mixing and agitation within the fluid. This can result in better heat transfer between the fluid and its surroundings. With higher kinetic energy, the fluid is better equipped to absorb and transfer heat. This can lead to an increase in the fluid temperature, especially if it is in contact with a heat source. The effect of the thermal radiation parameter (Rd) on the temperature profile is shown in figure 7a. It can be seen that an increase in Rd increases the temperature profile because Rd contributes to the radiation heat transfer in the system. An increase in Rd implies that the effect of radiation heat transmission is more significant and hence increase in temperature profile is observed. This principle is relevant in various engineering applications. For example, in industrial processes involving high-temperature furnaces or heat exchangers, understanding radiative heat transfer is crucial for designing systems that maintain or control fluid temperatures. Effect of Biot number (Bi) on the temperature profile is studied in figure 7b and it is observed that increase in Bi increases the temperature profile. Bi represents the ratio of heat transfer resistance within a solid to that of a solid–fluid interface. Higher Bi means that convective heat transfer from the hot fluid at the sheet’s bottom is more significant to the conductive heat transfer within the sheet. This leads to higher heat transfer rates and hence enhanced temperature profile. The variation in temperature due to change in solid volume fractions \(({{\phi }_{{{1}_{{}}}}}\) and \({{\phi }_{2}})\) is shown in figure 8a. It is noticed that an increase in \({{\phi }_{{{1}_{{}}}}}\) and \({{\phi }_{2}}\) increases the temperature profile for both \(\lambda >0 \) and \(\lambda <0\). Nanoparticles have higher surface-to-volume ratios and because of this they can interact with a larger portion of the surrounding fluid. An upsurge in the volume fraction leads to an increase in the absorption of heat resulting in a higher temperature profile. Figure 8b depicts the behaviour of temperature profile with an increase in heat source/sink parameter (Q). Increase in Q increases the temperature profile. A negative value of Q resembles the sink and a positive value of Q resembles the source parameters. The additional heat introduced into the system increases the temperature profile. In figures 6–8 it is observed that the temperature profile is more pronounced for shrinking sheets than for stretching sheets. In the case of a stretching sheet, the motion of the sheet promotes a larger region of interaction between the sheet and the surrounding fluid than the stretching sheet. In the case of a shrinking sheet, the flow converges towards the surface whereas in a stretching sheet it diverges away from the surface. Specifically, figure 9a illustrates the impact of the shapes of various nanoparticle on the properties of conductivity ratio. It is clarified that the increasing volume fraction helps in enhancing the conductivity ratio particularly using the Hamilton–Crosser model. Depending upon the shape, it is observed that the order of enhancement is displayed as \(\mathrm Spherical \le Brick \le Cylindrical\le Platelet\le Blade\). Figures 9b and 10a display the flow pattern simultaneously in the case of shrinking and stretching. Streamline figures provide a clear and intuitive visual representation of fluid flows through a system. By observing streamlines, one can identify important flow features such as vortices, stagnation points, separation points and recirculation zones. Streamlines provide information about the boundary layer, including boundary layer separation and transition from laminar to turbulent flow. When it comes to velocity streamlines, which represent the paths that fluid particles follow in a flow, shrinking and stretching can have significant impacts. The velocity streamlines often get compressed and converge through the diminishing centre when a fluid region experiences contraction. As a result, fluid molecules are compelled to cluster closer to one another in the direction of contraction. Hence, fluid particles are compressed and their distances decrease, leading to an increase in the velocity magnitude. The rate of change of velocity along the streamline becomes more pronounced, leading to higher acceleration of fluid particles. Further, stretching refers to the opposite effect, where a fluid region experiences expansion or elongation. As fluid particles move farther apart, the velocity decreases due to the conservation of mass. The rate of change of velocity along the streamline becomes less pronounced, leading to lower acceleration of fluid particles. In figure 10b, a comparison graph is presented, illustrating the consequence of the radiation parameter on the temperature distribution. This graph is drawn from a previous study and it serves to visually demonstrate the differences or similarities between the current findings and those of the earlier research. To optimise the fluid flow in various applications, such as in heat transfer and cooling systems, the skin friction coefficients \({{C}_{fx}}\) and \({{C}_{fy}}\) are studied for various parameters. Table 4 shows the calculated values of the skin friction coefficient along the x- and y-axes for both stretching and shrinking cases. It is observed that the increase in magnetic parameter increases \({{C}_{fx}}\) (magnitude) for both \(\lambda >0\) and \(\lambda <0\). \({{C}_{fy}}\) is found to decrease in magnitude with an increase in magnetic parameter. The increase in M makes the magnetic nanoparticles align near the surface and hence there arises a non-uniform distribution of the particles within the fluid. Due to this, flow pattern near the surface changes, leading to an increase in skin friction. It is also observed that changing the porosity parameter does not have much impact on the skin friction coefficients. There is a slight variation but overall, it is less significant. Similar to the porosity parameter, the rotational parameter also shows minor influence on the skin friction coefficients. For stretching, increasing volume fraction it is observed that skin friction coefficients decrease, indicating reduced resistance to flow. In the case of shrinking, decreasing volume fraction, the skin friction coefficient increases, indicating higher resistance to flow. In table 5, the Nusselt number (Nu) is calculated for different values of pertinent parameters. It is observed that increase in M decreases Nu for both stretching and shrinking cases. The porosity parameter has a minor effect on Nu. It is observed that the presence of porous media does not significantly influence heat transfer. The other parameters like Ec,  \(\Pr , \) Rd,  Bi show less variation in Nu with small variations in the respective parameters. It is observed that higher volume fractions of nanoparticles lead to effective heat transfer and hence lower Nu. The source/sink parameter appears to have a minor influence on the Nusselt number.

5 Conclusion

The present study analyses the effect of various parameters on a hybrid nanofluid which is considered to be flowing over a stretching/shrinking sheet. The study was based on both graphical and tabular forms.

  • The application of a magnetic field to the fluid resulted in a decrease in fluid velocity due to the development of Lorentz force, which opposes the fluid flow. It was observed for both stretching\(/\)shrinking cases.

  • Increasing the porosity parameter led to a decrease in fluid velocity.

  • The centrifugal force caused by rotation influences the flow of the fluid and because of that movement of nanoparticles was affected.

  • Higher volume fractions of nanoparticles led to higher temperature profiles.

  • Increase in thermal radiation and Biot number led to increase in the temperature profile.

The overall study provided valuable insights into the behaviour of hybrid nanofluid over stretching/shrinking sheets and their heat transfer characteristics. The results can have implications in various applications and can help while designing and optimising various practical applications like heat transfer and cooling systems.