Introduction

When determining viscosities of complex fluids that contain solids such as heavy oils, emulsions or slurries, the convectional viscometer types, i.e., concentric cylinders, or cone and plate, are often not suitable. This is because either the narrow gap or geometry would not accommodate the particle size (Roos et al. 2006), inability to maintain the particles suspended or inability to achieve the desired homogeneity. Vane or helical ribbon mixer geometry types have been proposed as potential candidates for slurry characterization (Roos et al. 2006; Metzner and Otto 1957; Patterson et al. 1979; Carreau et al. 1993).

The most challenging task for the helical ribbon geometry systems is transforming measurements into viscous information that is defining the shear stress and shear rate especially for complex rheology fluids (Guillemin et al. 2008; Glenn and Daubert 2003; Omura and Steffe 2003; Sulaiman et al. 2012; Glenn et al. 2000; Choplin and Marchal 1997; McNamee and Conrad 2011; La Fuente et al. 1996; Estellé and Lanos 2008; Thakur et al. 2004; Castell-Perez et al. 1991; Wu and Liu 2015; Kalombo et al. 2014; Hammad 2014). This is because it is not straightforward to establish the shear stress and shear rate relationships for complex geometry and complex rheology systems in terms of measured parameters and fluid properties. This difficulty may lead to rigorous and time-consuming data analysis and experimentation to establish the geometric constants which may be dependent on fluid rheology as well (Castell-Perez et al. 1991).

The challenges of defining geometry for complex mixers such as vane or helical ribbon can be addressed by employing the Couette analogy concept (Choplin and Marchal 1997; La Fuente et al. 1996). Choplin successfully applied the Couette analogy concept to helical ribbon geometry and obtained good results for Power-Law fluids of varying rheological parameters (Choplin and Marchal 1997).

In this study, an autoclave is modified by including a helical ribbon impeller and a torque sensor and calibrated with different fluids including Newtonian and Power-Law fluids. The Couette analogy concept is used to develop three different approaches of data interpretation including; analytical approach, dimensionless analysis, and empirical models. Using these three approaches, geometric constants are determined, and shear stress and shear rate definitions established.

Rotational mixer theory

The diameter of the helical ribbon impeller (real system) is approximated by an equivalent diameter of the corresponding concentric cylinder (virtual system) by use of the Couette analogy concept (Choplin and Marchal 1997; Wu and Liu 2015) as illustrated in Fig. 1. By defining torque at this equivalent diameter for a Power-Law fluid, the equivalent diameter can be defined as follows (Roos et al. 2006; Choplin and Marchal 1997).

$$d_{\text{e}} = D*\left[ {1 + \frac{2\omega }{n}\left( {\frac{{\pi hKD^{2} }}{2T}} \right)^{1/n} } \right]^{ - n/2}$$
(1)

where T is the generated torque at shaft speed ω, D is the vessel diameter, n is the flow behavior index, K is the consistency coefficient, and h is the vessel height.

Fig. 1
figure 1

Couette analogy principle (D = 0.083 m, d = 0.070 m, h = 0.114 m, d e = 0.076 m)

Full size image

The equivalent diameter can be determined by measuring torque at several rotational speeds using standard Power-Law fluids. Using this equivalent diameter, several other terms needed may be defined including Reynolds number, power number, shear rate, and shear stress. The following section discusses the different approaches that can be used to establish these definitions.

Method I: analytical

Starting with the equation of motion, it is easy to develop the following equation relating the measured torque to rotational speed for Power-Law fluids (Carreau et al. 1993).

$$T = 2\pi h \left[ {\frac{1}{{r_{\text{e}}^{ - 2/n} - R^{ - 2/n} }}} \right]^{n} \;K\left( {\frac{2 }{n}\omega } \right)^{n}$$
(2)

where r e is the equivalent radius and R is the vessel radius.

There are several ways in which Eq. (2) can be re-arranged into shear rate and shear stress components (Roos et al. 2006; Choplin and Marchal 1997; Steffe 2007). The two methods in which Eq. (2) can be re-arranged analytically are discussed next.

First analytical approach

The most common way is to define torque at the equivalent diameter for complex geometries. The drawback to this option is prior determination of the equivalent diameter. This option leads to following shear stress–shear rate relationship.

$$\frac{2}{{\pi hd_{\text{e}}^{2} }}T = K\left[ {\frac{2 }{n} \frac{\omega }{{1 - \left( {{\raise0.7ex\hbox{${d_{\text{e}} }$} \!\mathord{\left/ {\vphantom {{d_{\text{e}} } D}}\right.\kern-0pt} \!\lower0.7ex\hbox{$D$}}} \right)^{2/n} }}} \right]^{n}$$
(3)

Equation (3) is of form

$$\tau = K\dot{\gamma }^{n}$$
(4)

where

$$\tau = \left( {\frac{2}{{\pi hd_{\text{e}}^{2} }}} \right)T = k_{1}^{\prime \prime } T$$
(5)
$$\dot{\gamma } = \left( {\frac{2 }{n} \frac{1}{{1 - \left( {{\raise0.7ex\hbox{${d_{\text{e}} }$} \!\mathord{\left/ {\vphantom {{d_{\text{e}} } D}}\right.\kern-0pt} \!\lower0.7ex\hbox{$D$}}} \right)^{2/n} }}} \right)\omega = k_{1}^{\prime } \omega$$
(6)

Both \(k_{1}^{\prime \prime }\) and \(k_{1}^{\prime }\) are functions of geometry and fluid rheology. The dependence on rheology is weak and may be neglected (Metzner and Otto 1957). The variation of shear rate constant/coefficient \(k_{1}^{\prime }\) with equivalent diameter and flow behavior index can be examined theoretically. Figure 2 shows shear rate constant/coefficient \(k_{1}^{\prime }\) as a function of flow behavior index and vessel diameter to equivalent diameter ratio.

Fig. 2
figure 2

The dependence of shear constant/coefficient on equivalent diameter d e and flow behavior index n

Full size image

It can be seen from Fig. 2 that above flow behavior index of 0.4, there is little dependence of the shear rate constant/coefficient on the equivalent diameter and the flow behavior index.

The shape of trends in Fig. 2 is governed by two terms in brackets of Eq. (6), namely \(\frac{2 }{n}\) and \({\raise0.7ex\hbox{${d_{\text{e}} }$} \!\mathord{\left/ {\vphantom {{d_{\text{e}} } D}}\right.\kern-0pt} \!\lower0.7ex\hbox{$D$}}\). For an increase in flow behavior index from 0.1 to 0.4, \(\frac{2 }{n}\) decreases from 20 to 5, whereas an increase in flow behavior index from 0.4 to 0.8, \(\frac{2 }{n}\) decreases from 5 to 2.5. This results in a quick decrease of \(k_{1}^{\prime }\) up to flow behavior index of 0.4 and a gradual decrease of \(k_{1}^{\prime }\) above the flow behavior index of 0.4.

Considering \({\raise0.7ex\hbox{${d_{\text{e}} }$} \!\mathord{\left/ {\vphantom {{d_{\text{e}} } D}}\right.\kern-0pt} \!\lower0.7ex\hbox{$D$}}\) equals to 1.2, for example, an increase in flow behavior index from 0.8 to 1.2 leads \(k_{1}^{\prime }\) to decreases from 6.8 to 6.3. This change is small compared to the measurement uncertainties (estimated at 7 %) and can therefore be neglected for practical purposes. This observation is in support of the Metzner and Otto (1957) hypothesis which assumes that the shear rate coefficient is constant.

Second analytical (proposed) approach

Alternatively, Eq. (2) can be simplified by modifying the term in the first bracket as follows

$$\frac{T}{{2\pi h{r_{\text{r}}}^{2} }} = K\left[ {\frac{2 }{n} \omega } \right]^{n}$$
(7)

where

$$\frac{1}{{r_{\text{e}}^{ - 2/n} - R^{ - 2/n} }} \equiv \frac{1}{{{r_{\text{r}}}^{ - 2/n} }}$$
(8)

and \(r_{\text{r}}\) is an intermediary term used to simplify the equation of motion.

Similarly, Eq. (7) is of form shown in Eq. (4) where

$$\tau = \left( {\frac{1}{{2\pi h{r_{\text{r}}}^{2} }}} \right)T = k_{2}^{\prime\prime} T$$
(9)

and

$$\dot{\gamma } = \frac{2 }{n}\omega = k_{2}^{\prime } \omega$$
(10)

\(k_{2}^{\prime \prime }\) is a function of fluid rheology and system geometry but \(k_{2}^{\prime }\) is a function of fluid rheology only.

Method II: dimensionless analysis

A fundamental relationship based on dimensionless numbers can be developed by analyzing the power consumption of mixer-type viscometers using the Buckingham-Pi theorem (Steffe 2007). This analysis shows that the power number is related to several other dimensionless groups, such as Reynolds number, Froude number, Weissenberg number, and several geometrical ratios (Sulaiman et al. 2012; Castell-Perez et al. 1991; Steffe 2007). However, for homogenous fluids under laminar flow, the power number is inversely proportional to the Reynolds number and the constant of proportionality is geometry dependent (Metzner and Otto 1957; Sulaiman et al. 2012; Steffe 2007). The transition from laminar to turbulent is observed at a Reynolds number of 10 (Castell-Perez et al. 1991) but may be extended to Reynolds numbers around 100 when a helical blades type is used (La Fuente et al. 1996).

The Power number (N Po ) is related to the Reynolds number (N Re ) by the following relationship:

$$N_{Po} = \frac{A}{{N_{Re} }}$$
(11)

where

$$N_{Po} = \frac{T}{{\rho \omega^{2} d_{\text{e}}^{5} }}$$
(12)
$$N_{Re} = \frac{{\rho \omega d_{\text{e}}^{2} }}{\eta }$$
(13)

η is the apparent viscosity.

Combining Eqs. (11), (12) and (13), we find:

$$T = A^{\prime } \omega \eta$$
(14)

where

$$A^{\prime } = Ad_{\text{e}}^{3}$$
(15)

Considering a Power-Law fluid

$$\left. {\begin{array}{*{20}l} {T = A^{\prime } \eta \omega } \hfill \\ {\eta = K\dot{\gamma }^{n - 1} } \hfill \\ \end{array} } \right\}\quad T = KA^{\prime } \omega \dot{\gamma }^{n - 1}$$
(16)

Assuming a constant shear coefficient, \(k_{\text{MO}}^{\prime }\) proposed by Metzner and Otto, Eq. (16) can be expressed as

$$\left( {\frac{{k_{\text{MO}}^{\prime } }}{{A^{\prime } }}} \right)T = K\left( {k_{\text{MO}}^{\prime } \omega } \right)^{n}$$
(17)

Also, Eq. (17) is of form shown in Eq. (4) where

$$\tau = \left( {\frac{{k_{\text{MO}}^{\prime } }}{{A^{\prime } }}} \right)T = k_{\text{MO}}^{\prime \prime } T$$
(18)

and

$$\dot{\gamma } = k_{\text{MO}}^{\prime } \omega$$
(19)

\(k_{\text{MO}}^{\prime }\) and \(k_{\text{MO}}^{\prime \prime }\) are considered to be constant for a given geometry and are determined experimentally (Metzner and Otto 1957).

Method III: empirical

As shown in the above two methods, several parameters are involved in transforming the experimental data into viscous information. Several researchers have reported different values/models for these parameters. This has resulted in lack of common criteria to define these parameters and thus laboratory testing almost always has been preceded by tedious calibration testing for each setup. However, for some common geometries, correlations have been developed to simplify data interpretation.

Castell-Perez et al. (1991) showed that the average shear stress and average shear rate for anchor-like geometries could be estimated from geometrical parameters and the flow behavior index using the following equations (Castell-Perez et al. 1991):

$$\dot{\gamma } = \left\{ {2\left[ {\frac{{\left( {{\raise0.7ex\hbox{$D$} \!\mathord{\left/ {\vphantom {D d}}\right.\kern-0pt} \!\lower0.7ex\hbox{$d$}}} \right)^{{{\raise0.7ex\hbox{${\left( {2 - n} \right)}$} \!\mathord{\left/ {\vphantom {{\left( {2 - n} \right)} n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}} }}{{\left( {{\raise0.7ex\hbox{$D$} \!\mathord{\left/ {\vphantom {D d}}\right.\kern-0pt} \!\lower0.7ex\hbox{$d$}}} \right)^{{{\raise0.7ex\hbox{$n$} \!\mathord{\left/ {\vphantom {n 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} - 1}}} \right]\left[ {\frac{d}{h}} \right]^{{{\raise0.7ex\hbox{$n$} \!\mathord{\left/ {\vphantom {n 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} } \right\}\omega = k_{\text{CP}}^{\prime } \omega$$
(20)

Cheng and Davis (1969) proposed the following relation for narrow gap geometry

$$\dot{\gamma } = \left\{ {\frac{1}{{K_{R} }}\left[ {1 + \frac{{K_{R} }}{{n^{\prime } }} + \frac{1}{3}\left( {\frac{{K_{R} }}{{n^{\prime } }}} \right)^{2} \left( {1 - n^{\prime \prime } } \right)} \right]} \right\}\omega = k_{\text{CD}}^{\prime } \omega$$
(21)

where,

$$K_{R} = \ln \left( {\frac{D}{d}} \right),\quad n^{\prime } = \frac{d\ln \left( \tau \right)}{d\ln \left( \omega \right)},\quad n^{\prime \prime } = \frac{{d\ln \left( {n^{\prime } } \right)}}{d\ln \left( \omega \right)}$$
(22)

Metzner and Otto (1957) proposed the following relationship for Power-Law fluids,

$$\dot{\gamma } = k_{\text{MO}}^{\prime } \omega$$
(23)

Combining Eqs. (23) and (16), the following relationship is established

$$\left[ {\frac{T}{{KA^{\prime } \omega }}} \right]^{1/n - 1} = k_{\text{MO}}^{\prime } \omega$$
(24)

Metzner-Otto’s approach requires the use of a Newtonian fluid and Eq. (14) to determine the geometric constant A′. The determination of the shear rate constant \(k_{\text{MO}}^{\prime }\) also requires the use of a Power-Law fluid.

Experimentation: apparatus, fluids and procedures

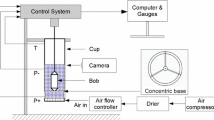
The mixing setup developed for this study consisted of a Parr autoclave (model 4547) equipped with a helical ribbon impeller, torque sensor, speed controller and an automated data acquisition system. In the device development process, the pitch blade turbine type impellers were replaced with the helical ribbon impeller, the internal cooling coils replaced with an external cooling jacket, and a torque sensor was installed. These modifications were employed following a guideline of good mixing and data quality, such as avoiding obstruction to flow field, avoiding hot spots, handling high viscosity and avoiding settling. The traditional autoclave is shown in Fig. 3, the modifications are represented in Fig. 4, whereas the new rheometer setup is shown in Fig. 5. The physical helical ribbon impeller diameter was 0.070 m (2.75 inches), and the cell diameter was 0.083 m (3.25 inches).

Fig. 3
figure 3

Traditional Parr autoclave model 4547

Full size image
Fig. 4
figure 4

Modified version of Parr autoclave

Full size image
Fig. 5
figure 5

Rheometers used in this study. a In-house rheometer, b MCR 301 rheometer

Full size image

The impeller-shaft system was rotated by a 93 W (0.125 hp) motor with variable speed control—from 0 to 32 rev/s. A torque sensor with an operating range of 0–1 Nm was installed to measure the torque on the shaft. The measured values of temperature, shaft speed and torque were recorded every second. A concentric cylinder rheometer, Anton Paar (MCR 301), was used to establish the rheological parameters of the fluids used in this study. The diameters of the cup and the bob used on the rheometer were 0.029 and 0.267 m, respectively. The cup and bob were both smooth surfaces. The samples were sheared from 0.01 to 1200 s−1.

Four Newtonian fluids were prepared and used in this study (Table 1). The viscosity of these fluids was determined at 21 °C within an error margin of ±5 %.

Table 1 Newtonian fluids
Full size table

Similarly, four non-Newtonian fluids were prepared using PAC powder at different concentrations and characterized with an Anton Paar (MCR 301) rheometer. The flow behavior index (n) and consistency coefficient (K) were determined at 21 °C within error bands of viscosity of ±10 and ±5 %, respectively. These rheological parameters were determined by directly fitting trend lines on to the flow curve generated from the MCR 301 rheometer data. However, the shear rate range of interested was 100–800 s−1 and therefore only data in this range were used in determining the rheological parameters of fluids. Table 2 shows the properties of the non-Newtonian fluids used in this study.

Table 2 Power-Law fluids
Full size table

During testing, fluid samples were placed in the autoclave and temperature equilibrated for at least 1800 s while mixing at 6.7 rev/s. Shaft speed was ramped up and down from 0 to 13.3 rev/s in steps of 0.8 rev/s. At each shaft speed, torque readings were recorded for about 60–180 s. Temperature was maintained at 21 ± 2 °C throughout the test by circulating glycol in the external jacket.

Results and discussion: calibration and rheological characterization

The average values of the measured torque at different shaft speeds are presented in Fig. 6. Fitting a trend line on N1 data gave an R-squared value of 0.98 indicating that the data is linear as expected for Newtonian fluids from Eq. (14). The first three data points of N2 were off the trend line, but when these points were removed, the remaining N2 data points gave an R 2 value of 0.99. N3 and N4 showed two slopes indicating transition from laminar or undeveloped flow to turbulent flow regime. The onset of turbulent flow leads to axial and radial velocity components, that is, flow in azimuthal direction. These other velocity components lead to additional energy consumption and, hence, increase in torque values. This early turbulent onset could be attributed to the low fluid viscosity. This implies that the device developed in this work may not be suitable for testing low-viscosity fluids. Figure 6 shows results of measured torque at different shaft speeds for the Newtonian fluids.

Fig. 6
figure 6

Average torque values at different shaft speeds for Newtonian fluids. The double arrow dotted lines indicate the multiple slopes observed with low-viscosity fluids

Full size image

Before starting data analysis, flow regimes need to be established, so that non-laminar data points can be discarded. Flow regimes were determined using power curves. Power curves for Newtonian fluids are presented in Fig. 7. From Eq. (11), a plot of power number against Reynolds number should yield an inverse line of slope A for a perfect laminar case. Since A is a geometric constant, all lines should have the same slope and should be closely aligned. The difference in N1 and N2 power curves is not significant and has almost the same slopes, whereas N3 and N4 were far apart and the difference between them is significant. This behavior could be due to the low viscosities of these fluids. Low-viscosity fluids transition to turbulent flow at low shaft speeds compared to high viscosity fluids. Since N3 and N4 did not achieve laminar flow regime, they were not used in the calibration process. For the high viscosity fluids, N1 and N2, the first few points did not align with the inverse line. This could be because flow is still developing, that is, not all the fluid is participating in flow until a certain shaft speed is reached. This undeveloped flow behavior is therefore responsible for the nonlinearity of the first few data points on the power curve for N1 and N2. Thus, the first five points data points for N1 and N2 were discarded because they were in the undeveloped flow region. These points can be clearly identified in Fig. 9, and this point will be discussed later.

Fig. 7
figure 7

Power curve showing undeveloped, laminar and turbulent regimes for the Newtonian fluids tested. The laminar data points are represented by the unfilled symbols. Only laminar data points were used in the calibration process

Full size image

Similarly, power curves were developed for the Power-Law fluids as shown in Fig. 8. Laminar flow was achieved at lower shaft speeds since Power-Law fluids have high apparent viscosity in this range of shaft speed. However, as shaft speed increases, Power-Law fluids experience turbulent flow due to reduced apparent viscosity. This is because as the apparent viscosity reduces turbulent eddies overcome the viscous forces and create additional velocity components which increases torque required to maintain a given flow velocity. Therefore, only data points that aligned well with the inverse line were selected for further analysis. For this case, only the first five data points for PL1 and PL2 were selected. It was not possible to identify at least three data points that were well aligned with the inverse line for PL3 and PL4 and thus all data points were considered to be turbulent.

Fig. 8
figure 8

Power curve showing laminar and turbulent regimes for the Power-Law fluids tested. The laminar data points are represented by the unfilled symbols. Only laminar data points were used in the calibration process

Full size image

In both cases above, Newtonian and Power-Law fluids, data analysis indicated that laminar flow existed at Reynolds numbers as high as 1000. This could be because the Reynolds number in this study was defined using the equivalent diameter concept. The equivalent diameter is bigger than the physical impeller diameter and the Reynolds number strongly depends on this value.

Determination of the geometric constants

The two geometric constants were determined namely the mixer constant A′, and the equivalent diameter, de. The mixer constant A′ was found to be 0.008 ± 0.0018 m3/rad determined using Newtonian fluids and Eq. (14). This value is a unique geometric parameter specific for the helical ribbon system used in this study. Also, the mixer constant A in Eq. (11) can be determined plotting the product of N Po and N Re against N Re as shown in Fig. 9. This plot should be a horizontal line in the laminar region and its value along the y-axis is the geometric constant A. The value of A for N1 and N2 are 16 and 20 rad−1, respectively, giving an average of 18 rad−1. The average value may be slightly affected by the number of data points used.

Fig. 9
figure 9

Variation of A with Reynolds number for Newtonian fluids—A is a constant in Eqs. 11 and 15. The laminar data points are represented by the unfilled symbols. Only laminar data points were used in determining constant A

Full size image

The equivalent diameter d e was determined from Eq. (1) using both Newtonian and Power-Law fluids and results are summarized in Fig. 10.

Fig. 10
figure 10

Equivalent diameter determined using several fluids

Full size image

The calculated d e using Newtonian fluids showed almost no dependence on viscosity or shaft speed. Since the apparent viscosities of Power-Law fluids decrease with increasing shaft speed which may results in turbulent flow, Newtonian fluids should be used in determining the equivalent diameter. For practical purposes, the equivalent diameter, d e, was assumed to be independent of shaft speed and fluid viscosity, and an average value of 0.076 ± 0.003 m was adopted for this set-up. Similarly, this value is a unique geometric parameter specific for the helical ribbon system used in this study.

Determination of the shear rate coefficient k′

There are five shear rate coefficient models presented in this work, some are to be determined from experimental data, whereas the others are to be calculated from geometric and rheological parameters. Analytical shear coefficient \(k_{1}^{\prime }\) can be calculated using Eq. (6), whereas \(k_{2}^{\prime }\) can be calculated using Eq. (10). The shear coefficient \(k_{\text{CP}}^{\prime }\) proposed by Castel-Perez, shear coefficient \(k_{\text{CD}}^{\prime }\) proposed by Cheng and Davis and shear coefficient \(k_{\text{MO}}^{\prime }\) proposed by Metzner and Otto can be can be calculated using Eqs. (20), (21) and (24), respectively. These shear coefficients were determined within a maximum error margin of ±15 %. This error margin was established using PL1 and PL2 data points since PL3 and PL4 data points were in turbulent region. Where experimental data are required, laminar data points were used (Table 3).

Table 3 Shear rate coefficient values
Full size table

With the exception of the shear coefficient values obtained using the Castel-Perez method, there was less variation in values obtained using a given method and different fluids compared to the variation in values obtained with different methods but same fluid.

The obtained values of \(k_{2}^{\prime }\) and \(k_{\text{MO}}^{\prime }\) were comparable to literature values of the similar geometry. The reported values using helical ribbon geometry range between 2 and 8 rad−1 (La Fuente et al. 1996; Castell-Perez et al. 1991; Steffe 2007). All the shear coefficient values were used to generate a flow curve for a fluid that had already been characterized with Anton Paar rheometer and when these flow curves were compared to that generated from Anton Paar rheometer data, \(k_{2}^{\prime }\) and \(k_{\text{MO}}^{\prime }\) provided a good match.

Since Metzner and Otto shear coefficient values gave the best match, the average shear coefficient value for this instrument was determined using \(k_{\text{MO}}^{\prime }\) values. Since most data points for PL3 and PL4 lay in the turbulent regime, average values were computed using PL1 and PL2. Therefore, the shear coefficient for this device was found to be 6 rad−1.

Determination of the shear stress coefficient k″

There are three shear stress models presented in this work, likewise, some are determined from experimental data, whereas the others are calculated from geometric and rheological parameters. The analytical shear stress coefficient \(k_{1}^{\prime \prime }\) can be calculated using Eq. (5) and \(k_{\text{MO}}^{\prime \prime }\) can be calculated using Eq. (18). On the other hand, the shear coefficient \(k_{2}^{\prime \prime }\) can be determined from experimental data by plotting Eq. (9).

Similarly, all the shear stress coefficient values were used to generate a flow curve for a fluid that had already been characterized with Anton Paar rheometer and once again Metzner and Otto shear stress coefficient values gave the best match. Therefore, the average shear stress coefficient value for this instrument was determined using \(k_{\text{MO}}^{\prime \prime }\) values which was found to be 750 m−3 (Table 4).

Table 4 Shear stress coefficient values
Full size table

The shear rate and shear stress definitions established in this work for this mixer-type viscometer are given in terms of the shaft speed and measured torque as follows

$$\begin{array}{*{20}l} {{\text{shear}}\;{\text{definition}}} \hfill \\ {{\text{for}}\;{\text{the}}\;{\text{device}}} \hfill \\ \end{array} \equiv \left\{ {\begin{array}{*{20}l} {\dot{\gamma } = k^{\prime } \omega = 6\omega } \hfill \\ {\tau = k^{\prime \prime } T = 750T} \hfill \\ \end{array} } \right.$$
(25)

Characterization of Power-Law fluids

The instrument was used to determine the rheological parameters of two unknown Power-Law fluids, and results were compared to Anton Paar rheometer measurements. Figure 11 shows performance and sensitivity of the device on these Power-Law fluids. The measured apparent viscosity values were with ±15 % of the Anton Paar values especially at low shear rates.

Fig. 11
figure 11

Sensitivity on the measured Power-Law fluid apparent viscosity

Full size image

Conclusions

A new mixer-viscometer was developed to characterize both settling and non-settling slurries. The geometry of this device is specifically important because it helps in suspending particles while minimizing vortex formation. The device was successfully calibrated using Newtonian and non-Newtonian liquids.

Couette analogy concept was used to develop mathematical models defining the equivalent diameter, shear rate and shear stress in terms of measurable parameters for the helical ribbon impeller. A new analytical methodology to simplify the relationship between the shear rate and the measured parameters was proposed. The equivalent diameter was used to define the power number and Reynolds number. An inverse line proved to be an important tool in identifying laminar flow data points on the power curve.

The dependence of the equivalent diameter on fluid rheology is weak and may be neglected for practical purposes. The shear rate coefficient was found to be a weak function of the fluid rheology and system geometry above the flow behavior index of 0.4. Metzner and Otto method gave the best shear coefficient and shear stress coefficient match when results were compared to Anton Paar rheometer (MCR 301). Therefore, shear coefficient and shear stress coefficient for this device were determined using average values from the Metzner and Otto method.

Testing a Power-Law fluid on the device showed excellent agreement with Anton Paar rheometer (MCR 301) measurements. The calibrated device can be used for any fluid rheology and not limited to the rheology of the fluid used to calibrate it. Also, using this device does not require prior knowledge of the fluid rheology of the sample to be characterized. We expect the developed device will help in charactering systems with solids.