1 Introduction

In the broadest sense, reliability is defined as a “measure of performance of the systems”. A design engineer is usually asked to maximize the system reliability and reduce its cost simultaneously. These conflicting objectives affect system efficiency. A system is considered more efficient if it achieves its optimum goals simultaneously. Niwas and Garg (2018) proposed an approach for analyzing the reliability and profit of an industrial system based on the cost-free warranty policy. However, multi-objective reliability models of the system design provide a better interpretation in such a situation. Moreover, various kinds of uncertainty such as vagueness, incompleteness, and unreliability of input information are found in the decision making of reliability. So, the models of real-world application should be more flexible and adaptable to the human judgment and decision-making process (Garg and Sharma 2013). Fuzzy set theory (Zimmermann 1996) deals with the kind of uncertainty that arises due to imprecision associated with the complexity of the system as well as vagueness of human judgement (Chen 1994; Utkin and Gurov 1996; Bing et al. 2000; Mohanta et al. 2004; Bag et al. 2009; Mahapatra and Roy (2009); Garg and Sharma 2012; Garg 2016, 2017; Mahata et al. 2018; Hussain et al. 2018; Salahshour et al. 2018; Mondal 2018).

The fuzzy optimization techniques to multi-objective reliability problems can be viewed in Park (1987), Dhingra (1992), Rao and Dhingra (1992), Huang (1997), Ravi et al. (2000), Mahapatra and Roy (2006), Huang et al. (2005, 2006), Kishor et al. (2009), Kumar and Yadav (2017, 2019), and Muhuri et al. (2018). Generally, achieving the optimal reliability design is considered quite difficult due to its NP-hard character (Chern 1992). To resolve it, various heuristic approaches for solving reliability optimization can be found in the literature such as Huang et al. (2009), Ayyoub and El-Sheikh (2009), Ebrahimipour and Sheikhalishahi (2011), Damghani et al. (2013), Mutingi and Mbohwa (2014), Garg and Sharma (2013), Garg (2014), Garg et al. (2014a; 2014b), Pant et al. (2015), Garg (2015a, b, c), Kim and Kim (2017) etc.

The preference-based approach (Deb 2001) suggests converting the multi-objective optimization problem (MOOP) to a single-objective optimization problem (SOOP) by emphasizing one Pareto-optimal solution at a time. In a practical situation, such a method needs to be applied many times for getting multiple Pareto-optimal solutions. The other drawback of such method is the dependency on a number of user-defined parameters, which are difficult to set in the arbitrary problem. To fix up these issues, a number of MOEAs have been suggested. The primary reason for their developments is to find multiple Pareto-optimal solutions in a single simulation run. MOEAs work with a population of solutions and generate a well-diverse set of solutions near the true Pareto-optimal region. Over the past decades, many generations of MOEAs emerged in the literature such as MOGA-Multi-Objective Genetic Algorithm (Fonseca and Fleming 1993), NPGA-Niched Pareto Genetic Algorithm (Horn et al. 1994), NSGA-Non-dominated Sorting Genetic Algorithm (Srinivas and Deb 1994), SPEA-Strength Pareto Evolutionary Algorithm (Zitzler and Thiele 1998), PAES-Pareto Archived Evolution Strategy (Knowles and Corne 1999), PESA-Pareto Envelop-based Selection Algorithm (Corne et al. 2000), MOMGA-Multiobjective Optimization with Messy Genetic Algorithm (Veldhuizen and Lamont 2000), PESA-II (Corne et al. 2001), SPEA2 (Zitzler et al. 2002), NSGA-II (Deb et al. 2002), MOEA/D-Multi-objective Evolutionary Algorithm based on Decomposition (Zhang and Li 2007), AGE-Approximation Guided Evolutionary-II (Wagner and Neumann 2013), NSGA-III (Jain and Deb 2013; Deb and Jain 2014) etc. NSGA-II is a very popular second-generation elitist MOEA which has significant applications in the engineering design problems. It is known of its some of the features like parameter-less sharing, elitist strategy, classifying the solutions into the fronts, and less computational complexity. Simulation results on difficult test problems show that NSGA-II gives much better convergence and diversity near the true Pareto-optimal front (Deb et al. 2002) compared to especially elitists MOEAs like SPEA, PAES. Many MOEAs and their solution approaches can be viewed in Deb (2001), Konak et al. (2006), Coello et al. (2007), Das and Panigrahi (2009), and Zhang and Xing (2017). MOEA approach is well-suited to multi-objective reliability problems which are addressed by some researchers such as Salazar et al. (2006), Taboada et al. (2007), Wang et al. (2009), Kishor et al. (2009), and Kumar and Yadav (2017).

In this paper, a methodology is proposed to find the best optimal system design in fuzzy multi-objective reliability optimization problem. However, Kishor et al. (2009) proposed interactive fuzzy multi-objective reliability optimization problem as per the preference of the Decision-Maker (DM) using convex-concave, concave-convex, and sigmoidal shapes of the membership functions, but it does not give the best trade-off optimal solution which is a demand of the system design for a practical purpose. This leads to the motivation for finding the best trade-off or compromise solution using various combination of linguistic modifiers such as very, more or less and indeed and FRBS. This is an ideal approach as suggested by Deb (2001), where an effort is made to find multiple trade-offs optimal solutions with a wide range of values for the objectives and then one of the obtained solutions is chosen using higher-level information. The advantage of using NSGA-II is to find a well distributive set of Pareto-optimal solutions in a single simulation run. The proposed approach shows the efficacy over the existing approach (Ravi et al. 2000), where various kinds of aggregate operators are used to determine the optimal system design. The proposed approach is comparatively studied with the existing approach using box-plot comparison. The rest of the paper is organized as follows. Section 2 gives some preliminaries such as basic definitions, fuzzy rule-based system and the mathematical model of the problem. Section 3 gives a brief description of the NSGA-II algorithm. Section 4 gives the proposed methodology with an illustrative example. Section 5 gives the results with its discussion and Sect. 6 gives the conclusions.

2 Preliminaries

Definition 1

In general, an MOOP is defined as follows (Miettinen 2001):

$$ {\text{Minimize}}\;\;F\left( X \right) = \left[ {f_{1} \left( X \right), f_{2} \left( X \right), \ldots , f_{k} \left( X \right)} \right]^{T} $$
(1)
$$ {\text{subject}}\;{\text{to}}\;\;X \in \varOmega , $$

involving \( \left( {k \ge 2} \right) \) conflicting objective functions \( f_{i} :{\mathbb{R}}^{n} \to {\mathbb{R}} \) need to be minimized simultaneously. The decision (variable) vector \( X = \left[ {x_{1} , x_{2} , \ldots , x_{n} } \right]^{T} \in \varOmega \subset {\mathbb{R}}^{n} \), where \( \varOmega \) is the feasible region formed by constraint functions. The image of the feasible region denoted by \( Z \subset {\mathbb{R}}^{k} \) and it is called a feasible objective region. The elements of Z are called objective vectors denoted by \( z = \left[ {f_{1} \left( X \right), f_{2} \left( X \right), \ldots , f_{k} \left( X \right)} \right]^{T} \) consisting of objective functions values. If fi is to be maximized, it is equivalent to minimize \( - f_{i} \). When all the objective and the constraint functions are linear then the problem is called multi-objective linear programming problem (MOLPP). If at least one of the functions is nonlinear then the problem is called a multi-objective nonlinear programming problem (MONLPP). Correspondingly, if all the objective functions and the feasible region are convex then the problem is convex and if some of the functions are non-convex then the problem is non-convex. The concept of optimality in the MOOP is studied in terms of Pareto terminology, which is defined as follows.

Definition 2

Pareto dominance (Ngatchou et al. 2006; Coello et al. 2007): A vector \( X \in \varOmega \) is said to dominate another \( Y \in \varOmega \) denoted by \( X\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \prec } Y \) iff \( f_{i} \left( X \right) \le f_{i} \left( Y \right) \forall i = 1, 2, \ldots ,k, \) and there exists at least one \( f_{j} \left( X \right) < f_{j} \left( Y \right), j \in \left\{ {1, 2, \ldots ,k} \right\}, j \ne i \).

Definition 3

Pareto-optimal solution (Jimenez and Bilbao 2009; Garg and Sharma 2013): A solution vector \( X \in \varOmega \) is said to be Pareto-optimal solution (Pareto optimal) iff there does not exist another vector \( X^{\prime} \in \varOmega \) which dominates \( X \in \varOmega \).

Definition 4

Pareto-optimal set (Coello et al. 2007; Garg and Sharma 2013): The Pareto-optimal set is defined as

$$ PS := \left\{ {X \in \varOmega {\mid }\neg \exists X^{\prime} \in \varOmega : X^{\prime}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \prec } X} \right\} $$

Definition 5

Pareto-optimal front (Garg and Sharma 2013; Kumar and Yadav 2019): The Pareto-optimal front is defined as

$$ PF := \left\{ {F\left( X \right) = \left[ {f_{1} \left( X \right),f_{2} \left( X \right), \ldots ,f_{k} \left( X \right)} \right]^{T} \in Z{\mid }X \in PS} \right\}. $$

Definition 6

Fuzzy set (Zimmermann 1996): Let X be a collection of objects generically denoted by x. A fuzzy set \( \tilde{A} \) in X is a set of ordered pair defined in the form as

$$ \tilde{A} = \left\{ {\left( {x, \mu_{{\tilde{A}}} \left( x \right)} \right):x \in X} \right\} $$

where \( \mu_{{\tilde{A}}}:X \to \left[ {0, 1} \right] \) is called the membership function and its function value is called grade of membership of x in \( \tilde{A} \).

Definition 7

Linguistic hedge (or modifier) (Zimmermann 1996; Kerre and De Cock 1999): A linguistic hedge (or a linguistic modifier) is an operation that modifies the meaning of the term. Suppose \( \tilde{H} \) is a fuzzy set in X, then the modifier m generates the composite term \( \tilde{M} = m(\tilde{H}) \). Modifiers are frequently used in mathematical models as follows.

Concentration:

It decreases the membership grades of all the members of \( \tilde{H} \) by spreading in the curve. It is defined as:

$$ \mu_{{con(\tilde{H})}} \left( x \right) = \left( {\mu_{{(\tilde{H})}} \left( x \right)} \right)^{2} \;\;{\text{for}}\;{\text{all}}\;\;x \in X $$

Dilation:

It increases the membership grades of all members by spreading out the curve. It is defined as:

$$ \mu_{{dil(\tilde{H})}} \left( x \right) = \left( {\mu_{{(\tilde{H})}} \left( x \right)} \right)^{1/2} \;\;{\text{for}}\;{\text{all}}\;x \in X $$

Contrast intensification:

It affects an increase of the membership grades greater than or equal to 0.5 and a decrease of the membership grades smaller than 0.5. It is defined as:

$$ \mu_{{int(\tilde{H})}} \left( x \right) = \left\{ {\begin{array}{*{20}l} {2\left( {\left( {\mu_{{(\tilde{H})}} \left( x \right)} \right)^{2} } \right),} \hfill & {\mu_{{(\tilde{H})}} \left( x \right) \in \left[ {0, 0.5} \right]} \hfill \\ {1 - 2\left( {1 - \mu_{{(\tilde{H})}} \left( x \right)} \right)^{2} ,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

Therefore, in general, strong and weak modifiers are given as: \( m_{\delta } \left( {\mu_{{(\tilde{H})}} \left( x \right)} \right) = \left( {\mu_{{(\tilde{H})}} \left( x \right)} \right)^{\delta } \) = a strong modifier or concentrator, if \( \delta > 1 \) and a weak modifier or dilator if \( \delta < 1 \).

The following linguistic hedges are associated with above mathematical operators: very\( \tilde{H} = con(\tilde{H}) \); more or less\( \tilde{H} = dil(\tilde{H}) \); Indeed\( \tilde{H} = Int(\tilde{H}) \); plus\( \tilde{H} = \tilde{H}^{1.25} \); slightly\( \tilde{H} \)= int[plus\( \tilde{H} \)and not (very\( \tilde{H} \)].

2.1 Fuzzy rule-based system (FRBS)

An FRBS (Cordon 2011) is one of the major applications of fuzzy set theory. In a broad sense, fuzzy rule-based system is a system of rule-based, where fuzzy sets and fuzzy logic are used as tools for representing different forms of knowledge, modeling the interactions, and relationships between its variables. The architecture of FRBS is as shown in Fig. 1. It consists of four principal units: the fuzzifier module, fuzzy inference engine, knowledge base, and the defuzzifier module. These units are described as follows.

Fig. 1
figure 1

Architecture of fuzzy rule-based system

Full size image

  • Fuzzifier module: The inputs of the system are usually given by the crisp values. Since the data manipulation in FRBS is based on fuzzy set theory, so fuzzification is necessary. In this process, the numerical values of each crisp input are converted into a set of the membership grades defined by the membership functions of the linguistic values. A knowledge base expert or an optimization algorithm usually determines the shape and distribution of the membership functions on the universe of discourse.

  • Knowledge-base: It contains the knowledge specific to the domain of application. An FRBS is characterized by a set of linguistic statements derived by a domain expert to map inputs to outputs. Domain knowledge is usually represented in the form of a set of “IF–THEN” rules, also known as production rules, and it is expressed as:

IF (a set of conditions are satisfied) THEN (a set of actions can be inferred).

  • Inference engine: To deal with the fuzzy information described above, the fuzzy inference engine employs the fuzzy knowledge-based methods such as Mamdani, Sugeno, etc., (Zimmermann 1996; Cordon 2011; Suptami et al. 2019) to simulate human decision-making and infer outputs.

  • Defuzzifier module: This module defuzzifizes the processed fuzzy data into the crisp data which suits to real-world applications.

2.2 Mathematical model of the problem

Reliability is one of the crucial design parameters that affect the system’s performance significantly. Practically, the problem of system reliability is constructed as a typical nonlinear programming problem with nonlinear cost functions. Suppose the system consists of m components, the reliability of each component is given by rj; j = 1, 2, …, m and their corresponding costs are denoted by \( C_{j} (r_{j} ) \). Moreover, in reliability optimization, we need to be optimized several mutually conflicting objectives subject to several design constraints. For instance, a design engineer is asked to improve the system reliability (RS) with the reduction of system cost (CS) simultaneously. Therefore, multiple objectives have become an essential part of the reliability-based design of the engineering systems. In addition, the cost of reliability is assumed to be a monotonically increasing function of reliability (Aggarwal and Gupta 1975; Huang et al. 2005). Therefore, a suitable multi-objective reliability optimization model (Garg et al. 2014b) of the system design by considering the system reliability and the system cost as objectives is given as follows:

$$ {\text{Maximize}}\;\;R_{S} \left( {r_{1} , r_{2} , , \ldots ,r_{m} } \right) = \left\{ {\begin{array}{*{20}c} {\mathop \prod \limits_{j = 1}^{m} r_{j} \;{\text{for}}\;{\text{series}}\;{\text{system}}} \\ {\text{or}} \\ {1 - \mathop \prod \limits_{i = 1}^{m} \left( {1 - r_{j} } \right)\;{\text{for}}\;{\text{parallel}}\;{\text{system}}} \\ {\text{or}} \\ {{\text{combination}}\;{\text{of}}\;{\text{series}}\;{\text{and}}\;{\text{parallel}}\;{\text{system}}} \\ \end{array} } \right. $$
(2)
$$ {\text{Minimize}}\;C_{S} \left( {r_{1} , r_{2} , \ldots ,r_{m} } \right) = \mathop \sum \limits_{j = 1}^{m} C_{j} \left( {r_{j} } \right) $$
$$ {\text{Or,}}\;{\text{Minimize}}\;( - R_{S} ,C_{S} ) $$

subject to \( r_{j,min} \le r_{j} \le 1 \), \( R_{S, min} \le R_{S} \le 1 \), for \( j = 1,2, \ldots ,m \).

3 Elitist non-dominated sorting genetic algorithm (NSGA-II)

Non-dominated sorting genetic algorithm (NSGA) was initially developed by Srinivas and Deb (1994). NSGA uses Goldberg’s domination criterion (1989) to rank the solutions and utilizes fitness sharing approach to maintain the diversity in the solution set. It has been criticizing especially for non-elitist approach, high computational complexity and specifying the sharing parameter. To cope up these issues, Deb et al. (2002) developed an improved version of NSGA and called it as NSGA-II by introducing some new features such as fast non-dominated sorting algorithm, crowding distance, crowded-comparison operator.

A fast-non-dominated sorting approach gives the worst-case computational complexity as \( O\left( {k\left( {2N} \right)^{2} } \right) \), where k is the number of objectives and N is the population size. This approach searches iteratively non-dominated solutions into different fronts. First, for each solution i in the population, the algorithm calculates two entities:

  1. (i)

    ni, the number of solutions dominating i,

  2. (ii)

    Si, a set of solutions dominated by i.

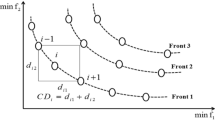
The solutions for which \( n_{i} = 0 \) belong to the first front. Second, for each member j in the set Si, the value of nj is reduced by one. If any nj is reduced to zero during this stage, the corresponding member j is put in the second front. The above process is continued with each member in the second front to identify the third front and so on. Furthermore, NSGA-II applies the concept of crowding-distance assignment with the worst-case computational complexity as \( O\left( {k\left( {2N} \right)\log \left( {2N} \right)} \right) \). The introduction of crowding-distance replaces the fitness sharing approach that requires a sharing parameter to be set by the user. The crowding-distance of the ith solution in the pth objective function is denoted by dip and its overall crowding-distance value is denoted by CDi (See Fig. 2). These values are calculated as follows:

$$ d_{ip} = \frac{{f_{p}^{i + 1} - f_{p}^{i - 1} }}{{f_{p}^{max} - f_{p}^{min} }} $$
(3)
$$ CD_{i} = \mathop \sum \limits_{p = 1}^{k} d_{ip} $$
(4)

where \( f_{p}^{i + 1} \) and \( f_{p}^{i - 1} \) denote the pth objective function of the \( \left( {i + 1} \right)^{th} \) and \( \left( {i - 1} \right)^{th} \) individual (solution) respectively, and \( f_{p}^{max} \) and \( f_{p}^{min} \) represent the maximum and minimum values of the pth objective function.

Fig. 2
figure 2

Fitness evaluation and individual crowding distance estimation of NSGA-II

Full size image

A higher value of crowding-distance gives the lesser crowded region and vice versa (Deb et al. 2002). So, the crowding-distance selects the solutions located in less-crowded regions which are extended up to the entire front for making diversity in the solution set. Finally, NSGA-II introduces an elitist strategy with the worst-case computational complexity \( O\left( {2N\log \left( {2N} \right)} \right) \). The elitist strategy (Zitzler et al. 2000; Laumanns et al. 2002) is used to enhance the convergence of an MOEA and avoid the loss of optimal solutions after getting it. In Fig. 3, an evaluation cycle of the NSGA-II is shown. First, an offspring Qt of size N is obtained by using the genetic operators such as selection, recombination, and mutation. A combined population Rt of size 2 N is then formed which consists of the current population Pt and the offspring population Qt. By using fast non-dominated sorting, Rt is divided into different fronts \( PF_{1} , PF_{2} , \ldots ,PF_{l} \). Let the number of solutions in each front PFi be Ni. Next, we choose members for the new population \( P_{t + 1} \) from the front PF1 to \( PF_{t - 1} \), noting that \( N_{1} + N_{2} + \cdots + N_{t} > N \) and \( N_{1} + N_{2} + \cdots + N_{t - 1} \le N \). Afterwards, to get the exactly N population members in \( P_{t + 1} \), we sort the solutions in front PFt using the crowding distance sorting procedure and choose the best solutions to fill any empty slot in the new population \( P_{t + 1} \). This process is continued until the termination condition is satisfied. The pseudo code of the NSGA-II algorithm is given as follows.

Fig. 3
figure 3

Evaluation cycle of the NSGA-II algorithm (Deb et al. 2002)

Full size image

Step 1. Initialize randomly a parent population P0 of size N. Set \( t = 0 \).

Step 2. Assign fitness (rank) according to non-domination level and crowded-comparison operator.

Step 3. whilet < number of maximum generations do

  1. (i)

    Create an offspring population Qt of size N applying selection, crossover, and mutation.

  2. (ii)

    Combine via \( R_{t} = P_{t} \cup Q_{t} \).

  3. (iii)

    Sort on Rt and classifying them into non-dominated fronts PFi, \( i = 1, 2, \ldots , {\text{etc}} \).

  4. (iv)

    Set a new population \( P_{t + 1} = \emptyset \) and set a counter \( i = 1 \).

while Parent population size \( \left| {P_{t + 1} } \right| + \left| {PF_{i} } \right| < N \)do

  1. (i)

    Calculate the crowding distance of PFi.

  2. (ii)

    Add the ith non-dominated front PFi to the parent population \( P_{t + 1} \).

  3. (iii)

    i = i + 1.

end while

  1. (v)

    Sort the PFi using the crowding distance-based comparison operator.

  2. (vi)

    Fill the parent population \( P_{t + 1} \) with the first \( N - \left| {P_{t + 1} } \right| \) solutions of PFi.

  3. (vii)

    Generate the offspring population \( Q_{t + 1} \).

  4. (viii)

    Set \( t = t + 1 \).

end while

Step 4. Collect the non-dominated solutions in vector P.

4 Proposed methodology

The proposed methodology is given step by step as follows.

Step 1. Fuzzification of the given model of the problem.

The values of the first objective RS in (2) belong to [0, 1]. The fuzzy set \( \tilde{R}_{S} \) is created as per the degree of satisfaction \( \alpha_{R} \) with values of RS. Similarly, the second objective in (2) is CS and its possible value lies in [0, \( \infty \)). The fuzzy set \( \tilde{C}_{S} \) is created as per the degree of satisfaction \( \alpha_{C} \) with values of CS. The membership functions of \( \tilde{R}_{S} \) and \( \tilde{C}_{S} \) are respectively, defined as:

$$ \mu_{{\tilde{R}_{S} }} = \left\{ {\begin{array}{*{20}c} {0, R_{S} \le R_{S}^{l} } \\ {h_{1} \left( {R_{S} } \right), R_{S}^{l} \le R_{S} \le R_{S}^{u} } \\ {1, R_{S} \ge R_{S}^{u} } \\ \end{array} } \right. $$
(5)
$$ \mu_{{\tilde{C}_{S} }} = \left\{ {\begin{array}{*{20}c} {1, C_{S} \le C_{S}^{l} } \\ {h_{2} \left( {C_{S} } \right), C_{S}^{l} \le C_{S} \le C_{S}^{u} } \\ {0, C_{S} \ge C_{S}^{u} } \\ \end{array} } \right. $$
(6)

where \( R_{S}^{l} \) and \( R_{S}^{u} \) are the lower and upper limits on RS; \( C_{S}^{l} \) and \( C_{S}^{u} \) are the lower and upper limits on CS; \( h_{1} \left( {R_{S} } \right) \) is a monotonically increasing function of RS; \( h_{2} \left( {C_{S} } \right) \) is a monotonically decreasing function of CS. These values are determined by the DM according to the actual situation. Each membership function is required to be maximized so that it could achieve the maximum degree of satisfaction (Kumar and Yadav 2017). The shapes of \( \mu_{{\tilde{R}_{S} }} \) and \( \mu_{{\tilde{C}_{S} }} \) are shown in Figs. 4 and 5 respectively. The mathematical model of the problem given in (2) is reformulated as follows.

Fig. 4
figure 4

Monotonically increasing membership function for system reliability

Full size image
Fig. 5
figure 5

Monotonically decreasing membership function for system cost

Full size image
$$ {\text{Maximize}}\;(\mu_{{\tilde{R}_{S} }} ,\mu_{{\tilde{C}_{S} }} ) $$
(7)
$$ {\text{or,}}\;{\text{Minimize}}\;( - \mu_{{\tilde{R}_{S} }} , - \mu_{{\tilde{C}_{S} }} ) $$
$$ {\text{subject}}\;{\text{to}}\;r_{j,min} \le r_{j} \le 1,j = 1, 2, \ldots ,m $$

Theorem 1

The Pareto-optimal solutions of the FMOOP (7) satisfy the MOOP (2).

Proof

Let R* be a Pareto-optimal solution vector of (7). Then by definition of Pareto-optimal solution,

\( {\nexists } R \in \varOmega \) (feasible region) such that \( - \mu_{{\tilde{R}_{S} }} \left( R \right) \le - \mu_{{\tilde{R}_{S} }} \left( {R^{*} } \right) \) and \( - \mu_{{\tilde{C}_{S} }} \left( R \right) < - \mu_{{\tilde{C}_{S} }} \left( {R^{*} } \right) \).

\( \Leftrightarrow {\nexists } R \in \varOmega \) such that \( - h_{1} \left[ {R_{S } \left( R \right)} \right] \le - h_{1} \left[ {R_{S} \left( {R^{*} } \right)} \right] \) and \( - h_{2} \left[ {C_{S } \left( R \right)} \right] < - h_{2} \left[ {C_{S} \left( {R^{*} } \right)} \right] \)

\( \Leftrightarrow {\nexists } R \in \varOmega \) such that \( h_{1} \left[ {R_{S } \left( R \right)} \right] \ge h_{1} \left[ {R_{S} \left( {R^{*} } \right)} \right] \) and \( h_{2} \left[ {C_{S } \left( R \right)} \right] > h_{2} \left[ {C_{S} \left( {R^{*} } \right)} \right] \)

\( \Leftrightarrow {\nexists } R \in \varOmega \) such that \( R_{S } \left( R \right) \ge R_{S} \left( {R^{*} } \right) \) and \( C_{S } \left( R \right) < C_{S} \left( {R^{*} } \right) \) (since h1 is a monotonically increasing and h2 is a monotonically decreasing function).

\( \Leftrightarrow {\nexists } R \in \varOmega \) such that \( - R_{S } \left( R \right) \le - R_{S} \left( {R^{*} } \right) \) and \( C_{S } \left( R \right) < C_{S} \left( {R^{*} } \right) \)

\( \Leftrightarrow R^{*} \in \varOmega \) is a Pareto-optimal solution of the MOOP given by (2). □

Step 2. Find the Pareto-optimal solutions (POF) of the fuzzy multi-objective reliability problem in terms of the membership grades.

NSGA-II is applied to the FMOOP (7). The POF is obtained by settings the parameters of NSGA-II such as crossover probability (pc), mutation probability (pm), maximum number of generations \( \left( {t_{max} } \right) \), distribution indices for crossover \( (\eta_{c} ) \) and mutation \( (\eta_{m} ) \). On the basis of rigorous experiments and tuning of the parameters, the best POF is obtained.

Step 3. Modify the Pareto-optimal solutions (POF) in various forms of linguistic hedges.

Linguistic hedges modify the membership function values of RS and CS as (Indeed high, Indeed low), (Indeed high, Very low), (Indeed high, Low), (Indeed high, More or less low), (Very high, Indeed low), (Very high, Very low), (Very high, Low), (Very high, More or less low), (High, Indeed low), (High, Very low), (High, low), (High, More or less low), (More or less high, Indeed low), (More or less high, Very low), (More or less high, low), (More or less high, More or less low). It can be defined as follows.

Indeed High (IDH): It is a linguistic form of modifier “intensification” applied to \( \tilde{R}_{S} \) defined by

$$ \mu_{{\tilde{R}_{S} }} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {R_{S} \le R_{S}^{l} } \hfill \\ {2\left( {\frac{{R_{S} - R_{S}^{l} }}{{R_{S}^{u} - R_{S}^{l} }}} \right)^{2} ,} \hfill & {R_{S}^{l} \le R_{S} \le (R_{S}^{u} + R_{S}^{l} )/2} \hfill \\ {1 - 2\left( {1 - \left( {\frac{{R_{S} - R_{S}^{l} }}{{R_{S}^{u} - R_{S}^{l} }}} \right)} \right)^{2} ,} \hfill & {(R_{S}^{u} + R_{S}^{l} )/2 \le R_{S} \le R_{S}^{u} } \hfill \\ {1,} \hfill & {R_{S} \ge R_{S}^{u} } \hfill \\ \end{array} } \right. $$

Very High (VH): It is a linguistic form of modifier “concentration” applied to \( \tilde{R}_{S} \) defined by

$$ \mu_{{\tilde{R}_{S} }} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {R_{S} \le R_{S}^{l} } \hfill \\ {\left( {\frac{{R_{S} - R_{S}^{l} }}{{R_{S}^{u} - R_{S}^{l} }}} \right)^{2} ,} \hfill & {R_{S}^{l} \le R_{S} \le R_{S}^{u} } \hfill \\ {1,} \hfill & {R_{S} \ge R_{S}^{u} } \hfill \\ \end{array} } \right. $$

High (H): It is a linguistic form but no modification is applied to \( \tilde{R}_{S} \) which is the linear membership function as:

$$ \mu_{{\tilde{R}_{S} }} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {R_{S} \le R_{S}^{l} } \hfill \\ {\left( {\frac{{R_{S} - R_{S}^{l} }}{{R_{S}^{u} - R_{S}^{l} }}} \right),} \hfill & {R_{S}^{l} \le R_{S} \le R_{S}^{u} } \hfill \\ {1,} \hfill & {R_{S} \ge R_{S}^{u} } \hfill \\ \end{array} } \right. $$

More or Less High (MOLH): It is a linguistic form of modifier “dilation” applied to \( \tilde{R}_{S} \) defined by

$$ \mu_{{\tilde{R}_{S} }} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {R_{S} \le R_{S}^{l} } \hfill \\ {\left( {\frac{{R_{S} - R_{S}^{l} }}{{R_{S}^{u} - R_{S}^{l} }}} \right)^{1/2} ,} \hfill & {R_{S}^{l} \le R_{S} \le R_{S}^{u} } \hfill \\ {1,} \hfill & {R_{S} \ge R_{S}^{u} } \hfill \\ \end{array} } \right. $$

Indeed Low (IDL): Similarly, it is a linguistic form of modifier “intensification” applied to \( \tilde{C}_{S} \) defined by \( \mu_{{\tilde{C}_{S} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {C_{S} \le C_{S}^{l} } \hfill \\ {2*\left( {\frac{{C_{S}^{u} - C_{S} }}{{C_{S}^{u} - C_{S}^{l} }}} \right)^{2} ,} \hfill & {C_{S}^{l} \le C_{S} \le (C_{S}^{u} + C_{S}^{l} )/2} \hfill \\ {1 - 2*\left( {1 - \left( {\frac{{C_{S}^{u} - C_{S} }}{{C_{S}^{u} - C_{S}^{l} }}} \right)} \right)^{2} ,} \hfill & {(C_{S}^{u} + C_{S}^{l} )/2 \le C_{S} \le C_{S}^{u} } \hfill \\ {0,} \hfill & {C_{S} \ge C_{S}^{u} } \hfill \\ \end{array} } \right. \)

Very Low (VL): It is a modifier “concentration” applied to \( \tilde{C}_{S} \) defined by

$$ \mu_{{\tilde{C}_{S} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {C_{S} \le C_{S}^{l} } \hfill \\ {\left( {\frac{{C_{S}^{u} - C_{S} }}{{C_{S}^{u} - C_{S}^{l} }}} \right)^{2} ,} \hfill & {C_{S}^{l} \le C_{S} \le C_{S}^{u} } \hfill \\ {0,} \hfill & {C_{S} \ge C_{S}^{u} } \hfill \\ \end{array} } \right. $$

Low (L): It is a linguistic form but no modification is applied to \( \tilde{C}_{S} \) which is the linear membership function as:

$$ \mu_{{\tilde{C}_{S} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {C_{S} \le C_{S}^{l} } \hfill \\ {\left( {\frac{{C_{S}^{u} - C_{S} }}{{C_{S}^{u} - C_{S}^{l} }}} \right),} \hfill & {C_{S}^{l} \le C_{S} \le C_{S}^{u} } \hfill \\ {0,} \hfill & {C_{S} \ge C_{S}^{u} } \hfill \\ \end{array} } \right. $$

More or Less Low (MOLL): It is a linguistic form of modifier “dilation” applied to \( \tilde{C}_{S} \) defined by

$$ \mu_{{\tilde{C}_{S} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {C_{S} \le C_{S}^{l} } \hfill \\ {\left( {\frac{{C_{S}^{u} - C_{S} }}{{C_{S}^{u} - C_{S}^{l} }}} \right)^{1/2} ,} \hfill & {C_{S}^{l} \le C_{S} \le C_{S}^{u} } \hfill \\ {0,} \hfill & {C_{S} \ge C_{S}^{u} } \hfill \\ \end{array} } \right. $$

Step 4. Construct the composition of fuzzy relations.

Let \( \tilde{R}_{1} \left( {x,y} \right),\left( {x,y} \right) \in X \times Y \) and \( \tilde{R}_{2} \left( {y,z} \right),\left( {y,z} \right) \in Y \times Z \) be two fuzzy relations. These are constructed as:

\( \tilde{R}_{1} \) = [MOLH H VH IDH]; \( \tilde{R}_{2} \) = [MOLL L VL IDL]; The composition of \( \tilde{R}_{1} \) and \( \tilde{R}_{2} \) is defined by “max–min” as:

\( \tilde{R} = \tilde{R}_{1} \circ \tilde{R}_{2} = \left\{ {\left[ {\left( {x, z} \right),max_{y} \left\{ {min\left\{ {\mu_{{\tilde{R}_{1} }} \left( {x,y} \right),\mu_{{\tilde{R}_{2} }} \left( {y,z} \right)} \right\}} \right\} } \right]|x \in X,y \in Y, z \in Z } \right\} \), \( \mu_{{\tilde{R}_{1} \circ \tilde{R}_{2} }} \) is the membership function of a fuzzy relation on fuzzy sets \( \tilde{R}_{S} \) and \( \tilde{C}_{S} \).

The fuzzy relation \( \tilde{R} \) is 4 by 4 composition matrix called the matrix of maximum satisfaction level achieved by each combination of fuzzy relation.

Step 5. Induce the FRBS in each combination.

In this Step, FRBS is induced to infer the output called the efficiency of the system for each element of the fuzzy relation \( \tilde{R} \). Input variables RS and CS are categorized as LOW, HIGH, MEDIUM and EXTREME while output ES (system efficiency) as POOR, BELOW AVERAGE, GOOD, VERY GOOD, EXCELLENT and OUTSTANDING. Triangular membership functions are used to define the membership grades for each variable. Mamdani type fuzzy inference and centroid defuzzification methods are adopted in this model. The efficiency matrix of the system is denoted by ES. The corresponding values of RS and CS to each element in \( \tilde{R} \) is substituted in rule-viewer of MATLAB Fuzzy Logic Toolbox. This value gives the system efficiency to each relation. The flow diagram of the proposed methodology is as shown in Fig. 6.

Fig. 6
figure 6

Flow diagram of the proposed methodology

Full size image

Step 6. Find the best trade-off or compromise solution.

The best compromise solution in the fuzzy relation \( \tilde{R} \) or find the best relation in \( \tilde{R} \) which gives the maximum satisfaction level as well as maximum efficiency in the system design. It is obtained by max–min composition as well. The optimal system design is proposed as:

$$ \mu_{S, max} = \tilde{R} \circ \tilde{E}_{S} $$

where ‘\( \circ \)’ is the composition defined in Step 4.

4.1 Illustration

Let us consider a life support system in a space capsule (Ravi et al. 2000). This system needs a single path to its success which contains two redundant subsystems. Each subsystem connects with two redundant components 1 and 4, and each of the redundant subsystems connects in series with component 2 and the resultant pair of series–parallel arrangement forms two equal paths. In order to back up for the pair, component 3 enters as a third path. This problem forms a continuous nonlinear optimization problem and consists of four components, each having component reliability \( r_{j} ,j = 1,2,3,4 \). The Mathematical model of the life-support system using block diagram (see Fig. 7) is given as follows.

$$ {\text{Maximize}}\;R_{S} = 1 - r_{3} \left[ {\left( {1 - r_{1} } \right)\left( {1 - r_{4} } \right)} \right]^{2} - \left( {1 - r_{3} } \right)\left[ {1 - r_{2} \left\{ {1 - \left( {1 - r_{1} } \right)\left( {1 - r_{4} } \right)} \right\}} \right]^{2} $$
(8)
$$ {\text{Minimize}}\;C_{S} = 2\mathop \sum \limits_{j = 1}^{4} K_{j} r_{j}^{{\alpha_{j} }} $$
$$ {\text{subject}}\;{\text{to}}\;0.5 \le r_{j} \le 1,\;\;j = 1, 2, 3, 4 $$

where different parameters values of Kj, as \( K_{1} = 100,K_{2} = 100,K_{3} = 200,K_{4} = 150 \) and \( \alpha_{j} \) as \( \alpha_{1} = \alpha_{2} = \alpha_{3} = \alpha_{4} = 0.6 \).

Fig. 7
figure 7

Block diagram of the life-support system

Full size image

The problem is posed as “Maximize system reliability as close as possible to 1 with approximate system cost of 641.8 (cost units)”.

The MOOP given in (8) is reformulated as FMOOP:

$$ {\text{Maximize}}\;\left( {\mu_{{\tilde{R}_{S} }} ,\mu_{{\tilde{C}_{S} }} } \right) $$
(9)
$$ {\text{subject}}\;{\text{to}}\;0.5 \le r_{j} \le 1,\;\;j = 1, 2, 3, 4; $$

where the linear membership functions of RS and CS are given by

$$ \mu_{{\tilde{R}_{S} }} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {R_{S} \le 0.9} \hfill \\ {\frac{{ R_{S} - 0.9}}{0.99 - 0.9},} \hfill & {0.9 \le R_{S} \le 0.99} \hfill \\ {1,} \hfill & {R_{S} \ge 0.99} \hfill \\ \end{array} } \right. $$
(10)
$$ \mu_{{\tilde{C}_{S} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {C_{S} \le 641} \hfill \\ {\frac{{700 - C_{S} }}{700 - 641},} \hfill & {641 \le C_{S} \le 700} \hfill \\ {0,} \hfill & {C_{S} \ge 700} \hfill \\ \end{array} } \right. $$
(11)

5 Results and discussion

After applying the proposed approach, the results are graphically shown. The parameter settings for the NSGA-II algorithm are given in Table 1. NSGA-II is applied to the FMOOP (9). Here, Population size is taken as 60, out of which 43 solutions are found non-dominated. Linguistic hedges applied to the given problem are as shown in Figs. 8 and 9. Tables 2 and 3 give the list of linguistic hedges values applied to a set of optimal values. The POFs for all possible cases are demonstrated in Fig. 10. Table 4 gives a composite relation (or maximum satisfaction level) to each possible combination of linguistic hedges. The proposed FRBS model (see Fig. 11) is then invoked in each possible case. Table 5 gives encoding rules for the FRBS. In Fig. 12, the domain of input variables changes dynamically in each case and its output shows as a surface plot correspondingly. On the basis of maximum satisfaction level \( (\mu_{max} ) \), the optimal values of input variables RS and CS are obtained. These values are put in the rule-viewer of MATLAB Fuzzy Logic Toolbox (Coleman et al. 1999) of FRBS for getting the efficiency of the system. Finally, Table 6 gives the list of the optimal solutions and their efficiencies towards the system. The DM can use this information of his/her own perspectives in the decision-making. From Table 6, it is observed that (MOLH, MOLL) achieves the maximum satisfaction level highest at 0.75962, while (IDH, L) achieves the maximum satisfaction level lowest at 0.00059. From the efficiency point of view, (VH, L) reaches the highest efficiency at 59% and (MOLH, MOLL) reaches the lowest efficiency at 53.9%. It is also observed that (VH, MOLL) attains the highest \( \mu_{S, max} = 0.582 \) with maximum satisfaction level at 0.60123 and its efficiency at 58.2%. This value is obtained as the best optimal value in all the possible cases by the proposed approach. Ravi et al. (2000) solved this problem using various kinds of aggregate operators to look into the impacts of system design and different optimal designs are found. The proposed approach does not need any kinds of aggregators in the formulation of the FMOOP and solves the problem in purely multi-objective manner as suggested by Deb (2001). Figure 13 shows a box-plot comparison between the optimal values obtained by Ravi et al. (2000) and the proposed approach.

Table 1 Parameter settings for NSGA-II
Full size table
Fig. 8
figure 8

Linguistic hedges applied to \( \tilde{R}_{S} \)

Full size image
Fig. 9
figure 9

Linguistic hedges applied to \( \tilde{C}_{S} \)

Full size image
Table 2 Linguistic hedges applied to the system reliability \( R_{S} = \tilde{R}_{1} \)
Full size table
Table 3 Linguistic hedges applied to the system cost \( C_{S} = \tilde{R}_{2} \)
Full size table
Fig. 10
figure 10figure 10

POFs obtained on the basis of all possible combinations of linguistic hedges

Full size image
Table 4 Composition matrix \( \tilde{R} = \tilde{R}_{1} \circ \tilde{R}_{2} \)
Full size table
figure a
Fig. 11
figure 11

The proposed FRBS model

Full size image
Table 5 Encoded-rules for the FRBS
Full size table
Fig. 12
figure 12figure 12figure 12figure 12

Surface viewer plot for each combination of linguistic hedges

Full size image
Table 6 The list of optimal system designs and their efficiencies for all possible combinations suggested by linguistic hedges and the significance of bold values is discussed in Sect. 5
Full size table
Fig. 13
figure 13

Box-plot comparison of the objective values with the existing approach

Full size image

6 Conclusions

In this paper, a methodology is developed to provide the best optimal system design in the fuzzy multi-objective reliability optimization problem. FMOOP is solved by an elitist MOEA, namely, NSGA-II and the Pareto-optimal solution set is obtained in terms of the membership grades. After that, linguistic hedges are used to modify the solution set in various cases and FRBS is invoked effectively to find the system efficiency in each case. The conclusions of the proposed approach are drawn as follows:

  • The proposed approach does not require any kind of aggregator operators and deals with the problem in a purely multi-objective manner.

  • The advantage of using NSGA-II is to get a well-distributive solution set in one simulation run, where the DM gets more information such as non-dominated and their characteristics.

  • Various combinations of linguistic hedges (or modifiers) are applied to determine the optimal system design and FRBS is used to evaluate its efficiency.

  • The optimal system design obtained by the combination (MOLH, MOLL) gives the highest maximum satisfaction (achievement) level, while (IDH, L) gives the lowest.

  • From an efficiency point of view, (VH, L) gives the maximum system efficiency, while (MOLH, MOLL) gives the minimum.

  • The combination (VH, MOLL) gives the best optimal system design in all possible cases.

  • A box-plot comparison shows that the proposed approach gives a better spread of the optimal values in the entire search space compared to the existing approach.

  • The proposed approach gives flexibility to the DM for choosing the best optimal system design of his/her own interests.

  • The proposed approach can be extended to other high levels of uncertainty techniques such as type-2 fuzzy set, intuitionistic fuzzy set, LR type intuitionistic fuzzy set, interval-valued intuitionistic fuzzy set, etc.

  • The proposed approach may be useful to determine the optimal design in an engineering system.