Classical and Bayesian analysis of reliability characteristics of a two-unit parallel system with Weibull failure and repair laws

Abstract

The present paper deals with analysis of reliability characteristics of a two-unit parallel system under classical and Bayesian set ups. The system consists of two non-identical units arranged in parallel configuration. System failure occurs when both the units stop functioning. Failure and repair time distributions of each unit are taken as Weibull with common shape parameter but different scale parameters. Using regenerative point technique, various measures of system effectiveness useful to system designers and operating managers have been obtained. Further, since the life testing experiments are time consuming and as such the parameters representing the reliability characteristics of the system/unit are assumed to be random variables. Therefore, a Monte Carlo simulation study is also carried out to illustrate the results for considered system model.

1 Introduction

In real life situations the systems are becoming complex day by day due to their automation and ever increasing demand of society. The improvement in effectiveness in respect of reliability, availability and net expected profit has therefore become important in recent years. Incorporation of redundancy is one of the methods to enhance the reliability of such types of systems. Standby redundant systems (Goel et al. 1983, 1985a, b; Goyal and Murari 1984; Gupta et al. 1983, 1986, 1988) have been analyzed under different set of assumptions such as random shocks, delayed replacement in repair and post repair, two types of operation and repair and imperfect switch etc., Gupta and Chaudhary (1992) also analysed a two non-identical priority unit cold standby system model by taking Rayleigh distribution only of the failure time of non-priority unit. But, sometimes when standby system takes some significant time to start the operation due to imperfect or slow switching device, then it will be wisable to use redundant unit in parallel form with the main unit so that the system does not fail if the main operative unit fails. Keeping this fact in view, Malik et al. (2000) analyzed a two unit parallel system by giving the priority in repair to main unit over the inspection to duplicate unit. Gupta and Shivakar (2003) dealt with the analysis of a two-unit parallel system assuming the concept of waiting time of repairman. Chaudhary et al. (2007) analyzed two unit parallel system model in which the repair of failed unit is completed in one or two phases. It is worth mentioning here that all the above system models were analyzed by using regenerative point technique. Regenerative point technique or regenerative process is a stochastic process with time points at which the process probabilistically restarts. It was first introduced by Smith (1955). Brkic (1990) dealt with the interval estimation of the parameters of Weibull distribution. Seo et al. (2003) estimated lifetime and reliability of a repairable redundant system subject to periodic alternation. Yadavalli et al. (2005) analyzed a two component system with common cause shock failure under Bayesian set up. However, most of the above studies were mainly concerned to obtain various reliability characteristics such as mean time to system failure (MTSF), point wise and steady state availabilities etc., by using exponential distribution as failure and repair time distribution of units and not to estimate the parameter(s) involved in the life time/repair time distribution of system/unit.

The purpose of the present paper is to analyze a two non-identical unit parallel system model by using Weibull distribution for both failure and repair times with common shape parameter but different scale parameters. For a more concrete study of the system model, a simulation study is also carried out.

We evaluate the following reliability characteristics of interest to system designers as well as operating managers by using regenerative point technique.

• 1. Steady state transition probability and mean sojourn times in different states.

• 2. Reliability of the system and MTSF.

• 3. Pointwise and steady state availabilities of the system.

• 4. Expected busy period of the repairman in time interval (0, t) and in steady state.

• 5. Net expected profit incurred by the system in time interval (0, t) and in steady state.

Further, since no system/unit is perfect, it may fail any time so parameter representing the life time of the system/unit is assumed to be a random variable. Therefore, a simulation study is conducted for analyzing the considered system model both in classical and Bayesian set ups. The Monte Carlo simulation technique has been used in conducting the numerical study. In classical setup, the maximum likelihood (ML) estimates of the parameters involved in the model and reliability characteristics along with their standard errors (SE) and width of confidence intervals are obtained. In Bayesian setup, Bayes estimates of the parameters and reliability characteristics along with their posterior standard errors (PSE) and width of highest posterior density (HPD) intervals are computed. In the end, the comparative conclusions are drawn to judge the performances of the MLE and Bayes estimates.

2 System model description, notations and states of the system

The system consists of two non-identical units (unit-1 and unit-2) arranged in parallel network. Each unit has two modes—Normal (N) and Total failure (F). Initially system starts its functioning from state S₀ in which both the units are in normal mode and operative. When system operates with only one unit then the operative unit has increased failure rate in comparison to the situation when both the units are operative. The system failure occurs when both the units stop functioning. A single repairman is always available with the system to repair a failed unit on First Come First Served (FCFS) basis. Each repaired unit works as good as new. The failure and repair time distributions of each unit are taken to be independent having the Weibull density with common shape parameter ‘p’ but different scale parameters α and β as follows:

$$ {\text{f}}_{\text{i}} \left( {\text{t}} \right) = \alpha_{\text{i}} {\text{pt}}^{{{\text{p}} - 1}} { \exp }( - \alpha_{\text{i}} {\text{t}}^{\text{p}} ), $$

and

$$ {\text{g}}_{\text{i}} \left( {\text{t}} \right) = \beta_{\text{i}} {\text{pt}}^{{{\text{p}} - 1}} { \exp }( - \beta_{\text{i}} {\text{t}}^{\text{p}} ) , $$

where t ≥ 0; α_i and β_i, p > 0 and i = 1, 2 respectively for unit-1 and unit-2.

A real life example based on the system model under study may be visualized as power supply in a colony by two transformers: transformer-1 and transformer-2 may be considered as unit-1 and unit-2 respectively. Both transformers are connected in parallel configuration. Transformer-1 and Transformer-2 fails with failure rates h₁ (.) and h₂ (.). When transformer-1 has failed, then complete load falls on transformer-2 and therefore, transformer-2 fails with increased failure rate r₂ (.) > h₂ (.). Similarly, when transformer-2 fails, then increased failure rate of transformer-1 is taken as r₁ (.) > h₁ (.).

2.1 Notations

E:

Set of regenerative states = {S_o, S₁, S₂}

α_i/ β_i (i = 1, 2):

Scale parameter of failure/repair time distribution for ith unit

p:

Shape parameter of failure/repair time distribution of each unit

h_i(t):

Failure rate of ith unit when both the units are operative in parallel network; ${\text{h}}_{\text{i}} \left( {\text{t}} \right) = {{\upalpha}}_{\text{i}} {\text{pt}}^{{{\text{p}} - 1}} ,\quad {{\upalpha}}_{\text{i}} ,{\text{ p}},{\text{ t}} > 0$

r_i(t):

Increased failure rate of ith unit having the form; ${\text{r}}_{\text{i}} \left( {\text{t}} \right) = {{\upmu}}_{\text{i}} {\text{pt}}^{{{\text{p}} - 1}} ;\quad {{\upmu}}_{\text{i}} ,{\text{ p}},{\text{ t}} > 0$

j_i(t):

Repair rate of ith unit; ${\text{j}}_{\text{i}} \left( {\text{t}} \right) = {{\upbeta}}_{\text{i}} {\text{pt}}^{{{\text{p}} - 1}} ,\quad {{\upbeta}}_{\text{i}} ,{\text{ p}},{\text{ t}} > 0$

${{{\text{q}}_{\text{ij}} \left( \cdot \right)} \mathord{\left/ {\vphantom {{{\text{q}}_{\text{ij}} \left( \cdot \right)} {{\text{Q}}_{\text{ij}} \left( \cdot \right)}}} \right. \kern-0pt} {{\text{Q}}_{\text{ij}} \left( \cdot \right)}}$ :

Pdf and cdf of one step or direct transition time from ${\text{S}}_{i} \in {\text{E}}$ to ${\text{S}}_{\text{j}} \in {\text{E}}$

${\text{p}}_{\text{ij}}$ :

Steady state transition probability from state ${\text{S}}_{\text{i}}$  to ${\text{S}}_{\text{j}}$ such that, ${\text{p}}_{\text{ij}} = \mathop { \lim }\limits_{{{\text{t}} \to \infty }} {\text{Q}}_{\text{ij}} ({\text{t}})$

${\text{p}}_{\text{ij}}^{{ ( {\text{k)}}}}$ :

Steady state transition probability from state ${\text{S}}_{\text{i}}$ to ${\text{S}}_{\text{j}}$  via ${\text{S}}_{\text{k}}$ such that, ${\text{p}}_{\text{ij}}^{{ ( {\text{k)}}}} = \mathop { \lim }\limits_{{{\text{t}} \to \infty }} {\text{Q}}_{\text{ij}}^{{\left( {\text{k}} \right)}} ({\text{t}})$

Z_i (t):

Probability that system sojourns in state S_i up to time t

${{\uppsi}}_{\text{i}}$ :

Mean sojourn time in state ${\text{S}}_{\text{i}}$ i.e., $\psi_{\text{i}} = \int_{0}^{\infty } {{\text{P}}[{\text{T}}_{\text{i}} > {\text{t}}]{\text{dt}}}$

${\text{R}}_{\text{i}} \left( {\text{t}} \right)$ :

Reliability of the system at time t when system starts from ${\text{S}}_{\text{i}} \in {\text{E}}$

${\text{A}}_{\text{i}} \left( {\text{t}} \right)$ :

Probability that the system will be operative in state ${\text{S}}_{\text{i}} \in {\text{E }}$at epoch t

${\text{B}}_{\text{i}} \left( {\text{t}} \right)$ :

Probability that the repairman will be busy in state ${\text{S}}_{\text{i}} \in {\text{E}}$ at epoch t

${{\upmu}}_{\text{up}} ({\text{t}})$ :

Expected up time of the system during interval (0, t) i.e., ${{\upmu}}_{\text{up}} ({\text{t}}) = \int_{0}^{\text{t}} {{\text{A}}_{0} ({\text{u}}){\text{du}}}$

${{\upmu}}_{\text{b}} \left( {\text{t}} \right)$ :

Expected busy period of repairman during interval (0, t) i.e., ${{\upmu}}_{\text{b}} \left( {\text{t}} \right) = \int_{0}^{\text{t}} {{\text{B}}_{0} ({\text{u}}){\text{du}}}$

${\text{P}}\left( {\text{t}} \right)$ :

Profit incurred by the system during interval (0, t)

$*$ :

Symbol for Laplace Transform of a function i.e., ${\text{q}}_{\text{ij}}^{ *} = \int_{0}^{\infty } {{\text{e}}^{{ - {\text{st}}}} {\text{q}}_{\text{ij}} ({\text{t}}){\text{dt}}}$

$\cdot$ :

Regenerative point

$\times$ :

Non-regenerative point

2.2 Symbols for the states of the system

${\text{N}}_{{ 1 {\text{o}}}}$ :

Unit-1 is in N-mode and operative

${\text{N}}_{{ 2 {\text{o}}}}$ :

Unit-2 is in N-mode and operative

${\text{F}}_{{ 1 {\text{r}}}}$ :

Unit-1 is in F-mode and under repair

${\text{F}}_{{ 2 {\text{r}}}}$ :

Unit-2 is in F-mode and under repair

${\text{F}}_{{ 1 {\text{w}}}}$ :

Unit-1 is in F-mode and waiting for repair

${\text{F}}_{{ 2 {\text{w}}}}$ :

Unit-2 is in F-mode and waiting for repair

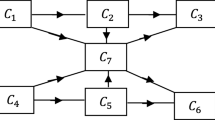
Using these symbols and assumptions stated earlier, the transition diagram of the system model along with all possible states and transitions is shown in Fig. 1. From Fig. 1, we observe that the states S₀, S₁ and S₂ are up states and S₃ and S₄ are failed states. We also observe that states S₃ and S₄ are non-regenerative since epochs of entrance from state S₁ to S₃ and S₂ to S₄ are non-regenerative whereas the other states are regenerative states.

Fig. 1

Transition diagram

3 Transition probabilities and sojourn times

The transition probability matrix (t.p.m) of the embedded Markov Chain is

$$ p_{\text{ij}} = \left( {\begin{array}{*{20}c} {{\text{p}}_{00} } & {{\text{p}}_{01} } & {{\text{p}}_{02} } \\ {{\text{p}}_{10} } & {{\text{p}}_{11} } & {{\text{p}}_{12}^{ ( 3 )} } \\ {{\text{p}}_{20} } & {{\text{p}}_{21}^{ ( 4 )} } & {{\text{p}}_{22} } \\ \end{array} } \right) $$

with non-zero elements.

As an illustration, to obtain ${\text{p}}_{01}$, the probability that the system transits from state ${\text{S}}_{0}$ to ${\text{S}}_{1}$ during time interval (0, ∞) we observe as follows¹ : ${\text{p}}_{01}$ = ∫[probability that the operating unit-1 in state ${\text{S}}_{0}$ fails during time (t, t + dt) and unit-2 does not fail up to time t]dt. Thus

$$ p_{01} = \int {\alpha_{1} pt^{p - 1} } e^{{ - \alpha_{1} t^{p} }} e^{{ - \alpha_{2} t^{p} }} dt = \frac{{\alpha_{1} }}{{\alpha_{1} + \alpha_{2} }} $$

Similarly,

$$ \eqalign{ p_{{02}} = & \frac{{\alpha _{2} }}{{\alpha _{2} + \alpha _{1} }};p_{{10}} = \frac{{\beta _{1} }}{{\mu _{2} + \beta _{1} }};p_{{12}}^{{(3)}} = \frac{{\mu _{2} }}{{\mu _{2} + \beta _{1} }}; \cr p_{{20}} = & \frac{{\beta _{2} }}{{\beta _{2} + \mu _{1} }};p_{{21}}^{{(4)}} = \frac{{\mu _{1} }}{{\mu _{1} + \beta _{2} }} \cr} $$

and the other elements of t.p.m will be zero.

It can be easily verified that

$$ \begin{gathered} {\text{p}}_{01} + {\text{p}}_{02} = 1 \hfill \\ {\text{p}}_{10} + {\text{p}}_{12}^{(3)} = 1;{\text{p}}_{20} + p_{21}^{(4)} = 1 \hfill \\ \end{gathered} $$

(1)

The mean sojourn time $\psi_{i}$ in state S_i is defined as the expected time for which the system stays in state S_i before transiting to any other state. If ${\text{T}}_{\text{i}}$ is the sojourn time in state ${\text{S}}_{\text{i}}$, then mean sojourn time in state ${\text{S}}_{\text{i}}$ is given by,

$$ \psi_{\text{i}} = \int {{\text{P}}({\text{T}}_{\text{i}} > {\text{t}}){\text{dt}}} $$

As an illustration, to obtain $\psi_{0}$, we observe as follows: $\psi_{0}$ = ∫[probability that the operating unit-1 and unit-2 in state ${\text{S}}_{0}$ do not fail up to time t] dt.

$$ \psi_{0} = \, \int {{\text{e}}^{{ - \alpha_{1} {\text{t}}^{\text{p}} }} {\text{e}}^{{ - \alpha_{2} {\text{t}}^{\text{p}} }} {\text{dt}}} = \frac{{\Upgamma (1 + \frac{1}{\text{p}})}}{{(\alpha_{1} + \alpha_{2} )^{{1/{\text{p}}}} }} $$

Similarly

$$ \begin{gathered} {{\uppsi}}_{1} = \, \int {{\text{e}}^{{ - {{\upbeta}}_{ 1} {\text{t}}^{\text{p}} }} {\text{e}}^{{ - {{\upmu}}_{2} {\text{t}}^{\text{p}} }}\, {\text{dt}}} = \int {{\text{e}}^{{ - ({{\upbeta}}_{1} + {{\upmu}}_{ 2} ){\text{t}}^{\text{p}} }}\, {\text{dt}}} = \frac{{\Upgamma \left( {1 + \frac{1}{\text{p}}} \right)}}{{({{\upbeta}}_{ 1} + {{\upmu}}_{ 2} )^{{1/{\text{p}}}} }} \hfill \\ {{\uppsi}}_{2} = \int {{\text{e}}^{{ - {{\upbeta}}_{2} {\text{t}}^{\text{p}} }} {\text{e}}^{{ - {{\upmu}}_{1} {\text{t}}^{\text{p}} }}\,{\text{dt}}} = \, \int {{\text{e}}^{{ - ({{\upbeta}}_{2} + {{\upmu}}_{1} ){\text{t}}^{\text{p}} }}\,{\text{dt}}} = \frac{{\Upgamma \left( {1 + \frac{1}{\text{p}}} \right)}}{{({{\upbeta}}_{2} + {{\upmu}}_{1} )^{{1/{\text{p}}}} }} \hfill \\ \end{gathered} $$

(2)

4 Analysis of characteristics

4.1 Reliability and MTSF

Let the random variable “T_i” be the time to system failure (TSF) when the system starts from $S_{i} \in \,E$, then the reliability of the system is given by

$$ {\text{R}}_{i} ({\text{t}}){\text{ = P [T}}_{\text{i}} > {\text{ t}}] $$

To determine the reliability of the system, we regard the failed states of the system as absorbing states i.e., those states in which system once reaches, remain there forever. By simple probabilistic arguments, we have the following recursive relations among R_i(t)’s (i = 0, 1, 2).

$$ {\text{R}}_{ 0} ( {\text{t) }} = {\text{ Z}}_{ 0} ( {\text{t) }} + {\text{ q}}_{ 0 1} ({\text{t}}) \, \copyright \,{\text{R}}_{1} ({\text{t}}) \, + {\text{ q}}_{ 0 2} ({\text{t}}) \, \copyright\,{\text{R}}_{2} ({\text{t}}) $$

(3)

$$ {\text{R}}_{ 1} ( {\text{t) }} = Z_{1} ({\text{t}}) \, + {\text{ q}}_{10} ({\text{t}}) \, \copyright\,{\text{R}}_{0} ({\text{t}}) $$

(4)

$$ {\text{R}}_{2} ({\text{t}}) = {\text{ Z}}_{2} ({\text{t}}) \, + {\text{ q}}_{20} ({\text{t}}) \, \copyright \,{\text{R}}_{0} ({\text{t}}) $$

(5)

where,

${\text{Z}}_{0} ({\text{t}}) = {\text{e}}^{{ - (\alpha_{1} + \alpha_{2} ){\text{t}}^{\text{p}} }} ,\;{\text{Z}}_{1} ({\text{t}}) = {\text{e}}^{{ - (\beta_{1} + \mu_{2} ){\text{t}}^{\text{p}} }}$ and ${\text{Z}}_{2} ({\text{t}}) = {\text{e}}^{{ - (\beta_{2} + \mu_{1} ){\text{t}}^{\text{p}} }}$

Taking the Laplace Transforms of relations (3, 4, 5) and simplifying for ${\text{R}}_{ 0}^{ *} ( {\text{s)}}$, omitting the argument ‘s’ for brevity, we get

$$ {\text{R}}_{ 0}^{ *} ( {\text{s)}} = \frac{{{\text{N}}_{ 1} ({\text{s}})}}{{{\text{D}}_{1} ({\text{s}})}} = \frac{{{\text{Z}}_{0}^{*} + {\text{q}}_{01}^{*} {\text{Z}}_{1}^{*} + {\text{q}}_{02}^{*} {\text{Z}}_{2}^{*} }}{{1 - {\text{q}}_{01}^{*} {\text{q}}_{10}^{*} - {\text{q}}_{02}^{*} {\text{q}}_{20}^{*} }} $$

(6)

where

$$ {\text{Z}}_{0}^{ *} ( {\text{s), Z}}_{1}^{ *} ( {\text{s)}} \;{\text{and}}\;{\text{Z}}_{2}^{ *} ( {\text{s)}} \;{\text{are the Laplace Transforms of}}\;{\text{Z}}_{ 0} ( {\text{t)}},\,{\text{Z}}_{1} ( {\text{t)}} \;{\text{and}}\;\;{\text{Z}}_{2} ( {\text{t)}}. $$

Taking the inverse Laplace Transform (ILT) of Eq. (6), we can get the reliability of the system when system starts from state S₀.

The MTSF can be obtained by using the well known formula-

$$ MTSF = E(T_{0} ) = \mathop {\lim }\limits_{s \to 0} R_{0}^{ * } (s) = \frac{{N_{1} (s)}}{{D_{1} (s)}} = \frac{{N_{1} (0)}}{{D_{1} (0)}} = \frac{{N_{1} }}{{D_{1} }} $$

(7)

Now using the results ${\text{q}}_{\text{ij}}^{*} (0) = {\text{p}}_{\text{ij}}$ and Z_i*(0) = $\psi_{\text{i}}$, we get

$$\eqalign{ N_{1} = & \psi _{0} + p_{{01}} \psi _{1} + p_{{02}} \psi _{2} \cr = & \frac{{\Gamma \left( {1 + \frac{1}{p}} \right)}}{{(\alpha _{1} + \alpha _{2} )^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 p}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$p$}}}} }} + \frac{{\alpha _{1} }}{{\alpha _{1} + \alpha _{2} }}\frac{{\Gamma \left( {1 + \frac{1}{p}} \right)}}{{(\beta _{1} + \mu _{2} )^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 p}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$p$}}}} }} \cr & + \frac{{\alpha _{2} }}{{\alpha _{1} + \alpha _{2} }}\frac{{\Gamma \left( {1 + \frac{1}{p}} \right)}}{{(\beta _{2} + \mu _{1} )^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 p}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$p$}}}} }} \cr D_{1} = & 1 - p_{{01}} p_{{10}} - p_{{02}} p_{{20}} \cr = & 1 - \frac{{\alpha _{1} }}{{\alpha _{1} + \alpha _{2} }}\frac{{\beta _{1} }}{{\beta _{1} + \mu _{2} }} - \frac{{\alpha _{2} }}{{\alpha _{1} + \alpha _{2} }}\frac{{\beta _{2} }}{{\beta _{2} + \mu _{1} }} \cr} $$

4.2 Availability analysis

Let us define A_i(t) as the probability that the system is up at time t when initially it starts from regenerative state ${\text{S}}_{\text{i}} \in \,{\text{E}}$. By simple probabilistic arguments, we have the following recursive relation among A_i (t)’s (i = 0, 1, 2).

$$ {\text{A}}_{0} ({\text{t}})\,\, = \,\,Z_{0} ({\text{t}}) \, + {\text{ q}}_{01} ({\text{t}}) \, \copyright\,{\text{A}}_{1} ({\text{t}}) \, + {\text{ q}}_{02} ({\text{t}}) \, \copyright\, {\text{A}}_{2} ({\text{t}}) $$

(8)

$$ {\text{A}}_{1} ({\text{t}})\,\, = \, \, Z_{1} ({\text{t}}) \, + {\text{ q}}_{10} ({\text{t}}) \, \copyright\, {\text{A}}_{0} ({\text{t}}) \, + {\text{ q}}_{12}^{(3)} ({\text{t}}) \, \copyright\, {\text{A}}_{2} ({\text{t}}) $$

(9)

$$ {\text{A}}_{2} ({\text{t}})\,\, = \, \, Z_{2} ({\text{t}}) \, + {\text{ q}}_{20} ({\text{t}}) \, \copyright \,{\text{A}}_{0} ({\text{t}}) \, + {\text{ q}}_{21}^{(4)} ({\text{t}}) \, \copyright \,{\text{A}}_{1} ({\text{t}}) $$

(10)

Taking the Laplace Transform of relations (8, 9, 10) and simplifying for ${\text{A }}_{ 0}^{ *} ( {\text{s)}}\,$, omitting the argument ‘s’ for brevity, we get

$$ {\text{A}}_{ 0}^{ * } ( {\text{s)}}\,\,{ = }\,\,\frac{{{\text{N}}_{ 2} ({\text{s}})}}{{{\text{D}}_{2} ({\text{s}})}} $$

(11)

where,

$${\text{N}}_{2} ({\text{s}})\,\, = {\text{Z}}_{0}^{*} \,\left( {1 - {\text{q}}_{{12}}^{{(3)*}} {\text{q}}_{{21}}^{{(4)*}} } \right)\, + \,{\text{q}}_{{01}}^{*} \,\left( {{\text{Z}}_{1}^{*} + {\text{Z}}_{2}^{*} {\text{q}}_{{12}}^{{(3)*}} } \right)\, + \,{\text{q}}_{{02}}^{*} \,\left( {{\text{Z}}_{1}^{*} {\text{q}}_{{21}}^{{(4)*}} + {\text{Z}}_{2}^{*} } \right)$$

and

$$ {\text{D}}_{2} ({\text{s}})\,\, = \,\,\left( {1 - \,{\text{q}}_{12}^{(3)*} {\text{q}}_{21}^{(4)*} } \right)\, - \,{\text{q}}_{01}^{*} \left( {{\text{q}}_{10}^{*} + \,{\text{q}}_{12}^{(3)*} {\text{q}}_{20}^{*} } \right)\, - \,{\text{q}}_{02}^{*} \left( {{\text{q}}_{10}^{*} {\text{q}}_{21}^{(4)*} + \,{\text{q}}_{20}^{*} } \right) $$

Taking the Inverse Laplace Transform of (11), we can get availability of the system when it starts from state S₀ for known values of the parameters.

In the long run, the steady state probability that the system will be operative, is given by,

$$ {\text{A}}_{ 0} \, = \, \mathop {\lim }\limits_{{{\text{t}} \to \infty }} {\text{ A}}_{ 0} ({\text{t}}) \, = \, \mathop {\lim }\limits_{{{\text{s}} \to 0}} {\text{ s A}}_{{}}^{ * } ({\text{s}}) \, = \, \frac{{{\text{N}}_{ 2} }}{{{\text{D}}_{2} }} $$

(12)

where,

$$ \begin{aligned} N_{2} & = \psi _{0} \left[ {p_{{10}} - p_{{20}} + p_{{10}} p_{{20}} } \right] \\ & \quad + \psi _{1} \left[ {p_{{01}} + p_{{02}} \left( {1 + p_{{20}} } \right)} \right] \\ & \quad + \psi _{2} \left[ {p_{{02}} + p_{{01}} \left( {1 - p_{{10}} } \right)} \right] \\ & = \frac{{\Gamma \left( {1 + \frac{1}{p}} \right)}}{{\left( {\alpha _{1} + \alpha _{2} } \right)^{{1/p}} }}\left[ {\frac{{\beta _{1} }}{{\beta _{1} + \mu _{2} }} - \frac{{\beta _{2} }}{{\beta _{2} + \mu _{1} }} + \frac{{\beta _{1} }}{{\beta _{1} + \mu _{2} }} \times \frac{{\beta _{2} }}{{\beta _{2} + \mu _{1} }}} \right] \\ & \quad + \frac{{\Gamma \left( {1 + \frac{1}{p}} \right)}}{{(\beta _{1} + \mu _{2} )^{{1/p}} }}\left[ {\frac{{\alpha _{1} }}{{\alpha _{1} + \alpha _{2} }} + \frac{{\alpha _{2} }}{{\alpha _{1} + \alpha _{2} }}\left( {{\text{1}} + \frac{{\beta _{2} }}{{\beta _{2} + \mu _{1} }}} \right)} \right] \\ & \quad + \frac{{\Gamma \left( {1 + \frac{1}{p}} \right)}}{{\left( {\beta _{2} + \mu _{1} } \right)^{{1/p}} }}\left[ {\frac{{\alpha _{2} }}{{\alpha _{1} + \alpha _{2} }} + \frac{{\alpha _{1} }}{{\alpha _{1} + \alpha _{2} }}\left( {{\text{1}} - \frac{{\beta _{1} }}{{\beta _{1} + \mu _{2} }}} \right)} \right] \\ \end{aligned} $$

and

$$\eqalign{ {\text{D}}_{2} = & \,\,\left( {{\text{p}}_{{10}} \, + \,{\text{p}}_{{12}}^{{(3)}} {\text{p}}_{{{\text{20}}}} } \right)\,\psi _{0} \cr & + \,\left( {{\text{p}}_{{01}} + {\text{p}}_{{02}} {\text{p}}_{{21}}^{{(4)}} } \right)\,{\text{m}}_{1} + \,\left( {{\text{p}}_{{01}} {\text{p}}_{{12}}^{{(3)}} + {\text{p}}_{{02}} } \right){\text{m}}_{2} \cr} $$

where

$$ {\text{m}}_{1} \,\, = \,\int {{\text{t}}\,\beta_{1} {\text{pt}}^{{{\text{p}} - 1}} {\text{e}}^{{ - \,\beta_{1} \,{\text{t}}^{\text{p}} }} \,{\text{dt}}} \,\, = \,\,\frac{{\Upgamma \left( {1 + \frac{1}{\text{p}}} \right)}}{{(\beta_{1} \,)^{{1/{\text{p}}}} }} $$

and

$$ {\text{m}}_{2} \,\, = \int {{\text{t}}\,\beta_{2} {\text{pt}}^{{{\text{p}} - 1}} {\text{e}}^{{ - \,\beta_{2} \,{\text{t}}^{\text{p}} }} {\text{dt}}} \,\, = \,\,\frac{{\Upgamma \left( {1 + \frac{1}{\text{p}}} \right)}}{{(\,\beta_{2} )^{{1/{\text{p}}}} }} $$

are the mean repair times of unit-1 and unit-2 respectively.

The expected up time of the system during (0, t) is given by-

$$ \,\mu \,_{\text{up}}^{{}} ({\text{t}})\,\, = \,\,\int\limits_{0}^{\text{t}} {{\text{A}}\,_{0} \left( {\text{u}} \right)\,{\text{du}}} $$

So that

$$ \mu_{\text{up}}^{*} ({\text{s}})\,\, = \,\,\frac{{{\text{A}}_{0}^{*} ({\text{s}})}}{\text{s}} $$

(13)

4.3 Busy period analysis

Let us define B_i(t) as the probability that the repairman is busy in repair of a failed unit at epoch t when the system starts from state ${\text{S}}_{\text{i}} \in \,{\text{E}}$. Using the probabilistic arguments, we have the following recursive relation among B_i(t)’s(i = 0, 1, 2).

$$ {\text{B}}_{0} ({\text{t}})\,\, = \,\,{\text{q}}_{01} ({\text{t}}) \, \copyright \,{\text{B}}_{1} ({\text{t}}) \, + {\text{ q}}_{02} ({\text{t}}) \, \copyright \,{\text{B}}_{2} ({\text{t}}) $$

(14)

$$ {\text{B}}_{1} ({\text{t}})\,\, = \,\,{\text{Z}}_{1}({\text{t}})\,\, + \,q_{10} (t) \, \copyright \,B_{0} (t) \, + \, q_{12}^{(3)} (t) \, \copyright \, B_{2} (t) $$

(15)

$$ {\text{B}}_{2} ({\text{t}})\, = \,\,{\text{Z}}_{2}({\text{t}})\,\, + \,{\text{q}}_{20} (t) \, \copyright \,{\text{B}}_{0} ({\text{t}}) \, + {\text{ q}}_{21}^{(4)} ({\text{t}}) \, \copyright \, {\text{B}}_{1} ({\text{t}}) $$

(16)

Taking the Laplace Transform of relations (14, 15, 16) and solving for B ^*₀ (s), omitting the argument ‘s’ for brevity, we get

$$ {\text{B}}_{ 0}^{ * } ( {\text{s)}}\,\,{ = }\,\,\frac{{{\text{N}}_{ 3} ({\text{s}})}}{{{\text{D}}_{2} ({\text{s}})}} $$

(17)

where,

$$ {\text{N}}_{3} ({\text{s}})\,\, = \,\,{\text{q}}_{01}^{*} (Z_{1}^{*} )\, - \,{\text{q}}_{02}^{*} ( - \,{\text{Z}}_{2}^{*} )\,\, = \,\,{\text{q}}_{01}^{*} {\text{Z}}_{1}^{*} + \,{\text{q}}_{02}^{*} {\text{Z}}_{2}^{*} $$

and D₂(s) is same as given in availability analysis.

Taking Inverse Laplace Transform of (17), we can get the probability that the repairman will be busy at a particular epoch for known values of the parameters.

In the long run, the probability that the repairman will be busy in repair of failed unit is given by

$$ {\text{B}}_{ 0} \, = \, \mathop {\lim }\limits_{{{\text{t}} \to \infty }} {\text{ B}}_{ 0} ({\text{t}}) = \, \mathop {\lim }\limits_{{{\text{s}} \to 0}} {\text{ s B}}_{ 0}^{ * } ({\text{s}}) \, = \, \mathop {\lim }\limits_{{{\text{s}} \to 0}} {\text{ s }}\frac{{{\text{N}}_{ 3} ({\text{s}})}}{{{\text{D}}_{2} ({\text{s}})}} \, = \, \frac{{{\text{N}}_{ 3} }}{{{\text{D}}_{2} }} $$

(18)

where,

$$ \begin{gathered} {\text{N}}_{3} \,\, = \,{\text{p}}_{01} {\text{m}}_{1} \, + \,{\text{p}}_{02} {\text{m}}_{2} \hfill \\ = \frac{{{{\upalpha}}_{ 1} }}{{{{\upalpha}}_{ 1} \, + \,{{\upalpha}}_{ 2} \,}} \frac{{\Upgamma \left( {1 + \frac{1}{\text{p}}} \right)}}{{ ( {{\upbeta}}_{ 1} \,)^{{1/{\text{p}}}} }} + \frac{{{{\upalpha}}_{ 2} }}{{\,{{\upalpha}}_{ 2} + {{\upalpha}}_{ 1} \,}} \frac{{\Upgamma \left( {1 + \frac{1}{\text{p}}} \right)}}{{(\,{{\upbeta}}_{ 2} )^{{1/{\text{p}}}} }} \hfill \\ \end{gathered} $$

and D₂ is same as given in availability analysis.

The expected busy period of the repairman in repair during (0, t) is given by

$$ \mu_{b}^{{}} ({\text{t}}) = \int\limits_{0}^{\text{t}} {{\text{B}}_{0}^{{}} ({\text{u}})\,{\text{du}}} $$

So that,

$$ \mu_{\text{b}}^{*} ({\text{s}})\,\, = \,\,\frac{{{\text{B}}_{0}^{*} ({\text{s}})}}{\text{s}} $$

(19)

4.4 Profit function analysis

Let us define

C₀ :

 = revenue (in Rs.) per-unit up time of the system

C₁ :

 = cost (in Rs.) per unit time when the repairman is busy in repair of a failed unit

Then, net expected profit incurred by the system during time interval (0, t) is given by

$$ \eqalign{ {\text{P }}\left( {\text{t}} \right)\,\, = & {\text{Expected total revenue in }}\left( {0,{\text{ t}}} \right) \cr & - {\text{ Expected total cost of repair in }}\left( {0,{\text{ t}}} \right) \cr = & {\text{C}}_{0} \mu _{{{\text{up}}}} ({\text{t}})\, - {\text{ C}}_{1} \mu _{{\text{b}}} ({\text{t}}) \cr} $$

(20)

The net expected profit per-unit time incurred by the system in steady-state is given by

$$ {\text{P }} = {\text{C}}_{0} {\text{A}}_{ 0}^{{}} - {\text{C}}_{ 1} {\text{B}}_{ 0}^{{}} $$

(21)

Where A₀ and B₀ have been given in (12) and (18) respectively.

5 Estimation of parameters, MTSF and profit function

5.1 Classical estimation

The failure, increased failure and repair times of units of system are assumed to be independently Weibull distributed random variables with failure rates h₁ (.), h₂ (.), increased failure rates r₁ (.), r₂ (.) and repair rates j₁(.), j₂(.) respectively.

where

h_i(t) = α_ipt^p−1, r_i(t) = μ_ipt^p−1, and j_i(t) = β_ipt^p−1; t ≥ 0, α_i, β_i, μ_i, p > 0 (i = 1, 2)

Here α_i, β_i, μ_i are scale parameters and p is the shape parameter.

In our study, we are interested with the ML estimation procedure as one of the most important classical procedures.

5.1.1 ML estimation

Let

$$ \begin{gathered} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{\text{X}}_{1} \, = \,({\text{x}}_{11} ,\,{\text{x}}_{12} , \ldots \ldots \ldots ,{\text{x}}_{{1n_{1} }} );\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{\text{X}}_{2} \, = \,({\text{x}}_{21} ,\,{\text{x}}_{22} , \ldots \ldots \ldots ,{\text{x}}_{{2{\text{n}}_{2} }} );\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{\text{X}}_{3} = \,({\text{x}}_{31} ,\,{\text{x}}_{32} ,{\text{x}}_{{3{\text{n}}_{3} }} )\,;\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{\text{X}}_{4} \, = \,({\text{x}}_{41} ,\,{\text{x}}_{42} , \ldots \ldots \ldots ,{\text{x}}_{{4n_{4} }} );\, \hfill \\ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{\text{X}}_{5} \, = \,({\text{x}}_{51} ,\,{\text{x}}_{52} , \ldots \ldots \ldots ,{\text{x}}_{{5{\text{n}}_{5} }} );\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{\text{X}}_{6} \, = \,({\text{x}}_{61} ,\,{\text{x}}_{62} , \ldots \ldots \ldots ,{\text{x}}_{{6{\text{n}}_{6} }} ) \hfill \\ \end{gathered} $$

be six independent random samples of sizes n_i (i = 1, 2, 3, 4, 5, 6) drawn from Weibull distribution with failure rates h₁ (.), h₂ (.), r₁ (.), r₂ (.) and repair rates j₁ (.), j₂ (.) respectively.

The likelihood function of the combined sample is

$$ \begin{aligned} L\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{X} _{1} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{X} _{2} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{X} _{3} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{X} _{4} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{X} _{5} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{X} _{6} \left| {\alpha _{1} ,\alpha _{2} ,\mu _{1} ,\mu _{2} ,\beta _{1} ,\beta _{2} } \right.} \right) & = \alpha _{1}^{{n_{1} }} \alpha _{2}^{{n_{2} }} \mu _{1}^{{n_{3} }} \mu _{2}^{{n_{4} }} \beta _{1}^{{n_{5} }} \beta _{2}^{{n_{6} }} p^{{n_{1} + n_{2} + n_{3} + n_{4} + n_{5} + n_{6} }} \\ & \quad \times Z_{1} Z_{2} Z_{3} Z_{4} Z_{5} Z_{6} e^{{ - (\alpha _{1} W_{1} + \alpha _{2} W_{2} + \mu _{1} W_{3} + \mu _{2} W_{4} + \beta _{1} W_{5} + \beta _{2} W_{6} )}} \\ \end{aligned} $$

(22)

Where,

$$ {\text{W}}_{\text{i}} \, = \,\sum\limits_{\text{j = 1}}^{{{\text{n}}_{\text{i}} }} {{\text{x}}_{\text{ij}}^{\text{p}} \,\,} {\text{and}}\,\,{\text{Z}}_{\text{i}} \, = \,\prod\limits_{\text{j = 1}}^{{{\text{n}}_{\text{i}} }} {{\text{x}}_{\text{ij}}^{{{\text{p}} - 1}} } ;\quad {\text{i}} = 1,\,2,\,3,\,4,\,5,\,6 $$

By using usual maximization likelihood approach, the M.L. estimates (say $\hat{\alpha }_{1} ,\hat{\alpha }_{2} ,\hat{\mu }_{1} ,\hat{\mu }_{2} ,\hat{\beta }_{1} ,\hat{\beta }_{2}$) of the parameters $\alpha_{1} ,\alpha_{2} ,\mu_{1} ,\mu_{2} ,\beta_{1} ,\beta_{2}$ are

$$ \hat{\alpha }_{1} \, = \,{\text{n}}_{1} /{\text{W}}_{1} ;\,\,\hat{\alpha }_{2} \, = \,n_{2} /{\text{W}}_{2} ;\,\,\hat{\mu }_{1} \, = \,{\text{n}}_{3} /{\text{W}}_{3} ;\,\,\hat{\mu }_{2} \, = \,{\text{n}}_{4} /{\text{W}}_{4} ;\,\hat{\beta }_{1} \, = \,{\text{n}}_{5} /{\text{W}}_{5} ;\,\,\hat{\beta }_{2} = \,{\text{n}}_{6} /{\text{W}}_{6} $$

(23)

Thus, by using the invariance property of MLE, the MLEs of MTSF and profit function, say, ${\hat{\text{M}}}\,{\text{and}}\,{\hat{\text{P}}}$ can be obtained. The asymptotic sampling distribution of

$$ \left( \begin{gathered} \hat{\alpha }_{1} - \alpha_{1} \, \hfill \\ \hat{\alpha }_{2} \, - \alpha_{2} \hfill \\ \hat{\mu }_{1} - \mu_{1} \, \hfill \\ \hat{\mu }_{2} - \,\mu_{2} \hfill \\ \hat{\beta }_{1} - \beta_{1} \, \hfill \\ \hat{\beta }_{2} - \beta_{2} \hfill \\ \end{gathered} \right)\sim {\text{N}}_{6} (0,\,{\text{I}}^{ - 1} ) $$

where I denotes the Fisher information matrix with diagonal elements

$$ {\text{I}}_{11} \, = \,\frac{{{\text{n}}_{1} }}{{\alpha_{1}^{2} \,}};\,\,{\text{I}}_{22} \, = \,\frac{{{\text{n}}_{2} }}{{\alpha_{2}^{2} }};\,\,{\text{I}}_{33} \, = \,\frac{{{\text{n}}_{3} }}{{\mu_{1}^{2} }};\,\,{\text{I}}_{44} \, = \,\frac{{{\text{n}}_{4} }}{{\mu_{2}^{2} }};{\text{I}}_{55} \, = \,\frac{{{\text{n}}_{5} }}{{\beta_{1}^{2} }};{\text{I}}_{66} \, = \,\frac{{{\text{n}}_{6} }}{{\beta_{2}^{2} }} $$

and non diagonal elements are all zero.

Also, the asymptotic distribution of $\left( {\,{\hat{\text{M}}} - \,{\text{M}}} \right)\,\sim \,{\text{N}}_{6}\left( {0,\,\,{\text{A}}'\,{\text{I}}^{ - 1} {\text{A}}} \right)$ and $\left( {{\hat{\text{P}}}\, - \,{\text{P}}} \right)\,\sim \,{\text{N}}_{6}\left( {0,\,{\text{B}}^{\prime}\,{\text{I}}^{ - 1} {\text{B}}} \right)$

where

$$ {\text{A}}^{\prime}\, = \,\left( {\frac{{\partial {\text{M}}}}{{\partial \alpha_{1} }},\,\frac{{\partial {\text{M}}}}{{\partial \alpha_{2} }},\,\frac{{\partial {\text{M}}}}{{\partial \mu_{1} }},\,\frac{{\partial {\text{M}}}}{{\partial \mu_{2} }},\frac{{\partial {\text{M}}}}{{\partial \beta_{1} }},\frac{{\partial {\text{M}}}}{{\partial \beta_{2} }}} \right),{\text{B}}^{\prime}\, = \,\left( {\frac{{\partial {\text{P}}}}{{\partial \alpha_{1} }},\,\frac{{\partial {\text{P}}}}{{\partial \alpha_{2} }},\,\frac{{\partial {\text{P}}}}{{\partial \mu_{1} }},\,\frac{{\partial {\text{P}}}}{{\partial \mu_{2} }},\frac{{\partial {\text{P}}}}{{\partial \beta_{1} }},\frac{{\partial {\text{P}}}}{{\partial \beta_{2} }}} \right) $$

5.2 Bayesian estimation

Since the natural family of conjugate priors of scale parameter in case of Weibull distribution when shape parameter is known is a gamma distribution. So in our case, the prior distributions of scale parameters $\alpha_{1} ,\alpha_{2} ,\mu_{1} ,\mu_{2} ,\beta_{1} ,\beta_{2}$ when the shape parameter p is known are assumed to be gamma with parameters (a_i, b_i)(i = 1, 2, 3, 4, 5, 6) and are given as follows:

$$ \alpha_{1} \sim \,{\text{Gamma}}\,({\text{a}}_{1} ,\,{\text{b}}_{1} ); $$

(24)

$$ \alpha_{2} \,\, \sim \,{\text{Gamma}}\,({\text{a}}_{2} ,\,{\text{b}}_{2} ); $$

(25)

$$ \mu_{1} \,\, \sim \,{\text{Gamma}}\,({\text{a}}_{3} ,\,{\text{b}}_{3} ); $$

(26)

$$ \mu_{2} \,\, \sim \,{\text{Gamma}}\,({\text{a}}_{4} ,\,{\text{b}}_{4} ); $$

(27)

$$ \beta_{1} \, \sim \,{\text{Gamma}}\,({\text{a}}_{6} ,\,{\text{b}}_{6} ) $$

(28)

$$ \beta_{2} \, \sim \,{\text{Gamma}}\,({\text{a}}_{6} ,\,{\text{b}}_{6} ) $$

(29)

Here the parameters of prior distributions are called hyper parameters. Using the likelihood function in (22) and prior distribution of α₁, α₂, μ₁, μ₂, β₁, β₂ (24, 25, 26, 27, 28, 29) the posterior distributions of these parameters are obtained as follows:

$$ \alpha_{1} \,\,\left| {\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{\text{X}}_{1} } \right.\, \sim \,{\text{Gamma}}\,({\text{n}}_{1} + \,{\text{a}}_{1} ,\,{\text{b}}_{1} \, + \,{\text{W}}_{1} ) $$

(30)

$$ \alpha_{2} \,\,\left| {\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{\text{X}}_{2} } \right.\, \sim \,{\text{Gamma}}\,({\text{n}}_{2} + \,{\text{a}}_{2} ,\,{\text{b}}_{2} \, + \,{\text{W}}_{2} ) $$

(31)

$$ \mu_{1} \,\,\left| {\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{\text{X}}_{3} } \right.\, \sim \,{\text{Gamma}}\,({\text{n}}_{3} + \,{\text{a}}_{3} ,\,{\text{b}}_{3} \, + \,{\text{W}}_{3} ) $$

(32)

$$ \mu_{2} \,\,\left| {\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{\text{X}}_{4} } \right.\, \sim \,{\text{Gamma}}\,({\text{n}}_{4} + \,{\text{a}}_{4} ,\,{\text{b}}_{4} \, + \,{\text{W}}_{4} ) $$

(33)

$$ \beta_{1} \,\,\left| {\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{\text{X}}_{5} } \right.\, \sim \,{\text{Gamma}}\,({\text{n}}_{5} + \,{\text{a}}_{5} ,\,{\text{b}}_{5} \, + \,{\text{W}}_{5} ) $$

(34)

$$ \beta_{2} \,\left| {\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\sim}$}}{\text{X}}_{6} } \right.\, \sim \,{\text{Gamma}}\,({\text{n}}_{6} + \,{\text{a}}_{6} ,\,{\text{b}}_{6} \, + \,{\text{W}}_{6} ) $$

(35)

Under squared error loss function, Bayes estimates of $\alpha_{1} ,\alpha_{2} ,\mu_{1} ,\mu_{2} ,\beta_{1} ,\beta_{2}$are respectively the means of posterior distribution given in Eqs. (30, 31, 32, 33, 34, 35, 36) and are as follows:

$$ \begin{aligned} \hat{\alpha }_{1} & = \left( {{\text{b}}_{1} + {\text{w}}_{1} } \right)/\left( {{\text{n}}_{1} + {\text{a}}_{1} } \right); \\ \hat{\alpha }_{2} & = \left( {{\text{b}}_{2} + {\text{w}}_{2} } \right)/\left( {{\text{n}}_{2} + {\text{a}}_{2} } \right); \\ \hat{\mu }_{1} & = \left( {{\text{b}}_{3} + {\text{w}}_{3} } \right)/\left( {{\text{n}}_{3} + {\text{a}}_{3} } \right); \\ \hat{\mu }_{2} & = \left( {{\text{b}}_{4} + {\text{w}}_{4} } \right)/\left( {{\text{n}}_{4} + {\text{a}}_{4} } \right); \\ \hat{\beta }_{1} & = \left( {{\text{b}}_{5} + {\text{w}}_{5} } \right)/\left( {{\text{n}}_{5} + {\text{a}}_{5} } \right); \\ \hat{\beta }_{2} & = \left( {{\text{b}}_{6} + {\text{w}}_{6} } \right)/\left( {{\text{n}}_{6} + {\text{a}}_{6} } \right) \\ \end{aligned} $$

(36)

6 Simulation study

We obtained, in the above section, MLE and Bayes estimates of scale parameters α₁, α₂, μ₁, μ₂, β₁, β₂ when the shape parameter p is known and hence the estimates of MTSF and profit function. In order to assess the statistical performances of these estimates, a simulation study is also conducted. The SE/PSE of the estimates and width of confidence/HPD intervals are used for comparison purpose. Random samples of sizes n₁ = n₂ = n₃ = n₄ = n₅ = n₆ = 180 have been drawn from the Weibull distribution for various values of parameters and based on these samples, the ML estimates of the MTSF and profit function are obtained. For Bayesian estimation of parameters, we generated 10,000 realizations from the posterior densities. Bayes estimates of the parameters with gamma priors are obtained by setting the values of hyper parameters as $\alpha_{ 1} = {\text{b}}_{ 1} /{\text{a}}_{ 1} ; \alpha_{2} = {\text{b}}_{2} /{\text{a}}_{2} ; \mu_{ 1} = {\text{b}}_{3} /{\text{a}}_{3} ; \mu_{2} = {\text{b}}_{4} /{\text{a}}_{4} ;\beta_{ 1} = {\text{b}}_{5} /{\text{a}}_{5} ;\beta_{2} = {\text{b}}_{6} /{\text{a}}_{6}$. The results of simulation study have been summarized in Tables 1, 2, 3, 4, 5, 6. All calculations are performed by using R.2.14.2 Software.

Table 1 Values of MTSF for fixed β₂ = 0.5, p = 1 and varying α₁

Table 2 Values of MTSF for fixed β₂ = 0.6, p = 1 and varying α₁

Table 3 Values of MTSF for fixed β₂ = 0.7, p = 1 and varying α₁

Table 4 Values of profit function for fixed β₂ = 0.5, p = 1 and varying α₁

Table 5 Values of profit function for fixed β₂ = 0.6, p = 1 and varying α₁

Table 6 Values of profit function for fixed β₂ = 0.7, p = 1 and varying α₁

For a more concrete study of the system behavior, by using values (Tables 1, 2, 3), we plot curves for true MTSF, its MLE and Bayes estimate (Figs. 2, 3, 4) w.r.t. failure rate $\alpha_{1}$ for different values of repair rate β₂(0.5,0.6,0.7) while the other parameters are kept fixed (p = 1.0; β₁ = 0.4; α₂ = 0.9; μ₁ = 0.5; μ₂ = 0.6).Curves for profit function, its MLE and Bayes estimates are also plotted (Figs. 5, 6, 7) by using values (Tables 4, 5, 6) for the same values of parameters as in case of MTSF and assuming the values of C₀ and C₁ as (C₀ = 100; C₁ = 50).

Fig. 2

Plot of MTSF for fixed β₂ = 0.5 and varying α₁

Fig. 3

Plot of MTSF for fixed β₂ = 0.6 and varying α₁

Fig. 4

Plot of MTSF for fixed β₂ = 0.7 and varying α₁

Fig. 5

Plot of profit for fixed β₂ = 0.5 and varying α₁

Fig. 6

Plot of profit for fixed β₂ = 0.6 and varying α₁

Fig. 7

Plot of profit for fixed β₂ = 0.7 and varying α₁

7 Conclusions

According to results obtained in Sect. 6, we observe from Tables 1, 2, 3, that for the fixed values of β₂ (0.5, 0.6, 0.7) and p(0.1) MTSF decreases as the failure rate α₁ increases. From these tables we also observe that for fixed values of β₂ and p _, both the SE of ML estimator and PSE of Bayes estimator of MTSF decrease with the increase in α_1. Also the SE of ML estimator is smaller than the PSE of Bayes estimator. Besides, the width of HPD intervals is smaller than the width of confidence intervals. Same trends are also observed from Tables 4, 5, 6 in case of profit function. It is also observed from Figs. 2, 3, 4 that MTSF, its MLE and Bayes estimate decrease with the increase in failure rate α₁ while all these increase with the increase in repair rate β₂. Same trends for profit function are also observed from Figs. 5, 6, 7. Hence, from the above discussion we suggest to use Bayes approach under squared error loss function than classical approach based on ML estimation for estimating the MTSF and profit function for the considered system model.