Reaction–diffusion approximation of nonlocal interactions using Jacobi polynomials

Abstract

Nonlocal interactions, which have attracted attention in various fields, result from the integration of microscopic information such as a transition possibility, molecular events, and signaling networks of living creatures. Nonlocal interactions are useful to reproduce various patterns corresponding to such detailed microscopic information. However, the approach is inconvenient for observing the specific mechanisms behind the target phenomena because of the compression of the information. Therefore, we previously proposed a method capable of approximating any nonlocal interactions by a reaction–diffusion system with auxiliary factors (Ninomiya et al., J Math Biol 75:1203–1233, 2017). In this paper, we provide an explicit method for determining the parameters of the reaction–diffusion system for the given kernel shape by using Jacobi polynomials under appropriate assumptions. We additionally introduce a numerical method to specify the parameters of the reaction–diffusion system with the general diffusion coefficients by the Tikhonov regularization.

1 Introduction

The mechanisms whereby various patterns observed in nature, such as the pigmentation patterns of animal skins, the arrangement of leaves in plants, and neural firing in the brain, are formed, are often complex. Many microscopic factors and substances are usually involved in these mechanisms through complex networks of interactions. This requires us to address the technical difficulties that arise from investigating the specific mechanisms, although corresponding techniques have been developed in experimental biology in recent years. Attempts to overcome the difficulties have led to the introduction of spatial long-range interactions to integrate complex and detailed events consisting of molecular or signaling networks. The use of these interactions, which are often known as nonlocal interactions, has attracted attention as a simple approach to treat the aforementioned phenomena. The advantage of using nonlocal interactions is that they enable us to easily investigate the way in which patterns are generated by conducting numerical simulations if the shape of the nonlocal interactions is detected [9, 19]. Various researchers have attempted to use these merits to study the pattern formations of animal skin, the dynamics of neural firing, and the phenomenon whereby the population density disperses [1,2,3,4, 6, 9, 14, 15, 18, 19]

Fig. 1

Typical examples of the Mexican-hat profile. The solid kernel is given by (2) with $d_1=1$, $d_2=2$, and the dashed one is given by $(d_1k^{d_1} -d_2 k^{d_2}) /(d_1-d_2)-(d_3k^{d_3} -d_4 k^{d_4}) /(d_3-d_4)$ with $d_1=1, d_2=2, d_3=4, d_4=6$ where $k^d$ is defined by (4). The vertical and horizontal axes correspond to the value of J(x) and the position x, respectively. The profiles of this kernel are similar to the shape of the Mexican-hat because of the short-range activation near the origin and the long-range inhibition at greater distances

Biological examples of the existence of nonlocal interactions have been reported for neural firing phenomena in the brain and the skin pigmentations of the zebrafish [9, 10, 16]. A typical example of nonlocal interactions is a lateral inhibition. This interaction activates objects near a point and conversely inhibits objects distant from the point. These observations can be described by a function with a profile similar to that in Fig. 1, by regarding a local activation and a long-range inhibition as positive and negative values, respectively. Based on this shape, this function is known as the Mexican hat (see [11, 12, 19]). Since a nonlocal interaction exerts influence globally in space, it can be imposed by a convolution with a suitable kernel in evolution equations (cf. [9, 14, 15, 18, 19]). Nonlocal interactions are typically modeled as follows [19]:

$$\begin{aligned} w*u (x):=\int w(x-y)u(y,t)dy. \end{aligned}$$

Here, u represents the concentration of a substance and w is termed a kernel of the convolution that characterizes the nonlocal interaction.

We next explain the various nonlocal evolution equations. One well-known example with a nonlocal interaction was proposed in [1] related to the neural firing phenomenon:

$$\begin{aligned} \tau \, u_t= -u +\int _{\mathbb {R}} w(x-y)H(u(y,t))dy +s(x,t), \end{aligned}$$

where u(x, t) is the membrane potential of the neurons at position x and time t, the time constant $\tau$ is positive, the function w is a kernel, the inhomogeneous term s is an external stimulus, and H is the Heaviside function. This equation has been analyzed for the dynamics of neural firing [1, 11, 12].

The next typical example is the model for the dispersal of biological organisms with the positive kernels. These nonlocal evolution equations are regarded as an extension of reaction–diffusion systems [8, 14]. They were actively analyzed for the traveling wave solutions [2, 3, 6]. The following nonlocal evolution equation is often analyzed for the traveling wave solutions:

$$\begin{aligned} u_t = \int k(x-y)u(y,t) dy -bu+f(u), \end{aligned}$$

(1)

where $u=u(x,t)$ is the population density of a single species, $k=k(x)$ is a non-negative kernel, b is a positive constant, and f is a nonlinear function of u. For the description of the dispersal phenomenon the reaction–diffusion systems are pivotally analyzed, and many theories are established. However, it has been reported that not only the local movement and interactions but also nonlocal ones are important to model such a phenomenon [8].

Furthermore, the effect of nonlocal saturation is considered as follows:

$$\begin{aligned} u_t -\varDelta u = \mu u \left( 1 - k * u\right) , \end{aligned}$$

where k(x) is a positive kernel and $\mu$ is a constant. These nonlocal competitive effects were introduced by [7, 13]. The existence of the traveling wave solution was also reported by [4]. Another example in the form of a mathematical model to investigate pattern formation in animal skins was proposed [9]. Interestingly, this author reproduced various patterns, such as spots, stripes, and nested patterns, by changing only the profile of the kernel.

Nonlocal interactions have several advantages in mathematical approaches for the pattern formations and the dynamics of the spatial dispersals [9, 19]. First, various patterns can be reproduced by changing only the kernel shape. Second, if the kernel shape can be detected in the phenomena, as reported in [10, 16], it enables us to investigate how patterns may be generated mathematically. However, nonlocal interactions are often inconvenient for the observation of specific mechanisms because of the difficulty presented by compression of the information. In response to this, we proposed a method capable of approximating the nonlocal interactions to the reaction–diffusion systems. In our previous study we showed that for any continuous even kernels, a multi-component reaction–diffusion system approximates the nonlocal evolution equations with a one-dimensional periodic boundary condition [18]. The key idea of the proof was to approximate the kernel by the linear sum of the Green kernels. However, we could not provide a method to determine the parameters in the corresponding reaction–diffusion system from the given kernel. To overcome this difficulty, we consider the problem in one-dimensional Euclidean space in this paper because the Green kernel is simpler than the periodic boundary case. Similar to [18], first we show that the reaction–diffusion system is also capable of approximating the nonlocal evolution equations for any kernels with certain conditions in one-dimensional Euclidean space. Moreover, we show that the coefficients of the reaction–diffusion system are explicitly obtained by using the Jacobi polynomials when the diffusion coefficients of multiple auxiliary factors are controlled. As we can explicitly calculate the parameters of the reaction–diffusion system for a given kernel shape, we can guess the strength of the influence of the auxiliary factors that construct the kernel for given kernel shapes. For the general setting of the diffusion coefficients we numerically calculate the parameters by using a typical method of optimizing problem for a given kernel shape. This approximation also enables us to approximate the traveling wave solutions of the nonlocal evolution equations with certain positive kernels such as $e^{-d |x|}, \sum _{j=1}^M \alpha _j e^{- d_j|x|}$, ($d, d_j>0, \alpha _j$ are constants) by that of the reaction–diffusion system. We numerically demonstrate that the speed of the traveling wave solution of a nonlocal evolution equation can be approximated by that of the reaction–diffusion system. We also explain numerically that the traveling wave solution of some nonlocal evolution equations cannot be approximated by our reaction–diffusion approximation.

This paper is organized as follows: In Sect. 2, we state the mathematical setting of the nonlocal equation in one-dimensional Euclidean space and the main result. In Sect. 3, we explain the proof of the reaction–diffusion approximation of any nonlocal interactions. Section 4 provides the proof for determining the coefficients of the reaction–diffusion system for given kernel shapes. In Sect. 5, we demonstrate the reaction–diffusion approximation to the traveling wave equations with certain kernels. In Sect. 6, we introduce a numerical method to calculate the coefficients of the reaction–diffusion system.

2 Mathematical settings and main results

We explain our main results by first stating the mathematical settings. As a mathematical model to describe various pattern formations by using nonlocal interactions, we consider the following initial value problem:

where $d_u$ is a positive constant, and $J*w$ is the convolution with respect to x for any $w\in BC(\mathbb {R})$, i.e.,

$$\begin{aligned} (J*w)(x):=\int _{\mathbb {R}}J(x-y)w(y)dy. \end{aligned}$$

Furthermore, we assume the following conditions for the functions g and J:

where $g_0,\ldots ,g_7$ are positive constants. Examples of g and J satisfying these hypotheses can be easily found such as

$$\begin{aligned} g(u,v)&=uv+au(1-u^2), \nonumber \\ J(x)&=\frac{1}{2\sqrt{d_1}}e^{-|x|/\sqrt{d_1}} -\frac{1}{2\sqrt{d_2}}e^{-|x|/\sqrt{d_2}}, \end{aligned}$$

(2)

where $d_1,\ d_2$, and a are positive constants with $d_2>d_1>0$. The example of mathematical model (1) in Sect. 1 satisfies these assumptions. The assumptions are the same as in [18] except for (H5) and the condition for stability in (H1).

First we consider the existence of solutions of the nonlocal evolution equation (P).

Theorem 1

(Global existence and global bounds for the solution of (P)) There exists a unique solution $u\in C([0,\infty ),BC(\mathbb {R}))$ of the problem (P) with an initial datum $u_0\in BC(\mathbb {R})$. Moreover,

$$\begin{aligned} \sup _{0\le t<\infty }\Vert u(\cdot ,t)\Vert _{BC(\mathbb {R})}<\infty . \end{aligned}$$

Because the proof is routine, it is included in the Appendix A.

Remark 1

Similar to Theorem 1, it is possible to prove the local existence of a unique solution $u\in C([0,T];H^1(\mathbb {R}))$ of (P) for any $T>0$ when the initial datum $u_0$ belongs to $H^1(\mathbb {R})$. Hence, we see that $u\in C^1((0,T];L^2(\mathbb {R}))\cap C((0,T];H^2(\mathbb {R}))$ and that it is a classical solution for $t\in (0,T]$ by the regularity theory for parabolic equations. We also note that $H^1(\mathbb {R})\subset BC(\mathbb {R})$.

We approximate the solution of the nonlocal evolution equation (P) by that of a reaction–diffusion system. Similar to [18], we introduce the following reaction–diffusion system ($\hbox {RD}_{\varepsilon }$) with $M+1$ components:

with

$$\begin{aligned} \left( u(\cdot ,0),v_j(\cdot ,0) \right) _{1\le j\le M} =\left( u_0(\cdot ),k^{d_j}*u_0(\cdot ) \right) _{1\le j\le M}, \end{aligned}$$

(3)

where

$$\begin{aligned} k^d(x):=\dfrac{1}{2\sqrt{d}}e^{-|x|/\sqrt{d}}. \end{aligned}$$

(4)

Remark 2

Similarly to the regularity of the solution to (P), we have the local existence of the solution $(u^{\varepsilon }, v_1^{\varepsilon },\ldots ,v_M^{\varepsilon })$ of ($\hbox {RD}_{\varepsilon }$) for any $T>0$. In particular, if the initial datum $u_0\in L^1(\mathbb {R})\cap H^1(\mathbb {R})$, then it follows that $u^{\varepsilon }, v_1^{\varepsilon },\ldots ,v_M^{\varepsilon }\in C([0,T];L^1(\mathbb {R})\cap H^1(\mathbb {R}))\cap C((0,T]; H^2(\mathbb {R})) \cap C^1((0,T];L^2(\mathbb {R}))$ for $1\le j\le M$ by the regularity theory for parabolic equations. See also the proofs of Propositions 2 and 3 in Appendix B. Therefore, the solution $(u^{\varepsilon }, v_1^{\varepsilon },\ldots , v_M^{\varepsilon })$ becomes the classical solution.

Comparing ($\hbox {RD}_{\varepsilon }$) with (P), it is clear that $J*u$ is approximated by the linear combination of $v_j$. The constants $\alpha _1,\ldots ,\alpha _M$ are specified later. We also remark that $w=k^d*u$ satisfies

$$\begin{aligned} dw_{xx}+u-w=0, \end{aligned}$$

namely, $k^d$ is the Green kernel.

Theorem 2

(Reaction–diffusion approximation) Let u(x, t) be a solution of (P) with an initial datum $u_0(\cdot )\in L^1(\mathbb {R})\cap H^1(\mathbb {R})$. For a sufficiently small $\varepsilon _0>0$ and each $\varepsilon \in (0,\varepsilon _0)$, if there exist a natural number M, constants $\alpha _j \in \mathbb {R}$, and positive constants $d_j$ $(j=1,\ldots ,M)$ such that

$$\begin{aligned} \left\| J- \sum _{j=1}^{M} \alpha _j k^{d_j} \right\| _{L^2(\mathbb {R})}\le \varepsilon , \end{aligned}$$

(5)

then for any $T>0$ there are positive constants $K_1(T)$ and $K_2(T)$ satisfying

$$\begin{aligned} \begin{aligned}&\sup _{0\le t\le T} \left\| u^{\varepsilon }(\cdot ,t) -u(\cdot ,t) \right\| _{H^1(\mathbb {R})} \le K_1(T)\, \varepsilon , \\&\sup _{0\le t\le T} \left\| v_j^{\varepsilon }(\cdot ,t) -k^{d_j}*u(\cdot ,t) \right\| _{H^1(\mathbb {R})} \le K_2(T)\, \varepsilon , \end{aligned} \end{aligned}$$

(6)

where $(u^{\varepsilon }, v_1^\varepsilon ,\ldots , v_M^\varepsilon )$ is the solution of ($\hbox {RD}_{\varepsilon }$) with (3).

This theorem is shown in Sect. 3.

Remark 3

If $g_7=0$ in (H3), the initial datum $u_0$ does not need the $L^1$-integrability over $\mathbb {R}$ in order to show Theorem 2.

In this theorem, we assumed that J is approximated by $\sum _{j=1}^M\alpha _jk^{d_j}$ as in (5). Accordingly, we encounter the following natural questions:

Can any function J be approximated by $\sum _{j=1}^M\alpha _jk^{d_j}$ ?

If so, how can we determine the constants $\alpha _1,\ldots ,\alpha _M$ ?

To answer these questions, we provide the following theorem:

Theorem 3

Assume that

besides (H5). For any positive sufficiently small $\varepsilon$, there exists a natural number M such that

$$\begin{aligned} \left\| J- \sum _{j=1}^{M} \alpha _j k^{d_j} \right\| _{L^2(\mathbb {R})}\le \varepsilon , \end{aligned}$$

(7)

where for any $j\in \mathbb {N}$

$$\begin{aligned} \left\{ \begin{aligned}&d_j=j^{-2}, \\&p_{k-1,\ell -1}=\frac{(-1)^{k+\ell }\sqrt{2\ell }(k+\ell -1)!}{(\ell -k)!k!(k-1)!},\\&\alpha _j=\frac{1}{j}\sum _{\ell =j}^{M} p_{j-1,\ell -1} \sum _{k=1}^{\ell } p_{k-1,\ell -1} \int _{\mathbb {R}} J(x) e^{-k|x|} \, dx. \end{aligned} \right. \end{aligned}$$

(8)

Previously [18], we proved the approximation theorem for the case of a periodic boundary condition in $[-L,L]$. Because the proof was based on the Stone–Weierstrass theorem, the coefficients $\alpha _1,\ldots , \alpha _M$ were determined implicitly. Theorem 3 guarantees choosing the coefficients $\alpha _1,\ldots ,\alpha _M$ explicitly (for more detail, see Sect. 4).

In this theorem, we assumed that $d_j=j^{-2}$; however, this is rather artificial. Thus, in Sect. 6, we introduce another approach to determine the constants $\alpha _1,\ldots ,\alpha _M$ for any given $d_1,\ldots ,d_M$. Unfortunately, we are unable to provide any proof to guarantee the method and leave it as an open problem.

3 Preliminaries and reaction–diffusion approximation of nonlocal interactions

To approximate the solution of (P) in Theorem 2, we state the auxiliary propositions. Firstly we give the boundedness of the solution for the nonlocal evolution equation (P) in $H^1(\mathbb {R})$.

Proposition 1

(Boundedness of the solution of (P)) The solution u of (P) with initial datum $u_0\in H^1(\mathbb {R})$ satisfies

$$\begin{aligned} \sup _{0\le t\le T}\Vert u(\cdot ,t)\Vert _{H^1(\mathbb {R})}\le C_0 \end{aligned}$$

for any $T>0$, where $C_0$ is a positive constant depending on only T and $u_0$.

Remark 4

It follows from Theorem 1, Proposition 1 and Remark 1 that the solution u(x, t) of (P) exists for any $(x,t)\in \mathbb {R}\times [0,\infty )$. We note that $\Vert u(\cdot ,t)\Vert _{BC(\mathbb {R}\times [0,\infty ))}$ is bounded, however $\Vert u(\cdot ,t)\Vert _{C([0,T];H^1(\mathbb {R})))}$ is not necessarily bounded as T tends to infinity. Actually, if we consider the propagating front starting from the initial function with a compact support, it diverges to infinity.

Next we investigate the boundedness of the solution for reaction–diffusion system ($\hbox {RD}_{\varepsilon }$) in $L^2(\mathbb {R})$ and $L^1(\mathbb {R})$.

Proposition 2

(Boundedness of the solution of ($\hbox {RD}_{\varepsilon }$)) Let $\varepsilon \in (0,1)$ be a constant and $u_0\in H^1(\mathbb {R})$. For any $T>0$, the solution $(u^{\varepsilon },v_1^{\varepsilon },\dots ,v_M^{\varepsilon })$ of ($\hbox {RD}_{\varepsilon }$) with initial datum (3) satisfies the following:

$$\begin{aligned}&\sup _{0\le t\le T}\Vert u^{\varepsilon }(\cdot ,t)\Vert _{L^2(\mathbb {R})}^2 \le K_3 e^{k_1T},\\&\sup _{0\le t\le T} \sum _{j=1}^{M} \left\| \alpha _j v_j^{\varepsilon }(\cdot ,t) \right\| _{L^2(\mathbb {R})}^2 \le K_4 \left( 1 +e^{k_1T} \right) , \\&\sup _{0\le t\le T}\Vert u_x^{\varepsilon }(\cdot ,t)\Vert _{L^2(\mathbb {R})}^2 \le K_5(T), \\&\sup _{0\le t\le T} \sum _{j=1}^{M} \left\| \alpha _j v_{j,x}^{\varepsilon }(\cdot ,t) \right\| _{L^2(\mathbb {R})}^2 \le K_6(T). \end{aligned}$$

Here, $k_1$, $K_3$, $K_4$, $K_5(T)$ and $K_6(T)$ are constants depending on only p, M, $g_j$, $\alpha _k$ ($j=0,\dots ,7$, $k=1,\dots ,M$), $\Vert J\Vert _{L^1(\mathbb {R})}$ and $\Vert u_0\Vert _{H^1(\mathbb {R})}$, and furthermore, $K_5(T)$ and $K_6(T)$ depend on T.

Proposition 3

($L^1$ boundedness for ($\hbox {RD}_{\varepsilon }$)) Assume $u_0\in L^1(\mathbb {R})\cap H^1(\mathbb {R})$ and the hypothesis of Proposition 2. Then, the solution $(u^{\varepsilon },v_1^{\varepsilon },\dots ,v_M^{\varepsilon })$ of ($\hbox {RD}_{\varepsilon }$) satisfies the following:

$$\begin{aligned} \sup _{0\le t\le T}\Vert u^{\varepsilon }(\cdot ,t)\Vert _{L^1(\mathbb {R})} \le K_7(T) \quad \text { and } \quad \sup _{0\le t\le T} \sum _{j=1}^{M} \left\| \alpha _j v_j^{\varepsilon }(\cdot ,t) \right\| _{L^1(\mathbb {R})} \le K_8(T), \end{aligned}$$

where $K_7(T)$ and $K_8(T)$ are positive constants independent of $\varepsilon$, $u^\varepsilon$ and $v_j^\varepsilon$.

We will give the proofs of these propositions in Appendix B. To show Theorem 2, we prepare the following lemma.

Lemma 1

Let $(u^{\varepsilon },v_1^{\varepsilon },\ldots , v_M^{\varepsilon })$ be the solution to ($\hbox {RD}_{\varepsilon }$). The following inequalities hold:

$$\begin{aligned} \left\| v_j^{\varepsilon }-k^{d_j}*u^{\varepsilon } \right\| _{L^2(\mathbb {R})} \le C_1\varepsilon \end{aligned}$$

(9)

for $1\le j\le M$, where $C_1$ is a positive constant independent of $\varepsilon$, $u^\varepsilon$ and $v_j^\varepsilon$.

This proof is shown in Appendix C. This is based on the energy method. Hereafter $C_j$ will denote a positive constant independent of $\varepsilon$.

We give the following proof for Theorem 2 based on the energy method.

Proof of Theorem 2

Let $U:=u^{\varepsilon }-u$ and $V_j:=v_j-k^{d_j}*u^{\varepsilon }$. Then, by ($\hbox {RD}_{\varepsilon }$) and (P), U is a solution of the following initial value problem:

$$\begin{aligned} \left\{ \begin{aligned}&U_t =d_u U_{xx} +g\left( u+U, \sum _{j=1}^{M} \alpha _jv_j^{\varepsilon } \right) -g\left( u,J*u \right)&\text { in } \; \mathbb {R}\times \{t>0\},\\&U(\cdot ,0)=0&\text { in } \; \mathbb {R}. \end{aligned} \right. \end{aligned}$$

(10)

First, we estimate the $L^2$-norm of U. Multiplying the equation of (10) by U and integrating it over $\mathbb {R}$, by (H2) and (H3), we see that

$$\begin{aligned}&\frac{d}{dt} \left( \frac{1}{2}\Vert U\Vert _{L^2(\mathbb {R})}^2 \right) \\&\quad \le -d_u \Vert U_x\Vert _{L^2(\mathbb {R})}^2 -g_0p\int _{\mathbb {R}} |u+\theta U|^{p-1}U^2 \, dx +g_4\int _{\mathbb {R}} \left| \sum _{j=1}^{M} \alpha _jv_j^{\varepsilon } \right| U^2 \, dx \\&\qquad +\,g_5 \int _{\mathbb {R}} U^2 \, dx +\int _{\mathbb {R}} \left( g_6 |u|+g_7 \right) \left| { \sum _{j=1}^{M}} \alpha _jv_j^{\varepsilon } -J*u \right| |U| \, dx. \end{aligned}$$

Recall that $u^{\varepsilon }$ and $v_j^{\varepsilon }$ are bounded in $H^1(\mathbb {R})$ from Proposition 2. By the Sobolev embedding theorem, both of $u^{\varepsilon }$ and $v_j^{\varepsilon }$ are uniformly bounded functions in $\mathbb {R}$. Moreover, since

$$\begin{aligned} \sum _{j=1}^{M} \alpha _j v_j^{\varepsilon }-J*u =\left( \sum _{j=1}^{M} \alpha _j k^{d_j}-J \right) *u^{\varepsilon } +\sum _{j=1}^{M} \alpha _j V_j+J*U \end{aligned}$$

where $V_j=v_j^{\varepsilon }-k^{d_j}*u^{\varepsilon }$, and (H5) holds, we see that

$$\begin{aligned} \begin{aligned} \frac{d}{dt} \left( \frac{1}{2}\Vert U\Vert _{L^2(\mathbb {R})}^2 \right)&\le C_2\Vert U\Vert _{L^2(\mathbb {R})}^2 +g_6 \int _{\mathbb {R}} |u| \left| \left( \sum _{j=1}^{M} \alpha _jk^{d_j}-J \right) *u^{\varepsilon } \right| |U| \, dx \\&\quad +g_7 \int _{\mathbb {R}} \left| \left( { \sum _{j=1}^{M}\,} \alpha _jk^{d_j}-J \right) *u^{\varepsilon } \right| |U| \, dx \\&\quad +\int _{\mathbb {R}} ( g_6 |u| +g_7 ) \left| { \sum _{j=1}^{M}\,} \alpha _j V_j \right| |U| \, dx. \end{aligned} \end{aligned}$$

(11)

By the assumption (5) and Proposition 2, for all $0\le t\le T$, we have

$$\begin{aligned}&g_6 \int _{\mathbb {R}} |u| \left| \left( \sum _{j=1}^{M} \alpha _jk^{d_j}-J \right) *u^{\varepsilon } \right| |U| \, dx \\&\quad \le g_6 \int _{\mathbb {R}} |u| \left\| \sum _{j=1}^{M} \alpha _jk^{d_j}-J \right\| _{L^2(\mathbb {R})} \Vert u^{\varepsilon } \Vert _{L^2(\mathbb {R})} |U| \, dx \\&\quad \le \frac{g_6}{2} \Vert u^{\varepsilon }\Vert _{L^2(\mathbb {R})} \left( \Vert u\Vert _{L^2(\mathbb {R})}^2 \Vert U\Vert _{L^2(\mathbb {R})}^2 +\varepsilon ^2 \right) \le C_3 \left( \Vert U\Vert _{L^2(\mathbb {R})}^2 +\varepsilon ^2 \right) . \end{aligned}$$

Using the Hölder inequality and the Young inequality for convolutions, assumption (5), and boundedness of $\Vert u^\varepsilon \Vert _{L^1(\mathbb {R})}$ in Proposition 3, we see that

$$\begin{aligned}&g_7 \int _{\mathbb {R}} \left| \left( \sum _{j=1}^{M} \alpha _jk^{d_j}-J \right) *u^{\varepsilon } \right| |U| \, dx \\&\quad \le g_7 \left\| \left( \sum _{j=1}^{M} \alpha _jk^{d_j}-J \right) *u^{\varepsilon } \right\| _{L^2(\mathbb {R})} \Vert U \Vert _{L^2(\mathbb {R})} \\&\quad \le g_7 \left\| \sum _{j=1}^{M} \alpha _jk^{d_j}-J \right\| _{L^2(\mathbb {R})} \Vert u^{\varepsilon } \Vert _{L^1(\mathbb {R})} \Vert U \Vert _{L^2(\mathbb {R})}\\&\quad \le g_7 \Vert u^{\varepsilon } \Vert _{L^1(\mathbb {R})} { \Vert U \Vert _{L^2(\mathbb {R})} \varepsilon }\\&\quad \le C_4 \left( \Vert U \Vert _{L^2(\mathbb {R})}^2 +\varepsilon ^2 \right) . \end{aligned}$$

Also, since $\Vert V_j\Vert _{L^2(\mathbb {R})}\le C_1\varepsilon$ by Lemma 1 and $u\in BC(\mathbb {R})$, we estimate the fourth term of (11) as follows:

$$\begin{aligned}&\int _{\mathbb {R}} \left( g_6 |u| +g_7 \right) \left| { \sum _{j=1}^{M}} \alpha _j V_j \right| |U| \, dx \\&\quad \le \frac{1}{2}\left( g_6 \Vert u \Vert _{BC(\mathbb {R})} +g_7 \right) \left( \left\| { \sum _{j=1}^{M}} \alpha _j V_j \right\| _{L^2(\mathbb {R})}^2 + \Vert U\Vert _{L^2(\mathbb {R})}^2 \, \right) \\&\quad \le C_5 \left( \Vert U\Vert _{L^2(\mathbb {R})}^2 +\varepsilon ^2 \right) . \end{aligned}$$

Summarizing these inequalities, we obtain

$$\begin{aligned} \frac{d}{dt} \left( \frac{1}{2} \Vert U\Vert _{L^2(\mathbb {R})}^2 \right) \le \frac{C_6}{2} \left( \Vert U\Vert _{L^2(\mathbb {R})}^2 +\varepsilon ^2 \right) . \end{aligned}$$

From the Gronwall inequality and $U(\cdot ,0)\equiv 0$, it follows that

$$\begin{aligned} \Vert U\Vert _{L^2(\mathbb {R})}^2 \le \left( e^{C_6T}-1 \right) \varepsilon ^2 \quad \text {for all}\quad 0\le t\le T. \end{aligned}$$

(12)

Therefore we have that $\sup _{0\le t\le T}\Vert U\Vert _{L^2(\mathbb {R})}=O(\varepsilon )$.

Finally, we estimate the $L^2$-norm of $U_x$. Integrating the equation of (10) multiplied by $-U_{xx}$ over $\mathbb {R}$ yields that

$$\begin{aligned}&\frac{d}{dt}\left( \frac{1}{2}\Vert U_x\Vert _{L^2(\mathbb {R})}^2 \right) \\&\quad \le -d_u\Vert U_{xx}\Vert _{L^2(\mathbb {R})}^2 -\int _{\mathbb {R}} \left\{ g\left( u+U, \sum _{j=1}^{M} \alpha _jv_j^{\varepsilon } \right) -g(u,J*u) \right\} U_{xx} \, dx \\&\quad \le -\frac{d_u}{2} \Vert U_{xx}\Vert _{L^2(\mathbb {R})}^2 +\frac{1}{2d_u} \left\| g\left( u+U, \sum _{j=1}^{M} \alpha _jv_j^{\varepsilon } \right) -g(u,J*u) \right\| _{L^2(\mathbb {R})}^2. \end{aligned}$$

Similarly to the estimate for $\Vert U \Vert _{L^2(\mathbb {R})}^2$, we see that

$$\begin{aligned} \frac{d}{dt}\left( \Vert U_x \Vert _{L^2(\mathbb {R})}^2 \right)&\le C_7 \left( \Vert U \Vert _{L^2(\mathbb {R})}^2 +\sum _{j=1}^{M} \Vert V_j\Vert _{L^2(\mathbb {R})}^2 +\left\| \sum _{j=1}^{M} \alpha _jk^{d_j}-J \right\| _{L^2(\mathbb {R})}^2 \right) . \end{aligned}$$

By Lemma 1, (5) and (12), we obtain

$$\begin{aligned} \Vert U_x \Vert _{L^2(\mathbb {R})}\le C_8\,\varepsilon \quad \text { for all } 0\le t\le T. \end{aligned}$$

Consequently, we see that $\sup _{0\le t\le T}\Vert U\Vert _{H^1(\mathbb {R})}\le K_1(T)\varepsilon$. $\square$

4 Approximation of a kernel by using Jacobi polynomials

4.1 Approximation of a kernel by the Stone–Weierstrass theorem

To consider the approximation of a kernel, we introduce the following functional space:

$$\begin{aligned} BC([0,\infty ]):= \{ \phi \in BC([0,\infty ))\ |\ \phi \text{ has } \text{ a } \text{ finite } \text{ limit } \phi _{\infty }:=\mathop {\lim }\limits _{{x \rightarrow \infty }}\phi (x) \}, \end{aligned}$$

with the norm

$$\begin{aligned} \Vert f\Vert _{BC([0,\infty ])}:=\sup _{x\in [0,\infty )}|f(x)|. \end{aligned}$$

Proposition 4

Every $\phi \in BC([0,\infty ])$ is uniformly approximated by a finite linear combination of a family $\{ e^{-j x} \}_{j=0}^{\infty }$.

The proof is similar to that of [18]. Therefore we put it in the Appendix D. This is based on the Stone–Weierstrass theorem.

4.2 Jacobi polynomials

In this subsection, we will approximate a kernel J representing a nonlocal interaction in (P), and propose how to determine the coefficients $\alpha _1,\ldots ,\alpha _M$ in Theorem 2 by using Jacobi polynomials.

Firstly we treat the series of functions $e^{-j x}$. Let us find $f_j(x)$ consisting of linear combinations of $\{e^{-jx}\}_{j=1}^{\infty }$ and satisfying

$$\begin{aligned} \int _0^\infty f_k(x)f_\ell (x) \, dx=\delta _{k\ell } =\left\{ \begin{aligned}&1&\text { if } \; k= \ell , \\&0&\text { if } \; k\ne \ell . \end{aligned} \quad \text { for } k,\ell =1,2, \dots \right. \end{aligned}$$

By changing variable x into y (recall $y=e^{-x}$), a series of $\{e^{-jx}\}_{j=1}^{\infty }$ is a power series in y, and the orthogonal condition is

$$\begin{aligned} \int _{0}^{1} \frac{f_k(-\log y)f_\ell (-\log y)}{y} \, dy=\delta _{k\ell } \quad \text { for } \; k,\ell =1,2,\dots . \end{aligned}$$

To show the convergence in Theorem 3, we introduce the space of absolutely convergent power series on [0, 1] with inner product

$$\begin{aligned} \int _{0}^{1} P(y)Q(y)y \, dy. \end{aligned}$$

The Gram–Schmidt process yields the orthonormal polynomial $P_j(y)$ of degree j which satisfies

$$\begin{aligned} \int _{0}^{1} P_i(y)P_j(y)y \, dy=\delta _{ij} \quad \text { for } \; i,j=0, 1, 2,\dots . \end{aligned}$$

(13)

In fact, we see that $P_0(y)=\sqrt{2}$, $P_1(y)=2 (3 y-2)$, $P_2(y)=\sqrt{6} (10 y^2 -12y+3)$, $P_3(y)=2\sqrt{2} (35y^3-60 y^2 +30 y -4)$. The recurrence formulae are

$$\begin{aligned} P_j(y)=(a_jy-b_j)P_{j-1}(y)-c_jP_{j-2}(y) \quad \text { for } j\ge 2 \end{aligned}$$

where

$$\begin{aligned}&a_j =\frac{2(2j+1)}{\sqrt{j(j+1)}}, \quad b_j =\frac{4j}{2j-1} \sqrt{\frac{j}{j+1}} \quad \text { and } \quad c_j =\frac{2j+1}{2j-1} \sqrt{\frac{j-1}{j+1}}. \end{aligned}$$

Since $P_j$ is a polynomial of degree $j\in \mathbb {N}\cup \{0\}$, there are coefficients $p_{0,j},\ldots , p_{j,j}$ such that

$$\begin{aligned} P_j(y)=\sum _{i=0}^{j} p_{i,j} \, y^i. \end{aligned}$$

(14)

Then it follows from (13) that

$$\begin{aligned} \int _0^1P_i(y)P_j(y)ydy= & {} \int _0^1\sum _{k=0}^{i} p_{k,i} \, y^k\sum _{\ell =0}^{j} p_{\ell ,j} \, y^\ell \cdot ydy\\= & {} \sum _{k=1}^{i+1} \sum _{\ell =1}^{j+1} \frac{p_{k-1,i} p_{\ell -1,j}}{k+\ell }=\delta _{ij}. \end{aligned}$$

Using this equality, we can inductively deduce

$$\begin{aligned} A\begin{pmatrix} p_{0,j}\\ p_{1,j} \\ \vdots \\ p_{j-1,j} \\ p_{j,j} \end{pmatrix} =\begin{pmatrix} 0\\ 0 \\ \vdots \\ 0 \\ 1/p_{j,j} \end{pmatrix}, \end{aligned}$$

where A is a $(j+1)\times (j+1)$ matrix the $(k,\ell )$-element of which equals $1/(k+\ell )$ ($1\le k,\ell \le j+1$). We denote the $(k,\ell )$-element of A by $(A)_{k\ell }$. Namely,$(A)_{k\ell }=1/(k+\ell )$ and

$$\begin{aligned} \mathrm{det\,} A = \frac{1}{2^{j+1}} \prod _{i=1}^j \frac{ (i+1)! (i!)^3 }{((2i +1)!)^2}. \end{aligned}$$

Calculating the inverse matrix $A^{-1}$ yields

$$\begin{aligned}&p_{j,j}^2=(A^{-1})_{j+1 \, j+1} =2(j+1) \left( \frac{(2j+1)!}{(j+1)! \, j!} \right) ^2,\\&p_{i,j}=(-1)^{i+j} \frac{(A^{-1})_{i+1 \, j+1}}{p_{j,j}} =\frac{(-1)^{i+j}}{p_{j,j}} \, \frac{2(i+1) (2j+1)! \, (i+j+1)!}{(j-i)! \, ((i+1)!)^2 \,(j!)^2} \end{aligned}$$

for $j=0,1,2,\dots ,$ and $i=0,\dots ,j-1$. We note that $0!\equiv 1$. Choosing $p_{j,j}$ as being positive, we have that

$$\begin{aligned} p_{i,j}=(-1)^{i+j} \sqrt{2(j+1)} \frac{(i+j+1)!}{(j-i)! \, (i+1)! \, i!} \quad \text { for } \; i=0,\dots ,j, \end{aligned}$$

which implies the second equality of (8).

Referring to [5], we denote the Jacobi polynomials of k degree by $Q_k^{(\alpha , \beta )}(x)$ satisfying

$$\begin{aligned}&\int _{-1}^1 Q_k^{(\alpha , \beta )}(x)Q_l^{(\alpha , \beta )}(x) (1-x)^\alpha (1+x)^\beta dx \\&\quad = \frac{2^{\alpha + \beta +1}\varGamma (l+\alpha +1)\varGamma (l+\beta +1) }{(2l+\alpha +\beta +1)\varGamma (l+\alpha +\beta +1)l!} \delta _{kl}. \end{aligned}$$

Actually, we see that $P_k(y) = \sqrt{2(k+1)}Q_k^{(0,1)}(2y-1)$ and $\int _0^1P_k(y)P_l(y)ydy=\delta _{kl}$. We note that these polynomials are normalized by (13).

If the limit of $J(x) e^x$ as $x\rightarrow \infty$ exists finitely, then

$$\begin{aligned} K(y):=\frac{J(-\log y)}{y} \end{aligned}$$

(15)

is continuous in [0, 1]. For $j \in \mathbb {N}$, put

$$\begin{aligned} q_{j-1}:=\int _{0}^{\infty } J(x) P_{j-1}(e^{-x})e^{-x} \, dx. \end{aligned}$$

By (14) and (15), we see that

$$\begin{aligned} q_{j-1}&\quad =\int _{0}^{1} K(y) P_{j-1}(y) y \, dy\nonumber \\&\quad =\sum _{k=1}^{j} \int _{0}^{1} J(-\log y) p_{k-1,j-1}y^{k-1} \, dy\nonumber \\&\quad =\frac{1}{2} \sum _{k=1}^{j} p_{k-1,j-1}\int _{\mathbb {R}} J(x) e^{-k|x|} \, dx. \end{aligned}$$

(16)

We note that if $K(y)=\sum _{k=1}^{\ell }\beta _{k-1}P_{k-1}(y)$ and $1\le j\le \ell$, then

$$\begin{aligned} q_{j-1} =\int _{0}^{1}\sum _{k=1}^{\ell }\beta _{k-1}P_{k-1}(y) P_{j-1}(y) y \, dy =\sum _{k=1}^{\ell }\beta _{k-1}\delta _{k-1 \, j-1} =\beta _{j-1}. \end{aligned}$$

Proof of Theorem 3

If J(x) satisfies (H6), then K(y) defined by (15) is continuous in [0, 1]. Hence, the polynomials approximate to K by the Stone–Weierstrass theorem. To be precise, for any $\varepsilon >0$, there exist a non-negative integer $\ell$ and constants $a_0,\ldots a_{\ell -1}$ such that

$$\begin{aligned} \sup _{0\le y\le 1} \left| K(y) - \sum _{j=1}^{\ell } a_{j-1}P_{j-1}(y) \right| \le \varepsilon . \end{aligned}$$

(17)

By the change of variable $y=e^{-x}$, we obtain

$$\begin{aligned}&\int _{0}^{\infty } \left| J(x) - \sum _{j=1}^{\ell } q_{j-1}P_{j-1}(e^{-x})e^{-x} \right| ^2 \, dx \\&\quad =\int _{0}^{1} \left| J(-\log y) - \sum _{j=1}^{\ell } q_{j-1} P_{j-1}(y) y \right| ^2 \frac{1}{y} \, dy \\&\quad =\int _{0}^{1} \left| K(y) - \sum _{j=1}^{\ell } q_{j-1}P_{j-1}(y) \right| ^2 y \, dy\\&\quad =\int _{0}^{1} \left| K(y) - \sum _{j=1}^{\ell } a_{j-1}P_{j-1}(y) - \sum _{j=1}^{\ell } (q_{j-1}-a_{j-1}) P_{j-1}(y) \right| ^2 y \, dy\\&\quad =\int _{0}^{1} \left| K(y) - \sum _{j=1}^{\ell } a_{j-1}P_{j-1}(y) \right| ^2 y \, dy -\sum _{j=1}^{\ell }(q_{j-1}-a_{j-1})^2. \end{aligned}$$

Using (17) yields

$$\begin{aligned} \int _{0}^{\infty } \left| J(x) - \sum _{j=1}^{\ell } q_{j-1}P_{j-1}(e^{-x})e^{-x} \right| ^2 \, dx \le \frac{\varepsilon ^2}{2} -\sum _{j=0}^{\ell -1}(q_j-a_j)^2 \le \frac{\varepsilon ^2}{2}. \end{aligned}$$

Since J(x) is an even function, we have that

$$\begin{aligned} \int _{\mathbb {R}} \left| J(x) - \sum _{j=1}^{\ell } q_{j-1}P_{j-1}(e^{-|x|})e^{-|x|} \right| ^2 \, dx \le \varepsilon ^2. \end{aligned}$$

This inequality implies

$$\begin{aligned} \left\| J - \sum _{j=1}^{\ell } q_{j-1}P_{j-1}(e^{-|x|})e^{-|x|} \right\| _{L^2(\mathbb {R})} \le \varepsilon \end{aligned}$$

with $\ell =M$. Next, we show the following:

$$\begin{aligned} \sum _{j=1}^{M}\alpha _jk^{d_j} =\sum _{j=1}^{M}q_{j-1}P_{j-1}(e^{-|x|})e^{-|x|}. \end{aligned}$$

It follows from the definition of $\{ \alpha _j\}_{j=1}^{M}$ in (8) and $k^{d_j}(x)=(j/2)e^{-j|x|}$ that

$$\begin{aligned} \sum _{j=1}^M\alpha _jk^{d_j} =\sum _{j=1}^M\frac{1}{2}\left( \sum _{\ell =j}^{M} p_{j-1,\ell -1} \sum _{k=1}^{\ell } p_{k-1,\ell -1} \int _{\mathbb {R}} J(x) e^{-k|x|} \, dx\, \right) e^{-j|x|}. \end{aligned}$$

By (14) and (16), we have

$$\begin{aligned} \sum _{j=1}^M\alpha _jk^{d_j}&=\sum _{j=1}^M \left( \sum _{\ell =j}^{M} p_{j-1,\ell -1} q_{\ell -1} \right) e^{-j|x|} =\sum _{\ell =1}^{M} q_{\ell -1}\sum _{j=1}^\ell p_{j-1,\ell -1} e^{-j|x|} \\&=\sum _{\ell =1}^{M}q_{\ell -1}P_{\ell -1} (e^{-|x|})e^{-|x|}. \end{aligned}$$

Consequently, the inequality (7) has shown. $\square$

Remark 5

This method is well known in the theory of orthogonal systems. See [5] for instance.

Remark 6

As shown in the above proof, by using (16), we have

$$\begin{aligned} \sum _{j=1}^M\alpha _jk^{d_j} =\sum _{j=1}^M c_{j,M}e^{-j|x|}, \end{aligned}$$

which satisfies (7), where

$$\begin{aligned} c_{j,M}=\sum _{\ell =j}^{M} p_{j-1,\ell -1} q_{\ell -1}. \end{aligned}$$

Fig. 2

The profiles of $J_1, J_2$ and the approximation of the kernels, and the distributions of $\alpha _1,\ldots ,\alpha _{10}$. a, b correspond to the results for $J_1$ and $J_2$, respectively. The profiles of $J_1$ and $J_2$ (Black solid thin curves) and the corresponding approximations of kernels with $d_j=j^{-2}$, $M= 10$ (gray dashed curves) are shown (upper). The distributions of $\alpha _1,\ldots ,\alpha _{10}$ are shown (lower). The vertical and horizontal axes correspond to the values of $\alpha _j$ and j, respectively

We numerically calculated the values of $\alpha _1,\ldots ,\alpha _M$ for the given kernel shapes by using the Jacobi polynomials. Let us consider the following two examples:

$$\begin{aligned} J_1(x):= & {} \frac{e^{-x^2}}{\sqrt{\pi }},\\ J_2(x):= & {} 3e^{-4|x|}-7x^2e^{-3|x|}+\frac{5x^4}{16}e^{-3|x|/2}. \end{aligned}$$

Then, the profiles of $J_1, J_2$ and the corresponding approximation functions are shown in Fig. 2 (upper), and the parameters $\alpha _1,\ldots ,\alpha _M$ determined by (8) are illustrated in Fig. 2 (lower). The effectiveness of this determination of $\alpha _1,\ldots ,\alpha _M$ is discussed in Sect. 7. We provide the examples of the values of $\alpha _1,\ldots ,\alpha _{5}$ for $J_1$ and $J_2$ which are explicitly calculated by (8) in the Appendix E. However, as see in the Appendix E, $\alpha _1, \ldots , \alpha _5$ are complicated even for a small number M.

Remark 7

If we allow to introduce the advection term, we may approximate more general kernels as in [18]. Here we give how to determine the the coefficients by the formal calculation. Let J be a continuous function satisfying $\lim _{|x| \rightarrow \infty } J(x)e^{|x|}=0$, and (H5). First we split the kernel J into even one $J^e$ and odd one $J^o$, i.e.,

$$\begin{aligned} J^e(x):=\dfrac{J(x)+J(-x)}{2},\quad J^o(x):=\dfrac{J(x)-J(-x)}{2},\quad J(x)=J^e(x)+J^o(x). \end{aligned}$$

As $J\in BC(\mathbb {R}) \cap L^1(\mathbb {R})$, we note that $J^e, J^o\in BC(\mathbb {R}) \cap L^1(\mathbb {R})$. By Theorem 3, for any $\varepsilon >0$, there are constants $d_j,\ \alpha _j$ ($j=1,\ldots ,M$) satisfying (7) with J replaced by the even part $J^e$.

For the approximation of the odd part, we set

$$\begin{aligned} {G}(x):=-\int _{-\infty }^xJ^o(y)dy=-\int _0^xJ^o(y)dy-\int _{-\infty }^0J^o(y)dy. \end{aligned}$$

We note that G(x) is the even continuous function. Since $\int _{\mathbb {R}}J^o(y)dy=0$,

$$\begin{aligned} \lim _{|x|\rightarrow \infty }{G}(x)=0. \end{aligned}$$

For any $\varepsilon >0$, there is a R such that $|J(x)|<\varepsilon e^{-|x|}$ for $|x|>R$. Thus $|J^0|<\varepsilon e^{-|x|}$ for $|x|>R$.

$$\begin{aligned} |G|\le \int _{-\infty }^x|J^0|dy\le \varepsilon e^{-|x|}, \end{aligned}$$

for $x<-R$. This implies that $\lim _{x\rightarrow -\infty }G(x)e^{|x|}=0$. Since

$$\begin{aligned} {G}(x)=-\int _\infty ^xJ^o(y)dy, \end{aligned}$$

we can show it similarly for $x>R$. Therefore $\lim _{|x|\rightarrow \infty }{G}(x)e^{|x|} = 0$. By integration by parts and $\int _\mathbb {R}J^o(x)dx=0$, we have $J^o*u={G}*u_x$. Thus it turns out that G is an even continuous kernel satisfying the assumption (H6). From Theorem 3 again, for any $\varepsilon >0$, there are constants $d_j$ and $\alpha _j$ $(j=M+1,\ldots ,K)$ such that

$$\begin{aligned} \left\| \sum _{j=M+1}^{K}\alpha _jk^{d_j}-G\right\| _{L^{2}(\mathbb {R})}\le \varepsilon . \end{aligned}$$

Thus, we can obtain

$$\begin{aligned} \left\| J*u-\sum _{j=1}^{M}\alpha _jk^{d_j}*u-\sum _{j=M+1}^{K}\alpha _jk^{d_j}*u_x\right\| _{L^2(\mathbb {R})}\le 2\varepsilon \Vert u\Vert _{{W^{1,1}(\mathbb {R})}} \end{aligned}$$

for any $u\in W^{1,1}(\mathbb {R})$. By summarizing the above arguments, for any continuous kernel J satisfying $\lim _{|x| \rightarrow \infty } J(x)e^{|x|}=0$, and (H5), there are constants $d_j$ and $\alpha _j$ $(j=1,\ldots , K)$ such that

$$\begin{aligned} \left\{ \begin{array}{ll} u_t &{}= d_uu_{xx}+g\left( u,{\displaystyle \sum _{j=1}^K}\alpha _jv_j \right) ,\\ 0 &{}= d_jv_{j,xx}+ u -v_j ,\quad (j=1,\ldots ,M)\\ 0 &{}=d_j v_{j,xx}+u_x-v_j,\quad (j=M+1,\ldots ,K) \end{array} \right. \end{aligned}$$

approximate (P).

In Theorem 3, we assume that $J(x)=O(e^{-|x|})$ as |x| tends to infinity. We can generalize this assumption to the assumption that J(x) decays exponentially. Hence, one obtain the following corollary:

Corollary 1

Let J(x) be an even continuous function with (H5). Assume that J(x) decays exponentially as $|x|\rightarrow \infty$, that is, there exists a constant $\gamma >0$ such that $J(x)=O(e^{-\gamma |x|})$ as $|x|\rightarrow \infty$. Then, for any sufficiently small $\varepsilon >0$, there exists $M\in \mathbb {N}$ such that

$$\begin{aligned} \left\| J-\sum _{j=1}^{M}\alpha _j^{(\gamma )} k^{d_j} \right\| _{L^2(\mathbb {R})} \le \gamma ^{-1/2} \, \varepsilon , \end{aligned}$$

where for any $j\in \mathbb {N}$

$$\begin{aligned} \left\{ \begin{aligned}&d_j = {\gamma ^{-2} j^{-2}},\\&\alpha _j^{(\gamma )}=\frac{1}{j}\sum _{\ell =j}^{M} p_{j-1,\ell -1}\sum _{k=1}^{\ell } p_{k-1,\ell -1} \int _{\mathbb {R}} J(x) e^{-k \, \gamma |x|} \, dx. \end{aligned} \right. \end{aligned}$$

(18)

where $p_{k-1, \ell -1}$ is the same as (8).

Proof

After (17) in the proof of Theorem 3, by changing variable $y=e^{-\gamma x}$ and calculating the $L^2$-norm of $J-\sum _{j=1}^{M}\alpha _j^{(\gamma )} k^{d_j}$, the assertion is proved. $\square$

By Corollary 1 and Theorem 2, we see that if any even and continuous function J(x) decays exponentially at infinity, then the solution of (P) can be approximated by the principal component of the solution for ($\hbox {RD}_{\varepsilon }$) with (18).

5 Numerical simulation

5.1 Periodic patterns induced by the short-range activation and the long-range inhibition

In this subsection, we firstly consider the kernel with Mexican hat, namely, the short-range activation and the long-range inhibition. As a simple example, we treat the case where J is given by $k^{d_1}-k^{d_2}$ and

$$\begin{aligned} g(u,v)=v+au(1-u^2). \end{aligned}$$

(19)

This nonlocal evolution equation can be approximated by the following simple reaction–diffusion system ($\hbox {RD}_{\varepsilon }$):

$$\begin{aligned} \left\{ \begin{aligned} u_t&= d_uu_{xx}+g(u,v_1-v_2),\\ v_{1,t}&= \frac{1}{\varepsilon } \left( d_1v_{1,xx}+ u -v_1 \right) , \\ v_{2,t}&= \frac{1}{\varepsilon } \left( d_2v_{2,xx} + u-v_2 \right) , \end{aligned} \right. \end{aligned}$$

(20)

where $0<d_1<d_2$. By using this reaction–diffusion system under the periodic boundary condition, we reported in [18] that the instability induced by the Mexican hat interaction can be regarded as the diffusion driven instability.

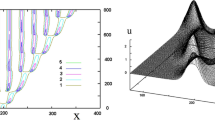
Setting the parameters and initial datum in one-dimensional space, we obtain the numerical solution u as in Fig. 3 (upper). As seen in Fig. 3, the solution u of (P) forms the periodic patterns locally. By forming positive and negative peaks alternately, the periodic pattern are generated as seen in Fig. 3 (upper). This formation is propagated to both direction of $|x| \rightarrow \infty$.

Fig. 3

The numerical results of (P) and ($\hbox {RD}_{\varepsilon }$) with the function (19), $J(x)=k^{d_1}-k^{d_2}$, $a=5$, $L=50$ and $d_1=1$, $d_2=2$ and $\varepsilon =0.001$ in (20). The initial conditions are equipped with $u_0(x)=e^{-x^2/20}$ in (P) and $(u^\varepsilon , v_1^{\varepsilon }, v_2^{\varepsilon })= (u_0, k^{d_1}*u_0, k^{d_2}*u_0)(x)$ in ($\hbox {RD}_{\varepsilon }$). Black line and gray line correspond to the solutions of (P) and ($\hbox {RD}_{\varepsilon }$), respectively. The estimation is $\sup _{0\le t \le 3.5} \Vert u -u ^\varepsilon \Vert _{L^2({\varOmega })}<0.219\ldots$ in this numerics

From (6) of Theorem 2, we see that $v_j$ converges to the quasi steady state,$v_j=k^{d_j}*u$. Thus, $v_1-v_2$ in the first equation of (20) becomes $(k^{d_1}-k^{d_2})*u$. As in Fig. 3 (lower), we can observe that the solution $u^\varepsilon$ of ($\hbox {RD}_{\varepsilon }$) also forms the spatial periodic solutions in one-dimensional space. From Theorem 2, we can expect that $\Vert u-u^\varepsilon \Vert _{L^2(\varOmega )}$ becomes a small value at which $\varOmega$ is a one-dimensional large interval $[-L,L]$. Actually, we obtain the estimation $\sup _{0 \le t \le 3.5}\left\| u -u ^\varepsilon \right\| _{L^2(\varOmega )}<0.219\ldots$ from the numerical simulations with the homogeneous Dirichlet boundary condition when $L=50$, and $\varepsilon = 0.001$.

Fig. 4

The numerical results of the superimposed traveling wave solutions by (P) and ($\hbox {RD}_{\varepsilon }$) with the function (21), J(x) defined in (22), $d_u=0.001$, $a=5$, and $M=2$, $d_j=j^{-2}$, $\varepsilon =0.001$, $\alpha _1=7/10$ and $\alpha _2=3/10$ in ($\hbox {RD}_{\varepsilon }$). The initial conditions are equipped with $u_0(x)=e^{-x^2/20}$ in (P) and $(u^\varepsilon , v_1^{\varepsilon }, v_2^{\varepsilon })= (u_0,k^{d_1}*u_0, k^{d_2}*u_0)(x)$ in ($\hbox {RD}_{\varepsilon }$). Black line and gray line correspond to the solutions of (P) and ($\hbox {RD}_{\varepsilon }$), respectively

5.2 Traveling wave solutions

In this subsection, we demonstrate that the traveling wave solution of (P) with certain kernels can be approximated by that of ($\hbox {RD}_{\varepsilon }$). Additionally, we will give an example of kernels for which we can not approximate the traveling wave solution of (P) by that of ($\hbox {RD}_{\varepsilon }$). In this subsection, let g be the function given by

$$\begin{aligned} g(u,v)=v-u+au(1-u). \end{aligned}$$

(21)

We note that the nonlinear term is the Fisher-KPP type. We consider the following form of the kernel in (P) for the case that the traveling wave solutions can be approximated by the reaction–diffusion system:

$$\begin{aligned} J(x)=\sum _{j=1}^M\alpha _j k^{d_j}(x), \quad \sum _{j=1}^M\alpha _j =1, \quad J(x)>0 \quad \text { for } x\in \mathbb {R}, \end{aligned}$$

(22)

where $\sum _{j=1}^M\alpha _j =1$ implies $\int _{\mathbb {R}}J(x)dx=1$. In the numerical simulation, we set the kernel by

$$\begin{aligned} J(x)= \dfrac{7}{10}k^{d_1}(x) + \dfrac{3}{10}k^{d_2}(x). \end{aligned}$$

Fig. 4 shows the results of the numerical simulation for the traveling wave solutions. Denoting the speeds of the traveling wave solution of (P) and ($\hbox {RD}_{\varepsilon }$) by $c_p$ and $c_{rd}$, respectively, we obtain from the numerical simulation that

$$\begin{aligned} c_p=7.917\ldots , \quad c_{rd}=7.879\ldots , \quad |c_p - c_{rd}| = 0.038\ldots . \end{aligned}$$

(23)

From [6], it is reported that there exists a critical speed $c^*$ such that for all $c>c^*$ there exist the traveling wave solutions of (P) by (21) without diffusion term. More precisely, the minimum speed is obtained by

$$\begin{aligned} c^*= \min _{\lambda >0}\frac{h(\lambda )}{\lambda }, \end{aligned}$$

where

$$\begin{aligned} h(\lambda ):= \int _{\mathbb {R}} J(z)e^{\lambda z}dz + g_u(0,0). \end{aligned}$$

Let us calculate the critical speed in the case of $J=\sum _{j=1}^M\alpha _j k^{j^{-2}}$ where $d_j=j^{-2}$ in (P). Since

$$\begin{aligned} \int _{\mathbb {R}} e^{-j|z|+\lambda z}dz =\frac{1}{j - \lambda } + \frac{1}{j+\lambda }=\frac{2j}{(j-\lambda )(j+\lambda )}, \end{aligned}$$

as $\lambda < 1$, we obtain

$$\begin{aligned} \begin{aligned} k(\lambda )&:=\min _{\lambda>0}\dfrac{h(\lambda )}{\lambda }= \min _{\lambda>0}\frac{1}{\lambda } \left( \int _{\mathbb {R}} \sum _{j=1}^{M} \frac{j\alpha _j}{2}e^{-j|z|+\lambda z}dz +a-1\right) \\&=\min _{\lambda >0}\frac{1}{\lambda } \left( \sum _{j=1}^{M}\frac{j^2 \alpha _j}{(j-\lambda )(j+\lambda )} +a-1\right) . \end{aligned} \end{aligned}$$

From this calculation, as $\lambda <1$ from the boundedness of h, the critical speed of Fig. 4 is numerically given by

$$\begin{aligned} c^*= \min _{\lambda \in [0,1]}k(\lambda )=k(0.788\ldots )=7.870\ldots . \end{aligned}$$

Thus, the speeds obtained by the numerical simulation (23) are near to the theoretical values although the small value of diffusion term is imposed.

Fig. 5

The numerical results of the superimposed traveling wave solutions by (P) and ($\hbox {RD}_{\varepsilon }$) with the function (21), $J(x)=e^{-x^2}/\sqrt{\pi }$, $d_u=0.001$, $a=5$, $d_j=j^{-2}$, $\varepsilon =0.01$, $M=6$, $\{\alpha _j\}_{j=1}^6$ obtained by (8). The initial conditions are equipped with $u_0(x)=e^{-x^2/20}$ in (P) and $(u^\varepsilon , v_1^{\varepsilon },\ldots , v_6^{\varepsilon })= (u_0,k^{d_1}*u_0, \ldots , k^{d_6}*u_0)(x)$ in ($\hbox {RD}_{\varepsilon }$). Black line and gray line correspond to the solutions of (P) and ($\hbox {RD}_{\varepsilon }$), respectively

On the other hand, in the case of $J(x)=e^{-x^2}/\sqrt{\pi }$, the difference between the critical value of the traveling wave solution of (P) and ($\hbox {RD}_{\varepsilon }$) is relatively large. Fig. 5 is the result of the numerical simulation. From the numerical simulation, we obtain the difference of the critical speeds after the speeds converge as

$$\begin{aligned} c_p=3.327\ldots , \quad c_{rd}=5.494\ldots , \quad |c_p - c_{rd}| = 2.166\ldots . \end{aligned}$$

We can calculate the critical speed similarly to the above. As $h(\lambda )=e^{\lambda ^2/4}$, we obtain that

$$\begin{aligned} c^*= \min _{\lambda >0}k(\lambda )=k(2.135\ldots )=3.337\ldots . \end{aligned}$$

On the other hand, the kernel is approximated by $\sum _{j=1}^{M}\alpha _{j}je^{-j|x|}/2$. Thus, as the parameters $\alpha _1,\ldots ,\alpha _6$ is calculated by Theorem 3, we can calculate $k(\lambda )$ of ($\hbox {RD}_{\varepsilon }$) as

$$\begin{aligned} k(\lambda )=k(0.959\ldots )=5.635\ldots . \end{aligned}$$

Thus, the speeds obtained theoretically are also quite different. This difference of speeds comes from the difference of the decay rates between the kernel J and the Green kernel.

6 Optimizing problem

In Sect. 4.2, we explained how to determine the values of $\{ \alpha _j \}_{j=1}^M$ for a given kernel shape J(x) by setting $d_j=j^{-2}$ and using the Gram–Schmidt process. In this section we numerically calculate the value of $\{ \alpha _j \}_{j=1}^M$ for the given J(x) and the other setting of $\{ d_j \}_{j=1}^M$ by using the typical method of the optimizing problem.

Assume that $\{ d_j\}_{j=1}^M$ and J(x) are given. Denoting $\{c_j\}_{j=1}^M$ as the unknown variables in this section, we consider the minimization of the following energy:

$$\begin{aligned} \left\| J(\cdot ) - {\sum _{j=1}^{M}} {c_j} e^{-|\cdot |/\sqrt{d_j} } \right\| ^2_{L^2(\varOmega )}, \end{aligned}$$

where $\varOmega := (0, L)$ is a one-dimensional region. Here we note that $\alpha _j = 2\sqrt{d_j} c_j$ because $c_j e^{-|x|/\sqrt{d_j}}=\alpha _j k^{d_j}$. By discretizing the spatial region $\varOmega$ and dividing it by N meshes, we have the following energy:

$$\begin{aligned} \sum _{i=0}^N \left( J(x_i) - {\sum _{j=1}^{M}} c_j e^{-|x_i|/\sqrt{d_j} } \right) ^2, \end{aligned}$$

where $x_i = Li/N$. For each i, we aim to find a solution $\{c_j\}_{j=1}^M$ satisfying$J(x_i) = \sum _{j=1}^Mc_j e^{-|x_i |/\sqrt{d_j} }$. Hence, by setting the matrix $H: \mathbb {R}^M \rightarrow \mathbb {R}^{N+1}$ as

$$\begin{aligned} H= ( h_{i,j})_{0\le i\le N, 1\le j\le M}, \quad h_{i,j}=e^{-|x_i |/\sqrt{d_j} }, \end{aligned}$$

and the column vectors as $\varphi = (c_1, \ldots , c_M)^T \in \mathbb {R}^M$ and $f= (J(x_0),\ldots ,J(x_N))^T \in \mathbb {R}^{N+1}$, this optimizing problem can be reproduced

$$\begin{aligned} H\varphi =f. \end{aligned}$$

We solve this optimizing problem by adapting the Tikhonov regularization [17]. Multiplying both sides by the adjoint operator $H^*$ and adding $\mu \varphi$ with a small constant $\mu >0$, we obtain the following equation

$$\begin{aligned} \mu \varphi +H^*H\varphi =H^*f. \end{aligned}$$

(24)

The operator $\mu I+H^*H$ is boundedly invertible. We perform a numerical simulation to calculate the value of $\{ \alpha _j\}_{j=1}^M$.

We demonstrate the approximation in the case of the function $J_1(x)$ by setting $d_j = j^{-1}$ and $d_j = j^{-1/2}$. As we cannot confirm whether f belongs to the range of the operator H in Eq. (24), we adapt an iterative method for the simultaneous equations. By denoting the error of the estimation as $\varepsilon _{error}$, we employ the stopping rule

$$\begin{aligned} \sum _{i=0}^N \left( J(x_i) - {\sum _{j=1}^{M}}c_j e^{-|x_i|/\sqrt{d_j} } \right) ^2 < \varepsilon _{error}. \end{aligned}$$

We also terminate the iteration if $\varepsilon _{pre}=\varepsilon _{error}$, where $\varepsilon _{pre}$ is the previous error in the iteration. Fig. 6 shows the results of the optimizing problem. The profiles of the original kernel and the approximation function are shown in the upper plots and the distributions of $\alpha _j$ are shown in lower.

Fig. 6

Numerical results with $L=20$, $M=10$, and $N=1000$. (upper) The profile of $J_1$ (black solid thin curves) and the corresponding approximation of kernels with $M=10$ (gray dashed curves). (lower) The distribution of $\alpha _1,\ldots ,\alpha _{10}$. The vertical and horizontal axes correspond to the values of $\alpha _j=2\sqrt{d_j} c_j$ and $j=1,\ldots ,10$, respectively. a $\mu =0.00001$ and $\varepsilon _{error} =0.004$ and b $\mu =0.00001$ and $\varepsilon _{error} =0.01$

7 Concluding remarks

We showed that any even continuous function satisfying (H6) can be approximated by the sum of fundamental solutions, thereby proving that the solution of a nonlocal evolution equation with any nonlocal interactions can be approximated by that of the reaction–diffusion system ($\hbox {RD}_{\varepsilon }$). Moreover, we explained in Theorem 3 that the coefficients $\alpha _1,\ldots ,\alpha _M$ of ($\hbox {RD}_{\varepsilon }$) can be explicitly determined by the Jacobi polynomials with the diffusion coefficients $d_j=j^{-2}$. We demonstrated that our method can be applied to the traveling wave solutions of the nonlocal equations with certain kernels. However, as the speed of a traveling wave solution depends on the decay rate of the kernel, it cannot be stated generally that every traveling wave solution can be approximated by ($\hbox {RD}_{\varepsilon }$).

For the general diffusion coefficients, we numerically calculated $\{ \alpha _j\}_{j=1}^{M}$ with the Tikhonov regularization as shown in Fig. 6. When kernel shapes are given, we can find the strength of the influence of the auxiliary activators and inhibitors $v_j$ to u, which depends on the diffusion coefficients. Nonlocal interaction is useful to reproduce various patterns, and to investigate how patterns are generated corresponding to the microscopic information such as signaling networks or mutual interactions of factors because we can regard the kernel as the reduction of microscopic information in the target phenomenon. Thus, it is compatible with various experiments [9, 19]. However, it is difficult to observe the structure of the original network that creates the kernel and to identify the essential factors in many mechanisms for real biological phenomena. Therefore, identification of the activator and the inhibitor with the strongest influence may be essential for the elucidation of the related mechanisms. Actually, the lower graph in Fig. 2 shows the distribution of ${\{ \alpha _j\}_{j=1}^{10}}$ for $J_2$. The largest absolute values among $\{ \alpha _j\}_{j=1}^{10}$ for the activator and the inhibitor were obtained when $j = 7$ and $j = 6$, respectively.

Fig. 7

Schematic network corresponding to ($\hbox {RD}_{\varepsilon }$) by assuming that the activations and the inhibitions in ($\hbox {RD}_{\varepsilon }$) are described by the arrows and T-shaped edges, respectively. The arrows from $v_j$ to u are determined by the sign of $\{ \alpha _j\}_{j=1}^{M}$

The network corresponding to system ($\hbox {RD}_{\varepsilon }$) can be described by the illustration in Fig. 7 by graphing the mutual activation and inhibition among u and $v_j$. This implies that the network in Fig. 7 is capable of reproducing any even kernels even though the original network of the nonlocal interactions is unknown. Thus, the network in Fig. 7 is a versatile system for pattern formation in one-dimensional space. However, the biological interpretation of this network in Fig. 7 to the real biological system is one of the future works.

A more complicated network can be considered. For example, consider the following reaction–diffusion system:

$$\begin{aligned} \left\{ \begin{aligned}&\begin{aligned}&u_t =d_u u_{xx} +g\left( u,{\sum _{j=1}^{M}\alpha _j v_j+\sum _{j=1}^{M}\beta _j w_j} \right)&\\&v_{j,t}=\frac{1}{\varepsilon } \left( d_{j,1} v_{j,xx} +u -v_j \right) \qquad \text { for } j=1,\dots ,M\\&w_{j,t}=\frac{1}{\varepsilon } \left( d_{j,2} w_{j,xx} +v_j -w_j \right) \qquad \text { for } j=1,\dots ,M \end{aligned}&\text { in } \mathbb {R}\times \{t>0\}, \end{aligned} \right. \end{aligned}$$

Then we can expect that

$$\begin{aligned} J=\sum _{j=1}^{M}\alpha _j k^{d_{j,1}}+\sum _{j=1}^{M}\beta _j k^{d_{j,2}}*k^{d_{j,1}}. \end{aligned}$$

Similarly, by increasing the number of components, we can imply that the kernel can be approximated by the linear combination of

$$\begin{aligned} k^{d_{j,m}}*k^{d_{j,m-1}}*\cdots *k^{d_{j,1}} \end{aligned}$$

We see that if $d_1\ne d_2$ and $x>0$, then

$$\begin{aligned} k^{d_2}*k^{d_1}(x)= & {} \int _{-\infty }^{\infty }\dfrac{1}{4\sqrt{d_1d_2}}e^{-|x-y|/\sqrt{d_2}-|y|/\sqrt{d_1}}dy =\dfrac{d_1k^{d_1}(x)-d_2k^{d_2}(x)}{d_1-d_2}. \end{aligned}$$

This function is continuously differentiable at $x=0$. If $d_1=d_2$, then

$$\begin{aligned} k^{d_1}*k^{d_1}(x)= & {} \dfrac{1}{2}k^{d_1}(x) +\dfrac{|x|}{2\sqrt{d_1}}k^{d_1}(x). \end{aligned}$$

Therefore, polynomial functions multiplied by the exponential decay can also be approximated.

We plan to extend our study to higher dimensional space. This development is expected to clarify our understanding of nonlocal interactions in various phenomena.

Appendices

Appendix

A: Existence and boundedness of a solution of the problem (P)

Proposition 5

(Local existence and uniqueness of the solution) There exist a constant $\tau >0$ and a unique solution $u\in C([0,\tau ];BC(\mathbb {R}))$ of the problem (P) with an initial datum $u_0\in BC(\mathbb {R})$.

This proposition is proved by the standard argument. That is based on the fixed point theorem for integral equation by the heat kernel.

In order to prove Theorem  1, we discuss the maximum principle as follows.

Lemma 2

(Global bounds for the solution of (P)) For a solution u of (P), it follows

$$\begin{aligned} \sup _{0\le t< \infty } \Vert u(\cdot ,t)\Vert _{BC(\mathbb {R})} < \infty . \end{aligned}$$

(25)

Proof

For a contradiction, we assume that there exists a constant $T>0$ such that

Then, we can take $\{T_n\}_{n\in \mathbb {N}}$ satisfying and

$$\begin{aligned} R_n:= \sup _{0\le t\le T_n} \Vert u(\cdot ,t)\Vert _{BC(\mathbb {R})} \rightarrow \infty \quad \text { as } n\rightarrow \infty \end{aligned}$$

Hence, for all $R>0$ there exists $N\in \mathbb {N}$ such that

$$\begin{aligned} R_n>R \qquad \text { for all } \; n\ge N. \end{aligned}$$

(26)

We suppose that $\sup _{0\le t\le T_n,x\in \mathbb {R}}u(x,t) =\sup _{0\le t\le T_n,x\in \mathbb {R}}|u(x,t)|$, (by replacing u(x, t) with $-u(x,t)$ if necessary).

Case 1: $u(x_n,t_n)=R_n$ for some $(x_n,t_n)\in \mathbb {R}\times [0,T_n]$.

Since $(x_n,t_n)$ is a maximum point of u on $\mathbb {R}\times [0,T_n]$, we see that

$$\begin{aligned} u_x(x_n,t_n)=0, \quad u_t(x_n,t_n)\ge 0, \quad u_{xx}(x_n,t_n)\le 0. \end{aligned}$$

For $r_0>0$ large enough, it holds that

$$\begin{aligned} -g_0 r^p +g_1\Vert J\Vert _{L^1(\mathbb {R})} r^2 +g_2\Vert J\Vert _{L^1(\mathbb {R})} r +g_3 r < -3 \quad \text { for all } r\ge r_0. \end{aligned}$$

(27)

Put $R=r_0$, $r=u(x_n,t_n)$. By (26), for all $u(x_n, t_n)>R$ we have

$$\begin{aligned} g\left( u(x_n,t_n),J*u(x_n,t_n) \right) <0. \end{aligned}$$

Substituting $(x_n,t_n)$ in the equation of (P), we obtain that

$$\begin{aligned} 0\le u_t(x_n,t_n) = d_u u_{xx}(x_n,t_n) +g\left( u(x_n,t_n),J*u(x_n,t_n) \right) <0. \end{aligned}$$

This yields a contradiction.

Case 2: $u(x,t)<R_n$ for all $(x,t)\in \mathbb {R}\times [0,T_n]$.

For any $n\in \mathbb {N}$, there exists a maximum point $t_n\in (0,T_n]$ of $\Vert u(\cdot ,t)\Vert _{BC(\mathbb {R})}$ such that $\Vert u(\cdot , t_n)\Vert _{BC(\mathbb {R})} =\max _{0\le t \le T_n} \Vert u(\cdot , t)\Vert _{BC(\mathbb {R})}=R_n$. If $s\in (0,t_n)$, then we see that

$$\begin{aligned} \Vert u(\cdot , t_n-s)\Vert _{BC(\mathbb {R})} \le \max _{0\le t \le T_n}\Vert u(\cdot , t)\Vert _{BC(\mathbb {R})}=R_n \end{aligned}$$

(28)

because $0<t_n-s\le T_n$. Here, since $\Vert u(\cdot , t_n-s)\Vert _{BC(\mathbb {R})}-s < \Vert u(\cdot ,t_n)\Vert _{BC(\mathbb {R})} =\sup _{x\in \mathbb {R}} |u(x,t_n)|$, there exists a point $x^{(n,s)}\in \mathbb {R}$ such that

$$\begin{aligned}&\Vert u(\cdot , t_n-s)\Vert _{BC(\mathbb {R})}-s < u(x^{(n,s)}, t_n) \quad \text { and } \end{aligned}$$

(29)

$$\begin{aligned}&u_{xx}(x^{(n,s)},t_n)\le 0. \end{aligned}$$

(30)

Let $n\in \mathbb {N}$ be a sufficiently large. Since $\Vert u(\cdot , t_n-s)\Vert _{BC(\mathbb {R})}$ is sufficiently large, we have $u(x^{(n,s)},t_n)>r_0$. Hence, by (27) it follows that

$$\begin{aligned} g(u(x^{(n,s)}, t_n), J*u(x^{(n,s)}, t_n))<-3. \end{aligned}$$

(31)

By (30), (31) and the equation of (P), it holds that $u_t(x^{(n,s)},t_n)\le -3$. Hence, there is a sufficient small constant $\eta _0>0$ such that for any $0<\eta <\eta _0$,

$$\begin{aligned} u(x^{(n,s)}, t_n) -u(x^{(n,s)}, t_n-\eta )<-2\eta . \end{aligned}$$

(32)

On the other hand, by (28) and (29), we obtain that for $s\in (0,t_n)$,

$$\begin{aligned}&u(x^{(n,s)},t_n) -u(x^{(n,s)},t_n-s)\\&\quad > \Vert u(\cdot ,t_n-s))\Vert _{BC(\mathbb {R})}-s - \Vert u(\cdot ,t_n-s))\Vert _{BC(\mathbb {R})} = -s. \end{aligned}$$

Choosing $0< s < \min \{\eta _0, t_n\}$ and taking $\eta =s$ in (32), we see that

$$\begin{aligned} -s< u(x^{(n,s)},t_n) -u(x^{(n,s)},t_n-s) < -2s. \end{aligned}$$

This inequality is a contradiction because s is positive. Thus, we have (25) because both of Case 1 and Case 2 imply a contradiction. $\square$

Proof of Theorem 1

Proposition 5 and Lemma 2 immediately imply Theorem 1. $\square$

B: Boundedness of the solution of the problems (P) and $\hbox {RD}_{\varepsilon }$

Here, we show several propositions.

Proof of Proposition 1

Multiplying the equation of (P) by u and integrating it over $\mathbb {R}$, we have

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\Vert u\Vert _{L^2(\mathbb {R})}^2 =-d_u \Vert u_x\Vert _{L^2(\mathbb {R})}^2 +\int _{\mathbb {R}} g(u,J*u)u \, dx. \end{aligned}$$

From (H1), the Schwarz inequality and the Young inequality for convolutions, one have

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\Vert u\Vert _{L^2(\mathbb {R})}^2&\le -d_u \Vert u_x\Vert _{L^2(\mathbb {R})}^2 -g_0\Vert u\Vert _{L^{p+1}(\mathbb {R})}^{p+1} +g_1 \Vert J\Vert _{L^1(\mathbb {R})} \Vert u\Vert _{L^2(\mathbb {R})} \Vert u\Vert _{L^4(\mathbb {R})}^2 \\&\quad +\left( g_2 \Vert J\Vert _{L^1(\mathbb {R})} +g_3 \right) \Vert u\Vert _{L^2(\mathbb {R})}^2. \end{aligned}$$

Moreover, using (H4), the interpolation for the Hölder inequality and the Young inequality, it holds that

$$\begin{aligned} g_1 \Vert J\Vert _{L^1(\mathbb {R})} \Vert u\Vert _{L^2(\mathbb {R})} \Vert u\Vert _{L^4(\mathbb {R})}^2&\le g_1 \Vert u\Vert _{L^{p+1}(\mathbb {R})}^{(p+1)/(p-1)} \Vert J\Vert _{L^1(\mathbb {R})} \Vert u\Vert _{L^2(\mathbb {R})}^{2(p-2)/(p-1)} \\&\le g_0 \Vert u\Vert _{L^{p+1}(\mathbb {R})}^{p+1} +C_9 \, \Vert J\Vert _{L^1(\mathbb {R})}^{(p-1)/(p-2)} \Vert u\Vert _{L^2(\mathbb {R})}^2. \end{aligned}$$

Hence we obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\Vert u\Vert _{L^2(\mathbb {R})}^2\le & {} -d_u \Vert u_x\Vert _{L^2(\mathbb {R})}^2 +C_9 \, \Vert J\Vert _{L^1(\mathbb {R})}^{(p-1)/(p-2)} \Vert u\Vert _{L^2(\mathbb {R})}^2 \\&+\left( g_2 \Vert J\Vert _{L^1(\mathbb {R})} +g_3 \right) \Vert u\Vert _{L^2(\mathbb {R})}^2. \end{aligned}$$

We therefore have

$$\begin{aligned} \frac{d}{dt}\Vert u\Vert _{L^2(\mathbb {R})}^2 \le C_{10} \Vert u\Vert _{L^2(\mathbb {R})}^2. \end{aligned}$$

(33)

Next, integrating the equation of (P) multiplied by $u_{xx}$ over $\mathbb {R}$, one have

$$\begin{aligned} -\frac{1}{2}\frac{d}{dt} \Vert u_x\Vert _{L^2(\mathbb {R})}^2= & {} d_u \Vert u_{xx}\Vert _{L^2(\mathbb {R})}^2 -\int _{\mathbb {R}} \left\{ g_u(u,J*u) |u_x|^2\right. \\&\left. +g_v(u,J*u)(J*u_x)u_x \right\} \, dx. \end{aligned}$$

From (H2), (H3), the Schwarz inequality and the Young inequality for convolutions, we can estimate the derivative of $\Vert u_x\Vert _{L^2}^2$ with respect to t as follows:

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \Vert u_x\Vert _{L^2(\mathbb {R})}^2&\le -d_u \Vert u_{xx}\Vert _{L^2(\mathbb {R})}^2 -g_0 p \int _{\mathbb {R}} |u|^{p-1} |u_x|^2 \, dx\\&\quad +g_4 \Vert J\Vert _{L^1(\mathbb {R})} \Vert u\Vert _{BC(\mathbb {R})} \Vert u_x\Vert _{L^2(\mathbb {R})}^2 \\&\quad +g_5 \Vert u_x\Vert _{L^2(\mathbb {R})}^2 +g_6 \int _{\mathbb {R}} |u| |J*u_x| |u_x| \, dx + g_7 \int _{\mathbb {R}} |J*u_x| |u_x| \, dx\\&\le g_4 \Vert J\Vert _{L^1(\mathbb {R})} \Vert u\Vert _{BC(\mathbb {R})} \Vert u_x\Vert _{L^2(\mathbb {R})}^2 -g_0 p \int _{\mathbb {R}} |u|^{p-1} |u_x|^2 \, dx \\&\quad +g_6 \int _{\mathbb {R}} |u| |J*u_x| |u_x| \, dx + g_5 \Vert u_x\Vert _{L^2(\mathbb {R})}^2 \\&\quad + g_7 \Vert J \Vert _{L^1(\mathbb {R})}\Vert u_x \Vert ^2_{L^2(\mathbb {R})}. \end{aligned}$$

By the Hölder and the Young inequalities, recalling that

$$\begin{aligned} g_6 \int _{\mathbb {R}} |u| |J*u_x| |u_x| \, dx \le g_0 p \int _{\mathbb {R}} |u|^{p-1} |u_x|^2 \, dx +C_{11} \, \Vert J\Vert _{L^1(\mathbb {R})}^{(p-1)/(p-2)} \Vert u_x\Vert _{L^2(\mathbb {R})}^2, \end{aligned}$$

we obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \Vert u_x\Vert _{L^2(\mathbb {R})}^2&\le \left\{ \left( g_4 \Vert u\Vert _{BC(\mathbb {R})}+g_7 \right) \Vert J\Vert _{L^1(\mathbb {R})} + g_5 \right\} \Vert u_x \Vert ^2_{L^2(\mathbb {R})} \nonumber \\&\quad +C_{11} \, \Vert J\Vert _{L^1(\mathbb {R})}^{(p-1)/(p-2)} \Vert u_x\Vert _{L^2(\mathbb {R})}^2. \end{aligned}$$

(34)

where $C_{11}$ is a positive constant and if $2\le p<3$, then $g_6=0$ which implies $C_{11}=0$ by (H4). By Lemma 2, since $\Vert u(\cdot ,t)\Vert _{BC(\mathbb {R})}$ is bounded in t, one see that

$$\begin{aligned} \frac{d}{dt} \Vert u_x\Vert _{L^2(\mathbb {R})}^2 \le C_{12} \Vert u_x\Vert _{L^2(\mathbb {R})}^2. \end{aligned}$$

(35)

Put $X(t):=\Vert u(\cdot ,t)\Vert _{L^2(\mathbb {R})}^2$ and $Y(t):=\Vert u_x(\cdot ,t)\Vert _{L^2(\mathbb {R})}^2$. By (33) and (35), it follows that

$$\begin{aligned} \left\{ \begin{aligned}&X(t)\le X(0)e^{C_{10} T}, \\&Y(t)\le Y(0)e^{C_{12} T} \end{aligned} \right. \quad \text { for all } \; 0\le t\le T. \end{aligned}$$

Consequently, we have

$$\begin{aligned} \sup _{0\le t\le T}\Vert u(\cdot ,t)\Vert _{H^1(\mathbb {R})} \le \Vert u_0\Vert _{H^1(\mathbb {R})}e^{k_0T}, \end{aligned}$$

where $2k_0=\max \{C_{10},C_{12}\}$. $\square$

Next we give the proof of Proposition 2.

Proof of Proposition 2

First, we show that $u^{\varepsilon }$ and $v_j^{\varepsilon }$ are bounded in $L^2(\mathbb {R})$ by the argument similar to the proof of Proposition 1. Multiplying the principal equation of ($\hbox {RD}_{\varepsilon }$) by $u^{\varepsilon }$ and integrating it over $\mathbb {R}$, we have

$$\begin{aligned} \frac{d}{dt} \Vert u^{\varepsilon }\Vert _{L^2(\mathbb {R})}^2 \le C_{13} \left( \Vert u^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2 + \sum _{j=1}^{M}\Vert \alpha _j v_j^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2 \right) . \end{aligned}$$

(36)

Also, multiplying the second equation of ($\hbox {RD}_{\varepsilon }$) by $v_j^{\varepsilon }$ and integrating it over $\mathbb {R}$, we see that

$$\begin{aligned} \frac{d}{dt} \Vert v_j ^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2 \le \frac{1}{\varepsilon } \left( \Vert u^{\varepsilon }\Vert _{L^2(\mathbb {R})}^2 -\Vert v_j ^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2 \right) . \end{aligned}$$

Multiplying the above inequality by $\alpha _j^2$ and adding those inequalities from $j=1$ to M, we obtain that

$$\begin{aligned} \frac{d}{dt} \sum _{j=1}^{M} \Vert \alpha _j v_j^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2 \le \frac{1}{\varepsilon } \left( C_{14} \Vert u^{\varepsilon }\Vert _{L^2(\mathbb {R})}^2 - \sum _{j=1}^{M} \Vert \alpha _j v_j^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2 \right) , \end{aligned}$$

(37)

where $C_{14}=\sum _{j=1}^{M}\alpha _j^2$. Here, put $X(t):=\Vert u^{\varepsilon }(\cdot ,t)\Vert _{L^2(\mathbb {R})}^2$, $Y(t):=\sum _{j=1}^{M} \Vert \alpha _j v_j^{\varepsilon } (\cdot ,t) \Vert _{L^2(\mathbb {R})}^2$. Hence, (36), (37) are described as follows:

$$\begin{aligned} \frac{dX}{dt} \le C_{13} (X + Y), \qquad \frac{dY}{dt} \le \frac{1}{\varepsilon } ( C_{14} X -Y ). \end{aligned}$$

(38)

Noticing that X(t), $Y(t)\ge 0$, we have

$$\begin{aligned} \frac{d}{dt}\left( X+C_{13}\varepsilon Y \right) \le C_{13}(1+C_{14}) ( X +C_{13}\varepsilon Y ), \end{aligned}$$

which implies

$$\begin{aligned} X(t) +C_{13}\varepsilon Y(t) \le \left\{ X(0) +C_{13}\varepsilon Y(0) \right\} e^{C_{13}(1+C_{14}) T} \qquad \text { for all } \; 0\le t\le T. \end{aligned}$$

Note that $\Vert v_j^{\varepsilon }(\cdot ,0)\Vert _{L^2(\mathbb {R})}=\Vert k^{d_j}*u_0\Vert _{L^2(\mathbb {R})} \le \Vert u_0\Vert _{L^2(\mathbb {R})}$ from $0<\varepsilon <1$ and $\Vert k^d\Vert _{L^1(\mathbb {R})}=1$. Recalling $X(t)=\Vert u^{\varepsilon }(\cdot ,t)\Vert _{L^2(\mathbb {R})}^2$, one see that

$$\begin{aligned} \Vert u^{\varepsilon }(\cdot ,t)\Vert _{L^2(\mathbb {R})}^2 \le \left( 1+C_{13} \sum _{j=1}^{M} \alpha _j^2 \right) \Vert u_0\Vert _{L^2(\mathbb {R})}^2 \, e^{C_{13}(1+C_{14}) T} \qquad \text { for all } \; 0\le t\le T. \end{aligned}$$

Using (38) again yields

$$\begin{aligned} Y(t)\le & {} \max \left\{ Y(0),\ \max _{0\le t\le T} X(t) \right\} \\\le & {} \max \left\{ \sum _{j=1}^{M} \alpha _j^2 ,\ \left( 1+ C_{13} \sum _{j=1}^{M} \alpha _j^2 \right) e^{C_{13}(1+C_{14})T} \right\} \Vert u_0\Vert _{L^2(\mathbb {R})}^2. \end{aligned}$$

Hence, it is shown that

$$\begin{aligned} \sum _{j=1}^{M}\Vert \alpha _j v_j^{\varepsilon } (\cdot ,t) \Vert _{L^2(\mathbb {R})}^2 \le C_{15} \Vert u_0\Vert _{L^2(\mathbb {R})}^2 \left( 1 +e^{ C_{13}(1+C_{14})T} \right) \quad \text {for all}\quad 0\le t\le T. \nonumber \\ \end{aligned}$$

(39)

Therefore, each component $u^{\varepsilon }$ and $v_j^{\varepsilon }$ of the solution is bounded in $L^2(\mathbb {R})$ by (36) and (39).

Next, let us show the boundedness of $u_x^{\varepsilon }$ and $v_{j,x}^{\varepsilon }$ in $L^2(\mathbb {R})$. Note that we use the $L^2$-boundedness of $u^{\varepsilon }$ and $v_j^{\varepsilon }$ in the proof. Multiplying the principal equation of ($\hbox {RD}_{\varepsilon }$) by $u_{xx}^{\varepsilon }$ and integrating it in $\mathbb {R}$, similarly to the proof of Proposition 1, one see that

$$\begin{aligned} \begin{aligned} \frac{1}{2}\frac{d}{dt} \Vert u_x^{\varepsilon }\Vert _{L^2(\mathbb {R})}^2&\le -d_u\Vert u_{xx}^{\varepsilon }\Vert _{L^2(\mathbb {R})}^2 +g_4\left\| {\sum _{j=1}^{M}}\alpha _j v_j^{\varepsilon } \right\| _{L^2(\mathbb {R})} \Vert u_x^{\varepsilon } \Vert _{L^4}^2 \\&\quad +C_{11} \Vert u_x^{\varepsilon }\Vert _{L^2}^{(p-3)/(p-2)} \left\| {\sum _{j=1}^{M}}\alpha _j v_{j,x}^{\varepsilon } \right\| _{L^2(\mathbb {R})}^{(p-1)/(p-2)} \\&\quad +g_5 \Vert u_x^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2 +g_7 \left( \Vert u_x^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2 +\left\| {\sum _{j=1}^{M}}\alpha _j v_{j,x}^{\varepsilon } \right\| _{L^2(\mathbb {R})}^2 \right) . \end{aligned} \end{aligned}$$

(40)

Here, $C_{11}$ is the same constant used by the inequality (34), and by (H4), $C_{11}=0$ if $2\le p<3$. By the Gagliardo–Nirenberg–Sobolev inequality, there is a positive constant $C_S$ satisfying

$$\begin{aligned} \Vert u_x^{\varepsilon }\Vert _{L^4(\mathbb {R})} \le C_S \Vert u_x^{\varepsilon }\Vert _{L^2(\mathbb {R})}^{3/4}\Vert u_{xx}^{\varepsilon }\Vert _{L^2(\mathbb {R})}^{1/4}. \end{aligned}$$

Applying this to (40) yields

$$\begin{aligned}&\frac{1}{2}\frac{d}{dt} \Vert u_x^{\varepsilon }\Vert _{L^2(\mathbb {R})}^2\\&\le -d_u\Vert u_{xx}^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2 +g_4\left\| {\sum _{j=1}^{M}}\alpha _j v_j^{\varepsilon } \right\| _{L^2(\mathbb {R})} C_S^2 \Vert u_x^{\varepsilon } \Vert _{L^2(\mathbb {R})}^{3/2}\Vert u_{xx}^{\varepsilon }\Vert _{L^2(\mathbb {R})}^{1/2} \\&\quad +C_{11} \Vert u_x^{\varepsilon }\Vert _{L^2}^{(p-3)/(p-2)} \left\| \sum _{j=1}^{M}\alpha _j v_{j,x}^{\varepsilon } \right\| _{L^2(\mathbb {R})}^{(p-1)/(p-2)} +g_5 \Vert u_x^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2\\&\qquad +g_7 \left( \Vert u_x^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2 +\left\| {\sum _{j=1}^{M}}\alpha _j v_{j,x}^{\varepsilon } \right\| _{L^2(\mathbb {R})}^2 \right) . \end{aligned}$$

By using the Young inequality, we have

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \Vert u_x^{\varepsilon }\Vert _{L^2(\mathbb {R})}^2\le & {} \frac{C_{16}}{2} \left[ \left\{ \Vert u_0\Vert _{L^2(\mathbb {R})}^{2/3} \left( 1+e^{2 C_{13}(1+C_{14}) T/3} \right) +1 \right\} \Vert u_x^{\varepsilon }\Vert _{L^2}^2 \right. \\&\left. + \sum _{j=1}^{M} \Vert \alpha _j v_{j,x}^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2 \right] . \end{aligned}$$

Hence, we get the following inequality:

$$\begin{aligned} \frac{d}{dt} \Vert u_x^{\varepsilon }\Vert _{L^2(\mathbb {R})}^2 \le C_{17} \left\{ \Vert u_x^{\varepsilon }\Vert _{L^2}^2 + \sum _{j=1}^{M} \Vert \alpha _j v_{j,x}^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2 \right\} . \end{aligned}$$

(41)

Also, integrating the second equation of ($\hbox {RD}_{\varepsilon }$) multiplied by $v_{j,xx}^{\varepsilon }$ over $\mathbb {R}$, from the Young inequality, it follows that

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \Vert v_{j,x}^{\varepsilon }\Vert _{L^2(\mathbb {R})}^2&=\frac{1}{\varepsilon } \left\{ -d_j \Vert v_{j,xx}^{\varepsilon }\Vert _{L^2(\mathbb {R})}^2 +\int _{\mathbb {R}} u_x^{\varepsilon } v_{j,x} \, dx -\Vert v_{j,x}^{\varepsilon }\Vert _{L^2(\mathbb {R})}^2 \right\} \\&\le \frac{1}{\varepsilon } \left( \frac{1}{2}\Vert u_x^{\varepsilon }\Vert _{L^2(\mathbb {R})}^2 -\frac{1}{2}\Vert v_{j,x}^{\varepsilon }\Vert _{L^2(\mathbb {R})}^2 \right) . \end{aligned}$$

Hence, multiplying this by $\alpha _j^2$ and adding those from $j=1$ to M yield the following:

$$\begin{aligned} \frac{d}{dt} \sum _{j=1}^{M} \Vert \alpha _jv_{j,x}^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2 \le \frac{ 1 }{\varepsilon } \left( C_{18} \Vert u_x^{\varepsilon }\Vert _{L^2(\mathbb {R})}^2 - \sum _{j=1}^{M} \Vert \alpha _jv_{j,x}^{\varepsilon } \Vert _{L^2(\mathbb {R})}^2 \right) , \end{aligned}$$

(42)

where $C_{18}=\sum _{j=1}^M \alpha _j^2$. Similarly to (36) and (37), (41) and (42) are represented as follows:

$$\begin{aligned} \frac{dX}{dt} \le C_{17} (X + Y), \qquad \frac{dY}{dt} \le \frac{ 1 }{\varepsilon } ( C_{18}X -Y ), \end{aligned}$$

where $X(t)=\Vert u_x^{\varepsilon }(\cdot ,t)\Vert _{L^2(\mathbb {R})}^2$ and $Y(t)=\sum _{j=1}^{M}\Vert \alpha _jv_{j,x}^{\varepsilon }(\cdot ,t)\Vert _{L^2(\mathbb {R})}^2$. Therefore, it follows that for any $0\le t\le T$,

$$\begin{aligned}&\Vert u_x^{\varepsilon }(\cdot ,t)\Vert _{L^2(\mathbb {R})}^2 \le \left( 1 +C_{17} \sum _{j=1}^{M} \alpha _j^2 \right) \Vert u_{0,x}\Vert _{L^2(\mathbb {R})}^2 \, e^{C_{17}(1+C_{18}) T} \quad \text { and } \\&\sum _{j=1}^{M}\Vert \alpha _j v_{j,x}^{\varepsilon }(\cdot ,t) \Vert _{L^2(\mathbb {R})}^2 \le C_{19} \Vert u_{0,x}\Vert _{L^2(\mathbb {R})}^2 \left( 1 +e^{C_{17}(1+C_{18}) T} \right) . \end{aligned}$$

$\square$

Proof of Proposition 3

Let $(u^{\varepsilon },v_j^{\varepsilon })$ be a solution of ($\hbox {RD}_{\varepsilon }$). For any $\delta >0$ and $k\in \mathbb {N}$, multiplying the first equation of ($\hbox {RD}_{\varepsilon }$) by $u^{\varepsilon } /\sqrt{\delta +(u^{\varepsilon })^2}$ and integrating it with respect to $x\in [-k,k]$, we have that

$$\begin{aligned} \int _{-k}^{k} u_t^{\varepsilon } \frac{u^{\varepsilon }}{\sqrt{\delta +(u^{\varepsilon })^2}} \,dx= & {} d_u \int _{-k}^{k} u_{xx}^{\varepsilon } \frac{u^{\varepsilon }}{\sqrt{\delta +(u^{\varepsilon })^2}} \,dx\nonumber \\&+\int _{-k}^{k} g\left( u^{\varepsilon }, \sum _{j=1}^{M} \alpha _j v_j^{\varepsilon } \right) \frac{u^{\varepsilon }}{\sqrt{\delta +(u^{\varepsilon })^2}} \, dx. \end{aligned}$$

(43)

For the left-hand side of (43), it holds that

$$\begin{aligned} \int _{-k}^{k} u_t^{\varepsilon } \frac{u^{\varepsilon }}{\sqrt{\delta +(u^{\varepsilon })^2}} \, dx =\frac{d}{dt} \int _{-k}^{k} \sqrt{\delta +(u^{\varepsilon })^2} \, dx \ \rightarrow \ \frac{d}{dt} \int _{-k}^{k} |u^{\varepsilon } | \, dx \quad \text { as } \delta \rightarrow 0 \end{aligned}$$

by using the dominated convergence theorem. Moreover, we calculate the first term of the right-hand side of (43) as follows:

$$\begin{aligned} d_u \int _{-k}^{k} u_{xx}^{\varepsilon } \frac{u^{\varepsilon }}{\sqrt{\delta +(u^{\varepsilon })^2}} \, dx&=-d_u \int _{-k}^{k} u_x^{\varepsilon } \left( \frac{u_x^{\varepsilon }}{\sqrt{\delta +(u^{\varepsilon })^2}} -\frac{(u^{\varepsilon })^2u_x^{\varepsilon }}{(\delta +(u^{\varepsilon })^2)^{3/2}} \right) \,dx \\&\quad +d_u\left[ u_x^{\varepsilon } \frac{u^{\varepsilon }}{\sqrt{\delta +(u^{\varepsilon })^2}} \right] _{x=-k}^{x=k} \\&=-d_u\delta \int _{-k}^{k} \frac{(u_x^{\varepsilon })^2}{(\delta +(u^{\varepsilon })^2)^{3/2}} \, dx +d_u \left( u_x^{\varepsilon } (k) - u_x^{\varepsilon }(-k) \right) \\&\le d_u \left( |u_x^{\varepsilon }(k) | +|u_x^{\varepsilon }(-k) | \right) . \end{aligned}$$

By (43), as $\delta \rightarrow 0$, it holds that for any $k\in \mathbb {N}$

$$\begin{aligned} \frac{d}{dt} \int _{-k}^{k} |u^{\varepsilon }| \, dx \le d_u \left( |u_x^{\varepsilon } (k)| +|u_x^{\varepsilon } (-k)| \right) +\int _{-k}^{k} g\left( u^{\varepsilon }, \sum _{j=1}^{M} \alpha _j v_j^{\varepsilon } \right) \frac{u^{\varepsilon }}{|u^{\varepsilon }|} \, dx. \end{aligned}$$

Similarly to the proof of Proposition 1,

$$\begin{aligned} \frac{d}{dt} \int _{-k}^{k} |u^{\varepsilon } | \, dx\le & {} d_u \left( |u_x^{\varepsilon } (k)| +|u_x^{\varepsilon } (-k)| \right) \nonumber \\&+C_{20}\left( \int _{-k}^{k} |u^{\varepsilon } | \, dx + \sum _{j=1}^{M} \int _{-k}^{k} |\alpha _j v_j^{\varepsilon } | \, dx \right) , \end{aligned}$$

(44)

where $C_{20}$ is a positive constant depending on $g_1$, $g_2$, $g_3$ and the boundedness of $\Vert u^{\varepsilon }\Vert _{BC(\mathbb {R})}$ by Proposition 2. By the similar argument for $v_j^{\varepsilon }$, we estimate

$$\begin{aligned} \frac{d}{dt} \int _{-k}^{k} |v_j^{\varepsilon }| \, dx \le \frac{1}{\varepsilon } \left( d_j \left( |v_{j,x}^{\varepsilon }(k)|+|v_{j,x}^{\varepsilon }(-k)| \right) +\int _{-k}^{k} |u^{\varepsilon }| \, dx -\int _{-k}^{k} |v_j^{\varepsilon }| \, dx \right) . \end{aligned}$$

Hence, we obtain that

$$\begin{aligned} \begin{aligned}&\frac{d}{dt} \sum _{j=1}^{M} \int _{-k}^{k} |\alpha _j v_j^{\varepsilon } | \, dx \\&\quad \le \frac{1}{\varepsilon } \left\{ \sum _{j=1}^{M} d_j |\alpha _j| \left( |v_{j,x}^{\varepsilon } (k)|+|v_{j,x}^{\varepsilon } (-k)| \right) + \left( \sum _{j=1}^{M} |\alpha _j|\right) \int _{-k}^{k} |u^{\varepsilon }| \, dx \right. \\&\qquad \left. - \sum _{j=1}^{M}\int _{-k}^{k} |\alpha _j v_j^{\varepsilon } | \, dx \right\} . \end{aligned} \end{aligned}$$

(45)

By calculating the sum of (44) and (45), we see that

$$\begin{aligned}&\frac{d}{dt} \int _{-k}^{k} \left( |u^{\varepsilon } |+C_{20}\varepsilon \sum _{j=1}^{M}|\alpha _j v_j^{\varepsilon } | \right) \, dx \le c_k(t) \nonumber \\&\quad + C_{21}\int _{-k}^{k} \left( |u^{\varepsilon } | +C_{20}\varepsilon \sum _{j=1}^{M} |\alpha _j v_j^{\varepsilon } | \right) \, dx, \end{aligned}$$

(46)

where $c_k(t)=d_u ( |u_x^{\varepsilon } (k,t)|+|u_x^{\varepsilon } (-k,t)| ) +C_{20}\sum _{j=1}^{M} d_j |\alpha _j| ( |v_{j,x}^{\varepsilon } (k,t)|+|v_{j,x}^{\varepsilon } (-k,t)| )$ depends on t and $C_{21}= C_{20}(1 + \sum _{j=1}^M | \alpha _j | )$. Here, from Proposition 2, $u_x^{\varepsilon } (\cdot ,t)$, $v_{j,x}^{\varepsilon }(\cdot ,t) \in L^2(\mathbb {R})$ for a fixed $0\le t\le T$. Hence, there is a subsequence $\{k_m\}_{m\in \mathbb {N}}$ satisfying $k_m\rightarrow \infty$ as $m\rightarrow \infty$ such that $u_x^{\varepsilon } (k_m,t)$, $u_x^{\varepsilon } (-k_m,t)$, $v_{j,x}^{\varepsilon }(k_m,t)$, $v_{j,x}^{\varepsilon }(-k_m,t)\rightarrow 0$ as $m\rightarrow \infty$. Hence, $c_{k_m}(t)\rightarrow 0$ as $m\rightarrow \infty$. Note that $k_m$ depends on a time t. Taking the limit of (46) on $k=k_m$ as $m\rightarrow \infty$, we have the following inequality

$$\begin{aligned}&\frac{d}{dt} \left( \Vert u^{\varepsilon } \Vert _{L^1(\mathbb {R})}+ C_{20} \varepsilon \sum _{j=1}^{M} \Vert \alpha _j v_j^{\varepsilon } \Vert _{L^1(\mathbb {R})} \right) \\&\quad \le C_{21} \left( \Vert u^{\varepsilon } \Vert _{L^1(\mathbb {R})}+ C_{20}\varepsilon \sum _{j=1}^{M} \Vert \alpha _j v_j^{\varepsilon } \Vert _{L^1(\mathbb {R})} \right) . \end{aligned}$$

Using the classical Gronwall Lemma, we have

$$\begin{aligned} \Vert u^{\varepsilon } \Vert _{L^1(\mathbb {R})} + C_{20}\varepsilon \sum _{j=1}^{M} \Vert \alpha _j v_j^{\varepsilon } \Vert _{L^1(\mathbb {R})} \le \left( 1+ C_{20} \varepsilon \sum _{j=1}^{M} |\alpha _j| \right) \Vert u_0 \Vert _{L^1(\mathbb {R})} \, e^{C_{21}T}. \end{aligned}$$

Therefore, we see that

$$\begin{aligned} \Vert u^{\varepsilon } \Vert _{L^1(\mathbb {R})}+ C_{20}\varepsilon \sum _{j=1}^{M} \Vert \alpha _j v_j^{\varepsilon } \Vert _{L^1(\mathbb {R})} \le C_{22}, \end{aligned}$$

and it is shown that $\sup _{0\le t\le T}\Vert u^{\varepsilon }(\cdot ,t)\Vert _{L^1(\mathbb {R})}$ is bounded. Furthermore, since (45) holds and $c_{k_m}(t)\rightarrow 0$ as $m\rightarrow \infty$, we obtain

$$\begin{aligned} \frac{d}{dt} \sum _{j=1}^{M} \int _{\mathbb {R}} |\alpha _j v_j^{\varepsilon }| \, dx \le \frac{1}{\varepsilon } \left( C_{23} -\sum _{j=1}^{M} \int _{\mathbb {R}} |\alpha _j v_j^{\varepsilon }| \, dx \right) , \end{aligned}$$

where $C_{23}= C_{22} \sum _{j=1}^{M} |\alpha _j|$. Hence, noting that $\Vert v_j^{\varepsilon }(\cdot ,0)\Vert _{L^1(\mathbb {R})}\le \Vert u_0\Vert _{L^1(\mathbb {R})}$, we have

$$\begin{aligned} \sum _{j=1}^{M} \int _{\mathbb {R}} |\alpha _j v_j^{\varepsilon }| \, dx\le & {} \max \left\{ C_{23}, \sum _{j=1}^{M} |\alpha _j| \Vert v_j^{\varepsilon }(\cdot ,0)\Vert _{L^1(\mathbb {R})} \right\} \\\le & {} \max \left\{ C_{23}, \sum _{j=1}^{M} |\alpha _j| \Vert u_0\Vert _{L^1(\mathbb {R})} \right\} . \end{aligned}$$

Consequently, we get the boundedness of $\sup _{0\le t\le T} \sum _{j=1}^{M} \Vert \alpha _j v_j^{\varepsilon }(\cdot ,t) \Vert _{L^1(\mathbb {R})}$, so that Proposition 3 is shown. $\square$

C: Proof of Lemma 1

Proof

Put $V_j:=v_j-k^{d_j}*u^{\varepsilon }$. Note that $k^{d_j}*u^{\varepsilon }$ is a solution of $d_j(k^{d_j}*u^{\varepsilon })_{xx}-k^{d_j}*u^{\varepsilon } +u^{\varepsilon }=0$. Since $u^{\varepsilon }$ is the first component of the solution to ($\hbox {RD}_{\varepsilon }$), we can calculate as follows:

$$\begin{aligned} k^{d_j}*u_t^{\varepsilon } =\frac{d_u}{d_j} \left( k^{d_j}*u^{\varepsilon }-u^{\varepsilon } \right) +k^{d_j}* \left( g\left( u^{\varepsilon }, \sum _{j=1}^{M}\alpha _jv_j^{\varepsilon } \right) \right) . \end{aligned}$$

Recalling that $\Vert k^{d_j}\Vert _{L^1(\mathbb {R})}=1$ and both of $\Vert u^{\varepsilon }\Vert _{L^2(\mathbb {R})}$ and $\Vert v_j^{\varepsilon }\Vert _{L^2(\mathbb {R})}$ are bounded with respect to $\varepsilon$ from Proposition 2, the right-hand side of the previous identity is bounded in $L^2(\mathbb {R})$. Hence, there exists a positive constant $C_{24}$ independent of $\varepsilon$ such that

$$\begin{aligned} \Vert k^{d_j}*u_t^{\varepsilon }\Vert _{L^2(\mathbb {R})}\le C_{24}. \end{aligned}$$

Recalling that $\varepsilon v_{j,t}^{\varepsilon }=d_jv_{j,xx}+u^{\varepsilon }-v_j^{\varepsilon }$, the equation of $V_j$ becomes

$$\begin{aligned} V_{j,t} =\frac{1}{\varepsilon }\left( d_j V_{j,xx} - V_j \right) -k^{d_j}*u_t^{\varepsilon }. \end{aligned}$$

Multiplying this equation by $V_j$ and integrating it over $\mathbb {R}$ yield

$$\begin{aligned} \frac{d}{dt}\frac{1}{2} \Vert V_j\Vert _{L^2(\mathbb {R})}^2&\le -\frac{d_j}{\varepsilon }\Vert V_{j,x}\Vert _{L^2(\mathbb {R})}^2 -\frac{1}{\varepsilon } \Vert V_j\Vert _{L^2(\mathbb {R})}^2 -\int _{\mathbb {R}} \left( k^{d_j}*u_t^{\varepsilon } \right) V_j \, dx \\&\le -\frac{1}{2\varepsilon } \Vert V_j\Vert _{L^2(\mathbb {R})}^2 +\frac{\varepsilon }{2} \left\| k^{d_j}*u_t^{\varepsilon } \right\| _{L^2(\mathbb {R})}^2 \le -\frac{1}{2\varepsilon } \Vert V_j\Vert _{L^2(\mathbb {R})}^2 +\frac{\varepsilon }{2}C^2_{24}. \end{aligned}$$

Since it is shown that

$$\begin{aligned} \frac{d}{dt} \Vert V_j\Vert _{L^2(\mathbb {R})}^2 \le -\frac{1}{\varepsilon } \Vert V_j\Vert _{L^2(\mathbb {R})}^2 +\varepsilon C^2_{24}, \end{aligned}$$

we get $\Vert V_j\Vert _{L^2(\mathbb {R})}^2\le \min \{\Vert V_j(\cdot ,0)\Vert _{L^2(\mathbb {R})}^2,\, (C_{24}\varepsilon )^2\}$. Noting that $V_j(\cdot ,0)=0$, we obtain that

$$\begin{aligned} \Vert V_j\Vert _{L^2(\mathbb {R})}\le C_{24}\varepsilon . \end{aligned}$$

Therefore, (9) is proved. $\square$

D: Polynomial approximation

Proof of Proposition 4

Let $\phi \in BC([0,\infty ])$. We change variables x in terms of y as follows:

$$\begin{aligned} y=e^{-x}, \qquad \psi (y):=\phi (x). \end{aligned}$$

(47)

Since y is decreasing in x and y belongs to [0, 1] when x belongs to $[0,\infty ]$, we have the inverse function of y and the inverse function is represented by $x=-\log y$. Also, since $\phi (x)$ is bounded at infinity by $\phi \in BC([0,+\infty ])$, one have $\psi \in C([0,1])$. Hence, applying the Stone–Weierstrass theorem to $\psi$, for any $\varepsilon$, there exists a polynomial function $p(y)=\sum _{j=0}^M\beta _j {y}^j$ such that

$$\begin{aligned} \left| \psi (y) - \sum _{j=0}^{M} \beta _j {y}^j\right| < \varepsilon \quad \text { for all } y\in [0,1]. \end{aligned}$$

Substituting $y=e^{-x}$ to the previous inequality, it follows that for all $x\in [0,+\infty ]$

$$\begin{aligned} \left| \phi (x) - \sum _{j=0}^{M} \beta _j e^{-jx}\right| < \varepsilon \end{aligned}$$

due to (47). $\square$

E: Examples of calculated parameters

We provide the examples of values of $\alpha _1,\ldots , \alpha _5$ which are explicitly calculated by using (8). We consider the case for $J_1$ and $J_2$.

In the case of $J_1(x)$, $\alpha _1,\ldots ,\alpha _5$ are calculated by

$$\begin{aligned} \begin{array}{l l l} \alpha _1&{}=&{} 30 \left( -140 e \text {erfc}(1)-504 e^4 \text {erfc}(2)+15 e^{\frac{1}{4}} \text {erfc}\left( \frac{1}{2}\right) +420 e^{\frac{9}{4}} \text {erfc}\left( \frac{3}{2}\right) \right. \\ &{}&{}\left. +210 e^{\frac{25}{4}} \text {erfc}\left( \frac{5}{2}\right) \right) \approx -0.3166,\\ \alpha _2 &{}=&{}-210 \left( -105 e \text {erfc}(1)-420 e^4 \text {erfc}(2)+10e^{\frac{1}{4}} \text {erfc}\left( \frac{1}{2}\right) +336 e^{\frac{9}{4}} \text {erfc}\left( \frac{3}{2}\right) \right. \\ &{}&{}\left. +180 e^{\frac{25}{4}} \text {erfc}\left( \frac{5}{2}\right) \right) \approx 1.619,\\ \alpha _3 &{}=&{}280 \left( -168 e \text {erfc}(1)-720 e^4 \text {erfc}(2)+15 e^{\frac{1}{4}} \text {erfc}\left( \frac{1}{2}\right) +560 e^{\frac{9}{4}} \text {erfc}\left( \frac{3}{2}\right) \right. \\ &{}&{}\left. +315 e^{\frac{25}{4}} \text {erfc}\left( \frac{5}{2}\right) \right) \approx 2.314, \\ \alpha _4 &{}=&{}-630 \left( -70 e \text {erfc}(1)-315 e^4 \text {erfc}(2)+6 e^{\frac{1}{4}} \text {erfc}\left( \frac{1}{2}\right) +240 e^{\frac{9}{4}} \text {erfc}\left( \frac{3}{2}\right) \right. \\ &{}&{}\left. +140e^{\frac{25}{4}} \text {erfc}\left( \frac{5}{2}\right) \right) \approx -4.438, \\ \alpha _5 &{}=&{}252 \left( -60 e \text {erfc}(1)-280 e^4 \text {erfc}(2)+5 e^{\frac{1}{4}} \text {erfc}\left( \frac{1}{2}\right) +210 e^{\frac{9}{4}} \text {erfc}\left( \frac{3}{2}\right) \right. \\ &{}&{}\left. +126 e^{\frac{25}{4}} \text {erfc}\left( \frac{5}{2}\right) \right) \approx 1.811, \\ \end{array} \end{aligned}$$

where

$$\begin{aligned} \text { erfc}(x):=1-\frac{2}{\sqrt{\pi }}\int _{0}^{x}e^{-t^2}dt. \end{aligned}$$

For the case of $J_2(x)$, $\alpha _1,\ldots ,\alpha _5$ are given by

$$\begin{aligned} \alpha _1&=\dfrac{3772961672081048906951}{251195073357821392800}\approx 15.02, \\ \alpha _2&=-\dfrac{1058305332396960720827}{17942505239844385200}\approx -58.98,\\ \alpha _3&=\dfrac{15614015192211958306819}{161482547158599466800}\approx 96.69, \\ \alpha _4&=-\dfrac{2167590862829621235761}{29904175399740642000}\approx -72.48, \\ \alpha _5&=\dfrac{4571014947001979131879}{209329227798184494000}\approx 21.84. \end{aligned}$$