1 Introduction

Recently there has been a surge in the analysis and simulation of mathematical models of reaction-diffusion type in the presence of so-called cross-diffusion. Cross-diffusion is a process in which the gradient in the concentration or density of one chemical or biological species induces a flux (either linear or nonlinear) of another species. This notion of cross-diffusion also includes the well-known cases of chemo- and haptotaxis modelling. Accordingly, the applications of reaction-cross-diffusion systems are abundant in the literature and include pattern forming in developmental biology [11], electrochemistry [3], cancer motility [5, 8, 12] and biofilms [15]. The introduction of cross-diffusion in standard reaction-diffusion models has been shown to prevent blow-up phenomena that are associated with such systems in the absence of cross-diffusion [9]. Explicit analytic solutions to these complex and often nonlinearly coupled systems of partial differential equations do rarely exist and thus several numerical methods have been applied to provide approximate solutions. Such methods are not only available for fixed spatial domains but also for simulations on continuously evolving spatial domains and surfaces [11]. In this contribution we present briefly the model system under consideration and discuss some state-of-the art analytical results and numerical tools as well as provide numerical solutions for some particular models.

2 A Multiple Species Reaction-Cross-Diffusion Model

Let \(\varOmega \subset {\mathbb {R}}^m\), m ∈{1, 2, 3}, be a simply connected bounded domain with ∂Ω ∈ C 0, 1. Moreover, let \( \mathbf {u} = \left ( u_1 \left ( \mathbf {x},t \right ),\cdots , u_n \left ( \mathbf {x},t \right ) \right )^T\) be a vector-valued function describing n species (chemical, biological, or otherwise) at position x ∈ Ω and time t ∈ I = [0, t F ], t F  > 0. The evolution equations for a reaction-cross-diffusion model can be obtained from the application of the law of mass conservation and are given by the following generalised non-dimensional system with zero-flux boundary conditions [11]

$$\displaystyle \begin{aligned} & \partial_t u_i = \nabla \cdot \left( \sum_{j=1}^n D_{ij} (\mathbf{u}) \nabla u_j \right)+ \gamma f_i (\mathbf{u}), & i =1,\cdots,n, \quad & \mathbf{x}\in\varOmega\,,\; t>0\,, {} \end{aligned} $$
(1a)
$$\displaystyle \begin{aligned} & \left(\sum_{j=1}^n D_{ij} (\mathbf{u}) \nabla u_j \right)\cdot {\nu} = 0,& i =1,\cdots,n, \quad & \mathbf{x}\in\partial\varOmega\,,\; t>0\,, {} \end{aligned} $$
(1b)
$$\displaystyle \begin{aligned} & \mathbf{u} (\mathbf{x},0) = \mathbf{u}_0 (\mathbf{x}),&& \mathbf{x}\in\varOmega\,,\; t=0.\,{}\end{aligned} $$
(1c)

In this framework, D ij (u) is the constant, linear, or nonlinear diffusion coefficient relating the jth species gradient with the flux of the ith species. γ is a non-dimensional scaling parameter describing the relative strength of the reaction kinetics f i (u) [13].

2.1 Analysis of Reaction-Cross-Diffusion Models

The general framework (1) encompasses the well-studied (Patlak-) Keller-Segel [9], Armstrong-Painter-Sherratt [2], and the Shigesada-Kawasaky-Teramoto [17] models. In many of these models, D ij (u) is highly nonlinear which makes rigorous mathematical analysis of such models, in particular if involving multiple species, challenging [4, 9, 14]—even in the absence of nonlinear reaction kinetics f i (u).

Analysis of Linear and Nonlinear Cross-Diffusion Models Some recent studies of reaction-diffusion systems with linear cross-diffusion show that such models enhance pattern formation for self-organised processes [7, 11]. In these works, the following two-species reaction-cross-diffusion system was studied

$$\displaystyle \begin{aligned} \partial_t {u} = \nabla \cdot \left( \nabla u + d_v \nabla v \right) + \gamma f(u,v), \qquad \partial_t {v} = \nabla \cdot \left( d\nabla v + d_u \nabla u \right) + \gamma g(u,v), \end{aligned} $$
(2)

where for illustrative purposes an activator-depleted model [13] with f(u, v) = a − u + u 2v and g(u, v) = b − u 2v was considered. On application of the linear stability theory, the following necessary conditions for cross-diffusion-driven instability were obtained and these generalise classical Turing diffusion-driven instability conditions in the absence of cross-diffusion

$$\displaystyle \begin{aligned} \begin{array}{rcl} f_u + g_v < 0, \; f_u\,g_v - f_v\,g_u > 0, \; d-d_u d_v > 0, \; d f_u + g_v - d_u\, f_v - d_v g_u &\displaystyle > 0, {} \end{array} \end{aligned} $$
(3)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \left(df_u+g_v-d_u\,f_v-d_vg_u\right)^2 -4(d-d_u d_v)\left(f_ug_v-f_vg_u)\right)&\displaystyle > 0. {} \end{array} \end{aligned} $$
(4)

The above generalisation implies that in the presence of cross-diffusion, a wide range of non-standard reaction-diffusion models can give rise to patterning that is induced by linear cross-diffusion. For example, activator-inhibitor, activator-activator, inhibitor-inhibitor kinetics can give rise to patterning either in the form of long-range inhibition, short-range activation (i.e., d > 1), or through short-range inhibition, long-range activation (d < 1), or through equal-range activation and inhibition (d = 1).

In Fig. 1 we exhibit Turing instability parameter regions for various diffusion and cross-diffusion coefficients: (a) in the absence of cross-diffusion, (b)-(e) positive cross-diffusion, and (f) negative cross-diffusion. We observe substantial changes in the range for instability in the (a, b)-parameter space as we introduce cross-diffusion, compare Fig. 1a–c. Cross-diffusion induces different parameter spaces. The non-empty parameter ranges for instability in Fig. 1d–e only exist due to the presence of cross-diffusion and they are empty in its absence.

Fig. 1
figure 1

Turing instability parameter regions for the reaction kinetic parameters (a, b) for the fixed diffusion and cross-diffusion parameters as given in each plot title. The blue region in each subplot is the region of Turing instability for (a, b)

Full size image

A drawback associated with reaction-diffusion models with linear cross-diffusion is that in some cases these fail to reproduce experimental observations, hence it becomes imperative to study nonlinear cross-diffusion models [4, 7]. Methods for nonlinear analysis of such models include perturbation methods [14] and weakly nonlinear analysis [7]. Unlike linear stability analysis which studies short-time behaviour of the system close to bifurcation points, nonlinear analysis allows the study of long-time behaviour of solutions far away from bifurcation points.

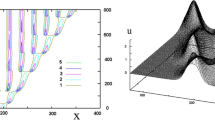
Positivity of Solutions for Reaction-Cross-Diffusion Models In many applications, the solution u of a reaction-cross-diffusion model (1) represents species concentration or densities or other non-negative quantities. It is therefore necessary that the evolving solution u, starting from any non-negative initial data u 0, stays non-negative for all times. If that holds then the system is called positivity-preserving. For single specie models satisfying the condition f 1(0) ≥ 0, the non-negativity of solutions is a consequence of the maximum principle [6, 16]. The situation is different and more involved in the case of systems. To this end, consider the simple case of a reaction-cross-diffusion system (1) with constant diffusion/cross-diffusion coefficients in Eq. (1a). A necessary condition for this system to be positivity-preserving is that the matrix D is diagonal, i.e. that all cross-diffusion terms vanish, see [18, Chap. 14] or [16]. That means for this system with non-vanishing cross-diffusion terms there exist non-negative initial data u 0 such that its solution u does not stay non-negative. Intuitively, in the equation for u 1, if D 1,2Δu 2 < 0 in some part of Ω then this leads to a decrease in u 1 independent of its actual value and thus to negative u 1 values if u 1 is sufficiently small (see Fig. 2). As a consequence of this negative result, nonlinear cross-diffusion terms are required for positivity-preserving systems. We refer the reader to, for instance, [16] for corresponding conditions on D ij and f i .

Fig. 2
figure 2

(a) Initial data u 1(x, 0) = 0.1 and \(u_2(x,0)=( \frac {1}{2}(1-\cos {}(2\pi x)))^{20}\) for system (1) with D = \(\begin {pmatrix}1&0.7\\ 0.7&1\end {pmatrix}\) , γ = 1, f = \(\begin {pmatrix}0\\ 0\end {pmatrix}\) in Ω = (0, 1). (b) Numerical solution of this system at t = 0.005

Full size image

3 Numerical Methods for Solving Reaction-Cross-Diffusion Models

In many physical modelling cases, the choice of the numerical method depends crucially on the physical properties of the model system. Reaction-cross-diffusion systems typically fall under parabolic partial differential equations for which numerous numerical methods exist. The simplest and most frequently used schemes are based on finite differences, e.g., [4, 16]. For positivity-preserving models involving, for instance, taxis terms, finite volume spatial discretisations, incorporating some form of flux-limiting for ensuring positivity of the discretised system, have been studied and used extensively [8]. Mass lumping has been shown to preserve positivity for finite element-based methods which deal more naturally with complex stationary and evolving domains/manifolds/surfaces [6, 11]. Other numerical methods such as spectral and meshless methods can be employed with considerable difficulties in treating complex geometries and nonlinear boundary conditions.

Numerical Example 1: Pattern Formation In Fig. 3 we exhibit finite element solutions for the reaction-diffusion system with linear cross-diffusion for system (2) on planar domains and surfaces [10]. Spot and stripe patterns are observed.

Fig. 3
figure 3

Finite element simulations revealing the patterning with or without cross-diffusion for the model system (2) with model parameter values (a) d = 10, d u  = 0, d v  = 0, a = 0.05, b = 1.1; (b) d = 10, d u  = 0, d v  = 1, a = 0.21, b = 0.26; (c) d = 10, d u  = 1, d v  = 0.5, a = 0.025, b = 1.1; (d) d = 0.75, d u  = 1, d v  = 0.5, a = 0.1, b = 0.08; (e) d = 1, d u  = 1, d v  = 0.5, a = 0.1, b = 0.08; and (f) d = 1, d u  = 1, d v  = 0.5, a = 0.1, b = 0.08

Full size image

Numerical Example 2: Cancer Invasion Our next example involves a cancer invasion model taken from [1, 5]. Here, the spatio-temporal interactions of two cancer cell populations, the extracellular matrix (ECM), and a matrix-degrading enzyme (MDE) are studied. Thus we define

$$\displaystyle \begin{aligned} \mathbf{u} = (\text{cell density } c_1, \text{cell density } c_2, \text{ECM density } v, \text{MDE concentration } m)\,. \end{aligned}$$

The densities and concentrations are scaled such that the volume fraction of occupied space reads ρ(u) = c 1 + c 2 + v ∈ [0, 1]; note that MDE does not take up space. The model without cross-diffusion terms reads

$$\displaystyle \begin{aligned} \partial_t c_1 &= \nabla \cdot \left[ D_{c,1} \nabla c_1 - c_1 \mathscr{A}_1(\mathbf{u}(t,\cdot)) \right] + \mu_{c,1} c_1(1-\rho(\mathbf{u})) - M(t,\mathbf{u}) c_1\,,{} \end{aligned} $$
(5a)
$$\displaystyle \begin{aligned} \partial_t c_2 &= \nabla \cdot \left[ D_{c,2} \nabla c_2 - c_2 \mathscr{A}_2(\mathbf{u}(t,\cdot)) \right] + \mu_{c,2} c_2(1-\rho(\mathbf{u})) + M(t,\mathbf{u}) c_1\,,{} \end{aligned} $$
(5b)
$$\displaystyle \begin{aligned} \partial_t v &= -\gamma m v + \mu_2(1-\rho(\mathbf{u}))^+\,, \end{aligned} $$
(5c)
$$\displaystyle \begin{aligned} \partial_t m &= \nabla \cdot \bigl[ D_m \nabla m \bigr] + \alpha_{c,1} c_1 + \alpha_{c,2} c_2 - \lambda m\,. \end{aligned} $$
(5d)

In the above, \(\mathscr {A}\) is a non-local operator modelling cell-cell and cell-matrix adhesion and M(t, u) accounts for mutations of cells from the less to the more invasive type (see [5] for full details). Note that the diffusion constants D c,1 and D c,2 are small so that diffusion (cell random motility) has, compared to adhesion and cell proliferation, only a small influence on the overall dynamics of the solution of (5). The modelling of cell random motility in (5) is rather simple and interactions between the two cell types and the ECM can be expected to affect random motility when the space gets locally filled, i.e., when ρ(u) locally tends to one. To this end, we introduce nonlinear cross-diffusion in (5) by replacing D c,1∇c 1 in (5a) with D c,1c 1∇ρ(u) = D c,1c 1∇c 1 + D c,1c 1∇c 2 + D c,1c 1∇v , and similarly for D c,2∇c 2 in (5b). Numerical simulations of system (5) without and with cross-diffusion are shown in Fig. 4. The introduction of cross-diffusion leaves the overall dynamics of the solution largely unaffected, Fig. 4b and c. However, the model with cross-diffusion exhibits a slightly slower speed of invasion of the cancer cells and the interface between the two cell types is significantly sharpened. This provides for a clear qualitative change of the model behaviour which may be of practical significance. Similar results are observed in a cell-sorting model with cross-diffusion [12].

Fig. 4
figure 4

(a) Initial data for model (5) at time t = 0. (b) Numerical solution of model (5) at time t = 120. (c) Same as (b) but for model (5) with cross-diffusion

Full size image

4 Conclusion and Open Research Questions

In this review we have highlighted some important aspects of cross-diffusion terms in reaction-diffusion models with respect to their analytic and numerical treatment together with some specific examples. Follow-up research non-exhaustively includes nonlinear stability analysis for the investigation of patterning mechanisms far away from bifurcation points, the development of higher-order numerical schemes for reaction-cross-diffusion systems that honour their positivity preservation properties, and the development of analytical and numerical tools for reaction-cross-diffusion systems on evolving domains. This research will also be driven by the needs of developmental and cellular biologists and other scientists who frequently use cross-diffusion in their applications.