Phase-field modeling through iterative splitting of hydraulic fractures in a poroelastic medium

Abstract

We study the propagation of hydraulic fractures using the fixed stress splitting method. The phase field approach is applied and we study the mechanics step involving displacement and phase field unknowns, with a given pressure. We present a detailed derivation of an incremental formulation of the phase field model for a hydraulic fracture in a poroelastic medium. The mathematical model represents a linear elasticity system with fading elastic moduli as the crack grows that is coupled with an elliptic variational inequality for the phase field variable. The convex constraint of the variational inequality assures the irreversibility and entropy compatibility of the crack formation. We establish existence of a minimizer of an energy functional of an incremental problem and convergence of a finite dimensional approximation. Moreover, we prove that the fracture remains small in the third direction in comparison to the first two principal directions. Computational results of benchmark problems are provided that demonstrate the effectiveness of this approach in treating fracture propagation. Another novelty is the treatment of the mechanics equation with mixed boundary conditions of Dirichlet and Neumann types. We finally notice that the corresponding pressure step was studied by the authors in Mikelić et al. (SIAM Multiscale Model Simul 13(1):367–398, 2015a).

1 Introduction

The coupling of flow and geomechanics in porous media is a major research topic in energy and environmental modeling. Of specific interest is induced hydraulic fracturing or hydrofracturing commonly known as fracking. This technique is used to release petroleum and natural gas that includes shale gas, tight gas, and coal seam gas for extraction. Here fracking creates fractures from a wellbore drilled into reservoir rock formations. In 2012, more than one million fracturing jobs were performed on oil and gas wells in the United States and this number continues to grow. Clearly there are economic benefits of extracting vast amounts of formerly inaccessible hydrocarbons. In addition, there are environmental benefits of producing natural gas, much of which is produced in the United States from fracking. Opponents to fracking point to environmental impacts such as contamination of ground water, risks to air quality, migration of fracturing chemical and surface contamination from spills to name a few. For these reasons, hydraulic fracturing is being heavily scrutinized resulting in the need for accurate and robust mathematical and computational models for treating fluid field fractures surrounded by a poroelastic medium.

Even in the most basic formulation, hydraulic fracturing is complicated to model since it involves the coupling of (i) mechanical deformation; (ii) the flow of fluids within the fracture and in the reservoir; and (iii) fracture propagation. Generally, rock deformation is modeled using the theory of linear elasticity, i.e. they are modeled as an impermeable elastic medium. Using Green’s function, an integral equation that determines a relationship between fracture width and the fluid pressure can be adopted. Fluid flow in the fracture is modeled using lubrication theory that relates fluid flow velocity, fracture width and the gradient of pressure.

Fluid flow in the reservoir is modeled as a Darcy flow and the respective fluids are coupled through a leakage term. The experiments show an analogy between hydraulic fracture propagation and crack propagation in fracture mechanics of solids. The criterion for fracture propagation is usually given by the conventional energy-release rate approach of linear elastic fracture mechanics (LEFM) theory; that is the fracture propagates if the stress intensity factor at the tip matches the rock toughness. Detailed discussions of the development of hydraulic fracturing models for use in petroleum engineering can be found in Adachi et al. (2007), Dean and Schmidt (2014), Hwang and Sharma (2013), McClure and Kang (2017) and in mechanical engineering and hydrology in de Borst et al. (2006), Gupta and Duarte (2014), Irzal et al. (2013), Schrefler et al. (2006) and in references cited therein.

In the literature, numerical models of fracture can be classified into two categories: discrete and continuum approaches. The discrete approach treats fractures as discontinuities. Its positive side is the simplicity in terms of modeling. One disadvantage is to consider topology changes in the implementation and mesh dependent fracture propagation is restricted to follow mesh lines. Some of these approaches, however, have difficulties with joining or branching fracture or with heterogeneous materials. For a detailed literature overview of various fracture propagation models, we refer the reader to Wick et al. (2016). In the following, we restrict our focus to a specific continuum approach, which has received a lot of attention.

In the last two decades, variational phase field models of brittle fracture gained popularity in fracture mechanics. In fracture mechanics, the fracture is a lower dimensional manifold. The phase-field variable is a smoothed indicator function that smoothly interpolates between the broken and unbroken regions. The change from the intact medium to a fracture takes place in a narrow mushy region. Francfort and Marigo developed in (1998) a variational formulation for quasi-static fracture evolution in a brittle material based on the minimization of the combined elastic energy in the bulk material and the fracture energy. It has been serving as a basis for a vast literature with numerical simulations and theoretical developments. The approach allows simulation of complex fracturing processes, such as branching and joining. Handling heterogeneous media does not pose major additional difficulties and updating the fracture shape is automatically contained in the model.

Because of the above mentioned analogy between fracture mechanics and hydraulic fracturing, it is appealing to simply borrow the approach of Francfort and Marigo. Nevertheless, it is important to recall that contrary to fracture mechanics, where Griffiths criterion has a deep physical meaning, using a phase field approach in hydraulic fracturing corresponds to a phenomenological overall behavior. The fractures are slender flow domains, but, nevertheless, their width is much bigger than the typical pore size of a porous medium. The mechanical interactions of the fracture interacting with the pore structure is not well understood and an open question. Furthermore, we do not consider the equations of fluid–structure, posed at the pore level, but their upscaled simplified form. Consequently, flow and deformation are described by Biot’s equations (e.g., Tolstoy 1992), which are not fundamental physical equations. This is a very important modeling aspect because one wants to couple the upscaled poroelastic medium possibly with Stokes or Navier–Stokes flow in the fracture, which are first principle equations. Here, interface conditions have to be carefully derived. An alternative is a lubrication approximation, which does not contain enough information about (the prediction) of the tip velocity. Hence there are difficulties with including a correct description of the interaction between the hydraulic fracture and the surrounding poroelastic medium. More physical reasoning based on the energy could be necessary. For correct modeling of these processes, only experiments can indicate how far the analogy of fracture behavior with solid mechanics works.

In this paper, we present our phase-field fracture model for pressurized fractures in a porous medium. Our approach is based on the observation that phase field models require the energy functional in the case of elasticity (Francfort and Marigo 1998) and a free energy in the case of poroelasticity (Mikelić et al. 2015b). The Biot equations are obtained by upscaling and for a hydraulic fracture being a lower dimensional manifold we do not know how to formulate such an energy functional. But in the elastic case, where the pressure is given, we can modify the regularized phase field elastic energy of Francfort and Marigo, and study the corresponding phase field system. We note that now the fracture is a three dimensional slender body. Similarly, in the case of the full Biot system, one would modify Biot’s free energy by inserting the phase field function.

Parts of this work are based on two preprints ICES-1315 (Mikelić et al. 2013) and ICES-1418 (Mikelić et al. 2014) that were published in the years 2013 and 2014 at the Institute of Computational Engineering and Sciences at the University of Texas at Austin.

The outline of this paper is as follows: First in Sect. 2, we provide general background information. In Sect. 3, we introduce an incremental formulation of a phase-field model for a pressurized crack. Here, the crack-pressure is incorporated with an interface law. In Sect. 4, we present a mathematical analysis of the incremental problem. In Sect. 5, a numerical formulation is briefly described. Finally in Sect. 6 we provide numerical experiments for classical benchmark cases, e.g. Sneddon’s pressurized crack with constant fluid pressure (see Sect. 6.1 and Sneddon 1946). Here, we also focus on the behavior when working with mixed boundary conditions of Dirichlet and Neumann types.

2 Fundamental background information

In this section, we explain the idea of our approach and provide background information. We finish with a current literature overview of phase-field models used for hydraulic facturing.

2.1 The Biot system and fixed-stress iterative coupling

Major difficulties in simulating hydraulic fracturing in a deformable porous medium are treating crack propagation induced by high-pressure slick water injection and later the coupling to a multiphase reservoir simulator for production. A computational effective procedure in modeling coupled multiphase flow and geomechanics is to apply an iterative coupling algorithm as described in Mikelić and Wheeler (2012), and Mikelić et al. (2014).

Iterative coupling is a sequential procedure where either the flow or the mechanics is solved first followed by solving the other problem using the latest solution information. At each time step the procedure is iterated until the solution converges within an acceptable tolerance. There are four well-known iterative coupling procedures and we are interested primarily in one referred to as the fixed stress split iterative method.

In order to fix ideas we address the simplest model of real applied importance, namely, the quasi-static single phase Biot system. Let $\mathcal {C}$ denote any open set homeomorphic to an ellipsoid strictly contained in $(0,L)^3 \subset \mathbb {R}^3$ (a crack set). Its boundary is a closed surface $\partial \mathcal {C}$. In most applications $\mathcal {C}$ is a curved 3d domain, with two dimensions significantly smaller than the dominant one. Nevertheless, we consider $\mathcal {C}$ as a 3d domain and use its particular geometry only when discussing the stress interface conditions. The boundary of $(0,L)^3$ is denoted by $\partial (0,L)^3 = \partial \varOmega {\setminus }\partial \mathcal {C}$ divided into Dirichlet and Neumann parts, $\partial _D \varOmega$ and $\partial _N (0,L)^3$ respectively. We assume that meas$(\partial _D\varOmega )>0$. Boundary conditions on $\partial (0,L)^3 = \partial _D\varOmega \cup \partial _N (0,L)^3$ for the above situation involve displacements and tractions as well as pressure and flux.

Remark 1

We notice that in many references on fracture propagation, the crack $\mathcal {C}$ is considered as a lower dimensional manifold and the lubrication theory is applied to describe the fluid flow (see e.g. Adachi et al. 2007; Ganis et al. 2014; Girault et al. 2015). We recall that the 3d flow in $\mathcal {C}$ can be reconstructed from a lower dimensional lubrication approximation (see Mikelić et al. 2015a), except at the tips where a law for their displacements has to be added separately.

The quasi-static Biot equations (see e.g. Tolstoy 1992) are an elliptic-parabolic system of PDEs, valid in the poroelastic domain $\varOmega = (0,L)^3{\setminus }\overline{\mathcal {C}}$, where for every $t\in (0,T)$ we have

$$\begin{aligned}&\sigma ^{por} -\sigma _0 =\mathcal {G} e (\mathbf {u} ) -\alpha p I ; \quad - \text{ div } \{ \sigma ^{por} \} = { \rho }_b \mathbf {g} ; \end{aligned}$$

(1)

$$\begin{aligned}&\partial _t \left( \frac{1}{M} p + \text{ div } ( \alpha \mathbf {u} ) \right) + \text{ div } \left\{ \frac{\mathcal {K} }{ \eta } ( \rho _f \mathbf {g} - \nabla p ) \right\} =f , \end{aligned}$$

(2)

where $\sigma _0$ is the reference state total stress and $\mathbf {g}$ is the gravity and f represents volume sources/sinks, respectively. By I, be denote the identity matrix. In the following, we set $\mathbf {g} = 0$ and $\sigma _{0} =0$. The important parameters and unknowns are given in Table 1.

Table 1 Unknowns and effective coefficients

The fixed stress split iterative method consists in imposing constant volumetric mean total stress $\sigma _v$. This means that the stress $\displaystyle \sigma _v = K_{dr} \text{ div } \mathbf {u} I -\alpha p I$ is kept constant at the half-time step.

The iterative process reads as follows:

$$\begin{aligned}&\left( \frac{1}{M} +\frac{\alpha ^2}{K_{dr}} \right) \partial _t p^{n+1} + \text{ div } \left\{ \frac{\mathcal {K} }{ \eta } ( \rho _f \mathbf {g} - \nabla p^{n+1} ) \right\} \nonumber \\&\quad = - \frac{\alpha }{K_{dr}} \partial _t \sigma _v^{n} + f =f- \alpha \text{ div } \partial _t \mathbf {u}^{n} + \frac{\alpha ^2}{K_{dr}} \partial _t p^n ; \end{aligned}$$

(3)

$$\begin{aligned}&\quad - \text{ div } \{ \mathcal {G} e (\mathbf {u}^{n+1} ) { \} } + \alpha \nabla p^{n+1} =0 . \end{aligned}$$

(4)

Remark 2

We remark that the fixed stress approach is useful in employing existing reservoir simulators in that (3) can be extended to treat the mass balance equations arising in black oil or compositional flows and allows decoupling of multiphase flow and elasticity.

Remark 3

Interest in the system (3)–(4) is based on its robust numerical convergence. Under mild hypothesis on the data, the convergence of the iterations was studied in Mikelić and Wheeler (2012) and it was proven that the solution operator ${\mathcal {S}}$, mapping $\{ \mathbf {u}^{n} , p^{n} \}$ to $\{ \mathbf {u}^{n+1} , p^{n+1} \}$ is a contraction on appropriate functional spaces with the contraction constant $\gamma _{FS} = \frac{M \alpha ^2}{ K_{dr} + M \alpha ^2 } <1$. The corresponding unique fixed point satisfies equations (1)–(2). Further important recent studies on the fixed-stress scheme have been undertaken in Both et al. (2017), Castelletto et al. (2015), Gaspar and Rodrigo (2017). For phase-field fracture, a very detailed computational analysis of the fixed-stress scheme was performed in Lee et al. (2017a).

Remark 4

We finally notice that the (discretized) Biot equations (without fractures) form a mixed system that is subject to a (discrete) inf-sup condition. Theoretical studies were undertaken in Murad and Loula (1992, 1994). Various finite element pairs have been investigated in Ferronato et al. (2010), Liu (2004), Philips and Wheeler (2003). More recent references can be found in Lee (2016), Rodrigo et al. (2016), Lee et al. (2017c), Hong and Kraus (2018). Important is the choice of the pressure space, which should be locally mass conservative, but can be still of lowest order. For these reasons, fluid-filled phase-field fractures using the entire Biot system have been formulated either with linear/linear elements for the displacements/pressure (see e.g., Mikelić et al. 2015a) or linear/enriched-linear elements (Lee et al. 2016a), where an enriched Galerkin formulation for the pressures ensures local mass conservation.

2.2 Focus on crack propagation in the fixed-stress elasticity step

Because of the complexity of this coupled nonlinear fluid-mechanics system, we follow the above splitting strategy and restrict our attention to a simplified model in which we assume that the pressure has been computed from the previous fixed-stress fluid iteration step. Our focus in this paper is therefore on crack propagation in the framework of the fixed-stress mechanics step (4) and we call this approach a fluid filled crack with a given pressure.

Remark 5

The extension to the full poroelastic system for crack propagation and therefore employing a phase-field formulation of the pressure step (3) is studied in Mikelić et al. (2015a) and called fluid-filled crack propagation in a poroelastic medium. In the fixed stress iterative splitting, the pressure is known in the mechanics step and can be included into the forcing terms. Then we arrive exactly in the situation studied in the current article.

In the following, we present an incremental formulation of the hydraulic fracture with a given pressure field surrounded by a poroelastic medium. The mathematical model involves the coupling of a linear elasticity system with an elliptic variational inequality for the phase field variable. With this approach, branching of fractures and heterogeneities in mechanical properties can be effectively treated as demonstrated numerically in Sect. 6.

Our formulation follows in Miehe et al. (2010) and is a thermodynamically consistent framework for phase-field models of quasi-static crack propagation in elastic solids, together with incremental variational principles. The work by Miehe et al. (2010) is further based on the variational approach to elastic fractures formulated by Francfort and Marigo (1998); see also Bourdin et al. (2008). Our contribution represents an extension to a phase-field pressurized fracture model in a poroelastic medium that we describe in the following in more detail.

Following Griffith’s criterion, we suppose that the crack propagation occurs when the elastic energy restitution rate reaches its critical value $G_c$. In the classical setting the crack $\mathcal {C}$ is a lower dimensional manifold and for a traction force $\tau$ applied at the part of the boundary $\partial _N \varOmega$, then we associate to the crack $\mathcal {C}$ the following total energy

$$\begin{aligned} E (\mathbf {u} , \mathcal {C} ) = \int _\varOmega \frac{1}{2} \mathcal {G} e(\mathbf {u}): e(\mathbf {u}) \ dx - \int _{\partial _N \varOmega } \tau \mathbf {u} \ dS - \int _\varOmega \alpha p_B \text{ div } \mathbf {u} \ dx + G_c \mathcal {H}^2 (\mathcal {C}), \end{aligned}$$

(5)

where $p_B$ is the poroelastic medium pressure calculated in the previous iterative coupling step and $\alpha \in (0,1)$ is the Biot coefficient. In (5), the first three terms stem from (4) and the last term, $G_c \mathcal {H}^2(\mathcal {C})$ is the surface energy related to the fracture.

This energy functional is then minimized with respect to the kinematically admissible displacements $\mathbf {u}$ and any crack set satisfying a crack growth condition. The computational modeling of this minimization problem treats complex crack topologies and requires approximation of the crack location and of its length. This was overcome by regularizing the sharp crack surface topology in the solid by diffusive crack zones described by a scalar auxiliary variable. This variable is a phase-field that interpolates between the unbroken and the broken states of the material, which is introduced through a time-dependent $\varphi$ (the crack phase field), defined on $(0,L)^3 \times (0,T)$. The functional from (5) is regularized using the phase field unknown and the new crack functional (the last term in (5) divided by $G_c$) reads

$$\begin{aligned} \varGamma _\varepsilon (\varphi ) = \int _{(0,L)^3 } \left( \frac{1}{2\varepsilon } (1-\varphi )^2 + \frac{\varepsilon }{2} | \nabla \varphi |^2 \right) \ dx = \int _{(0,L)^3 } \gamma (\varphi , \nabla \varphi ) \ dx, \end{aligned}$$

(6)

where $\gamma$ is the crack surface density per unit volume. This regularization of $\mathcal {H}^2 (\mathcal {C})$, in the sense of the $\varGamma -$limit when $\varepsilon \rightarrow 0$, was used in Bourdin et al. (2000).

The model proposed in this paper is a simple extension of the crack functional (6) that, after the time discretization, can be analyzed both as a minimization problem and as a variational PDE formulation. For simplicity the presentation of the time discretized (or the incremental problem) here is based on energy minimization, whereas our treatment of the corresponding variational formulation can be found in Mikelić et al. (2013) and the current paper. For the full quasi-static problem we refer to Mikelić et al. (2015c).

2.3 Energy minimization versus the variational PDE formulation

In the numerical analysis of fracture propagation in solid mechanics, solving the minimization problem (Francfort and Marigo 1998; Bourdin et al. 2008) by considering the variational formulation is for instance treated in Burke et al. (2010). Most other works also start from the energy level. We base our computational framework on the variational PDE formulation since more additional realistic physical interfacial effects (see Fig. 1 and Adachi et al. 2007) and associated dissipative terms and nonlinear physical models can be employed. Moreover, the Biot system does not correspond to an energy minimization formulation in $\mathbf {u}$ and p, but has a free energy linked to a Lyapunov functional. For these reasons, the variational PDE formulations allow for more general settings, with the drawback that only stationary points are computed and not only the minimizers.

2.4 Literature on hydraulic phase-field fracture modeling

In our knowledge, applying the phase field approach to the simulation of propagation of pressurized fractures in an elastic medium was initiated by the SPE conference paper (Bourdin et al. 2012). The pressurized fracture was described through a boundary term $\int _{\mathcal {C}} p [\mathbf {u\cdot n}]$, with the crack $\mathcal {C}$ being a surface and $[\mathbf {u\cdot n}]$ the displacement jump across the crack (see also Remark 7 in Sect. 3.2). The phase field handling of such terms goes back to the work presented in Chambolle (2004).

Fig. 1

Illustration of our approach for a 2d situation: a crack $\mathcal {C}\subset \mathbb {R}$ embedded in a porous medium $(0,L)^2$. Here, the dimensions of the crack are assumed to be much larger than the pore scale size (black dots) of the porous medium (color figure online)

In the years Mikelić et al. (2013) and (2014), the first model for pressurized fractures in porous media (including Biot’s coefficient $\alpha$) was proposed and rigorously investigated. Here the displacement phase-field system was modeled in a monolithic framework. Later, a decoupled model was investigated in Mikelić et al. (2015c) for which a corresponding robust numerical augmented Lagrangian approach was developed in Wheeler et al. (2014). We also notice the development of a sharp interface model for pressurized fractures using variational techniques in Almi et al. (2014). The efficient and robust numerical solution of pressurized phase-field models based on quasi-monolithic approaches was presented in Heister et al. (2015), Wick et al. (2015). Based on the first models (Mikelić et al. 2013, 2014) (and also the current paper), fully monolithic solution techniques for pressurized fractures have been developed in Wick (2017a, b). For a different treatment of the decoupled model (Mikelić et al. 2015c), using the discontinuous Galerkin (DG) formulation for the displacements, we refer to Engwer and Schumacher (2017). Various adaptive mesh refinement schemes for pressurized phase-field fracture, with focus on the crack path or other quantities of interest, have been proposed in Heister et al. (2015), Lee et al. (2016b), Wick (2016b).

The pressurized phase-field method has been then further extended to fluid-filled fractures in which a Darcy type equation is used for modeling fracture flow (Mikelić et al. 2015a) and similar studies have appeared simultaneously (Miehe and Mauthe 2016; Miehe et al. 2015; Markert and Heider 2015). A rigorous mathematical analysis including detailed numerical studies of a fully-coupled fluid geomechanics phase-field model in porous media was first presented in Mikelić et al. (2015b). Here, the important phenomenon of negative pressures at fracture tips was observed. This feature is known to appear in such configurations, but was not yet quantified using a phase-field method. In the year 2016, we note further contributions to fluid-filled phase-field fractures from Heider and Markert (2017), Lee et al. (2016b). To reduce the computational cost, we notice that parallel computation frameworks have been implemented in most groups, e.g., Bourdin et al. (2012), Heister et al. (2015), Miehe et al. (2015), Lee et al. (2016b). Coupling to other codes and reservoir simulators has been first accomplished in Wick et al. (2016). However, further research is necessary because the current modeling, the coupling algorithm, and the treatment of the multi-scale nature of the problem must be further improved.

Recent results concentrated on the extension to proppant flow (Lee et al. 2016a), two-phase flow inside the fracture (Lee et al. 2018), single phase-flow for nonlinear poroelastic media (van Duijn et al. 2018), fractures in partially saturated porous media (Cajuhi et al. 2017), fracture initialization with probability maps of fracture networks (Lee et al. 2017b), consequences on further multiphysics coupling of the pressurized fractures interface law (Wick 2016a), more accurate crack width computations and computational analysis of fixed-stress splitting (Lee et al. 2017a), a phase-field formulation (in elasticity) with a lower-dimensional lubrication formulation (Santillan et al. 2017), and a multirate analysis in which different time steps for different regimes are used (Almani et al. 2017).

3 An incremental phase field formulation

We introduce the time-dependent crack phase field $\varphi$, defined on $(0,L)^3 \times (0,T)$. The regularized crack functional is given by (6). Our further considerations are based on the fact that the evolution of cracks is fully dissipative in nature. First, the crack phase field $\varphi$ is intuitively a regularization of $1- \mathbb {1}_{\mathcal {C} }$ and we impose its negative evolution

$$\begin{aligned} \partial _t \varphi \le 0. \end{aligned}$$

(7)

3.1 A global constitutive dissipation functional

Next we follow Miehe et al. (2010) and Bourdin et al. (2000) and replace the energy (5) by a global constitutive dissipation functional for a rate independent fracture process. That is

$$\begin{aligned}&E_\varepsilon (\mathbf {u} , \varphi ) = \int _{(0,L)^3} \frac{1}{2} \left( (1-k) \varphi ^2 +k \right) \mathcal {G} e(\mathbf {u}): e(\mathbf {u}) \ dx - \int _{\partial _N \varOmega } \tau \mathbf {u} \ dS \nonumber \\&\quad -\int _{(0,L)^3} \alpha \varphi ^{2} p_B \text{ div } \mathbf {u} \ dx + G_c \int _{(0,L)^3} \left( \frac{1}{2\varepsilon } (1-\varphi )^2 + \frac{\varepsilon }{2} | \nabla \varphi |^2 \right) \ dx. \end{aligned}$$

(8)

We remark that $\partial _N\varOmega$ contains both the outer boundary and the fracture boundary. Moreover, k is a positive regularization parameter for the elastic energy, with $k\ll \varepsilon$, e.g., Braides (1998). We notice that $k>0$ is necessary for quasi-static phase-field fracture models in order to avoid a singular discrete system. For dynamic fracture, $k = 0$ may be chosen, see e.g., Borden et al. (2012). Due to the presence of the acceleration term, in the limit $\varphi \rightarrow 0$ non-zero respective matrix entries are assured, removing the degeneracy.

We note that the pressure cross term reads

$$\begin{aligned} \int _{(0,L)^3} \alpha \varphi ^{2} p_B \text{ div } \mathbf {u}\, dx, \end{aligned}$$

instead of

$$\begin{aligned} \int _{(0,L)^3} \alpha \varphi p_B \text{ div } \mathbf {u} \, dx. \end{aligned}$$

This is linked to the behavior for negative values of the phase field variable. Moreover, if $\varphi \le 0$, there should be no contribution. Therefore instead of

$$\begin{aligned} \int _{(0,L)^3} \alpha \varphi ^2 p_B \text{ div } \mathbf {u} \, dx, \end{aligned}$$

we use

$$\begin{aligned} \int _{(0,L)^3} \alpha \varphi _+^2 p_B \text{ div } \mathbf {u} \, dx. \end{aligned}$$

Using $\varphi _+^2$ yields a higher regularity and avoids difficulties in the differentiation since we need first and second order derivatives for Newton’s method. We notice that for $0\le \varphi \le 1$, using $\varphi _+^{2}$, instead of $\varphi _+$ in the pressure cross term should not affect the phase field approximation. If $\varphi = \mathbb {1}_{\mathcal {C}}$, we do not see any difference.

We explain this choice in more detail in the following. In the incremental formulation, the entropy condition $\partial _t \varphi \le 0$ leads to a condition similar to the obstacle problem, which guarantees that $\varphi \le 1$. On the contrary, the presence of the pressure gradient can lead to negative values of the phase field variable. Later in Theorem 2, we show for the incremental, continuous in space problem that $\varphi \ge 0$. For the formulation which is discretized in space, the approximation for $\varphi$ is not necessarily nonnegative. It becomes nonnegative only when passing to the space continuous problem. For this reason, working with $\varphi _+$ is a safeguard choice, which in the end does not modify the original problem and is numerically stable. There are formulations with good estimates for the time derivatives in which $\varphi$ is nonnegative only in the space–time continuous formulation, which has been proven in Mikelić et al. (2015c).

In the following, we consider a quasi-static formulation where velocity changes are small. First, we derive an incremental form, i.e., we replace the time derivative in inequality (7) with a discretized version; more precisely

$$\begin{aligned} \partial _t \varphi \rightarrow \partial _{\varDelta t} \varphi = (\varphi - \varphi _p )/(\varDelta t), \end{aligned}$$

where $\varDelta t>0$ is the time step and $\varphi _p$ is the phase field from the previous time step. After time discretization, our quasistatic constrained minimization problem becomes a stationary problem, called the incremental problem.

3.2 Interface coupling of a pressurized crack with a porous medium

The crack is filled with a fluid and, consequently, it is pressurized. However, the energy $E_\varepsilon$ given by (8) is incomplete though and we need to include the crack-pressure. To this end, we work with an internal interface between the fracture and the porous medium and derive appropriate interface conditions. A general description of a crack embedded in a porous medium is illustrated in Fig. 1. Here, we consider a setting in which the complex interface crack/pore structure is simplified. We notice that such a complex structure would require the solution of a variational problem since the formulation as energy minimization might not be well defined. Furthermore, we assume that the crack is a 3d thin domain with a width much less than its length, then lubrication theory can be applied. Hence, the leading order of the stress in $\mathcal {C}$ is $-p_f I$.

At the crack boundary, we assume the continuity of the pressures and the continuity of contact forces:

$$\begin{aligned} p_f = p_B, \qquad \sigma \mathbf {n} = (\mathcal {G} e (\mathbf {u}) -\alpha p_B I) \mathbf {n} = -p_f \mathbf {n}, \end{aligned}$$

(9)

where $p_f$ denotes the fracture fluid pressure and $\mathbf {n}$ the normal vector. We recall that $\partial \varOmega$ consists of $\partial \mathcal {C}$, $\partial _N \varOmega {\setminus }\partial \mathcal {C} = \partial _N (0,L)^3$ and $\partial _D \varOmega = \partial _D (0,L)^3$. The Neumann and interface boundary parts can be written as $\partial _N \varOmega = \partial _N (0,L)^3 \cup \partial \mathcal {C}$. On $\partial _D (0,L)^3$ we set the Dirichlet condition $\mathbf {u}=0$ and on $\partial _N (0,L)^3$, we have $\sigma \mathbf {n}=\tau$.

Before introducing the phase field variable, we eliminate the traction crack surface integrals and obtain

$$\begin{aligned}&\int _{\varOmega } \alpha p_B \text{ div } \mathbf {w} \ dx + \int _{\partial \mathcal {C}} \sigma \mathbf {n} \mathbf {w} \ dS \nonumber \\&\quad = \int _{\varOmega } \alpha p_B \text{ div } \mathbf {w} \ dx - \int _{\partial \mathcal {C}} p_f w_n \ dS \nonumber \\&\quad = \int _{\varOmega } \alpha p_B \text{ div } \mathbf {w} \ dx - \int _{\varOmega } \text{ div } (p_B \mathbf {w} ) \ dx + \int _{\partial _N (0,L)^3} p_B w_n \ dS\nonumber \\&\quad = \int _{\varOmega } (\alpha -1) p_B \text{ div } \mathbf {w} \ dx - \int _{\varOmega } \nabla p_B \mathbf {w} \ dx + \int _{\partial _N (0,L)^3} p_B w_n \ dS, \end{aligned}$$

(10)

where $\mathbf {w}\cdot \mathbf {n}$ denotes the normal component of the vector function $\mathbf {w}$, where $\mathbf {n}$ is oriented towards interior of $\mathcal {C}$.

Remark 6

To date, in most studies dealing with pressurized fractures, the outer domain boundary conditions are of homogeneous Dirichlet type. Here, the test function $\mathbf {w}$ cancels $\int _{\partial _N (0,L)^3} p_B w_n \ dS$. However, this last integral is important when Neumann boundary conditions are prescribed, where the test function $\mathbf {w}$ does not vanish. We present such a case in Sect. 6.2.

In the above calculations, surface integrals are now treated with Gauss’ divergence theorem:

$$\begin{aligned}&- \int _{\partial _N (0,L)^3} \tau \mathbf {w} \ dS + \int _{ \partial \mathcal {C} } p w_{n} \ dS- \int _{\varOmega } \alpha p \text{ div } \mathbf {w} \ dx \nonumber \\&\quad = - \int _{\varOmega } (\alpha -1) p \text{ div } \mathbf {w} \ dx + \int _{\varOmega } \nabla p \mathbf {w} \ dx -\int _{\varOmega } \text{ div } (\mathcal {T} \mathbf {w} ) \ dx \nonumber \\&\quad = -\int _{\varOmega } (\alpha -1) p \text{ div } \mathbf {w} \ dx + \int _{\varOmega } (\nabla p - \text{ div } \mathcal {T} ) \mathbf {w} \ dx - \int _{\varOmega } \mathcal {T} : e(\mathbf {w} ) \ dx, \end{aligned}$$

(11)

where $\mathcal {T}$ is a smooth symmetric $3\times 3$ matrix with compact support in a neighborhood of $\partial (0,L)^3$, such that $\mathcal {T} \mathbf {n} =\tau + p \mathbf {n}$ on $\partial _N (0,L)^3$. The tensor $\mathcal {T}$ is introduced in order to handle the phase field only in volume terms. Assuming that the crack $\mathcal {C}$ does not interact with $\partial _N \varOmega$, it can be eliminated by using Green’s formula. Hence the solution does not depend on the choice of $\mathcal {T}$. We set

$$\begin{aligned} \mathcal {F}= - (\alpha -1) p I - \mathcal {T} ,\qquad \mathbf {f}=\nabla p - \text{ div } \mathcal {T} . \end{aligned}$$

(12)

In the case of $\partial _N \varOmega = \emptyset$, we have $\mathcal {T}\equiv 0$. Then, the terms in (12) for $\mathcal {F}$ and $\mathbf {f}$ reduce to $\mathcal {F} = -(\alpha -1)pI$ and $\mathbf {f} = \nabla p$.

After the above transformation and after taking $\sigma _0=0$ and neglecting the gravity term $\rho _b g$, the weak formulation of problem (1) reads as follows

$$\begin{aligned} 0&=\int _\varOmega \sigma ^{por} : e(\mathbf {w}) \ dx - \int _{\partial _N \varOmega } \tau \cdot \mathbf {w} \ dS \nonumber \\&= \int _\varOmega \mathcal {G} e(\mathbf {u}) : e(\mathbf {w}) \ dx - \int _\varOmega (\alpha -1) p \text{ div } \mathbf {w} \ dx + \int _\varOmega \nabla p\cdot \mathbf {w} \ dx \nonumber \\&\quad - \int _{\partial _N \varOmega {\setminus }\partial \mathcal {C}} (\tau + p\mathbf {n})\cdot \mathbf {w} \ dS \nonumber \\&= \int _\varOmega \mathcal {G} e(\mathbf {u}) : e(\mathbf {w}) \ dx + \int _\varOmega \left( \mathcal {F}: e(\mathbf {w}) + \mathbf {f} \cdot \mathbf {w} \right) \ dx \end{aligned}$$

(13)

for all $\mathbf {w} \in \{ \mathbf {w} \in H^1 (\varOmega )^3 | \; \mathbf {w}=0\; \text{ on } \, \partial _D \varOmega \}$. To the variational equation (13) corresponds the following variant of the energy functional (8):

$$\begin{aligned} {\tilde{E}}_\varepsilon (\mathbf {u} , \varphi )&= \int _{(0,L)^3} \frac{1}{2} \left( (1-k) \varphi ^2 +k \right) \mathcal {G} e(\mathbf {u}): e(\mathbf {u}) \ dx \nonumber \\&\quad +\int _{(0,L)^3} \varphi ^{2} (\mathcal {F}: e( \mathbf {u}) + \mathbf {f}\cdot \mathbf {u}) \ dx \nonumber \\&\quad + G_c \int _{(0,L)^3} \left( \frac{1}{2\varepsilon } (1-\varphi )^2 + \frac{\varepsilon }{2} | \nabla \varphi |^2 \right) \ dx. \end{aligned}$$

(14)

Remark 7

We note that introduction of the phase field approximation of the pressured fracture in this section was introduced, differs from Bourdin et al. (2012). In fact, the presence of the term $\int _\varOmega p\mathbf {u} \cdot \nabla \varphi \ dx$ must be treated carefully numerically and we have derived therefore a different phase field energy functional. The $\varGamma -$limit of our formulation was calculated for a particular one dimensional setting in Engwer and Schumacher (2017), which leads to the same formulation for the lower dimensional fracture as in Bourdin et al. (2012).

Remark 8

We emphasize that the previous choice $p_B = p_f$ on the fracture boundary is one possible modeling choice. It may be justified to assume that $p_f \gg p_B$ such that a discontinuous pressure could be more appropriate. Such a modeling is left for future studies.

Remark 9

In the fixed stress splitting $\mathcal {F}$ and f depend on the pressure. For details we refer the reader to Mikelić et al. (2015b).

3.3 The final energy functional

In the case of elastic cracks it can be shown that the phase field unknown satisfies $0\le \varphi \le 1$. In order to establish this property for the spatially continuous incremental problem, we first modify (14) for negative values of $\varphi$. As previously discussed, we now use $\varphi _+$ instead of $\varphi$ in terms where negative $\varphi$ could lead to incorrect physics in the bulk energy, traction and pressure forces. With this modification, the final energy functional reads

$$\begin{aligned} {{\mathcal {E}}}_\varepsilon (\mathbf {u} , \varphi )&= \int _{(0,L)^3} \frac{1}{2} \left( (1-k) \varphi _+^2 +k \right) \mathcal {G} e(\mathbf {u}): e(\mathbf {u}) \ dx \nonumber \\&\quad +\int _{(0,L)^3} \varphi ^{2}_+ (\mathcal {F}: e( \mathbf {u}) + \mathbf {f}\cdot \mathbf {u}) \ dx \nonumber \\&\quad + G_c \int _{(0,L)^3} \left( \frac{1}{2\varepsilon } (1-\varphi )^2 + \frac{\varepsilon }{2} | \nabla \varphi |^2 \right) \ dx. \end{aligned}$$

(15)

As functional space of admissible displacements, we choose

$$\begin{aligned} V_U = \{ \mathbf {z} \in H^1 ((0,L)^3)^3 \ | \ \mathbf {z} =0 \, \text{ on } \; \partial _D \varOmega \} . \end{aligned}$$

The entropy condition (7) is imposed in its discretized form and we introduce a convex set K:

$$\begin{aligned} K=\{ \psi \in H^1 ( (0,L)^3 ) \ | \ \psi \le \varphi _p \le 1 \; \text{ a.e. } \text{ on } \ (0,L)^3 \} , \end{aligned}$$

(16)

where $\varphi _p (x)$ is the value of the phase field from the previous time step. The incremental minimization problem now reads:

Definition 1

Find $\mathbf {u} \in V_U$ and a nonnegative $\varphi \in K$ such that

$$\begin{aligned} \mathcal {E}_\varepsilon ( \mathbf {u} , \varphi )=\min _{ \{ \mathbf {v} , \psi \} \in V_U \times K } \mathcal {E}_\varepsilon ( \mathbf {v} , \psi ) . \end{aligned}$$

(17)

Note that the value of the phase field unknown $\varphi$ from the previous time step enters only the convex set K, as the obstacle $\varphi _p$. The goal of Sect. 4 is to establish a solution to the minimization problem (17).

3.4 The Euler–Lagrange equations in strong form

From the energy functional, we obtain by differentiation and application of the fundamental lemma of calculus of variations the strong formulation: Find $u:(0,L)^3 \rightarrow \mathbb {R}^3$ and $\varphi :(0,L)^3 \rightarrow \mathbb {R}$ such that

$$\begin{aligned}&- \text{ div } \left( \left( (1-k) \varphi _+^2 +k \right) \mathcal {G} e(\mathbf {u})\right) + \varphi _+^{2} \mathbf {f} - \text{ div } (\varphi _+^{2} \mathcal {F} )=0 \quad \text{ in } (0,L)^3,\qquad \end{aligned}$$

(18)

$$\begin{aligned}&\mathbf {u} =0 \quad \text{ on } \partial _D (0,L)^3, \end{aligned}$$

(19)

$$\begin{aligned}&\left( (1-k) \varphi _+^2 +k \right) \mathcal {G} e(\mathbf {u}) \mathbf {n} = -\varphi _+^{2} \mathcal {F} \mathbf {n} \quad \text{ on } \partial _N (0,L)^3, \end{aligned}$$

(20)

and

$$\begin{aligned}&\partial _{\varDelta t} \varphi \le 0 \quad \text{ on } (0,L)^3 \quad \text{ and } \quad \frac{\partial \varphi }{\partial \mathbf {n}} =0 \quad \text{ on } \quad \partial (0,L)^3, \end{aligned}$$

(21)

$$\begin{aligned}&-G_c \varepsilon \varDelta \varphi -\frac{G_c}{\varepsilon }(1-\varphi ) + (1-k) \mathcal {G} e(\mathbf {u}): e(\mathbf {u}) \varphi _+ \nonumber \\&\quad +2 \varphi _+ (\mathcal {F} : e(\mathbf {u}) + \mathbf {f}\cdot \mathbf {u} )\le 0 \quad \text{ in } (0,L)^3 , \end{aligned}$$

(22)

$$\begin{aligned}&\left\{ -G_c \varepsilon \varDelta \varphi -\frac{G_c}{\varepsilon } (1-\varphi ) + (1-k) \mathcal {G} e(\mathbf {u}): e(\mathbf {u}) \varphi _+ \nonumber \right. \\&\left. \quad +2 \varphi _+ (\mathcal {F} : e(\mathbf {u}) + \mathbf {f} \cdot \mathbf {u} )\right\} \partial _{\varDelta t} \varphi =0 \; \text{ in } \; (0,L)^3, \end{aligned}$$

(23)

where (23) is the strong form of Rice’ condition (which is a well-known complementarity condition). This two-field formulation can be compared with the Model I formulation given in Miehe et al. (2010) (see p. 1289). The main difference is that the system (18)–(23) is a variational inequality; and in Miehe et al. (2010) a penalization term is used for solving the inequality.

4 Well-posedness of the model

4.1 Existence of a minimizer to the energy functional $\mathcal {E}_\varepsilon$

In this section, we seek for a solution to the minimization problem (17). The strategy is to consider the integrand of (15), using the notation $\mathbf {z} := (\mathbf {v}, \varphi )$, and $\xi$ stands for the components of the gradient of the displacements and the gradient of the phase-field function. With $z_{4}$, we access the fourth component of $\mathbf {z}$, namely the phase-field function. Lastly, $z_{4+}$ denotes the positive part of the phase-field unknown. Then,

$$\begin{aligned} g( x, \mathbf {z} , \xi )= & {} \frac{1}{2} \left( (1-k) (\inf \{ z_{4+} , 1 \})^2 +k \right) \sum _{i,j,k, r=1}^3 \mathcal {G}_{ijkr} \xi _{kr} \xi _{ij} + G_c ( \frac{1}{2\varepsilon } (1-z_4)^2 \nonumber \\&+\frac{\varepsilon }{2} | \nabla z_4 |^2 ) + (\inf \{ z_{4+} , 1 \})^{2} \left( \sum _{i,j=1}^3 F_{ij} \xi _{ij} + \sum _{i=1}^3 f_i z_i\right) , \end{aligned}$$

(24)

defined on $(0,L)^3 \times \mathbb {R}^4 \times \mathbb {R}^{12} \rightarrow \mathbb {R} \cup \{ +\infty \}$. It is convex in $\xi$ and we will prove that it is

• (i) a Caratheodory function (i.e. a continuous function on $\mathbb {R}^4 \times \mathbb {R}^{12}$ for every x from $(0,L)^3$ and a measurable function on $(0,L)^3$ for every $\{ \mathbf {z} , \xi \}$ from $\mathbb {R}^4 \times \mathbb {R}^{12}$);

• (ii) the energy functional (15) is coercive.

Then Corollary 3.24, p. 97, from Dacorogna’s monograph (2008) yields the lower semi-continuity of the energy functional. Proving existence of at least one point of minimum is then a classical task.

We start with a result which follows directly from the basic theory:

Lemma 1

Let $\mathbf {f}$ and $\mathbf {F} \in L^{2}$; and $G_c$, b be nonnegative constants. Let $\varepsilon$ be a positive small parameter. Then the integrand $g(\cdot ,\cdot ,\cdot )$ given by (24) is a Caratheodory function.

Proposition 1

Under the assumptions of Lemma 1, the functional

$$\begin{aligned} \varPhi (\mathbf {v}, \varphi )= \int _{(0,L)^3} g( x, \{ \mathbf {v}, \varphi \} , \{ e(\mathbf {v}), \nabla \varphi \}) \ dx \end{aligned}$$

(25)

is coercive over $V_U \times H^1 ((0,L)^3)\cap K$, i.e.

$$\begin{aligned} \lim \varPhi (\mathbf {v}, \varphi ) \rightarrow \infty , \qquad \text{ when }\quad || \mathbf {v} ||_{V_U} +|| \varphi ||_{H^1} \rightarrow \infty . \end{aligned}$$

(26)

Proof

Let us introduce the abbreviation ${{\tilde{\varphi }}}= \inf \{ \varphi _+ , 1 \}$. Let c be a generic constant. We estimate all terms one by one:

$$\begin{aligned} \left| \int _{(0,L)^3} ({{\tilde{\varphi }}} )^{2} (\mathbf {f} \mathbf {v} + \mathcal {F} : e(\mathbf {v} ) \ dx \right| \le || \mathbf {v} ||_{L^2} \ || \mathbf {f} ||_{L^2} + || {{\tilde{\varphi }}} e(\mathbf {v}) ||_{L^2} \ || \mathcal {F} ||_{L^2} . \end{aligned}$$

(27)

The elastic energy terms yield

$$\begin{aligned} \int _{(0,L)^3} \left( (1-k) ({{\tilde{\varphi }}})^2 +k \right) \mathcal {G} e(\mathbf {v}): e(\mathbf {v}) \ dx \ge c k || e(\mathbf {v}) ||_{L^2}^2 + c (1-k) || {{\tilde{\varphi }}} e(\mathbf {v}) ||_{L^2}^2 . \end{aligned}$$

(28)

We recall that, by Korn’s inequality,

$$\begin{aligned} || \mathbf {v} ||_{H^1 ((0,L)^3)} \le C_K || e(\mathbf {v}) ||_{L^2 ((0,L)^3)}, \qquad \forall \mathbf {v}\in V_U . \end{aligned}$$

(29)

Therefore, putting together (27) and (28), and using (29), yields

$$\begin{aligned}&\varPhi (\mathbf {v}, \varphi ) \ge G_c \int _{(0,L)^3} \left( \frac{(1-\varphi )^2}{2\varepsilon } +\varepsilon |\nabla \varphi |^2 \right) \ dx + \frac{c k}{4} || e(\mathbf {v}) ||_{L^2}^2 \nonumber \\&\quad +\frac{ c (1-k)}{4} || {{\tilde{\varphi }}} e(\mathbf {v}) ||_{L^2}^2 - \frac{|| \mathcal {F} ||_{L^2}^2 }{c(1-k)} - \frac{C_K^2|| \mathbf {f} ||_{L^2}^2}{ck} . \end{aligned}$$

(30)

The coerciveness property (26) follows from (30). $\square$

Our goal is to prove the following theorem:

Theorem 1

(Existence of a minimizer to the incremental phase field problem) Let $\varepsilon ,k>0$ and $\mathcal {F}$, $\mathbf {f}\in L^{2}$, $\varphi _p \in H^1$, $0\le \varphi _p \le 1$ a.e. on $(0,L)^3$. Then the minimization problem (17) has at least one solution $\{ \mathbf {u} , \varphi \} \in V_U \times K$ and $\varphi \ge 0$ a.e. on $(0,L)^3$.

Proof

Let $\{ \mathbf {u}^k , \varphi ^k \}_{k\in \mathbb {N}} \in V_U \times K$ be a minimizing sequence for the minimization problem (17) for $\varPhi$; that is a sequence of elements of $V_U \times K$ such that $\varPhi ( \mathbf {u}^k , \varphi ^k ) \rightarrow \inf _{V_U \times K} \varPhi ( \mathbf {v} , \varphi )$. By proposition (1) and the inequality (30) $\inf _{V_U \times K} \varPhi ( \mathbf {v} , \varphi ) \ne -\infty$. The sequence $\{ \mathbf {u}^k , \varphi ^k \}_{k\in \mathbb {N}}$ is uniformly bounded in $V_U \times K$ and $\{ \varphi _+^k \}_{k\in \mathbb {N}}$ is uniformly bounded in $L^\infty ((0,L)^3)$. Therefore there exists $\{ \mathbf {u} , \varphi \}$ and a subsequence, denoted by the same superscript, such that for $k\rightarrow \infty$

$$\begin{aligned}&\{ \mathbf {u}^k , \varphi ^k \} \rightarrow \{ \mathbf {u} , \varphi \} \quad \text{ weakly } \text{ in } \; V_U \times H^1 ((0,L)^3), \nonumber \\&\quad \text{ strongly } \text{ in } \; L^q ((0,L)^3)^4, \; q<6, \nonumber \\&\quad \text{ and } \text{ a.e. } \text{ on } \quad (0,L)^3. \end{aligned}$$

(31)

Next, inequality (30) yields

$$\begin{aligned} g( x, \mathbf {v} , \xi ) \ge \langle a(x), \xi \rangle + B, \qquad \text {for } \{ \mathbf {v} , \xi \} \in \mathbb {R}^4\times \mathbb {R}^{12} \quad \text{ and } \text{ a.e. } \quad x\in (0,L)^3, \end{aligned}$$

with $a\in L^2((0,L)^3)$ and $B\in \mathbb {R}$. Consequently, we are in a situation to apply Corollary 3.24, p. 97, from Dacorogna (2008). This result yields the weak lower semicontinuity of the functional $\varPhi$ and hence

$$\begin{aligned} \varPhi (\mathbf {u} , \varphi ) \le \lim \inf \varPhi (\mathbf {u}^k , \varphi ^k) =\inf _{V_U \times K} \varPhi ( \mathbf {v} , \varphi ). \end{aligned}$$

(32)

Since

$$\begin{aligned} \varPhi (\mathbf {v}, \psi ) = {{\mathcal {E}}}_\varepsilon (\mathbf {v}, \psi ) \quad \text {on } V_u \times K, \end{aligned}$$

we have proven that $\{ \mathbf {u} , \varphi \} \in V_U \times H^1 ((0,L)^3)\cap K$ is a solution for the minimization problem.

It remains to prove that $\varphi$ is nonnegative. We evaluate the functional $\varPhi$ at the point $\{ \mathbf {u} , \varphi _+ \}$. Obviously $\varphi _+ \in K$. A direct calculation yields

$$\begin{aligned} \varPhi (\mathbf {u} , \varphi _+ ) = \varPhi (\mathbf {u} , \varphi ) - \frac{ G_c}{2\varepsilon } \int _{(0,L)^3} \varphi _- ( \varphi _- -2 ) \ dx -\frac{\varepsilon G_C}{2} \int _{(0,L)^3} | \nabla \varphi _- |^2 \ dx. \end{aligned}$$

(33)

Therefore $\{ \mathbf {u} , \varphi \}$ can be a point of minimum only if $\varphi _-=0$ and we conclude that $\varphi \ge 0$ a.e. on $(0,L)^3$. $\square$

Corollary 1

(Euler–Lagrange weak PDE formulation) Let the hypotheses of Theorem 1 be satisfied. Then the Euler–Lagrange equations corresponding to the minimization problem (17)

$$\begin{aligned} \int \limits _{(0,L)^3}\!\!\!\! \left( (1-k) \varphi ^2 +k \right) \mathcal {G} e(\mathbf {u}): e(\mathbf {w}) \ dx +\!\!\!\! \int \limits _{(0,L)^3}\!\!\!\! \varphi ^{2} ( \mathcal {F} : e( \mathbf {w}) + \mathbf {f}\cdot \mathbf {w} ) \ dx=0,\qquad \end{aligned}$$

(34)

for all $\mathbf {w} \in V_U$, and

$$\begin{aligned}&\int \limits _{(0,L)^3} (1-k) \varphi \psi \mathcal {G} e(\mathbf {u}): e(\mathbf {u}) \ dx + G_c \int \limits _{(0,L)^3} \left( -\frac{1}{\varepsilon } (1-\varphi ) \psi + \varepsilon \nabla \varphi \cdot \nabla \psi \right) \ dx \nonumber \\&\quad + 2\!\!\int _{(0,L)^3} \varphi ( \mathbf {f} \cdot \mathbf {u} + \mathcal {F} : e (\mathbf {u}) ) \psi \, dx \le 0, \end{aligned}$$

(35)

for all $\psi \in H^1 ((0,L)^3), \, \psi \ge 0 \text{ a.e. } \text{ on } \; (0,L)^3$, and

$$\begin{aligned}&\int \limits _{(0,L)^3} (1-k) \varphi (\varphi _p -\varphi ) \mathcal {G} e(\mathbf {u}): e(\mathbf {u}) \ dx + G_c \int \limits _{(0,L)^3} \left( -\frac{1}{\varepsilon } (1-\varphi ) (\varphi _p -\varphi ) \nonumber \right. \qquad \\&\left. \quad +\varepsilon \nabla \varphi \cdot \nabla (\varphi _p -\varphi ) \right) \ dx + 2 \int \limits _{(0,L)^3} \varphi ( \mathbf {f}\cdot \mathbf {u} + \mathcal {F} : e (\mathbf {u}) ) (\varphi _p -\varphi ) \ dx = 0,\qquad \end{aligned}$$

(36)

admit a solution $\{ \mathbf {u} , \varphi \} \in V_U \times H^1 ((0,L)^3)\cap K$, such that $\varphi \ge 0$ a.e. on $(0,L)^3$. We observe that equation (36) is the Rice condition (see e.g. Francfort 2011).

In the next result, we show that our crack cannot become a ‘fat’ (balloon-like) crack, but remains tiny in the third direction:

Corollary 2

Let the hypotheses of Theorem 1 be satisfied. Let in addition the previous phase-field values $\varphi _p$ satisfy

$$\begin{aligned} \int _{(0,L)^3} (1-\varphi _p)^2 \, dx = || 1-\varphi _p ||_{L^2((0,L)^3)}^2 = C\varepsilon \end{aligned}$$

and

$$\begin{aligned} \Vert \sqrt{\varepsilon } \nabla \varphi _p \Vert _{L^2((0,L)^3)} \le C. \end{aligned}$$

Then the current phase-field variable $\varphi$ satisfy the same estimates:

$$\begin{aligned} \int _{(0,L)^3} (1-\varphi )^2 \, dx = || 1-\varphi ||_{L^2((0,L)^3)}^2 = C\varepsilon \end{aligned}$$

and

$$\begin{aligned} \int _{\{\varphi \le q\}} \, dx = meas \{ \varphi \le q\} \le \frac{C\varepsilon }{(1-q)^2} \quad \forall q\in [0,1). \end{aligned}$$

Proof

We evaluate

$$\begin{aligned} \varPhi (0,\varphi _p)&= G_c \int _{(0,L)^3} \left( \frac{1}{2\varepsilon } (1 - \varphi _p)^2 + \varepsilon | \nabla \varphi _p|^2 \right) \\&= \underbrace{G_c \varepsilon \int _{(0,L)^3} | \nabla \varphi _p|^2}_{\le c} + \frac{G_c}{2\varepsilon } \int _{((0,L)^3)} (1-\varphi _p)^2 \, dx \\&\le C. \end{aligned}$$

Since $\varPhi (u,\varphi ) \le \varPhi (0,\varphi _p)$ we use (30) and obtain the claimed estimates. $\square$

Remark 10

This theoretical property in Corollary 2 has also been confirmed in our numerical simulations in Sect. 6 in which the crack stays tiny in the second (2d) or third direction (3d), but grows into the other (2d) or two other (3d) directions.

4.2 A finite dimensional approximation

The finite dimensional approximation serves for two purposes. First, we continue our well-posedness study. Secondly, by specifying the discrete basis function through finite element functions with small support, we obtain a numerical procedure for a computer implementation. Let $\{ \psi _r \}_{r\in \mathbb {N}}$ be a basis for $H^1 ((0,L)^3 )$ and $\{ \mathbf {w}^r \}_{r\in \mathbb {N}}$ be a basis for $V_U$. We start by defining a finite dimensional approximation to the minimization problem (17).

Definition 2

(of a penalized approximation)

Let us suppose the assumptions of Theorem 1 and a penalization parameter $\delta \in \mathbb {R}$ and in particular, let $\delta :=M\in \mathbb {N}$ in this section. Let ${{\tilde{\varphi }}} =\inf \{ 1, \varphi _+ \}$. The pair $\{ \mathbf {u}^M , \varphi ^M \}$, $\mathbf {u}^M =\sum ^M_{r=1} a_r \mathbf {w}^r$ and $\varphi ^M =\sum ^M_{r=1} b_r \psi _r$, is a finite dimensional approximative solution for problem (17) if it is a minimizer to the problem

$$\begin{aligned} \inf _{V_U^M \times W^M} \left\{ \varPhi (\mathbf {v} , \varphi ) + \int _{(0,L)^3} \frac{\delta }{2} (\varphi - \varphi _p^M)^2_+ \ dx \right\} , \end{aligned}$$

(37)

where $V_U^M =$ span $\{ \mathbf {w}^r \}_{r=1, \dots , M}$, $W^M =$ span $\{ \psi _r \}_{r=1, \dots , M}$ and $\varphi _p^M$ is a projection of $\varphi _p$ on $W^M$.

Formulation 1

(Discrete weak formulation) Each solution for the problem (37) satisfies the discrete variational formulation

$$\begin{aligned}&\int _{(0,L)^3} \left( (1-k) ({{\tilde{\varphi }}}^M)^2 +k \right) \mathcal {G} e(\mathbf {u}^M): e(\mathbf {w}^r) \ dx \nonumber \\&\quad +\int _{(0,L)^3} ({{\tilde{\varphi }}}^M)^{2} ( \mathcal {F} : e(\mathbf {w}^r) + \mathbf {f} \mathbf {w}^r ) \ dx =0, \quad \forall r=1, \dots , M, \end{aligned}$$

(38)

$$\begin{aligned}&G_c \int _{(0,L)^3} \left( -\frac{1}{\varepsilon } (1-\varphi ^M) \psi _r + \varepsilon \nabla \varphi ^M \cdot \nabla \psi _r \right) \ dx + \int _{(0,L)^3} \delta ( \varphi ^M -\varphi _p^M)_+ \psi _r \ dx \nonumber \\&\quad +2 \int _{(0,L)^3} ({{\tilde{\varphi }}}^M) ( \mathcal {F} : e( \mathbf {u}^M) + \mathbf {f} \cdot \mathbf {u}^M ) \psi _r \ dx \nonumber \\&\quad +\int _{(0,L)^3} (1-k) {{\tilde{\varphi }}}^M \psi _r \mathcal {G} e(\mathbf {u}^M): e(\mathbf {u}^M) \ dx =0, \quad \forall \; r=1, \dots , M. \end{aligned}$$

(39)

Proposition 2

We assume the hypotheses of Theorem 1. Then there exists a penalized finite dimensional approximation for problem (37) that satisfies the a priori estimate

$$\begin{aligned}&G_c \int _{(0,L)^3} \frac{(1-\varphi ^M)^2}{\varepsilon } \ dx + \int _{(0,L)^3} M ( \varphi ^M - \varphi _p^M)_+^2 \ dx \nonumber \\&\quad +k || e(\mathbf {u}^M) ||_{L^2}^2 + || {{\tilde{\varphi }}}^M e(\mathbf {u}^M) ||_{L^2}^2 \le c , \end{aligned}$$

(40)

where c is independent of M.

Proof

This is a consequence of (30) in Proposition (1) and the continuity of the integrand. $\square$

Theorem 2

Assume the hypotheses of Theorem 1. Then there exists a subsequence of $\{ \mathbf {u}^M , \varphi ^M \} \in V_U^M \times W^M$, denoted by the same symbol, and $\{ \mathbf {u} , \varphi \} \in V_U \times H^1 ((0,L)^3)\cap K$, $\varphi \ge 0$ a.e., being a minimizer to the problem (17) and such that

$$\begin{aligned} \{ \mathbf {u}^M , \varphi ^M \} \rightarrow \{ \mathbf {u} , \varphi \} \quad \text{ in } \quad V_U \times H^1 ((0,L)^3). \end{aligned}$$

(41)

Proof

By Proposition 2 there is a solution $\{ \mathbf {u}^M , \varphi ^M \}$ for problem (37), satisfying the a priori estimate (40). Therefore there exists $\{ \mathbf {u} , \varphi \}$ and a subsequence, denoted by the same superscript, such that

$$\begin{aligned}&\{ \mathbf {u}^M , \varphi ^M \} \rightarrow \{ \mathbf {u} , \varphi \} \quad \text{ weakly } \text{ in } \; V_U \times H^1 ((0,L)^3),\nonumber \\&\quad \text{ strongly } \text{ in } \; L^q ((0,L)^3)^4, \; q<6, \nonumber \\&\quad \text{ and } \text{ a.e. } \text{ on } \quad (0,L)^3, \; \text{ as } \; M\rightarrow \infty . \end{aligned}$$

(42)

Obviously $(\varphi ^M -\varphi _p^M )_+ \rightarrow 0$, as $M\rightarrow \infty$, and $\varphi \in K$.

Next, let

$$\begin{aligned} \varphi \in K^N = \{z\in W^N : z(x) \le \varphi _p^M(x) \text { a.e. on }(0,L)^3\}, N\le M. \end{aligned}$$

Then we have

$$\begin{aligned} \varPhi (\mathbf {u}^M , \varphi ^M) + \int _{(0,L)^3} \frac{M}{2} (\varphi ^M - \varphi _p^M)^2_+ \ dx \le \varPhi (\mathbf {v} , \varphi ) , \end{aligned}$$

for all $\{ \mathbf {v} , \varphi \} \in V_U^N \times W^N \cap K$. The limit $M\rightarrow \infty$ yields

$$\begin{aligned} \varPhi (\mathbf {u} , \varphi ) \le \varPhi (\mathbf {v} , \varphi ) , \quad \forall \{ \mathbf {v} , \varphi \} \in V_U^N \times W^N \cap K . \end{aligned}$$

After passing to the limit $N\rightarrow \infty$, we conclude that $\{ \mathbf {u} , \varphi \} \in V_U \times H^1 ((0,L)^3) \cap K$ is a solution to problem (17). As before, it still can be shown that $\varphi$ is nonnegative.

It remains to establish strong convergence of the gradients. Passing to the limit in equation (38) is straightforward and we conclude that $\{ \mathbf {u} , \varphi \}$ satisfies equation (34). Next we choose $\mathbf {w}= \mathbf {u}^M$ as test function in (38) and pass to the limit $M\rightarrow \infty$. Thus,

$$\begin{aligned}&\int _{(0,L)^3} \left( (1-k) ({ \varphi }_+)^2 +k \right) \mathcal {G} e(\mathbf {u}): e(\mathbf {u}) \ dx \nonumber \\&\quad +\int _{(0,L)^3} ({\varphi }_+)^{2} ( \mathcal {F} : e(\mathbf {u} ) + \mathbf {f} \cdot \mathbf {u} ) \ dx=0. \end{aligned}$$

(43)

Therefore we have the convergence of the weighted elastic energies

$$\begin{aligned}&\lim _{M\rightarrow \infty } \int _{(0,L)^3} \left( (1-k) ({{\tilde{\varphi }}}^M)^2 +k \right) \mathcal {G} e(\mathbf {u}^M): e(\mathbf {u}^M) \ dx \nonumber \\&\quad =\int _{(0,L)^3} \left( (1-k) ({ \varphi }_+)^2 +k \right) \mathcal {G} e(\mathbf {u}): e(\mathbf {u}) \ dx . \end{aligned}$$

(44)

Using Fatou’s lemma we have

$$\begin{aligned}&\int _{(0,L)^3} \liminf _{M\rightarrow \infty } \left( (1-k) ({{\tilde{\varphi }}}^M)^2 +k \right) \mathcal {G} e(\mathbf {u}^M): e(\mathbf {u}^M) \ dx \nonumber \\&\quad \le \liminf _{M\rightarrow \infty } \int _{(0,L)^3} \left( (1-k) ({{\tilde{\varphi }}}^M)^2 +k \right) \mathcal {G} e(\mathbf {u}^M): e(\mathbf {u}^M) \ dx \nonumber \\&\quad =\int _{(0,L)^3} \left( (1-k) ({ \varphi }_+)^2 +k \right) \mathcal {G} e(\mathbf {u}): e(\mathbf {u}) \ dx . \end{aligned}$$

(45)

Consequently

$$\begin{aligned} \mathbf {u}^M \rightarrow \mathbf {u} \quad \text{ strongly } \text{ in } \quad V_U ,\quad \text{ as } \; M\rightarrow \infty . \end{aligned}$$

(46)

For every $\psi \in L^\infty ((0,L)^3)\cap H^1 ((0,L)^3)$, (46) implies

$$\begin{aligned} \lim _{M\rightarrow \infty } | \int _{(0,L)^3} { {\tilde{\varphi }}}^M \psi \mathcal {G} e(\mathbf {u}^M -\mathbf {u}): e(\mathbf {u}^M -\mathbf {u}) \ dx | \rightarrow 0, \quad \text{ as } \; M\rightarrow \infty , \end{aligned}$$

and

$$\begin{aligned}&\int _{(0,L)^3} { {\tilde{\varphi }}}^M \psi \mathcal {G} e(\mathbf {u}^M ): e(\mathbf {u}^M ) \ dx = \int _{(0,L)^3} { {\tilde{\varphi }}}^M \psi \mathcal {G} e(\mathbf {u}^M - \mathbf {u}): e(\mathbf {u}^M -\mathbf {u}) \ dx \nonumber \\&\quad +2 \int _{(0,L)^3} { {\tilde{\varphi }}}^M \psi \mathcal {G} e(\mathbf {u}^M ): e(\mathbf {u} ) \ dx - \int _{(0,L)^3} { {\tilde{\varphi }}}^M \psi \mathcal {G} e(\mathbf {u} ): e(\mathbf {u} ) \ dx \nonumber \\&\quad \rightarrow \int _{(0,L)^3} { \varphi }_+ \psi \mathcal {G} e(\mathbf {u} ): e(\mathbf {u} ) \ dx, \quad \text{ as } \; M\rightarrow \infty . \end{aligned}$$

(47)

Next we use Minty’s lemma and write equation (39) in the equivalent form

$$\begin{aligned}&\int _{(0,L)^3} (1-k) \inf \{ \varphi ^M_+ , 1\} (\psi -\varphi ^M) \mathcal {G} e(\mathbf {u}^M): e(\mathbf {u}^M) \ dx \nonumber \\&\quad + G_c \int _{(0,L)^3} \left( \frac{( \psi -1)}{\varepsilon } (\psi -\varphi ^M) \nonumber \right. \\&\left. \quad +\varepsilon \nabla \psi \cdot \nabla (\psi -\varphi ^M) \right) dx \nonumber \\&\quad + 2 \int _{(0,L)^3} (\inf \{ \varphi ^M_+ , 1\}) \ ( \mathbf {f}\cdot \mathbf {u}^M + \mathcal {F} : e (\mathbf {u}^M) ) (\psi -\varphi ^M) dx \nonumber \\&\quad + \int _{(0,L)^3} M ( \psi - \varphi _p^M)_+ (\psi -\varphi ^M) \ dx \ge 0, \quad \forall \ \psi \in W^M . \end{aligned}$$

(48)

After taking $\psi =\varphi _p^M$, we use the convergence (47) pass to the limit $M \rightarrow \infty$ (see e. g. Kinderlehrer and Stampacchia 2000), and obtain

$$\begin{aligned}&\lim _{M\rightarrow \infty } G_c \int _{(0,L)^3} \varepsilon | \nabla \varphi ^M |^2 \ dx = - \int _{(0,L)^3} (1-k) \varphi (\varphi -\varphi _p ) \mathcal {G} e(\mathbf {u}): e(\mathbf {u}) \ dx \nonumber \\&\quad +\int _{(0,L)^3} \left( \frac{G_c}{\varepsilon } (1-\varphi _p) (\varphi -\varphi _p ) - \frac{G_c}{\varepsilon } (\varphi -\varphi _p )^2 + \varepsilon \nabla \varphi \cdot \nabla \varphi _p \right) \ dx \nonumber \\&\quad -2 \int _{(0,L)^3} \varphi _{+} \ ( \mathbf {f} \cdot \mathbf {u} + \mathcal {F} : e (\mathbf {u}) ) (\varphi -\varphi _p ) \ dx = G_c \int _{(0,L)^3} \varepsilon | \nabla \varphi |^2 \ dx. \end{aligned}$$

(49)

This finishes the proof. $\square$

5 Numerical approximation

We now formulate finite element approximations to (35)–(34), which are analogous to equations (38)–(39). For spatial discretization, we apply a standard Galerkin finite element method on quadrilaterals (2d) and hexahedra (3d), respectively. Specifically, we approximate displacements by continuous bilinears (2d) or trilinears (3d) and refer to the finite element space as $V_h$. Also, we take $\varphi$ to be bilinears (2d) and trilinears (3d), and denote this space as $W_h$; see e.g. Ciarlet (1987). Here h represents the standard approximation parameter. We deal with:

Formulation 2

(Weak form) Find $\{u^h,\varphi ^h\}\in V_h \times W_h$ such that

$$\begin{aligned}&\int _{(0,L)^3} \left( (1-k) ({{\tilde{\varphi }}}^h)^2 +k \right) \mathcal {G} e(\mathbf {u}^h): e(\mathbf {w} ) \ dx \nonumber \\&\quad +\int _{(0,L)^3} ({{\tilde{\varphi }}}^h)^{2} ( \mathcal {F} : e(\mathbf {w}) + \mathbf {f}\cdot \mathbf {w} ) \ dx =0 \quad \forall \mathbf {w}\in V_h , \end{aligned}$$

(50)

$$\begin{aligned}&G_c \int _{(0,L)^3} \left( -\frac{1}{\varepsilon } (1-\varphi ^h) \psi + \varepsilon \nabla \varphi ^h \cdot \nabla \psi \right) \ dx + \int _{(0,L)^3} \delta (\partial _{\varDelta t} \varphi ^h)_+ \psi \ dx \nonumber \\&\quad +2 \int _{(0,L)^3} ({{\tilde{\varphi }}}^h) ( \mathcal {F} : e( \mathbf {u}^h) + \mathbf {f} \cdot \mathbf {u}^h ) \psi \ dx \nonumber \\&\quad +\int _{(0,L)^3} (1-k) {{\tilde{\varphi }}}^h \psi \mathcal {G} e(\mathbf {u}^h): e(\mathbf {u}^h) \ dx =0 \quad \forall \; \psi \in W_h. \end{aligned}$$

(51)

The incremental formulation (50)–(51) corresponds to the (pseudo-) time stepping scheme based on a difference quotient approximation with backward differences for the time derivatives. In the quasi-static model the time derivative $\delta [\partial _t \varphi ]_+$ is present and is discretized as follows

$$\begin{aligned} {\delta } [\partial _{ t} \varphi ]_+&\rightarrow {\delta } [\partial _{\varDelta t} \varphi ]_+ = {\delta } \frac{[\varphi - \varphi ^{n-1}]_+}{\varDelta t}, \end{aligned}$$

with the time step size $\varDelta t$, where $n-1$ is used to indicate the preceding time step. We then obtain for the weak form:

$$\begin{aligned} {\delta } (\varphi _+ - \varphi _+^{n-1}, \psi )_{L^2} + \varDelta t ( B,\psi )_{L^2} = 0, \quad \forall \psi \in W_h . \end{aligned}$$

(52)

Here, $( \cdot , \cdot )$ denotes the discrete scalar product in $L^2$ and A and B denote the operators of all remaining terms for the present time step in the weak formulation, where the equation (52) is related to equations (50) and (51). Finally, the spatially discretized semi-linear form can be written in the following way:

Finite Element Formulation 1

Find $\mathbf {U}^h:=\{\mathbf {u}^h,\varphi ^h\}\in V_h\times W_h$ such that:

$$\begin{aligned} A(\mathbf {U}^h)({\varvec{\Psi }} ) = {\delta } ([\varphi ^h - \varphi ^{h,n-1}]_+,\psi )_{L^2} + \varDelta t A_S (\mathbf {U}^h)({\varvec{\Psi }} ) = 0, \end{aligned}$$

with

$$\begin{aligned}&A_S (\mathbf {U}^h)({\varvec{\Psi }} ) = \left( ((1-k) (\inf \{ \varphi _+^h , 1\})^2 + k) \mathcal {G}e(\mathbf {u}^h), e(\mathbf {w}) \right) _{L^2} - \langle {\tau }, \mathbf {w} \rangle _{\partial _N \varOmega }\\&\quad - ((\inf \{ \varphi _+^h , 1\})^{2}(\alpha -1)p_B, \nabla \cdot \mathbf {w})_{L^2} + (\nabla p_B (\inf \{ \varphi _+^h , 1\})^{2}, \mathbf {w})_{L^2}\\&\quad +\left( (1-k) \mathcal {G}e(\mathbf {u}^h) : e(\mathbf {u}^h) (\inf \{ \varphi _+^h , 1\}), \psi \right) _{L^2} - \frac{G_c}{\epsilon } (1-\varphi ^h,\psi )_{L^2}\\&\quad + G_c \epsilon (\nabla \varphi ^h, \nabla \psi )_{L^2}- 2 \left( (\inf \{ \varphi _+^h , 1\}) { \left( (\alpha -1)p_B \nabla \cdot \mathbf {u}^h - \nabla p_B \cdot \mathbf {u}^h \right) }, \psi \right) _{L^2} \end{aligned}$$

for all ${\varvec{\Psi }} =\{\mathbf {w},\psi \}\in V_h\times W_h$, where $A_S (\cdot )(\cdot )$ is the sum of equations (50) and (51) and equality (11) is applied in the relation between $\tau$ and $\mathcal{T}$.

5.1 Linearization and Newton’s method

The nonlinear problem is solved with Newton’s method. For the iteration steps $m=0,1,2,\ldots$, it holds:

$$\begin{aligned} A'(\mathbf {U}^{h,m})(\varvec{\Delta } \mathbf{U }^h, {\varvec{\Psi }} ) = - A(\mathbf {U}^{h,m})({\varvec{\Psi }} ) , \quad \mathbf {U}^{h,m+1} = \mathbf {U}^{h,m} + \lambda {\varvec{\Delta } \mathbf{U }}^{h}, \end{aligned}$$

(53)

with ${\varvec{\Delta } \mathbf{U }}^{h}=\{\varvec{\Delta } \mathbf{U }^h , \varDelta \varphi ^h\}$, and a line search parameter $\lambda \in (0,1]$. Here, we need the (approximated) Jacobian of Finite Element Formulation 1 (defined without using the subscript h):

$$\begin{aligned} A'(\mathbf {U})({\varvec{\Delta } \mathbf{U }}, {\varvec{\Psi }} ) = {\delta } (\varDelta [\varphi - \varphi ^{n-1}]_+,\psi )_{L^2} + \varDelta t A_S '(\mathbf {U})( {\varvec{\Delta } \mathbf{U }}, {\varvec{\Psi }} ), \end{aligned}$$

with

$$\begin{aligned}&A_S '(\mathbf {U})( {\varvec{\Delta } \mathbf{U }}, {\varvec{\Psi }} ) {=} \left( 2(1-k) \inf \{ \varphi _+ , 1\} H(1-\varphi ) \varDelta \varphi \mathcal {G}e(\mathbf {u}) + ((1-k)(\inf \{ \varphi _+ , 1\})^2 \right. \\&\quad \left. + k)\mathcal {G}e(\varDelta \mathbf {u}), e(\mathbf {w}) \right) _{L^2} - (2 (\inf \{ \varphi _+ , 1\}) H(1-\varphi ) \varDelta \varphi (\alpha -1)p_B, \nabla \cdot \mathbf {w})_{L^2}\\&\quad + ( 2 (\inf \{ \varphi _+ , 1\}) H(1-\varphi ) \varDelta \varphi \nabla p_B, \mathbf {w})_{L^2} + \left( 2(1-k) \mathcal {G}e(\mathbf {u}) : e(\varDelta \mathbf {u}) \inf \{ \varphi _+ , 1\} \right. \\&\quad \left. {+} (1-k)\mathcal {G}e(\mathbf {u}) : e(\mathbf {u}) H(1-\varphi ) \varDelta \varphi , \psi \right) _{L^2} {+} \frac{G_c}{\epsilon } (\varDelta \varphi ,\psi )_{L^2} + G_c \epsilon (\nabla \varDelta \varphi , \nabla \psi )_{L^2} \\&\quad -(\alpha -1) 2 (p_B ( H(1-\varphi ) \varDelta \varphi \nabla \cdot \mathbf {u} + (\inf \{ \varphi _+ , 1\}) \nabla \cdot \varDelta \mathbf {u}), \psi )_{L^2} \\&\quad + 2 \left( \nabla p_B \cdot ( H(1-\varphi ) \varDelta \varphi \mathbf {u} + (\inf \{ \varphi _+ , 1\}) \varDelta \mathbf {u}),\psi \right) _{L^2}, \end{aligned}$$

for all ${\varvec{\Psi }} =\{\mathbf {w},\psi \}\in V_h\times W_h$. Here, $H (\cdot )$ is Heaviside’s function.

Remark 11

The realization of (53) is based on a modified Newton method with dynamic Jacobian modification developed in Wick (2017b), where the terms related to the nonconvex parts (i.e., in the displacement equation) are scaled accordingly. Other monolithic solvers worthy to mention are Gerasimov and Lorenzis (2016) and Wick (2017a) in which line-search assisted or error-oriented Newton methods were developed, respectively. Alternatively, a robust and efficient technique is to replace $\varphi ^h$ in the elasticity equation by a time-lagged extrapolated $\varphi ^h$, which has been demonstrated computationally to provide a robust and stable numerical scheme Heister et al. (2015) (2d) and Lee et al. (2016b) (3d).

6 Numerical tests

We perform four numerical tests. The first test assumes a constant pressure $p_B = 10^{-3}$ that acts in the pressure [Sneddon’s 2d benchmark (Sneddon and Lowengrub 1969)]. The second example considers again Sneddon’s 2d benchmark, but with Neumann conditions on the bottom and top boundaries. In the third example, we study two interacting propagating fractures subject to a nonconstant pressure. In the fourth test, we address Sneddon’s 3d benchmark in which a penny-shaped fracture is subject to a constant pressure, again $p_B = 10^{-3}$. The programming code is based on the finite element software deal.II (see Arndt et al. 2017; Bangerth et al. 2007) and the underlying monolithic numerical treatment is described in detail in Wick (2017a, b).

6.1 Constant pressure in a crack (Sneddons’s 2d benchmark)

The first example is motivated by Bourdin et al. (2012), Wheeler et al. (2014) and is based on Sneddon’s theoretical calculations (1969, 1946). Specifically, we consider a 2d problem where a (constant) pressure $p_B$ is used to drive the deformation and crack propagation. We assume a dimensionless form of the equations.

Fig. 2

Example 1: Configuration (left) and crack pattern (right)

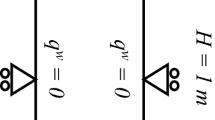
The configuration is displayed in Fig. 2. We prescribe the initial crack implicitly (see e.g. Borden et al. 2012 and specifically for this setting Wheeler et al. 2014). Therefore, we deal with the following geometric data: $\varOmega = (0,4)^2$ and a (prescribed) initial crack with length $2l_0 = 0.4$ on $\varOmega _C = (1.8,2.2)\times (2-h, 2-h) \subset \varOmega$ where h is the local mesh size. Thus, we deal with a 2d crack with a length much larger than its width. As boundary conditions we set the displacements zero on $\partial \varOmega$. The test is stationary, but we perform two (pseudo) time steps in order to account for the crack irreversibility condition.

Applying the theory of $\varGamma$-convergence based on a related finite element analysis in Bourdin (1999), we choose $h\ll k\ll \epsilon$, i.e., $k = 0.25\sqrt{h}$ and $\epsilon = 0.5\sqrt{h}$. Furthermore, it is well-known that $\delta$ must depend on h, i.e., here, we choose $\delta = 100\times h^{-2}$. The Biot coefficient and critical energy release rate are chosen as $\alpha = 0$ and $G_c = 1.0$, respectively. The mechanical parameters are Young’s modulus and Poisson’s ratio are set to be $E = 1.0$ and $\nu _s = 0.2$. The applied fracture pressure is $p_B = 10^{-3}$.

The goal is to measure the crack opening displacement (COD) and the volume of the crack under spatial mesh refinement. To this end, we observe u along $\varOmega _C$. Specifically, the width is determined as the jump of the normal displacements $COD := w:= w(x,y) = [\mathbf {u}\cdot \mathbf {n}].$ This expression can be written in integral form as follows:

$$\begin{aligned} COD := w:= w(x,y) = \int _{-\infty }^{\infty } \mathbf {u}\cdot \nabla \varphi \, dy. \end{aligned}$$

(54)

We note that the integration is perpendicular to the crack direction. Here, the crack is aligned with the x-axis and therefore integration into the normal direction coincides with the y-direction.

Fig. 3

Example 1: COD for different h. Sneddon’s turquoise line with squares corresponds to his analytical solution. It is well observed that the crack tips must be resolved correctly as they are not well approximated on coarse meshes (color figure online)

The COD formula (54) is obvious since the phase-field variable $\varphi$ can be related to a level-set function. This level-set can be used to compute the (unit) normal vector, e.g., Nguyen et al. (2016), Lee et al. (2017a). Here, the normal vector is in the y-direction and therefore, the above formula is obtained corresponding to $[\mathbf {u}\cdot \mathbf {n}]$ for $\varepsilon = 0$.

Second, following (Dean and Schmidt 2014, p. 710), the volume of the fracture is $V = \pi w l_0.$ The analytical expression for the width (to which we compare) Dean and Schmidt (2014) is $w = 4 \frac{(1 - \nu _s^2)l_0 p}{E}.$ Then, the analytical expression for the volume becomes

$$\begin{aligned} V = 2 \pi \frac{(1 - \nu _s^2)l_0^2 p}{E}. \end{aligned}$$

(55)

In contrast to Bourdin et al. (2012), we use the numerical approximation of the phase-field function instead of a synthetic choice of the crack indicator function.

The crack pattern and the corresponding mesh are displayed in Fig. 2. Our findings for different spatial mesh parameters h are summarized in Fig. 3. Specifically, we observe overall convergence to Sneddon’s analytical solution (Sneddon and Lowengrub 1969) as well as much better approximation of the crack tips under local mesh refinement. The obtained crack volumes are displayed in Table 2 in which the exact value is computed by Formula (55).

Table 2 Example 1: Fracture volume

6.2 Sneddon’s 2d-benchmark with mixed boundary conditions

Fig. 4

Example 2: phase-field function for Case 1 and Case 2 at left and the Cases 3 and 4 at right

In this second test, the domain and parameters are the same as in the previous example. The only (major) change concerns the boundary conditions. The top $\varGamma _{top}$ and bottom $\varGamma _{bottom}$ boundaries form now a Neumann boundary $\partial _N (0,L)^2 = \varGamma _{top} \cup \varGamma _{bottom}$. Here, we prescribe Neumann conditions $\tau$ of homogeneous and nonhomogeneous type. Then, we compare these results to the previous setting. In total we design the following tests:

• Case 1: $\partial _N (0,L)^2 = \emptyset$ and $u=0$ on $\partial _D (0,L)^2$;

• Case 2: $\tau = (0,0)^T$ on $\partial _N (0,L)^2$ and $u=0$ on $\partial _D (0,L)^2$;

• Case 3: $\tau = (0,0.001)^T$ on $\varGamma _{top}$, $\tau = (0,-0.001)^T$ on $\varGamma _{bottom}$

  and $u=0$ on $\partial _D (0,L)^2$;

• Case 4: $\tau = (0,0.1)^T$ on $\varGamma _{top}$, $\tau = (0,-0.1)^T$ on $\varGamma _{bottom}$

  and $u=0$ on $\partial _D (0,L)^2$.

These computations are performed on a 7 times uniformly refined mesh with $h = 0.044$. The phase-field function is displayed in Fig. 4.

Fig. 5

Example 2: the y-displacements for all four cases

The maximal crack width openings $w_{max}$ at $x=2$ computed with the help of (54) in the middle of the fracture are:

• Case 1: $w_{max}(x=2;\; 0\le y\le 4) = 5.25244\times 10^{-4}$;

• Case 2: $w_{max}(x=2;\; 0\le y\le 4) = 5.52572\times 10^{-4}$;

• Case 3: $w_{max}(x=2;\; 0\le y\le 4) = 1.31092\times 10^{-3}$;

• Case 4: $w_{max}(x=2;\; 0\le y\le 4) = 7.67588\times 10^{-2}$.

These findings are plausible: in Case 2 zero traction forces are applied on the top and the bottom boundaries and the fracture pressure keeps the fracture open. In addition, the maximal crack opening displacement is very similar (as expected) to Case 1. We further remark that the pressure boundary term $\int _{ \partial _N (0,L)^2} p_B w_n \ dS$ in (10) is important when working with Neumann conditions. For instance, when $\int _{ \partial _N (0,L)^2} p_B w_n \ dS$ is not used in Case 2, we obtain a negative width, which is of course nonphysical for this setting. The influence is significant for all cases when $\Vert \tau \Vert < \Vert p\mathbf {n}\Vert$ (Case 2) and $\Vert \tau \Vert \approx \Vert p\mathbf {n}\Vert$ (Case 3). In the Cases 3 and 4, the domain is pulled, since now the traction forces are strictly positive/negative, respectively. Consequently the fracture opens more than in the first two cases. Specifically, when the traction force is increased by a magnitude of order 2, the fracture width is also higher about a magnitude of order 2. The y-displacement fields (here directly to the crack opening displacements since the fracture is aligned with the x-axis) are displayed in Fig. 5.

6.3 Two-crack interaction subject to non-constant pressure

In this third example, we extend the previous setting to study the interaction of two different fractures that are subject to a linearly increasing pressure $p_B$. In the first part, a homogeneous material is considered and in the second part a heterogenous material field. The pressure function is given by $p_B(t) = 0.1 + t \cdot 0.1,$ where t denotes the total time, and Young’s modulus is set to be $E=1$ in the first part and it varies between 1.1 and 11.0 in the second part. Poisson ratio is 0.2. The penalization parameter is chosen as $\delta = 10h^{-2}$. The remaining parameters are chosen as in the previous example. Our results in the Figs. 6 and 7 show two propagating, interacting fractures. Specifically, they curve away due to stress-shadowing effects (see e.g., Castonguay et al. 2013). The extension to nonconstant pressure evolution using Darcy’s law and application of the fixed-stress splitting is studied in Wick et al. (2016) and Mikelić et al. (2015a).

Fig. 6

Example 3: crack evolution in red in a homogeneous material at times $T=0, 15, 30$ (color figure online)

Fig. 7

Example 3: crack evolution in red in a heterogeneous material at times $T=30, 40, 50$. The light blue regions denote smooth material $E\approx 1$ and dark blue stands for $E\approx 11.0$ (color figure online)

6.4 Sneddons’s 3d benchmark with a constant pressure in a penny-shaped crack

The last example is again based on Sneddon’s theoretical calculations (Sneddon and Lowengrub 1969, Section 3.3, pp. 138–139). Specifically, we consider a 3d problem where a (constant) pressure $p_B=10^{-3}$ is used to open a penny-shaped fracture.

The configuration is displayed in Fig. 8 and $\varOmega = (0,10)^3$. We prescribe the initial crack implicitly by setting the intial value of the phase-field variable to zero in the $y=5$-plane with origin (5, 5, 5). The radius of the fracture is $\rho =1$. As boundary conditions we set the displacements zero on $\partial \varOmega$. We perform five (pseudo) time steps.

We choose $k=10^{-12}$ and $\varepsilon = 2h$ and $h_{min} = 1.08, 0.54, 0.27, 0.135$. The Biot coefficient and critical energy release rate are chosen as $\alpha = 0$ and $G_c = 1.0$, respectively. The mechanical parameters are Young’s modulus and Poisson’s ratio are set to be $E = 1.0$ and $\nu _s = 0.2$. The applied fracture pressure is $p_B = 10^{-3}$.

The locally refined mesh on the finest level and the penny-shaped fracture are shown in Fig. 8. Specifically, we observe that the fracture remains thin in the third direction as shown theoretically in Corollary 2. The crack opening displacement (here the displacements in y direction) and the corresponding plots for the four different h values are shown in Fig. 9. We notice that $\varepsilon$ depends on h. For this reason, we cannot expect ‘convergence’ in the classical sense. Such results however have been shown in our other papers in which $\varepsilon$ was fixed and only h was varied Lee et al. (2016b), Wheeler et al. (2014).

Fig. 8

Example 4: A penny-shaped fracture and locally refined mesh (left) and zoom-in at right. Specifically, the fracture remains thin in the third direction as shown theoretically in Corollary 2

Fig. 9

Example 4: Crack opening displacements. Graphical illustration of the y displacements (left) and evaluation of the crack opening displacements for the four different h values. The reference curve of Sneddon has been computed with the formula given in Sneddon and Lowengrub (1969) on p. 139

7 Conclusion

In this paper, we discussed the mechanics step of hydraulic phase-field fractures with a given pressure field for propagating cracks in a poroelastic medium. The phase-field algorithm is based on an incremental formulation and existence of a minimizer is established. We rigorously show that if the initial crack size was of order $\varepsilon$ (with a reasonable control of the gradient of its initial phase-field description), then the phase-field function at the next (future) time step has the same property. Consequently, in our model, the initially slender fractures remain indeed thin in the second (in 2d) or third (3d) space dimensions during the incremental evolution. Numerical benchmarks are demonstrating the correctness of the theory. Specifically, a numerical test with mixed boundary conditions (Dirichlet and Neumann) was designed in which our modeling of the pressure interface conditions was further confirmed. The modeling of this paper forms the basis for extensions to crack growth in heterogeneous porous media, fluid-filled, and proppant-filled crack evolutions.