1 Introduction

Soil is a granular material, a product of rock fragmentation and weathering processes. Geotechnical engineers investigate the mechanical behavior of soil and predict its response to applied forces and/or movements. In several geotechnical problems, large and, sometimes, non-topological deformations, e.g., pile penetration, excavation, or landslides are encountered. Therefore, a soil grain does not maintain the same grains as neighbors during a large deformation. This fact distinguishes soil from other engineering materials, e.g., reinforced concrete, steel. In this case, traditional Finite Element Methods (FEM) encounter numerical problems due to element distortion and, hence, resort to remeshing techniques. On the contrary, meshfree methods are techniques without fixed connectivities among the points representing the domain and, thus, are promising to treat large deformations. Applications of meshfree methods in geomechanics can be found in (Bardenhagen et al. 2000; Beuth et al. 2011; Blanc 2008; Blanc and Pastor 2013; Bui and Fukagawa 2011; Coetzee 2005; Cuéllar et al. 2009; Holmes et al. 2011; Jassim et al. 2012; Khoshghalb and Khalili 2010, 2012; Murakami et al. 2005; Pastor et al. 2008; Vermeer et al. 2008; Zhu et al. 2006), to name a few. They show the growing interest in meshfree techniques.

In soil mechanics, two benchmark problems are usually considered to, e.g., check new material laws such as barodesy (described in Sect. 3) or to classify different soils. These are the oedometric and the triaxial test which are described in more detail in Sect. 2. In this contribution, they are considered as test scenarios for the presented meshfree approaches. Boundary-value continuum problems in engineering and physics are formulated using partial differential equations (PDEs). While the exact solution satisfies those equations in all points of the problem domain in question, it can only be given analytically (since the number of points in a continuum is infinite) and is usually only available for the most simple cases. Approximate solutions (see, e.g., Fries and Matthies 2003) are given in a finite number of points. They either satisfy the PDEs in these points exactly (strong form of the PDE) or in some integral sense taking into account the function values in between the solution points via interpolation (weak form). Since both meshfree methods which are discussed in this contribution are based on the strong formulation, we present the weighted moving least squares (WMLS) procedure in Sect. 4 (see, e.g., Lancaster and Salkauskas 1981) which is used to approximate the required function values and derivatives of functions defined on a finite set of points. The description of the meshfree approaches—Finite Pointset Method (FPM) and Soft PARticle Code (SPARC)—for the described applications can be found in Sects. 5 and 6 including a short comparison. Numerical results for specific test scenarios will be presented and discussed in “Part II: Numerical Examples” of this contribution in the near future.

2 Two benchmark problems in soil mechanics

2.1 Oedometric test

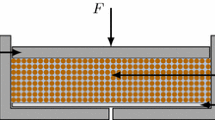
An oedometric test simulates one-dimensional compression. The soil sample is loaded in vertical/axial direction, whereas rigid side walls hinder any lateral expansion (see Fig. 1a). The obtained stress-strain curves are nonlinear and anelastic, i.e., irreversible (see Fig. 1b). During the loading phase, the soil sample becomes stiffer because of the hindered lateral displacement. The vertical velocity is prescribed at the upper plate; the horizontal velocity at the side walls vanishes and so does the vertical velocity at the bottom plate. These kinematic boundary conditions make the oedometric test easy to simulate. It is assumed that the deformation is homogeneous and the contact between side walls and soil sample is frictionless.

Fig. 1
figure 1

a Oedometric test apparatus. b Stress-strain curve (in axial direction) with alternating loading and unloading phases using the hypoplastic constitutive law of barodesy (see Sect. 3 and Kolymbas 2011 for further details)

Full size image

2.2 Triaxial test

The triaxial test is a common method to extract mechanical parameters of granular materials in engineering practice. In a conventional triaxial test, a cylindrical soil sample is enclosed in a thin rubber membrane and placed between two rigid plates inside a pressure chamber, as shown in Fig. 2a. The soil sample is loaded by the stress component \(\sigma _{1}\) in axial direction and by constant lateral stresses \(\sigma _{2}=\sigma _{3}\). Positive stresses denote compression. Initially, the sample is under hydrostatic pressure \(\sigma _{1}=\sigma _{2}=\sigma _{3}=\sigma _\mathrm c \) with \(\sigma _\mathrm c >0\). Thereafter, the upper plate can move vertically and apply axial load or displacement to the specimen. During the test, the minimum principal stress is equal to the confining pressure \(\sigma _{2}=\sigma _{3}=\sigma _\mathrm c \) and the maximum principal stress \(\sigma _{1} (=\!\sigma _\mathrm c + \Delta \sigma \)) increases. The axial stress increases until the soil sample reaches a limit state which is manifested by vanishing incremental stiffness. The sample becomes shorter while bulging. The axial strain of the sample is controlled through the displacement of the upper plate \(\varepsilon _{1}=\Delta h/h_{0}\) with \(h_{0}\) being the initial sample height. In the obtained stress-strain diagram, the maximum \(\sigma _{1}\) value is denoted as the peak and is obtained by using dense samples, whereas by loose samples a peak is not obtained and the stress-strain curve asymptotically approaches the maximum (see Fig. 2b). Moreover, dense soil samples have the tendency to increase their volume under shear. This effect is called dilatancy. On the contrary, loose samples decrease their volume under shear, an effect called contractancy. The triaxial test is more complex than the oedometric test: The assumption of homogeneity of deformation in the course of the triaxial test does not agree with the reality due to friction at the end plates.

Fig. 2
figure 2

a Triaxial test apparatus. b Stress difference vs. axial strain (top) and volumetric strain vs. axial strain (bottom) for loose (void ratio \(e=0.9\)) as well as dense (void ratio \(e=0.67\)) Hostun sand using the hypoplastic constitutive law of barodesy (see Sect. 3 and Kolymbas 2011 for further details)

Full size image

3 Barodesy for sand

A constitutive equation governs the relationship between stresses and strains inside a sample. It is formulated in tensorial form and should conform to basic mechanical properties of the material. The anelastic soil behavior is characterized by irreversible deformations. Besides elastoplastic constitutive laws also hypoplastic ones are capable of describing anelastic behavior. The latter neither use a plastic potential and yield surface nor distinguish between elastic and plastic deformations. Barodesy is a new version of hypoplasticity (see Kolymbas 2011, 2012 for further details) of the general form \({\mathring{ \mathbf T }={ \mathbf H }({ \mathbf T },{ \mathbf D }},e)\), where \(\mathbf{T }\) is the Cauchy stress tensor (\(\varvec{\sigma }=-\mathbf T \) with principal stresses \(\sigma _1,\sigma _2,\sigma _3\) in axial and lateral directions), \(\mathbf{D }\) is the stretching tensor (the symmetric part of the velocity gradient, i.e., \(\mathbf{D } = \frac{1}{2}(\nabla \mathbf{v }^\mathrm{T } + (\nabla \mathbf{v }^\mathrm{T })^\mathrm{T })\), and \(e\) is the void ratio. More specifically:

$$\begin{aligned} {\mathring{ \mathbf T }} = h(\sigma )\cdot (f { \mathbf R }^{0} + g{{ \mathbf T }}^{0})\cdot |{ \mathbf D } |, \end{aligned}$$
(3.1)

where \(\sigma := |\mathbf{T } |=\sqrt{\mathrm{tr }(\mathbf{T }^2)}\). The tensorial function \(\mathbf{H }(\mathbf{T },\mathbf{D },e)\) is subjected to two general mathematical restrictions: nonlinearity in \(\mathbf{D }\) as well as homogeneity in \(\mathbf{D }\) and \(\mathbf{T }\). It should be homogeneous of the first degree in \(\mathbf{D }\) in order to describe rate independent materials and homogeneous in \(\mathbf T \) in order to describe proportional stress paths in case of proportional strain paths. Herein, the superscript “\(^{0}\)” indicates a normalized tensor, i.e., \({ \mathbf T }^{0}:={ \mathbf T }/ |{ \mathbf T } |. {\mathring{ \mathbf T }}\) denotes the co-rotational Jaumann-Zaremba stress rate ensuring the material frame-indifference:

$$\begin{aligned} {\mathring{ \mathbf T }} = \dot{ \mathbf T } - { \mathbf W }{ \mathbf T } + { \mathbf T }{ \mathbf W } \end{aligned}$$

with \(\dot{\mathbf{T }}\) denoting the time derivative of the Cauchy stress tensor and \(\mathbf W \) being the antisymmetric part of the velocity gradient (spin tensor). The function \(\mathbf R \) expressing the directions of stress paths (see Kolymbas 2011) reads \(\mathbf R = \mathrm tr (\mathbf D ^{0}) \mathbf I + c_{1} \text{ exp } (c_{2} \mathbf D ^{0})\), where \(\mathbf I \in \mathbb R ^{3\times 3}\) denotes the identity matrix. The functions \(f, g\), and \(h\) in (3.1) are given as follows:

$$\begin{aligned} f = c_{4} \mathrm tr (\mathbf D ^{0}) + c_{5}(e-e_\mathrm c ) + c_{6},\quad g = -c_{6},\quad h = \sigma ^{c_{3}}, \end{aligned}$$

where \(c_{1},\ldots , c_{6}\) are material constants and \(e\) is the void ratio defined as the ratio \(V_\mathrm p /V_\mathrm s \), where \(V_\mathrm p \) and \(V_\mathrm s \) are the volume of pores and solids (grains), respectively. For the considered sand, the value of \(e\) ranges between \(0.63\) and \(0.9. e_\mathrm c \) denotes the critical void ratio: \(e_\mathrm c =(1+e_\mathrm c0 ) \mathrm exp \left( \frac{\sigma ^{1-c_{3}}}{c_{4}(1-c_{3})}\right) -1\) (see Desrues et al. 2000). As an example, the material constants for Hostun sand read: \(c_{1} = -1.7637, c_{2} = -1.0249, c_{3} = 0.5517, c_{4} = -1174, c_{5} = -4175, c_{6} = 2218, e_\mathrm c0 =0.8703\). Note that stresses are expressed in kPa.

4 Discrete approximation

In this section, we describe the weighted moving least squares procedure which is used to approximate spatial partial derivatives of arbitrary order on a finite pointset. The method is used in FPM (see Sect. 5) as well as SPARC (see Sect. 6).

Assume that a discrete domain \(\Gamma =\{\mathbf{x }_i\}_{i=1,\ldots ,N}\subset \mathbb{R }^3\) is given containing only a finite number \(N\in \mathbb{N }\) of points. Let \(V\) be the vector space of all functions \(f:\mathbb R ^3\rightarrow \mathbb R \). Consider the Hilbert space \(W\) with pointwise basis \(\{\varphi _j:\Gamma \rightarrow \mathbb{R }\}_{j=1,\ldots ,D}(D=\mathrm dim (W))\) as a subspace of \(V\). Our aim is to determine \(g\in W\) as an optimal (in the sense of weighted subspace projection) pointwise approximation of a pointwise given function \(f\in V\). Using the representation of \(g\) with the help of the basis \(\{\varphi _j\}_{j=1,\ldots ,D}\), the error \(\mathcal{E }\) of the weighted projection with given weight function \(w: \Gamma \rightarrow \mathbb{R }^+\) has to be minimized over the unknown coefficients \(a_j (j=1,\ldots ,D)\):

$$\begin{aligned} \mathcal E ^2&=\sum \limits _{i=1}^N\left[ w(\mathbf x _i)\left( f(\mathbf x _i)-\sum \limits _{j=1}^{D} a_j\varphi _j(\mathbf x _i)\right) \right] ^2. \end{aligned}$$
(4.1)

For clearer notation, we introduce the following matrices and vectors:

$$\begin{aligned} \mathbf W&= \left( \begin{array}{cccc} w(\mathbf x _1) &{} 0 &{} \cdots &{} 0 \\ 0 &{} w(\mathbf x _2) &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} w(\mathbf x _N) \end{array} \right) , \qquad {\varvec{\Phi }}= \left( \begin{array}{cccc} \varphi _1(\mathbf x _1) &{} \varphi _2(\mathbf x _1) &{} \cdots &{} \varphi _D(\mathbf x _1) \\ \varphi _1(\mathbf x _2) &{} \varphi _2(\mathbf x _2) &{} \cdots &{} \varphi _D(\mathbf x _2) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \varphi _1(\mathbf x _N) &{} \varphi _2(\mathbf x _N) &{} \cdots &{} \varphi _D(\mathbf x _N) \end{array} \right) ,\\ \mathbf f&= (f(\mathbf x _1), \ldots , f(\mathbf x _N))^\mathrm T , \qquad \mathbf a =(a_1, \ldots , a_D)^\mathrm T . \end{aligned}$$

We can now rephrase (4.1) as

$$\begin{aligned} \mathcal E ^2=\mathbf f ^\mathrm T \mathbf W ^2 \mathbf f - \mathbf f ^\mathrm T \mathbf W ^2 {\varvec{\Phi }}\mathbf a -\mathbf a ^\mathrm T {\varvec{\Phi }}^\mathrm T \mathbf W ^2 \mathbf f +\mathbf a ^\mathrm T {\varvec{\Phi }}^\mathrm T \mathbf W ^2{\varvec{\Phi }} \mathbf a . \end{aligned}$$

The error \(\mathcal E ^2\) is minimized if

$$\begin{aligned} \frac{\partial }{\partial \mathbf a }\mathcal E ^2=\mathbf 0 \Longleftrightarrow {\varvec{\Phi }}^\mathrm T \mathbf W ^2{\varvec{\Phi }} \mathbf a&={\varvec{\Phi }}^\mathrm T \mathbf W ^2 \mathbf f . \end{aligned}$$
(4.2)

Provided that \({\varvec{\Phi }}^\mathrm T \mathbf W ^2{\varvec{\Phi }}\) is invertible, the solution of (4.2) is given by

$$\begin{aligned} \mathbf a =({\varvec{\Phi }}^\mathrm T \mathbf W ^2{\varvec{\Phi }})^{-1} {\varvec{\Phi }}^\mathrm T \mathbf W ^2 \mathbf f =\mathbf S \mathbf f ,\quad \mathbf g = {\varvec{\Phi }} \mathbf a =(g(\mathbf x _1),\ldots ,g(\mathbf x _N))^\mathrm T . \end{aligned}$$

For brevity, we introduced the matrix \(\mathbf S =( {\varvec{\Phi }}^\mathrm T \mathbf W ^2 {\varvec{\Phi }})^{-1} {\varvec{\Phi }}^\mathrm T \mathbf W ^2\). Assuming that the \(\mathbf x _i\) are linearly independent (non-coplanar) points, the matrix \({\varvec{\Phi }}^\mathrm T \mathbf W ^2 {\varvec{\Phi }}\) is invertible if \(N\ge D\).

4.1 Expansion to continuous approximation and approximate derivatives

In the preceding paragraph we obtained \(\mathbf g \) as an optimal (in the sense of subspace projection) pointwise approximation of a pointwise function \(\mathbf f \). The vector \(\mathbf g \) was given in terms of the coefficient vector \(\mathbf a \) with respect to the pointwise basis matrix \({\varvec{\Phi }}: g(\mathbf x _i)=\sum _{j=1}^D a_j\varphi _j(\mathbf x _i), \mathbf x _i\in \Gamma \). Provided that the functions \(\varphi _j\) are defined on some continuous domain \(\Omega \supset \Gamma \), we can define a new function

$$\begin{aligned} \tilde{f}(\mathbf x )&=\sum \limits _{j=1}^D a_j\varphi _j(\mathbf x ),\qquad x\in \Omega . \end{aligned}$$

The function \(\tilde{f}\) is the interpolant of \(g\) on \(\Omega \supset \Gamma \) (since \(\tilde{f}(\mathbf x _i)=g(\mathbf x _i)\)) as well as the approximation of \(\mathbf f \) on \(\Omega \) (optimal in the sense of best projection in the discrete domain).

Given a pointwise function \(f\) on \(\Gamma \) (represented by the vector \(\mathbf f \)), derivatives of \(f\) are undefined as \(\Gamma \) consists only of a countable number of points. If suitable basis and weight functions are chosen, an optimal approximation \(\tilde{f}\) can be derived. As \(\tilde{f}\) is defined on a continuous domain \(\Omega \), derivatives of \(\tilde{f}\) are meaningful. This leads to the idea that an approximate derivative can be defined by the derivative of the approximation \(\tilde{f}: \tilde{\partial }_* f=\partial _*\tilde{f}\), where “\(*\)” is a placeholder for either \(0\) (identity/function value operator \(\partial _0\)) or derivative variables (\(\partial _1, \partial _{1,2}\), etc.). Exploiting the linearity of the differential operator \(\partial _*\), we can write

$$\begin{aligned} \tilde{\partial }_* f=\partial _*\tilde{f}=\partial _*\left( \sum _{j=1}^D\varphi _j a_j\right) = \sum _{j=1}^D \underbrace{\partial _*\varphi _j}_{(b_*)_j} a_j =\sum _{j=1}^D (b_*)_j a_j = \mathbf b ^\mathrm T _* \mathbf a = \mathbf b ^\mathrm T _* \mathbf S \mathbf f . \end{aligned}$$

The linear operator \(\tilde{\partial }_*\) is determined by two independent components, namely the vector \(\mathbf b _*\) and the matrix \(\mathbf S \). This independence can be exploited by reusing the \(\mathbf b _*\)-vectors and the matrix \(\mathbf S \) in computations on the same discrete domain and pointwise basis but with different function \(\hat{f}\).

Along the same lines, we can generalize the presented one-dimensional procedure for the multi-dimensional case which is used in FPM and SPARC. We can, e.g., define the approximate gradient operator in \(\mathbb R ^3\) for a function \(\mathbf f : \Gamma \rightarrow \mathbb R ^3\) by

$$\begin{aligned} \tilde{\nabla }\mathbf{f} = \left( {\begin{array}{l@{\quad }l@{\quad }l} {\bar{\partial }_{1} \mathbf{f _{1}}} &{} {\bar{\partial }_{1} \mathbf{f_{2}}} &{} {\bar{\partial }_{1} \mathbf{f_{3}}} \\ {\bar{\partial }_{2} \mathbf{f_{1} }} &{} {\bar{\partial }_{2} \mathbf{f_{2}}} &{} {\bar{\partial }_{2} \mathbf{f_{3}}} \\ {\bar{\partial }_{3} \mathbf{f_{1}}} &{} {\bar{\partial }_{3} \mathbf{f_{2}}} &{} {\bar{\partial }_{3} \mathbf{f_{3}}} \\ \end{array}} \right) = \left( { \begin{array}{l} {\mathbf{b}_{1}^{T} } \\ {\mathbf{b}_{2}^{T} } \\ {\mathbf{b}_{3}^{T} } \\ \end{array}}\right) \mathbf{S}\underbrace{{\left( { \begin{array}{c@{\quad }c@{\quad }c} {\left( {\mathbf{{f}}\left( {\mathbf{x}_{1} } \right) } \right) _{1} } &{} {\left( {\mathbf{f}\left( {\mathbf{x}_{1} } \right) } \right) _{2} } &{} {\left( {\mathbf{f}\left( {\mathbf{x}_{1} } \right) } \right) _{3} } \\ {\left( {\mathbf{f}\left( {\mathbf{x}_{2} } \right) } \right) _{1} } &{} {\left( {\mathbf{f}\left( {\mathbf{x}_{2} } \right) } \right) _{2} } &{} {\left( {\mathbf{f}\left( {\mathbf{{x}}_{2} } \right) } \right) _{3} } \\ \vdots &{} \vdots &{} \vdots \\ {\left( {\mathbf{f}\left( {\mathbf{x}}_{D} \right) } \right) _{1} } &{} {\left( {\mathbf{f}\left( {\mathbf{x}}_{D} \right) } \right) _{2} } &{} {\left( {\mathbf{f}\left( {\mathbf{x}}_{D} \right) }\right) _{3} } \\ \end{array} } \right) }}_\mathbf{F}. \end{aligned}$$

Note that the matrix \(\mathbf F \) plays the role of the vector \(\mathbf f \) in the one-dimensional case.

4.2 One-dimensional numerical example

The following example shows the influence of the weight function and of the basis \(\varvec{\varphi }\) on the corresponding approximation. We use the pointwise function \(\mathbf f =({-0.6,0,-0.2,2,3.4})^\mathrm T \) with \(\Gamma =({0.5, 1.6, 2.4, 3.2, 3.8})^\mathrm T \). Furthermore, the monomial bases of second and third degree, i.e., \(\varvec{\varphi }=(1,x,x^2)^\mathrm T \) and \(\varvec{\varphi }=(1,x,x^2,x^3)^\mathrm T \), are considered. We employ the truncated Gaussian weight function often used with the weighted moving least squares method adapted from (Tiwari et al. 2007):

$$\begin{aligned} w(r,h)&= \left\{ \begin{array}{l@{\quad }l} \exp \left( -\gamma \frac{r}{h}\right) -\exp \left( -\gamma \frac{1}{h}\right) &{} \hbox {if }\frac{r}{h}\le 1, \\ 0 &{} \hbox {otherwise} \end{array} \right. \end{aligned}$$
(4.3)

with \(r=|\mathbf x _i-\mathbf x |\). The second term in the first case in (4.3) is added to ensure continuity of \(w\) at the truncation points. This is important if the approximation is employed in computations with time-dependent \(\Gamma \): If a new point appears in the support of \(w\), the resulting approximations should not change abruptly. The parameter \(\gamma \) determines the speed of the decay towards zero. We use \(\gamma =6\) following (Tiwari et al. 2007). The weighting radius \(h\) (which corresponds to the radius of influence to determine the neighboring points in the meshfree methods FPM and SPARC) can be space-dependent to account for varying local densities of the points within \(\Gamma \). Larger values of \(h(\mathbf x )\) enhance the ability of the approximation to capture global trends of the pointwise function \(\mathbf f \), whereas smaller values improve the ability to capture local details. This is demonstrated in Fig. 3.

Fig. 3
figure 3

Influence of the weighting radius \(h\) (or \(\mathrm supp (w)\) in general, bottom) on the resulting approximation (continuous approximations, top) with the help of the monomial basis of a second degree and b third degree

Full size image

5 Finite pointset method

The FPM is a meshfree approach to numerically solve (coupled) PDEs based on their strong solution in a sufficiently dense cloud of points carrying the physical information (such as velocity, pressure, etc.). Since a Lagrangian formulation is used, these discrete points move with the occurring velocity field. In order to determine the required approximations of spatial partial derivatives of arbitrary order, the WMLS algorithm (which is described in Sect. 4) employing the numerical data known at the discrete points of the domain is applied. Due to the compact support of the weighting function, only the values in a defined neighborhood influence the approximations and, thus, accelerate the computation compared to simulations with global weighting functions. Time derivatives are formed by simple finite differences. Thus, FPM is a generalized finite difference method. Over the last ten years, the fields of application have steadily expanded: computational fluid dynamics (CFD), especially gas dynamics and incompressible flows (see, e.g., Hietel et al. 2005; Iliev and Tiwari 2002; Tiwari and Kuhnert 2002a, b, 2004, 2005, 2007); fluid structure interaction (see Tiwari et al. 2007); continuum mechanics, in particular plastic and visco-elasto-plastic material behavior (see Kuhnert et al. 2012).

In this contribution, we present the use of FPM to solve the coupled PDEs governed by the material law of barodesy for the oedometric and triaxial test. The numerical (discrete) formulation of the problem is described in Sect. 5.1; the necessary boundary conditions are discussed in Sect. 5.2.

5.1 Numerical model

The starting point of the numerical model is the equation of motion

$$\begin{aligned} \dot{\mathbf{v }}=\frac{1}{\rho }(\nabla ^\mathrm T \mathbf T )^\mathrm T +\mathbf g , \end{aligned}$$
(5.1)

where \(\mathbf v \in \mathbb R ^3\) denotes the velocity field, \(\rho \in \mathbb R^+ \) denotes the density, \(\mathbf T \in \mathbb R ^{3\times 3}\) denotes the Cauchy stress tensor, and \(\mathbf g \in \mathbb R ^3\) denotes the vector of body forces, respectively. Throughout this contribution, the operator \(\nabla ^\mathrm T \) denotes the divergence of the subsequent quantity.

The simple implicit model for a sufficiently dense discrete pointset \(X=\{\mathbf{x }_i\}_{i=1,\ldots ,N}\subset \mathbb{R }^3\) (\(N\in \mathbb{N }\)) and time steps \(t_n\), \(t_{n+1}=t_n+\Delta t\) is given by

$$\begin{aligned} \frac{\mathbf{v }_i^{n+1}-\mathbf{v }_i^n}{\Delta t}=\frac{1}{\rho _i}(\nabla ^\mathrm{T }\mathbf{T }_i^{n+1})^\mathrm{T }+\mathbf{g }_i. \end{aligned}$$
(5.2)

The indices \(i\) and \(n, n+1\) correspond to the index of the numerical point and of the considered time step, respectively. The determination/approximation of spatial partial derivatives such as \(\nabla ^\mathrm T \mathbf T _i^{n+1}\) at a point \(\mathbf{x }_i\) by surrounding neighbor points in a defined ball of influence with radius \(h\), called smoothing length, is based on the WMLS method described in Sect. 4.

At time step \(t_n\), we only know the current stress tensor \(\mathbf{T }_i^n\). Thus, the estimation of the future stress tensor \(\mathbf{T }_i^{n+1}\) is necessary to solve (5.2). In order to do this, we linearize the considered nonlinear constitutive law of the stress tensor (the barodesy model as described in Sect. 3) locally for each point \(\mathbf{x }_i\) and form the linearized implicit model

$$\begin{aligned} \mathbf T _i^{n+1}=\mathbf T _i^n+\Delta t\cdot \frac{1}{3}C_i^{n+1}(\nabla ^\mathrm T \mathbf v _i^{n+1})\mathbf I +\Delta t\cdot 2\mu _i^{n+1}\mathbf D _i^{n+1}. \end{aligned}$$
(5.3)

\(C\) is the compression modulus in the sense that the pressure \(p\) rises if the volume of the material is changed, i.e.,

$$\begin{aligned} \frac{dp}{dt}=-\frac{1}{3}C\nabla ^\mathrm T \mathbf v . \end{aligned}$$
(5.4)

Relation (5.4) is similar to the law of mass conservation – the density also increases if the volume is decreased:

$$\begin{aligned} \frac{d\rho }{dt}=-\rho \nabla ^\mathrm T \mathbf v . \end{aligned}$$
(5.5)

From (5.4) and (5.5) we can derive a relation which connects the compression modulus with the partial derivative of the density with respect to the pressure by \(\frac{\partial \rho }{\partial p}=\frac{3\rho }{C}\). The associated shear modulus is denoted by \(\mu \). Both the determination of the compression and the shear modulus for the considered material law of barodesy will be described below in (5.13)–(5.15). \(\mathbf D \in \mathbb R ^{3\times 3}\) is the stretching tensor, as described in Sect. 3. Due to (5.4), the linearized implicit model (5.3) can be rewritten as

$$\begin{aligned} \mathbf T _i^{n+1}=\mathbf T _i^n-(p_i^{n+1}-p_i^n)\mathbf I +\Delta t\cdot 2\mu _i^{n+1}\mathbf D _i^{n+1}. \end{aligned}$$

Assuming that the difference \(p_i^{n+1}-p_i^n=:\epsilon _i^{n+1}\) is just the correction/penalty pressure (see below for details), the above equation simplifies to

$$\begin{aligned} \mathbf T _i^{n+1}=\mathbf T _i^n-\epsilon _i^{n+1}\mathbf I +\Delta t\cdot 2\mu _i^{n+1}\mathbf D _i^{n+1}. \end{aligned}$$
(5.6)

Embedding the estimation of the future stress tensor (5.6) in the numerical model (5.2) for the velocity, we obtain

$$\begin{aligned} \frac{\mathbf{v }_i^{n+1}-\mathbf{v }_i^n}{\Delta t}=\frac{1}{\rho _i}\left( \nabla ^\mathrm{T }(\mathbf{T }_i^n-\epsilon _i^{n+1}\mathbf{I }+\Delta t\cdot 2\mu _i^{n+1}\mathbf{D }_i^{n+1})\right) ^\mathrm{T }+\mathbf{g }_i. \end{aligned}$$

After reordering, this yields

$$\begin{aligned} \frac{\mathbf{v }_i^{n+1}-\mathbf{v }_i^n}{\Delta t}+\frac{1}{\rho _i}\nabla \epsilon _i^{n+1}-\frac{1}{\rho _i}\left( \nabla ^\mathrm{T }(\Delta t\cdot 2\mu _i^{n+1}\mathbf{D }_i^{n+1})\right) ^\mathrm{T }=\frac{1}{\rho _i}(\nabla ^\mathrm{T }\mathbf{T }_i^n)^\mathrm{T }+\mathbf{g }_i. \end{aligned}$$

Defining the system viscosity by \(\hat{\eta }_i^{n+1}:=\Delta t \cdot \mu _i^{n+1}\) and the derived forces by \(\hat{\mathbf{g }}_i^n:=\frac{1}{\rho _i}(\nabla ^\mathrm T \mathbf T _i^n)^\mathrm T +\mathbf g _i\), the above equation can be simplified to

$$\begin{aligned} \frac{\mathbf{v }_i^{n+1}-\mathbf{v }_i^n}{\Delta t}+\frac{1}{\rho _i}\nabla \epsilon _i^{n+1}-\frac{1}{\rho _i}\left( \nabla ^\mathrm{T }(2\hat{\eta }_i^{n+1}\mathbf{D }_i^{n+1})\right) ^\mathrm{T }=\hat{\mathbf{g }}_i^n. \end{aligned}$$
(5.7)

The complete numerical scheme takes (5.7) and combines it with the penalty formulation we employ for any viscous flow under some compressibility constraint, i.e., the penalty pressure \(\epsilon _i^{n+1}\) is given by

$$\begin{aligned} \nabla ^\mathrm T \mathbf v _i^{n+1}+\nabla ^\mathrm T \left( \frac{\Delta t_\mathrm virt }{\rho _i}\nabla \epsilon _i^{n+1}\right) =\nabla ^\mathrm T (\mathbf{v _\mathrm tg })_i^{n+1} \end{aligned}$$
(5.8)

with virtual time step \(\Delta t_\mathrm virt \) depending on the current time step, the mean distance of the points, and the geometry (for further details see Kuhnert et al. 2012). This is in fact a Poisson equation which determines the penalty (correction) pressure in such a way that the velocity \(\mathbf v _i^{n+1}\) might be corrected towards the target velocity \((\mathbf{v _\mathrm tg })_i^{n+1}\) (depending on a constraint for its divergence) such that \(\mathbf v _i^{n+1}+\frac{\Delta t_\mathrm virt }{\rho _i}\nabla \epsilon _i^{n+1}=(\mathbf{v _\mathrm tg })_i^{n+1}\). The constraint for the divergence of the target velocity is given by the law of mass conservation (cf. (5.5)), namely \(\frac{d\rho }{dt}=\frac{\partial \rho }{\partial p}\frac{dp}{dt}=-\rho \nabla ^\mathrm T \mathbf v _\mathrm tg \). A simple implicit model yields

$$\begin{aligned} \left( \frac{\partial \rho }{\partial p}\right) _i^{n+1}\frac{p_i^{n+1}-p_i^n}{\Delta t}=\left( \frac{\partial \rho }{\partial p}\right) _i^{n+1}\frac{\epsilon _i^{n+1}}{\Delta t}=-\rho _i\nabla ^\mathrm T (\mathbf v _\mathrm tg )_i^{n+1}. \end{aligned}$$

Subsequently, we obtain

$$\begin{aligned} \nabla ^\mathrm T (\mathbf v _\mathrm tg )_i^{n+1}=\frac{1}{\rho _i}\left( \frac{\partial \rho }{\partial p}\right) _i^{n+1}\frac{\epsilon _i^{n+1}}{\Delta t}. \end{aligned}$$
(5.9)

Combining (5.8) and (5.9) gives

$$\begin{aligned} \nabla ^\mathrm T \mathbf v _i^{n+1}+\nabla ^\mathrm T \left( \frac{\Delta t_\mathrm virt }{\rho _i}\nabla \epsilon _i^{n+1}\right) -\frac{1}{\rho _i}\left( \frac{\partial \rho }{\partial p}\right) _i^{n+1}\frac{\epsilon _i^{n+1}}{\Delta t}=0. \end{aligned}$$
(5.10)

Remember, \(\left( \frac{\partial \rho }{\partial p}\right) _i^{n+1}=\frac{3\rho _i}{C_i^{n+1}}\). The resulting implicit, linear system which has to be solved is finally given by (5.7), (5.10), as well as the barodesy model for the stress tensor and the implicit formulation for the void ratio \(e\):

$$\begin{aligned} \begin{aligned}&\frac{\mathbf{v }_i^{n+1}-\mathbf{v }_i^n}{\Delta t}+\frac{1}{\rho _i}\nabla \epsilon _i^{n+1}-\frac{1}{\rho _i}\left( \nabla ^\mathrm T (2\hat{\eta }_i^{n+1}\mathbf{D }_i^{n+1})\right) ^\mathrm{T }=\hat{\mathbf{g }}_i,\\&\nabla ^\mathrm{T } \mathbf{v }_i^{n+1}+\nabla ^\mathrm{T }\left( \frac{\Delta t_\mathrm{virt }}{\rho _i}\nabla \epsilon _i^{n+1}\right) -\frac{1}{\rho _i}\left( \frac{\partial \rho }{\partial p}\right) _i^{n+1}\frac{\epsilon _i^{n+1}}{\Delta t}=0,\\&\mathbf{T }_i^{n+1}=\mathbf{T }_i^n+\Delta t\cdot ( \mathbf{W }_i^{n+1}\mathbf{T }_i^n - \mathbf{T }_i^n \mathbf{W }_i^{n+1} + \mathbf{H }(\mathbf{T }_i^n,\mathbf{D }_i^{n+1},e_i^{n+1}) ),\\&e_i^{n+1}=\frac{\Delta t\cdot \mathrm{tr }(\mathbf{D }_i^{n+1})+e_i^n}{1-\Delta t\cdot \mathrm{tr }(\mathbf{D }_i^{n+1})}, \end{aligned} \end{aligned}$$
(5.11)

where \({ \mathbf H }\) denotes the nonlinear material law of barodesy (see Sect. 3). Note that \({ \mathbf H }({ \mathbf T },{ \mathbf D },e)={ \mathring{ \mathbf T }}=\dot{ \mathbf T }-{ \mathbf W }{ \mathbf T }+{ \mathbf T }{ \mathbf W }\) is used. The first two equations are solved simultaneously for the velocity and pressure update; then, the resulting velocity is used to determine the stress tensor and the void ratio update.

Now we answer the question how to obtain the future compressibility and shear moduli from the material law of barodesy required for the linearization (5.3). First we consider the “linearized” shear modulus. The constitutive law of time evolution of the stress tensor is given by

$$\begin{aligned} \dot{\mathbf{T }}=\mathbf W \mathbf T -\mathbf T \mathbf W +\mathbf H (\mathbf T ,\mathbf D ,e). \end{aligned}$$
(5.12)

Our approach is to test this equation for a typical state and deformation. Let us assume that we know the current stress tensor \(\mathbf T _i^n\) and the current stretching tensor \(\mathbf D _i^n\) as well as the current spin tensor \(\mathbf W _i^n\). Then we can simply determine \((\mathbf D _i^n)_\mathrm{check }^{\mu }=\mathbf D ^{\star ,n}_i=\mathbf D _i^n-\frac{1}{3}\mathrm tr (\mathbf D _i^n)\mathbf I \). \((\mathbf D _i^n)_\mathrm{check }^{\mu }\) describes a pure shear deformation which does not contain compression or expansion. The constitutive law (5.12) suggests to check the growth of the stress tensor under this given shear deformation by \((\mathbf T _i^{n+1})_\mathrm{check }^{\mu }=\mathbf T _i^n+\Delta t\cdot ( \mathbf W _i^n\mathbf T _i^n -\mathbf T _i^n\mathbf W _i^n + \mathbf H (\mathbf T _i^n,(\mathbf D _i^n)_\mathrm{check }^{\mu },e_i^{n+1}((\mathbf D _i^n)_\mathrm{check }^{\mu })) )\). Eventually, there are two ways to define the future shear modulus – either

$$\begin{aligned} \mu _i^{n+1}=\frac{\Vert (\mathbf T _i^{n+1})_\mathrm{check }^{\mu } - \mathbf T _i^n\Vert _\mathrm{Mises }}{\Delta t \cdot 2 \Vert (\mathbf D _i^n)_\mathrm{check }^{\mu }\Vert _\mathrm{Mises }} \end{aligned}$$
(5.13)

or

$$\begin{aligned} \mu _i^{n+1}=\max \left( 0,\frac{\Vert (\mathbf T _i^{n+1})_\mathrm{check }^{\mu }\Vert _\mathrm{Mises } - \Vert \mathbf T _i^n\Vert _\mathrm{Mises }}{\Delta t \cdot 2 \Vert (\mathbf D _i^n)_\mathrm{check }^{\mu }\Vert _\mathrm{Mises }}\right) , \end{aligned}$$
(5.14)

where the von Mises stress norm is given by \(\Vert \mathbf T \Vert _\mathrm{Mises }^{2}=\frac{1}{2}\big (({T}_{11}-{T}_{22})^2+({T}_{22}-{T}_{33})^2+({T}_{33} -{T}_{11})^2\big )+3({T}_{12}^2+{T}_{23}^2+{T}_{31}^2)\). In the same fashion, we are able to define a checking deformation for the compression by \((\mathbf D _i^n)_\mathrm{check }^{C}=\mathbf D ^{\star ,n}_i+\frac{1}{3}\alpha \mathbf I =\mathbf D _i^n-\frac{1}{3}\mathrm tr (\mathbf D _i^n)\mathbf I +\frac{1}{3}\alpha \mathbf I \). This tensor contains regular isotropic compression with the divergence of the velocity equal to \(\alpha \in \mathbb R \) (e.g., \(\alpha =\mathrm tr (\mathbf D _i^n)\)). The quantity \(\alpha \) should be chosen suitable for the considered test scenario. Again, we can determine a fictitious value of the future stress tensor under the checking deformation by \((\mathbf T _i^{n+1})_\mathrm{check }^{C}=\mathbf T _i^n+\Delta t\cdot ( \mathbf W _i^n\mathbf T _i^n -\mathbf T _i^n\mathbf W _i^n + \mathbf H (\mathbf T _i^n,(\mathbf D _i^n)_\mathrm{check }^{C},e_i^{n+1}((\mathbf D _i^n)_\mathrm{check }^{C})) )\). The future compression modulus is then easily computed with the help of (5.4) by

$$\begin{aligned} C_i^{n+1}=\max \left( 0,\frac{\frac{1}{3}\mathrm tr ((\mathbf T _i^{n+1})_\mathrm{check }^{C})-\frac{1}{3}\mathrm tr (\mathbf T _i^n)}{\alpha \Delta t}\right) . \end{aligned}$$
(5.15)

Due to the chosen definitions in (5.13)–(5.15), it is guaranteed that the future shear and compression moduli are non-negative which prevents numerical instabilities.

Note that as the sample is homogeneous and lateral movement is hindered during the oedometric test, we have no rotations, i.e., \(\mathbf W =\mathbf 0 \). Thus, the simplified relation \(\dot{ \mathbf T }={\mathring{ \mathbf T }}={ \mathbf H }({ \mathbf T },{ \mathbf D },e)\) is valid in this case.

5.2 Boundary conditions

In this subsection, we consider the necessary boundary conditions for the two test scenarios.

5.2.1 Oedometric test

Usually, in the experimental setup a cubic test apparatus and sample are employed. The side walls and the bottom plate are rigid, whereas the upper plate is moved in axial direction, here \(x_1\)-direction, with a prescribed velocity \(v_\mathrm p \) (\(v_\mathrm p <0\) in case of loading, \(v_\mathrm p >0\) in case of unloading). For the velocity and the pressure at the side walls as well as at both plates a slip condition (ideal slip without drag) and a homogeneous Neumann condition is used, respectively.

5.2.2 Triaxial test

Due to the geometry of the considered triaxial test, we have two types of boundaries in this scenario. On the one hand, we are confronted with the boundary representing the contact of the sample with the upper plate compressing it and the fixed bottom plate. The top and the bottom of the sample are lubricated in order to reduce friction. Thus, a slip condition representing ideal slip without drag should be used for the velocity at the upper and bottom plates. Furthermore, the upper plate is moved down with a prescribed velocity \(v_\mathrm p <0\) in \(x_1\)-direction, whereas the bottom plate is fixed. For the pressure we assume that the derivative in normal direction is equal to zero at both plates, i.e., a homogeneous Neumann condition has to be satisfied. On the other hand, we have a free surface which corresponds to the curved surface of the sample/membrane which is subject to the confining pressure \(\sigma _\mathrm c \in \mathbb R ^+\) (see also Sect. 2.2). Let us suppose at time step \(t_n\) the vector \(\mathbf n _i\in \mathbb R ^3\) is the surface normal at a free surface point \(\mathbf x _i\). The vectors \(\mathbf a _i,\mathbf b _i\in \mathbb R ^3\) are mutually perpendicular vectors which are tangential to the free surface at \(\mathbf x _i\). The unknown future stress tensor \(\mathbf T _i^{n+1}\) has to satisfy at least the following conditions:

$$\begin{aligned} \mathbf a _i^\mathrm T \mathbf T _i^{n+1}\mathbf n _i=0,\quad \mathbf b _i^\mathrm T \mathbf T _i^{n+1}\mathbf n _i=0,\quad \mathbf n _i^\mathrm T \mathbf T _i^{n+1}\mathbf n _i=-\sigma _\mathrm c . \end{aligned}$$
(5.16)

These conditions imply that there are no shear stresses at the free surface and that the component normal to the free surface is equal to the applied confining pressure. The future stress tensor is determined by a simple implicit method analogous to the ones used to compute the “linearized” shear and compression moduli (see Sect. 5.1). The task is now to find \(\mathbf D _i^{n+1}\) such that the conditions (5.16) are satisfied. As \(\mathbf D _i^{n+1}\) has six independent components, we additionally require

$$\begin{aligned} \begin{aligned} \mathbf a _i^\mathrm T \mathbf D _i^{n+1}\mathbf a _i&=\mathbf a _i^\mathrm T \mathbf D _i^n\mathbf a _i,\quad \mathbf b _i^\mathrm T \mathbf D _i^{n+1}\mathbf b _i=\mathbf b _i^\mathrm T \mathbf D _i^n\mathbf b _i,\\ \mathbf a _i^\mathrm T \mathbf D _i^{n+1}\mathbf b _i&=\mathbf a _i^\mathrm T \mathbf D _i^n\mathbf b _i, \end{aligned} \end{aligned}$$
(5.17)

i.e., we retain the \((\mathbf a _i,\mathbf b _i)\)-components of the deformation tensor of the current time step. After the determination of \(\mathbf D _i^{n+1}\) by (5.16) and (5.17), e.g., with the help of the Newton iteration method, we can finally derive conditions for the future velocity \(\mathbf v _i^{n+1}\) at the free surface:

$$\begin{aligned} \begin{aligned} \frac{\partial (\mathbf n _i^\mathrm T \mathbf v _i^{n+1})}{\partial \mathbf n }-\frac{1}{3}\nabla ^\mathrm T \mathbf v _i^{n+1}&=\mathbf n _i^\mathrm T \mathbf D _i^{n+1}\mathbf n _i,\\ \frac{1}{2}\left( \frac{\partial (\mathbf a _i^\mathrm T \mathbf v _i^{n+1})}{\partial \mathbf n }+\frac{\partial (\mathbf n _i^\mathrm T \mathbf v _i^{n+1})}{\partial \mathbf a }\right)&=\mathbf a _i^\mathrm T \mathbf D _i^{n+1}\mathbf n _i,\\ \frac{1}{2}\left( \frac{\partial (\mathbf b _i^\mathrm T \mathbf v _i^{n+1})}{\partial \mathbf n }+\frac{\partial (\mathbf n _i^\mathrm T \mathbf v _i^{n+1})}{\partial \mathbf b }\right)&=\mathbf b _i^\mathrm T \mathbf D _i^{n+1}\mathbf n _i. \end{aligned} \end{aligned}$$
(5.18)

The three linear conditions (5.18) are well applicable to solve the system (5.11).

6 Soft PARticle code

In this section, we first discuss the numerical formulation used in SPARC (see Sect. 6.1); the chosen boundary conditions are presented in Sect. 6.2. A short comparison of FPM and SPARC can be found in Sect. 6.3.

6.1 Numerical model

The Soft PARticle Code (SPARC) is a new particle-based numerical simulation method in which a continuum is represented by a number of particles (similar to the FPM approach, see Sect. 5). These particles are mass points and carry the physical information of the material, such as density (\(\rho \)), void ratio (\(e\)), Cauchy stress tensor (\(\mathbf T \)), velocity (\(\mathbf v \)), position (\(\mathbf x \)), etc. The word “soft” indicates that the boundaries between particles are not conceived as those in discrete element methods, where each particle has exact size, shape, and boundary as well as contact laws governing the interactions with neighboring particles. Instead, in SPARC, each particle \(i\) has a set of neighboring particles (support) and Cauchy’s equation of motion governs the movement of this particle (see also (5.1)), i.e.,

$$\begin{aligned} \dot{\mathbf{v }}_i=\frac{1}{\rho _i}(\nabla ^\mathrm T \mathbf T _i)^\mathrm T +\mathbf g _i. \end{aligned}$$
(6.1)

Just like in FPM, the neighboring particles provide the necessary information for computing the spatial derivatives of quantities at particle \(i\) (e.g., \(\nabla ^\mathrm T \mathbf T _i\)) with the help of the WMLS method described in Sect. 4.

Equation (6.1) is solved using the implicit method:

$$\begin{aligned} \frac{\mathbf{v }_i^{n+1}-\mathbf{v }_i^n}{\Delta t}=\frac{1}{\rho _i^n}(\nabla ^\mathrm{T }\mathbf{T }_i^{n+1})^\mathrm{T }+\mathbf{g }_i. \end{aligned}$$

The velocity of a particle is known at the current time step \(n\). Given kinematic boundary conditions, the unknown velocity at the future time step \(n+1\) can be obtained by the following process.

  • Step 1. Compute the future stress tensor for each particle. First the velocity gradient tensor \(\mathbf L _i^n\) is calculated from the current velocity field in the support using the described WMLS algorithm:

    $$\begin{aligned} \mathbf{L }_i^n = \nabla (\mathbf{v }_i^n)^\mathrm{T }. \end{aligned}$$

    The stretching tensor \(\mathbf D _i^n\) and the spin tensor \(\mathbf W _i^n\), which account for the deformation and rotation rates, respectively, are the symmetric and antisymmetric parts of the velocity gradient (cf. Sect. 3):

    $$\begin{aligned} \mathbf{D }_i^n = \frac{\mathbf{L }_i^n+(\mathbf{L }_i^n)^\mathrm{T }}{2},\quad \mathbf{W }_i^n = \frac{\mathbf{L }_i^n-(\mathbf{L }_i^n)^\mathrm{T }}{2}. \end{aligned}$$

    The constitutive model accounting for the material behavior, here, barodesy (see Sect. 3), is then used for predicting the rate of the stress tensor (\(\dot{\mathbf{T }}\)). Thus, the stress tensor at future time step \(n+1\) is obtained by the explicit method

    $$\begin{aligned} \mathbf T _i^{n+1} = \mathbf T _i^n + \Delta t \cdot ( \mathbf W _i^n\mathbf T _i^n-\mathbf T _i^n\mathbf W _i^n+ \mathbf H (\mathbf T _i^n,\mathbf D _i^n,e_i^n) ). \end{aligned}$$

  • Step 2. Solve the nonlinear system of equations for the future velocity. In (6.1), the term \(\nabla ^\mathrm T \mathbf T _i^{n+1}\) is determined using the WMLS method. This results in a nonlinear system of equations which has to be solved for the unknown future velocity:

    $$\begin{aligned} \mathbf v _i^{n+1}&= \mathbf v _i^n+\Delta t \cdot \frac{1}{\rho _i^n}\left( \nabla ^\mathrm T (\mathbf T _i^n+\Delta t \cdot ( \mathbf W _i^n\mathbf T _i^n-\mathbf T _i^n\mathbf W _i^n+ \mathbf H (\mathbf T _i^n,\mathbf D _i^n,e_i^n)) ) \right) ^\mathrm{T }\\&\quad +\Delta t \cdot \mathbf g _i, \end{aligned}$$

    \(i=1,\ldots ,N\) (\(N\in \mathbb N \) is the number of particles). This is done with the help of the Newton iteration method.

The described process shows that SPARC is a meshfree generalized finite difference method using the strong formulation for solving PDE (6.1). The future position, void ratio, and density are computed after obtaining the solution for the future velocity \(\mathbf v _i^{n+1}\):

$$\begin{aligned} \mathbf x _i^{n+1} = \mathbf x _i^n + \Delta t \cdot \mathbf v _i^{n+1},\quad e_i^{n+1} = e_i^n + \Delta t \cdot (1+e_i^n) \nabla ^\mathrm T \mathbf v _i^{n+1}. \end{aligned}$$

Note that \(\nabla ^\mathrm T \mathbf v _i^{n+1}\) is calculated using the vector field in the support of particle \(i\) in the WMLS procedure. The balance of mass (\(\dot{\rho } + \rho \nabla ^\mathrm T \mathbf v = 0\)) yields

$$\begin{aligned} \rho _i^{n+1}&= \rho _i^n - \Delta t \cdot \rho _i^n \cdot \nabla ^\mathrm T \mathbf v _i^{n+1}. \end{aligned}$$

As discussed in Sect. 5.1, \(\mathbf{W }=\mathbf{0 }\) and, hence, \(\dot{\mathbf{T }}=\mathring{\mathbf{T }}=\mathbf{H }(\mathbf{T },\mathbf{D },e)\) for the oedometric test.

6.2 Boundary conditions

The chosen boundary conditions are described in this section for the considered test scenarios.

6.2.1 Oedometric test

The simulation of the oedometric test is performed in \(\mathbb R ^3\), where \(\mathbf e _i\) for \(i=1,2,3\) denote the canonic basis vectors. Here, \(\mathbf e _1\) is defined as the vertical direction along which the upper plate moves. As the side walls of the specimen container are considered rigid, instead of using a cylindrical specimen, the oedometric test can also be simulated by using a cube filled with soft particles (cf. Sect. 5.2.1). For particles at the upper plate and at the bottom of the sample, the velocity component along \(\mathbf e _1\) is prescribed as \(v_\mathrm p \) and \(0\), respectively. \(v_\mathrm p \) is the given speed of the upper plate. For particles at the side walls with \(\mathbf e _j\) (\(j=2,3\)) as their normal vectors, due to the constrained lateral deformation, the velocity components \(v_j\) \((j=2,3)\) are prescribed as \(0\).

6.2.2 Triaxial test

As more complicated boundary conditions are present in the case of the triaxial test, the cylindrical shape of the sample is modeled in the simulation. For particles at the upper and bottom plate, the velocity component along the axial direction is prescribed as in the case of the oedometric test. Due to the balance of forces, Cauchy’s equation has to be satisfied for particles at the membrane/free surface:

$$\begin{aligned} \mathbf t = \mathbf T \cdot \mathbf n , \end{aligned}$$
(6.2)

where the stress vector \(\mathbf t \) is always normal to the membrane surface with normal vector \(\mathbf n \) and \(\mathbf t =-\sigma _\mathrm c \mathbf n \) is satisfied. As the confining pressure is constant during the test (see also Sect. 2.2), the time rate change of the stress vector is given by \(\dot{\mathbf{t }} = -\sigma _\mathrm c \dot{\mathbf{n }}\). As a result, instead of (6.2) the following condition is prescribed for all particles at the membrane:

$$\begin{aligned} \dot{\mathbf{T }}\cdot \mathbf n + \mathbf T \cdot \dot{\mathbf{n }} = -\sigma _\mathrm c \dot{\mathbf{n }}. \end{aligned}$$

6.3 Comparison of FPM and SPARC

Compared to the procedure used in FPM (see Sect. 5), the explicit determination of the future stress tensor in SPARC undoes the necessity of local linearization (cf. (5.3)). However, the resulting system for the future velocity is nonlinear. The solution of this system requires more computing time than a comparable linear one in FPM.

Regarding the numerical implementation, it can be observed that also for the triaxial test both FPM and SPARC yield almost exactly the same numerical results when only \({\mathring{{ \mathbf T }}}=\dot{ \mathbf{T }}\) is used, i.e., rotations are not removed, instead of taking into account the objective time rate \({\mathring{ \mathbf T }}=\dot{ \mathbf T }-{ \mathbf W }{ \mathbf T }+{ \mathbf T }{ \mathbf W }\) with rotations of the observer or of the reference frame removed (see Kolymbas 2011, 2012) as described above. This will be discussed in more detail in “Part II: Numerical Examples” of this contribution.

7 Conclusion

In order to classify different soils and verify new material laws, standard laboratory tests are used in soil mechanics. We presented two meshfree approaches—FPM and SPARC—to simulate two standard benchmark problems in soil mechanics, namely the oedometric and the triaxial test. Meshfree techniques have the advantage that there are no fixed connectivities among the points representing the domain. Only the information of points in a radius of influence is required in our methods.

The presented material law of barodesy (for sand) reflects the anelastic behavior of the material and the nonlinear dependence of the time rate of the stress tensor from the symmetric part of the velocity gradient/strain tensor. Both meshfree methods solve the occurring PDEs in the strong form. Thus, spatial partial derivatives of different orders have to be determined for any point of the finite pointset representing the domain. The approximation of these derivatives at a certain point is done with the help of a weighted moving least squares procedure only incorporating a restricted neighborhood of the considered point.

In the approach based on FPM, the physical model is solved with a fully implicit ansatz which necessitates the local linearization of the stress tensor including the determination of corresponding shear and compression moduli. In case of the triaxial test, the prescribed boundary condition at the free surface is obtained with the help of the Newton iteration method. In contrast to the linear system that has to be solved in the FPM approach, the method used in SPARC leads to a nonlinear system for the velocity which can be solved with the Newton iteration method: The stress tensor is determined explicitly, thereafter the velocity is determined implicitly employing the result of the stress tensor integration.

The theoretical description of the presented methods will be complemented by a discussion of numerical results in “Part II: Numerical Examples” of this contribution including separate studies on the critical parameters for the two meshfree methods, a comparison of the results of the FPM and SPARC simulations, as well as a comparison of the best simulation results for each method with the corresponding results of the laboratory test.