Some novel distance and similarity measures for probabilistic dual hesitant fuzzy sets and their applications to MAGDM

Abstract

Probabilistic dual hesitant fuzzy set is a more powerful and important tool to express uncertain information. As we all know, the distance and similarity measures are very useful tool in decision-making field. In this study, the distance measure and similarity measure of probabilistic dual hesitation fuzzy set are systematically proposed from the perspectives of discrete and continuous, ordered and unordered, which provides a theoretical support for the research of decision-making problems in probabilistic dual hesitation fuzzy environment. Firstly, we proposed some novel distance and similarity degrees for two probabilistic dual hesitant fuzzy sets and their weighted forms. Secondly, we proposed a decision technique based on the novel built weighted distance and similarity measures to solve the multi-attribute group decision-making problem in the PDHF environment. Finally, the proposed technique was applied to the suitability evaluation of new urbanization. Meanwhile, the technique built in this study was compared with the existed methods to verify the practicability and feasibility, and the superiorities of the built in this study were put forward, which has a better effect in solving multi-attribute group decision-making problems.

1 Introduction

Due to uncertainty of people’s cognition for the objective world and the objective needs, to deal with these problems with uncertain information, accordingly, the fuzzy set (FS) was built by Zadeh [1]. With the development of FS and its extensions, it has been applied in many fields, scholars have proposed different decision-making (DM) methods [2,3,4,5,6] for the problems they have solved. Since it was proposed, many scholars have studied and extended FS in detail, and put forward different dimensional FSs [7,8,9] from different perspectives on the basis of FS. Atanassov, Atanassov and Gargov, [10, 11] proposed intuitionistic FS (IFS) and interval IFS (IVIFS) depend on FS, they include two aspect of membership degree (MD) and non-membership degree (NMD), it is more in line with people’s cognition of things, some scholars put forward some interesting DM methods [12,13,14,15] and applied them to practical problems. but these FSs can’t reflect the situation that the DM gives multiple possible values to the decision object, in order to better reflect this situation, Torra [16] proposed the hesitant FS (HFS), and the its MD contains several possible values, some scholars put forward some DM methods [17,18,19,20,21,22] for HFS and applied them to some real problems. Zhu et al. [23] proposed the dual HFS (DHFS) based on HFS. It contains not only MD but also NMD. Both MD and NMD are composed of several possible values, it is found that IFS and IVIFS are special cases of DHFS.

According to some actual situations in real life, DHFS can’t reflect the probability information of MD and NMD, some DM methods [24,25,26,27,28,29,30,31] are proposed for DHFS and applied to some real problems. Based on this, Hao et al. [32] introduces probability into DHFS, put forward the probabilistic DHFS (PDHFS) and probabilistic dual hesitant fuzzy element (PDHFE), and gave the basic operation laws, at the same time, two PDHFEs are compared by using the score and deviation degree of PDHFE, and the calculation formula of entropy of PDHFE was given. Since the PDHFS was put forward, there have been some studies on the PDHFS, some novel multi-attribute decision-making (MADM) and multi-attribute group decision-making (MAGDM) methods have been built. Zhao et al. [33] gave the DM technique by PROMETHEE-II method to solve PDHF MCGDM problem. Garg and Kaur [34] presented a correlation coefficient for PDHFS, and applied the decision method to project managers’ evaluation of a software company. Ren et al. [35] extended conventional TODIM method to PDHF environment and it was applied to enterprise strategic assessment. Zhang et al. [36] presented a MAGDM model with MULTIMOORA and applied it to the evaluation of the P-J fit algorithm. Garg and Kaur [37] applied the MSM operator to PDHF environment to solve the medical diagnosis problem. Although there have been some studies on the DM methods for PDHFS, on the whole, there are few studies on DM method under PDHF setting.

Distance and similarity measures are very important concepts in some MAGDM problems, from the literatures, there have been many studies on distance and similarity measures for multifarious extended FSs. For example, distance and similarity measures of FS [38, 39]. Distance and similarity measures of IFS and IVIFS [40, 41]. Distance and similarity measures of HFS [42,43,44,45,46,47]. Distance and similarity measures of DHFS [48, 49].

Through literatures reviewed, we find that there are few studies on the distance and similarity measures of PDHFS. Ren et al. [35] studied the distance of PDHFS, in this study, two PDHFEs with different probability distributions are transformed into PDHFEs with the same probability distribution by probability splitting algorithm. Thus, the distance between two PDHFEs is calculated, but the calculation method is more complex. Garg and Kaur [50] also defined the distance between two PDHFEs, but from the definition of distance, the distance calculated according to this distance formula will be smaller than the real distance. The distance proposed in the paper is a generalization of the famous Hamming distance, Euclidean distance and Hausdorff metric, which is more representative and will not change the original value of the distance. Moreover, the calculation method is simple. At the same time, the systematic research is carried out for discrete and continuous cases, ordered and unordered cases, which plays a basic theoretical support for the research of distance and similarity measures in PDHF environment, which will play a very important role in the MADM/MAGDM whose decision information is PDHFS.

Therefore, the ultimate goal of this study is to systematically propose the distance measure and similarity measure between two PDHFS, and propose a novel MAGDM technique based on these distance measures and similarity measures. Finally, by applying the novel MAGDM technique to evaluate the sustainability of new urbanization, the flexibility of the proposed MAGDM technique is verified by parameter analysis, and the effectiveness of the proposed MAGDM technique is verified by comparative analysis with existing decision-making methods.

The motivation of this paper as follows: (1) In the increasingly complex decision-making environment, it is very important to obtain evaluation information effectively. PDHFS can more comprehensively and extensively express the preference information of decision makers (DMs). (2) We can find the famous Hamming distance, Euclidean distance, Hausdorff metric have been successfully extended into many fuzzy setting, we divide the distance into discrete and continuous cases, ordered and unordered cases, and extend the several famous distance measures to PDHF setting. (3) The existing distance does not take into account the psychological behavior of decision-makers. It is necessary to propose some novel distance measures that not only meets the axiomatic definition of distance measure, but also reflects the psychological behavior of decision-makers. (4) It is very important to evaluate the sustainability of new urbanization, which can play the most basic theoretical support for relevant departments on how to better develop new urbanization. Unscientific evaluation methods will lead to incalculable wrong results. (5) Finally, the flexibility of the proposed MAGDM technique is verified by parameter analysis, and the effectiveness of the proposed MAGDM technique is verified by comparative analysis with existing decision-making methods.

The main contributions of this paper are as follow: (1) Before defining the distance and similarity measures, axiomatic definitions of the distance and similarity measures between two PDHFSs are proposed. (2) The famous Hamming distance, Euclidean distance and Hausdorff metric are extended to the PDHF environment, and some distance measures with very interesting properties are proposed. At the same time, some similarity measures are proposed according to the relationship between distance and similarity measures. (3) Some distance measures put forward fully consider the psychological behavior of decision-makers, and make decision-makers more flexible in the process of use. (4) parameter analysis verifies the flexibility of the proposed technique and the comparative analysis with the existing methods further proves the effectiveness and superiority of the proposed technique. (5) the proposed approach gives DMs more options in dealing with uncertain problems and provides some reference for the further extension of these distance and similarity measures method in other decision environments.

The rest parts are listed in the following. Section 2 reviewed some basic concepts about PDHFS and some classical distance measures. In Sect. 3, some novel concepts for PDHFE were defined, and some novel distance measures (unordered and ordered distance measures) for PDHFE were proposed, these novel works laid a solid foundation for proposing the distance measures for PDHFS; Sect. 4 proposed the distance measures of PDHFS in eight cases on the basis of Sect. 3; Sect. 5 proposed some similarity measures for PDHFE based on the distance measures proposed in Sect. 4; In Sect. 6, the similarity measures proposed above were applied to the suitability evaluation of new urbanization, and compared with the existed MADM methods, which showed the effectiveness of the study; Sect. 7 analyzed the advantages and puts forward the advantages of the study; In Sect. 8, some conclusions and future works were put forward.

2 Preliminaries

2.1 Probabilistic dual hesitant fuzzy set

In the subsection, we will review some basic conception, score function, accuracy function, comparison method and aggregation operator for PDHFS.

Definition 1

[32]. Let $X$ be a fixed set, a PDHFS on $X$ is recorded as:

$$P = \left\{ {\left. {\left\langle {x,\left. {h\left( x \right)} \right|p\left( x \right),\left. {g\left( x \right)} \right|q\left( x \right)} \right\rangle x \in X} \right|} \right\}$$

(1)

The components $\left. {\hbar \left( \ell \right)} \right|\tau \left( \ell \right)$ and ${\lambda\kern-8pt^{-}} (\ell) | \upsilon (\ell)$ are some possible elements of MD and NMD, where $\hbar \left( \ell \right)$ and ${\lambda\kern-8pt^{-}} \left( \ell \right)$ are the MD and NMD of $\ell \in X$, respectively. $\tau \left( \ell \right)$ and $\upsilon \left( \ell \right)$ are the probabilistic information for $\hbar \left( \ell \right)$ and ${\lambda\kern-8pt^{-}} \left( \ell \right)$. Meanwhile,

$$0 \le \gamma ,\eta \le 1,\quad 0 \le \gamma^{ + } + \eta^{ + } \le 1,$$

(2)

and

$$p_{i} \in \left[ {0,1} \right],\;q_{j} \in \left[ {0,1} \right],\;\sum\limits_{i = 1}^{\# h} {p_{i} } = 1,\;\sum\limits_{i = 1}^{\# g} {q_{i} } = 1,$$

(3)

where $\gamma \in \hbar \left( \ell \right)$, $\eta \in {\lambda\kern-8pt^{-}} \left( \ell \right)$, $\gamma^{ + } \in \hbar^{ + } \left( x \right) = \cup_{\gamma \in \hbar \left( x \right)} \max \left\{ \gamma \right\}$, ${\eta ^ + } \in {{\lambda\kern-8pt^{-}} ^ + }\left( x \right) = { \cup _{\gamma \in {\lambda\kern-8pt^{-}} \left( x \right)}}\max \left\{ \eta \right\}$, $\tau_{i} \in \tau \left( \ell \right)$ and $\upsilon_{i} \in \upsilon \left( \ell \right)$. The symbols $\# \hbar$ is the number of elements in the components $\left. {\hbar \left( \ell \right)} \right|\tau \left( \ell \right)$, the symbols $\# {\lambda\kern-8pt^{-}}$ is the number of elements in $\left. {{\lambda\kern-8pt^{-}} \left( \ell \right)} \right|\upsilon \left( \ell \right)$.

In order to be more convenient in the process of use and calculation, the pair $p = \left\langle {\left. {h\left( x \right)} \right|p\left( x \right),\left. {g\left( x \right)} \right|q\left( x \right)} \right\rangle$ is called as the PDHFE [32], denoted by $p = \left\langle {\left. h \right|p,\left. g \right|q} \right\rangle$.

Under conditions $0 < \sum\nolimits_{i = 1}^{\# h} {p_{i} } < 1$ and $0 < \sum\nolimits_{i = 1}^{\# g} {q_{i} } < 1$, the decision-making offers only partial information, in view of this situation, we need to normalize the PDHFS by the following formula [32]:

$$P = \left\{ {\left. {\left\langle {x,\left. {h\left( x \right)} \right|p\left( x \right),\left. {g\left( x \right)} \right|q\left( x \right)} \right\rangle x \in X} \right|} \right\}$$

(4)

where the elements in $p\left( x \right)$ and $q\left( x \right)$ are calculated by $p\left( x \right) = {{p_{i} } \mathord{\left/ {\vphantom {{p_{i} } {\sum\nolimits_{i = 1}^{\# h} {p_{i} } }}} \right. \kern-\nulldelimiterspace} {\sum\nolimits_{i = 1}^{\# h} {p_{i} } }}$ and $q\left( x \right) = {{q_{i} } \mathord{\left/ {\vphantom {{q_{i} } {\sum\nolimits_{i = 1}^{\# h} {q_{i} } }}} \right. \kern-\nulldelimiterspace} {\sum\nolimits_{i = 1}^{\# h} {q_{i} } }}$, respectively.

In order to compare the size of two PDHFEs, Hao et al. [32] defined the score function, Xu and Zhou [51] defined the accuracy function of PDHFE.

Definition 2

[32]. Let $p = \left\langle {\left. h \right|p,\left. g \right|q} \right\rangle$ be a PDHFE, then the score function for PDHFE is defined as:

$$S\left( p \right) = \sum\limits_{i = 1\;\gamma \in h}^{\# h} {\gamma_{i} \cdot p_{i} } - \sum\limits_{j = 1\;\gamma \in g}^{\# g} {\eta_{j} \cdot q_{j} }$$

(5)

Definition 3

[51]. Let $p = \left\langle {\left. h \right|p,\left. g \right|q} \right\rangle$ be a PDHFE, the accuracy function for PDHFE is defined as:

$$H\left( p \right) = \sum\limits_{i = 1\;\gamma \in h}^{\# h} {\gamma_{i} \cdot p_{i} } { + }\sum\limits_{j = 1\;\gamma \in g}^{\# g} {\eta_{j} \cdot q_{j} }$$

(6)

Xu and Zhou [51] proposed the method used to compare the size of two PDHFEs as follows.

Definition 4

[51]. Let $p_{i} \left( {i = 1,2} \right)$ be two PDHFEs, $S\left( {p_{i} } \right)\left( {i = 1,2} \right)$ and $H\left( {p_{i} } \right)\left( {i = 1,2} \right)$ are the score function and accuracy function, respectively. Then.

• 1. If $S\left( {p_{1} } \right) > S\left( {p_{2} } \right)$, then the PDHFE $p_{1}$ is superior to $p_{2}$, denoted by $p_{1} > p_{2}$; On the contrary, there is $p_{1} < p_{2}$.

• 2. If $S\left( {p_{1} } \right) = S\left( {p_{2} } \right)$, then

  • (1) If $H\left( {p_{1} } \right) < H\left( {p_{2} } \right)$, the PDHFE $p_{1}$ is superior to $p_{2}$, denoted by $p_{1} > p_{2}$;

  • (2) If $H\left( {p_{1} } \right) > H\left( {p_{2} } \right)$, the PDHFE $p_{1}$ is inferior to $p_{2}$, denoted by $p_{1} < p_{2}$;

  • (3) If $H\left( {p_{1} } \right) = H\left( {p_{2} } \right)$, the PDHFE $p_{1}$ is equal to $p_{2}$, denoted by $p_{1} = p_{2}$.

How to use the information aggregation operator to effectively aggregate the information provided by decision-maker for better decisions is very important, Hao et al. [32] defined the PDHF weighted averaging operator.

Definition 5

[32]. Let $p_{i} = \left\langle {\left. {h_{i} } \right|p_{{h_{i} }} ,\left. {g_{i} } \right|q_{{g_{i} }} } \right\rangle \left( {i = 1,2, \cdots ,n} \right)$ be $n$ PDHFEs and $\omega_{j} \left( {j = 1,2, \cdots ,n} \right)$ be the weight with $\omega_{j} \in \left[ {0,1} \right]\left( {j = 1,2, \cdots ,n} \right)$ and $\sum\nolimits_{j = 1}^{n} {\omega_{j} } = 1$. Then the PDHFWA operator is defined as:

$$\begin{gathered} PDHFWA\left( {P_{1} ,P_{2} , \cdots ,P_{n} ,} \right){ = }\mathop \oplus \limits_{j = 1}^{n} \omega_{j} p_{j} \hfill \\ { = }\mathop \cup \limits_{\begin{subarray}{l} \gamma_{1} \in h_{1} ,\gamma_{2} \in h_{2} , \cdots ,\gamma_{n} \in h_{n} \\ \eta_{1} \in g_{1} ,\eta_{2} \in g_{2} , \cdots ,\eta_{n} \in g_{n} \end{subarray} } \left\{ {\left\{ {\left. {\left( {1 - \mathop \Pi \limits_{i = 1}^{n} \left( {1 - \gamma_{i} } \right)^{{\omega_{i} }} } \right)} \right|\mathop \Pi \limits_{i = 1}^{n} p_{{\gamma_{i} }} } \right\},\left\{ {\left. {\left( {\mathop \Pi \limits_{j = 1}^{n} \eta_{j}^{{\omega_{j} }} } \right)} \right|\mathop \Pi \limits_{j = 1}^{n} q_{{\eta_{i} }} } \right\}} \right\} \hfill \\ \end{gathered}$$

(7)

2.2 Some classical distance measures

In the field of scientific research, distance and similarity measures are very important tools, which are widely used in important decision-making problems such as machine learning, pattern recognition, bilateral matching and so on. In most studies, the distance for two fuzzy sets $A$ and $B$ on $X = \left\{ {x_{1} ,x_{2} , \cdots ,x_{n} } \right\}$ mainly includes the following distance measures, here we give several distance measures [52,53,54]:

• (1) The Hamming distance: $h\left( {A,B} \right) = \sum\nolimits_{i = 1}^{n} {\left| {\mu_{A} \left( {x_{i} } \right) - \mu_{B} \left( {x_{i} } \right)} \right|}$.

• (2) The normalized Hamming distance: $h_{n} \left( {A,B} \right) = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left| {\mu_{A} \left( {x_{i} } \right) - \mu_{B} \left( {x_{i} } \right)} \right|}$.

• (3) The Euclidean distance: $e\left( {A,B} \right) = \left( {\sum\nolimits_{i = 1}^{n} {\left( {\mu_{A} \left( {x_{i} } \right) - \mu_{B} \left( {x_{i} } \right)} \right)^{2} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}$.

• (4) The normalized Euclidean distance: $e_{n} \left( {A,B} \right) = \left( {\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {\mu_{A} \left( {x_{i} } \right) - \mu_{B} \left( {x_{i} } \right)} \right)^{2} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}$.

• (5) The Hausdorff metric: $h_{m} \left( {A,B} \right) = \max \left| {\mu_{A} \left( {x_{i} } \right) - \mu_{B} \left( {x_{i} } \right)} \right|$

where $\mu_{A} \left( {x_{i} } \right)$ and $\mu_{B} \left( {x_{i} } \right)$ represent the MD of $A$ and $B$, and satisfy condition $0 \le \mu_{A} \left( {x_{i} } \right),\mu_{B} \left( {x_{i} } \right) \le 1$.

3 Some distance measures between PDHFEs

Since PDHFS is different from existing FSs, the existing distance measures of various FSs can’t calculate the distance between two PDHFSs. Hence, this chapter will solve this problem.

From the literatures review, most studies on distance measure have given the axiomatic definition for distance measure. Next, before giving the distance measure between two PDHFSs, we first built the axiomatic definition of distance measure for two PDHFEs.

Definition 6

Let $\tau = \left\langle {\left. {h_{\tau } } \right|p_{\tau } ,\left. {g_{\tau } } \right|q_{\tau } } \right\rangle$ and $\upsilon = \left\langle {\left. {h_{\upsilon } } \right|p_{\upsilon } ,\left. {g_{\upsilon } } \right|q_{\upsilon } } \right\rangle$ be two PDHFSs, then $d\left( {\tau ,\upsilon } \right)$ is named as distance measure between two PDHFEs, if $d\left( {\tau ,\upsilon } \right)$ satisfies:

• (A1) $0 \le d\left( {\tau ,\upsilon } \right) \le 1$;

• (A2) $d\left( {\tau ,\upsilon } \right) = 0$ if and only if $\tau = \upsilon$;

• (A3) $d\left( {\tau ,\upsilon } \right) = d\left( {\upsilon ,\tau } \right)$.

Remark 1

For two different PDHFEs, if the lengths of two PDHFEs are different, the shorter PDHFE should be extended by adding the minimum element under pessimistic criterion until the two PDHFEs have the same length, adding the maximum element under the optimism criterion, and the probability of those added elements is equal to zero. In fact, we can extend the shorter PDHFE by adding any element according to the preference and actual situation of the decision-maker until it has the same length as the longer PDHFE.

Remark 2

Some definitions of deviation degree under different cases.

• (1) The deviation degree in discrete unordered case:

  If $\# \left( {\left. {h_{\tau } } \right|p_{\tau } } \right) = \# \left( {\left. {h_{\upsilon } } \right|p_{\upsilon } } \right) = \Phi$ and $\# \left( {\left. {g_{\tau } } \right|q_{\tau } } \right) = \# \left( {\left. {g_{\upsilon } } \right|q_{\upsilon } } \right) = \Psi$, then the discrete unordered deviation degrees of MD and NMD from PDHFEs $\tau$ to $\upsilon$ are defined as follows:

  The discrete unordered deviation degree of MD:

  $$p_{DUMD} \left( {\tau ,\upsilon } \right){ = }\left| {h_{\tau }^{j} p_{\tau }^{j} - h_{\upsilon }^{j} p_{\upsilon }^{j} } \right|$$

  The discrete unordered deviation degree of NMD:

  $$p_{DUNMD} \left( {\tau ,\upsilon } \right){ = }\left| {g_{\tau }^{j} q_{\tau }^{j} - g_{\upsilon }^{j} q_{\upsilon }^{j} } \right|$$

• (2) The deviation degree in discrete ordered case:

  If $\# \left( {\left. {h_{\tau } } \right|p_{\tau } } \right) \ne \# \left( {\left. {h_{\upsilon } } \right|p_{\upsilon } } \right)$, $\# \left( {\left. {g_{\tau } } \right|q_{\tau } } \right) \ne \# \left( {\left. {g_{\upsilon } } \right|q_{\upsilon } } \right)$, let $\Gamma = \max \left( {\# \left( {\left. {h_{\tau } } \right|p_{\tau } } \right),\# \left( {\left. {h_{\upsilon } } \right|p_{\upsilon } } \right)} \right)$, $\Upsilon = \max \; \left( {\# \left( {\left. {g_{\tau } } \right|q_{\tau } } \right),\# \left( {\left. {g_{\upsilon } } \right|q_{\upsilon } } \right)} \right)$.

  The discrete ordered deviation degrees of MD and NMD from $\tau$ to $\upsilon$ are defined as follows:

  The discrete ordered divergences of MD:

  $$p_{DOMD} \left( {\tau ,\upsilon } \right){ = }\left| {h_{\tau }^{\sigma \left( j \right)} p_{\tau }^{\sigma \left( j \right)} - h_{\upsilon }^{\sigma \left( j \right)} p_{\upsilon }^{\sigma \left( j \right)} } \right|$$

  The discrete ordered divergences of NMD:

  $$p_{DONMD} \left( {\tau ,\upsilon } \right){ = }\left| {g_{\tau }^{\sigma \left( j \right)} q_{\tau }^{\sigma \left( j \right)} - g_{\upsilon }^{\sigma \left( j \right)} q_{\upsilon }^{\sigma \left( j \right)} } \right|$$

  where $\left. {h_{\tau }^{\sigma \left( j \right)} } \right|p_{\tau }^{\sigma \left( j \right)} \left( {j = 1,2, \cdots ,\# \left. {h_{\tau }^{\sigma \left( j \right)} } \right|p_{\tau }^{\sigma \left( j \right)} } \right)$ is the $i{\varvec{th}}$ smallest in $\left. {h_{\tau } } \right|p_{\tau }$; $\left. {h_{\upsilon }^{\sigma \left( j \right)} } \right|p_{\upsilon }^{\sigma \left( j \right)} \left( {j = 1,2, \cdots ,\# \left. {h_{\upsilon }^{\sigma \left( j \right)} } \right|p_{\upsilon }^{\sigma \left( j \right)} } \right)$ is the $i{\varvec{th}}$ smallest in $\left. {h_{\upsilon } } \right|p_{\upsilon }$; $\left. {g_{\tau }^{\sigma \left( j \right)} } \right|q_{\tau }^{\sigma \left( j \right)} \left( {j = 1,2, \cdots ,\# \left. {g_{\tau }^{\sigma \left( j \right)} } \right|q_{\tau }^{\sigma \left( j \right)} } \right)$ is the $i{\varvec{th}}$ smallest in $\left. {g_{\tau } } \right|q_{\tau }$; $\left. {g_{\upsilon }^{\sigma \left( j \right)} } \right|q_{\upsilon }^{\sigma \left( j \right)} \left( {j = 1,2, \cdots ,\# \left. {g_{\upsilon }^{\sigma \left( j \right)} } \right|q_{\upsilon }^{\sigma \left( j \right)} } \right)$ is the $i{\varvec{th}}$ smallest in $\left. {g_{\upsilon } } \right|q_{\upsilon }$, and $h_{\tau }^{\sigma \left( j \right)} p_{\tau }^{\sigma \left( j \right)} \le h_{\tau }^{{\sigma \left( {j + 1} \right)}} p_{\tau }^{{\sigma \left( {j + 1} \right)}}$, $h_{\upsilon }^{\sigma \left( j \right)} p_{\upsilon }^{\sigma \left( j \right)} \le h_{\upsilon }^{{\sigma \left( {j + 1} \right)}} p_{\upsilon }^{{\sigma \left( {j + 1} \right)}}$, $g_{\tau }^{\sigma \left( j \right)} q_{\tau }^{\sigma \left( j \right)} \le g_{\tau }^{{\sigma \left( {j + 1} \right)}} q_{\tau }^{{\sigma \left( {j + 1} \right)}}$, $g_{\upsilon }^{\sigma \left( j \right)} q_{\upsilon }^{\sigma \left( j \right)} \le g_{\upsilon }^{{\sigma \left( {j + 1} \right)}} q_{\upsilon }^{{\sigma \left( {j + 1} \right)}}$.

3.1 Some unordered distance measures for PDHFE

Let $\tau = \left\langle {\left. {h_{\tau } } \right|p_{\tau } ,\left. {g_{\tau } } \right|q_{\tau } } \right\rangle$ and $\upsilon = \left\langle {\left. {h_{\upsilon } } \right|p_{\upsilon } ,\left. {g_{\upsilon } } \right|q_{\upsilon } } \right\rangle$ be two PDHFEs, then some distances between $\tau$ and $\upsilon$ are defined as follows.

• (1) The generalized unordered normalized distance (GUND) between $\tau$ and $\upsilon$ is defined as:

  $$d_{gund} \left( {\tau ,\upsilon } \right) = \left[ {\frac{1}{2}\left( {\frac{1}{\Phi }\sum\nolimits_{j = 1}^{\Phi } {p_{UMD}^{\lambda } \left( {\tau ,\upsilon } \right)} + \frac{1}{\Psi }\sum\nolimits_{j = 1}^{\Psi } {p_{UNMD}^{\lambda } \left( {\tau ,\upsilon } \right)} } \right)} \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $\lambda > 0$.

  If $\lambda { = }1$, GUND becomes the unordered normalized Hamming distance (UNHD); If $\lambda { = 2}$, GUND becomes the unordered normalized Euclidean distance (UNED).

• (2) The generalized unordered normalized Hausdorff distance (GUNHD) between $\tau$ and $\upsilon$ is defined as:

  $$d_{gunhd} \left( {\tau ,\upsilon } \right) = \left( {\mathop {\max }\limits_{j} \left( {p_{UMD}^{\lambda } \left( {\tau ,\upsilon } \right),p_{UNMD}^{\lambda } \left( {\tau ,\upsilon } \right)} \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $\lambda > 0$.

  If $\lambda { = }1$, GUNHD becomes the unordered normalized Hamming–Hausdorff distance (UNHHD); If $\lambda { = 2}$, GUNHD becomes the unordered normalized Euclidean–Hausdorff distance (UNEHD).

  Also, some unordered hybrid distance measures can be built as follows:

• (3) The generalized unordered hybrid normalized distance (GUHND) between $\tau$ and $\upsilon$ is defined as:

  $$d_{guhnd} \left( {\tau ,\upsilon } \right) = \left\{ {\frac{1}{2}\left[ \begin{gathered} \frac{1}{2}\left( {\frac{1}{\Phi }\sum\nolimits_{j = 1}^{\Phi } {p_{UMD}^{\lambda } \left( {\tau ,\upsilon } \right)} + \frac{1}{\Psi }\sum\nolimits_{j = 1}^{\Psi } {p_{UNMD}^{\lambda } \left( {\tau ,\upsilon } \right)} } \right) \hfill \\ + \mathop {\max }\limits_{j} \left( {p_{UMD}^{\lambda } \left( {\tau ,\upsilon } \right),p_{UNMD}^{\lambda } \left( {\tau ,\upsilon } \right)} \right) \hfill \\ \end{gathered} \right]} \right\}^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  If $\lambda { = }1$, GUHND becomes the unordered hybrid normalized Hamming distance (UHNHD); If $\lambda { = 2}$, GUHND becomes the unordered hybrid normalized Euclidean distance (UHNED).

3.2 Some ordered distance measures for PDHFE

Let $\tau = \left\langle {\left. {h_{\tau } } \right|p_{\tau } ,\left. {g_{\tau } } \right|q_{\tau } } \right\rangle$ and $\upsilon = \left\langle {\left. {h_{\upsilon } } \right|p_{\upsilon } ,\left. {g_{\upsilon } } \right|q_{\upsilon } } \right\rangle$ be two PDHFEs, then some ordered normalized distances between $\tau$ and $\upsilon$ are defined as follows.

• (1) The generalized ordered normalized distance (GOND) between $\tau$ and $\upsilon$ is defined as:

  $$d_{gond} \left( {\tau ,\upsilon } \right) = \left[ {\frac{1}{2}\left( {\frac{1}{\Gamma }\sum\nolimits_{j = 1}^{\Gamma } {p_{OMD}^{\lambda } \left( {\tau ,\upsilon } \right)} + \frac{1}{\Upsilon }\sum\nolimits_{j = 1}^{\Upsilon } {p_{ONMD}^{\lambda } \left( {\tau ,\upsilon } \right)} } \right)} \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  If $\lambda { = }1$, GOND becomes the ordered normalized Hamming distance (ONHD); If $\lambda { = 2}$, GOND becomes the ordered normalized Euclidean distance (ONED).

• (2) The generalized ordered normalized Hausdorff distance (GONHD) between $\tau$ and $\upsilon$ is defined as:

  $$d_{gonhd} \left( {\tau ,\upsilon } \right) = \left( {\mathop {\max }\limits_{j} \left( {p_{OMD}^{\lambda } \left( {\tau ,\upsilon } \right),p_{ONMD}^{\lambda } \left( {\tau ,\upsilon } \right)} \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $\lambda > 0$.

  If $\lambda { = }1$, GONHD becomes the ordered normalized Hamming–Hausdorff distance (ONHHD); If $\lambda { = 2}$, GONHD becomes the ordered normalized Euclidean–Hausdorff distance (ONEHD).

  Additionally, some ordered hybrid distance measures can be built for PDHFE as follows:

• (3) The generalized ordered hybrid normalized distance (GOHND) between $\tau$ and $\upsilon$ is defined as:

  $$d_{gohnd} \left( {\tau ,\upsilon } \right) = \left\{ {\frac{1}{2}\left[ \begin{gathered} \frac{1}{2}\left( {\frac{1}{\Gamma }\sum\nolimits_{j = 1}^{\Gamma } {p_{OMD}^{\lambda } \left( {\tau ,\upsilon } \right)} + \frac{1}{\Upsilon }\sum\nolimits_{j = 1}^{\Upsilon } {p_{ONMD}^{\lambda } \left( {\tau ,\upsilon } \right)} } \right) \hfill \\ + \mathop {\max }\limits_{j} \left( {p_{OMD}^{\lambda } \left( {\tau ,\upsilon } \right),p_{ONMD}^{\lambda } \left( {\tau ,\upsilon } \right)} \right) \hfill \\ \end{gathered} \right]} \right\}^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  If $\lambda { = }1$, GOHND becomes the ordered hybrid normalized Hamming distance (OHNHD); If $\lambda { = 2}$, GOHND becomes the ordered hybrid normalized Euclidean distance (OHNED).

4 Distance measures between two collections of PDHFSs

Before giving distance measures between two collections of PDHFSs, we firstly give some basic and necessary remarks.

Remark 4

Some definitions of deviation degree under different cases.

• (1) The deviation degree in discrete unordered case:

  Let $\# \left( {\left. {h_{M} \left( {x_{i} } \right)} \right|p_{M} \left( {x_{i} } \right)} \right) = \# \left( {\left. {h_{N} \left( {x_{i} } \right)} \right|p_{N} \left( {x_{i} } \right)} \right) = \Phi_{{x_{i} }},$ $\# \left( {\left. {g_{M} \left( {x_{i} } \right)} \right|q_{M} \left( {x_{i} } \right)} \right) = \# \left( {\left. {g_{N} \left( {x_{i} } \right)} \right|q_{N} \left( {x_{i} } \right)} \right) = \Psi_{{x_{i} }}.$

  The discrete unordered divergences of MD and NMD from PDHFSs $M$ to $N$ on $X = \left\{ {x_{1} ,x_{2} , \cdots ,x_{n} } \right\}$ are defined as follows:

  The discrete unordered deviation degree of MD:

  $$p_{DUMD} \left( {M,N} \right){ = }\left| {h_{M}^{j} \left( {x_{i} } \right)p_{M}^{j} \left( {x_{i} } \right) - h_{N}^{j} \left( {x_{i} } \right)p_{N}^{j} \left( {x_{i} } \right)} \right|$$

  The discrete unordered deviation degree of NMD:

  $$p_{DUNMD} \left( {M,N} \right){ = }\left| {g_{M}^{j} \left( {x_{i} } \right)q_{M}^{j} \left( {x_{i} } \right) - g_{N}^{j} \left( {x_{i} } \right)q_{N}^{j} \left( {x_{i} } \right)} \right|$$

  In the next subsection, we firstly proposed some distances under.

• (2) The deviation degree in continuous unordered case:

  If $\# \left( {\left. {h_{M} \left( x \right)} \right|p_{M} \left( x \right)} \right) = \# \left( {\left. {h_{N} \left( x \right)} \right|p_{N} \left( x \right)} \right) = \Phi_{x},$$\# \left( {\left. {g_{M} \left( x \right)} \right|q_{M} \left( x \right)} \right) = \# \left( {\left. {g_{N} \left( x \right)} \right|q_{N} \left( x \right)} \right) = \Psi_{x}.$

  The unordered continuous deviation degrees of MD and NMD from PDHFSs $M$ to $N$ on $x \in X$:

  The continuous unordered deviation degree of MD:

  $$p_{CUMD} \left( {M,N} \right){ = }\left| {h_{M}^{j} \left( x \right)p_{M}^{j} \left( x \right) - h_{N}^{j} \left( x \right)p_{N}^{j} \left( x \right)} \right|$$

  The continuous unordered deviation degree of NMD:

  $$p_{CUNMD} \left( {M,N} \right){ = }\left| {g_{M}^{j} \left( x \right)q_{M}^{j} \left( x \right) - g_{N}^{j} \left( x \right)q_{N}^{j} \left( x \right)} \right|$$

• (3) The deviation degree in discrete ordered case:

  If $\# \left( {\left. {h_{M} \left( {x_{i} } \right)} \right|p_{M} \left( {x_{i} } \right)} \right) \ne \# \left( {\left. {h_{N} \left( {x_{i} } \right)} \right|p_{N} \left( {x_{i} } \right)} \right)$, $\# \left( {\left. {g_{M} \left( {x_{i} } \right)} \right|q_{M} \left( {x_{i} } \right)} \right) \ne \# \left( {\left. {g_{N} \left( {x_{i} } \right)} \right|q_{N} \left( {x_{i} } \right)} \right)$, let $\Gamma_{{x_{i} }} = \max \left( {\# \left( {\left. {h_{M} \left( {x_{i} } \right)} \right|p_{M} \left( {x_{i} } \right)} \right),\# \left( {\left. {h_{N} \left( {x_{i} } \right)} \right|p_{N} \left( {x_{i} } \right)} \right)} \right)$ and $\Upsilon_{{x_{i} }} = \max \left( {\# \left( {\left. {g_{M} \left( {x_{i} } \right)} \right|q_{M} \left( {x_{i} } \right)} \right),\# \left( {\left. {g_{N} \left( {x_{i} } \right)} \right|q_{N} \left( {x_{i} } \right)} \right)} \right)$.

  The discrete ordered deviation degrees of MD and NMD from PDHFSs $M$ to $N$ on $X = \left\{ {x_{1} ,x_{2} , \cdots ,x_{n} } \right\}$:

  The discrete ordered deviation degree of MD degree:

  $$p_{DOMD} \left( {M,N} \right){ = }\left| {h_{M}^{\sigma \left( j \right)} \left( {x_{i} } \right)p_{M}^{\sigma \left( j \right)} \left( {x_{i} } \right) - h_{N}^{\sigma \left( j \right)} \left( {x_{i} } \right)p_{N}^{\sigma \left( j \right)} \left( {x_{i} } \right)} \right|$$

  The discrete ordered deviation degree of NMD:

  $$p_{DONMD} \left( {M,N} \right){ = }\left| {g_{M}^{\sigma \left( j \right)} \left( {x_{i} } \right)q_{M}^{\sigma \left( j \right)} \left( {x_{i} } \right) - g_{N}^{\sigma \left( j \right)} \left( {x_{i} } \right)q_{N}^{\sigma \left( j \right)} \left( {x_{i} } \right)} \right|$$

  where $\left. {h_{M}^{{\varsigma_{j} }} \left( {x_{i} } \right)} \right|p_{M}^{{\varsigma_{j} }} \left( {x_{i} } \right)\left( {i = 1,2, \cdots ,\# \left. {h_{M} \left( {x_{i} } \right)} \right|p_{M} \left( {x_{i} } \right)} \right)$ is the $i{\varvec{th}}$ smallest in $\left. {h_{M} \left( {x_{i} } \right)} \right|p_{M} \left( {x_{i} } \right)$; $\left. {h_{N}^{{\varsigma_{j} }} \left( {x_{i} } \right)} \right|p_{N}^{{\varsigma_{j} }} \left( {x_{i} } \right)\left( {i = 1,2, \cdots ,\# \left. {h_{N} \left( {x_{i} } \right)} \right|p_{N} \left( {x_{i} } \right)} \right)$ is the $i{\varvec{th}}$ smallest in $\left. {h_{N} \left( {x_{i} } \right)} \right|p_{N} \left( {x_{i} } \right)$; $\left. {g_{M}^{{\varsigma_{j} }} \left( {x_{i} } \right)} \right|q_{M}^{{\varsigma_{j} }} \left( {x_{i} } \right)\left( {i = 1,2, \cdots ,\# \left. {h_{M} \left( {x_{i} } \right)} \right|p_{M} \left( {x_{i} } \right)} \right)$ is the $i{\varvec{th}}$ smallest in $\left. {g_{M} \left( {x_{i} } \right)} \right|q_{M} \left( {x_{i} } \right)$; $\left. {g_{N}^{{\varsigma_{j} }} \left( {x_{i} } \right)} \right|q_{N}^{{\varsigma_{j} }} \left( {x_{i} } \right)\left( {i = 1,2, \cdots ,\# \left. {g_{N} \left( {x_{i} } \right)} \right|q_{N} \left( {x_{i} } \right)} \right)$ is the $i{\varvec{th}}$ smallest in $\left. {g_{N} \left( {x_{i} } \right)} \right|q_{N} \left( {x_{i} } \right)$, and $h_{M}^{{\varsigma_{j} }} \left( {x_{i} } \right)p_{M}^{{\varsigma_{j} }} \left( {x_{i} } \right) \le h_{M}^{{\varsigma_{j + 1} }} \left( {x_{i} } \right)p_{M}^{{\varsigma_{j + 1} }} \left( {x_{i} } \right)$, $h_{N}^{{\varsigma_{j} }} \left( {x_{i} } \right)p_{N}^{{\varsigma_{j} }} \left( {x_{i} } \right) \le h_{N}^{{\varsigma_{j + 1} }} \left( {x_{i} } \right)p_{N}^{{\varsigma_{j + 1} }} \left( {x_{i} } \right)$, $g_{M}^{{\varsigma_{j} }} \left( {x_{i} } \right)q_{M}^{{\varsigma_{j} }} \left( {x_{i} } \right) \le g_{M}^{{\varsigma_{j + 1} }} \left( {x_{i} } \right)q_{M}^{{\varsigma_{j + 1} }} \left( {x_{i} } \right)$, $g_{N}^{{\varsigma_{j} }} \left( {x_{i} } \right)q_{N}^{{\varsigma_{j} }} \left( {x_{i} } \right) \le g_{N}^{{\varsigma_{j + 1} }} \left( {x_{i} } \right)q_{N}^{{\varsigma_{j + 1} }} \left( {x_{i} } \right)$.

• (4) The deviation degree in continuous ordered case:

  If $\# \left( {\left. {h_{M} \left( x \right)} \right|p_{M} \left( x \right)} \right) \ne \# \left( {\left. {h_{N} \left( x \right)} \right|p_{N} \left( x \right)} \right)$, $\# \left( {\left. {g_{M} \left( x \right)} \right|q_{M} \left( x \right)} \right) \ne \# \left( {\left. {g_{N} \left( x \right)} \right|q_{N} \left( x \right)} \right)$, let $\Gamma_{x} = \max \left( {\# \left( {\left. {h_{M} \left( x \right)} \right|p_{M} \left( x \right)} \right),\# \left( {\left. {h_{N} \left( x \right)} \right|p_{N} \left( x \right)} \right)} \right)$ and $\Upsilon_{x} = \max \left( {\# \left( {\left. {g_{M} \left( x \right)} \right|q_{M} \left( x \right)} \right),\# \left( {\left. {g_{N} \left( x \right)} \right|q_{N} \left( x \right)} \right)} \right)$,

  The continuous ordered distance measures for PDHFS, we give the continuous ordered divergences of MD and NMD from PDHFSs $M$ to $N$:

  The continuous ordered divergences of MD:

  $$p_{COMD} \left( {M,N} \right){ = }\left| {h_{M}^{\sigma \left( j \right)} \left( x \right)p_{M}^{\sigma \left( j \right)} \left( x \right) - h_{N}^{\sigma \left( j \right)} \left( x \right)p_{N}^{\sigma \left( j \right)} \left( x \right)} \right|$$

  The continuous ordered divergences of NMD:

  $$p_{CONMD} \left( {M,N} \right){ = }\left| {g_{M}^{\sigma \left( j \right)} \left( x \right)q_{M}^{\sigma \left( j \right)} \left( x \right) - g_{N}^{\sigma \left( j \right)} \left( x \right)q_{N}^{\sigma \left( j \right)} \left( x \right)} \right|$$

  where $\left. {h_{M}^{{\varsigma_{j} }} \left( x \right)} \right|p_{M}^{{\varsigma_{j} }} \left( x \right)\left( {i = 1,2, \cdots ,\# \left. {h_{M} \left( x \right)} \right|p_{M} \left( x \right)} \right)$ is the $i{\varvec{th}}$ smallest in $\left. {h_{M} \left( x \right)} \right|p_{M} \left( x \right)$; $\left. {h_{N}^{{\varsigma_{j} }} \left( x \right)} \right|p_{N}^{{\varsigma_{j} }} \left( x \right)\left( {i = 1,2, \cdots ,\# \left. {h_{N} \left( x \right)} \right|p_{N} \left( x \right)} \right)$ is the $i{\varvec{th}}$ smallest in $\left. {h_{N} \left( x \right)} \right|p_{N} \left( x \right)$; $\left. {g_{M}^{{\varsigma_{j} }} \left( x \right)} \right|q_{M}^{{\varsigma_{j} }} \left( x \right)\left( {i = 1,2, \cdots ,\# \left. {h_{M} \left( x \right)} \right|p_{M} \left( x \right)} \right)$ is the $i{\varvec{th}}$ smallest in $\left. {g_{M} \left( x \right)} \right|q_{M} \left( x \right)$; $\left. {g_{N}^{{\varsigma_{j} }} \left( x \right)} \right|q_{N}^{{\varsigma_{j} }} \left( x \right)\left( {i = 1,2, \cdots ,\# \left. {g_{N} \left( x \right)} \right|q_{N} \left( x \right)} \right)$ is the $i{\varvec{th}}$ smallest in $\left. {g_{N} \left( x \right)} \right|q_{N} \left( x \right)$, and $h_{M}^{{\varsigma_{j} }} \left( x \right)p_{M}^{{\varsigma_{j} }} \left( x \right) \le h_{M}^{{\varsigma_{j + 1} }} \left( x \right)p_{M}^{{\varsigma_{j + 1} }} \left( x \right)$, $h_{N}^{{\varsigma_{j} }} \left( x \right)p_{N}^{{\varsigma_{j} }} \left( x \right) \le h_{N}^{{\varsigma_{j + 1} }} \left( x \right)p_{N}^{{\varsigma_{j + 1} }} \left( x \right)$, $g_{M}^{{\varsigma_{j} }} \left( x \right)q_{M}^{{\varsigma_{j} }} \left( x \right) \le g_{M}^{{\varsigma_{j + 1} }} \left( x \right)q_{M}^{{\varsigma_{j + 1} }} \left( x \right)$, $g_{N}^{{\varsigma_{j} }} \left( x \right)q_{N}^{{\varsigma_{j} }} \left( x \right) \le g_{N}^{{\varsigma_{j + 1} }} \left( x \right)q_{N}^{{\varsigma_{j + 1} }} \left( x \right)$.

The distances between two PDHFEs can only calculate the distance between two fuzzy elements, but in the process of practical decision-making, each decision alternative has several multiple decision attributes, and each decision attribute corresponds to a PDHFE. The distance between two PDHFSs cannot be calculated, and different decision attributes have different importance, the weight of each decision attribute is different. To solve these problems, we propose some distance measures for PDHFS.

4.1 Unordered weighted distance measures between two collections of PDHFSs in discrete case

Let $M = \left\langle {\left. {h_{M} \left( {x_{i} } \right)} \right|p_{M} \left( {x_{i} } \right),\left. {g_{M} \left( {x_{i} } \right)} \right|q_{M} \left( {x_{i} } \right)} \right\rangle$ and $N = \left\langle {\left. {h_{N} \left( {x_{i} } \right)} \right|p_{N} \left( {x_{i} } \right),\left. {g_{N} \left( {x_{i} } \right)} \right|q_{N} \left( {x_{i} } \right)} \right\rangle$ be two PDHFSs on $X = \left\{ {x_{1} ,x_{2} , \cdots ,x_{n} } \right\}$. In practical problems, we believe that the weight of each element should be considered. For example, in the field of MADM, the importance of each decision attribute is different and should be given different weights, then some discrete unordered weighted distances between $M$ and $N$ are defined as follows.

• (1) The generalized discrete unordered weighted distance (GDUWD) between $M$ and $N$ is recorded as:

  $$d_{gdu\omega d} \left( {M,N} \right) = \left[ {\frac{1}{2}\sum\nolimits_{i = 1}^{n} {\omega_{i} \left( {\frac{1}{{\Phi_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Phi_{{x_{i} }} }} {p_{DUMD}^{\lambda } \left( {M,N} \right)} + \frac{1}{{\Psi_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Psi_{{x_{i} }} }} {p_{DUNMD}^{\lambda } \left( {M,N} \right)} } \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $\lambda > 0$.

  If $\lambda { = }1$, GDUWD becomes the discrete unordered weighted Hamming distance (DUWHD); If $\lambda = 2$, GDUWD becomes the discrete unordered weighted Euclidean distance (DUWED).

• (2) The generalized discrete unordered weighted hausdorff distance (GDUWHD) between $M$ and $N$ is defined as:

  $$d_{gdu\omega hd} \left( {M,N} \right) = \left[ {\sum\nolimits_{i = 1}^{n} {\omega_{i} \left( {\mathop {\max }\limits_{j} \left( {p_{DUMD}^{\lambda } \left( {M,N} \right),p_{DUNMD}^{\lambda } \left( {M,N} \right)} \right)} \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  If $\lambda { = }1$, GDUWHD becomes the discrete unordered weighted Hamming-Hausdoff distance (DUWHHD); If $\lambda = 2$, GDUWHD becomes the discrete unordered weighted Euclidean-Hausdorff distance (DUWEHD).

  Similarly, some discrete unordered hybrid weighted distance measures can be defined. Next, we define some discrete unordered hybrid weighted distance measures.

• (3) The generalized discrete unordered hybrid weighted distance (GDUHWD) between $M$ and $N$ is defined as

  $$d_{gduh\omega d} \left( {M,N} \right) = \left[ {\frac{1}{2}\sum\limits_{i = 1}^{n} {\omega_{i} \left( \begin{gathered} \frac{1}{2}\left( {\frac{1}{{\Phi_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Phi_{{x_{i} }} }} {p_{DUMD}^{\lambda } \left( {M,N} \right)} + \frac{1}{{\Psi_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Psi_{{x_{i} }} }} {p_{DUNMD}^{\lambda } \left( {M,N} \right)} } \right) \hfill \\ + \mathop {\max }\limits_{j} \left( {p_{DUMD}^{\lambda } \left( {M,N} \right),p_{DUNMD}^{\lambda } \left( {M,N} \right)} \right) \hfill \\ \end{gathered} \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $\lambda > 0$.

  If $\lambda = 1$, GDUHWD becomes the discrete unordered hybrid weighted Hamming distance (DUHWHD); If $\lambda = 2$, GDUHWD becomes the discrete unordered hybrid weighted Euclidean distance (DUHWED).

4.2 Unordered weighted distance measures between two collections of PDHFSs in continuous case

Some continuous unordered weighted distances between $M$ and $N$ are defined as follows.

• (1) The generalized continuous unordered weighted distance (GCUWD) between $M$ and $N$ is defined as:

  $$d_{gcu\omega d} \left( {M,N} \right) = \left[ {\frac{1}{2}\int_{a}^{b} {\omega \left( x \right)\left( {\frac{1}{{\Phi_{x} }}\sum\nolimits_{j = 1}^{{\Phi_{x} }} {p_{CUMD}^{\lambda } \left( {M,N} \right)} + \frac{1}{{\Psi_{x} }}\sum\nolimits_{j = 1}^{{\Psi_{x} }} {p_{CUNMD}^{\lambda } \left( {M,N} \right)} } \right)dx} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $\lambda > 0$ , where $\omega \left( x \right) \in \left[ {0,1} \right]$ and $\int_{a}^{b} {\omega \left( x \right)dx} = 1$.

If $\lambda = 1$, GCUWD becomes the continuous unordered weighted Hamming distance (CUWHD); If $\lambda = 2$, GCUWD becomes the continuous unordered weighted Euclidean distance (CUWED); If $\omega \left( x \right) = \frac{1}{b - a}$, GCUWD becomes the generalized continuous unordered equal weighted distance (GCUEWD); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\lambda = 1$, GCUWD becomes the continuous unordered equal weighted Hamming distance (CUEWHD); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\lambda = 2$, GCUWD becomes the continuous unordered equal weighted Euclidean distance (CUEWED).

Next, we define the generalized continuous unordered weighted Hausdorff distance (GCUWHD) between $M$ and $N$ is defined as:

$$d_{gcu\omega hd} \left( {M,N} \right) = \left\{ {\int_{a}^{b} {\omega \left( x \right)\left( {\mathop {\max }\limits_{j} \left( {p_{CUMD}^{\lambda } \left( {M,N} \right),p_{CUNMD}^{\lambda } \left( {M,N} \right)} \right)} \right)dx} } \right\}^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

where $\lambda > 0$.

If $\lambda = 1$, GCUWHD becomes the continuous unordered weighted Hamming-Hausdorff distance (CUWHHD); If $\lambda = 2$, GCUWHD becomes the continuous unordered weighted Euclidean-Hausdorff distance (CUWEHD); If $\omega \left( x \right) = \frac{1}{b - a}$, GCUWHD becomes the generalized continuous unordered equal weighted Hausdorff distance (GCUEWHD); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\lambda = 1$, GCUWHD becomes the continuous unordered equal weighted Hamming-Hausdorff distance (CUEWHHD); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\lambda = 2$, GCUWHD becomes the continuous unordered equal weighted Euclidean-Hausdorff distance (CUEWDHD).

Similarly, some hybrid continuous unordered weighted distance measures can be defined. Next, we define the generalized continuous unordered hybrid weighted distance (GCUHWD):

$$d_{gcuh\omega d} \left( {M,N} \right) = \left[ {\frac{1}{2}\int_{a}^{b} {\omega \left( x \right)\left( \begin{gathered} \frac{1}{2}\left( {\frac{1}{{\Phi_{x} }}\sum\nolimits_{j = 1}^{{\Phi_{x} }} {p_{CUMD}^{\lambda } \left( {M,N} \right)} + \frac{1}{{\Psi_{x} }}\sum\nolimits_{j = 1}^{{\Psi_{x} }} {p_{CUNMD}^{\lambda } \left( {M,N} \right)} } \right) \hfill \\ + \mathop {\max }\limits_{j} \left( {p_{CUMD}^{\lambda } \left( {M,N} \right),p_{CUNMD}^{\lambda } \left( {M,N} \right)} \right) \hfill \\ \end{gathered} \right)dx} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

where $\lambda > 0$.

If $\lambda = 1$, GCUHWD becomes the continuous unordered hybrid weighted Hamming distance (CUHWHD); If $\lambda = 2$, GCUHWD becomes the continuous unordered hybrid weighted Euclidean distance (CUHWED); If $\omega \left( x \right) = \frac{1}{b - a}$, GCUHWD becomes the generalized continuous unordered hybrid equal weighted distance (GCUHEWD); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\lambda = 1$, GCUHWD becomes the hybrid continuous equal weighted Hamming distance (HCEWHD); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\lambda = 2$, GCUHWD becomes the continuous unordered hybrid equal weighted Euclidean distance (CUHEWED).

4.3 Ordered weighted distance measures between two collections of PDHFSs in discrete case

Some ordered weighted distances between $M$ and $N$ is defined as follows.

• (1) The generalized discrete ordered weighted distance (GDOWD) between $M$ and $N$ is defined as:

  $$d_{gdo\omega d} \left( {M,N} \right) = \left[ {\frac{1}{2}\sum\nolimits_{i = 1}^{n} {\omega_{i} \left( {\frac{1}{{\Gamma_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Gamma_{{x_{i} }} }} {p_{DOMD}^{\lambda } \left( {M,N} \right)} + \frac{1}{{\Upsilon_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Upsilon_{{x_{i} }} }} {p_{DONMD}^{\lambda } \left( {M,N} \right)} } \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  (8)

  where $\lambda > 0$.

  If $\lambda { = }1$, GDOWD becomes the discrete ordered weighted Hamming distance (DOWHD); If $\lambda { = 2}$, GDOWD becomes the discrete ordered weighted Euclidean distance (DOWED).

• (2) The generalized discrete ordered weighted Hausdorff distance (GDOWHD) between $M$ and $N$ is defined as:

  $$d_{gdo\omega hd} \left( {M,N} \right) = \left( {\sum\nolimits_{i = 1}^{n} {\omega_{i} \mathop {\max }\limits_{j} \left( {p_{DOMD}^{\lambda } \left( {M,N} \right),p_{DONMD}^{\lambda } \left( {M,N} \right)} \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  If $\lambda { = }1$, GDOWHD becomes the discrete ordered weighted Hamming–Hausdorff distance (DOWHHD); If $\lambda { = 2}$, GDOWHD becomes the discrete ordered weighted Euclidean–Hausdorff distance (DOWEHD).

  Next, we define the generalized discrete ordered hybrid weighted distance (GDOHWD) between $M$ and $N$ is defined as:

  $$d_{gdohwd} \left( {M,N} \right) = \left\{ {\frac{1}{2}\sum\nolimits_{i = 1}^{n} {\omega_{i} \left[ \begin{gathered} \frac{1}{2}\left( {\frac{1}{{\Gamma_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Gamma_{{x_{i} }} }} {p_{DOMD}^{\lambda } \left( {M,N} \right)} + \frac{1}{{\Upsilon_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Upsilon_{{x_{i} }} }} {p_{DONMD}^{\lambda } \left( {M,N} \right)} } \right) \hfill \\ + \mathop {\max }\limits_{j} \left( {p_{DOMD}^{\lambda } \left( {M,N} \right),p_{DONMD}^{\lambda } \left( {M,N} \right)} \right) \hfill \\ \end{gathered} \right]} } \right\}^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $\lambda > 0$.

  If $\lambda = 1$, GDOHWD becomes the discrete ordered hybrid weighted Hamming distance (DOHWHD); If $\lambda = 2$, GDOHWD becomes the discrete ordered hybrid weighted Euclidean distance (DOHWED).

4.4 Ordered weighted distance measures between two collections of PDHFSs in continuous case

Some continuous ordered weighted distances between $M$ and $N$ are defined as follows.

• (1) The generalized continuous ordered weighted distance (GCOWD) between $M$ and $N$ is defined as:

  $$d_{gco\omega d} \left( {M,N} \right) = \left[ {\frac{1}{2}\int_{a}^{b} {\omega \left( x \right)\left( {\frac{1}{{\Gamma_{x} }}\sum\nolimits_{j = 1}^{{\Gamma_{x} }} {p_{COMD}^{\lambda } \left( {M,N} \right)} + \frac{1}{{\Upsilon_{x} }}\sum\nolimits_{j = 1}^{{\Upsilon_{x} }} {p_{CONMD}^{\lambda } \left( {M,N} \right)} } \right)dx} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $\lambda > 0$, $\omega \left( x \right) \in \left[ {0,1} \right]$ and $\int_{a}^{b} {\omega \left( x \right)} dx = 1$.

If $\lambda = 1$, GCOWD becomes the continuous ordered weighted Hamming distance (COWHD); If $\lambda = 2$, GCOWD becomes the continuous ordered weighted Euclidean distance (COWED); If $\omega \left( x \right) = \frac{1}{b - a}$, GCOWD becomes the generalized continuous ordered equal weighted distance (GCOEWD); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\lambda = 1$, GCOWD becomes the continuous ordered equal weighted Hamming distance (COEWHD); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\lambda = 2$, GCOWD becomes the continuous ordered equal weighted Euclidean distance (COEWED).

Next, we define a generalized continuous ordered weighted Hausdorff distance (GCOWHD) between $M$ and $N$ is defined as:

$$d_{gco\omega hd} \left( {M,N} \right) = \left\{ {\int_{a}^{b} {\omega \left( x \right)\left( {\mathop {\max }\limits_{j} \left( {p_{COMD}^{\lambda } \left( {M,N} \right),p_{CONMD}^{\lambda } \left( {M,N} \right)} \right)} \right)dx} } \right\}^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

where $\lambda > 0$.

If $\lambda = 1$, GCOWHD becomes the continuous ordered weighted Hamming-Hausdorff distance (COWHHD); If $\lambda = 2$, GCOWHD becomes the continuous ordered weighted Euclidean-Hausdorff distance (COWEHD); If $\omega \left( x \right) = \frac{1}{b - a}$, GCOWHD becomes the generalized continuous ordered equal weighted Hausdorff distance (GCOEWHD); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\lambda = 1$, GCOWHD becomes the continuous ordered equal weighted Hamming-Hausdorff distance (COEWHHD); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\lambda = 2$, GCOWHD becomes the continuous ordered equal weighted Euclidean-Hausdorff distance (COEWEHD).

Similarly, some continuous ordered hybrid continuous weighted distance measures can be defined.

• (1) The generalized continuous ordered hybrid weighted distance (GCOHWD) between $M$ and $N$ is defined as:

  $$d_{gcoh\omega d} \left( {M,N} \right) = \left[ {\frac{1}{2}\int_{a}^{b} {\omega \left( x \right)\left( \begin{gathered} \frac{1}{2}\left( {\frac{1}{{\Gamma_{x} }}\sum\nolimits_{j = 1}^{{\Gamma_{x} }} {p_{COMD}^{\lambda } \left( {M,N} \right)} + \frac{1}{{\Upsilon_{x} }}\sum\nolimits_{j = 1}^{{\Upsilon_{x} }} {p_{CONMD}^{\lambda } \left( {M,N} \right)} } \right) \hfill \\ + \mathop {\max }\limits_{j} \left( {p_{COMD}^{\lambda } \left( {M,N} \right),p_{CONMD}^{\lambda } \left( {M,N} \right)} \right) \hfill \\ \end{gathered} \right)dx} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $\lambda > 0$.

If $\lambda = 1$, GCOHWD becomes the continuous ordered hybrid weighted Hamming distance (COHWHD); If $\lambda = 2$, GCOHWD becomes the continuous ordered hybrid weighted Euclidean distance (COHWED); If $\omega \left( x \right) = \frac{1}{b - a}$, GCOHWD becomes the generalized continuous ordered hybrid equal weighted distance (GCOHEWD); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\lambda = 1$, GCOHWD becomes the continuous ordered hybrid equal weighted Hamming distance (COHEWHD); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\lambda = 2$, GCOHWD becomes the hybrid continuous equal weighted Euclidean distance (COHEWED).

4.5 Unordered two-stage weighted distance measures between two collections of PDHFSs in discrete case

Some discrete unordered two-stage weighted distances between ${\rm M}$ and ${\rm N}$ are defined as follows.

• (1) The generalized discrete unordered two-stage weighted distance (GDUT-SWD) between $M$ and $N$ is defined as:

  $$d_{gdut - s\omega d} \left( {M,N} \right) = \left[ {\frac{1}{2}\sum\nolimits_{i = 1}^{n} {\left( {\frac{{w_{i} }}{{\Phi_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Phi_{{x_{i} }} }} {p_{DUMD}^{\lambda } \left( {M,N} \right)} + \frac{{\eta_{i} }}{{\Psi_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Psi_{{x_{i} }} }} {p_{DUNMD}^{\lambda } \left( {M,N} \right)} } \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $w_{i} \left( {i = 1,2, \cdots ,n} \right)$ with $\sum\nolimits_{i = 1}^{n} {w_{i} } = 1$ and $\eta_{i} \left( {i = 1,2, \cdots ,n} \right)$ with $\sum\nolimits_{i = 1}^{n} {\eta_{i} } = 1$ be the weights assigned to MD and NMD of PDHFS.

  If $\lambda { = }1$, GDUT-SWD becomes the discrete unordered two-stage weighted Hamming distance (DUT-SWHD); If $\lambda = 2$, GDUT-SWD becomes the discrete unordered two-stage weighted Euclidean distance (DUT-SWED).

• (2) The generalized discrete unordered two-stage weighted hausdorff distance (GDUT-SWHD) between $M$ and $N$ is defined as:

  $$d_{gdut - s\omega hd} \left( {M,N} \right) = \left[ {\sum\nolimits_{i = 1}^{n} {\left( {\mathop {\max }\limits_{j} \left( {w_{i} p_{DUMD}^{\lambda } \left( {M,N} \right),\eta_{i} p_{DUNMD}^{\lambda } \left( {M,N} \right)} \right)} \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $\lambda > 0$.

  If $\lambda { = }1$, GDUT-SWHD becomes the discrete unordered two-stage weighted Hamming-Hausdoff distance (DUT-SWHHD); If $\lambda = 2$, GDUT-SWHD becomes the discrete unordered two-stage weighted Euclidean-Hausdorff distance (DUT-SWEHD).

  Combining the GDUT-SWD and the GDUT-SWHD, the generalized discrete unordered two-stage hybrid weighted distance (GDUT-SHWD) between $M$ and $N$ is defined as:

  $$d_{gdut - sh\omega d} \left( {M,N} \right) = \left\{ {\frac{1}{2}\sum\nolimits_{i = 1}^{n} {\left[ \begin{gathered} \frac{1}{2}\left( {\frac{{w_{i} }}{{\Gamma_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Gamma_{{x_{i} }} }} {p_{DUMD}^{\lambda } \left( {M,N} \right)} + \frac{{\eta_{i} }}{{\Upsilon_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Upsilon_{{x_{i} }} }} {p_{DUNMD}^{\lambda } \left( {M,N} \right)} } \right) \hfill \\ + \mathop {\max }\limits_{j} \left( {w_{i} p_{DUMD}^{\lambda } \left( {M,N} \right),\eta_{i} p_{DUNMD}^{\lambda } \left( {M,N} \right)} \right) \hfill \\ \end{gathered} \right]} } \right\}^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $\lambda > 0$.

  If $\lambda = 1$, GDUT-SHWD becomes the discrete unordered two-stage hybrid weighted Hamming distance (DUT-SHWHD); If $\lambda = 2$, GDUT-SHWD becomes the discrete unordered two-stage hybrid weighted Euclidean distance (DUT-SHWED).

4.6 Unordered two-stage weighted distance measures between two collections of PDHFSs in continuous case

Some continuous unordered two-stage weighted distances between $M$ and $N$ are defined as follows.

• (1) The generalized continuous unordered two-stage weighted distance (GCUT-SWD) between $M$ and $N$ is defined as:

  $$d_{gcut - s\omega d} \left( {M,N} \right) = \left[ {\frac{1}{2}\int_{a}^{b} {\left( {\frac{w\left( x \right)}{{\Phi_{x} }}\sum\nolimits_{j = 1}^{{\Phi_{x} }} {p_{CUMD}^{\lambda } \left( {M,N} \right)} + \frac{\eta \left( x \right)}{{\Psi_{x} }}\sum\nolimits_{j = 1}^{{\Psi_{x} }} {p_{CUNMD}^{\lambda } \left( {M,N} \right)} } \right)dx} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $\lambda > 0$, $w\left( x \right)$ with $\int_{a}^{b} {w\left( x \right)dx = 1}$ and $\eta \left( x \right)$ with $\int_{a}^{b} {\eta \left( x \right)dx = 1}$ be the weights assigned to MD and NMD of PDHFS.

If $\lambda = 1$, GCUT-SWD becomes the continuous unordered two-stage weighted Hamming distance (CUT-SWHD); If $\lambda = 2$, GCUT-SWD becomes the continuous unordered two-stage weighted Euclidean distance (CUT-SWED); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\eta \left( x \right) = \frac{1}{b - a}$, GCUT-SWD becomes the generalized continuous unordered two-stage equal weighted distance (GCUT-SEWD); If $\omega \left( x \right) = \frac{1}{b - a}$, $\eta \left( x \right) = \frac{1}{b - a}$ and $\lambda = 1$, GCUT-SWD becomes the continuous unordered two-stage equal weighted Hamming distance (CUT-SEWHD); If $\omega \left( x \right) = \frac{1}{b - a}$, $\eta \left( x \right) = \frac{1}{b - a}$ and $\lambda = 2$, GCUT-SWD becomes the continuous unordered two-stage equal weighted Euclidean distance (CUT-SEWED).

Next, we define a generalized continuous unordered two-stage weighted Hausdorff distance (GCUT-SWHD) between $M$ and $N$ is defined as:

$$d_{gcut - s\omega hd} \left( {M,N} \right) = \left\{ {\int_{a}^{b} {\left( {\mathop {\max }\limits_{j} \left( {w\left( x \right)p_{CUMD}^{\lambda } \left( {M,N} \right),\eta \left( x \right)p_{CUNMD}^{\lambda } \left( {M,N} \right)} \right)} \right)dx} } \right\}^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

where $\lambda > 0$.

If $\lambda = 1$, GCUT-SWHD becomes the continuous unordered two-stage weighted Hamming-Hausdorff distance (CUT-SWHHD); If $\lambda = 2$, GCUT-SWHD becomes the continuous unordered two-stage weighted Euclidean-Hausdorff distance (CUT-SWEHD); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\eta \left( x \right) = \frac{1}{b - a}$, GCUT-SWHD becomes the generalized continuous unordered two-stage equal weighted Hausdorff distance (GCUT-SEWHD); If $\omega \left( x \right) = \frac{1}{b - a}$, $\eta \left( x \right) = \frac{1}{b - a}$ and $\lambda = 1$, GCUT-SWHD becomes the continuous unordered two-stage equal weighted Hamming-Hausdorff distance (CUT-SEWHHD); If $\omega \left( x \right) = \frac{1}{b - a}$, $\eta \left( x \right) = \frac{1}{b - a}$ and $\lambda = 2$, GCUT-SWHD becomes the continuous unordered two-stage equal weighted Euclidean-Hausdorff distance (CUT-SEWEHD).

Similarly, some hybrid continuous unordered two-stage weighted distance measures can be defined. Next, we define the generalized continuous unordered two-stage hybrid weighted distance (GCUT-SHWD):

$$d_{gcut - sh\omega d} \left( {M,N} \right) = \left[ {\frac{1}{2}\int_{a}^{b} {\left( \begin{gathered} \frac{1}{2}\left( {\frac{w\left( x \right)}{{\Phi_{x} }}\sum\nolimits_{j = 1}^{{\Phi_{{x_{i} }} }} {p_{CUMD}^{\lambda } \left( {M,N} \right)} + \frac{\eta \left( x \right)}{{\Psi_{x} }}\sum\nolimits_{j = 1}^{{\Psi_{{x_{i} }} }} {p_{CUNMD}^{\lambda } \left( {M,N} \right)} } \right) \hfill \\ + \mathop {\max }\limits_{j} \left( {w\left( x \right)p_{CUMD}^{\lambda } \left( {M,N} \right),\eta \left( x \right)p_{CUNMD}^{\lambda } \left( {M,N} \right)} \right) \hfill \\ \end{gathered} \right)dx} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

where $\lambda > 0$.

If $\lambda = 1$, GCUT-SHWD becomes the continuous unordered two-stage hybrid weighted Hamming distance (CUT-SHWHD); If $\lambda = 2$, GCUT-SHWD becomes the hybrid continuous two-stage weighted Euclidean distance (CUT-SHWED); If $\omega \left( x \right) = \frac{1}{b - a}$ and $\eta \left( x \right) = \frac{1}{b - a}$, GCUT-SHWD becomes the generalized continuous unordered two-stage hybrid equal weighted distance (GCUT-SHEWD); If $\omega \left( x \right) = \frac{1}{b - a}$, $\eta \left( x \right) = \frac{1}{b - a}$ and $\lambda = 1$, GCUT-SHWD becomes the continuous unordered two-stage hybrid equal weighted Hamming distance (CUT-SHEWHD); If $\omega \left( x \right) = \frac{1}{b - a}$, $\eta \left( x \right) = \frac{1}{b - a}$ and $\lambda = 2$, GCUT-SHWD becomes the continuous unordered two-stage hybrid equal weighted Euclidean distance (CUT-SHEWED).

4.7 Ordered two-stage weighted distance measures between two collections of PDHFSs in discrete case

The generalized discrete ordered two-stage weighted distance (GDOT-SWD) and generalized discrete ordered two-stage weighted Hausdorff distance (GDOT-SWHD) between $M$ and $N$ are defined as:

$$d_{gdot - s\omega d} \left( {M,N} \right) = \left[ {\frac{1}{2}\sum\limits_{i = 1}^{n} {\left( {\frac{{w_{i} }}{{\Gamma_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Gamma_{{x_{i} }} }} {p_{DOMD}^{\lambda } \left( {M,N} \right)} + \frac{{\eta_{i} }}{{\Upsilon_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Upsilon_{{x_{i} }} }} {p_{DONMD}^{\lambda } \left( {M,N} \right)} } \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

(9)

$$d_{gdot - s\omega hd} \left( {M,N} \right) = \left( {\sum\limits_{i = 1}^{n} {\mathop {\max }\limits_{j} \left( {w_{i} p_{DOMD}^{\lambda } \left( {M,N} \right),\eta_{i} p_{DONMD}^{\lambda } \left( {M,N} \right)} \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

where $\lambda > 0$.

If $\lambda { = }1$, GDOT-SWD and GDOT-SWHD become the discrete ordered two-stage weighted Hamming distance (DOT-SWHD) and the discrete ordered two-stage weighted Hamming–Hausdorff distance (DOT-SWHHD), respectively. If $\lambda { = 2}$, GDOT-SWD and GDOT-SWHD become the discrete ordered two-stage weighted Euclidean distance (DOT-SWED) and the discrete ordered two-stage weighted Euclidean–Hausdorff distance (DOT-SWEHD). Combining the GDOT-SWD and the GDOT-SWHD, the generalized discrete ordered two-stage hybrid weighted distance (GDOT-SHWD) between $M$ and $N$ is defined as:

$$d_{gdot - sh\omega d} \left( {M,N} \right) = \left\{ {\frac{1}{2}\sum\nolimits_{i = 1}^{n} {\left[ \begin{gathered} \frac{1}{2}\left( {\frac{{w_{i} }}{{\Gamma_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Gamma_{{x_{i} }} }} {p_{DOMD}^{\lambda } \left( {M,N} \right)} + \frac{{\eta_{i} }}{{\Upsilon_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Upsilon_{{x_{i} }} }} {p_{DONMD}^{\lambda } \left( {M,N} \right)} } \right) \hfill \\ + \mathop {\max }\limits_{j} \left( {w_{i} p_{DOMD}^{\lambda } \left( {M,N} \right),\eta_{i} p_{DONMD}^{\lambda } \left( {M,N} \right)} \right) \hfill \\ \end{gathered} \right]} } \right\}^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

where $\lambda > 0$.

If $\lambda = 1$, GDOT-SHWD becomes the discrete ordered two-stage hybrid weighted Hamming distance (DOT-SHWHD); If $\lambda = 2$, GDOT-SHWD becomes the discrete ordered two-stage hybrid weighted Euclidean distance (DOT-SHWED).

4.8 Ordered two-stage weighted distance measures between two collections of PDHFSs in continuous case

Some continuous ordered two-stage weighted distances between $M$ and $N$ are defined as:

• (1) The generalized continuous ordered two-stage weighted distance (GCOT-SWD) between $M$ and $N$ is defined as:

  $$d_{{g{\text{co}} t - s\omega d}} \left( {M,N} \right) = \left[ {\frac{1}{2}\int_{a}^{b} {\left( {\frac{w\left( x \right)}{{\Gamma_{x} }}\sum\nolimits_{j = 1}^{{\Gamma_{x} }} {p_{COMD}^{\lambda } \left( {M,N} \right)} + \frac{\eta \left( x \right)}{{\Upsilon_{x} }}\sum\nolimits_{j = 1}^{{\Upsilon_{x} }} {p_{CONMD}^{\lambda } \left( {M,N} \right)} } \right)dx} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $\lambda > 0$.

If $\lambda = 1$, GCOT-SWD becomes the continuous ordered two-stage weighted Hamming distance (COT-SWHD); If $\lambda = 2$, GCOT-SWD becomes the continuous ordered two-stage weighted Euclidean distance (COT-SWED); If $w\left( x \right) = \frac{1}{b - a}$ and $\eta \left( x \right) = \frac{1}{b - a}$, GCOT-SWD becomes the generalized continuous ordered two-stage equal weighted distance (GCOT-SEWD); If $w\left( x \right) = \frac{1}{b - a}$, $\eta \left( x \right) = \frac{1}{b - a}$ and $\lambda = 1$, GCOT-SWD becomes the continuous ordered two-stage equal weighted Hamming distance (COT-SEWHD); If $w\left( x \right) = \frac{1}{b - a}$, $\eta \left( x \right) = \frac{1}{b - a}$ and $\lambda = 2$, GCOT-SWD becomes the continuous ordered two-stage equal weighted Euclidean distance (COT-SEWED).

Next, we define a generalized continuous ordered two-stage weighted Hausdorff distance (GCOT-SWHD) between $M$ and $N$ is defined as:

$$d_{gcot - s\omega hd} \left( {M,N} \right) = \left\{ {\int_{a}^{b} {\left( {\mathop {\max }\limits_{j} \left( {w\left( x \right)p_{COMD}^{\lambda } \left( {M,N} \right),\eta \left( x \right)p_{CONMD}^{\lambda } \left( {M,N} \right)} \right)} \right)dx} } \right\}^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

where $\lambda > 0$.

If $\lambda = 1$, GCOT-SWHD becomes the continuous ordered two-stage weighted Hamming-Hausdorff distance (COT-SWHHD); If $\lambda = 2$, GCOT-SWHD becomes the continuous ordered two-stage weighted Euclidean-Hausdorff distance (COT-SWEHD); If $w\left( x \right) = \frac{1}{b - a}$ and $\eta \left( x \right) = \frac{1}{b - a}$, GCOT-SWHD becomes the generalized continuous ordered two-stage equal weighted Hausdorff distance (GCOT-SEWHD); If $w\left( x \right) = \frac{1}{b - a}$, $\eta \left( x \right) = \frac{1}{b - a}$ and $\lambda = 1$, GCOT-SWHD becomes the continuous ordered two-stage equal weighted Hamming-Hausdorff distance (COT-SEWHHD); If $w\left( x \right) = \frac{1}{b - a}$, $\eta \left( x \right) = \frac{1}{b - a}$ and $\lambda = 2$, GCOT-SWHD becomes the continuous ordered two-stage equal weighted Euclidean-Hausdorff distance (COT-SEWEHD).

Similarly, some continuous ordered hybrid continuous weighted distance measures can be defined.

• (1) The generalized continuous ordered two-stage hybrid weighted distance (GCOT-SHWD):

  $$d_{gcot - sh\omega d} \left( {M,N} \right) = \left[ {\frac{1}{2}\int_{a}^{b} {\left( \begin{gathered} \frac{1}{2}\left( {\frac{w\left( x \right)}{{\Gamma_{x} }}\sum\nolimits_{j = 1}^{{\Gamma_{x} }} {p_{COMD}^{\lambda } \left( {M,N} \right)} + \frac{\eta \left( x \right)}{{\Upsilon_{x} }}\sum\nolimits_{j = 1}^{{\Upsilon_{x} }} {p_{CONMD}^{\lambda } \left( {M,N} \right)} } \right) \hfill \\ + \mathop {\max }\limits_{j} \left( {w\left( x \right)p_{COMD}^{\lambda } \left( {M,N} \right),\eta \left( x \right)p_{CONMD}^{\lambda } \left( {M,N} \right)} \right) \hfill \\ \end{gathered} \right)dx} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}$$

  where $\lambda > 0$.

If $\lambda = 1$, GCOT-SHWD becomes the continuous ordered two-stage hybrid weighted Hamming distance (COT-SHWHD); If $\lambda = 2$, GCOT-SHWD becomes the continuous ordered two-stage hybrid weighted Euclidean distance (COT-SHWED); If $w\left( x \right) = \frac{1}{b - a}$ and $\eta \left( x \right) = \frac{1}{b - a}$, GCOT-SHWD becomes the generalized continuous ordered two-stage hybrid equal weighted distance (GCOT-SHEWD); If $w\left( x \right) = \frac{1}{b - a}$, $\eta \left( x \right) = \frac{1}{b - a}$ and $\lambda = 1$, GCOT-SHWD becomes the continuous ordered two-stage hybrid equal weighted Hamming distance (COT-SHEWHD); If $w\left( x \right) = \frac{1}{b - a}$, $\eta \left( x \right) = \frac{1}{b - a}$ and $\lambda = 2$, GCOT-SHWD becomes the continuous ordered two-stage hybrid equal weighted Euclidean distance (COT-SHEWED).

Theorem 1

From the form of the formula given above in Sects. 4.1–4.8, the distance measures in Sect. 4.1 is special case of the distance measures in Sect. 4.5; the distance measures in Sect. 4.2 is special case of the distance measures in Sect. 4.6; the distance measures in Sect. 4.3 is special case of the distance measures in Sect. 4.7; the distance measures in Sect. 4.4 is special case of the distance measures in Sect. 4.8.

5 Some similarity measures for PDHFSs

In the field of MADM, similarity measure is a very important tool in solving the MADM problems. Researchers have proposed some similarity measures for FS, type-2FS, IFS, IVIFS, HFS, DHFS, and so on. For example, Beg and Ashraf [55] proposed the similarity measure for FS. The similarity measures for type-2 fuzzy sets were proposed [56,57,58,59,60,61]. The similarity measures for IFS [62,63,64,65,66,67]. The similarity measures for PFS [68,69,70,71,72]. The similarity measures for IVIFS [73,74,75,76]. Hu et al. [77] proposed the similarity measure for HFS. The similarity measures for DHFS [78, 79]. From the literatures, there is no research on the similarity measure of PDHFS, and the existing similarity measures can’t calculate the similarity of two PDHFSs, so it is necessary to study the similarity measure of PDHFS.

From the literatures review, most studies on similarity measure have given the axiomatic definition of similarity measure. Next, before giving the similarity measure between two PDHFSs, we first give the axiomatic definition of similarity measure for PDHFS, then we will define the similarity measure between two PDHFSs with the help of the distance measure between two PDHFSs proposed above.

Definition 6

Let $M$ and $N$ be two PDHFSs on $X$, then $s\left( {M,N} \right)$ is called as similarity measure between ${\rm M}$ and ${\rm N}$, if $s\left( {M,N} \right)$ satisfies:

• (A1) $0 \le s\left( {M,N} \right) \le 1$;

• (A2) $s\left( {M,N} \right) = 1 - d\left( {M,N} \right)$;

• (A3) $s\left( {M,N} \right) = 1$ if and only if $M = N$;

• (A4) $s\left( {M,N} \right) = s\left( {N,M} \right)$ if and only if $M = N$.

Based on Eq. (3), we obtain the similarity measure corresponding to the distance measure as follows:

$$\begin{gathered} s\left( {M,N} \right) = 1 - d_{gdu\omega d} \left( {M,N} \right) \hfill \\ \quad \quad \quad \;\, = 1 - \left[ {\frac{1}{2}\sum\nolimits_{i = 1}^{n} {\omega_{i} \left( {\frac{1}{{\Phi_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Phi_{{x_{i} }} }} {p_{DUMD}^{\lambda } \left( {M,N} \right)} + \frac{1}{{\Psi_{{x_{i} }} }}\sum\nolimits_{j = 1}^{{\Psi_{{x_{i} }} }} {p_{DUNMD}^{\lambda } \left( {M,N} \right)} } \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} \hfill \\ \end{gathered}$$

(10)

Using the distance defined in Sects. 4.1–4.8 instead of $d_{gdu\omega d} \left( {M,N} \right)$ in the above similarity measure, we can get the corresponding similarity measure.

6 A numerical example and comparative analysis

In this subsection, we applied our proposed making technique to select the optimal alternative in MAGDM with PDHF information in discrete ordered cases.

The following is a basic description of a PDHF MAGDM problem. Let $X = \left\{ {X_{1} ,X_{2} , \cdots ,X_{m} } \right\}$ be a set of alternatives, and $C = \left\{ {C_{1} ,C_{2} , \cdots ,C_{n} } \right\}$ be decision attributes for a MAGDM with PDHFSs, and $E = \left\{ {e_{1} ,e_{2} , \cdots ,e_{p} } \right\}$ be a set of decision experts, whose weight vector is $\omega = \left( {\omega_{1} ,\omega_{2} , \cdots ,\omega_{p} } \right)^{T}$. The decision-making provides decision information with PDHFSs $d_{ij} = \left( {\left. {h_{ij} } \right|p_{ij} ,\left. {g_{ij} } \right|q_{ij} } \right)\left( {i = 1,2, \cdots ,m;j = 1,2, \cdots ,n} \right)$, thus, we obtain the decision matrix $D = \left( {d_{ij} } \right)_{mn}$. In order to better identify the optimal alternative from the alternative sets, the concept of ideal point is proposed. In this study, let $C^{ + } { = }\left( {C_{1}^{ + } ,C_{2}^{ + } , \cdots ,C_{n}^{ + } } \right)$ be the most ideal PDHFS in the PDHFSs. Because PDHFS is divided into MD and NMD, in practice, the weights of these two parts should also be different, so we let $w_{j} \in \left[ {0,1} \right],j = 1,2, \cdots ,l_{{x_{i} }}$, $\sum\nolimits_{j = 1}^{n} {w_{j} } = 1$ and $\eta_{j} \in \left[ {0,1} \right],j = 1,2, \cdots ,m_{{x_{i} }}$, $\sum\nolimits_{j = 1}^{n} {\eta_{j} } = 1$ be the weighting assigned to MD and NMD in each alternative, respectively.

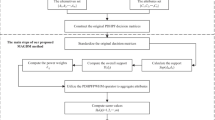
Then, basic calculation steps of the proposed decision-making technique is as follows:

• Step 1: Obtain the PDHF decision matrix $D = \left( {d_{ij} } \right)_{m \times n} \left( {i = 1,2, \cdots ,m;j = 1,2, \cdots ,n} \right)$;

• Step 2: Obtain the normalized decision matrix $D^{^{\prime}} = \left( {d_{ij}^{C} } \right)_{m \times n}$;

• Step 3: Obtain the collective assessment information matrix for six alternatives under four attributes through aggregating the opinion of three experts according to the Eq. (7).

• Step 4: Calculate the ideal point vector $X^{ + } { = }\left( {C_{1}^{ + } ,C_{2}^{ + } , \cdots ,C_{n}^{ + } } \right)$ of attributes according to the Definition 2;

• Step 5: Calculate $d_{gdo\omega d}$ and $d_{gdot - s\omega d}$ between alternative $X_{i} \left( {i = 1,2, \cdots ,m} \right)$ and $X^{ + }$ according to the Eqs. (8) and (9);

• Step 6: Calculate the similarity measure between alternative $X_{i} \left( {i = 1,2, \cdots ,m} \right)$ and the ideal point vector $X^{ + }$ using $s_{gdo\omega d} \left( {X_{i} ,X^{ + } } \right) = 1 - d_{gdo\omega d} \left( {X_{i} ,X^{ + } } \right)$ and $s_{gdot - s\omega d} \left( {X_{i} ,X^{ + } } \right) = 1 - d_{gdot - s\omega d} \left( {X_{i} ,X^{ + } } \right)$, respectively;

• Step 7: Sort the alternatives by values of similarity measure;

• Step 8: Select the optimal alternative according to the value of maximum similarity measure.

6.1 A numerical example

6.1.1 Application of MAGDM technique in sustainability assessment of new urbanization

New urbanization is a necessary historical process after China’s economic and social development to a certain extent. The 17th National Congress of the Communist Party of China clearly put forward that the 18th and 19th national congresses further emphasized the path of urbanization with Chinese characteristics. In recent years, a large number of scholars have invested in the research on the measurement of the development level of new urbanization, and analyzed the possibility of building a new urbanization evaluation system from different aspects, so as to measure the quality of urbanization development and evaluate the suitability of new urbanization. In the illustrative example (adapted from Ref. [32]), there are six alternatives $X_{i} \left( {i = 1,2, \cdots ,6} \right)$ to be evaluated. Four decision attributes are employed: the infrastructure factor ($C_{1}$), the economic and development factor ($C_{2}$), the ecological environment factor ($C_{3}$) and the equity factor ($C_{4}$). In the evaluation process, there are three experts $E_{i} \left( {i = 1,2,3} \right)$ to give the original preference values, whose weight vector is $\nu = \left( {0.2,0.3,0.5} \right)^{T}$, the three experts give the original evaluation values of $X_{1}$, $X_{2}$, $X_{3}$, $X_{4}$, $X_{5}$, and $X_{6}$ under $C_{1}$, $C_{2}$, $C_{3}$ and $C_{4}$. The weight vector of attribute is in the distance measure $d_{gdo\omega d} \left( {X_{i} ,X^{ + } } \right)$ is $\omega = \left( {0.1,0.4,0.2,0.3} \right)$, the weight vectors of MD and NMD are $w = \left( {0.2,0.4,0.1,0.3} \right)$ and $\eta = \left( {0.1,0.35,0.25,0.3} \right)$ in the distance measure $d_{gdot - s\omega d} \left( {X_{i} ,X^{ + } } \right)$, where $\lambda = 2$. All assessments values are given by three experts in Tables 1, 2 and 3.

Table 1 The PDHF decision matrix given by $E_{1}$

Table 2 The PDHF decision matrix given by $E_{2}$

Table 3 The PDHF decision matrix given by $E_{3}$

Next steps, the proposed MAGDM technique is used to evaluate the suitability of new urbanization.

According to the steps 1–8, we can give the ranking of six alternatives is $X_{1} \succ X_{5} \succ X_{2} \succ X_{4} \succ X_{3} \succ X_{6}$ (by $s_{gdo\omega d} \left( {X_{i} ,X^{ + } } \right)$) and $X_{1} \succ X_{2} \succ X_{5} \succ X_{4} \succ X_{3} \succ X_{6}$ (by $s_{gdot - s\omega d} \left( {X_{i} ,X^{ + } } \right)$)(“$\succ$” means “super to”), respectively.

6.1.2 Application of MAGDM technique in sustainability assessment of new urbanization

In the illustrative example, there are four substation sites $X_{i} \left( {i = 1,2,3,4} \right)$ to be evaluated. Three attributes are employed: the geographical factor ($C_{1}$), the technical factor ($C_{2}$) and the environmental factor ($C_{3}$), two experts $e_{i} \left( {i = 1,2} \right)$ give the original preference values of $X_{1}$, $X_{2}$, $X_{3}$ and $X_{4}$ under $C_{1}$, $C_{2}$ and $C_{3}$, the weight vector of two experts is $\nu = \left( {0.4,0.6} \right)^{T}$. Two decision information matrices $\Re^{1}$ and $\Re^{2}$ are showed in Tables 4 and 5 by two experts.

Table 4 The PDHF decision information matrix $\Re^{1}$ obtained by $e_{1}$

Table 5 The PDHF decision information matrix $\Re^{2}$ obtained by $e_{2}$

According to the steps 1–8, we can give the ranking of four alternatives is $X_{2} \succ X_{1} \succ X_{3} \succ X_{4}$ (by $s_{gdo\omega d} \left( {X_{i} ,X^{ + } } \right)$) and $X_{2} \succ X_{1} \succ X_{3} \succ X_{4}$ (by $s_{gdot - s\omega d} \left( {X_{i} ,X^{ + } } \right)$)(“$\succ$” means “super to”), respectively.

6.2 Comparative analysis

6.2.1 Comparative analysis 1

Here, we compare the method proposed in this study with the BASD model based PROMETHEE-II method proposed by Ref. [33], let’s bring the data into the model.

Calculate the overall BASD degrees $H\left( {X_{i} } \right)\left( {i = 1,2, \cdots ,6} \right)$ for alternatives $X_{i} \left( {i = 1,2, \cdots ,6} \right)$, respectively, the overall BASD degrees are listed in Table 6.

Table 6 The overall BASD degrees $H^{ + } \left( {X_{i} } \right)$ and $H^{ - } \left( {X_{i} } \right)$

Thus, the ranking of alternatives is $X_{1} \succ X_{5} \succ X_{2} \succ X_{3} \succ X_{4} \succ X_{6}$. Although the order of alternatives a little different, the optimal alternative is $X_{1}$.

6.2.2 Comparative analysis 2

Here, we compare the method proposed in this study with the visualization model based on the entropy of PDHFS proposed by Ref. [32], let’s bring the data into the model. We can get $X_{1} \succ X_{4} \succ X_{5} \succ X_{2} \succ X_{3} \succ X_{6}$.

Although the order of alternatives a little different, the optimal alternative is $X_{1}$.

From the comparison with the two methods, although the ranking is slightly different, the best alternative is $X_{1}$, which shows that the MAGDM technique built in this study is effective, but the following analysis can also see the advantages of our proposed method.

7 Advantages of the proposed method

(1) On the basis of reviewing the famous Hamming distance, Euclidean distance, Hausdorff metric and their generalization, we divide the distance into discrete and continuous cases, ordered and unordered cases. We develop some PDHF distance measures and their weighted forms, and discussed their properties and relations as their parameters change.

(2) From the comparison and analysis of the two methods, the research results given by the method proposed in this study are basically consistent with results obtained by Refs. [32] and [33].

(3) We analyze the change of the ranking of the evaluated alternatives with the change of risk attribute parameter $\lambda$, which is more in line with the reality and gives DMs more choices. From the results, the ranking results are relatively stable, and the best alternative is always $X_{1}$, which also shows the superiority and effectiveness of the method proposed in this study.

(4) We can observe the change of the ranking of the evaluated alternatives with the change of values of risk attribute parameter $\lambda$ and weights $\omega$, $w$, $\eta$. From the results, the ranking is relatively stable, and the best object is always, which also shows the superiority and effectiveness of the method proposed in this study.

Because the ranking results of alternatives are mainly affected by the risk attribute parameter $\lambda$, the weight $\omega$ of attribute is in the distance measure $d_{gdo\omega d} \left( {X_{i} ,X^{ + } } \right)$, the weights $w$ and $\eta$ of MD and NMD in the distance measure $d_{gdot - s\omega d} \left( {X_{i} ,X^{ + } } \right)$. Next, we analyze the change of the ranking of the evaluated alternatives with the different changes of DMs’ attitude $\lambda$, weight $\omega$, weights $w$ and $\eta$ of MD and NMD.

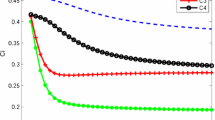
(1) Analysis of the change of the ranking of the evaluated alternatives with the different $\lambda$ and $\omega = \left( {0.1,0.4,0.2,0.3} \right)$, the ranking changes of alternatives are shown in Table 7 and Fig. 1.

Table 7 The $s_{gdo\omega d} \left( {X_{i} ,X^{ + } } \right)$ for different values of DMs’ attitude $\lambda$

Fig. 1

The change of $s_{gdo\omega d} \left( {X_{i} ,X^{ + } } \right)$ for different values of DMs’ attitude $\lambda$

Next, we analyze the change of the ranking of the evaluated alternatives with the change of $\lambda$ value.

(2) Analysis of the change of the ranking of the evaluated alternatives with the different $\lambda$ and different weights $w$ and $\eta$ of MD and NMD, the results are listed in Tables 8, 9, 10, 11 and Fig. 2.

Table 8 The $s_{gdot - s\omega d} \left( {X_{i} ,X^{ + } } \right)$ for different $w$, $\eta$ and different $\lambda$

Table 9 The $s_{gdot - s\omega d} \left( {X_{i} ,X^{ + } } \right)$ for different $w$, $\eta$ and different $\lambda$

Table 10 The $s_{gdot - s\omega d} \left( {X_{i} ,X^{ + } } \right)$ for different $w$, $\eta$ and different $\lambda$

Table 11 The $s_{gdot - s\omega d} \left( {X_{i} ,X^{ + } } \right)$ for different $w$, $\eta$ and different $\lambda$

Fig. 2

The change of $s_{gdot - s\omega d} \left( {X_{i} ,X^{ + } } \right)$ for different $w$, $\eta$ and different $\lambda$

8 Conclusions

As we all know, distance and similarity measures play a very important role in the field of decision-making. Through literatures analysis, we find that the research on distance and similarity measures of PDHFS is relatively lacking. In this study, we study the distance and similarity measures of PDHFS. On the basis of reviewing the famous Hamming distance, Euclidean distance, Hausdorff metric and their generalization, we divide the distance into discrete and continuous cases, ordered and unordered cases. We develop some PDHF distance measures, and discussed their properties and relations as their parameters change. We also give various weighted distance measures of PDHFS. Using the relationship between distance measure and similarity measure, the corresponding similarity measures of PDHFS are obtained. It should be noted that all the above measures are based on two assumptions: if the different PDHFEs have the different lengths or same length, if the lengths are different, the shorter PDHFE should be extended by adding the minimum or maximum element until the two PDHFSs have the same length. In fact, we can extend the shorter PDHFE by adding any element according to the preference and actual situation of the decision-maker until it has the same length as the longer PDHFE. In the future research, In the next research work, we will continue to focus on the research of decision-making methods and aggregation operators, such as QUALIFLEX method, BWM method, ARAS method, WASPAS method [80,81,82,83] with the PDHF environment, study the PDHF aggregation operator, and propose some new MADM method. It is also committed to applying the decision-making method proposed in this study to uncertain MAGDM problems such as pattern recognition and substation optimization.