Global exponential stability of uncertain memristor-based recurrent neural networks with mixed time delays

Abstract

The global exponential stability of the equilibrium point for uncertain memristor-based recurrent neural networks is studied in this paper. The memristor-based recurrent neural networks considered in this paper are based on a realistic memristor model, and can be considered as the extension of some existing memristor-based recurrent neural networks. By virtue of homomorphic theory, it is proved that the uncertain memristor-based recurrent neural networks have a unique equilibrium point under some mild assumptions. Moreover, the unique equilibrium point is proved to be globally exponentially stable by constructing a suitable Lyapunov functional. Finally, the obtained results are applied to determine the dynamical behaviors and circuit design of the memristor-based recurrent neural networks by some numerical examples.

1 Introduction

In 1971, Professor Chua [1] theoretically predicted the existence of a new two-terminal circuit element called the memristor (a contraction for memory and resistor). Chua believed that memristor has every right to be the fourth fundamental passive circuit element. However, until 2008, the Williams group built the first solid-state memristor, which was modeled as a thin semiconductor film ($\hbox {TiO}_2$) sandwiched between two metal contacts [2]. Because of the important memory feature, the memristor has generated unprecedented worldwide interest since its potential applications in next generation computers and powerful brain-like neural computers (see [3, 4]).

In recent years, various recurrent neural networks have been proposed and their dynamic behaviors are studied extensively since their wide applications in pattern recognition, image processing, associative memory, neurodynamic optimization problems and so on (see [5,6,7,8,9,10,11,12,13,14,15]). Meanwhile, more and more researchers observe that time delays are unavoidable and can influence greatly the dynamical behaviors of neural networks (see [16,17,18,19,20]). In general, these delays include discrete delays, time-varying delays, distributed delays and so on. However, the conventional recurrent neural network’s connection weights are implemented by resistors, and do not have any memory property. The memristor works like a biological synapse, with its conductance varying with experience, or with the current flowing through it over time [21, 22]. Compared with the resistor, the memristor is more suitably used as synapse in neural networks since its nanoscale size, automatic information storage, and nonvolatile characteristic with respect to long periods of power-down [23]. This special behavior can be applied in artificial neural networks, i.e., memristor-based neural network (see [21]). Memristor-based neural networks have proven as a promising architecture in neuromorphic systems for the non-volatility, high-density, and unique memristive characteristic. There exist several different mathematical models for the memristor-based neural networks. For example, in 2010, Hu and Wang [24] proposed a mathematical model for the memristor-based neural networks and studied its global uniform asymptotic stability by a constructing proper Lyapunov functional. In [25], combining with the typical current–voltage characteristics of memristor, Wu et.al introduced a simple model of the memristor-based recurrent neural networks.

It is well known that the applications of neural networks rely heavily on the dynamical behaviors of the networks, such as stability, periodic oscillatory, chaos, and so on. Meanwhile, the analysis of dynamical behaviors of the memristor-based neural networks has been found useful to address a number of interesting engineering applications and therefore have been studied extensively (see [22, 26,28,29,30,31,32,32]). Based on a realistic memristor model and differential inclusion theory, authors in [22] studied the convergence and attractivity of memristor-based cellular neural networks with time delays. Wu et al. in [28] introduced some Lagrange stability criteria dependent on the network parameters for the Lagrange stability of the memristor-based recurrent neural networks with discrete and distributed delays. The paper [33] presented some new theoretical results on the invariance and attractivity of memristor-based cellular neural networks with time-varying delays. In [34], Wu et.al designed a simple memristor-based neural network model. Based on the fuzzy theory and Lyapunov method, they studied the problem of global exponential synchronization of a class of memristor-based recurrent neural networks with time-varying delays. In [35], the global asymptotic stability and synchronization of a class of fractional-order memristor-based delayed neural networks were investigated.

Meanwhile, the estimation errors are unavoidable for the numerical values of the neural network parameters including the neuron fire rate and the weight coefficients depending on certain resistance and capacitance. Moreover, some other external disturbances such as noise are also unavoidable. It should be noted that the uncertainty may change the stability of the neural network. On the other hand, transmission delay is also unavoidable when signals are communicated among neurons, and the transmission delay may lead to some undesired complex dynamical behaviors. In general, the transmission delay includes discrete delays, time-varying delays and distributed delays and so on. For example, by exploiting all possible information in mixed time delays, two discrete-time mixed delay neural networks were studied separately in [36, 37]. So, it is reasonable to study the dynamical behaviors of the uncertain memristor-based neural networks with time delays. Recently, more and more literatures focus on the stability of uncertain neural networks with mixed time delays (see [36,38,39,39]). For example, in [38], author studied the global asymptotic robust stability of delayed neural networks with norm-bounded uncertainties. The problems of robust stability analysis and robust controller designing of an uncertain memristive neural networks were studied in [40]. Reference [41] was concerned with the global robust synchronization of multiple memristive neural networks with nonidentical uncertain parameters.

However, as far as we know, there are very few literatures concerning on the stability of the uncertain memristor-based recurrent neural networks with time-varying delays and distributed delays. Motivated by the above works, we will study the existence and global exponential stability of the equilibrium point for a class of the uncertain memristor-based recurrent neural networks with time-varying delays and distributed delays. The neural network considered in this paper can be considered as an extension of the neural network in [34]. The structure of this paper is outlined as follows. In Sect. 2, we introduce the memristor-based recurrent neural network model and some related preliminaries. In Sect. 3, we prove the existence and global exponential stability of the equilibrium point for a class of the uncertain memristor-based recurrent neural networks. In Sect. 4, we present several numerical simulations to show the effectiveness of our results. Finally, the main conclusions drawn in the paper are summarized.

$\mathbf{Notation }$ Given the vector $x=(x_1,x_2,\ldots ,x_n)^T$, where the superscript T is the transpose operator, we let $\Vert x\Vert :=(\sum \nolimits _{i=1}^nx_i^2)^\frac{1}{2}$. ${\mathbb{R}}$ is the set of real numbers. Let $A=(a_{ij})\in {\mathbb{R}}^{n\times n}$ and define $\Vert A\Vert =\sqrt{\lambda _M(A^TA)}$, where $\lambda _M(A)$ stands for the operation of taking the maximum eigenvalue of A. $I\in {\mathbb{R}}^{n\times n}$ is the $n\times n$ identity matrix. For a real symmetric matrix A, $A<0(>0)$ means that A is negative (positive) definite.

Fig. 1

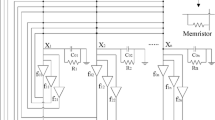
Circuit of memristor-based recurrent neural network in [34]

2 Neural network model and preliminaries

As shown in [34], the memristor-based recurrent neural network can be implemented by very large scale of integration circuits with memristors (see Fig. 1). By Kirchoff’s current law, the following memristor-based recurrent neural network was introduced in [34],

$$\begin{aligned} \begin{aligned} C_{i}\dot{x}_i(t)=&-\left[ \sum \limits _{j=1}^n\left( \frac{1}{R_{f_{ij}}} +\frac{1}{R_{g_{ij}}}\right) +W_i(x_i(t))\right] x_i(t)\\&+\sum \limits _{j=1}^n\frac{\text {sign}_{ij}}{R_{f_{ij}}}f_j(x_j(t))\\&+\sum \limits _{j=1}^n\frac{\text {sign}_{ij}}{R_{g_{ij}}}f_j(x_j(t-\tau _j(t))) +I_i,\\ \end{aligned} \end{aligned}$$

(1)

where $f_j$ is the activation function, $\tau _j(t)$ is the time-varying delay, and $x_i(t)$ is the voltage of the capacitor $C_i$. $R_{f_{ij}}$ is the resistor between the feedback function $f_j(x_j(t))$ and $x_i(t)$, and $R_{g_{ij}}$ is the resistor between the feedback function $f_j(x_j(t-\tau _j(t)))$ and $x_i(t)$. $\text {sign}_{ij}$ is defined as

$$\begin{aligned} \text {sign}_{ij}=\left\{ \begin{aligned}&1, \,\,&\text{ if } \quad i\ne j;\\&0, \,\,&\text{ if } \quad i= j. \end{aligned}\right. \end{aligned}$$

(2)

$W_i$ is the memductance of the i-th memristor satisfying

$$\begin{aligned} W_i(x_i(t))=\left\{ \begin{aligned}&W_i', \,\,&\text{ if } \quad x_i(t)\le 0;\\&W_i'', \,\,&\text{ if } \quad x_i(t)>0. \end{aligned}\right. \end{aligned}$$

(3)

$I_i$ is an external input or bias. Let

$$\begin{aligned} s(x_{i}(t)):=\left\{ \begin{aligned}&-1, \,\,\text{ if } \quad x_{i}(t)\le 0;\\&1, \,\,\text{ if } \quad x_{i}(t)>0, \end{aligned}\right. \end{aligned}$$

(4)

and

$$\begin{aligned} {m_i}:=\frac{W''_{i}-W'_{i}}{2C_{i}}. \end{aligned}$$

(5)

Then, by (3), we obtain that

$$\begin{aligned} \frac{W_i(x_i(t))}{C_{i}}={m_i}s(x_i(t))+\frac{W_i'+W_i''}{2C_{i}}. \end{aligned}$$

For simplicity, we let

$$\begin{aligned} \begin{aligned} d_i&=\sum \limits _{j=1}^n\left[ \frac{1}{C_{i}R_{f_{ij}}} +\frac{1}{C_{i}R_{g_{ij}}}\right] +\frac{W_i'+W_i''}{2C_{i}},\\ \;a_{ij}&=\frac{\text {sign}_{ij}}{C_{i}R_{f_{ij}}},\; b_{ij}=\frac{\text {sign}_{ij}}{C_{i}R_{g_{ij}}},\; U_{i}=\frac{I_{i}}{C_{i}}. \end{aligned} \end{aligned}$$

(6)

It follows that $[\sum \nolimits _{j=1}^n(\frac{1}{C_{i}R_{f_{ij}}}+\frac{1}{C_{i}R_{g_{ij}}})+\frac{W_i(x_i)}{C_{i}}]x_i =[d_i+{m_i}s(x_i)]x_i=d_ix_i+{m_i}|x_i|$. Hence, the memristor-based neural network (1) can be simplified as follows,

$$\begin{aligned} \begin{aligned} \dot{x}_i(t)=&-d_ix_i(t)-{m_i}|x_i(t)| +\sum \limits _{j=1}^na_{ij}f_j(x_j(t))\\&+\sum \limits _{j=1}^nb_{ij}f_j(x_j(t-\tau _j(t)))+U_i, \end{aligned} \end{aligned}$$

(7)

or,

$$\begin{aligned} \begin{aligned} \dot{x}(t)=&-Dx(t)-M|x(t)|+Af (x (t))\\&+Bf (x (t-\tau (t)))+U , \end{aligned} \end{aligned}$$

(8)

where $D=\text {diag}\{d_1,d_2,\ldots ,d_n\}$, ${M}=\text {diag}\{{m}_1,{m}_2,\ldots ,{m}_n\}$, $A=(a_{ij})_{n\times n}$, $B=(b_{ij})_{n\times n}$, $|x(t)|=(|x_1(t)|,\ldots ,|x_n(t)|)^T$, $\tau (t)=(\tau _1(t),\tau _2(t),\ldots ,\tau _n(t))^T$, $x (t-\tau (t))=(x_1(t-\tau _1(t)),\ldots ,x_n(t-\tau _n (t)))^T$, and $U=(U_{1},U_{2},\ldots ,U_{n})^{T}.$

Throughout the paper, we also need the following assumptions introduced in [34].

${\mathbf{(A_1)}}$ For $i\in \{1, 2,\ldots , n\}$, the activation function $f_i$ is Lipschitz continuous. That is, there exists $l_i>0$ such that for all $r_1, r_2\in {\mathbb{R}}$ with $r_1\ne r_2$,

$$\begin{aligned} 0\le \frac{f_i(r_1)-f_i(r_2)}{r_1-r_2}\le l_i. \end{aligned}$$

(9)

Here, we let $L=\text {diag}\{l_1,l_2,\ldots ,l_n\}$.

${\mathbf{(A_2)}}$ For $i\in \{1, 2, \ldots , n\}$, $\tau _i(t)$ satisfies

$$\begin{aligned} 0\le \tau _i(t)\le {\overline{\tau }}_i,\quad \dot{\tau }_i(t)\le 0. \end{aligned}$$

(10)

Here, we let ${\overline{\tau }}=\max \{{\overline{\tau }}_1,\ldots ,{\overline{\tau }}_n\}$.

Different from [34], we will study the following memristor-based neural network with time-varying delays and distributed delays,

$$\begin{aligned} \begin{aligned} \dot{x}_i(t)=&-d_ix_i(t)-{M_i}|x_i(t)|+\sum \limits _{j=1}^na_{ij}f_j(x_j(t))\\&+\,\sum \limits _{j=1}^nb_{ij}f_j(x_j(t-\tau _j(t)))\\&+\,\sum _{j=1}^ne_{ij}\int _{t-\mu _{j}}^{t}f_j(x_j(s))ds+U_i, \end{aligned} \end{aligned}$$

(11)

$i=1,2,\ldots ,n$. Neural network (11) can be considered as an extension of neural network (7). $e_{ij}$ and the time delay $\mu _j>0$ are two constants, and $\int _{t-\mu _{j}}^{t} f_j(x_j(s))ds$ is the distributed delay. The memristor-based neural network (11) can be rewritten as follows,

$$\begin{aligned} \begin{aligned} \dot{x}(t)=&-Dx(t)-M|x(t)|+Af(x(t))+Bf (x (t-\tau (t)))\\&+\,E\int _{t-\mu }^{t}f(x(s))ds+U, \end{aligned} \end{aligned}$$

(12)

where $E=(e_{ij})_{n\times n}$. It is clear that the neural network (12) can be considered as an extension of the neural network in [34] (i.e., (7) in this paper).

Next, we introduce the assumptions about the connection weight matrices as follows.

${\mathbf{(A_3)}}$ The parameters $D=\text {diag}\{d_1,d_2,\ldots ,d_{n}\}$, ${M}=\text {diag}\{{m}_1,{m}_2,\ldots ,{m}_n\}$, $A=(a_{ij})_{n \times n}$, $B=(b_{ij})_{n \times n}$, and $E=(e_{ij})_{n \times n}$ are assumed to be intervalised as follows,

$$\begin{aligned} \begin{aligned} D_{\mathcal {I}}&:=\{D=\text {diag}\{d_{i}\}: 0< {\underline{d_{i}}}\le d_{i}\le \overline{d_{i}}, \forall i=1,\ldots ,n\},\\ {M}_{\mathcal {I}}&:=\{{M}=\text {diag}\{{m}_{i}\}: {\underline{{m}}}_{i}\le {m}_{i}\le \overline{{m}}_{i}, \forall i=1,\ldots ,n\},\\ A_{\mathcal {I}}&:=\{A=(a_{ij})_{n\times n}: {\underline{a}}_{ij}\le a_{ij}\le \overline{a}_{ij}, \forall i,j=1,\ldots ,n\},\\ B_{\mathcal {I}}&:=\{B=(b_{ij})_{n\times n}: {\underline{b}}_{ij}\le b_{ij}\le {\overline{B}}_{ij}, \forall i,j=1,\ldots ,n\},\\ E_{\mathcal {I}}&:=\{E=(e_{ij})_{n\times n}: {\underline{e}}_{ij}\le e_{ij}\le {\overline{E}}_{ij}, \forall i,j=1,\ldots ,n\}. \end{aligned} \end{aligned}$$

(13)

Here, we let ${\underline{A}}=({\underline{a}}_{ij})_{n\times n}$, ${\underline{B}}=({\underline{b}}_{ij})_{n\times n}$, ${\underline{E}}=({\underline{e}}_{ij})_{n\times n}$, $\overline{A}=(\overline{a}_{ij})_{n\times n}$, ${\overline{B}}=({\overline{B}}_{ij})_{n\times n}$, and ${\overline{E}}=({\overline{E}}_{ij})_{n\times n}$. From the above assumption ${\mathbf{(A_3)}}$, the diagonal matrix D is invertible.

Lemma 1

If$H(x)\in {\mathcal {C}}^{0}$satisfies the following conditions

$$\begin{aligned}&(i)\, H(x)\ne H(y) \, \text{ for } \text{ all } x\ne y,\\&(ii) \,\Vert H(x)\Vert \rightarrow \infty \, as\, \Vert x\Vert \rightarrow \infty , \end{aligned}$$

then, H(x) is a homeomorphism of${\mathbb{R}}^{n}$.

The following lemmas are necessary for proving the existence and global exponential stability of the equilibrium point for the uncertain memristor-based recurrent neural network (11).

Lemma 2

[42] For$x\in {\mathbb{R}}^{n}$, $A\in A_{\mathcal {I}}$and any positive diagonal matrixP, we have

$$\begin{aligned} x^{T}(PA+A^{T}P)x\le x^{T}(PA^{*}+A^{*T}P+\parallel PA_{*}+A^{T}_{*}P\parallel I)x, \end{aligned}$$

where$A^{*}=\frac{1}{2}({\underline{A}}+\overline{A})$and$A_{*}=\frac{1}{2}(\overline{A}-{\underline{A}}).$

Lemma 3

[42] For any$B\in B_{\mathcal {I}}$and$E\in E_{\mathcal {I}}$, we have

$$\begin{aligned} \parallel B\parallel \le {\mathrm {b}},\quad \parallel E\parallel \le {\varrho}, \end{aligned}$$

where

$$\begin{aligned} {\mathrm {b}}= & {} \min \{\parallel B^{*}\parallel +\parallel B_{*}\parallel ,\parallel \hat{B}\parallel ,\\&\sqrt{\parallel B^{*}\parallel ^{2}+\parallel B_{*}\parallel ^{2}+2\parallel B^{T}_{*}\mid B^{*}\mid \parallel }\},\\ {\varrho }= & {} \min \{\parallel E^{*}\parallel +\parallel E_{*}\parallel ,\parallel \hat{E}\parallel ,\\&\sqrt{\parallel E^{*}\parallel ^{2}+\parallel E_{*}\parallel ^{2}+2\parallel E^{T}_{*}\mid E^{*}\mid \parallel }\}. \end{aligned}$$

$B^{*}=\frac{1}{2}({\underline{B}}+{\overline{B}})$, $B_{*}=\frac{1}{2}({\overline{B}}-{\underline{B}})$, $E^{*}=\frac{1}{2}({\underline{E}}+{\overline{E}})$, $E_{*}=\frac{1}{2}({\overline{E}}-{\underline{E}})$. $\hat{B}=(\hat{b}_{ij})_{n\times n}$ with $\hat{b}_{ij}=\max \{\mid {\underline{b}}_{ij}\mid ,\mid {\overline{B}}_{ij}\mid \}$, and $\hat{E}=(\hat{e}_{ij})_{n\times n}$ with $\hat{e}_{ij}=\max \{\mid {\underline{e}}_{ij}\mid ,\mid {\overline{E}}_{ij}\mid \}$.

Lemma 4

[43] For any constant matrix$\chi \in {\mathbb{R}}^{n\times n}$,$\chi =\chi ^{T}$, scalar$v>0$, vector function$F:[0,v]\rightarrow {\mathbb{R}}^{n}$such that the integrations concerned are well-defined, we have,

$$\begin{aligned} v\int _{0}^{v}F^{T}(s)\chi F(s)ds\ge \left( \int _{0}^{v}F(s)ds\right) ^{T}\chi \left( \int _{0}^{v}F(s)ds\right) . \end{aligned}$$

3 Main results

In this section, we will study the existence and global exponential stability of the equilibrium point for the uncertain memristor-based neural network (11). For simplicity, we let

$$\begin{aligned} \begin{aligned} {\widehat{M}}&=\text {diag}\{\widehat{m}_{i}\},\quad \widehat{m}_{i}:=\max \{| {{\underline{{m}}}}_{i}|,| {\overline{{m}}}_{i}|\},\\ \mu&=\text {diag}\{\mu _1,\ldots ,\mu _n\}, \quad \mu _0:=\max \{\mu _1,\ldots ,\mu _n\}, \end{aligned} \end{aligned}$$

(14)

where ${\underline{{m}}}_{i},{\overline{{m}}}_{i}$ are from (13), and $\mu _i$ is from (11).

Theorem 1

Under the assumptions (${\mathbf{A_1}}$),(${\mathbf{A_2}}$), and (${\mathbf{A_3}}$), if the diagonal matrix${\underline{D}}-{\widehat{M}}>0$and there exists a positive diagonal matrix$P=\text {diag}\{p_1,p_2,\ldots ,p_n\}$such that

$$\begin{aligned} \begin{aligned} \varPsi :=&-2P({\underline{D}}-\widehat{M})L^{-1}+(PA^{*}+A^{*T}P\\&+\parallel PA_{*}+A^{T}_{*}P\parallel I)+2\Vert P\Vert ({\mathrm {b}}+\varrho \mu _0)I<0, \end{aligned} \end{aligned}$$

(15)

then, the memristor-based neural network (11) has a unique equilibrium point.

Proof

Let $H(x)=-Dx-{M}|x|+(A+B+E\mu )f(x)+U$. It is obvious that $H(x^*)=0$ if and only if $x^*$ is an equilibrium point of the memristor-based neural network (11). Next, based on Lemma 1, we will prove that $H(\cdot )$ a homeomorphism of ${\mathbb{R}}^{n}$, and then the memristor-based neural network (11) has a unique equilibrium point.

$\mathbf{Step\,1: }$ We first prove $H(\cdot )$ is injective, i.e., the hypothesis (i) in Lemma 1 holds. In fact, for any $x,y\in {\mathbb{R}}^{n}$ with $x\ne y$, we have

$$\begin{aligned} \begin{aligned} H(x)-H(y)=&-D(x-y)-{M}(|x|-|y|)\\&+(A+B+E\mu )(f(x)-f(y)). \end{aligned} \end{aligned}$$

(16)

The proof of this step is divided into two following cases:

$\mathbf{Case\,1: }$$f(x)-f(y)=0$. If $f(x)-f(y)=0$, then $H(x)-H(y)=-D(x-y)-{M}(|x|-|y|)$, and

$$\begin{aligned} \begin{aligned}&(x-y)^T(H(x)-H(y))\\&\quad =-(x-y)^TD(x-y)-(x-y)^T{M}(|x|-|y|)\\&\quad \le -(x-y)^TD(x-y)+(x-y)^T|{M}|(x-y)\\&\quad =-(x-y)^T(D-|{M}|)(x-y)\\&\quad \le (x-y)^T(\widehat{M}-{\underline{D}})(x-y)\\&\quad <0. \end{aligned} \end{aligned}$$

(17)

Hence, $H(x)-H(y)\ne 0$.

$\mathbf{Case\,2: }$$f(x)-f(y)\ne 0$. In this case, multiplying both sides of (16) by $2(f(x)-f(y))^TP$, we have

$$\begin{aligned} \begin{aligned}&2(f(x)-f(y))^TP(H(x)-H(y))\\&\quad =-\,2(f(x)-f(y))^TPD(x-y)\\&\qquad -\,2(f(x)-f(y))^TP{M}(|x|-|y|)\\&\qquad +\,2(f(x)-f(y))^TP(A+B+E\mu )(f(x)-f(y)). \end{aligned} \end{aligned}$$

(18)

By the assumption (${\mathbf{A_1}}$) and the fact that P and M are two diagonal matrices, it is clear that

$$\begin{aligned} \begin{aligned}&-2(f(x)-f(y))^TP{M}(|x|-|y|)\\&\quad \le 2|f(x)-f(y)|^TP|{M}||x-y|\\&\quad = 2(f(x)-f(y))^TP|{M}|(x-y)\\&\quad \le 2(f(x)-f(y))^TP{\widehat{M}}(x-y). \end{aligned} \end{aligned}$$

(19)

Meanwhile,

$$\begin{aligned} \begin{aligned}&2(f(x)-f(y))^TP(A+B+E\mu )(f(x)-f(y))\\&\le (f(x)-f(y))^T(PA+A^TP)(f(x)-f(y))\\&\quad +\,2(f(x)-f(y))^T\Vert P\Vert (\Vert B\Vert +\Vert E\mu \Vert )(f(x)-f(y)). \end{aligned} \end{aligned}$$

(20)

Substituting (20) into (18), we have

$$\begin{aligned} \begin{aligned}&2(f(x)-f(y))^TP(H(x)-H(y))\\&\le -2(f(x)-f(y))^TP({\underline{D}}-{\widehat{M}})L^{-1}(f(x)-f(y))\\&\quad +\,(f(x)-f(y))^T\big (PA+A^TP+2\Vert P\Vert (\Vert B\Vert \\&\quad +\,\Vert E\mu \Vert )I\big )(f(x)-f(y))\\&=(f(x)-f(y))^T\big [-2P({\underline{D}}-{\widehat{M}})L^{-1}\\&\quad +\,PA+A^TP+2\Vert P\Vert (\Vert B\Vert +\Vert E\mu \Vert )I\big ](f(x)-f(y))\\&\le (f(x)-f(y))^T\varPsi (f(x)-f(y)). \end{aligned} \end{aligned}$$

(21)

Hence, by (21), considering the assumptions that $\varPsi$ is negative definite and $f(x)-f(y)\ne 0$, we obtain

$$\begin{aligned} \begin{aligned} 2(f(x)-f(y))^TP(H(x)-H(y))<0, \end{aligned} \end{aligned}$$

(22)

which means $H(x)-H(y)\ne 0$.

Thus, from $\mathbf{Cases\,1 }$ and $\mathbf{2 }$, it follows that H is injective.

$\mathbf{Step\,2: }$ We next prove that the hypothesis (ii) in Lemma 1 holds, i.e., $\Vert H(x)\Vert \rightarrow \infty$ as $\Vert x\Vert \rightarrow \infty$. In fact, by the definition of H, we have

$$\begin{aligned} \begin{aligned}&\Vert H(x)\Vert \\&\quad =\Vert -Dx-{M}|x|+(A+B+E\mu )f(x)+U\Vert \\&\quad \ge \Vert -Dx\Vert -\Vert {M}|x|\Vert -\Vert (A+B+E\mu )f(x)\Vert -\Vert U\Vert \\&\quad \ge (\Vert {\underline{D}}\Vert -\Vert {\widehat{M}}\Vert )\Vert x\Vert -\Vert A+B+E\mu \Vert \Vert f(x)\Vert -\Vert U\Vert . \end{aligned} \end{aligned}$$

(23)

It is noted that $\Vert {\underline{D}}\Vert -\Vert {\widehat{M}}\Vert>0$ since the diagonal matrix ${\underline{D}}-\widehat{M}$ is positive definite. On the other hand, letting $y=0$ in (21), we have

$$\begin{aligned} \begin{aligned}&2(f(x)-f(0))^TP(H(x)-H(0))\\&\quad \le (f(x)-f(0))^T\varPsi (f(x)-f(0))\\&\quad \le \lambda _M(\varPsi )\Vert f(x)-f(0)\Vert ^2. \end{aligned} \end{aligned}$$

That is,

$$\begin{aligned} \begin{aligned}&-2(f(x)-f(0))^TP(H(x)-H(0))\\&\quad \ge -\lambda _M(\varPsi )\Vert f(x)-f(0)\Vert ^2. \end{aligned} \end{aligned}$$

(24)

Then, by (24), it follows that $\Vert 2P\Vert \Vert H(x)-H(0)\Vert \ge -\lambda _M(\varPsi )\Vert f(x)-f(0)\Vert$, and consequently,

$$\begin{aligned} \begin{aligned} \Vert H(x)\Vert&\ge \frac{-\Vert H(0)\Vert -\lambda _M(\varPsi )\Vert f(x) -f(0)\Vert }{\Vert 2P\Vert }\\&\ge \frac{-\Vert H(0)\Vert -\lambda _M(\varPsi )\Vert f(x)\Vert +\lambda _M(\varPsi ) \Vert f(0)\Vert }{\Vert 2P\Vert }. \end{aligned} \end{aligned}$$

(25)

It is also noted that $-\lambda _M(\varPsi )>0$. Hence,

$$\begin{aligned} \begin{aligned} \Vert H(x)\Vert \ge&\max \bigg \{(\Vert {\underline{D}}\Vert -\Vert {\widehat{M}}\Vert )\Vert x\Vert \\&-\,\Vert A+B+E\mu \Vert \Vert f(x)\Vert -\Vert U\Vert ,\\&\times \,\left[ -\Vert H(0)\Vert -\lambda _M(\varPsi )\Vert f(x)\Vert \right. \\&\left. +\,\lambda _M(\varPsi )\Vert f(0)\Vert \right] /\Vert 2P\Vert \bigg \}. \end{aligned} \end{aligned}$$

(26)

Thus, we obtain that $\Vert H(x)\Vert \rightarrow \infty$ as $\Vert x\Vert \rightarrow \infty$.

Then, by Lemma 1, $H(\cdot )$ is a homeomorphism of ${\mathbb{R}}^{n}$, and consequently the memristor-based neural network (11) has a unique equilibrium point. $\square$

We next study the global exponential stability of the equilibrium point for the memristor-based neural network (11).

Theorem 2

Under the assumptions in Theorem 1, the unique equilibrium point of the memristor-based neural network (11) is globally exponentially stable.

Proof

From Theorem 1, the memristor-based neural network (11) has a unique equilibrium point. Let $x^*=(x_1^*,x_2^*,\ldots ,x_n^*)^T$ be the unique equilibrium point of the memristor-based neural network (11). Then, by the definition of the equilibrium point, we have

$$\begin{aligned} 0=-Dx^*-M|x^*|+Af (x^*)+Bf (x^*)+E\mu f(x^*)+U. \end{aligned}$$

To simplify the proof, we make the following transformation

$$\begin{aligned} \begin{aligned} z=x-x^*. \end{aligned} \end{aligned}$$

(27)

Then, the memristor-based neural network (11) can be expressed equivalently as follows,

$$\begin{aligned} \begin{aligned} \dot{z}(t)=&-Dz(t)-{M}(|z(t)+x^*|-|x^*|)\\&+\,Ag(z(t))+Bg(z(t-\tau (t)))+E\int _{t-\mu }^{t}g(z(s))ds, \end{aligned} \end{aligned}$$

(28)

where $g(z(t))=f(z(t)+x^*)-f(x^*)$ and $g(z(t-\tau (t)))=f(z(t-\tau (t))+x^*)-f(x^*)$.

We consider the following Lyapunov function,

$$\begin{aligned} V(t,z)=V_1(t,z)+V_2(t,z)+V_3(t,z), \end{aligned}$$

(29)

where

$$\begin{aligned} \begin{aligned} V_1(t,z)=&e^{\delta t}z^TD^{-1}z,\\ V_2(t,z)=&2\alpha e^{\delta t}\sum \limits _{i=1}^n p_i \int _0^{z_i}g_i(s)ds,\\ V_3(t,z)=&(\alpha \gamma _1+\beta _1)\sum \limits _{i=1}^n \int _{t-\tau _i(t)}^{t}g_i^2(z_i(s))e^{\delta (s+{\overline{\tau }}_i)}ds\\&+\,(\alpha \gamma _2+\beta _2)\sum _{i=1}^{n}\int _{-\mu _i}^{0} \int _{t+\theta }^{t}e^{\delta (s-\theta )}g_{i}^{2}(z_{i}(s))dsd\theta . \end{aligned} \end{aligned}$$

(30)

Here, $\alpha ,\beta _j,\gamma _j$, and $\delta$ are some positive constants to be determined, $j=1,2$.

First, calculating the time derivative of $V_1(t,z)$ along the trajectories of the memristor-based neural network (28), we have

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}V_1(t,z(t))\\&\quad =\delta e^{\delta t}z^T(t)D^{-1}z(t)+2e^{\delta t}z^T(t)D^{-1}\dot{z}(t)\\&\quad =\delta e^{\delta t}z^T(t)D^{-1}z(t)-2e^{\delta t}z^T(t){z}(t)\\&\qquad -\,2e^{\delta t}z^T(t)D^{-1}{M}(|z(t)+x^*|-|x^*|)\\&\qquad +\,2e^{\delta t}z^T(t)D^{-1}Ag(z (t))\\&\qquad +\,2e^{\delta t}z^T(t)D^{-1}Bg(z (t-\tau (t)))\\&\qquad +\,2e^{\delta t}z^T(t)D^{-1}E\int _{t-\mu }^{t}g(z(s))ds. \end{aligned} \end{aligned}$$

(31)

Since D and M are all diagonal matrices, we have

$$\begin{aligned} \begin{aligned}&-2e^{\delta t}z^T(t)D^{-1}{M}(|z(t)+x^*|-|x^*|)\\&\quad \le 2e^{\delta t}|z(t)|^T D^{-1}|{M}|\cdot \big |(|z(t)+x^*|-|x^*|)\big |\\&\quad \le 2e^{\delta t}z^T(t)D^{-1}|{M}|z(t). \end{aligned} \end{aligned}$$

(32)

Substituting (32) into (31), we obtain that

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}V_1(t,z(t))\\&\quad \le e^{\delta t}z^T(t)(\delta D^{-1}-2I+2D^{-1}|{M}|)z(t)\\&\qquad +\,2e^{\delta t}z^T(t)D^{-1}Ag(z (t))\\&\qquad +\,2e^{\delta t}z^T(t)D^{-1}Bg(z (t-\tau (t)))\\&\qquad +\,2e^{\delta t}z^T(t)D^{-1}E\int _{t-\mu }^{t}g(z(s))ds\\&\quad \le e^{\delta t}z^T(t)\left( \delta D^{-1}-2I+2D^{-1}|{M}|+\frac{3}{k}\right) z(t)\\&\qquad +\,ke^{\delta t}g^T(z (t))\Vert D^{-1}A\Vert ^2g(z (t))\\&\qquad +\,ke^{\delta t}g^T(z (t-\tau (t)))\Vert D^{-1}B\Vert ^2g(z (t-\tau (t)))\\&\qquad +\,ke^{\delta t}\big [\int _{t-\mu }^{t}g(z(s))ds\big ]^T\Vert D^{-1} E\Vert ^2\int _{t-\mu }^{t}g(z(s))ds, \end{aligned} \end{aligned}$$

(33)

where k is a positive constant to be determined later.

Second, we calculate the time derivative of $V_2(t,z)$ along the trajectories of the memristor-based neural network (28) as follows,

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}V_2(t,z(t))\\&\quad =2\delta \alpha e^{\delta t}\sum \limits _{i=1}^n p_i \int _0^{z_i}g_i(s)ds\\&\qquad +\,2\alpha e^{\delta t}g^T(z (t))P\dot{z}(t)\\&\quad \le 2\delta \alpha e^{\delta t}g^T(z (t))P{z}(t)-2\alpha e^{\delta t}g^T(z (t))PD{z}(t)\\&\qquad -\,2\alpha e^{\delta t}g^T(z (t))P{M}(|z(t)+x^*|-|x^*|)\\&\qquad +\,2\alpha e^{\delta t}g^T(z (t))PAg(z (t))\\&\qquad +\,2\alpha e^{\delta t}g^T(z (t))PBg(z (t-\tau (t)))\\&\qquad +\,2\alpha e^{\delta t}g^T(z (t))PE\int _{t-\mu }^{t}g(z(s))ds. \end{aligned} \end{aligned}$$

(34)

Similarly to (32), and by the fact that $g_i$ is nondecreasing with $g_i(0)=0$, we have

$$\begin{aligned} \begin{aligned}&-2\alpha e^{\delta t}g^T(z (t))P{M}(|z(t)+x^*|-|x^*|)\\&\quad \le 2\alpha e^{\delta t}g^T(z (t))P|{M}|z(t). \end{aligned} \end{aligned}$$

(35)

Based on the assumption that ${\underline{D}}-{\widehat{M}}$ is positive definite, it can be obtained that the diagonal matrix $D-|{M}|$ is positive definite. Hence, we can choose a sufficient small constant $\delta>0$ such that

$$\begin{aligned} \delta I-D+|{M}|<0. \end{aligned}$$

(36)

Meanwhile, by the assumption (${\mathbf{A_1}}$) and the transformation (27), we have

$$\begin{aligned} g^T(z (t)){z}(t)\ge g^T(z (t))L^{-1}g(z (t)). \end{aligned}$$

(37)

Thus, substituting (35) and (37) into (34), we obtain

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}V_2(t,z(t))\\&\quad \le 2\alpha e^{\delta t}g^T(z (t))P(\delta I-D+|{M}|){z}(t)\\&\qquad +\,2\alpha e^{\delta t}g^T(z (t))PAg(z (t))\\&\qquad +\,2\alpha e^{\delta t}g^T(z (t))PBg(z (t-\tau (t)))\\&\qquad +\,2\alpha e^{\delta t}g^T(z (t))PE\int _{t-\mu }^{t}g(z(s))ds\\&\quad \le \alpha e^{\delta t}g^T(z (t))\big [2P(\delta I-D+|{M}|)L^{-1}+PA+A^TP\\&\qquad +\,\Vert PB\Vert I+\mu _0\Vert PE\Vert I\big ]g(z (t))\\&\qquad +\,\alpha e^{\delta t}g^T(z (t-\tau (t)))\Vert PB\Vert g(z (t-\tau (t)))\\&\qquad +\,\alpha e^{\delta t}\big [\int _{t-\mu }^{t}g(z(s))ds \big ]^T\mu _0^{-1}\Vert PE\Vert \int _{t-\mu }^{t}g(z(s))ds, \end{aligned} \end{aligned}$$

(38)

since $2g^T(z (t))PAg(z (t)) =g^T(z (t))(PA+A^TP)g(z (t))$ and $2g^T(z (t))PBg(z (t-\tau (t)))$$\le g^T(z (t))\Vert PB\Vert g(z (t))$$+g^T(z (t-\tau (t)))\Vert PB\Vert g(z (t-\tau (t))).$

Third, calculating the time derivative of $V_3(t,z)$ along the trajectories of the memristor-based neural network (28), we have

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}V_3(t,z(t))\\&\quad =(\alpha \gamma _1+\beta _1)\sum \limits _{i=1}^n e^{\delta (t+{\overline{\tau }}_i)} g_i^2(z_i (t))\\&\qquad -\, (\alpha \gamma _1+\beta _1)\sum \limits _{i=1}^n (1-\dot{\tau }_i(t))e^{\delta (t-\tau _i(t)+{\overline{\tau }}_i)}g_i^2(z_i (t-\tau _i(t)))\\&\qquad +\,(\alpha \gamma _2+\beta _2)\sum _{i=1}^{n}g_{i}^{2}(z_{i}(t))\delta ^{-1}e^{\delta t}(e^{\delta \mu _i}-1)\\&\qquad -\,(\alpha \gamma _2+\beta _2)e^{\delta t}\sum \limits _{i=1}^n \int _{t-\mu _i}^{t}g_{i}^{2}(z_{i}(s))ds\\&\quad \le e^{\delta t}\big [(\alpha \gamma _1+\beta _1)e^{\delta {\overline{\tau }}}\\&\qquad +\,(\alpha \gamma _2+\beta _2)\delta ^{-1}(e^{\delta \mu _0}-1) \big ]g^T(z (t))g(z (t))\\&\qquad -\,(\alpha \gamma _1+\beta _1) e^{\delta t}g^T(z (t-\tau (t)))g(z (t-\tau (t)))\\&\qquad -\,(\alpha \gamma _2+\beta _2)e^{\delta t}\sum \limits _{i=1}^n \int _{t-\mu _i}^{t}g_{i}^{2}(z_{i}(s))ds. \end{aligned} \end{aligned}$$

(39)

Meanwhile, according to Lemma 4, we have

$$\begin{aligned}&-\mu _0\sum \limits _{i=1}^n\int _{t-\mu _i}^{t}g_{i}^{2}(z_{i}(s))ds\\&\quad \le -\left[ \int _{t-\mu }^{t}g(z(s))ds\right] ^T\int _{t-\mu }^{t}g(z(s))ds. \end{aligned}$$

Hence, by (33), (38), and (39), the time derivative of V(t, z) can be calculated as follows,

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}V(t,z(t))\\&\quad =\frac{d}{dt}V_1(t,z(t))+\frac{d}{dt}V_2(t,z(t))+\frac{d}{dt}V_3(t,z(t))\\&\quad \le e^{\delta t}z^T(t) \bigg [\delta D^{-1}-2I+2D^{-1}|{M}| +\frac{3}{k}I\bigg ]z(t)\\&\qquad +\,\alpha e^{\delta t}g^T(z (t))\bigg [k\alpha ^{-1}\Vert D^{-1}A\Vert ^2\\&\qquad +\,2P(\delta I-D+|{M}|)L^{-1}+PA+A^TP\\&\qquad +\,\Vert PB\Vert I+\mu _0\Vert PE\Vert I+\alpha ^{-1}\big [(\alpha \gamma _1+\beta _1) e^{\delta {\overline{\tau }}}\\&\qquad +\,(\alpha \gamma _2+\beta _2)\delta ^{-1}(e^{\delta \mu _0}-1)\big ]I\bigg ]g(z (t))\\&\qquad +\,e^{\delta t}g^T(z (t-\tau (t)))\bigg [k\Vert D^{-1}B\Vert ^2+\alpha \Vert PB\Vert \\&\qquad -\, (\alpha \gamma _1+\beta _1)\bigg ]g(z (t-\tau (t)))\\&\qquad +\,e^{\delta t}\bigg [k\Vert D^{-1}E\Vert ^2+\alpha \mu _0^{-1} \Vert PE\Vert -(\alpha \gamma _2\\&\qquad +\,\beta _2)\mu _0^{-1}\bigg ]\big [\int _{t-\mu }^{t}g(z(s))ds \big ]^T\int _{t-\mu }^{t}g(z(s))ds. \end{aligned} \end{aligned}$$

(40)

Next, we let

$$\begin{aligned} \begin{aligned} \gamma _1&={\Vert PB\Vert },\,\,\beta _1={k}\Vert D^{-1}B\Vert ^2,\\ \gamma _2&= \Vert PE\Vert ,\,\,\beta _2=k\mu _0\Vert D^{-1}E\Vert ^2. \end{aligned} \end{aligned}$$

(41)

Then, under the assumption ${\mathbf{(A_3)}}$, by Lemmas 2 and 3, we have

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}V(t,z(t))\\&\quad \le e^{\delta t}z^T(t) \bigg [\delta {\underline{D}}^{-1}-2I +2{\underline{D}}^{-1}|{\widehat{M}}|+\frac{3}{k}I\bigg ]z(t)\\&\qquad +\,\alpha e^{\delta t}g^T(z (t))\bigg [k\alpha ^{-1}\Vert D^{-1}A\Vert ^2I+2\delta P+\varPsi \\&\qquad -\,\Vert P\Vert (b+\varrho \mu _0)I+\alpha ^{-1}\big [(\alpha \gamma _1+\beta _1) e^{\delta {\overline{\tau }}}\\&\qquad +\,(\alpha \gamma _2+\beta _2)\delta ^{-1}(e^{\delta \mu _0}-1)\big ]I\bigg ]g(z (t)). \end{aligned} \end{aligned}$$

(42)

Here, $\varPsi$ is from (15). By Lemma 3 and the choices of $\gamma _1$ and $\beta _1$ in (41), we have

$$\begin{aligned} \begin{aligned}&-\Vert P\Vert b+\alpha ^{-1}\big (\alpha \gamma _1+\beta _1)e^{\delta {\overline{\tau }}}\\&\quad = -\Vert P\Vert b+\Vert PB\Vert +\alpha ^{-1}{k}\Vert D^{-1}B\Vert ^2e^{\delta {\overline{\tau }}}\\&\quad \le \frac{k}{\alpha }\Vert D^{-1}B\Vert ^2e^{\delta {\overline{\tau }}}. \end{aligned} \end{aligned}$$

(43)

Similarly, we also have

$$\begin{aligned} \begin{aligned}&-\Vert P\Vert \varrho \mu _0+\alpha ^{-1}\big (\alpha \gamma _2+\beta _2) \delta ^{-1}(e^{\delta \mu _0}-1)\\&\quad =-\Vert P\Vert \varrho \mu _0+\Vert PE\Vert \delta ^{-1}(e^{\delta \mu _0}-1)\\&\qquad +\,\alpha ^{-1}k\mu _0\Vert D^{-1}E\Vert ^2\delta ^{-1}(e^{\delta \mu _0}-1)\\&\quad \le \Vert P\Vert \varrho [-\mu _0+\delta ^{-1}(e^{\delta \mu _0}-1)]\\&\qquad +\,\alpha ^{-1}k\mu _0\Vert D^{-1}E\Vert ^2\delta ^{-1}(e^{\delta \mu _0}-1). \end{aligned} \end{aligned}$$

(44)

Then, letting $\alpha =k^2$ and $\delta =\frac{1}{k}$, and substituting (43) and (44) into (42), we obtain that

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}V(t,z(t))\\&\quad \le e^{\delta t}z^T(t) {\underline{D}}^{-1}\bigg [-2({\underline{D}} -|{\widehat{M}}|)+\big (\frac{1}{k}I+\frac{3}{k}{\underline{D}}\big )\bigg ]z(t)\\&\qquad +\,k^2e^{\delta t}g^T(z (t))\bigg [\varPsi +2k^{-1}P\\&\qquad +\,\big [k^{-1}\Vert D^{-1}A\Vert ^2+k^{-1}\Vert D^{-1}B\Vert ^2e^{k^{-1}{\overline{\tau }}}\\&\qquad +\,\Vert P\Vert \varrho [-\mu _0+k(e^{k^{-1} \mu _0}-1)]\\&\qquad +\,\mu _0\Vert D^{-1}E\Vert ^2(e^{k^{-1} \mu _0}-1)\big ]I\bigg ]g(z (t)). \end{aligned} \end{aligned}$$

(45)

The facts that

$$\begin{aligned} \begin{aligned} \text{(i) }\,\, \varPsi _1:=&\frac{1}{k}I+\frac{3}{k}{\underline{D}} \rightarrow 0,\, \text{ as } k\rightarrow +\infty ; \\ \text{(ii) }\,\,\varPsi _2:=&\frac{\Vert D^{-1}A\Vert ^2+\Vert D^{-1}B \Vert ^2e^{k^{-1}{\overline{\tau }}}}{k}\\&+\Vert P\Vert \varrho [k(e^{k^{-1} \mu _0}-1)-\mu _0]\\&+\mu _0\Vert D^{-1}E\Vert ^2(e^{k^{-1} \mu _0}-1)\rightarrow 0,\, \text{ as } k\rightarrow +\infty \end{aligned} \end{aligned}$$

imply that we can choose a sufficiently large k such that both (36) and the following inequalities hold,

$$\begin{aligned} \begin{aligned}&\text{(I) }\, -2({\underline{D}}-|{\widehat{M}}|)+\varPsi _1<0; \\&\text{(II) }\,\varPsi +2k^{-1}P+\varPsi _2I<0. \end{aligned} \end{aligned}$$

(46)

Hence, by (45), we have

$$\begin{aligned} \begin{aligned} \frac{d}{dt}V(t,z(t))\le 0, \end{aligned} \end{aligned}$$

which means that

$$\begin{aligned} e^{\delta t}z^T(t)D^{-1}z(t)=V_1(t,z(t))\le V(t,z(t))\le V(0,z(0)). \end{aligned}$$

More precisely,

$$\begin{aligned} \begin{aligned} \Vert x(t)-x^*\Vert =\Vert z(t)\Vert \le M e^{-\frac{\delta }{2} t}, \end{aligned} \end{aligned}$$

where $M=[d_{m}V(0,z(0))]^\frac{1}{2}$ and $d_{m}=\max \{d_i:i=1,\ldots ,n\}$. That is, the unique equilibrium point $x^*$ of the memristor-based neural network (11) is globally exponentially stable. $\square$

Remark 1

Recently, researchers propose several different mathematical models of the memristor-based neural networks, and study their dynamical behaviors extensively [24, 25, 33, 34]. These dynamical behaviors include the stability of equilibrium point, periodic solution, almost-periodic solution and synchronization and so on. For example, the global exponential synchronization and periodic solution of memristor-based neural network (11) were separately studied in [34, 44]. However, as far as we know, there are very few related conclusions about uncertain memristor-based recurrent neural network (11) with distributed delays.

Meanwhile, Theorems 1 and 2 can also be used to verify the global exponential stability of the equilibrium point not only for the memristor-based recurrent neural network in [34] but also for the general uncertain recurrent neural networks in [16, 18]. Hence, the conclusions in this paper can be considered as the generalization and improvement of the previous related works.

Corollary 1

Under the assumptions (${\mathbf{A_1}}$) and (${\mathbf{A_2}}$), if the diagonal matrix${D}-{\widehat{M}}>0$and there exists a positive diagonal matrix$P=diag\{p_1,p_2,\ldots ,p_n\}$such that

$$\begin{aligned} \begin{aligned} \varPsi :=&-2P({D}-\widehat{M})L^{-1}+(PA+A^{T}P\\&+\parallel PA+A^{T}P\parallel I)+2\Vert P\Vert {\mathrm {b}}I<0, \end{aligned} \end{aligned}$$

(47)

then, memristor-based neural network (1) has a unique equilibrium point, which is globally exponentially stable.

4 Numerical examples

In this section, we present some illustrative examples to show the effectiveness and application of the obtained results.

4.1 Analysis of dynamical behaviors of network (11)

First, we choose randomly the values of capacitor $C_{i}$, external input $I_{i}$, memductance $W'_{i}$, $W''_{i}$, resistors $R_{f_{ij}}$, and $R_{g_{ij}}$ in (1) in Tables 1 and 2, and let $R_{f_{ij}}=R_{g_{ij}}$ for $i,j=1,2,3,4.$

Table 1 Parameter values in (1)

Table 2 Resistors between $f_{j}(x_{j}(t))$ and $x_{i}(t)$ in (1)

Then, substituting the parameter values in Tables 1 and 2 into (11), we have

$$\begin{aligned} D= & {} \text {diag}\{7.5,4.0,7.4759,1.5884\},\\ {M}= & {} \text {diag}\{0.75,-0.25,-0.5,0.1786\},\\ U= & {} (4.5,1.0,2.75,0.8571)^{T},\\ A= & {} \left[ \begin{array}{cccc} 0 &{} 0.1667 &{}0.3333 &{}0.25\\ 0.1667 &{} 0 &{}0.0556 &{}0.0278\\ 0.2278&{}0.1923&{}0&{}0.1250\\ 0.0204 &{}0.0476&{}0.0357&{}0 \end{array}\right] ,\\ B= & {} \left[ \begin{array}{cccc} 0 &{} 0.1250 &{} 0.1111 &{} 0.2000\\ 0.3333 &{} 0 &{} 0.0417 &{} 0.1667\\ 0.1786 &{} 0.1087 &{} 0 &{} 0.2500\\ 0.0286 &{} 0.1429 &{} 0.0476 &{} 0\\ \end{array}\right] . \end{aligned}$$

Additionally, the parameter ${e_{ij}}$ in (11) are uniformly distributed pseudorandom numbers generated by rand in Matlab. In this numerical experiment,

$$\begin{aligned} E=\left[ \begin{array}{cccc} 0.7094 &{} 0.6551 &{} 0.9597 &{} 0.7513\\ 0.7547 &{} 0.1626 &{} 0.3404 &{} 0.2551\\ 0.2760 &{} 0.1190 &{} 0.5853 &{} 0.5060\\ 0.6797 &{} 0.4984 &{} 0.2238 &{} 0.6991\\ \end{array}\right] . \end{aligned}$$

The activation functions are given:

$$\begin{aligned} f_{1}(x)=f_{2}(x)=\frac{1}{2}(|x+1|-|x-1|). \end{aligned}$$

(48)

Then, by (9), we have $L=\text {diag}\{1,1,1,1\}.$ Let $\mu =\text {diag}\{0.6,0.6,0.6,0.6\}$ and $\tau _{i}(t)=1$ for $i=1,2,3,4$ in (11).

Second, the assumption $({\mathbf{A_3}})$ about the matrices D, M, A, B and E in (12) is shown as follows,

$$\begin{aligned}\begin{aligned} D_{\mathcal {I}}&:=\{D=\text {diag}\{d_{i}\}: 0.9d_{i}\le d_{i}\le 1.1d_{i}, \forall i\},\\ {M}_{\mathcal {I}}&:=\{{M}=\text {diag}\{{m}_{i}\}: 0.9m_{i}\le {m}_{i}\le 1.1m_{i}, \forall i\},\\ A_{\mathcal {I}}&:=\{A=(a_{ij})_{n\times n}: 0.9{a}_{ij}\le a_{ij}\le 1.1{a}_{ij}, \forall i,j\},\\ B_{\mathcal {I}}&:=\{B=(b_{ij})_{n\times n}: 0.9{b}_{ij}\le b_{ij}\le 1.1{b}_{ij}, \forall i,j\},\\ E_{\mathcal {I}}&:=\{E=(e_{ij})_{n\times n}: 0.9{e}_{ij}\le e_{ij}\le 1.1{e}_{ij}, \forall i,j\}. \end{aligned} \end{aligned}$$

Furthermore, by Lemmas 2, 3, and (14), we can calculate $A^{*}$, $A_{*}$, $\widehat{M}$, $\varrho =2.1649$, ${\mathrm {b}}= 0.5515$, and $\mu _{0}=0.6$. It is clear that ${\underline{D}}-{\widehat{M}}$ is positive and there exists a positive definite diagonal matrix

$$\begin{aligned} P=\text {diag}\{ 19.1338, \, 19.1338, \, 19.1338, \, 19.1338\} \end{aligned}$$

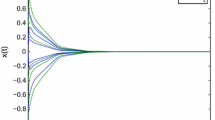
such that (15) holds. Thus, by Theorems 1 and 2, the unique equilibrium point of the memristor-based neural network (11) is globally exponentially stable. The initial values of the neural network (11) are set to be $(0.1,0.1,0.1,0.1)^{T}$, $(0.5,0.5,0.5,0.5)^{T}$, and $(1,1,1,1)^{T}$, respectively. The solution trajectories of (11) are illustrated in Fig. 2.

Fig. 2

Solution trajectories of the memristor-based neural network (11)

4.2 Applications

In this section, we apply the proposed results to analysis the dynamic behaviors and design the circuit of memristor-based neural network in [34].

4.2.1 Analysis of the dynamical behaviors of (1)

We fix the values of parameters $C_{i}$, $I_{i}$, $R_{f_{ij}}$, $R_{g_{ij}}$, $\tau _{j}(t)$ for $i,j=1,2,3,4.$ in Section 4.1. It is clear that ${D}-{\widehat{M}}$ is positive and there exists a positive definite diagonal matrix

$$\begin{aligned} P=\text {diag}\{ 0.1372, 0.1372, 0.1372, 0.1372\} \end{aligned}$$

such that (47) holds. Thus, by Corollary 1, the unique equilibrium point of the memristor-based neural network (1) is globally exponentially stable. The initial values of the neural network (1) are set to be $(0.1,0.1,0.1,0.1)^{T}$, $(0.5,0.5,0.5,0.5)^{T}$, and $(1,1,1,1)^{T}$, respectively. The solution trajectories of (1) are illustrated in Fig. 3.

Fig. 3

Solution trajectories of the memristor-based neural network (1)

4.2.2 Design of network (1)

In this section, we apply the obtained results in Corollary 1 to design the circuit of memristor-based neural network with a unique globally exponentially stable equilibrium point. First, we fix the values of parameters $C_{i}$, $I_{i}$, $R_{f_{ij}}$, and $R_{g_{ij}}$ in (1). Then, we apply the obtained results to determine $d_{i}$ and $m_i$ in (1). Furthermore, we calculate the memductances $W_{i}'$ and $W_{i}''$ of the $i-$th memristor, and finish the design of the circuit.

The design process of memristor-based neural network is described by three steps as follows.

Step 1 We fix a positive definite matrix P in (47). Based on the matrix inequality (47), we add the following two matrix inequalities

$$\begin{aligned} {D}-|\widehat{M}|> & {} 0, \end{aligned}$$

(49)

$$\begin{aligned} {D}-|\widehat{M}|< & {} {D} \end{aligned}$$

(50)

to solve the matrix ${D}-|\widehat{M}|.$ Here, the conditions (49) and (50) guarantee that $D-|\widehat{M}|$ and $|\widehat{M}|$ are positive definite in both Theorem 1 and Corollary 1, respectively.

Step 2 By (5) and (6), if $m_{i}\ge 0$, then we have

$$\begin{aligned} d_i-|m_{i}|=\sum \limits _{j=1}^n\left[ \frac{1}{C_{i}R_{fij}} +\frac{1}{C_{i}R_{gij}}\right] +\frac{W_i'}{C_{i}}. \end{aligned}$$

Furthermore, we calculate $W_{i}'$ for $i\in \{1,2,\cdots ,n\}$. Meanwhile, the corresponding $W_{i}''$ can be assigned the arbitrary value satisfied $m_{i}=\frac{W_{i}''-W_{i}'}{2C_{i}}>0$ theoretically.

If $m_{i}<0$, then we have

$$\begin{aligned} d_i-|m_{i}|=\sum \limits _{j=1}^n\left[ \frac{1}{C_{i}R_{fij}} +\frac{1}{C_{i}R_{gij}}\right] +\frac{W_i''}{C_{i}}. \end{aligned}$$

Similarly, we obtain the $W_{i}'$ and $W_{i}''$ in (1).

Step 3 Substituting $W_{i}'$ and $W_{i}''$ into (5) and (6), we obtain $d_{i}$ and $m_{i}$. That is, we complete the design of memristor-based neural network.

Now we set activation function $f_{i}(x)$ represented by (48), and the values of parameters $C_{i}$, $I_{i}$, $R_{f_{ij}}$, and $R_{g_{ij}}$ in (1) as same as in Tables 1 and 2. $\tau _{i}(t)$ are given as same as in Sect. 4.1. Consequently, we obtain the matrices U, A, B, and L as same as in Sect. 4.1. Next, we give a positive definite matrix

$$\begin{aligned} P=\text {diag}\{1,1,1,1\}. \end{aligned}$$

By Step 1, we have

$$\begin{aligned} {D}-|\widehat{M}|=\text {diag}\{0.0143, 2.1977,1.5685,3.5865\}. \end{aligned}$$

By Step 2, letting $m_{i}>0$ for $i=1,2,3,4$, we have $W_{1}'= -1.7109,\, W_{2}'= 0.1170,\, W_{3}'= -0.6748,\, W_{4}'= 4.8468.$ Moreover, fix $W_{1}''=1.2891,\, W_{2}''=3.1170,\, W_{3}''=2.3252,$ and $W_{4}''=7.8468.$ Then, by Step 3, we obtain

$$\begin{aligned} D= & {} \text {diag}\{ 1.5143,3.1977, 3.0685, 4.0150\},\\ \widehat{M}= & {} \text {diag}\{1.5000,1.0000,1.5000,0.4286\}. \end{aligned}$$

The initial values of the neural network (1) are set to be $(0.2,0.2,0.2,0.2)^{T}$, $(0.8,0.8,0.8,0.8)^{T}$, and $(2,2,2,2)^{T}$, respectively. We depict the solution trajectories of (1) in Fig. 4.

Fig. 4

Solution trajectories of the designed memristor-based neural network (1)

Remark 2

It should be noted that the obtained conclusions in this paper can also be applied to verify the global exponential stability of the equilibrium point for the general uncertain recurrent neural networks as follows,

$$\begin{aligned} \begin{aligned} \dot{x}_i(t)=&-d_ix_i(t)+\sum \limits _{j=1}^na_{ij}f_j(x_j(t))\\&+\sum \limits _{j=1}^nb_{ij}f_j(x_j(t-\tau _j(t)))\\&+\sum _{j=1}^ne_{ij}\int _{t-\mu _{j}}^{t}f_j(x_j(s))ds+U_i, \end{aligned} \end{aligned}$$

which has been studied extensively (see [17, 38, 39]). However, the influence of the distributed delays were not considered in [17, 38, 39]. Hence, the obtained conclusions in this paper improve the previous related works.

5 Conclusion

The analysis of dynamical behaviors of the memristor-based neural networks is necessary when the engineering applications of such networks become more and more popular. In this paper, we study the existence and global exponential stability of the equilibrium point for a class of memristor-based recurrent neural networks. By virtue of homeomorphic theory, we prove that the memristor-based neural network has a unique equilibrium point. Furthermore, we prove that the unique equilibrium point is globally exponentially stable by constructing a suitable Lyapunov functional. From the circuit of memristor-based recurrent network, we present some conditions for the amplifiers, connection resistors between the amplifiers, the capacitors, and the memductances of memristor to guarantee the existence and global exponential stability of the equilibrium point of the circuit. Finally, some numerical examples are used to show the effectiveness of our main results. In the future, we will focus on the delay-distribution probability problem for memristor-based recurrent neural networks.