Combined constraint-based with metric-based in semi-supervised clustering ensemble

Abstract

Recently, both semi-supervised clustering and cluster ensemble have received tremendous attention due to their accurate and reliable performance. There are mainly two kinds of existing semi-supervised clustering algorithms called constraint-based and metric-based. In this paper, we present a semi-supervised clustering ensemble approach which takes both pairwise constraints and metric measure into account. Firstly, under the assistance of supervised information included pairwise constraints and labeled data, the approach generates different base clustering partitions respectively using constraint-based semi-supervised clustering and metric-based semi-supervised clustering, in which the latter develops a new metric function. Given the spatial particularity of image pixels, the metric considers spatial distribution of surrounding pixels besides inherent features of pixels in the process of image feature extraction. And then the target clustering is obtained by integrating those base clustering partitions into an ensemble function. Finally, we conduct experimental verification on general data sets and image data sets, and compare clustering performance of our approach with those of other approaches. Both theoretical analysis and experimental results demonstrate that the proposed method produces considerable improvement in clustering accuracy and yields superior clustering results over a number of representative clustering methods.

1 Introduction

Clustering is acknowledged as one of the most important unsupervised learning methods in machine learning field. As a pre-processing technique, clustering has been frequently researched and widely applied to all kinds of practical scenes. It aims to categorize unlabeled samples into multiple classes based on the similarity between samples, and these multiple classes are often called clusters. In contrast to unsupervised learning, supervised learning needs a mass of labeled samples to assist cluster process. Nevertheless, labeled samples are relatively less in the real world because they are fairly difficult to get, so that it leads to undesirable clustering without the aid of labeled samples. Hence, the semi-supervised clustering [1] method emerges at the proper time. With a small amount of prior knowledge provided in advance, it divides plentiful unlabeled examples into several groups with higher clustering performance, and has become a hot spot in current research.

Despite a variety of clustering methods have been proposed, none is applicable to all data sets and achieves satisfactory clustering goals for all data sets. That is to say each clustering algorithm has own merits and demerits. Due to different data sets and different algorithms, as well as different parameters in the same algorithm, all these will lead to different results. By this token, how to select the proper algorithm is a significant and hard task for the users. The emerging cluster ensemble approach presented by Strehl et al. [2] can just ameliorate this puzzle. Du et al. [3] propose a novel self-supervised learning framework for clustering ensemble. Hao et al. [4] propose an improved clustering ensemble method based link analysis. In general, the basic idea of cluster ensemble is to integrate a variety of clustering partitions by using a specific consensus function to generate the final decision that outperforms individual clustering.

Semi-supervised clustering ensemble applies these two strategies simultaneously, namely semi-supervised clustering and cluster ensemble. Similarly, it combines different clustering results of various semi-supervised clustering algorithms by using ensemble function to create a single target clustering with more optimal performance than those of individual semi-supervised clustering. What’s more, it has strengths of low sensitivity to noise, outliers and variables. Yu et al. [5] propose a feature selection method based semi-supervised cluster ensemble framework for tumor clustering from bio-molecular data. Yu et al. [6] propose an incremental semi-supervised clustering ensemble framework for high dimensional data clustering.

At present, two typical approaches of semi-supervised clustering called constraint-based and metric-based are researched a lot. The former revises objective function of algorithm to guide the process of clustering by using supervised information provided in advance. Xiong et al. [7] study the active learning problem of selecting pairwise constraints for semi-supervised clustering. Wang et al. [8] propose a semi-supervised nonnegative matrix factorization method with pairwise constraints. The latter exploits a specific distance/similarity metric for clustering to satisfy the given pairwise constraints. Yan et al. [9] propose a semi-supervised clustering method with multi-viewpoint based similarity measure. Yin et al. [10] develop a semi-supervised fuzzy clustering algorithm with metric learning and entropy regularization simultaneously (SMUC). Although the two kinds of methods have their own singular focus respectively, they aren’t not only separated completely, but also exists symbiotic relationship between them. Inspired by the work of Bilenko et al. [11], many scholars have begun to turn their attention to the field of exploitation of hybrid approaches, which aims to combine the advantages of constraint-based with that of metric-based. In order to sufficiently solve the violation problem of pairwise constraints and to mitigate the problem of manually tuning the kernel parameters owing to the fact that no sufficient supervision, an adaptive semi-supervised clustering kernel method based on metric learning (SCKMM) is proposed by Yin et al. [12]. Arzeno and Vikalo [15] present an extension of soft-constraint semi-supervised affinity propagation (E-SCSSAP) which incorporates metric learning in the optimization objective and acquires desirable clusters. Reviewing previous related literature, we found that most researchers just take single objective function of the two factors into account, but relatively few researchers synthesize the two different kinds of algorithms adopted the mechanism of ensemble. Different from these conventional methods, this paper presents a semi-supervised clustering ensemble approach in conjunction with the both.

Additionally, most of image data metric measures used in previous literature are merely based on intrinsic properties of pixels. As we all known, one pixel and its surrounding pixels are tightly linked, so that it is necessary and reasonable to incorporate spatial characteristic in objective function. However, the most common way used in existing methods is selecting various means or statistical operators in a designated area around pixel as its spatial information, whose results still exist more or less deviation with the actual features. To mitigate the deviation, the paper concerns the intrinsic feature of pixel as well as spatial characteristic of its surroundings in metric measure simultaneously. Comparison experiments and analysis are made to validate the superiority of our method. The main contributions of this paper can be summarized as three aspects.

Firstly, this paper improves the performance of semi-supervised clustering by introducing ensemble mechanism, which unites different results respectively produced from constraint-based algorithm and metric-based algorithm. They have certain preoccupations in their fields that one concentrates on the adjustment of objective function according to pairwise constraints while the other is concerned with the introduction of metric function to measure the distance/similarity between samples more precisely. The combination method obtains benefits beyond what a single algorithm achieves.

Secondly, this paper proposes a metric-based semi-supervised clustering algorithm, in which the metric measure is formulated by two styles. One is used for measuring the distance between general data samples, and the other is for image pixel samples. Out of consideration for pixels’ spatial properties, we conclude the point that metric between pixels should be collectively based on the inherent feature of pixels and its neighboring spatial information. The metric evaluation function is expressed as the ratio of the feature similarity based on spatial information to the distance based on inherent feature. This new perspective breaks through traditional single idea for pixels metric, and significantly improve the accuracy.

Thirdly, we conduct two group experiments respectively on general data sets and image data sets for performance evaluation of clustering. On the basis of the proposed approach, the former simply employs ensemble mechanism integrated a constraint-based method and a metric-based method with a general metric measure. Besides the stages of the former, the latter adds a space-based pixel similarity to general metric measure that measures the similarity based on the inherent feature of pixels. It follows that our method not only applies to clustering of general data sets, but also to clustering of image data sets. Both of the two experiments complete targeted clustering on different data sets with high precision.

We organize the remainder of this paper into four sections. Section 2 surveys related works about what we have done. In Sect. 3, the new semi-supervised clustering ensemble approach is illustrated and the process of clustering with our proposed approach is described in detail. Section 4 provides experiment results and analysis. Finally we come to conclusions and look forward to several issues for future works in Sect. 5.

2 Related works

Semi-supervised clustering and clustering ensemble have been studied extensively, and the research topics in the fields of related are mainly distributed into three parts.

The first one is semi-supervised clustering learning approach. In real application, various useful prior knowledge, such as class labels or pairwise constraints, are taken into account in clustering process. This strategy of technique is called semi-supervised clustering [16]. The popular semi-supervised clustering approach is mainly composed of two categories called constraint-based method [16–20] and metric-based method [10, 21–23]. For the former, the linear-time constrained vector quantization error algorithm (LCVQE) [17] concerns on the problem of clustering with soft instance level constraints, in which a more intuitive objective function is introduced with lower computational complexity. Pairwise constrained maximum margin clustering approach (PMMC) [19] develops a set of effective loss functions for discouraging the violation of given pairwise constraints. For the later, the information theoretic metric method (ITML) [21] learns a Mahalanobis distance function by minimizing the differential relative entropy between two multivariate Gaussian under constraints on the distance function. Large margin nearest neighbor classification (LMNN) [22] focuses on how to learn a Mahalanobis distance metric for large margin nearest neighbor from labeled example so that the k-nearest neighbors always belong to the same class while examples from different classes are separated by a large margin. But beyond that, several hybrid approaches have been proposed gradually. For instance, Bilenko et al. [11] integrate the constraint-based method and distance-function learning method to form a hybrid method, which is a metric pairwise constrained k-means algorithm incorporated both metric learning and the use of pairwise constraints in a uniform and principled manner (MPCK). Yin et al. [12] propose an adaptive semi-supervised clustering kernel method based on metric learning (SCKMM), where the parameter of Gaussian kernel can be estimated through the objective function from pairwise constraints, and the pairwise constraint-based K-means is used to solve the violation of constraints. In addition, Lin et al. [13] proposes a semi-supervised grid clustering algorithm based on rough reduction (RSGrid). Zhang and Lu [14] provide a semi-supervised clustering approach using the kernel-based method based on KFCM (SSKFCM).

The second one is cluster ensemble learning approach. From the generation perspective, a set of diverse ensemble members is generated and known as base clustering in various forms. Base clustering can result from different views, different initialization parameter, different methods, and so on. But then it is difficult to learn a suitable consensus function to summarize the base clusterings and search for an optimal unified clustering decision. In light of that theoretical analysis, a great amount of well-known ensemble methods emerge. Three graph-based ensemble methods are introduced in study [2], all of which partition clusters based on a constructed similarity graph. The cluster-based similarity partition algorithm (CSPA) uses METIS to partition the induced similarity graph. The hyper-graph partition algorithm (HGPA) uses HMETIS to partition the hyper-graph. The meta-clustering algorithm (MCLA) collapses related hyper-edges and assigns each object to the collapsed hyper-edge in which it participates most strongly. An iterative voting consensus (IVC) [24] is a feature-based approach, in which each base clustering provides a cluster label as a new feature describing each data point that is utilized to formulate the final solution. By exploiting the significance of attribute defined in rough set theory, Wang et al. [25] apply the proposed two feature selection algorithms to a cluster ensemble selection problem.

The third one is semi-supervised clustering ensemble learning approach. Due to the lack of prior knowledge about cluster labels, cluster ensemble is still a challenging problem. By leveraging limited supervision information in cluster ensemble, semi-supervised clustering ensemble offers an effective solution to overcome this limitation and obtains accurate, robust and stable results. Wang et al. [26] construct semi-supervised cluster ensemble based on binary similarity matrix (BSMSCE), which takes the strengths of known information to improve the quality of clustering. Chen et al. [27] analyze convergence of semi-supervised clustering ensemble and proposed a new relabeling approach for semi-supervised clustering ensemble by majority voting (we called it MVSCE for short). Yu et al. [5] view the expert’s knowledge as constraints in the process of clustering and propose a framework called FS-SSCE, which not only applies the feature selection technique to perform gene selection on the gene dimension, but also selects an optimal subset of representative clustering solutions in the ensemble and improve the performance of tumor clustering using the normalized cut algorithm.

3 The proposed approach

3.1 An overview of the proposed approach

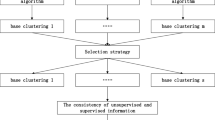
With the high stability and robustness, it is verified that cluster ensemble is an ideal alternative for a single clustering algorithm. For the purpose of improving performance of individual semi-supervised clustering algorithm, the paper makes great efforts to study about semi-supervised clustering ensemble, and introduces ensemble technique combining constraint-based semi-supervised clustering method and metric-based semi-supervised clustering method. We refer to the proposed hybrid semi-supervised clustering ensemble algorithm as HSCE for short. The procedure of our proposed approach is showed in Fig. 1.

Fig. 1

An overview of the proposed approach

Figure 1 shows the clustering process based on the proposed semi-supervised clustering ensemble approach. Based on the semi-supervised clustering ensemble model, the clustering process of HSCE can be described concisely as follows. (a) Supervised information (also called prior knowledge, such as class labels, pairwise constraints and the number of clusters) are specified in advance for further clustering. (b) It is the second step—clustering and partition generation—that seems to be the most essential step. From the generation perspective, with assistance of supervised information, data points are divided into different clustering groups by using constraint-based semi-supervised clustering approach and metric-based semi-supervised clustering approach respectively. Thus, several clustering partitions are generated and known as base clustering decisions. (c) Decisions integration. The consensus function employs a specific form of meta-level information matrix that stacks up all the previous base partition results, and it is available for deriving the final results with appealing properties superior to any individual one.

3.2 The constraint-based semi-supervised clustering Approach

3.2.1 Pairwise constraints

Generally, we hope to get more constraint information to aid clustering, because it is more easily obtained than class label information in practice. The pairwise constraints reflect prior knowledge about whether a pair of samples should be grouped together or not. It contains two types, namely must-link and cannot-link. Must-link indicates the two data points must be grouped in the same cluster marked as $M=\left\{ \left( {{x}_{i}},{{x}_{j}} \right) \right\}$ while cannot-link indicates the two data points must be grouped in different clusters marked as $C=\left\{ \left( {{x}_{i}},{{x}_{j}} \right) \right\}$. Pairwise constraints have transitivity and symmetry properties. Assume ${{x}_{i}},{{x}_{j}},{{x}_{k}}\in X$, the properties are showed as follows.

(1) Transitivity: $\left( {{x}_{i}},{{x}_{k}} \right)\in M\And \left( {{x}_{k}},{{x}_{j}} \right)\in M\Rightarrow \left( {{x}_{i}},{{x}_{j}} \right)\in M$,

$$\left( {{x}_{i}},{{x}_{k}} \right)\in M\And \left( {{x}_{k}},{{x}_{j}} \right)\in C\Rightarrow \left( {{x}_{i}},{{x}_{j}} \right)\in C$$

(2) Symmetry: $\left( {{x}_{i}},{{x}_{j}} \right)\in M\Rightarrow \left( {{x}_{j}},{{x}_{i}} \right)\in M$, $\left( {{x}_{i}},{{x}_{j}} \right)\in C\Rightarrow \left( {{x}_{j}},{{x}_{i}} \right)\in C$.

3.2.2 The semi-supervised spectral clustering algorithm based on pairwise constraints

In the section, the semi-supervised spectral clustering algorithm based on pairwise constraints (SSCA) [20] is used as the constraint-based semi-supervised clustering approach in our approach. The process of SSCA is briefly described as below. Firstly, it revises distance matrix of samples according to pairwise constraints information. If $\left( {{x}_{i}},{{x}_{j}} \right)\in M$ then ${{D}_{ij}}=0$; if $\left( {{x}_{i}},{{x}_{j}} \right)\in C$, then ${{D}_{ij}}=\infty$. Secondly, it constructs the similarity matrix of samples according to this equation: ${{\overline{w}}_{ij}}=\exp \left( -\frac{{{\left\| {{x}_{i}}-{{x}_{j}} \right\|}^{2}}}{{{\sigma }_{i}}{{\sigma }_{j}}} \right)$, where ${{\sigma }_{i}}=\frac{1}{k}\sum\limits_{n=1}^{k}{\left\| {{x}_{i}}-{{x}_{n}} \right\|}$ is a corresponding parameter for each data point. And then spectral clustering algorithm is used to solve the eigenvalues and eigenvectors of Laplacian matrix, to which is transformed by the similarity matrix. Finally, it divides the sample set X into k clusters combining with kernel fuzzy c-means (KFCM) clustering [28].

3.3 The metric-based semi-supervised clustering approach

3.3.1 The large margin nearest cluster distance metric (LMNC)

From the study provided by Huang et al. [23], we learn that LMNC metric is a generalized inspired by Mahalanobis metric. One common goal for metric learning is min–max principle: minimize the distances between same-cluster samples meanwhile maximize the distances between different-cluster samples. A set of n labeled data is denoted as $\left\{ \left( {{x}_{i}},{{y}_{i}} \right) \right\}_{i=1}^{n},$ where ${{x}_{i}}\in {{R}^{d}}$, ${{y}_{i}}\in \left\{ 1,2,...,K \right\}$ represents discrete class labels. Let M be the symmetric matrix of size $d\times d$, for any two given data points ${{x}_{i}}$ and ${{x}_{j}}$ on a vector space ${{R}^{d}}$, the squared distance measure between them can be expressed by Eq. (1).

$$D\left( {{x}_{i}},{{x}_{j}} \right)={{\left( {{x}_{i}}-{{x}_{j}} \right)}^{T}}M\left( {{x}_{i}}-{{x}_{j}} \right)$$

(1)

In general, M is a positive semi-definite matrix, i.e. $\mathbf{M}\ge 0$. To learn matrix $\mathbf{M}\in {{R}^{d\times d}}$, a cost function over this distance metric can be constructed by Eq. (2).

$$\varepsilon \left( L \right) = \sum\limits_{{ij}} {a_{{ij}} } \left( {x_{i} - z_{j} } \right)^{T} M\left( {x_{i} - z_{j} } \right) + {\text{ }}c\sum\limits_{{ijl}} {a_{{ij}} } \left( {1 - a_{{ij}} } \right)\left[ {1 + \left( {x_{i} - z_{j} } \right)^{T} M\left( {x_{i} - z_{j} } \right) - \left( {x_{i} - z_{l} } \right)^{T} M\left( {x_{i} - z_{l} } \right)} \right]_{ + }$$

(2)

where the weight matrix ${{a}_{ij}}\in \left\{ 0,1 \right\}$ indicates that ${{a}_{ij}}=1$ if the class labels ${{y}_{i}}$ and ${{y}_{j}}$ match, otherwise ${{a}_{ij}}=0$. ${{z}_{j}}$ represents the center of the ${{j}^{th}}$ cluster, $c>0$ is a positive constant, ${{\left[ f \right]}_{+}}=\max \left( f,0 \right)$ denotes the loss function. To reach min–max goal, we transform the loss metric problem into an optimization problem (3).

$$\text{Min}\sum\limits_{ij}{{{a}_{ij}}}{{\left( {{x}_{i}}-{{z}_{j}} \right)}^{T}}M\left( {{x}_{i}}-{{z}_{j}} \right)+c\sum\limits_{ijl}{{{a}_{ij}}\left( 1-{{a}_{ij}} \right)}{{\xi }_{ijl}}$$

(3)

s.t. (1) ${{\xi }_{ijl}}\ge 0$, (2) $M\ge 0$, (3) ${{\left( {{x}_{i}}-{{z}_{l}} \right)}^{T}}M\left( {{x}_{i}}-{{z}_{l}} \right)-{{\left( {{x}_{i}}-{{z}_{j}} \right)}^{T}}M\left( {{x}_{i}}-{{z}_{j}} \right)\ge 1-{{\xi }_{ijl}}$.

This expression induces a slack variables ${{\xi }_{ijl}}$ to represent the loss function. This optimization problem can be solved by means of the gradient projection algorithm [29].

3.3.2 The similarity metric of image pixels based on spatial information (SMIP)

In contrast to ordinary approaches, the innovation of the pixel affinity presented by Na and Yu [30], is the affinity based on patch [31] and the edge information on the lines of two pixels.

The first step is to solve patch-based similarity. For an image I(x, y), the similarity of arbitrary two pixels i and j is denoted as ${{S}_{ij}}\in \left[ 0,1 \right]$. Normally, the more i similar to j is, the higher the value of ${{S}_{ij}}$is. Pixel’s neighbor information should be considered to obtain stable feature due to the greater difference of the visual feature of single pixel. So the affinity based on patch can reflect the similarity between pixels veritably and satisfactorily. Using the average L*a*b* color space, the weighted average features of pixels in certain patch can be calculated by $\overset{\wedge }{\mathop{I}}\,\left( x,y \right)=I\left( x,y \right)*{{G}_{\sigma }}\left( x,y \right)=I\left( x,y \right)*{{G}_{\sigma }}\left( x \right)*{{G}_{\sigma }}\left( y \right)$, where * represents convolution operation, (x, y) describes one pixel’s coordinate, ${{G}_{\sigma }}\left( x,y \right)$denotes a two-dimensional Gaussian kernel function used ${{\sigma }^{2}}$ as a variance, $\sigma$ is designed for controlling the size. ${{\sigma }_{I}}$ is the scale parameter for color feature. The patch-based similarity can be described as Eq. (4).

$$S_{ij}^{\left( 1 \right)}=\exp \left( \frac{-\left\| \overset{\wedge }{\mathop{I}}\,\left( i \right)-\overset{\wedge }{\mathop{I}}\,\left( j \right) \right\|_{2}^{2}}{\sigma _{I}^{2}} \right)$$

(4)

The second step is to solve edge-based similarity. In the light of the model conveyed by Cour et al. [32], we assume $E\left( x,y \right)$ is edge information of image $I\left( x,y \right)$, then the edge-based similarity between two pixels i and j is formulated by Eq. (5).

$$S_{ij}^{\left( 2 \right)}=\exp \left( \frac{-{{\max }_{p\in line\left( i,j \right)}}{{\left\| E\left( {{p}_{x}},{{p}_{y}} \right) \right\|}^{2}}}{\sigma _{E}^{2}} \right)$$

(5)

where P indicates one of the pixels in the line from pixel i to j, $\left( {{p}_{x}},{{p}_{y}} \right)$means its corresponding coordinate, $\sigma _{E}^{2}$ represents the scale parameter of edge-based similarity.

According to the study of Martin et al. [33], the patch that centers on one pixel p can be cut into two parts by diameter from one angle. The feature difference between two parts can be denoted as $E\left( x,y,\theta ,r \right)=\left| {{E}_{+}}\left( x,y \right)-{{E}_{-}}\left( x,y \right) \right|$, where $\theta$ is a cutting angle, ${{E}_{+}}$ and ${{E}_{-}}$ respectively represent the features of two sides, $r$ means radius. By adjusting cutting angle, the direction of cutting may be as near to the actual one as possible until the biggest difference generates. At this point, the edge information can be denoted as $E\left( x,y \right)=\underset{\theta \in \left[ 0,180 \right)}{\mathop{\max }}\,E\left( x,y,\theta ,r \right)$. Applying the convolution theorem, the edge information at specific angle $\theta$ can be calculated by equation ${{E}_{\theta }}\left( x,y \right)=\left| I\left( x,y \right)*{{\nabla }_{\theta }}G\left( x,y \right) \right|$. For higher calculating speed, the edge feature is approximately represented by that at four angles 0°, 45°, 90°, 135°, transformed to $E\left( x,y \right)\approx {{E}_{0}}\left( x,y \right)+{{E}_{45}}\left( x,y \right)+{{E}_{90}}\left( x,y \right)+{{E}_{135}}\left( x,y \right)$.

On account of convolution property: ${{G}_{\theta }}\left( x,y \right)=G\left( x,y \right)*{{\nabla }_{\theta }}$, further transformation, $E\left( x,y \right)\approx \left| {{I}_{2}}\left( x,y \right)*{{\nabla }_{0}} \right|+\left| {{I}_{2}}\left( x,y \right)*{{\nabla }_{45}} \right|+\left| {{I}_{2}}\left( x,y \right)*{{\nabla }_{90}} \right|+\left| {{I}_{2}}\left( x,y \right)*{{\nabla }_{135}} \right|$, where ${{\nabla }_{0}},{{\nabla }_{45}},{{\nabla }_{90}},{{\nabla }_{135}}$ denote corresponding partial derivatives filters ($v=0.5\sigma \sqrt{2\pi }$, called normalizing factor).

$${{\nabla }_{\mathbf{0}}}=\left[ \begin{array}{*{20}l} -\mathbf{v} & \mathbf{0} & \mathbf{v} \\\end{array} \right],{{\nabla }_{\mathbf{45}}}=\left[ \begin{array}{*{20}l} \mathbf{-v} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{v} \\\end{array} \right],{{\nabla }_{\mathbf{90}}}=\left[ \begin{array}{*{20}l} \mathbf{-v} \\ \mathbf{0} \\ \mathbf{v} \\\end{array} \right],{{\nabla }_{\mathbf{135}}}=\left[ \begin{array}{*{20}l} \mathbf{0} & \mathbf{0} & \mathbf{-v} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{v} & \mathbf{0} & \mathbf{0} \\\end{array} \right]$$

The third step is to solve final similarity. Integrating with the aforementioned approaches, we convey the final similarity as Eq. (6).

$${{S}_{ij}}=\sqrt{S_{ij}^{\left( 1 \right)}\times S_{ij}^{\left( 2 \right)}}$$

(6)

3.3.3 The proposed metric-based semi-supervised clustering approach

In this part, we combine the two methods aforementioned, namely LMNC and SMIP, to form a new metric function firstly. And then the generated combination function is applied to a semi-supervised clustering algorithm [34] by substituting its objective function to form a new metric-based semi-supervised clustering algorithm. This algorithm proposed is called LSSC for short, which is used as the metric-based semi-supervised clustering approach in our proposed approach. Specifically, we formulate the similarity between ${{x}_{i}}$ and ${{x}_{j}}$ by using a new metric function. The metric function is denoted as Eq. (7).

$${{\overset{\wedge }{\mathop{D}}\,}_{ij}}=\frac{{{S}_{ij}}}{D\left( {{x}_{i}},{{x}_{j}} \right)}$$

(7)

It is applied to cases where samples are pixels of one image, ${{\overset{\wedge }{\mathop{D}}\,}_{ij}}=\frac{{{S}_{ij}}}{D\left( {{x}_{i}},{{x}_{j}} \right)}$ is the similarity for image pixel samples, where ${{S}_{ij}}$ is the space-based similarity calculated by Eq. (6). Otherwise ${{S}_{ij}}=1$, in the case of general data similarity, and then ${{\overset{\wedge }{\mathop{D}}\,}_{ij}}=\frac{1}{D\left( {{x}_{i}},{{x}_{j}} \right)}$ is the similarity for general data samples, where $D\left( {{x}_{i}},{{x}_{j}} \right)$ is the LMNC distance metric. The larger ${{\overset{\wedge }{\mathop{D}}\,}_{ij}}$ is, the more similar the pair samples are. The LSSC algorithm is described in Algorithm 1.

3.4 Consensus function

The CSPA algorithm [2] aims to obtain the final clustering ${{\pi }^{*}}$ from the set of M base clustering results marked as $\prod =\left\{ {{\pi }_{1}},{{\pi }_{\text{2}}},...,{{\pi }_{M}} \right\}$. In details, this algorithm constructs a $N\times N$ similarity matrix for each base clustering ${{\pi }_{m}}$, and it is denoted as ${{S}_{m}}$, $m\in \left\{ 1,...,M \right\}.$ For two data samples ${{x}_{i}}$ and ${{x}_{j}}$ in ${{\pi }_{m}}$, if ${{x}_{i}}$ and ${{x}_{j}}$ have the same class labels $C\left( {{x}_{i}} \right)=C\left( {{x}_{j}} \right)$, ${{S}_{m}}\left( {{x}_{i}},{{x}_{j}} \right)=1$; if not ${{S}_{m}}\left( {{x}_{i}},{{x}_{j}} \right)=0$. Then the M similarity matrix are merged to form a co-association (CO) matrix, which represented as $CO\left( {{x}_{i}},{{x}_{j}} \right)=\frac{1}{M}\sum\nolimits_{m=1}^{M}{{{S}_{m}}}\left( {{x}_{i}},{{x}_{j}} \right)$. This algorithm creates a similarity graph, where vertexes represent data points and edges’ weight represent similarity scores obtained from the CO matrix. Following that, the graph partitioning algorithm METIS is used to partition the similarity graph into k clusters and yield the final partition decision.

3.5 Complexity analysis

We also analyze the computational complexity of the HSCE algorithm. We refer to the corresponding time complexity of HSCE as T _HSCE, which is estimated as follows:

T _HSCE = T _SSCA + T _LSSC + T _CSPA.

where T _SSCA is the computational cost of the constraint-based SSCA algorithm and T _LSSC is the computational cost of the metric-based LSSC algorithm. T _SSCA and T _LSSC serves as the computational complexity of the original ensemble member generation algorithm. T _CSPA is the computational complexity of the final ensemble decision generation algorithm.

Concretely, T _SSCA is affected by the number of instances n as follows: T _SSCA = O($n\mathrm{log}n$) [20]. For LSSC, step 1 requires to determine k cluster centers, and thus has a complexity of O(k). Step 2 divide n instances into k clusters, therefore requires O(nk). Step 3 recalculates the cluster centers and its complexity is O(n). Step 2 and step 3 compose an iteration process and the max-number of iterations is t. So T _LSSC is estimated as follows: T _LSSC = O(k) + O((O(nk) + O(n))t). The computational complexity of CSPA are as follows: T _CSPA = O (n ² km) [2], where n is the number of instances, k denotes the number of clusters in the final result, and m denotes the number of the original ensemble members (base clusterings). Overall, the computational complexity of HSCE is approximately O(n ² km).

The space complexity of HSCE mainly depends on the initial size of the data sets, and thus the space complexity is O(mn), where m denotes the number of instances, n denotes the number of dimensions for general data sets, and m*n denotes the matrix of an image for image data sets.

4 Experiments

In this section, we apply the proposed approach to implement two groups of experiments. The first group makes some contrast tests on the proposed algorithm with the other related algorithms to verify clustering performance on general test data sets. The second group conducts comparison experiments for image data clustering comparing with several representative algorithms to evaluate the clustering result.

We use Matlab as the programing language in our experiment. The running environment consists of software and hardware. The configurations are described as follows. (a) Software: windows 64-bit operating system, MATLAB R2013a. (b) Hardware: CPU/Intel(R) Xeon(R), Graphics card/NVIDIA Quadro 5000, RAM/DDRA3 8 GB.

4.1 Comparison experiments on general data sets

4.1.1 Data set and experimental setting

In order to validate the effectiveness of our proposed clustering algorithm, eight data sets are selected from UCI Machine Learning Repository [35] for following considerations. Firstly, these data sets are widely used as benchmark data sets for machine learning and data mining research. In addition, these data sets enjoy different properties, of which three are binary-class and five are multiple-class. Furthermore, the dimensional representations are with distributions ranging from low to high. The detailed description of these data sets are showed in Table 1.

Table 1 The characteristics of these data sets

In this section, the SMIP need to be ignored. So, the metric function of LSSC algorithm uses the general form, i.e., ${{\overset{\wedge }{\mathop{D}}\,}_{ij}}=\frac{1}{D\left( {{x}_{i}},{{x}_{j}} \right)}$, where $D\left( {{x}_{i}},{{x}_{j}} \right)$ is the LMNC distance metric between two instances. Some related parameters are set as reported in literature [20, 23]. In LSSC algorithm, the maximum of iterations is set as 150. The number of clusters k is set as the same as the ground-true class number. Next, we conduct three comparison experiments on UCI data sets. For each dataset, we repeat experiments for 20 trials.

On one hand, the number of supervised information (included pairwise constraints and labels) has effect on the result of semi-supervised clustering ensemble algorithm. In order to test the effectiveness of supervised information, we investigate the impact of supervised information on the performance of HSCE. In our experiments, we select the percent of supervised information as 0, 5, 10, 15, 20, 25% to analyze the effect of supervised information, where 0% means without any supervised information.

On the other hand, HSCE is compared with the following eight representation semi-supervised clustering algorithms. Two constraint-based clustering algorithms are LCVQE [17] and PMMC [19]. Two metric-based clustering algorithms are ITML [21] and LMNN [22]. Three hybrid clustering algorithms which combined constraint-based and metric-based are MPCKM [11], SCKMM [12] and ESCSSAP [15]. One semi-supervised clustering ensemble algorithm is MVSCE [27]. For the sake of fair comparison with other algorithms, we employ 20% of all the samples of each class as labeled samples, then those labeled samples are used to produce pairwise constraints in metric-based method. Meanwhile, we select 20% must-link constraints of all instances’ must-link constraints and 20% cannot-link constraints of all instances’ cannot-link constraints for each class in constraint-based method.

Furthermore, to obtain a better understanding of our work, we compare the proposed method with other semi-supervised clustering algorithms based on the average running times, included LCVQE [17], ITML [21], SMUC [10] and RSGrid [13]. In this part of experiment, we test the time performance of HSCE on the whole dataset and employ 20% of supervised information for each dataset.

4.1.2 Evaluation criterion

In our experiments, we adopt two popular evaluation criteria on the clustering performance.

• a. Normalized mutual information (NMI for short). It reflects the coherence between the inferred clustering and the ground truth aggregation [36]. Let C be the random variable denoting the cluster assignments of data points, and K be the random variable denoting the underlying class labels, and then the NMI measure is defined as

  $$NMI=\frac{2I\left( C;K \right)}{H(C)+H(K)}$$

  where I(X;Y) = H(X) − H(X|Y) is the mutual information between the random variables X and Y, H(X) is the Shannon entropy of X, and H(X|Y) is the conditional entropy of X given Y. The normalization by the average entropy of C and K makes the value of NMI stay between 0 and 1.

• b. F-Measure. It evaluates the clustering result based on the underlying classes and considers the same-cluster pairs. Pairwise F-measure relies on the traditional information retrieval measures. It consists of precision index and recall index. The value of F-measure stays between 0 and 1. F-Measure is defined as

  $$Precision=\frac{\#\text{Samples Correctly Predicted In Same Cluster}}{\text{ }\!\!\#\!\!\text{ Total Samples Predicted In Same Cluster}}$$
  $$Recall=\frac{\#\text{Samples Correctly Predicted In Same Cluster}}{\#\text{Total Samples In Same Cluster}}$$
  $$F-Measure=\frac{2\times Precision\times Recall}{Precision+Recall}$$

For both two evaluation indexes, the larger the value it is, the more similar the groupings by clustering and those by the ground true class labels.

4.1.3 Experimental results and analysis

To obtain a comprehensive understanding of our work, we add the number of supervised information in the experimental process for each data set gradually. For each case, the average NMI and F-measure values of HSCE are shown in Fig. 2. From these results, we get some interesting points. NMI and F-measure values of HSCE are considerably improved as the percentage of supervised information increases. The more supervised information make the better performance of semi-supervised clustering ensemble. This is due to the fact that more abundant labeled instances are, more reliable the metric measure is. At the same time, the more pairwise constraints are, the more completely the violation issue of pairwise constraints is solved. As a result, HSCE achieve better performance through adding prior knowledge.

Fig. 2

NMI and F-measure values with supervised information increasing

Tables 2 and 3 separately summarize the NMI and F-Measure performance of the proposed semi-supervised clustering algorithm and the other eight algorithms based on the same proportion of constraints over different data sets. In the both tables, the top highest NMI and F-measure scores are highlighted in bold font. Table 4 reports the average running times of all the algorithms. From these comparison results, these semi-supervised clustering algorithms demonstrate the significantly different degree on clustering performance. The detailed analysis of this group experiment is summarized as follows.

Table 2 Evaluation of clustering performance on NMI for nine algorithms

Table 3 Evaluation of clustering performance on F-Measure for nine algorithms

Table 4 Comparison of average running times (s)

Firstly, as a whole, we observe that SCKMM, E-SCSSAP, MVSCE and HSCE can consistently achieve comprehensive better-performance with higher value on both two indexes, and outperform other algorithms obviously. This is due to the fact that a combination method of both pairwise constraints and metric measure can obtain performance superior to other traditional single clustering methods (either constraint-based or metric-based). MVSCE and HSCE work well than other algorithms distinctly, we can verify that the cluster ensemble approaches are able to integrate multiple clustering solutions and provide a more accurate, robust and stable final result when compared with standard clustering algorithms.

Secondly, as can be seen from results, the two metric-based methods achieve a little higher performance than the two constraint-based methods on most data sets. This observation can be explained that sufficient pairwise constraints and labeled instances are good for measuring the distance between instances with an accurate metric function, which can easily enforce samples from the same cluster closely and samples from different clusters far apart.

Thirdly, although HSCE fails to achieve the best performance on few date sets, its values still extremely close to the best ones. This can be attributed to the fact that the proposed HSCE algorithm is considerably effective in utilizing the pairwise constraints and learning accurate metric measure to improve clustering performance. In addition, HSCE refers to combine a number of base partitions for a particular data set into a consensus clustering solution. Cluster ensemble sufficiently improved the clustering result of individual clustering algorithm. Thus, the HSCE algorithm provides an appealing clustering performance with high accurate, stable and meaningful.

Fourthly, two different evaluation metric are used to evaluate results, namely NMI and F-measure. The two index results are not always consistent on all data sets. For example, on the same data set Vowel, the NMI value of E-SCSSAP is slightly higher than HSCE. And yet, the F-measure performance of HSCE is better than E-SCSSAP. This phenomenon indicates the chosen of evaluation index is important for evaluating the performance of clustering algorithm. Adopting more than one evaluation index can measure clustering results more accurately and comprehensively.

In this section, the average time consumptions for 20 trials of each clustering algorithm are reported in Table 4. In addition to the aforementioned factors about running environment, the runtime of proposed method is related to data sets, the attributes of data sets, the number of iterations and the number of clusters, and so on. From these experimental results, it can be seen that the time performance of HSCE is generally efficient and considerable within an acceptable time. Although it is not the fastest algorithm on most data sets, we can learn from the experimental results that HSCE works stably. Furthermore, it demonstrates the proposed method is feasible, reasonable and ideal on the efficiency.

4.2 Comparison experiments on image data sets

4.2.1 Data set and experimental setting

To illustrate the implementation of the proposed method for image pixels clustering, eight images in the size of 481 × 321 are randomly chosen from the Berkeley Segmentation Data Set (BSDS500) [37], as showed in Table 5. For comparison, we also implement image data clustering using the following four methods. (a) K-means, an unsupervised clustering algorithm. (b) LSSC, a metric-based semi-supervised clustering algorithm proposed in this paper. (c) SSKFCM [14], a semi-supervised clustering approach using the kernel-based method based on KFCM; (d) BSMSCE [26], a semi-supervised clustering ensemble algorithm.

Table 5 The eight chosen original images

Feature extraction is a foundational step and a premise to generate satisfied clustering results for image data. In the experiments, we extract two parts of characteristics of an image, namely immanent characteristic and spatial information. On one hand, the immanent characteristic we need to extract concretely included the color feature at one pixel site, the surrounding texture feature LBP value, and the color gradient which denotes sudden change when meeting region edge or noise pixels. On the other hand, from the perspective of spatial information, we extract the color feature of pixels based on CIE L*A*B* space and the edge information of image. The result of feature extraction fits more closely with human perception.

In this section, LMNC and SMIP are combined to form the metric function of LSSC algorithm, which is conveyed as ${{\overset{\wedge }{\mathop{D}}\,}_{ij}}=\frac{{{S}_{ij}}}{D\left( {{x}_{i}},{{x}_{j}} \right)}$. The LMNC metric method for SSCA algorithm mainly measures based on the extracted immanent characteristic, which are the color gray value at one pixel site, the color gradient value calculated by Sobel operator and the texture feature LBP value of neighborhood pixels (with 3 × 3 windows). Meanwhile the SMIP metric method considers the patch-based color feature similarity and the edge-based spatial feature similarity. In other words, the extracted spatial information is used to compute the SMIP metric.

Likewise, the experimental conditions are set as reported in literature [20, 23, 30]. Firstly, the maximum of iterations is set as 150 in LSSC algorithm. In addition, we need to provide some information. We randomly sample some pixels from different partitions of an image as labeled data. Those labeled pixels are used in metric-based LSSC algorithm. The pixels with the same label indicate they are similar, while with different labels dissimilar. Then the set of must-links M and the set of cannot-links C can be obtained respectively. Those constraint information are used in constraint-based SSCA algorithm. The number of clusters k is set as the same as the ground-true class number.

4.2.2 Evaluation criterion

Here, we set the number of clusters equal to the number of ground-true clusters. Clustering accuracy (ACC) metric is used to compare the clusters generated by these algorithms with the ground-true clusters to evaluate the image data clustering performance [38]. Clustering accuracy discovers the one-to-one relationship between clusters and ground-true clusters and measures the extent to which each cluster contain data points from the corresponding ground-true cluster. It sums up the whole matching degree between all pair ground-true cluster-clusters. ACC can be computed as $Acc=\frac{1}{N}\max \left( \sum\limits_{{{C}_{k}},{{L}_{m}}}{T\left( {{C}_{k}},{{L}_{m}} \right)} \right)$, where N is the total number of pixels in an image, ${{C}_{k}}$ denotes the k-th cluster in final results, and ${{C}_{k}}$ denotes the ground-truth m-th cluster. From the perspective of an image, $T\left( {{C}_{k}},{{L}_{m}} \right)$ is the number of pixels belonging to ground-true cluster m that are assigned to cluster k. ACC computes the maximum sum of $T\left( {{C}_{k}},{{L}_{m}} \right)$ for all pairs of clusters and ground-true clusters, and these pairs have no overlaps. The greater clustering accuracy means the better clustering performance.

4.2.3 Experimental results and analysis

Figure 3 illustrates the graphical ACC results of the five methods with different numbers of labeled pixels. As the percent of labeled pixels increases, the unsupervised clustering K-means algorithm is used as the baseline clustering, whose performance is still a steadily numerical value. While the accuracy of other semi-supervised clustering algorithms reveals gradually increasing trend as a whole with the increase of labeled data. What’s more, Table 6 displays the experiment results of image data clustering performance on ACC with 40% of labeled pixels, which shows the accuracy of the five algorithms with numerical value intuitively. From these results, we obtain several attractive insights.

Fig. 3

Clustering performance with different percent of labeled pixels

Table 6 ACC results with 40% of labeled pixels

Firstly, we observe that SSKFCM and LSSC often achieve the better performance than K-means on the eight images. K-means gets better grade only with few supervised information on image 2. But when the percent of labeled pixels reaches a certain number, both SSKFCM and LSSC algorithms behave better and better, and far exceeds K-means. It demonstrates that comparing with unsupervised clustering, semi-supervised clustering methods can improve the clustering accuracy by effectively exploring the available information that is usually in the form of pairwise constraints and instance labels. As a result, the semi-supervised clustering algorithms outperform other traditional unsupervised clustering methods.

Secondly, we can observe that the performance of the LSSC algorithm is always comparable to, and better than the SSKFCM algorithm when there are enough labeled information, even better than BSMSCE and HSCE few times. It can be understandable that the proposed LSSC method takes into full account of the intrinsic properties and spatial information of each pixel so that the metric function can measure the similarity more accurately, and easily make points from different clusters far apart and those from the same clusters closely. Thus, LSSC provides a more satisfying clustering results.

Thirdly, BSMSCE and HSCE can consistently outperform better than SSKFCM and LSSC in most of our experiments. This observation can be explained by the fact that both BSMSCE and HSCE respectively have a cluster ensemble mechanism in the process of determining accurate and robust clustering decision from an ensemble of base clustering results. In other words, cluster ensemble combined different solutions of various clustering methods can achieve accuracy superior to those of individual clustering.

Fourthly, compare to HSCE, the performance of BSMSCE has a little advantage on image 3, image 4 and image 8, and the performance of LSSC behave a little advantage on image 7. Nonetheless, for overall perspective, HSCE displays better than BSMSCE and LSSC in most cases. In view of image peculiarity, HSCE also obtains more supervised information by propagating limited pairwise constraints and considerably effective in utilizing the pairwise constraints, so that it not only performs the metric accurately, but also solve the violation issue effectively. Thereby, the clustering performance of HSCE is sufficiently improved.

It is worth noting that HSCE improves the robustness as well as the quality of clustering results. HSCE nearly always achieves the best performance with steady development trend on the eight images. This observation can be explained by the fact summing up the above.

5 Conclusion

In this paper, we present a novel semi-supervised clustering ensemble approach for data clustering. Our method is different from the previous studies that integrates the constraint-based method and the metric method into a semi-supervised clustering ensemble approach in the hope of gaining the more optimal accuracy, robustness and stability of clustering dramatically. Specifically, we construct a new metric function with two forms in our proposed metric-based semi-supervised clustering algorithm. One is for general data clustering based on the LMNC distance metric. The other is for image data clustering by combining the similarity of image pixels with the LMNC metric from the image perspective, concretely it builds collections of the inherent attributes and spatial information of pixels, which efficiently and accurately reflects the relationship between image pixels. Moreover, we conduct two group comparison experiments, respectively on general data sets and image data sets. Multiple comparison results indicate that this proposed scheme can achieve better clustering performance than a number of competing clustering algorithms on the whole. Empirically as well as theoretically, it confirms the feasibility and effectiveness of the proposed method with encouraging results.

However, what we are done still leaves much to be desired. For instance, we should add noise factors into the experiments to test the sensitivity of clustering algorithms to noise, which can reveal the stability and robustness of clustering approaches. At the same time, there are a great many interesting directions to extend our work. As we all known, clustering is often viewed as a foundation technology in image process and computer vision. To investigate further, our future work will develop clustering into the mapping process from low-level features of images to high-level semantic comprehension in conjunction with other related techniques.