1 Introduction

Formal concept analysis [1] mainly discusses how to obtain binary concepts and their hierarchy from a given binary relation between objects and attributes. Now, this theory has been applied to a variety of fields such as knowledge discovery, data mining and software engineering [2–8]. However, in the real world, the relation between objects and attribute is often established under certain conditions. In order to widen the application scope, Lehmann and Wille [9] extended classical formal concept analysis into triadic concept analysis. More studies on triadic concept analysis can be found in [10–15].

Formal decision context was proposed by Zhang and Qiu [16] in 2005 for decision-making analysis of the data, and in recent years it has been studied by many scholars. For example, Shao [17] and Qu et al. [18] discussed rule acquisition in formal decision contexts. Wei et al. [19] put forward two types of attribute reduction methods for formal decision contexts and Hong et al. [27] gave another one. Wang and Zhang [20] divided formal decision contexts into two categories: consistent and inconsistent ones, and developed attribute reduction approaches for consistent decision contexts. Based on granular computing, Wu et al. [21] defined a new kind of consistent decision contexts. Shao et al [22] also investigated the issue of attribute reduction in consistent decision contexts from the viewpoint of rule acquisition. Considering that an inconsistent decision context appears more often than a consistent one, Li et al. [23] presented an attribute reduction technology for inconsistent decision contexts. Since computing a minimal reduct of a formal decision context is computationally expensive, Li et al. [24] designed a heuristic attribute reduction method for formal decision contexts. For making better decision analysis, Li et al. [25] gave a rule acquisition oriented attribute reduction approach for general formal decision contexts. Also, it deserves to be mentioned that the issue of object reduction was discussed in [26] for formal decision contexts. Except the classical formal decision contexts, rule acquisition and attribute reduction were investigated in generalized decision contexts such as incomplete [28], fuzzy [29, 30] and real ones [31–33].

According to the above discussion, although some researchers investigated rule acquisition and attribute (object) reduction in classical, incomplete, fuzzy and real decision contexts, little work has been done on these topics for triadic decision contexts. Motivated by this problem, the current study focuses on the issues of rule acquisition and attribute reduction in triadic decision contexts, which can be regarded as an information fusion technology for decision-making analysis since a triadic decision context can be viewed as multi-source data if one treats the data under each condition as a single-source data.

The rest of this paper is organized as follows. Section 2 briefly recalls some basic notions related to triadic context, triadic concept and triadic decision context. Section 3 discusses how to derive implication rules from a triadic decision context and puts forward a rule acquisition method. Section 4 constructs discernibility matrix and Boolean function to compute all reducts of a triadic decision context. The paper is then concluded with a summary.

2 Triadic concept analysis

In this section, we briefly introduce some basic notions about triadic concept analysis to facilitate our subsequent discussion.

Definition 1

[9] A triadic context is a quadruple \((U,A,\,C,I),\) where U is a nonempty and finite set of objects, A is a nonempty and finite set of attributes, C is a nonempty and finite set of conditions, and I is a ternary relation between U, A and C (i.e., \(I\subseteq U\times A\times C).\) Here, \((x,a,c)\in I\) means that the object x owns the attribute a under the condition c.

For a triadic context (U, A, C, I), we can build three binary contexts \((X\times A,C,I^{(1)}),\) \((U,B\times C,I^{(2)})\) and \((U,A\times H,I^{(3)})\) by fixing the nonempty object set \(X\subseteq U,\) nonempty attribute set \(B\subseteq A\) and nonempty condition set \(H\subseteq C,\) respectively. Note that here X, B and H are all treated as a whole. To be more concrete, for any \(X\times \{a\}\subseteq X\times A\) and \(c\in C,\) the relationship \((X\times \{a\},c)\in I^{(1)}\) means that for every object \(x\in X,\) there is \((x,a,c)\in I.\) Similarly, for any \(x\in U\) and \(B\times \{c\}\subseteq B\times C,\) the relationship \((x,B\times \{c\})\in I^{(2)}\) means that for every attribute \(a\in B,\) there is \((x,a,c)\in I;\) for any \(x\in U\) and \(\{a\}\times H\subseteq A\times H,\) the relationship \((x,\{a\}\times H)\in I^{(3)}\) means that for every condition \(c\in H,\) there is \((x,a,c)\in I.\)

Hereinafter, we say that \((X\times A,C,I^{(1)}),\) \((U,B\times C,I^{(2)})\) and \((U,A\times H,I^{(3)})\) are projected contexts of the triadic context (U, A, C, I) by fixing the nonempty object set \(X\subseteq U,\) nonempty attribute set \(B\subseteq A\) and nonempty condition set \(H\subseteq C,\) respectively. Similar to other binary contexts, we can define concept-forming operators for the projected contexts \((X\times A,C,I^{(1)}),\) \((U,B\times C,I^{(2)})\) and \((U,A\times H,I^{(3)}).\)

Definition 2

[15] Let \((X\times A,C,I^{(1)})\) be a projected context of (U, A, C, I) with \(X\subseteq U.\) For \(B\subseteq A\) and \(H\subseteq C,\) we define

$$\begin{aligned} \begin{array}{c} B^{X^{(1)}}=\{c\in C \mid \forall a\in B,(X\times \{a\},c)\in I^{(1)}\},\\ H^{X^{(1)}}=\{a\in A \mid \forall c\in H,(X\times \{a\},c)\in I^{(1)}\}, \end{array} \end{aligned}$$

where \(X^{(1)}\) is a mapping from the power set \(2^A\) to the power set \(2^C,\) and it is also used as a mapping from \(2^C\) to \(2^A\) when there is no confusion.

Definition 3

[15] Let \((U,B\times C,I^{(2)})\) be a projected context of (U, A, C, I) with \(B\subseteq A.\) For \(X\subseteq U\) and \(H\subseteq C,\) we define

$$\begin{aligned} \begin{array}{c} X^{B^{(2)}}=\{c\in C \mid \forall x\in X,(x,B\times \{c\})\in I^{(2)}\},\\ H^{B^{(2)}}=\{x\in U \mid \forall c\in H,(x,B\times \{c\})\in I^{(2)}\}, \end{array} \end{aligned}$$

where \(B^{(2)}\) is a mapping from the power set \(2^U\) to the power set \(2^C,\) and it is also used as a mapping from \(2^C\) to \(2^U\) when there is no confusion.

Definition 4

[15] Let \((U,A\times H,I^{(3)})\) be a projected context of (U, A, C, I) with \(H\subseteq C.\) For \(X\subseteq U\) and \(B\subseteq A,\) we define

$$\begin{aligned} \begin{array}{c} X^{H^{(3)}}=\{a\in A \mid \forall x\in X,(x,\{a\}\times H)\in I^{(3)}\},\\ B^{H^{(3)}}=\{x\in U \mid \forall a\in B,(x,\{a\}\times H)\in I^{(3)}\}, \end{array} \end{aligned}$$

where \(H^{(3)}\) is a mapping from the power set \(2^U\) to the power set \(2^A,\) and it is also used as a mapping from \(2^A\) to \(2^U\) when there is no confusion.

Definition 5

[15] Let (U, A, C, I) be a triadic context. For \(X\subseteq U,\) \(B\subseteq A\) and \(H\subseteq C,\) the ordered pair (X, B, H) is called a triadic concept of (U, A, C, I) if \(B=H^{X^{(1)}},\) \(H=B^{X^{(1)}},\) \(X=H^{B^{(2)}},\) \(H=X^{B^{(2)}},\) \(X=B^{H^{(3)}}\) and \(B=X^{H^{(3)}}.\) Here X, B and H are termed as the extent, intent and modus of the triadic concept (X, B, H), respectively.

In other words, the concept-forming operators for projected contexts are employed in Definition 5 to define triadic concepts. Such a way of formalizing a triadic concept is equivalent to the one given in [9]. For convenience, we denote the set of all triadic concepts of (U, A, C, I) by \(\underline{{\mathfrak {B}}}(U,A,C,I).\)

Proposition 1

Let (U, A, C, I) be a triadic context. For \(X,X_1,X_2\subseteq U,\) \(B,B_1,B_2\subseteq A\) and \(H\subseteq C,\) the following conclusions hold:

  1. (i)

    \(X_1\subseteq X_2\Rightarrow X_2^{H^{(3)}}\subseteq X_1^{H^{(3)}};\)

  2. (ii)

    \(B_1\subseteq B_2\Rightarrow B_2^{H^{(3)}}\subseteq B_1^{H^{(3)}};\)

  3. (iii)

    \(X\subseteq X^{H^{(3)}H^{(3)}}, B\subseteq B^{H^{(3)}H^{(3)}}.\)

Proof

  1. (i)

    For any \(a\in X^{H^{(3)}}_2,\) we have \((x,\{a\}\times H)\in I^{(3)}\) for every \(x\in X_2.\) Since \(X_1\subseteq X_2,\) it follows \((x,\{a\}\times H)\in I^{(3)}\) for every \(x\in X_1,\) which yields \(a\in X^{H^{(3)}}_1.\) Then, \(X^{H^{(3)}}_2\subseteq X^{H^{(3)}}_1\) is at hand.

  2. (ii)

    For any \(x\in B^{H^{(3)}}_2,\) we have \((x,\{a\}\times H)\in I^{(3)}\) for every \(a\in B_2.\) Since \(B_1\subseteq B_2,\) it follows \((x,\{a\}\times H)\in I^{(3)}\) for every \(a\in B_1,\) which leads to \(x\in B^{H^{(3)}}_1.\) That is, \(B_2^{H^{(3)}}\subseteq B_1^{H^{(3)}}\) is established.

  3. (iii)

    For any \(x\in X,\) we have \((x,\{a\}\times H)\in I^{(3)}\) if \(a\in X^{H^{(3)}},\) which implies \(x\in X^{H^{(3)}H^{(3)}}.\) As a result, \(X\subseteq X^{H^{(3)}H^{(3)}}.\) In a similar manner, we can prove \(B\subseteq B^{H^{(3)}H^{(3)}}.\) \(\square\)

Similar to the case in binary contexts, the ordered pair \((X,B\times H)\) is called a concept of the projected context \((U,A\times H,I^{(3)})\) if \(X=B^{H^{(3)}}\) and \(B=X^{H^{(3)}}.\) Then, we denote the set of all concepts of \((U,A\times H,I^{(3)})\) by \(\underline{{\mathfrak {B}}}(U,A\times H,I^{(3)}).\) Moreover, we define meet, join and partial order relation on \(\underline{{\mathfrak {B}}}(U,A\times H,I^{(3)})\) as follows:

$$\begin{aligned}&(i)\quad (X_1,B_1\times H)\wedge (X_2,B_2\times H)\\&\quad \quad =(X_1\cap X_2,(B_1\cup B_2)^{H^{(3)}H^{(3)}}\times H),\\&(ii)\quad (X_1,B_1\times H)\vee (X_2,B_2\times H)\\&\quad \quad =((X_1\cup X_2)^{H^{(3)}H^{(3)}},(B_1\cap B_2)\times H),\\&(iii)\quad (X_1,B_1\times H)\preceq (X_2,B_2\times H) \Leftrightarrow X_1\subseteq X_2.\\ \end{aligned}$$

Definition 6

[15] Let \((U,A\times H,I^{(3)})\) be a projected context of (U, A, C, I), \(E\subseteq A\) and \(I^{(3)}_E=I^{(3)} \cap (U\times (E\times H)).\) Then, the binary context \((U,E\times H,I^{(3)}_E)\) is called a sub-context of \((U,A\times H,I^{(3)}).\)

Moreover, we define

$$\begin{aligned} \begin{array}{l}X^{H^{(3)}_E}=\{a\in E\mid \forall x\in X, (x,\{a\}\times H)\in I^{(3)}_E\},\\ B^{H^{(3)}_E}=\{x\in U\mid \forall a\in B, (x,\{a\}\times H)\in I^{(3)}_E\}. \end{array} \end{aligned}$$

Then, \((X,B\times H)\) is called a concept of the sub-context \((U,E\times H,I^{(3)}_E)\) if \(X=B^{H^{(3)}_E}\) and \(B=X^{H^{(3)}_E}.\) Similarly, we denote the set of all concepts of \((U,E\times H,I^{(3)}_E)\) by \(\underline{{\mathfrak {B}}}(U,E\times H,I^{(3)}_E)\) and

$$\begin{aligned} {\mathfrak {U}}(U,E\times H,I^{(3)}_E)=\{X|(X,B\times H)\in \underline{{\mathfrak {B}}}(U,E\times H,I^{(3)}_E)\}. \end{aligned}$$

Proposition 2

Let \((U,A\times H,I^{(3)})\) be a projected context of (U, A, C, I) and \(E\subseteq A.\) For \(X,X_1,X_2\subseteq U\) and \(B,B_1,B_2\subseteq E,\) the following conclusions hold:

  1. (i)

    \(X^{H^{(3)}_E}=X^{H^{(3)}}\cap E,\) \(B^{H^{(3)}_E}=B^{H^{(3)}};\)

  2. (ii)

    \(X_1\subseteq X_2\Rightarrow X_2^{H^{(3)}_E}\subseteq X_1^{H^{(3)}_E};\)

  3. (iii)

    \(B_1\subseteq B_2 \Rightarrow B_2^{H^{(3)}_E}\subseteq B_1^{H^{(3)}_E};\)

  4. (iv)

    \(X\subseteq X^{H^{(3)}_E H^{(3)}_E},\) \(B\subseteq B^{H^{(3)}_E H^{(3)}_E};\)

  5. (v)

    \((X^{H^{(3)}_E H^{(3)}_E},X^{H^{(3)}_E}\times H),(B^{H^{(3)}_E},B^{H^{(3)}_EH^{(3)}_E}\times H)\in \underline{{\mathfrak {B}}}(U,E\times H,I^{(3)}_E).\)

Proof

(i) \(X^{H^{(3)}_E}=\{a\in E\mid \forall x\in X, (x,\{a\}\times H)\in I^{(3)}_E\}=\{a\in A \mid \forall x\in X,(x,\{a\}\times H)\in I^{(3)}\}\cap E=X^{H^{(3)}}\cap E.\) That is, \(X^{H^{(3)}_E}=X^{H^{(3)}}\cap E\) is at hand. Moreover, \(B^{H^{(3)}_E}=\{x\in U\mid \forall a\in B, (x,\{a\}\times H)\in I^{(3)}_E\}=\{x\in U \mid \forall a\in B,(x,\{a\}\times H)\in I^{(3)}\}=B^{H^{(3)}}.\) That is, \(B^{H^{(3)}_E}=B^{H^{(3)}}\) is established.

The proofs of (ii), (iii) and (iv) are similar to those of (i), (ii) and (iii) in Proposition 1. The remainder is to prove (v).

Note that \(X\subseteq X^{H^{(3)}_E H^{(3)}_E}\) holds due to (iv), which leads to \(X^{H^{(3)}_E H^{(3)}_E H^{(3)}_E}\subseteq X^{H^{(3)}_E}.\) On the other hand, \(X^{H^{(3)}_E}\subseteq X^{H^{(3)}_E H^{(3)}_E H^{(3)}_E}\) is true according to (iv). To sum up, it follows \(X^{H^{(3)}_E}=(X^{H^{(3)}_E H^{(3)}_E})^{H^{(3)}_E}.\) By combining it with \(X^{H^{(3)}_E H^{(3)}_E}=(X^{H^{(3)}_E})^{H^{(3)}_E},\) we conclude \((X^{H^{(3)}_E H^{(3)}_E},X^{H^{(3)}_E}\times H)\in \underline{{\mathfrak {B}}}(U,E\times H,I^{(3)}_E).\) Moreover, \((B^{H^{(3)}_E},B^{H^{(3)}_EH^{(3)}_E}\times H)\in \underline{{\mathfrak {B}}}(U,E\times H,I^{(3)}_E)\) can be proved in a similar manner. \(\square\)

Proposition 3

Let \((U,A\times H,I^{(3)})\) be a projected context of (U, A, C, I) and \(F\subseteq E\subseteq A.\) Then \({\mathfrak {U}}(U,F\times H,I^{(3)}_F)\subseteq {\mathfrak {U}}(U,E\times H,I^{(3)}_E).\)

Proof

For any \(X\in {\mathfrak {U}}(U,F\times H,I^{(3)}_F),\) there exists \(B\subseteq A\) such that \((X,B\times H)\in \underline{{\mathfrak {B}}}(U,F\times H,I^{(3)}_F).\) Let \(S=E\backslash F.\)

Case 1 If \(X^{H^{(3)}_S}=\emptyset ,\) then \((X,B\times H)\in \underline{{\mathfrak {B}}}(U,E\times H,I^{(3)}_E).\) As a result, \(X\in {\mathfrak {U}}(U,E\times H,I^{(3)}_E).\)

Case 2 If \(X^{H^{(3)}_S}\not =\emptyset ,\) we, without loss of generality, suppose \(X^{H^{(3)}_S}=B^\prime .\) Then, \((X,(B\cup B^\prime )\times H)\in \underline{{\mathfrak {B}}}(U,E\times H,I^{(3)}_E).\) That is, \(X\in {\mathfrak {U}}(U,E\times H,I^{(3)}_E)\) still holds.

To sum up, \({\mathfrak {U}}(U,F\times H,I^{(3)}_F)\subseteq {\mathfrak {U}}(U,E\times H,I^{(3)}_E)\) is at hand. \(\square\)

Definition 7

A triadic decision context is a septuple \((U,A,C_A,I,D,C_D,J),\) where \((U,A,C_A,I)\) and \((U,D,C_D,J)\) with \(A\cap D=\emptyset\) and \(C_A\cap C_D=\emptyset\) are two triadic contexts. Here, A and D are called the conditional and decision attribute sets, respectively.

Example 1

Table 1 shows a triadic decision context \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J),\) where \(U=\{x_1,x_2,x_3,x_4\}\) means four days: Monday, Tuesday, Wednesday, Thursday, \(A=\{a_1,a_2,a_3,a_4,a_5\}\) means five kinds of ingredients: Potatoes, Tomatoes, Eggs, Milk, Pork, \(C_A=\{c_1,c_2\}\) means two suppliers: Supermarket 1 and Supermarket 2 (the dates of the two supermarkets providing ingredients are uncertain, but there is at least one supermarket providing ingredients everyday), \(D=\{h_1,h_2,h_3\}\) means three kinds of food: Sandwich, Hamburg, Pizza, and \(C_D=\{c_3,c_4\}\) means two restaurants: Restaurant 1 and Restaurant 2.

Table 1 A triadic decision context \((U,A,C_A,I,D,C_D,J)\)
Full size table

Firstly, we design Algorithm 1 to compute the triadic concepts of the triadic context (U, A, C, I) whose main idea is as follows: for every condition set \(H\subseteq C,\) check whether the concepts of the projected context \((U,A\times H,I^{(3)})\) are triadic concepts of (U, A, C, I).

figure a

It is easy to observe that the time complexity of Algorithm 1 is exponential.

Now, we employ Algorithm 1 to compute all triadic concepts of \((U,A,C_A,I)\) and \((U,D,C_D,J)\) which can be found in Tables 2 and 3, respectively.

Table 2 All triadic concepts of \((U,A,C_A,I)\)
Full size table
Table 3 All triadic concepts of \((U,D,C_D,J)\)
Full size table

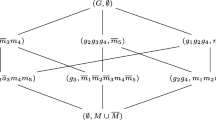
Moreover, we depict the diagrams of \(\underline{{\mathfrak {B}}}(U,A,C,I)\) and \(\underline{{\mathfrak {B}}}(U,D,C_D,J)\) in Figs. 1 and 2, respectively. In the first figure, the geometric structure of the triadic concepts is represented by the triangular pattern in the center of the diagram. The circles represent the triadic concepts and the lines the equivalence classes. The perforated lines indicate the connection to the extent diagram on the right, to the intent diagram on the lower left, and to the modus diagram above. A circle of the line diagram on the right represents the extent consisting of those objects whose signs are attached to this circle below. The intents and modi can analogously be read from the diagram where the intents get larger from the upper left to the lower right and the modi get larger from the upper right to the lower left. For instance, the second circle from bottom to top connects horizontally with the extent \(\{x_3\},\) to the lower left with the intent \(\{a_1,a_3,a_4\},\) and to the upper left with the modus \(\{c_2\};\) hence it represents the triadic concept \((\{x_3\},\{a_1,a_3,a_4\},\{c_2\}).\)

Fig. 1
figure 1

The diagram of \(\underline{{\mathfrak {B}}}(U,A,C,I)\)

Full size image
Fig. 2
figure 2

The diagram of \(\underline{{\mathfrak {B}}}(U,D,C_D,J)\)

Full size image

3 A rule acquisition based knowledge reduction framework for triadic decision contexts

In this section, we discuss how to derive implication rules from a triadic decision context and put forward a corresponding knowledge reduction framework.

Definition 8

Let \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J)\) be a triadic decision context, E be a nonempty subset of A, H be a nonempty subset of \(C_A,\) and K be a nonempty subset of \(C_D.\) For any \((X,B\times H)\in \underline{{\mathfrak {B}}}(U,E\times H,I^{(3)}_E)\) and \((Y,G\times K)\in \underline{ {\mathfrak {B}}}(U,D\times K,J^{(3)}),\) if \(X\subseteq Y\) and X, Y, B, G are all nonempty, we say that \((Y,G\times K)\) can be implied by \((X,B\times H),\) which is denoted by \((X,B\times H)\rightarrow (Y,G\times K).\)

The following conclusion can be drawn from \((X,B\times H)\rightarrow (Y,G\times K)\): if \(x\in U\) is shared by all the attributes in B under every condition of H, then x possesses all the attributes in G under each condition of K. That is, we can obtain a constrained decision rule “If B under H, then G under K” which is denoted by \(B\times H\rightarrow G\times K.\) Note that constrained decision rules in triadic decision contexts are special implication rules [9] in triadic contexts.

Let \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J)\) be a triadic decision context. For any nonempty subset \(E\subseteq A,\) \(H\subseteq C_A\) and \(K\subseteq C_D,\) we denote by \({\mathfrak {R}}(E,H,D,K)=\{B\times H\rightarrow G\times K\mid (X,B\times H)\in {\mathfrak {B}}(U,E\times H,I^{(3)}_E), (Y,G\times K)\in {\mathfrak {B}}(U,D\times K,J^{(3)})\}\) the set of all the constrained decision rules between the concepts of \({\mathfrak {B}}(U,E\times H,I^{(3)}_E)\) and those of \({\mathfrak {B}}(U,D\times K,J^{(3)}).\)

Definition 9

Let \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J)\) be a triadic decision context, \(E\subseteq A,\) \(H\subseteq C_A\) and \(K\subseteq C_D.\) For \(B'\times H\rightarrow G'\times K\in {\mathfrak {R}}(E,H,D,K)\) and \(B''\times H\rightarrow G''\times K\in {\mathfrak {R}}(A,H,D,K),\) if \(B'\subseteq B''\) and \(G''\subseteq G',\) we say that \(B''\times H\rightarrow G''\times K\) can be implied by \(B'\times H\rightarrow G'\times K\) and denote this implication relationship by \(B'\times H\rightarrow G'\times K\Rightarrow B''\times H\rightarrow G''\times K.\)

Definition 10

Let \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J)\) be a triadic decision context, \(E\subseteq A,\) \(H\subseteq C_A,\) \(K\subseteq C_D,\) \(\varSigma \subseteq {\mathfrak {R}}(E,H,D,K)\) and \(\varOmega \subseteq {\mathfrak {R}}(A,H,D,K).\) If for any \(B\times H\rightarrow G\times K\in \varOmega ,\) there exists \(B_0\times H\rightarrow G_0\times K\in \varSigma\) such that \(B_0\times H\rightarrow G_0\times K\Rightarrow B\times H\rightarrow G\times K,\) we say that \(\varOmega\) can be implied by \(\varSigma ,\) which is denoted by \(\varSigma \Rightarrow \varOmega .\)

Definition 11

For a triadic decision context \({\mathbb {F}}=(U,A, C_A,I,D,C_D,J),\) \(E\subseteq A,\) \(H\subseteq C_A\) and \(K\subseteq C_D,\) if \({\mathfrak {R}}(E,H,D,K)\Rightarrow {\mathfrak {R}}(A,H,D,K),\) then E is called an HK-consistent set of \({\mathbb {F}};\) otherwise, E is called an HK-inconsistent set of \({\mathbb {F}}.\) Furthermore, if E is an HK-consistent set and any \(S\subset E\) is not an HK-consistent set of \({\mathbb {F}},\) then E is called an HK-reduct of \({\mathbb {F}}.\) The intersection of all the HK-reducts is called the HK-core of \({\mathbb {F}}.\)

Thus, a HK-reduct E of a given triadic decision context \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J)\) is such a minimal subset of A that all the constrained decision rules of \({\mathbb {F}}\) can be implied by the constrained decision rules of the reduced triadic decision context \((U,E,H,I_E,D,K,J).\)

Definition 12

Let \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J)\) be a triadic decision context, \(H\subseteq C_A\) and \(K\subseteq C_D.\) \(a\in A\) is called an HK-dispensable attribute of \({\mathbb {F}}\) if \(A\backslash \{a\}\) is an HK-consistent set of \({\mathbb {F}};\) otherwise, \(a\in A\) is called an HK-indispensable attribute of \({\mathbb {F}}.\)

Definition 13

Let \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J)\) be a triadic decision context, \(E\subseteq A,\) \(H\subseteq C_A\) and \(K\subseteq C_D.\) \(B\times H\rightarrow G\times K\in {\mathfrak {R}}(E,H,D,K)\) is said to be redundant in \({\mathfrak {R}}(E,H,D,K)\) if there exists another \(B_0\times H\rightarrow G_0\times K\in {\mathfrak {R}}(E,H,D,K)\) such that \(B_0\times H\rightarrow G_0\times K \Rightarrow B\times H\rightarrow G\times K.\) Otherwise, \(B\times H\rightarrow G\times K\) is said to be non-redundant.

Generally speaking, it is more appealing to derive non-redundant constrained decision rules from a triadic decision context because the redundant ones can be implied by others.

Let \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J)\) be a triadic decision context, \(E\subseteq A,\) \(H\subseteq C_A\) and \(K\subseteq C_D.\) We denote

$$\begin{aligned}&{\mathfrak {U}}^*(U,E\times H,I^{(3)}_E)\\&\quad =\{X\in {\mathfrak {U}}(U,E\times H,I^{(3)}_E)\mid X\not =\emptyset ,X^{H^{(3)}_E}\not =\emptyset \},\\&{\mathfrak {U}}^*(U,D\times K,J^{(3)})\\&\quad =\{Y\in {\mathfrak {U}}(U,D\times K,J^{(3)})\mid Y\not =\emptyset ,Y^{K^{(3)}}\not =\emptyset \}. \end{aligned}$$

Then three mappings \(\alpha _E,\) \(\beta _E,\) \(\gamma _E\): \({\mathfrak {U}}^*(U,E\times H,I^{(3)}_E)\) \(\times {\mathfrak {U}}^*(U,D\times K,J^{(3)}) \rightarrow \{0,1\}\) are defined as follows:

$$\begin{aligned} \alpha _E^{HK}(X,Y)= & {} \Bigg \{ \begin{array}{ll} 1, &{} \quad \text{ for } \text{ any } X'\in {\mathfrak {U}}^*(U,E\times H,I^{(3)}_E), \text{ if }\\ &{} X\subseteq Y \text{ and } X\subset X', \text{ then } X'\nsubseteq Y,\\ 0, &{} \quad \text{ otherwise, } \end{array}\\ \beta _E^{HK}(X,Y)= & {} \Bigg \{ \begin{array}{ll} 1, &{} \quad \text{ for } \text{ any } Y'\in {\mathfrak {U}}^*(U,D\times K,J^{(3)}), \text{ if }\\ &{} X\subseteq Y \text{ and } Y'\subset Y, \text{ then } X\nsubseteq Y',\\ 0, &{} \quad \text{ otherwise, } \end{array}\\ \gamma _E^{HK}(X,Y)= & {} \Bigg \{ \begin{array}{ll} 1, &{} \quad \text{ if } \alpha _E^{HK}(X,Y)=1 \text{ and } \beta _E^{HK}(X,Y)=1,\\ &{} \\ 0, &{} \quad \text{ otherwise. } \end{array} \end{aligned}$$

Theorem 1

For a triadic decision context \({\mathbb {F}}=(U,A,\,C_A,I,D,C_D,J),\) \(E\subseteq A,\) \(H\subseteq C_A\) and \(K\subseteq C_D,\) let \((X,B\times H)\in {\mathfrak {B}}(U,E\times H,I^{(3)}_E),\) \((Y,G\times K)\in {\mathfrak {B}}(U,D\times K,J^{(3)})\) and \(B\times H\rightarrow G\times K.\) Then \(B\times H\rightarrow G\times K\) is redundant in \({\mathfrak {R}}(E,H,D,K)\) if and only if \(\gamma _E^{HK}(X,Y)=0,\) or equivalently, \(B\times H\rightarrow G\times K\) is non-redundant in \({\mathfrak {R}}(E,H,D,K)\) if and only if \(\gamma _E^{HK}(X,Y)=1.\)

Proof

Since \((X,B\times H)\in {\mathfrak {B}}(U,E\times H,I^{(3)}_E),\) \((Y,G\times K)\in {\mathfrak {B}}(U,D\times K,J^{(3)})\) and \(B\times H\rightarrow G\times K,\) it follows from Definition 8 that \(X\ne \emptyset ,\) \(X^{H^{(3)}_E}\ne \emptyset ,\) \(Y\ne \emptyset ,\) \(Y^{K^{(3)}}\ne \emptyset .\) Thus, \(X\in {\mathfrak {U}}^*(U,E\times H,I^{(3)}_E)\) and \(Y\in {\mathfrak {U}}^*(U,D\times K,J^{(3)}).\)

“\(\Leftarrow\)” If \(\gamma _E^{HK}(X,Y)=0,\) we have \(\alpha _E^{HK}(X,Y)=0\) or \(\beta _E^{HK}(X,Y)=0.\) If \(\alpha _E^{HK}(X,Y)=0,\) then there exists \((X_0,B_0\times H)\in {\mathfrak {B}}(U,E\times H,I^{(3)}_E)\) such that \(X\subset X_0\) and \(X_0\subseteq Y.\) Thus, \(B_0\times H\rightarrow G\times K\in {\mathfrak {R}}(E,H,D,K)\) and \(B_0\subset B.\) It can be known from Definition 13 that \(B\times H \rightarrow G\times K\) is redundant in \({\mathfrak {R}}(E,H,D,K)\) since \(B_0 \times H\rightarrow G\times K\Rightarrow B\times H\rightarrow G\times K.\) If \(\beta _E^{HK}(X,Y)=0,\) we can prove in a similar manner that \(B\times H\rightarrow G\times K\) is redundant in \({\mathfrak {R}}(E,H,D,K).\)

“\(\Rightarrow\)” If the constrained decision rule \(B\times H\rightarrow G\times K\) is redundant in \({\mathfrak {R}}(E,H,D,K),\) there exists \(B_0\times H\rightarrow G_0\times K\in {\mathfrak {R}}(E,H,D,K)\setminus \{B\times H\rightarrow G\times K\}\) such that \(B_0\times H\rightarrow G_0\times K\Rightarrow B\times H \rightarrow G\times K.\) Hence, \(B_0\subset B\) and \(G\subseteq G_0\) or \(B_0\subseteq B\) and \(G\subset G_0.\) That is, \(X\subset X_0\) and \(Y_0\subseteq Y,\) or \(X\subseteq X_0\) and \(Y_0\subset Y,\) where \((X_0,B_0\times H)\in {\mathfrak {B}}(U,E\times H,I^{(3)}_E)\) and \((Y_0,G_0\times K)\in {\mathfrak {B}}(U,D\times K,J^{(3)}).\) Noting that \(X\subseteq Y\) and \(X_0\subseteq Y_0,\) we have \(X\subseteq Y,\) \(X\subset X_0\) and \(X_0\subseteq Y_0\subseteq Y,\) or \(X\subseteq Y,\) \(Y_0\subset Y\) and \(X\subseteq X_0\subseteq Y_0.\) Therefore, \(\alpha _E^{HK}(X,Y)=0\) or \(\beta _E^{HK}(X,Y)=0,\) which implies \(\gamma _E^{HK}(X,Y)=0.\) \(\square\)

Let \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J)\) be a triadic decision context, \(E\subseteq A,\) \(H\subseteq C_A\) and \(K\subseteq C_D.\) Then we denote

$$\overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)}=\{X\in {\mathfrak {U}}^*(U,E\times H,I^{(3)}_E)\mid \text{ there } \text{ is } Y\in {\mathfrak {U}}^*(U,D\times K,J^{(3)})\,\text{ such } \text{ that }\,\gamma _E^{HK}(X,Y)=1\},$$
$$\overline{{\mathfrak {R}}(E,H,D,K)}=\{B\times H\rightarrow G\times K\in {\mathfrak {R}}(E,H,D,K)\mid \gamma (B^{H^{(3)}_E},G^{K^{(3)}})=1\}.$$

That is, \(\overline{{\mathfrak {R}}(E,H,D,K)}\) is just the set of all non-redundant constrained decision rules of \({\mathfrak {R}}(E,H,D,K).\)

Example 2

Continued with Example 1. Take \(E=A,\) \(H=C_A\) and \(K=C_D.\) It can be seen from Tables 2 and 3 that

$$\begin{aligned} {\mathfrak {U}}^*(U,E\times H,I^{(3)}_E)=\{\{x_1\}, \{x_2\},\{x_1,x_3\},\{x_1,x_4\}\} \end{aligned}$$

and

$$\begin{aligned} {\mathfrak {U}}^*(U,D\times K,J^{(3)})=\{\{x_1\},\{x_2\},\{x_2,x_3\}\}. \end{aligned}$$

Then, we obtain

$$\begin{aligned} \gamma _E^{HK}(\{x_1\},\{x_1\})= & {} 1,\\ \gamma _E^{HK}(\{x_2\},\{x_2\})= & {} 1, \end{aligned}$$

and

$$\begin{aligned} \gamma _E^{HK}(X,Y)=0\,\,\text{ for } \text{ other }\,X\,\text{ and }\,Y, \end{aligned}$$

which leads to \(\overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)}=\{\{x_1\},\{x_2\}\}.\) Moreover, it is easy to verify that

$$\begin{aligned}&\overline{{\mathfrak {R}}(E,H,D,K)}=\{\{a_2,a_4\}\times \{c_1,c_2\} \rightarrow \{h_2\}\times \{c_3,c_4\},\\&\{a_1\}\times \{c_1,c_2\}\rightarrow \{h_1,h_3\}\times \{c_3,c_4\}\} \end{aligned}$$

In what follows, we put forward an equivalent condition for judging whether a given attribute set is an HK-consistent set of a triadic decision context.

Proposition 4

Let \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J)\) be a triadic decision context, \(E\subseteq A,\) \(H\subseteq C_A\) and \(K\subseteq C_D.\) Then both \({\mathfrak {R}}(E,H,D,K)\Rightarrow \overline{{\mathfrak {R}}(E,H,D,K)}\) and \(\overline{{\mathfrak {R}}(E,H,D,K)}\Rightarrow {\mathfrak {R}}(E,H,D,K)\) are true.

Proof

Since \(\overline{{\mathfrak {R}}(E,H,D,K)}\) is a subset of \({\mathfrak {R}}(E,H,D,K),\) it follows \({\mathfrak {R}}(E,H,D,K)\Rightarrow \overline{{\mathfrak {R}}(E,H,D,K)}\) according to Definition 10. The remainder is to prove \(\overline{{\mathfrak {R}}(E,H,D,K)}\) \(\Rightarrow {\mathfrak {R}}(E,H,D,K).\)

For any \(B\times H\rightarrow G\times K\in {\mathfrak {R}}(E,H,D,K),\) if it is non-redundant in \({\mathfrak {R}}(E,H,D,K),\) then \(B\times H\rightarrow G\times K\in \overline{{\mathfrak {R}}(E,H,D,K)}\) and it can imply itself; if \(B\times H\rightarrow G\times K\) is redundant in \({\mathfrak {R}}(E,H,D,K),\) then there exists \(B_1\times H\rightarrow G_1\times K\in {\mathfrak {R}}(E,H,D,K)\setminus \{B\times H \rightarrow G\times K\}\) such that \(B_1\times H\rightarrow G_1\times K\Rightarrow B\times H\rightarrow G\times K.\) If \(B_1\times H\rightarrow G_1\times K\) is non-redundant in \({\mathfrak {R}}(E,H,D,K),\) then \(B_1\times H\rightarrow G_1\times K\in \overline{{\mathfrak {R}}(E,H,D,K)}\) and \(B_1\times H\rightarrow G_1\times K\Rightarrow B\times H\rightarrow G\times K;\) otherwise, there exists \(B_2\times H\rightarrow G_2\times K\in {\mathfrak {R}}(E,H,D,K)\setminus \{B\times H\rightarrow G\times K,B_1\times H\rightarrow G_1\times K\}\) such that \(B_2\times H\rightarrow G_2\times K\Rightarrow B\times H\rightarrow G\times K.\) Since \({\mathfrak {R}}(E,H,D,K)\) is a finite set of constrained decision rules, it is true even in the worst case that there exists \(B_n\times H\rightarrow G_n\times K\in {\mathfrak {R}}(E,H,D,K)\setminus \{B\times H\rightarrow G\times K,B_1\times H\rightarrow G_1\times K,...,B_{n-1}\times H\rightarrow G_{n-1}\times K\}\) such that \(B_n\times H\rightarrow G_n\times K\) is non-redundant in \({\mathfrak {R}}(E,H,D,K)\) and \(B_n\times H\rightarrow G_n\times K\Rightarrow B\times H\rightarrow G\times K.\) Therefore, \(\overline{{\mathfrak {R}}(E,H,D,K)}\Rightarrow {\mathfrak {R}}(E,H,D,K).\) \(\square\)

Theorem 2

For a triadic decision context \({\mathbb {F}}=(U,A,\,C_A,I,D,C_D,J),\) \(E\subseteq A\) is an HK -consistent set of \({\mathbb {F}}\) if and only if \(\overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)}=\overline{{\mathfrak {U}} (U,A\times H,I^{(3)})}.\)

Proof

“\(\Rightarrow\)” If \(E\subseteq A\) is an HK-consistent set of \({\mathbb {F}},\) it follows from Definition 11 that \({\mathfrak {R}}(E,H,D,K)\Rightarrow {\mathfrak {R}}(A,H,D,K).\) According to Proposition 4, we obtain \(\overline{{\mathfrak {R}}(E,H,D,K)}\Rightarrow {\mathfrak {R}} (E,H,D,K)\Rightarrow {\mathfrak {R}}(A,H,D,K)\Rightarrow \overline{ {\mathfrak {R}}(A,H,D,K)}.\) Now, we are to prove \(\overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)}\) \(=\overline{{\mathfrak {U}} (U,A\times H,I^{(3)})}.\)

For any \(X\in \overline{{\mathfrak {U}}(U,A\times H,I^{(3)})},\) there exist \(B\subseteq A\) and \((Y,G\times K)\in {\mathfrak {B}}(U,D\times K,J^{(3)})\) such that \(\gamma _A^{HK}(X,Y)\) \(=1\) and \(B\times H\rightarrow G\times K\in \overline{{\mathfrak {R}}(A,H,D,K)}.\) Since \(\overline{{\mathfrak {R}}(E,H,D,K)}\Rightarrow \overline{{\mathfrak {R}}(A,H,D,K)},\) there exists \(B_0\times H\rightarrow G_0\times K\in \overline{{\mathfrak {R}}(E,H,D,K)}\) such that \(B_0\subseteq B\) and \(G\subseteq G_0.\) That is, \(X_0\in \overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)},\) \(X\subseteq X_0\) and \(Y_0\subseteq Y,\) where \((X_0,B_0\times H)\in {\mathfrak {B}}(U,E\times H,I^{(3)}_E)\) and \((Y_0,G_0\times K)\in {\mathfrak {B}}(U,D\times K,J^{(3)}).\) If \(X_0\ne X,\) we have \(X\subset X_0\subseteq Y_0\subseteq Y.\) Noting that \(X_0\in {\mathfrak {U}}(U,E\times H,I^{(3)}_E)\subseteq {\mathfrak {U}}(U,A\times H,I^{(3)}),\) we obtain \(\alpha _A^{HK}(X,Y)=0,\) which is in contradiction with \(\gamma _A^{HK}(X,Y)=1.\) So, \(X=X_0\in \overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)}.\) Therefore, we conclude \(\overline{{\mathfrak {U}}(U,A\times H,I^{(3)})}\subseteq \overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)}.\)

On the other hand, for any \(X\in \overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)},\) there exist \(B\subseteq E\) and \((Y,G\times K)\in {\mathfrak {B}}(U,D\times K,J^{(3)})\) such that \(\gamma _E^{HK}(X,Y)=1.\) If \(X\notin \overline{{\mathfrak {U}}(U,A\times H,I^{(3)})},\) we obtain \(\gamma _A^{HK}(X,Y)=0.\) Noting that \(\beta _A^{HK}(X,Y)=\beta _E^{HK}(X,Y)=1,\) we have \(\alpha _A^{HK}(X,Y)=0.\) Then, there exists \(X_0\in {\mathfrak {U}}(U,A\times H,I^{(3)})\) such that \(\alpha _A^{HK}(X_0,Y)=1\) and \(X\subset X_0.\) Furthermore, it is easy to conclude that \(\beta _A^{HK}(X_0,Y)=1\) based on \(\alpha _A^{HK}(X_0,Y)=1,\) \(\beta _A^{HK}(X,Y)\) \(=1\) and \(X\subset X_0.\) Hence, \(\gamma _A^{HK}(X_0,Y)=1\) and \(X\subset X_0.\) Since \(\overline{{\mathfrak {U}}(U,A\times H,I^{(3)})}\subseteq \overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)}\) has been proved above, it follows \(X_0\in \overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)}\) and \(X\subset X_0\subseteq Y.\) Therefore, \(\alpha _E^{HK}(X,Y)=0,\) which is in contradiction with \(\alpha _E^{HK}(X,Y)=1.\)

“\(\Leftarrow\)” If \(\overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)}=\overline{{\mathfrak {U}}(U,A\times H,I^{(3)})},\) then for any \(B\times H\rightarrow G\times K\in \overline{{\mathfrak {R}}(A,H,D,K)},\) there exists \(B_0\times H\rightarrow G\times K\in \overline{{\mathfrak {R}}(E,H,D,K)}\) such that \(X=X_0,\) where \((X,B\times H)\in {\mathfrak {B}}(U,A\times H,I^{(3)}),\) \((Y,G\times K)\in {\mathfrak {B}}(U,D\times K,J^{(3)})\) and \((X_0,B_0\times H)\in {\mathfrak {B}} (U,E\times H,I^{(3)}_E).\) So, \(B_0=X_0^{H^{(3)}_E}=X_0^{H^{(3)}}\cap E=X^{H^{(3)}}\cap E=B\cap E\subseteq B,\) which means \(B_0\times H\rightarrow G\times K\Rightarrow B\times H\rightarrow G\times K.\) Therefore, we get \(\overline{{\mathfrak {R}}(E,H,D,K)}\Rightarrow \overline{{\mathfrak {R}}(A,H,D,K)}\) and hence \({\mathfrak {R}}(E,H,D,K)\Rightarrow \overline{{\mathfrak {R}} (E,H,D,K)}\Rightarrow \overline{{\mathfrak {R}}(A,H,D,K)}\) \(\Rightarrow {\mathfrak {R}}(A,H,D,K).\) Consequently, E is an HK-consistent set of \({\mathbb {F}}.\) \(\square\)

Finally, we design Algorithm 2 to derive the non-redundant constrained decision rules from a triadic decision context.

figure b

It is easy to observe that the time complexity of Algorithm 2 is exponential.

Example 3

Continued with Example 1. Take \(H=C_A=\{c_1,c_2\}\) and \(K=C_D=\{c_3,c_4\}.\) Then, according to Algorithm 2, all the non-redundant constrained decision rules hidden in \({\mathbb {F}}\) are as follows:

\(r_1^{HK}\): If Supermarket 1 and Supermarket 2 provide Tomatoes and Milk, then Restaurant 1 and Restaurant 2 sell Hamburg.

\(r_2^{HK}\): If Supermarket 1 and Supermarket 2 provide Potatoes, then Restaurant 1 and Restaurant 2 sell Sandwich and Pizza.

Moreover, it can be verified with Theorem 2 that \(E=\{a_1,a_2,a_4\}\) is an HK-consistent set of \({\mathbb {F}}.\)

4 Knowledge reduction in triadic decision contexts

In the previous section, we have put forward a novel reduction framework for triadic decision contexts. With this framework, we can obtain all the non-redundant constrained decision rules from a triadic decision context. Note that, generally speaking, the implementation of knowledge reduction makes the discovery of constrained decision rules easier. Motivated by this, we discuss below how to implement knowledge reduction under the proposed framework.

Definition 14

Let \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J)\) be a triadic decision context, \(H\subseteq C_A\) and \(K\subseteq C_D.\) For \((X_i,B_i\times H),(X_j,B_j\times H)\in {\mathfrak {B}}(U,A\times H,I^{(3)}),\) we denote

$$\begin{aligned}&P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))\\&\quad =\Bigg \{ \begin{array}{ll} B_i\lozenge B_j, &{} \quad \text{ if } X_i\nsubseteq X_j\in \overline{{\mathfrak {U}}(U,A\times H,I^{(3)})} \text{ or }\\ &\quad X_j\nsubseteq X_i\in \overline{{\mathfrak {U}}(U,A\times H,I^{(3)})},\\ \emptyset , &{} \quad \text{ otherwise, } \end{array} \end{aligned}$$

where \(B_i\lozenge B_j=(B_i\cup B_j)\setminus (B_i\cap B_j).\) We call \(P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))\) the HK-discernibility attribute set of \((X_i,B_i\times H)\) and \((X_j,B_j\times H),\) and \({\mathfrak {P}}^{\vartriangle }=\{P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))\mid (X_i,B_i\times H),(X_j,B_j\times H)\in {\mathfrak {B}}(U,A\times H,I^{(3)})\}\) the HK-discernibility matrix of \({\mathbb {F}}.\)

Proposition 5

Let \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J)\) be a triadic decision context, \(H\subseteq C_A,\) \(K\subseteq C_D\) and \((X_i,B_i\times H),(X_j,B_j\times H),(X_k,B_k\times H)\in {\mathfrak {B}}(U,A\times H,I^{(3)}).\) Then

  1. (i)

    \(P^{\vartriangle }((X_i,B_i\times H),(X_i,B_i\times H))=\emptyset;\)

  2. (ii)

    \(P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))=P^{\vartriangle }((X_j,B_j\times H),(X_i,B_i\times H));\)

  3. (iii)

    \(P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))\subseteq P^{\vartriangle }((X_i,B_i\times H),(X_k,B_k\times H))\cup P^{\vartriangle }((X_k,B_k\times H),(X_j,B_j\times H))\) if \(X_i,X_j,X_k\in \overline{{\mathfrak {U}}(U,A\times H,I^{(3)})}.\)

Proof

According to Definition 14, the proofs of (i) and (ii) are trivial. The remainder is to prove (iii).

For any \(a\in P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H)),\) we have that \(a\in B_i\) but \(a\notin B_j,\) or \(a\in B_j\) but \(a\notin B_i.\)

If \(a\in B_i,\) \(a\notin B_j\) and \(a\notin B_k,\) then \(a\in P^{\vartriangle }((X_i,B_i\times H),(X_k,B_k\times H));\) if \(a\in B_i,\) \(a\notin B_j\) and \(a\in B_k,\) then \(a\in P^{\vartriangle }((X_k,B_k\times H),(X_j,B_j\times H)).\) Thus, \(P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))\subseteq P^{\vartriangle }((X_i,B_i\times H),(X_k,B_k\times H))\cup P^{\vartriangle }((X_k,B_k\times H),(X_j,B_j\times H))\) when \(a\in B_i\) but \(a\notin B_j.\)

Similarly, we can prove \(P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))\subseteq P^{\vartriangle }((X_i,B_i\times H),(X_k,B_k\times H))\cup P^{\vartriangle }((X_k,B_k\times H),(X_j,B_j\times H))\) when \(a\in B_j\) but \(a\notin B_i.\) \(\square\)

In what follows, from the viewpoint of the HK-discernibility attribute set, we put forward an equivalent condition for judging whether a given attribute set is an HK-consistent set of a triadic decision context. Before embarking on this issue, we explain the relationship between the HK-discernibility attribute set and an HK-consistent set.

For any nonempty set \(P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))\in {\mathfrak {P}}^{\vartriangle },\) it follows from Definition 14 that the concepts \((X_i,B_i\times H)\) and \((X_j,B_j\times H)\) can be distinguished from one to another by the attribute set \(P^{\vartriangle }((X_i,\) \(B_i\times H),(X_j,B_j\times H)).\) Now, consider such a case that we remove the attributes in the complement set of E in A in order to avoid redundancy. Under such a circumstance, if \(E\cap P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))=\emptyset ,\) then both \((X_i,B_i\times H)\) and \((X_j,B_j\times H)\) will be degenerated into the same concept. Without loss of generality, we assume that this degenerated concept is \((X_k,B_k\times H).\) The following discussion is divided into two cases.

Case 1 \(X_i\nsubseteq X_j\in \overline{{\mathfrak {U}}(U,A\times H,I^{(3)})}\)

Under this case, there are two circumstances for the relationship among \((X_i,B_i\times H),\) \((X_j,B_j\times H)\) and \((X_k,B_k\times H).\) See Figs. 3 and 4 for details. No matter which circumstance it occurs, it always follows \(X_j\notin \overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)}.\) As a result, we can conclude that \(\overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)}\not =\overline{{\mathfrak {U}}(U,A\times H,I^{(3)})}.\) Then, according to Theorem 2, E is not an HK-consistent set of \({\mathbb {F}}.\)

Case 2 \(X_j\nsubseteq X_i\in \overline{{\mathfrak {U}}(U,A\times H,I^{(3)})}\)

In a similar manner, \(X_i\notin \overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)}\) but \(X_i\in \overline{{\mathfrak {U}}(U,A\times H,I^{(3)})}\) can be proved, which leads to \(\overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)}\not =\overline{{\mathfrak {U}}(U,A\times H,I^{(3)})}.\) Consequently, E is not an HK-consistent set of \({\mathbb {F}}.\)

To sum up, in order to obtain that E is an HK-consistent set of \({\mathbb {F}},\) it is necessary to guarantee \(E\cap P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))\not =\emptyset\) for every nonempty set \(P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))\in {\mathfrak {P}}^{\vartriangle }.\)

Fig. 3
figure 3

The relationship among \((X_i,B_i\times H),\) \((X_j,B_j\times H)\) and \((X_k,B_k\times H)\)

Full size image
Fig. 4
figure 4

The relationship among \((X_i,B_i\times H),\) \((X_j,B_j\times H)\) and \((X_k,B_k\times H)\)

Full size image

Theorem 3

Let \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J)\) be a triadic decision context, \(H\subseteq C_A\) and \(K\subseteq C_D.\) Then \(E\subseteq A\) is an HK -consistent set of \({\mathbb {F}}\) if and only if \(E\cap P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))\not =\emptyset\) for every nonempty set \(P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))\in {\mathfrak {P}}^{\vartriangle }.\)

Proof

“\(\Rightarrow\)” It is trivial according to the aforementioned analysis.

“\(\Leftarrow\)” For any \(X\in \overline{{\mathfrak {U}} (U,A\times H,I^{(3)})},\) there exists \(B\subseteq A\) such that \((X,B\times H)\in {\mathfrak {B}}(U,A\times H,I^{(3)}).\) Moreover, it can be known from Proposition 2 that \(((B\cap E)^{H^{(3)}},(B\cap E)^{H^{(3)}H^{(3)}}\times H)\in {\mathfrak {B}}(U,A\times H,I^{(3)}).\) If \((B\cap E)^{H^{(3)}}=X,\) then \((X,(B\cap E)\times H)\in {\mathfrak {B}}(U,E\times H,I^{(3)}_E)\) and hence \(X\in \overline{{\mathfrak {U}}(U,E\times H,I^{(3)}_E)}\) is at hand. Otherwise, \((B\cap E)^{H^{(3)}}\not =X.\) Under such a case, it in fact satisfies \((B\cap E)^{H^{(3)}}\nsubseteq X.\) Based on Definition 14, \(P^{\vartriangle }((X,B\times H),((B\cap E)^{H^{(3)}},(B\cap E)^{H^{(3)}H^{(3)}}\times H))\not =\emptyset .\) According to the assumption, we obtain \(E\cap P^{\vartriangle }((X,B\times H),((B\cap E)^{H^{(3)}},(B\cap E)^{H^{(3)}H^{(3)}}\times H))\not =\emptyset ,\) which yields \(E\cap B\not =E\cap (B\cap E)^{H^{(3)}H^{(3)}}.\) However,

$$\begin{aligned} \begin{array}{ll} E\cap B\subseteq B&{}\Rightarrow (E\cap B)^{H^{(3)}}\supseteq B^{H^{(3)}}=X\\ &{}\Rightarrow (E\cap B)^{H^{(3)}H^{(3)}}\subseteq B\\ &{}\Rightarrow E\cap (E\cap B)^{H^{(3)}H^{(3)}}\subseteq E\cap B. \end{array} \end{aligned}$$

On the other hand,

$$\begin{aligned} E\cap B\subseteq (E\cap B)^{H^{(3)}H^{(3)}}\Rightarrow E\cap B\subseteq E\cap (E\cap B)^{H^{(3)}H^{(3)}}. \end{aligned}$$

Therefore, \(E\cap B=E\cap (B\cap E)^{H^{(3)}H^{(3)}},\) a contradiction. As a result, \(\overline{{\mathfrak {U}}(U,A\times H,I^{(3)})}\subseteq \overline{{\mathfrak {U}} (U,E\times H,I^{(3)}_E)}.\)

Moreover, similar to the case in the proof of Theorem 2, we can draw the conclusion \(\overline{{\mathfrak {U}} (U,E\times H,I^{(3)}_E)}\subseteq \overline{{\mathfrak {U}}(U,A\times H,I^{(3)})}\) with the help of \(\overline{{\mathfrak {U}}(U,A\times H,I^{(3)})}\subseteq \overline{{\mathfrak {U}} (U,E\times H,I^{(3)}_E)}.\)

To sum up, \(\overline{{\mathfrak {U}}(U,A\times H,I^{(3)})}=\overline{{\mathfrak {U}} (U,E\times H,I^{(3)}_E)}\) is established. According to Theorem 2, E is an HK-consistent set of \({\mathbb {F}}.\) \(\square\)

Proposition 6

Let \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J)\) be a triadic decision context, \(H\subseteq C_A\) and \(K\subseteq C_D.\) \(a\in A\) is an HK -indispensable attribute of \({\mathbb {F}}\) if and only if there exists \(P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))\in {\mathfrak {P}}^ {\vartriangle }\) such that \(P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))=\{a\}.\)

Proof

“\(\Rightarrow\)” If \(a\in A\) is an HK-indispensable attribute of \({\mathbb {F}},\) it follows from Definition 12 that \(A\setminus \{a\}\) is an HK-inconsistent set of \({\mathbb {F}}.\) Based on Theorem 3, there exists \(P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))\in {\mathfrak {P}}^ {\vartriangle }\) such that \((A\setminus \{a\})\cap P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))=\emptyset ,\) which yields \(P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))=\{a\}.\)

“\(\Leftarrow\)” If there exists \(P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))\in {\mathfrak {P}}^ {\vartriangle }\) such that \(P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))=\{a\},\) then \((A\setminus \{a\})\cap P^{\vartriangle }((X_i,B_i\times H),(X_j,B_j\times H))=\emptyset .\) Hence, it follows from Theorem 3 that \(A\setminus \{a\}\) is an HK-inconsistent set of \({\mathbb {F}}.\) Consequently, a is an HK-indispensable attribute of \({\mathbb {F}}.\) \(\square\)

Definition 15

For a triadic decision context \({\mathbb {F}}=(U,A,\,C_A,I,D,C_D,J)\) with \(H\subseteq C_A\) and \(K\subseteq C_D,\) let \({\mathfrak {P}}^{\vartriangle }\) be the HK-discernibility matrix of \({\mathbb {F}}.\) We call \(F_{\vartriangle }=\bigwedge \nolimits _{P^{\vartriangle }\in {\mathfrak {P}}^ {\vartriangle },P^{\vartriangle }\not =\emptyset }\bigvee P^{\vartriangle }\) the HK-discernibility function of \({\mathbb {F}}.\)

Theorem 4

For a triadic decision context \({\mathbb {F}}=(U,A,\,C_A,I,D,C_D,J)\) with \(H\subseteq C_A\) and \(K\subseteq C_D,\) let \(F_{\vartriangle }=\bigvee \nolimits ^{k}_{t=1}(\bigwedge \nolimits ^{r_t}_{s=1}a_s)\) be the minimal disjunctive normal form of the HK -discernibility function \(F_{\vartriangle },\) where \(\bigwedge \nolimits ^{r_t}_{s=1}(a_s)\) \((t\leqslant k)\) are all the prime implicants of the HK -discernibility function \(F_{\vartriangle }.\) Then \(E_t=\{a_s\mid s\leqslant r_t\}\) \((t\leqslant k)\) are all the HK -reducts of \({\mathbb {F}}.\)

Proof

According to the definition of the minimal disjunctive normal form of a Boolean function, the proof is immediate from Theorem 3 and Proposition 6. \(\square\)

Example 4

Continued with Example 1. Take \(H=C_A\) and \(K=C_D.\) Then, Table 4 shows the HK-discernibility matrix of \({\mathbb {F}}=(U,A,C_A,I,D,C_D,J).\) According to Theorem 4, we can compute all the HK-reducts of \({\mathbb {F}}\) as follows:

$$\begin{aligned} \begin{array}{ll} F_{\vartriangle }&{}=\bigwedge \limits _{P^{\vartriangle }\in {\mathfrak {P}}^ {\vartriangle },P^{\vartriangle }\not =\emptyset }\bigvee P^{\vartriangle }\\ &{}=(a_1\vee a_4)\wedge (a_2\vee a_4)\wedge (a_1\vee a_2)\\ &{}\quad \wedge (a_1\vee a_2\vee a_4)\wedge a_1\wedge a_2\wedge a_4\\ &{}=a_1\wedge a_2\wedge a_4. \end{array} \end{aligned}$$

Thus, \({\mathbb {F}}\) has one HK-reduct \(E=\{a_1,a_2,a_4\}.\) By this HK-reduct, we can obtain the reduced triadic decision context \((U,E,C_A,I_E,D,C_D,J).\) Table 5 shows all triadic concepts of \((U,E,C_A,I_E),\) and Fig. 5 depicts the diagram of \(\underline{{\mathfrak {B}}}(U,E,C_A,I_E).\) Based on Tables 3 and 5, all the non-redundant constrained decision rules hidden in \((U,E,C_A,I_E,D,C_D,J)\) are as follows:

\(r_3^{HK}\): If Supermarket 1 and Supermarket 2 provide Tomatoes and Milk, then Restaurant 1 and Restaurant 2 sell Hamburg.

\(r_4^{HK}\): If Supermarket 1 and Supermarket 2 provide Potatoes, then Restaurant 1 and Restaurant 2 sell Sandwich and Pizza.

Comparing \(r_3^{HK}\) and \(r_4^{HK}\) with \(r_1^{HK}\) and \(r_2^{HK}\) in Example 3, we find that the non-redundant constrained decision rules derived from the reduced triadic decision context are the same as those derived from the original dataset \({\mathbb {F}}.\)

Table 4 The HK-discernibility matrix of \({\mathbb {F}}\)
Full size table
Table 5 All triadic concepts of \((U,E,C_A,I_E)\)
Full size table
Fig. 5
figure 5

The diagram of \(\underline{{\mathfrak {B}}}(U,E,C_A,I_E)\)

Full size image

5 Conclusion

This study has put forward a novel rule acquisition method for triadic decision contexts and discussed the issue of attribute reduction to make the original constrained decision rules more compact for making better decision analysis of the data. It deserves to be mentioned that the proposed method can be regarded as an information fusion technology since a triadic decision context can be viewed as multi-source data if one takes the data under each condition to be a single-source data.

The study of the triadic concept analysis is still in its infancy. At present, this theory has been mainly applied to mining triadic hierarchy structure [34], association rules [35], searching for optimal patterns [36] and analyzing triadic security context [37] from ternary relation. So, the proposed method will also be applied to these potential applications in the near future.

In fact, the discussion of triadic decision contexts is a challenging problem since the dimension of the data is three. As is well known, building a concept lattice of a two-dimension data is computationally expensive, let alone a three-dimension data. So, it is still necessary to improve the efficiency of mining knowledge from triadic decision contexts. Maybe concept learning [38] can provide a feasible way of solving this kind of problems.

Last but not least, the results in this paper on constrained decision rules of a triadic decision context should be generalized into the fuzzy environment because the data under consideration may often be fuzzy in the real world. Note that there have been many excellent studies (e.g. [39–41]) for our reference on this aspect. In our opinion, the problems to be investigated include fuzzy decision tree induction, generalization of fuzzy decision rules, and so on. We will try to find possible solutions to these problems in our forthcoming work.