1 Introduction

Support vector machine (SVM) [1, 2], being widely used for pattern classification and regression problems, was introduced by Vapnik and his co-workers in the early 1990s. Previous studies demonstrated the superiority of SVM [3–5]. By employing the structural risk minimization (SRM) principle [6], SVM tries to find a decision hyperplane that separates data points from two classes well by constructing two parallel support hyperplanes that the margin between them is maximized. However, SVM needs to solve a quadratic programming problem (QPP), which restricts its application to large scale problems. To address this issue, numerous approaches have been proposed [7–12].

For binary classification, some nonparallel hyperplane classifiers have attracted much attention. Mangasarian and Wild [9] proposed a generalized eigenvalue proximal support vector machine (GEPSVM) which aims at finding two nonparallel hyperplanes such that each hyperplane is closer to its own class and far from the other class as much as possible. This idea leads to solving two generalized eigenvalue problems which in turn reduces computation cost compared with SVM. Subsequently, an improved version of GEPSVM, called IGEPSVM [13], is proposed to remove the possible singularity problem of GEPSVM. In the spirit of GEPSVM, Jayadeva et. al. [10] proposed the twin support vector machine (TWSVM). Different from SVM, TWSVM solves two smaller sized QPPs rather than a single large one, which makes the learning speed of TWSVM be approximately four times faster than that of SVM. Both GEPSVM and TWSVM share the idea of nonparallel SVMs, which is in fact has been studied extensively [14–20].

Instead of finding nonparallel hyperplanes, the idea of seeking projection axes for SVMs has also been established. Ye et. al. [21] proposed a multi-weight vector projection support vector machine (MVSVM), whose purpose is to find two optimal weight vector projection directions, such that each class is centered around its own class centroid while is separated as much as possible from the other class in the projected space. Inspired by TWSVM and MVSVM, projection twin support vector machine (PTSVM) [22, 23] is proposed recently. The central thought of PTSVM is to find a projection axis one for each class, such that the within-class variance of the projected data points of its own class is minimized meanwhile projected data points of the other class scatter away as far as possible. PTSVM can be extended to find multiple orthogonal directions by a recursive procure. To accelerate the training speed of PTSVM, Shao et al. [24] adopted the idea of least squares [7, 14] and proposed a least squares projection twin support vector machine (LSPTSVM) by considering the equality constraints. An extra regularization term is introduced in the primal problem of LSPTSVM to remove the singularity problem that may appear in PTSVM.

As a natural extension of binary classification problem, multi-class classification has also drawn many attentions. Among all the methods, SVM and its variants [25–29] have been confirmed to have outstanding performance. Generally speaking, two types of strategies are widely used when SVMs are applied. One is the “decomposition-reconstruction” strategy which involves solving a series of small sized optimization problems, including the classical “one versus one” and “one versus rest” techniques [26–29]. The other one is the “all-together” strategy through solving one large scale optimization problem [25].

Being a successful multi-class classification tool, multiple recursive projection twin support vector machine (MPTSVM) [29] is a recently proposed SVM-type classifier, which is established based on binary PTSVM by utilizing the “one versus rest” technique. Though MPTSVM performs satisfactorily, it is computationally expensive since a series of QPPs are needed to be solved. For this purpose, in this paper, we extend the LSPTSVM to multi-class classification problem, and propose a multiple least squares recursive projection twin support vector machine (MLSPTSVM). Instead of solving complex QPPs in MPTSVM, our MLSPTSVM solves a series of linear equations, which leads to relatively fast training speed. For \(K(K>2)\) classes classification problem, our MLSPTSVM determines K groups of projection axes, one group for each class, such that the within-class variance of the projected data points of its own class is minimized while each projected class is far awat from the projected centers of the other classes. Specially, we apply the classical “one versus rest” multi-class classification technique to our MLSPTSVM by considering its advantage on computational efficiency. Preliminary experimental results on several real-world datasets and large datasets show the advantages of MLSPTSVM over MPTSVM and other SVM related methods for multi-class classification problem. The following are the highlights of our MLSPTSVM:

  1. 1.

    MLSPTSVM considers both the linear and the nonlinear models, while the binary LSPTSVM ignores the nonlinear case.

  2. 2.

    MLSPTSVM solves a series of linear equations, which makes it can handle the large datasets easily.

  3. 3.

    MLSPTSVM could generate multiple orthogonal projection directions for each class, which may notably enhance its performance.

  4. 4.

    The Sherman–Morrison–Woodbury (SMW) formulation and the reduced kernel technique are employed to reduce the complexity of nonlinear MLSPTSVM.

The rest of the paper is organized as follows: In Sect. 2, we provide the basic notations and give a brief review of TWSVM, PTSVM and LSPTSVM. Section 3 presents the details of MLSPTSVM under different requirement and its computational complexity. A variety of experimental results are demonstrated in Sect. 4. Finally, Sect. 5 concludes this paper.

2 Preliminaries

In this section, we consider the binary classification problem of classifying m data points in the n-dimensional real space \(\mathbb R^{n}\), with data points in class 1 and class 2 are represented by the matrices \(A=({\rm a}_{1},\ldots ,{\rm a}_{m_1})^{T}\in \mathbb {R}^{m_1\times n}\) and \(B=({\rm b}_{1},\ldots ,{\rm b}_{m_2})^{T}\in \mathbb {R}^{m_2\times n}\) respectively, where \(m=m_1+m_2\). In the following, we will give a brief review of TSVM, PTSVM and LSPTSVM.

2.1 Twin support vector machine

Twin support vector machine (TWSVM) [10] aims at determining two nonparallel hyperplanes \(x^{T}w^{(1)}+b^{(1)}=0\) and \(x^{T}w^{(2)}+b^{(2)}=0\), such that each hyperplane is close to data points of one class and far from the data points of the other class. The two hyperplanes are obtained by solving a pair of SVM-type QPPs as the following

$$\begin{aligned} \underset{w^{(1)},b^{(1)},\xi }{\min }& \frac{1}{2}(A w^{(1)}+e_1b^{(1)})^{T}(A w^{(1)}+e_1b^{(1)})+c_1e_2^{T}\xi \nonumber \\ \hbox {s.t.}\;& -(B w^{(1)}+e_2b^{(1)})+\xi \ge e_2,\quad \xi \ge 0 \end{aligned}$$
(1)

and

$$\begin{aligned} \underset{w^{(2)},b^{(2)},\eta }{\min }& \frac{1}{2}(B w^{(2)}+e_2b^{(2)})^{T}(B w^{(2)}+e_2b^{(2)})+c_2e_1^{T}\eta \nonumber \\ \hbox {s.t.}\;& (A w^{(2)}+e_1b^{(2)})+\eta \ge e_1,\quad \eta \ge 0, \end{aligned}$$
(2)

where \(c_1\), \(c_2 > 0\) are penalty parameters, \(e_1\in \mathbb {R}^{m_1}\) and \(e_2\in \mathbb {R}^{m_2}\) are vectors of ones, and \(\xi ,\,\eta\) are vectors of nonnegative slack variables.

Through the K.K.T conditions [30], we can obtain the Wolf dual forms of problems (1) and (2) as follows

$$\begin{aligned} \underset{\alpha }{\min }& \frac{1}{2}\alpha ^{T}P(Q^{T}Q)^{-1}P^{T}\alpha -e_2^{T}\alpha \nonumber \\ \hbox {s.t.}\;& 0\le \alpha \le c_1e_2 \end{aligned}$$
(3)

and

$$\begin{aligned} \underset{\gamma }{\min }& \frac{1}{2}\gamma ^{T}Q(P^{T}P)^{-1}Q^{T}\gamma -e_1^{T}\gamma \nonumber \\ \hbox {s.t.}\;& 0\le \gamma \le c_1e_1. \end{aligned}$$
(4)

Here, \(Q=[A,e_1]\), \(P=[B,e_2]\), and \(\alpha =(\alpha _{1},\alpha _{2},\ldots ,\alpha _{m_2})^T\) and \(\gamma =(\gamma _{1},\gamma _{2},\ldots ,\gamma _{m_1})^T\) are the vectors of Lagrange multipliers.

Define \(u=[w^{(1)},b^{(1)}]^{T}\) and \(v=[w^{(2)},b^{(2)}]^{T}\). Then the two nonparallel hyperplanes can be obtained from the solution of problems (3) and (4), which are given by

$$\begin{aligned} u=-(Q^{T}Q)^{-1}P^{T}\alpha \end{aligned}$$
(5)

and

$$\begin{aligned} v=(P^{T}P)^{-1}Q^{T}\gamma \end{aligned}$$
(6)

respectively. Once vectors u and v are known from (5) and (6), the two separating hyperplanes \(x^{T}w^{(1)}+b^{(1)}=0\) and \(x^{T}w^{(2)}+b^{(2)}=0\) are obtained and the training process is finished. For predicting, a new data point \(\mathrm x\in \mathbb {R}^{n}\) is assigned to class \(i (i=1,2)\), depending on which of the two hyperplanes it lies closer to, i.e.,

$$\begin{aligned} label({\rm x})=\hbox {arg} \underset{i=1,2}{\min }|{\rm x}^{T} w^{(i)}+b^{(i)}|, \end{aligned}$$
(7)

where \(|\cdot |\) is the absolute value operation that computes perpendicular distance of \(\mathrm x\) to each hyperplane.

It should be noted that, \(Q^{T}Q\) and \(P^{T}P\) in (5) and (6) are positive semidefinite, and hence it is possible that they may not be well defined when taking inverse. Therefore, a regularization term \(\epsilon I\) can be introduced to avoid the possible ill-condition of \(Q^{T}Q\) and \(P^{T}P\), where \(\epsilon > 0\) and I is the identity matrix of appropriate dimension.

2.2 Projection twin support vector machine

Different from TWSVM who finds nonparallel hyperplanes, projection twin support vector machine (PTSVM) [22] aims at finding two projection axes \(w_1\) and \(w_2\), one for each class, such that the within-class variance of projected data points of its own class is minimized while projected data points from other class scatter away as far as possible. This idea leads to the formulations of PTSVM as

$$\begin{aligned} \underset{w_{1}}{\min }& \frac{1}{2}\sum _{i=1}^{m_{1}}\left( w_{1}^T{\rm a}_{i}-w_{1}^T\frac{1}{m_{1}}\sum _{j=1}^{m_{1}}{\rm a}_{j}\right) ^{2}+c_{1}\sum _{k=1}^{m_2}\xi _{k}\nonumber \\ \hbox {s.t.}\;& w_{1}^{T}{\rm b}_k-w_{1}^{T}\frac{1}{m_{1}}\sum _{j=1}^{m_{1}}{\rm a}_{j}+\xi _{k}\ge 1,\quad \xi _{k}\ge 0,\quad k=1,2,\ldots ,m_2 \end{aligned}$$
(8)

and

$$\begin{aligned} \underset{w_{2}}{\min }& \frac{1}{2}\sum _{i=1}^{m_{2}}\left( w_{2}^T{\rm b}_{i}-w_{2}^T\frac{1}{m_{2}}\sum _{j=1}^{m_{2}}{\rm b}_{j}\right) ^{2}+c_{2}\sum _{k=1}^{m_1}\eta _{k}\nonumber \\ \hbox {s.t.}\;& -\left( w_{2}^{T}{\rm a}_k-w_{2}^{T}\frac{1}{m_{2}}\sum _{j=1}^{m_{2}}{\rm b}_{j}\right) +\eta _{k}\ge 1,\quad \eta _{k}\ge 0,\quad k=1,2,\ldots ,m_1, \end{aligned}$$
(9)

where \(c_{1}\) and \(c_{2}\) are trade-off parameters, and \(\xi _k,\,\eta _k\) are nonnegative slack variables.

Before determining solutions of (8) and (9), we first define

$$\begin{aligned} S_1=\sum _{i=1}^{m_{1}}\left( {\rm a}_{i}-\frac{1}{m_{1}}\sum _{j=1}^{m_{1}}{\rm a}_{j}\right) \left( {\rm a}_{i}-\frac{1}{m_{1}}\sum _{j=1}^{m_{1}}{\rm a}_{j}\right) ^T \end{aligned}$$
(10)

and

$$\begin{aligned} S_2=\sum _{i=1}^{m_{2}}\left( {\rm b}_{i}-\frac{1}{m_{2}}\sum _{j=1}^{m_{2}}{\rm b}_{j}\right) \left( {\rm b}_{i}-\frac{1}{m_{2}}\sum _{j=1}^{m_{2}}{\rm b}_{j}\right) ^T, \end{aligned}$$
(11)

as the covariance matrices of the first and second class, respectively. Then problems (8) and (9) can be solved through their Wolf dual forms [30] which are given by

$$\begin{aligned} \underset{\alpha }{\min }& \frac{1}{2}\alpha ^{T}\left( B-\frac{1}{m_{1}}e_2e_{1}^{T}A\right) S_{1}^{-1}\left( B-\frac{1}{m_{1}}e_2e_{1}^{T}A\right) ^{T}\alpha -e_2^{T}\alpha \nonumber \\ \hbox {s.t.}\;& 0\le \alpha \le c_{1}e_2 \end{aligned}$$
(12)

and

$$\begin{aligned} \underset{\gamma }{\min }& \frac{1}{2}\gamma ^{T}\left( A-\frac{1}{m_{2}}e_1e_{2}^{T}B\right) S_{2}^{-1}\left( B-\frac{1}{m_{2}}e_1e_{2}^{T}B\right) ^{T}\gamma -e_1^{T}\gamma \nonumber \\ \hbox {s.t.}\;& 0\le \gamma \le c_{2}e_1, \end{aligned}$$
(13)

respectively, where \(\alpha =(\alpha _{1},\alpha _{2},\ldots ,\alpha _{m_2})^T\) and \(\gamma =(\gamma _{1},\gamma _{2},\ldots ,\gamma _{m_1})^T\) are Lagrange multiplier vectors, \(e_1\in \mathbb {R}^{m_1}\) and \(e_2\in \mathbb {R}^{m_2}\) are vectors of ones.

After obtaining \(\alpha\) and \(\beta\), \(w_{1}\) and \(w_{2}\) can be expressed by

$$\begin{aligned} w_{1}&=S_{1}^{-1}\left( B-\frac{1}{m_{1}}e_2e_{1}^{T}A\right) ^{T}\alpha ,\nonumber \\ w_{2}&=S_{2}^{-1}\left( A-\frac{1}{m_{2}}e_1e_{2}^{T}B\right) ^{T}\gamma . \end{aligned}$$
(14)

For a new coming data point \(\mathrm x\in \mathbb {R}^{n}\), it is assigned to class \(i (i=1,2)\) depending on which of the two projected class centers it is closer to, i.e.,

$$\begin{aligned} label({\rm x})=\hbox {arg} \underset{i=1,\,2}{\min }\{d_1,\,d_2\}, \end{aligned}$$
(15)

where \(d_1\) and \(d_2\) represent the distances between the projection of \(\mathrm x\) and the projected center of corresponding class, which are given by

$$\begin{aligned} d_1&=\left| w_{1}^{T}{\rm x}-w_{1}^{T}\frac{1}{m_1}\sum _{j=1}^{m_{1}}{\rm a}_{j}\right| \end{aligned}$$
(16)

and

$$\begin{aligned} d_2&=\left| w_{2}^{T}{\rm x}-w_{2}^{T}\frac{1}{m_2}\sum _{j=1}^{m_{2}}{\rm b}_{j}\right| , \end{aligned}$$
(17)

respectively.

It should be noticed that the above procedure requires the two variance matrices defined by (10) and (11) to be nonsingular. However, when there are not sufficient samples, the two variance matrices can be singular. To deal with this problem, PCA plus LDA [31, 32] technique has been employed in PTSVM. Furthermore, to enhance the performance, a recursive procure is introduced in PTSVM to obtain multiple projection axes for each class.

2.3 Least squares projection twin support vector machine

By considering equality constraints in the primal problems of PTSVM, least squares projection twin support vector machine (LSPTSVM) [24] is proposed. However, LSPTSVM is not a direct least squares version of PTSVM. In fact, LSPTSVM introduces a regularization term in the primal objective function to remove the singularity problem that may happen in PTSVM and gains better generalization ability. This leads to following optimal problems

$$\begin{aligned} \underset{w_{1}}{\min }& \frac{1}{2}\sum _{i=1}^{m_{1}}\left( w_{1}^T{\rm a}_{i}-w_{1}^T\frac{1}{m_{1}}\sum _{j=1}^{m_{1}}{\rm a}_{j}\right) ^{2}+\frac{c_1}{2}\sum _{k=1}^{m_2}\xi _{k}^{2}+\frac{v_1}{2}\Vert w_1\Vert ^2 \nonumber \\ \hbox {s.t.}\;& w_{1}^{T}{\rm b}_k-w_{1}^{T}\frac{1}{m_{1}}\sum _{j=1}^{m_{1}}{\rm a}_{j}+\xi _{k}=1,\quad k=1,2,\ldots ,m_2 \end{aligned}$$
(18)

and

$$\begin{aligned} \underset{w_{2}}{\min }& \frac{1}{2}\sum _{i=1}^{m_{2}}\left( w_{2}^T{\rm b}_{i}-w_{2}^T\frac{1}{m_{2}}\sum _{j=1}^{m_{2}}{\rm b}_{j}\right) ^{2}+\frac{c_2}{2}\sum _{k=1}^{m_1}\eta _{k}^{2}+\frac{v_2}{2}\Vert w_2\Vert ^2 \nonumber \\ \hbox {s.t.}\;& -\left( w_{2}^{T}{\rm a}_k-w_{2}^{T}\frac{1}{m_{2}}\sum _{j=1}^{m_{2}}{\rm b}_{j}\right) +\eta _{k}=1,\quad k=1,2,\ldots ,m_1, \end{aligned}$$
(19)

where \(c_1>0, c_2>0\) are trade-off parameters, \(v_1>0, v_2>0\) are regularization parameters, and \(\xi _k,\,\eta _k\) are slack variables.

By substituting the equality constraint into the objective function, we can derive the optimal axes \(w_1\) and \(w_2\) of (18) and (19) as

$$\begin{aligned} w_{1}&=\left[ \frac{S_1}{c_1}+\left( -B+\frac{1}{m_{1}}e_2e_{1}^{T}A\right) ^{T}\left( -B+\frac{1}{m_{1}}e_2e_{1}^{T}A\right) +\frac{v_1}{c_1}I\right] ^{-1}\nonumber \\&\quad \times \left( B-\frac{1}{m_{1}}e_2e_{1}^{T}A\right) ^{T}e_2 \end{aligned}$$
(20)

and

$$\begin{aligned} w_{2}&=-\left[ \frac{S_2}{c_2}+\left( A-\frac{1}{m_{2}}e_1e_{2}^{T}B\right) ^{T}\left( A-\frac{1}{m_{2}}e_1e_{2}^{T}B\right) +\frac{v_2}{c_2}I\right] ^{-1}\nonumber \\&\quad \,\times \left( A-\frac{1}{m_{2}}e_1e_{2}^{T}B\right) ^{T}e_1, \end{aligned}$$
(21)

where \(e_1\in \mathbb {R}^{m_1}\), \(e_2\in \mathbb {R}^{m_2}\) are vectors of ones, I is the identity matrix with appropriate dimension, and \(S_1, S_2\) are defined as in (10) and (11) respectively. It is clear that different from PTSVM, LSPTSVM will not encounter the singularity problem due to the nonsingularity of the involved matrices \((\frac{S_1}{c_1}+(-B+\frac{1}{m_{1}}e_2e_{1}^{T}A)^{T}(-B+\frac{1}{m_{1}}e_2e_{1}^{T}A)+\frac{v_1}{c_1}I)\) and \((\frac{S_2}{c_2}+(A-\frac{1}{m_{2}}e_1e_{2}^{T}B)^{T}(A-\frac{1}{m_{2}}e_1e_{2}^{T}B)+\frac{v_2}{c_2}I)\). This makes LSPTSVM much more stable.

In order to further enhance the performance of LSPTSVM, multiple orthogonal directions for each class can also be obtained by using a recursive procedure. Suppose that the two groups of desired projection axes are \(W_1=\{w_1^{(t)},t=1,2,\ldots ,r\}\) and \(W_2=\{w_2^{(t)},t=1,2,\ldots ,r\}\), where \(w_1^{(t)}\) and \(w_2^{(t)}\) are obtained from (20) and (21) recursively, and r is the desired number of projection axes for each class. For testing, the label of a new coming data point \(\mathrm x\in \mathbb {R}^{n}\) can be similarly determined by (15), but with \(d_1\) and \(d_2\) are newly defined by

$$\begin{aligned} d_1&=\left| \left| W_{1}^{T}{\rm x}-W_{1}^{T}\frac{1}{m_1}\sum _{j=1}^{m_{1}}{\rm a}_{j}\right| \right| \end{aligned}$$
(22)

and

$$\begin{aligned} d_2&=\left| \left| W_{2}^{T}{\rm x}-W_{2}^{T}\frac{1}{m_2}\sum _{j=1}^{m_{2}}{\rm b}_{j}\right| \right| , \end{aligned}$$
(23)

respectively, where \(||\cdot ||\) represents the 2-norm of a vector.

3 Multi-class least squares recursive projection twin support vector machine

In this section, we consider multi-class classification problem with the dataset \(T=\{(X,Y)\}\) contains \(K\ge 2\) classes, where \(X=\{{{\rm x}_1},\ldots ,{{\rm x}_m}\}\) consists of m data points and each data point is an n-dimensional vector, and \(Y\in \mathbb {R}^m\) is the corresponding output with each element belonging to \(\{1,\ldots ,K\}\). We further organize data points in the i-th class as \(A_i=({\rm x}_{i1},\ldots ,{\rm x}_{im_i})^{T}\in \mathbb {R}^{m_i\times n}\) and define \(B_i=({\rm \overline{x}}_{i1},\ldots ,{\rm \overline{x}}_{i\overline{m}_i})^{T}\in \mathbb {R}^{\overline{m}_i\times n}\) as the set of the rest \(K-1\) classes, where \(m_i\) is the number of data points in the i-th class and \(\overline{m}_i=m-m_i\) represents the number of data points in the rest \(K-1\) classes. In the following, we will present our multi-class least squares recursive projection twin support vector machine (MLSPTSVM) for the above K classes classification problem.

3.1 Linear MLSPTSVM

3.1.1 One projection axis

For K classes classification problem, linear MLSPTSVM generates K projection axes in the primal space, one for each class that separates one class from all the other classes in the same manner of binary LSPTSVM. Specifically, it requires that the projected points of one class are close to its projected center as much as possible while the distance from the projected center to the rest \(K-1\) classes are far away to some extent. Denote \(w_{i}\) the projection axis for the i-th class, \(i=1,2,\ldots K\). Then linear MLSPTSVM considers the following problem

$$\begin{aligned} \underset{w_{i}}{\min }& \frac{1}{2}\sum _{j=1}^{m_{i}}\left( w_{i}^T{\rm x}_{ij}-w_{i}^T\frac{1}{m_{i}}\sum _{s=1}^{m_{i}}{\rm x}_{is}\right) ^{2}+\frac{c_i}{2}\sum _{k=1}^{\overline{m}_i}\xi _{k}^{2}+\frac{v_{i}}{2}\Vert w_i\Vert ^2 \nonumber \\ \hbox {s.t.}\;& w_{i}^{T}{\rm \overline{x}}_{ik}-w_{i}^{T}\frac{1}{m_{i}}\sum _{s=1}^{m_{i}}{\rm x}_{is}+\xi _{k}=1,\quad k=1,2,\ldots ,\overline{m}_i, \end{aligned}$$
(24)

where \(c_i>0\) is the trade-off parameter, \(v_{i}>0\) is the regularization parameter, and \(\xi _k\) are slack variables. We now give the geometric interpretation of problem (24). By employing the quadratic loss function, the first two terms of the objective function and the constraint are committed to minimize the empirical risk, which ensures the projected points of its own class are clustered around its projected center meanwhile the distances from the projected center to the rest classes are far away to some extents. Note that the nonnegative constraints of \(\xi _k\) are abandoned due to the usage of quadratic loss function. The last term in the objective function is a regularization term which is utilized to avoid the singularity problem of our model and reach better generalization ability, which is similar to classical SVM [1, 2] and improved TWSVM [15].

Problem (24) can be solved by the following process. We first define the within-class variance matrix \(S_i\) for the i-th class as

$$\begin{aligned} S_i=\left( A_i-\frac{1}{m_i}e_ie_i^{T}A_i\right) ^{T}\left( A_i-\frac{1}{m_i}e_ie_i^{T}A_i\right) \!, \end{aligned}$$
(25)

where \(e_i\in \mathbb {R}^{m_i}\) is the vector of ones. Substituting the constraint into the objective function, problem (24) is converted into an unconstrained problem which is given by

$$\begin{aligned} \underset{w_{i}}{\min } \frac{1}{2}w_i^T S_i w_i+\frac{c_i}{2}\left\| -B_i w_i+\frac{1}{m_i}\overline{e}_ie_i^TA_i w_i+\overline{e}_i\right\| ^2+\frac{v_{i}}{2}\Vert w_i\Vert ^2, \end{aligned}$$
(26)

where \(\overline{e}_i\in \mathbb {R}^{\overline{m}_i}\) is the vector of ones. Set the gradient of the objective function in (26) with respect to \(w_i\) to zero, then

$$\begin{aligned} S_iw_{i}+c_i\left( -B_i+\frac{1}{m_{i}}\overline{e_i}e_{i}^{T}A_i\right) ^{T}\left( -B_iw_i+\frac{1}{m_{i}}\overline{e_i}e_{i}^{T}A_iw_i+\overline{e_i}\right) +v_{i}w_i=0. \end{aligned}$$
(27)

For simplicity, we define \(H_i=(A_i-\frac{1}{m_i}e_ie_i^{T}A_i)\in \mathbb {R}^{m_{i}\times n}\) and \(G_i=(B_i-\frac{1}{m_{i}}\overline{e_i}e_{i}^{T}A_i)\in \mathbb {R}^{\overline{m}_i\times n}\). Therefore, the optimal projection vector \(w_i\) of problem (24) can be obtained from (27) by

$$\begin{aligned} w_{i}=\left( \left( \frac{1}{c_{i}}H_i^{T}H_i+\frac{v_{i}}{c_{i}}I\right) +G_i^{T}G_i\right) ^{-1}G_i^{T}\overline{e_i}. \end{aligned}$$
(28)

Here I is the identity matrix with appropriate dimension. Owes to the extra regularization term in problem (24), the singularity issue is ruled out since the involved matrix in (28) is positive definite.

After K optimal projection axes \(w_i (i=1,\ldots ,K)\) are obtained from (28), the training stage is complete. For predicting, the label of a new coming data point \(\mathrm x\in \mathbb {R}^{n}\) is determined depending on which of the class center it is closer to in the projected space:

$$\begin{aligned} label({\rm x})=\hbox {arg} \underset{i=1,\ldots ,K}{\min }\left| w_{i}^T{\rm x}-w_{i}^T\frac{1}{m_{i}}e_i^TA_i\right| \!. \end{aligned}$$
(29)

The whole process above leads to the following Algorithm 1.

figure a

3.1.2 Multiple orthogonal projection axes

In order to further enhance the performance of our MLSPTSVM, we can obtain multiple orthogonal projection axes for each class by a recursive procure. The recursive procure contains two steps: \((\mathrm i)\) determine projection axes \(w_i (i=1,\ldots ,K)\) one for each class by carrying out Algorithm 1, and normalize \(w_i\) to have unit norm, i.e., \(w_i = w_i /\Vert w_i\Vert\); \((\mathrm ii)\) generate new data points by projecting the original data points into projection subspace which is orthogonal to projection axis \(w_i\).

Denote \(W_i=\{w_i^{(j)}|j=1,\ldots ,r\}\) (\(1\le i\le K\)) as the set of multiple projection axes of the i-th class, where \(w_i^{(j)}\) is the j-th projection axis and r is the desired number of projection axes of the i-th class, respectively. Then, the decision function of a new coming data \(\mathrm x\in \mathbb {R}^{n}\) for multiple projection axes case is given by

$$\begin{aligned} label({\rm x})=\hbox {arg} \underset{i=1,\ldots ,K}{\min }\left\| W_{i}^{T}{{\rm x}}-W_{i}^{T}\frac{1}{m_i}e_i^TA_i\right\| \!. \end{aligned}$$
(30)

Suppose that \(X^{(j)}\) is the j-th projected dataset and \({\rm x}_l^{(j)}\) is the l-th data point in dataset \(X^{(j)}\) (\(j=1,\ldots ,r; l=1,\ldots ,m\)). Then, the proposed recursive MLSPTSVM algorithm works as in Algorithm 2.

figure b

We show that the multiple projection axes obtained for each class by Algorithm 2 is actually orthogonal to each other.

Theorem 1

By implementing Algorithm 2, the resulting \(W_i\) is an orthonormal set for each \(i = 1,\ldots ,K\).

Proof

We here take the similar strategy in [22, 33, 34]. Since each \(w_i^{(j)}\) is a unit vector by performing Algorithm2, we need only to prove that \(w_i^{j}\) is orthogonal to \(w_i^{(j-k)}\) for all \(k = 1,\,2,\ldots ,j-1\). According to the definition of \(G_i\) and \(\overline{e_i}\) in Sect. 3.1.1, \(G_i^{T}\overline{e_i}\) is a linear combination of the row vectors of matrices \(A_i\) and \(B_i\), i.e. the input samples. By observing (28), this implies that in the j-th iteration, each projection axis \({w_i^{(j)}}\) is a linear combination of the input samples \({\rm x}_l^{(j)}\), where \(l=1,\ldots ,m\). For the newly obtained projected data in the j-th iteration (Step (3) in Algorithm 2), by multiplying \({w_i^{(j-1)}}^T\), we have

$$\begin{aligned} {w_i^{(j-1)}}^T{\rm x}_l^{(j)}={w_i^{(j-1)}}^T{\rm x}_l^{(j-1)}-{w_i^{(j-1)}}^T w_i^{(j-1)}{w_i^{(j-1)}}^T{\rm x}_l^{(j-1)}=0. \end{aligned}$$

This means \(w_i^{(j-1)}\) is orthogonal to the input samples \({\rm x}_l^{(j)}\), which in turn implies that \(w_i^{(j)}\) is orthogonal to \(w_i^{(j-1)}\).

In the same way, we can justify that \(w_i^{(j)}\) is orthogonal to \(w_i^{(j-k)}\) for all \(k = 2,\ldots ,j-1\). Therefore, \(W_i\) is an orthonormal set for each \(i = 1,\ldots ,K\) and the proof is completed.

From Theorem 1, we see that each \(W_i\) spans an orthogonal subspace such that the discriminative information for classification are contained as much as possible.

3.2 Nonlinear MLSPTSVM

In this subsection, we extend the linear MLSPTSVM to the nonlinear case, which is ignored in LSPTSVM [24]. Consider the nonlinear kernel \(\mathcal {K}\), and let \(C = [A_1,\ldots ,A_K]^{T}\). Then the within-class variance of the i-th class in the kernel space can be written as

$$\begin{aligned} (S_{i})^{\phi }=\left( \mathcal {K}(A_i,C^T)-\frac{1}{m_i}e_ie_i^{T}\mathcal {K}(A_i,C^T)\right) ^{T}\left( \mathcal {K}(A_i,C^T)-\frac{1}{m_i}e_ie_i^{T}\mathcal {K}(A_i,C^T)\right) \!, \end{aligned}$$
(31)

and nonlinear MLSPTSVM leads to the following unconstraint problem

$$\begin{aligned} \begin{array}{ll} \underset{w_{i}}{\min }&{} \frac{1}{2}w_i^T (S_{i})^{\phi } w_i\\ &{} +\frac{c_i}{2}\Vert -\mathcal {K}(B_i,C^T) w_i+\frac{1}{m_i}\overline{e_i}e_i^T\mathcal {K}(A_i,C^T) w_i+\overline{e_i}\Vert ^2+\frac{v_{i}}{2}\Vert w_i\Vert ^2, \end{array} \end{aligned}$$
(32)

where \(c_i>0\) is the trade-off parameter, \(v_{i}>0\) is the regularization parameter, and \(e_i\in \mathbb {R}^{m_i}\), \(\overline{e_i}\in \mathbb {R}^{\overline{m}_i}\) are vectors of ones. The optimal solution of problem (32) can be determined by

$$\begin{aligned} w_{i}=\left( \left( \frac{1}{c_{i}}\overline{H}_i^{T}\overline{H}_i+\frac{v_{i}}{c_{i}}I\right) +\overline{G}_i^{T}\overline{G}_i\right) ^{-1}\overline{G}_i^{T}\overline{e_i}, \end{aligned}$$
(33)

where \(\overline{H}_i=\mathcal {K}(A_i,C^T)-\frac{1}{m_{i}}e_ie_i^{T}\mathcal {K}(A_i,C^T)\) and \(\overline{G}_i=\mathcal {K}(B_i,C^T)-\frac{1}{m_{i}}\overline{e_i}e_{i}^{T}\mathcal {K}(A_i,C^T)\).

After the K optimal projection axes \(w_{i}\) (\(i = 1,\ldots ,K\)) are obtained, the label of a new coming data point \(\mathrm x\) is classified in the same way as the linear case. To get multiple projection axes, the similar procedure can be taken as in Algorithm 2, which will be omitted here.

3.3 Computational analysis

We analyze the computation complexity of our MLSPTSVM in this subsection. Suppose r is the desired number of projection axes for each class. From (28), we see that linear MLSPTSVM solves K classes classification problem mainly by giving K matrix inverses of size \(n \times n\), where \(n \ll m\). Thus the time complexity of linear MLSPTSVM is about \(O(Krn^3)\). Similarly, by observing (33), the nonlinear MLSPTSVM requires K matrix inverses of order \(m \times m\), and it takes \(O(Krm^3)\) time.

In order to reduce the time complexity when calculating matrix inverses for nonlinear MLSPTSVM, we resort to the following Sherman–Morrison–Woodbury (SMW) formula [30]

$$\begin{aligned} (A+UV^{T})^{-1} = A^{-1} - A^{-1}U(I + V^{T}A^{-1}U)^{-1}V^{T}A^{-1}. \end{aligned}$$
(34)

Specifically, by (34), we can rewrite (33) as

$$\begin{aligned} w_{i}=(Y_i - Y_i\overline{G}_i^{T}(I + \overline{G}_iY_i\overline{G}_i^{T})^{-1}\overline{G}_iY_i)\overline{G}_i^{T}\overline{e_i}, \end{aligned}$$
(35)

where \(Y_i=(\frac{1}{c_{i}}\overline{H}_i^{T}\overline{H}_i+\frac{v_{i}}{c_{i}}I)^{-1}\) that can be further rewritten by (34) as

$$\begin{aligned} Y_i=\frac{c_{i}}{v_{i}}\left( I-\frac{1}{v_{i}}\overline{H}_i^{T}(I+\frac{1}{v_{i}}\overline{H}_i\overline{H}_i^{T})^{-1}\overline{H}_i\right) \!. \end{aligned}$$
(36)

As we can observe from (35) and (36), the calculation of matrix inverse in (33) is converted into two smaller sized \(m \times m\) matrix inverses, that is, \((I+\frac{1}{v_{i}}\overline{H}_i\overline{H}_i^{T})^{-1}\in \mathbb {R}^{{m}_{i}\times {m}_{i}}\) and \((I + \overline{G}_iY_i\overline{G}_i^{T})^{-1}\in \mathbb {R}^{\overline{m}_{i}\times \overline{m}_{i}}\). Therefore, the computation complexity of nonlinear MLSPTSVM can be reduced to \(O(Krd^3)\), where \(d = max\{m_i, \overline{m}_i|i=1,\ldots ,K\}\).

Furthermore, if the number of data points m in dataset T is very large, then the rectangular kernel technique [8, 35] can be applied to reduce the dimensionality of nonlinear MLSPTSVM. Specifically, we can reduce \(\mathcal {K}(A_i,C^T)\) of size \(m_{i}\times m\) and \(\mathcal {K}(B_i,C^T)\) of size \(\overline{m}_i\times m\) to much smaller sizes \(m_{i}\times \widetilde{m}\) and \(\overline{m}_i\times \widetilde{m}\), respectively. Here \(\widetilde{m}\) is as small as 1–10 % of m and \(\overline{C}\) is an \(\widetilde{m} \times n\) random submatrix of C. Thus the complexity of nonlinear MLSPTSVM can be largely reduced. The rectangular kernel technique not only makes large scale problem tractable, but also leads to improved generalization performance by avoiding data overfitting [8].

4 Experimental results

To demonstrate the classification ability of MLSPTSVM, we perform our MLSPTSVM, the recently proposed MPTSVM [29], together with other four state-of-the-art binary classification methods, including SVM [1, 2], GEPSVM [9], TWSVM [10], and LSTSVM [14] on artificial datasets, publicly available UCI datasets [36] and some large datasets [37]. Note that the SVM, GEPSVM, TWSVM and LSTSVM are applied here to multi-class classification problem by using one vs rest technique. To clarify the fact that these binary classifiers are used in the multi-classification context, we re-term them as MSVM, MGEPSVM, MTWSVM, and MLSTSVM respectively, where the first letter “M” represents “multiple”. All the methods are implemented in MATLAB 2013a environment on a PC with Intel i5 processor (2.67 GHz), 2 GB RAM. MSVM is implemented by LIBSVM [38] due to its fast training speed. The dual QPPs arising in MSVM, MTWSVM and MPTSVM are solved using Mosek optimization toolbox, the eigenvalue problems in MGEPSVM are solved by a function ‘eig’, and the matrix inverse problems in several methods including MLSPTSVM are solved by calling operation ‘\(\backslash\)’. For parameter selection, all the parameters except for the number of projection axes in MPTSVM and MLSPTSVM, are selected from \(2^{-8}\) to \(2^{8}\) by employing the standard tenfold cross-validation technique [39]. Experiments are repeated five times on each dataset and the corresponding results are recorded, including the means and standard deviations of test accuracies, computing time which are obtained under the best parameters, and p values which are calculated by performing paired t-test in 5 % significance level. Specially, in order to compare the performances of various methods intuitively, we mark the highest accuracy on each dataset in bold.

4.1 Artificial examples

We first conduct experiments on two artificial examples to evaluate the performance of our MLSPTSVM in comparison to MPTSVM. The first dataset is a three-dimensional Xor dataset that consists of 153 samples with three classes of the same size, as shown in Fig. 1. This three-dimensional Xor dataset is obtained by randomly perturbing points around three intersecting lines. The second dataset is a cross plane dataset containing three classes, with 600 samples are generated in a two-dimensional plane, as shown in Fig. 2.

Fig. 1
figure 1

A three-dimensional Xor dataset with three classes

Full size image
Fig. 2
figure 2

A two-dimensional crossplane dataset with three classes

Full size image

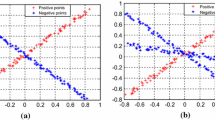
For the experiment on the first dataset, the number of projection axes for each class is set to 1 for both MLSPTSVM and MPTSVM. Fig. 3a, b show the classification results by plotting the distance distributions of MPTSVM and MLSPTSVM. Specifically, \(d_i\) (\(i=1,2,3\)) in Fig. 3 are the distances between the projected points and the i-th projected center. MLSPTSVM classifies the Xor dataset well with just two misclassified points, which is the same for MPTSVM.

For the second artificial dataset, Fig. 4a, b depict the three projection directions obtained by MPTSVM and MLSPTSVM, respectively. From Fig. 4, we see that the resulting directions for these two methods are very similar. To make the comparison clearer, the specific performances of MPTSVM and MLSPTSVM on the two datasets are reported in Table 1. As we can observe in Table 1, MLSPTSVM has comparable classification accuracy to that of MPTSVM but with considerably less computing time. Furthermore, by observing the p values, we see that 0.775 and 0.799 are much greater than 0.05, which implies that the performance of these two methods are essentially similar.

Fig. 3
figure 3

Distance distribution of MPTSVM and MLSPTSVM on Xor dataset

Full size image
Fig. 4
figure 4

Projection directions of MPTSVM and MLSPTSVM on crossplane dataset

Full size image
Table 1 Performance comparison of MPTSVM and MLSPTSVM on artificial datasets
Full size table

4.2 UCI datasets

In this subsection, we further experiment on six UCI benchmark datasets [36], whose details are listed in Table 2. The experimental results for linear and nonlinear cases of our MLSPTSVM, as well as the other five methods, i.e., MSVM, MGEPSVM, MTWSVM, MLSTSVM and MPTSVM are summarized in Tables 3 4, respectively. For nonlinear classifiers, Gaussian kernel is selected for all the methods. The SMW technique [30] is employed to simplify the calculation of matrix inverses for our nonlinear MLSPTSVM. The optimal numbers of projection axes that are selected from 1 to the dimension of each dataset are listed in the brackets for MPTSVM and MLSPTSVM.

Table 2 Details of the benchmark UCI datasets
Full size table

For the linear case, from Table 3, we observe that MLSPTSVM and MPTSVM can obtain the highest accuracies on most of the datasets among all the methods, which indicate that they have better generalization capability than the others. Furthermore, we see that MLSPTSVM has comparable accuracies to those of MPTSVM since most of p values between them are larger than 0.05. On the other side, MLSPTSVM takes significantly less computing time than MPTSVM as one can see in Table 3. For example, MLSPTSVM takes 0.017(s) on Glass dataset while MPTSVM needs almost 0.431(s). However, MLSPTSVM is a bit slower than MGEPSVM and MLSTSVM, which mainly because multiple projection axes are needed on most datasets for MLSPTSVM.

Table 3 Performance comparison for various methods using the linear kernel
Full size table

For the nonlinear case, the employed Gaussian kernel is defined by \({\mathcal {K}}(x,z) = \exp \left( { - \frac{{\left\| {x - z} \right\|^{2} }}{{2p^{2} }}} \right)\), where p is the kernel parameter. From Table 4, we can see that MLSPTSVM and MPTSVM outperform the other methods in terms of classification accuracy, while these two methods achieve comparable performance by observing both the accuracies and p values. For example, MPTSVM and MLSPTSVM obtain accuracies 97.47 and 98.01 % on Pathbased dataset, while the corresponding p value is 0.084. With regard to time consumption, from Table 4, it can be seen that MLSPTSVM takes almost the fewest computing time compared with its competitors. Specially, MLSPTSVM takes significantly less time than MPTSVM as in the linear case. Furthermore, only one projection axis is enough for MLSPTSVM to get the highest accuracy on three datasets, i.e., Seeds, Wine and Pathbased, while the corresponding computing times are very competitive. This demonstrates the superiority of our MLSPTSVM.

In summary, from Tables 3 and 4, we conclude that MLSPTSVM and MPTSVM outperform other methods in both linear and nonlinear cases, and there is no statistical difference in classification accuracy between these two methods since most of corresponding p values are larger than 0.05. However, it is evident that MLSPTSVM takes considerable less computing time compared with MPTSVM. In addition, the optimal number of projection axes varies from different datasets for both MPTSVM and our MLSPTSVM.

Table 4 Performance comparison for various methods using the nonlinear kernel
Full size table

4.3 Large datasets

As one observes in Sect. 3, our MLSPTSVM tends to extremely fast since it only needs to solve a series of linear equations. In this subsection, we argue the above viewpoint by exhibiting the ability of our MLSPTSVM on dealing with large scale datasets. Note that MSVM, MTWSVM and MPTSVM involve solving complex QPPs with high computational complexity, which makes them fail on large datasets. Therefore, we only present the experimental results of our MLSPTSVM, MGEPSVM and MLSTSVM. Eight large datasets [37] are used for comparison, whose details are summarized in Table 5. Here, the Mnist dataset is generated by randomly selecting 30 % samples in each class of the original dataset, and the other datasets are combined by the training set and testing set. Since our linear MLSPTSVM requires to determine the inversion of matrices whose orders are input space dimension, we perform dimensionality reduction step before classifying on high-dimensional datasets. Therefore, we first employ LDA [31] on USPS, Reuster300 and Mnist datasets for dimensionality reduction. Furthermore, the number of projection axes are selected from 1 to 8 for the convenience of further analyzing in Sect. 4.4.

Table 5 Details of the large datasets
Full size table

For the linear case, we report the experimental results of the three involved methods on the above large datasets in Table 6. Table 6 demonstrate that our MLSPTSVM outperforms MLSTSVM and MGEPSVM on most datasets in terms of classification accuracy, and the corresponding p values between them are all much smaller than 0.05, which indicates the effectiveness of our MLSPTSVM over MLSTSVM and MGEPSVM. For example, for Shuttle dataset, MGEPSVM and MLSTSVM gain 67.77 and 90.12 % accuracy respectively while MLSPTSVM can reach to 91.19 %. Meanwhile, the two corresponding p values are all close to 0. It can also be observed that our MLSPTSVM is a bit slower than MGEPSVM and MLSTSVM, which is mainly because that the optimal number of projection axes is needed to be searched. However, this also the source of great performance of MLSPTSVM. In conclusion, the results in Table 6 demonstrate the feasibility of our linear MLSPTSVM on large datasets.

Table 6 Performance comparison on large datasets when using the linear kernel
Full size table

For the nonlinear case, four datasets in Table 5 are considered, i.e., Page-blocks, Satimage, Pendigits and Mnist, and the Gaussian kernel is used in nonlinear MLSPTSVM. We employ the rectangular kernel technique [8, 35] to reduce the dimensionality and select 1 % of training samples to perform the kernel transformation. The corresponding experimental results of nonlinear MGEPSVM, MLSTSVM and MLSPTSVM on these four large datasets are reported in Table 7. From Table 7, we find that nonlinear MLSPTSVM also handle large datasets well while with acceptable computational time. For example, for Pendigis dataset, nonlinear MLSPTSVM gains as high as 98.42 % accuracy compared with 90.55 % for linear MLSPTSVM, but with 1.56(s) computational time. The phenomena further confirms the ability of our MLSPTSVM to deal with large scale datasets. Besides, nonlinear MLSPTSVM can obtain comparable classification accuracy with MLSTSVM, while these two methods outperform MGEPSVM to a large extent.

Table 7 Performance comparison on large datasets when using the nonlinear kernel
Full size table

4.4 Parameters analysis

Linear MLSPTSVM contains two sets of penalty parameters \(c_i\) and \(v_i\), \(i = 1,2,\ldots ,K\), which are needed to be selected independently. Moreover, the number of projection axes is also considered as a parameter. In this subsection, we analyze the influence of these parameters to the performance of our MLSPTSVM on four large datasets, i.e., Page-blocks, USPS, Pendigits and Shuttle, respectively. For convenience, we use the same \(c_i\) and \(v_i\) for each \(i = 1,2,\ldots ,K\), that is, \(c_i\) = c and \(v_i\) = v for some c and v.

We first consider the effect of parameters c and v on the test accuracy, which is shown in Fig. 5. Here, the grid search method is employed, and the corresponding accuracy is obtained under the optimal number of projection axes, while parameters c and v are changing within the set \(\{2^{-8},\ldots ,2^{8}\}\). From Fig. 5, we observe that the accuracy varies greatly along with the change of parameters c and v, which implies that c and v have a great impact on the classification accuracy. Thus, to achieve better performance, it is necessary to select the suitable parameters c and v.

Fig. 5
figure 5

Relationship between parameters c, v and classification accuracy

Full size image

We next depict the relationship between the number of projection axes and classification accuracy in Fig. 6. Here, the number of projection axes is selected from 1 to 8. As we can see from Fig. 6, multiple orthogonal projection axes are required for the four datasets in order to reach higher accuracy, and for different datasets, the optimal number of projection axes varies. For example, USPS dataset needs six projection axes while Shuttle dataset only needs two. However, it should be noted that sometimes one projection axis is enough for MLSPTSVM, as we can observe in Tables 3 and 4. This shows that on one hand, multiple orthogonal projection axes may necessary for some datasets; on the other hand, for some datasets, redundant projection axes may bring confused classification information [40]. Moreover, by observing Fig. 6, we see that with the increase of the number of projection axes, the accuracy increases until it is up to a maximum, and then decreases in general, although there may be some specifications as in Fig. 6a. In summary, a proper number of projection axes can improve the performance of MLSPTSVM to a much extent.

Fig. 6
figure 6

Relationship between the numbers of projection axes and classification accuracy

Full size image

For nonlinear MLSPTSVM, the kernel parameter p needs to be considered. We next show the relationship between kernel parameter p and classification accuracy on four UCI datasets in Table 2, i.e., Seeds, Dermatology, Wine, and Pathbased. We draw the parameter-accuracy curves in Fig. 7 on these four datasets with parameter p belonging to \(\{2^{-8},\ldots ,2^{8}\}\). Here, each accuracy is obtained under the optimal parameters c, v and the number of projection axes. From Fig. 7, we can see that kernel parameter p has a great influence on classification accuracy. For example, for dataset Wine, the lowest accuracy is 38.12 % while the highest one can reach to 100 %. Thus, a suitable kernel parameter is crucial for nonlinear MLSPTSVM to achieve better performance.

Fig. 7
figure 7

Relationship between the kernel parameter and classification accuracy

Full size image

5 Conclusions

In this paper, a novel multiple least squares recursive projection twin support vector machine for multi-class classification is proposed, termed as MLSPTSVM. For K classes classification problem, our MLSPTSVM solves K groups of primal problems directly by solving a series of linear equations, which leads to its fast training speed. A recursive procure is further introduced to MLSPTSVM to generate multiple projection directions. Preliminary experimental results show that our MLSPTSVM has comparable classification accuracy with MPTSVM but with dramatically less computing time. Besides, experiments on some large datasets further demonstrate the effectiveness of our MLSPTSVM. For practical convenience, we upload our MLSPTSVM MATLAB code upon http://www.optimal-group.org/Resource/MLSPTSVM.html. As we know, extracting features is crucial for classification, especially when faced with high-dimensional data. Thus, exploring effective feature selection/extraction methods to improve the performance of MLSPTSVM will be one of our future works.