A fuzzy approach to multicriteria assignment problem using exponential membership functions

Abstract

In this paper, we extend the classical assignment problem to the multicriteria assignment problem by considering three criteria: cost, time and quality subject to many realistic constraints including multi-job assignment and a knapsack-type resource constraint. The paper addresses the uncertainty of the real-life assignment problem by formulating a fuzzy cost–time–quality assignment problem using exponential membership functions. We define fuzzy goal for each criterion as per the preferences of the decision-maker and aggregate the fuzzy goals using product operator. In order to obtain optimal assignment plans, the resultant nonlinear 0-1 optimization problem is solved using genetic algorithm for different choices of the shape parameters in the exponential membership functions. As an illustrative example, we consider a fuzzy manpower planning problem.

1 Introduction

Assignment problem is of great use in many important decision-making problems such as resource allocation problem, personnel scheduling and manpower planning. One may refer to the recent survey paper of Pentico [27] for details on assignment problems. The classical assignment problem is usually considered either as the cost minimizing problem or as the time minimizing problem. Cost minimizing problem aims at finding the optimal assignment that minimizes the total project cost, whereas the time minimizing problem search for the shortest duration, when the total project time is of vital concern. However, assigning jobs only based on cost and/or time cannot efficiently model the real-world situations. Therefore, generalized assignment problems are proposed in the literature that include factors other than cost and time while making the allocation decisions.

In the real-world scenario, the various parameters responsible for an optimal assignment plan need not be deterministic. Moreover, assignment problems are also affected by vagueness and ambiguity associated with the use of linguistic expressions such as “high cost”, “longer time” and “poor quality” by the decision-maker. In such situations, the assignment problem is modeled as fuzzy assignment problem. The real-world decision-making problems in general and the assignment problem in particular have benefited greatly from the fuzzy set theory [38, 39, 42] in terms of integrating quantitative and qualitative information, subjective preferences of the decision-maker. With respect to the fuzzy model of the assignment problem and its variants, one may refer to the works of Belacela and Boulasselb [1], De and Yadav [5], Feng and Yang [7], Huang et al. [12], Kagade and Bajaj [14], Kumar and Gupta [15], Li et al. [18], Lin and Wen [19], Lin et al. [20], Liu and Gao [22], Liu and Li [23], Mukherjee and Basu [25], Qin et al. [28], Ridwan [29], Sakawa et al. [31], Tada and Ishii [32], Tsai et al. [34], Wang and Watada [37], Yang and Liu [41].

In this paper, we study a new model of multicriteria assignment problem based upon cost, time, and quality objectives subject to many realistic constraints including multi-job assignment and a knapsack-type resource constraint. We propose an efficient fuzzy approach to solve it using exponential membership functions. The paper is organized as follows. In Sect. 2, we describe and formulate the multicriteria assignment problem. In Sect. 3, we formulate fuzzy multicriteria assignment problem. In Sect. 4, we present details of the genetic algorithm (GA) to solve the model of the fuzzy multicriteria assignment problem. Numerical illustrations of fuzzy manpower planning are provided in Sect. 5 to demonstrate the proposed methodology and the concluding remarks are made in Sect. 6.

2 Problem formulation

2.1 Problem description, assumptions and notations

In the real-world allocation problems, the managers hope not only to maximize the profit (minimize the cost) and minimize the time but also wish to promote the quality of each job/task performed when assigned to a specific worker. The amounts of cost needed and time required to accomplish a task with certain level of quality are highly interrelated with the difficulty of the job and the capability of the worker. Moreover, the level of quality does not necessarily relate to the time taken and cost incurred, because a job can be completed on time consuming reasonable budget, while the quality is unacceptable. Therefore, a trade-off among the cost, time and quality is required to make the allocation decision. The multicriteria assignment problem considered in this paper is described as under.

Assume that there are n tasks and n workers are available to perform the tasks. We wish to find an optimal assignment plan satisfying the following requirements:

• 1. Consider three goals, namely, minimize the total cost of finishing tasks, minimize the total time in which all the tasks are completed and maximize the overall quality level achieved. A project is said to be accomplished if all n tasks are completed with an acceptable level of quality. It is then expected that the project can be optimally assigned and efficiently conducted so that resources utilized can also be minimized. An optimal assignment implies that the task is assigned to the most suitable worker, explicitly, the most capable or skillful worker, requiring the least resources, i.e., cost and time and resulting in the highest quality level. In other words, if worker i has ability to undertake some tasks and it is believed that he will probably account for more cost or consume very long time or is not meeting the quality standards, in such situations, the worker i will be deprived of opportunity to undertake such tasks.

• 2. All the tasks must be completed and each task is completed by only one worker. A worker can undertake more than one task, i.e., multi-job assignment is permissible.

• 3. It is allowed not to assign any task to some worker(s).

• 4. In order to balance amount of work among the workers, it is necessary to stipulate the number of workers who have been assigned to various tasks. In this paper, we assume that this number should be at least s, 0 < s ≤ n.

• 5. In the process of decision-making, the working ability of each worker is considered. We define the maximum number of tasks that can be assigned to the worker i by l _i , 0 < l _i  ≤ n.

• 6. There is an additional knapsack-type resource constraint subject to a maximum limit on the overall distribution of resources.

For each worker i finishing task j, we denote the cost, the consumed time, the quality level and the consumed resource by c _ij , t _ij , q _ij and $d_{ij}, i = 1, 2,\ldots,n, j = 1, 2,\ldots,n,$ respectively. In order to model the above-mentioned multicriteria assignment problem, the following variables are employed:

$$ x_{ij}=\left\{\begin{array}{ll} 1,&\hbox {if task $j$ is assigned to worker $i$},\\ 0,&\hbox {otherwise}. \\ \end{array} \right. $$

2.2 Objectives

2.2.1 Cost

Let f ₁(x,C) denote the total cost after all tasks are completed, i.e.,

$$ f_1(x,C)= \sum_{i=1}^n \sum_{j=1}^n c_{ij}x_{ij}.\\ $$

2.2.2 Time

The total consumed time after all tasks assigned to worker i are completed, is given by

$$ \sum_{j=1}^n t_{ij}x_{ij},\quad i=1,2,\ldots,n.\\ $$

Assuming every worker started simultaneously, the total consumed time denoted by f ₂(x,T) when all the tasks are finished, is given as

$$ f_2(x,T)= \max_{1\leq i \leq n}\sum_{j=1}^n t_{ij}x_{ij}.\\ $$

2.2.3 Quality

Let f ₃(x,Q) denote the total quality achieved after all the tasks are completed, i.e.,

$$ f_3(x,Q)= \sum_{i=1}^n \sum_{j=1}^n q_{ij}x_{ij}.\\ $$

In this paper, the quality of the tasks completed has been considered at five different levels, where level 1 is the best and level 5 is the worst. Thus, for maximizing total quality we need to minimize f ₃(x,Q). This is done so in order to maintain consistency in the nature of all the three objective functions. It may be noted that the quality level can be decided by the project manager and may represent the perceived quality of the work, the ease of communication, the reputation of a firm or an individual.

2.3 Constraints

 

• Each task must be completed by only one worker and all the tasks should be finished, therefore, we have

  $$ \begin{aligned} &\sum_{i=1}^{n} \sum_{j=1}^n x_{ij}=n,\\ &\sum_{i=1}^{n} x_{ij}=1,\quad j=1,2,\ldots,n. \end{aligned} $$

• The number of tasks that are finished by worker i can not be larger than $l_i (i=1,2,\ldots,n)$ and the number of workers who undertake some tasks must be at least s, therefore, we have

  $$ \begin{aligned} &\sum_{j=1}^n x_{ij}\leq l_i,\quad i= 1,2,\ldots,n,\\ &\sum_{i=1}^n \min\left\{1,\sum_{j=1}^n x_{ij}\right\}\geq s.\\ \end{aligned} $$

• The knapsack-type resource constraint subject to a maximum limit b on the overall distribution of resources is expressed as

  $$ \sum_{i=1}^n \sum_{j=1}^n d_{ij}x_{ij}\leq b.\\ $$

2.4 The decision problem

The constrained multicriteria assignment model is written as follows:

$$ \begin{aligned} &\hbox {(P1)} \min f_1(x,C)= \min \sum_{i=1}^n \sum_{j=1}^n c_{ij}x_{ij} \\ &\min f_2(x,T)= \min \left(\max_{1\leq i \leq n}\sum_{j=1}^n t_{ij}x_{ij}\right)\\ &\min f_3(x,Q)= \min \sum_{i=1}^n \sum_{j=1}^n q_{ij}x_{ij}\\ \end{aligned} $$

$$ \hbox{subject to} \sum_{i=1}^n \sum_{j=1}^n x_{ij}=n, $$

(1)

$$ \sum_{i=1}^n x_{ij}=1,\quad j=1,2,\ldots,n , $$

(2)

$$ \sum_{j=1}^n x_{ij}\leq l_i,\quad i= 1,2,\ldots,n, $$

(3)

$$ \sum_{i=1}^n \min \left\{1,\sum_{j=1}^n x_{ij}\right\}\geq s , $$

(4)

$$ \sum_{i=1}^n \sum_{j=1}^nd_{ij}x_{ij}\leq b , $$

(5)

$$ x_{ij} \in \{0,1\},\quad i=1,2,\ldots,n ,\quad j= 1,2,\ldots,n. $$

(6)

3 Fuzzy multicriteria assignment problem

Operationally, formulating an assignment problem requires an estimate of the cost, time and quality for various possible allocations among workers and tasks. In real-world problems, these estimates cannot be determined exactly because cost, time and quality are affected by various indefinite and uncertain factors that cannot be measured precisely. Also, the decision-maker’s assessment about the estimates may be based on incomplete knowledge about the project itself, which may affect the decision of allocation of a task to a particular worker. Hence, making a decision based upon a crisp model is not the best decision. Under such circumstances, the issue of allocation of tasks becomes one of a choice from a “fuzzy” set of subjective/intuitive interpretations.

In this section, we present fuzzy model of the multicriteria assignment problem based on vague aspiration levels of the decision-maker to determine the best allocation strategy. We assume that the decision-maker may decide aspiration levels on the basis of past experiences and knowledge possessed by him. The best allocation decision is resulted from the intersection of all the fuzzy goals and the constraints.

3.1 Representation of fuzzy goals

The vague aspiration levels of the decision-maker can be characterized by using the fuzzy membership functions, for example, linear [42, 43], piecewise linear [13], exponential [3, 17], tangent [16]. A linear membership function is most commonly used because it is simple and it is defined by fixing two points: the upper and lower levels of acceptability. However, there are some difficulties in using linear membership functions, see Watada [40]. Furthermore, if the membership function is interpreted as fuzzy utility of the decision-maker, describing the behavior of indifference, preference or aversion towards uncertainty, then a nonlinear membership function provides a better representation than a linear membership function. Moreover, it should be emphasized that unlike linear membership functions, for nonlinear membership functions the marginal rate of increase(or decrease) of membership values as a function of model parameters is not constant—a technique that reflects reality better than the linear case.

We transform the multicriteria assignment problem (P1) into a fuzzy multicriteria assignment problem using the exponential membership functions characterizing vague aspiration levels of the decision-maker with regard to the objective functions of cost, time and quality. The advantage of using the exponential form of membership function is that it is not as restrictive as the linear form, but flexible enough to describe the grades of precision in the parameter values. Let $\mu_{Z_1}(x),\,\mu_{Z_2}(x),\,and\,\mu_{Z_3}(x)$ represents the membership functions in respect of cost, time, and quality objectives, respectively. It may be noted that 0 ≤ $\mu_{Z_j}(x)$ ≤ 1; j = 1, 2, 3. The following steps are used in the construction of the exponential fuzzy membership functions:

• Step 1: Find Z ^worst _j (upper bound), Z ^* _j (lower bound) and D _j (tolerance) of each objective function as follows:

  • (a) Obtain individual Z ^worst _j (worst solution) by maximizing the cost objective, time objective and quality objective subject to all the constraints of the problem (P1).

  • (b) Obtain individual Z ^* _j (best solution) by minimizing the cost objective, time objective and quality objective subject to all the constraints of the problem (P1).

  • (c) Obtain the tolerance D _j  = Z ^worst _j  − Z ^* _j for each objective function.

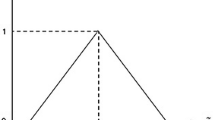
• Step 2: Define the exponential membership function $\mu_{Z_j}(x)$, j = 1, 2, 3 as follows, see Fig. 1:

  $$ \mu_{Z_j}(x)=\left\{ \begin{array}{ll} 1, & Z_j \leq Z_j^*\\ {{1-\exp\left({{K_j(Z_j^{\rm worst}-Z_j)}\over {D_j}}\right) }\over {1-\exp(K_j) }},& Z_j^* < Z_j \leq Z_j^{\rm worst}\\ 0,& Z_j > Z_j^{\rm worst} \end{array} \right. $$

As Fig. 1 shows, for K _j  < 0 (K _j  > 0), the membership function $\mu_{Z_j}(x)$ is strictly concave (convex) in [Z ^* _j , Z ^worst _j ]. The values of the shape parameter K _j of the fuzzy membership function allows us to model the grades of precision in the corresponding objective function. It may be noted that by changing the shape parameters, we can capitalize on an advantage of the exponential membership functions: they explore the different fuzzy utilities of the decision-maker.

3.2 Aggregation of fuzzy goals

Once the fuzzy membership functions are defined, the fuzzy goals are aggregated using the “product operator”. Further, the aspiration levels of the various fuzzy goals are used in the constraints to achieve the desired compromise solution. Therefore, the fuzzy multicriteria assignment problem becomes:

$$\hbox {(P2)} \max W= (\mu_{Z_1}(x)\cdot \mu_{Z_2}(x) \cdot \mu_{Z_3}(x)) $$

subject to constraints (1–6)

$$ \mu_{Z_1}(x)-\overline{\mu}_{Z_1}(x)\geq 0 , $$

(7)

$$ \mu_{Z_2}(x)-\overline{\mu}_{Z_2}(x)\geq 0 , $$

(8)

$$ \mu_{Z_3}(x)-\overline{\mu}_{Z_3}(x)\geq 0. $$

(9)

Here, ($\mu_{Z_1}(x)$ · $\mu_{Z_2}(x)$ · $\mu_{Z_3}(x)$) denotes the product term. Further, $\overline{\mu}_{Z_1}(x), \overline{\mu}_{Z_2}(x)$ and $\overline{\mu}_{Z_3}(x)$ are the desired aspiration levels of the fuzzy goals corresponding to the three objective functions. The model (P2) can be solved for varying aspiration levels of the decision-maker regrading the achievement of various fuzzy goals.

Fig. 1

Fuzzy membership functions

4 Solution methodology

The fuzzy multicriteria assignment problem (P2) is a single objective nonlinear 0-1 optimization problem with the knapsack-type constraint and is “NP-hard” problem [26]. To deal with such “NP-hard” problems many heuristic methods have been developed. Herrera et al. [9] presented a personnel assignment problem with verbal information using a GA. Toroslu and Arslanoglu [33] presented GA solutions for different versions of the personnel assignment problem with multiple objectives based on hierarchical and set constraints. Wang et al. [35] presented a two-stage fuzzy facility location problem with Value-at-Risk (VaR) which results in a two-stage fuzzy zero-one integer programming problem. They also proposed an approximate approach to compute the VaR by making use of the discretization method of fuzzy variables and a hybrid genotype-phenotype-mutation-based binary particle swarm optimization algorithm to compute the VaR. Wang et al. [36] proposed a hybrid mutation-based binary ant-colony optimization approach to the two-stage fuzzy-random facility-location model. Lin et al. [21] presented a particle swarm optimization algorithm combined with the random-key encoding scheme for solving a bi-objective personnel assignment problem. In this paper, we propose to use GA to solve fuzzy multicriteria assignment problem (P2). The GA is a well-known random search and global optimization method based on the idea of natural selection and evolution. Rather than relying on the gradient information, it searches the optimal solution by simulating the natural evolution process. The GA is proven to be a suitable method for solving large-scale optimization problems which are nonlinear, non-convex and discrete. It has demonstrated several significant advantages, such as strong robustness, convergence to global optimum and parallel search capability. As large-scale parallel stochastic search and optimization algorithms, the GAs have a good provenance in the resolution of diverse NP-hard problems [6, 10], including network optimization and resource assignment [24, 30].

4.1 Genetic algorithm

GA, a general adaptive optimization search methodology based on a direct analogy to Darwinian natural selection and genetics in biological systems, is a promising alternative to conventional heuristic methods and is based on the principle of “survival of the fittest” [4, 8, 11]. An overview of basic GA is as follows.

To solve a problem with GA, an encoding mechanism must first be designed to represent each solution as a chromosome. A fitness function is then defined to measure the goodness of a chromosome. The GA searches the solution space using a population which is a set of chromosomes at each generation. During each generation, the three genetic operators: selection, crossover and mutation, are applied to the population several times to form a new population. Selection operation results in forming a parent population for creating the next generation. Crossover operation with a crossover rate recombines the two selected chromosomes to form offsprings. Mutation operation with a mutation rate randomly alter selected positions in a selected chromosome. New population is then generated by replacing some chromosomes in the parent population with the offsprings. This process is repeated until some termination condition, e.g., the number of generations is reached.

It may be noted that while solving the model (P2), in each GA run, the decision-maker is required to provide values of the shape parameters K ₁, K ₂ and K ₃ based on his estimates of vagueness in the objective functions of cost, time and quality, respectively. The following are the technical details of the algorithm used.

4.1.1 Chromosome encoding

A gene in a chromosome is characterized by two factors: locus (i.e., the position of the gene located within the structure of chromosome), and allele (i.e., the value the gene takes). In the proposed encoding method, the length of the chromosome is taken to be n, same as the number of jobs that need to be allocated. Thus, a solution is represented as a chromosome Ch _k , which is encoded as an array, as follows:

$$ {\text{Ch}}_{k}= X_{k}[j]=a_j, j=1,2, \ldots, n, k=1, 2,\ldots, {\text {popsize}}.\\ $$

Here, popsize defines the number of chromosomes initialized to constitute population of one generation. The initialization algorithm to create first generation of size popsize is as follows:

• Step 1 For k = 1 to popsize, repeat Step 2.

• Step 2 For j = 1 to n, repeat Step 3.

• Step 3 Randomly generate an integer $a_j \in [1, n].$ Initialize X _k [j] = a _j .

Here, a _j takes an integer value in [1, n], indicating that the jth task is assigned to worker a _j . For example, a ₁ = 2 indicates that the job 1 is assigned to worker 2. After decoding this solution, we can get the corresponding values of decision variables x _ij :

$$ x_{ij}=\left\{ \begin{array}{ll} 1,\quad \hbox {if } i=a_j\\ 0,\quad \hbox {otherwise}\\ \end{array} \right. $$

where $i=1, 2,\ldots, n,$ denotes the worker and $j=1, 2,\ldots, n,$ is the job-id. It can be verified easily that this solution satisfies the constraints (1), (2) and (6) of the model (P2). If it also satisfies other constraints of the model, then it is a feasible solution.

4.1.2 Fitness evaluation

The fitness function is another important issue in GA for solving any problem. The design of the chromosome takes care of the constraints (1), (2) and (6) of the model (P2). Any violation in the left out constraints (3)−(5) and (7)−(9) will lead to infeasibility. We use penalty parameter approach to put selective pressure on the infeasible chromosomes, thus assigning them lesser fitness and leading to their elimination in subsequent generations. Absolute values of all the violations in the constraints (3)–(5) and (7)–(9) are clubbed together to get the net violation V. We use a static penalty parameter P to penalize the net violation V. In general, the use of penalty parameter is to put enough selective pressure on the fitness function to avoid infeasibility of the chromosomes. In case of no violation of the inequality constraints (3)–(5) and (7)–(9), the penalty parameter P will be zero and positive otherwise. It may be noted that if the penalty is too high or too low then the problem might become very difficult for the GA. A large penalty discourages the exploration of the infeasible region since the very beginning of the search process. On the other hand, if the penalty is too low, a lot of the search time (generations) will be spent exploring the infeasible region because the penalty will be negligible with respect to the objective function. The resultant fitness function fit _k for chromosome ${\text{Ch}}_{k}, k=1,2,\ldots, {\text{popsize}}$ is thus expressed as:

$$ {\text{fit}}_{k}=(\mu_{Z_1}(x) \cdot \mu_{Z_2}(x) \cdot \mu_{Z_3}(x))- P*V \\ $$

where

$$ P=\left\{ \begin{array}{ll} 10^3,&\quad \hbox {if } V > 0\\ 0,&\quad \hbox {otherwise}\\ \end{array} \right. $$

The objective is to find the solution chromosome Ch _k corresponding to the best found (maximum value) fitness, for the function fit _k .

4.1.3 Elitism

In order to preserve and use previously found best solution in subsequent generations, an elite-preserving operator is often used. In addition to an overall increase in performance, there is another advantage of using elitism. In an elitist GA, the statistics of the population-best solutions cannot degrade with generations. The elite count (t) indicates the number of individuals that are guaranteed to be carried forward to the next generation without performing selection, crossover and mutation operations. In this paper, we use t = 1 to retain the most fit individual of the current population for the population comprising the next generation.

4.1.4 Selection

The selection method determines how chromosomes are selected from the current population to be considered as parents for crossover. The goal of selection (reproduction) operator is to choose individuals that, on average, are more fit than others to pass on their genes to the next generation. We employ 4-player tournament selection as a selection mechanism in this study. Four individuals are randomly selected and the one with the highest fitness is selected for the parent population. It may be recalled that we already have one member of the next generation as an outcome of performing elitism. Let ${\text{Ch}}^\prime_k, k=2, 3,\ldots, {\text{popsize}}$ constitutes the parent population which will give rise to remaining popsize − 1 members of the next generation after the crossover and mutation operations are performed. The remaining popsize − 1 chromosomes for the parent population are generated using 4-player tournament selection as follows:

• Step 1 For k = 2 to popsize, repeat Step 2 to Step 5.

• Step 2 Randomly generate four integers ${\text{sel}}_1, {\text{sel}}_2, {\text{sel}}_3, {\text{sel}}_4 \in [1, {\text{popsize}}].$ These represents the selection of chromosomes $Ch_{sel_1},\,Ch_{sel_2},\,Ch_{sel_3},\,Ch_{sel_4}$ for 4-player tournament selection.

• Step 3 If $fit_{sel_1}$ ≥ $fit_{sel_2}$, let m = sel₁ else m = sel₂.

• Step 4 If $fit_{sel_3}$ ≥ $fit_{sel_4}$, let t = sel₃ else t = sel₄.

• Step 5 If fit _m  ≥ fit _t , let ${\text{Ch}}^\prime_k$ = Ch _m , else ${\text{Ch}}^\prime_k$ = Ch _t .

4.1.5 Crossover operator

Crossover is the main genetic operator. The two parent chromosomes, if selected for mating pool, reproduce two child chromosomes (offsprings) using the crossover operation. The crossover probability $p_c \in (0,1)$ represents the statistical chance that the two selected chromosomes will crossover. For each potential crossover, a random number between 0 and 1 is generated. If the number of selected chromosome is odd then the above procedure is repeated until one more chromosome gets selected or the number of selected chromosomes become an even number. Two-point crossover is used here between the selected parents to exchange the gene values between the two randomly selected crossover points in both parent chromosomes to produce offsprings. The algorithm of the two-point crossover operation is given below:

• Step 1 For k = 2 to popsize, repeat Step 2.

• Step 2 Randomly generate a real number r from interval (0,1). The chromosome ${\text{Ch}}^\prime_k$ is selected as a parent if r < p _c .

• Step 3 Denote the selected parents as $S_1,S_2,\ldots$ and divide them into following pairs $(S_1, S_2),(S_3, S_4),\ldots.$

• Step 4 For each pair of selected parents, for example (S ₁, S ₂), randomly select two positions $pos_1, pos_2 \in [1,n].$

• Step 5 Exchange the gene values between the two selected positions pos₁ and pos₂, for the two selected parents.

Figure 2 depicts the two point crossover operation between two randomly generated positions, pos ₁ = 2 and pos ₂ = 4, for the selected parents.

Fig. 2

Two point crossover operation

4.1.6 Mutation operator

Mutation is another operator which produce spontaneous random changes in various chromosomes by altering one or more genes. In this paper, out of several available mutation operators, we use swap mutation. With some probability of mutation $p_{\rm m} \in (0,1),$ a chromosome is selected for the process of mutation. The mutation process is summarized as follows:

• Step 1 Set k = 2.

• Step 2 If k ≤ popsize, go to Step 3, otherwise stop.

• Step 3 Randomly generate a real number r from interval (0,1). If r < p _m, select the chromosome ${\text{Ch}}^\prime_k$ for mutation and go to Step 4 else k = k + 1 and go to Step 2.

• Step 4 Randomly select two positions, ${\text{pos}}_1, {\text{pos}}_2 \in [1,n]$ and swap the gene values at the two selected positions.

Figure 3 depicts the process of mutation in a selected chromosome with pos₁ = 3 and pos₂ = 5. Here, in the selected chromosome, pos₁ = 3 corresponds to task 3 is assigned to worker 6, i.e., x ₆₃ = 1 and pos₂ = 5 corresponds to task 5 is assigned to worker 4, i.e., x ₄₅ = 1. After swap mutation is performed, task 3 is assigned to worker 4, i.e., x ₄₃ = 1 and task 5 is assigned to worker 6, i.e., x ₆₅ = 1.

Fig. 3

Swap mutation operation

4.2 Step-wise description of the proposed solution approach

The step-wise description of the proposed solution approach for obtaining the optimal assignment plans of the fuzzy assignment problem is as follows:

• Step 1 Express fuzzy goal of each objective function of the problem (P1) using exponential fuzzy membership function and aggregate different fuzzy goals using product operator.

• Step 2 Use aspiration level of each fuzzy goal to guide the solution search.

• Step 3 Use GA to solve the resultant nonlinear 0-1 optimization problem (P2) for different choices of the shape parameters in the exponential fuzzy membership functions.

5 Numerical illustrations: results and analysis

In this section, we present numerical illustrations of the fuzzy manpower planning problem. The proposed GA is coded in C++ on a personal computer with Intel Core2Duo CPU, having a speed of 2.8 GHz and a 4 GB RAM. The following settings of the parameters are used to solve different problem instances: number of tasks (n) = number of workers (n) = 6, l _i  = 2 ∀ i, s = 5, b = 30, p _c  = 0.5, p _m = 0.1, popsize = 100, generations = 2,000. Table 1 provides necessary data in respect of cost, time, quality and resource requirements. Table 2 gives the upper bound (Z ^worst _j ), lower bound (Z ^* _j ) and the tolerance (D _j ) for each objective function. These values are used to construct the exponential membership functions of the three objectives.

Table 1 The cost–time–quality–resource matrix

Table 2 The worst-best solution payoff matrix

Optimal assignment plans are reported in Tables 3, 4, 5 for different values of the shape parameters and different estimates of aspiration levels indicated by the decision-maker. For each combination of the shape parameters (K ₁, K ₂, K ₃), we have presented results by taking two different estimates of the aspiration levels $(\overline{\mu}_{Z_1}(x),\overline{\mu}_{Z_2}(x),\overline{\mu}_{Z_3}(x)).$

Table 3 Optimal assignment plan-I

Table 4 Optimal assignment plan-II

Table 5 Optimal assignment plan-III

Figures 4, 5, 6 show the variations in the degree of satisfaction of the goals of cost, time and quality corresponding to different choices of the shape parameters. Generally, the achievement levels may not be large enough to satisfy the decision-maker because of multiple objective nature of the problem and also considering the fact that we are dealing with 0-1 programming problem. Accepting a high deterioration in one of the objective functions may provide higher improvement(s) in the remaining objective functions. In most cases, it is possible that poor performance on one criterion may be compensated by good performance on other criteria. Thus, corresponding to decision-maker’s preferences, many different solutions can be reached at different satisfaction degrees.

Fig. 4

The degree of satisfaction of the goal of the total cost

Fig. 5

The degree of satisfaction of the goal of the total time

Fig. 6

The degree of satisfaction of the goal of the overall quality

The above-obtained optimal assignment plans clearly shows the advantage of using exponential membership functions in the fuzzy multicriteria assignment problem. If the decision-maker is not satisfied with the obtained assignment plan, more assignment plans can be obtained by varying values of the shape parameters in the exponential membership functions enabling us to explore different fuzzy utilities of the decision-maker. In the proposed methodology, all the three objectives are treated equivalently. However, the decision-maker can choose different solutions according to his needs in different situations. For example, cost can be the most important objective for the decision-maker in a determined period of allocation plan. Then, the decision-maker will choose the solution which satisfies the cost objective function the most. However, this can cause poor performance of the satisfaction degree of other objective functions. The proposed solution method provides a wide range of information and flexibility in the sense that by changing shape parameters in the exponential membership functions interactively provides different scenario analysis for imprecise allocation plans. Also, it is possible that the upper bound Z ^worst _j and lower bound Z ^* _j of the objective functions can be changed using decision-maker’s preferences so that new membership functions are generated. This will lead to the formulation of a new crisp 0-1 programming problem.

5.1 Comparison of the proposed approach with the approach of Tsai et al. [34]

To further assess the performance of the proposed approach, we compare the experimental results of the proposed approach with the experimental result produced by the approach of Tsai et al. [34]. In their approach, the linear membership functions have been used to capture the vague aspiration levels of the decision-maker and max–min approach proposed by Bellman and Zadeh [2] is used to aggregate all the fuzzy goals. Table 6 presents the corresponding optimal assignment plan obtained using the approach of Tsai et al. [34].

Table 6 Optimal assignment plan

The comparison of the optimal assignment plans presented in Tables 3, 4, 5 with the optimal assignment plan presented in Table 6, clearly shows that the individual achievement level of each fuzzy goal is better in most of the assignment plans obtained using the proposed approach. In other words, the proposed approach not only provides better assignment plans but also provides flexibility in the sense that if the decision-maker is not satisfied with the obtained assignment plan, more assignment plans can be obtained by varying values of the shape parameters in the exponential membership functions enabling us to explore different fuzzy utilities of the decision-maker. It is important to point out that the flexibility to explore different fuzzy utilities of the decision-maker is not possible in the approach of Tsai et al. [34] since the linear membership functions are defined by fixing both the upper and lower levels of acceptability.

6 Conclusions

In this paper, we have discussed a fuzzy multicriteria assignment problem to deal with an uncertain environment in the real-world applications of the assignment problem. We considered overall quality in finishing all the tasks along with cost and time objectives. The solution of the proposed model is a trade-off among the cost, time and quality objectives. The exponential fuzzy membership functions have been used to efficiently model the fuzzy assignment problem using product operator. The shape parameters in the exponential membership functions are used to describe the grades of precision in the objective functions. The resultant nonlinear 0-1 optimization problem with a knapsack-type resource constraint is “NP-hard” and thus has been solved using GA. Optimal assignment plans have been reported corresponding to many choices of the shape parameters describing different fuzzy utilities of the decision-maker and the various combinations of desired aspiration levels of the objectives indicated by the decision-maker.