1 Introduction

Nanofluids, commonly identified as NPs simply NPs, are fluids made up of embedded nanoparticles that are used to transmit heat. A wide range of basic liquids, such as water, organic compound fluids, fuel, and bioliquids, are frequently included in base liquids. These and other basic liquids make up base liquids, which are often made of them. The ability of fluid stability and heat transport to be greatly enhanced by nanoparticles that are both much smaller but with considerably bigger area of surface. Increased thermal conductivity of nanofluids was initially developed by Choi [1]. Nanofluids are used in a numerous fields of disciplines, with science and management. Numerous uses for nanoparticles have been discovered by analysis of fluid flow, including electrochemical reactions, tiny electronics, and energy production: Because of their special qualities, nanofluids are particularly successful in a variety of heat control processes. Thermal conductivity is the key framework when it comes to issues with heat transfer. In their study, Motlagh and Kalteh [2] examined how heat is transported while taking into account the shape and aggregation of nanoparticles. Researchers found that the nanoparticles shape and aggregation had a disproportionate impact upon the velocity of nanoliquids. Swain and Mahanthesh [3] studied nanoparticle collection’s impact on nanoliquid distribution, finding it increases temperature. Sabu et al. [4] examined nanoparticle collection’s kinematics on a slanted surface. As the plate’s raise increased, the velocity appearance considerably reduced while the temperature appearance increased dramatically. Mahanthesh [5] examined how the creation of nanoparticles affects heat transfer through the nanoparticles. In this section, they mentioned that the act of collecting nanoparticles accelerates the movement of the nanoliquid. Makhdoum et al. [6] addressed the consequences of entropy generation and nanoparticle collection at the point when nanofluid flow is zero across stretching surfaces via angled Lorentz forces. By utilizing the computational strategy, Bilal et al. [7] investigated the impact of bidirectional diffusion on Prandtl nanofluid through stretched areas. Using boundary conditions for heat as well as mass flux, Hayat et al. [8] explored 3-D nanofluid flows across an gradually stretched area. In a Darcy-Forchheimer form, Wang et al. [9] explored the dissolving rheology of a 3-D Maxwell nanofluid (graphene-engine oil) flow having slip circumstance across an extensible surface. Using a computational technique, Sohail and Naz [10] investigated the mass and heat transfer models within the MHD flow of Sutterby nanofluid in stretched cylinder. Azeem Khan and Hussain [11] investigated the effects of stimulation energy on the dynamics within the time-varying Sutterby nanofluid.

In general, mass and heat transmission mechanisms work as intended, for instance, storing of eliminating trappings over mechanical operations, storing of electronic parts in computers, the heating and cooling of constructions and residences, cooking, and the temperature control of returning of spacecraft. Further research into the significance of such devices is possible in the fields of power plants, MHD accelerators, polyethylene the extruding refrigeration spirals, electrical modifications, boundary layer control, and transpiration progressions in aerodynamics. Turkyilmazoglu [12] demonstrated the two distinct stages of fluid flow and the MHD flow for various fluids using a rotating stretchable disk and a moving substrate. According to Zohr et al. [13], the magnetic effect and the Stefan puffing situation have an impact on the flow of tiny organisms in nanofluids. Doh et al. [14]studied hydromagnetic nanofluid flow, homogeneous and heterogeneous procedures, and boundary layer flow of magneto pass through nanoliquid. Xiong et al. [15] studied magneto pass through nanoliquid, and Khan et al. [16] studied Maxwell fluid flow characteristics.

Due to the temperature differences between two bodies or inside the same body, the transmission of heat is a significant role in the current environment. The “Cattaneo-Christov heat flux model” (CCHFM) was an improvised Fourier’s theory that Christov developed to overcome the limitations of parabolic expression of energy. Waqas et al. [17] recently clarified how the revised Fourier law affects the flow of Burger fluid. Shehzad et al. [18] provide an illustration of the Oldroyd-B material flow’s Robin’s criteria and adapted Fourier law-based Darcy-Forchheimer occurrence. Ahmed et al. [19] made use of a rotating disk for analyzing the nanofluid flow using CCHFM. Hayat et al. [20] investigated the Oldroyd-B tiny particles ascent utilizing the hydromagnetic static point theory. Shah et al. [21] evaluated the governing equations that use a modified version of the Fourier law to depict the flow of mixed convective fluid across a surface. Through the use of a gyrating frame and CCHFM, Ali et al. [22] explored the magnetized Oldroyd-B tiny particle occurrences. CCHFM has been employed by Reddy et al. [23] to describe the improvement in heat transfer during micropolar nanofluid flow.

Entropy is associated with disorder; however, this disorder is one that describes the variety of states that a system might assume. As time goes on, there is less energy available to carry out worthwhile tasks. Since irreversibilities exist, entropy generation is directly tied to them. Entropy intensification causes a drop in efficiency, which is why entropy minimization has grown in importance in the thermo-fluid area [24]. The impacts on entropy production for hydromagnetic mix convection with Ohmic heating and loss of energy were investigated by Sparrow-Quack-Boerner local nonsimilarity technique which was used by Afridi et al. [25]. Almakki et al. [26] utilized the bivariate spectral quasi-linearization technique to explore the intermittent MHD micropolar nanofluid including the production of entropy. Khan and Alzahrani [27] explored expected convection mechanisms and combined convective flow via the production of entropy and the stimulation energy effect. Ijaz Khan and Alzahrani [27] studied at the mathematical modeling for mixed convective transport of non-Newtonian fluid including entropy and stimulation energy. CoFe2O4 and water as a base fluid in a tube estimated with two different models like ANFIS and MLP were studied by Sundar and Mewada [28] for empirical entropy, efficiency of energy, and thermal stability element. Further relevent work is reported in [29,30,31,32,33,34] and studies reported therein. Kumar and Sharma [35] use radiative flux to take the Dufour and Soret phenomenon. This work aims to study the creation of entropy in a hybrid nanofluid flow of \(\mathrm{Cu}+{\mathrm{TiO}}_{2}/{\mathrm{H}}_{2}\mathrm{O}\) through a spinning disk that rotates vertically and has partial slip and thermal radiation. In their study, Kumar and Sharma [36] investigate the effects of Stefan puffing on the three-dimensional Reiner-Rivlin fluid flow on a spinning disk traversing vertically.

In this research, the primary goal is to examine the entropy generation on a permeable, stretching sheet over an MHD and different shapes of nanoparticle with the impact of Cattaneo-Christov heat flux model. Copper (Cu) and titanium dioxide (TiO2) hybrid nanoparticles were used in this study, with water acting as the base fluid. The identical variables are used to convert the non-linear partial differential equations into non-linear ordinary differential equations. The OHAM method is applied to analytically resolve the newly revised equations. This research is beneficial for biofluidic engineering, blood cancer treatment, and biological aspects. On a graphic representation, the influence of several physical parameters and variables on velocity, temperature, and entropy generation is illustrated.

2 Model Features and Nathematical Evaluation

The following list shows the distinctive qualities of current work:

  • \(\mathrm{Cu}+{\mathrm{TiO}}_{2}/{\mathrm{H}}_{2}\mathrm{O}\) hybrid nanofluid flow across a dual-direction stretching surface in three dimensions via the origin constant is taken into consideration and their empirical relation is presented in Table 1 and numerical values are shown in Table 2;

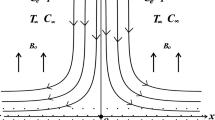
  • It is also thought that the surface moves with speeds \(\widetilde{{u}^{*}}={U}_{w}\left(x\right)=ax,\widetilde{{v}^{*}}={V}_{w}(y)=by\) where \(a\) and \(b\) are positive numbers which indicate stretching in the \(x-y\) directions;

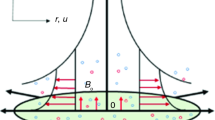
  • According to the fluid model, the magnetic dipole has been taken that is orthogonal to the surface;

  • In this research, we discuss different nanoparticle shapes, including spheres, bricks, cylinders, platelets, and blades whose values are listed in Table 3;

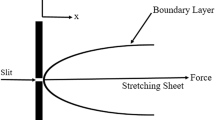
  • The boundary layer theory is used to present the transport rheology under investigation;

  • Nonlinear thermal radiations and heat absorption/generation and magneto-hydrodynamic are taken;

  • The geometry of the model is depicted in Fig. 1.

Table 1 Parameters of hybrid nanofluids with mathematical formulation [37, 38] 
Full size table
Table 2 Thermal properties of \({\mathrm{TiO}}_{2}\) and \(\mathrm{Cu}\) within the base liquid
Full size table
Table 3 Shapes of nanoparticles related with sizes
Full size table
Fig. 1
figure 1

Geometry of the model 

Full size image

Using the preceding supposition, a system of PDEs is created, and non-linear PDEs are represented as [37]: 

$$\frac{\partial \widetilde{{u}^{*}}}{\partial x}+\frac{\partial \widetilde{{v}^{*}}}{\partial y}+\frac{\partial \widetilde{{w}^{*}}}{\partial z}=0$$
(1)
$$\widetilde{{u}^{*}}\frac{\partial \widetilde{{u}^{*}}}{\partial x}+\widetilde{{v}^{*}}\frac{\partial \widetilde{{u}^{*}}}{\partial y}+\widetilde{{w}^{*}}\frac{\partial \widetilde{{u}^{*}}}{\partial z}={v}_{hnf}\frac{{\partial }^{2}\widetilde{{u}^{*}}}{\partial {z}^{2}}-\frac{{\sigma }_{hnf}}{{\rho }_{hnf}}{B}^{2}\widetilde{{u}^{*}}$$
(2)
$$\widetilde{{u}^{*}}\frac{\partial \widetilde{{v}^{*}}}{\partial x}+\widetilde{{v}^{*}}\frac{\partial \widetilde{{v}^{*}}}{\partial y}+\widetilde{{w}^{*}}\frac{\partial \widetilde{{v}^{*}}}{\partial z}={v}_{hnf}\frac{{\partial }^{2}\widetilde{{v}^{*}}}{\partial {z}^{2}}-\frac{{\sigma }_{hnf}}{{\rho }_{hnf}}{B}^{2}\widetilde{{v}^{*}}$$
(3)
$$\widetilde{{u}^{*}}\frac{\partial T}{\partial x}+\widetilde{{v}^{*}}\frac{\partial T}{\partial y}+\widetilde{{w}^{*}}\frac{\partial T}{\partial z}+{\lambda }_{E}{\phi }_{E}={\alpha }_{hnf}\frac{{\partial }^{2}T}{\partial {z}^{2}}+\frac{{\mu }_{hnf}}{{\left(\rho {C}_{P}\right)}_{hnf}}{\left(\frac{\partial \widetilde{{u}^{*}}}{\partial z}\right)}^{2}+\frac{Q}{{\left(\rho {C}_{P}\right)}_{hnf}}\left(T-{T}_{\infty }\right)+\frac{16{\delta }^{*}{{T}_{\infty }}^{3}}{{3{K}^{*}\left({\rho C}_{P}\right)}_{hnf}}\left(\frac{{\partial }^{2}T}{\partial {z}^{2}}\right)$$
(4)

Associated boundary conditions are:

$$\begin{array}{c}\widetilde{{u}^{*}}={U}_{w}\left(x\right)=ax, T={T}_{w},\widetilde{{v}^{*}}={V}_{w}(y)=by, \widetilde{{w}^{*}}=0:z=0\\ \widetilde{{u}^{*}}\to 0, \widetilde{{v}^{*}}\to 0, T\to {T}_{\infty }:z\to \infty \end{array}$$
(5)

where \({\phi }_{E}\) is the diffusion of heat flux:

$${\phi }_{E}={\widetilde{{u}^{*}}}^{2}\frac{{\partial }^{2}T}{\partial {x}^{2}}+{\widetilde{{v}^{*}}}^{2}\frac{{\partial }^{2}T}{\partial {y}^{2}}+{\widetilde{{w}^{*}}}^{2}\frac{{\partial }^{2}\widetilde{T}}{\partial {z}^{2}}+2\widetilde{{u}^{*}}\widetilde{{v}^{*}}\frac{{\partial }^{2}T}{\partial x\partial y}+2\widetilde{{v}^{*}}\widetilde{{w}^{*}}\frac{{\partial }^{2}T}{\partial y\partial z}+2\widetilde{{u}^{*}}\widetilde{{w}^{*}}\frac{{\partial }^{2}T}{\partial x\partial z}+\left(\widetilde{{u}^{*}}\frac{\partial \widetilde{{u}^{*}}}{\partial x}+\widetilde{{v}^{*}}\frac{\partial \widetilde{{u}^{*}}}{\partial y}+\widetilde{{w}^{*}}\frac{\partial \widetilde{{u}^{*}}}{\partial z}\right)\frac{\partial T}{\partial x}+\left(\widetilde{{u}^{*}}\frac{\partial \widetilde{{v}^{*}}}{\partial x}+\widetilde{{v}^{*}}\frac{\partial \widetilde{{v}^{*}}}{\partial y}+\widetilde{{w}^{*}}\frac{\partial \widetilde{{v}^{*}}}{\partial z}\frac{\partial T}{\partial y}\right)+\left(\widetilde{{u}^{*}}\frac{\partial \widetilde{{w}^{*}}}{\partial x}+\widetilde{{v}^{*}}\frac{\partial \widetilde{{w}^{*}}}{\partial y}+\widetilde{{w}^{*}}\frac{\partial \widetilde{{w}^{*}}}{\partial z}\right)\frac{\partial T}{\partial z}$$
(6)

Similarity transformation [37] and [39] of given problem is described as:

$$\widetilde{{u}^{*}}=ax{f}{'}\left(\zeta \right), \widetilde{{v}^{*}}=by{g}{'}\left(\zeta \right), \widetilde{{w}^{*}}=-\sqrt{a{v}_{f}}\left(f\left(\zeta \right)+cg\left(\zeta \right)\right), \zeta =\sqrt{\frac{a}{{v}_{f}}}z,\uptheta \left(\zeta \right)=\frac{{T-T}_{\infty }}{{T}_{w}-{T}_{\infty }}, c=\frac{b}{a}$$
(7)

Applying Eq. \((7\)) in Eqs. \((1-4)\), non-linear ODEs are produce as:

$${\varepsilon }_{1}{f}^{{'}{'}{'}}+\left(f+cg\right){f}^{{'}{'}}-{\left({f}{'}\right)}^{2}-M{\varepsilon }_{3}{f}{'}=0$$
(8)
$${\varepsilon }_{1}{g}^{\mathrm{^{'}}\mathrm{^{'}}\mathrm{^{'}}}+\left(f+cg\right){g}^{\mathrm{^{'}}\mathrm{^{'}}}-c{\left({g}^{\mathrm{^{'}}}\right)}^{2}-M{\varepsilon }_{3}{g}^{\mathrm{^{'}}}=0$$
(9)
$${{(\varepsilon }_{2}+Rd)\uptheta }^{\boldsymbol{^{'}}\boldsymbol{^{'}}}+Pr\left(f+cg\right){\theta }{'}+Pr\lambda \theta +PrEc{\left({f}^{{'}{'}}\right)}^{2}-Pr{\delta }_{t}{\{\left(f+cg\right)}^{2}{\theta }^{{'}{'}}+(f+cg)({f}{'}+cg{'})\theta {'}\}=0$$
(10)

According to those boundary criteria:

$$\begin{array}{c}f\left(0\right)=0, {f}{'}\left(0\right)=1, g\left(0\right)=0, g{'}\left(0\right)=a,\theta \left(0\right)=1, :\zeta =0\\ {f}{'}\left(\infty \right)\to 0, {g}{'}\left(\infty \right)\to 0,\theta (\infty )\to o :\zeta \to \infty .\end{array}$$
(11)

where fluid parameters are differentiated as:

$$M=\frac{{B}_{0}^{2}{\sigma }_{hnf}}{a{\rho }_{hnf}},Ec=\frac{{U}^{2}}{{C}_{P}\left({T}_{s}-T\right)}, Pr=\frac{\nu }{{\alpha }_{hnf}}, \lambda =\frac{Q}{a{({\rho C}_{P})}_{hnf}}, Rd=\frac{16{\delta }^{*}{{T}_{\infty }}^{3}}{{3{K}^{*}\left(k\right)}_{hnf}} and c=\frac{b}{a}$$
(12)

Now, the descriptions of the parameters \({\varepsilon }_{1}, {\varepsilon }_{2},\) and \({\varepsilon }_{3}\) are as follows:

$${\varepsilon }_{1}=\frac{(1+{Z}^{1}\varphi +{Z}^{2}{\varphi }^{2})}{(1-\varphi +\varphi \frac{{\rho }_{s}}{{\rho }_{f}})},{\varepsilon }_{2}=\frac{\frac{{k}_{nf}}{k}}{1-\varphi +\varphi \frac{{(\rho {C}_{P})}_{s}}{{(\rho {C}_{P})}_{f}}}, {\varepsilon }_{3}=\frac{(1-\varphi +\varphi \frac{{\sigma }_{s}}{{\sigma }_{f}})}{(1-\varphi +\varphi \frac{{\rho }_{s}}{{\rho }_{f}})}$$
(13)

The skin-friction coefficient and the local Nusselt number are defined as:

$${C}_{fx}=\frac{2{\mu }_{hnf}{\left(\frac{\partial u}{\partial z}\right)}_{z=0}}{{\rho }_{hnf}{U}^{2}};R{e}_{x}^{1/2}{C}_{fx}=\left(\frac{{\mu }_{hnf}}{{\mu }_{f}}\right){f}^{{'}{'}}\left(0\right)$$
(14)
$${C}_{fy}=\frac{2{\mu }_{hnf}{\left(\frac{\partial v}{\partial z}\right)}_{z=0}}{{\rho }_{hnf}{U}^{2}};R{e}_{y}^{1/2}{C}_{fy}=\left(\frac{{\mu }_{hnf}}{{\mu }_{f}}\right){g}^{{'}{'}}\left(0\right)$$
(15)
$$N{u}^{*}={\frac{{-x{k}_{hnf}\left(\frac{\partial T}{\partial z}\right)}_{z=0}}{{k}_{f}({T}_{s}-{T}_{0})}; Re}^{-1/2}N{u}^{*}=-\frac{{k}_{hnf}}{{k}_{f}}{\uptheta }{'}\left(0\right)$$
(16)

2.1 Entropy Generation

According to the mathematical model, the description of entropy generation is [40].

$${E}_{G}=\frac{{k}_{f}}{{T}_{\infty }^{2}}\left(\frac{{k}_{hnf}}{{k}_{f}}\right){\left(\frac{\partial T}{\partial z}\right)}^{2}+\frac{{k}_{f}}{{T}_{\infty }^{2}}\left(\frac{{{16\delta }^{*}T}_{\infty }^{3}}{3{k}_{f}{k}^{*}}\right){\left(\frac{\partial T}{\partial z}\right)}^{2}+\frac{{\mu }_{hnf}}{{T}_{\infty }}{\left(\frac{\partial \widetilde{u}}{\partial z}\right)}^{2}+\frac{{\sigma }_{nf}}{{T}_{\infty }}\left(\widetilde{u}+\widetilde{v}\right){B}^{2}$$
(17)

The definition of dimensionless entropy generation is given below:

$$NG=\frac{{T}_{\infty }^{2}{a}^{2}{E}_{G}}{{k}_{f}{\left({T}_{w}-{T}_{\infty }\right)}^{2}}$$
(18)

We obtained the following dimensionless variant of the entropy equation using Eq. \((17)\).

$$NG=Re\left(\frac{{k}_{hnf}}{{k}_{f}}+Rd\right){\theta {'}}^{2}+{B}_{r}Re{\left({f}^{{'}{'}}\right)}^{2}+MEcPrRe\frac{1}{A}\left({{f}{'}}^{2}+{{g}{'}}^{2}\right)$$
(19)

Here,

$$Re=\frac{{a}^{2}U}{{\nu }_{f}x}, {B}_{r}=\frac{{{\mu }_{nf}U}^{2}}{{k}_{f}({T}_{w}-{T}_{\infty })}, A=\frac{{T}_{w}-{T}_{\infty }}{{T}_{\infty }}$$
(20)

3 Optimal Homotopy Analysis Method

Different scholars have employed a variety of different methods to formulate nonlinear differential equations. OHAM is a most common method used to solve nonlinear differential equations [40]. This can be done using Mathematica programming. The technique needs some initial assumptions and linear operator values, which are explained in given below.

$$\widehat{f}\left(\zeta \right)=1-\mathrm{exp}\left(-\zeta \right)$$
(21)
$$\widehat{g}\left(\zeta \right)=a(1-\mathrm{exp}\left(-\zeta \right))$$
(22)
$$\widehat{\theta }\left(\zeta \right)=\mathrm{exp}\left(-\zeta \right)$$
(23)
$${\mathcal{L}}_{\widehat{f}}=\frac{{d}^{3}\widehat{f}}{d{\zeta }^{3}}-\frac{d\widehat{f}}{d\zeta }, {\mathcal{L}}_{\widehat{g}}=\frac{{d}^{3}\widehat{g}}{d{\zeta }^{3}}-\frac{d\widehat{g}}{d\zeta }, {\mathcal{L}}_{\widehat{\theta }}=\frac{{d}^{2}\widehat{\theta }}{d{\zeta }^{2}}-\widehat{\theta }$$
(24)

The prior linear operators satisfy the basic requirements:

$${\mathcal{L}}_{\widehat{f}}\left\{{\mathcal{B}}_{1}^{*}+{\mathcal{B}}_{2}^{*}\mathrm{exp}\left(\xi \right)+{\mathcal{B}}_{3}^{*}\mathrm{exp}\left(-\xi \right)\right\}=0$$
(25)
$${\mathcal{L}}_{\widehat{g}}\left\{{\mathcal{B}}_{4}^{*}+{\mathcal{B}}_{5}^{*}\mathrm{exp}\left(\xi \right)+{\mathcal{B}}_{6}^{*}\mathrm{exp}\left(-\xi \right)\right\}=0$$
(26)
$${\mathcal{L}}_{\widehat{\theta }}\left\{{\mathcal{B}}_{7}^{*}\mathrm{exp}\left(\xi \right)+{\mathcal{B}}_{8}^{*}\mathrm{exp}\left(-\xi \right)\right\}=0$$
(27)

The above constants \({\mathcal{B}}_{j}^{*}=j=(1-8)\) which BC can help you find.

3.1 Optimal Convergence Parameters

It should be noted that in approximation homotopic techniques, the non-zero convergence control parameters \({h}_{f, }{ h}_{g}\), and \({h}_{\theta }\) determine the convergence zone and the progression of homotopic methods. As recommended by Liao [41], we have expressed the average squared residual errors using the notion of minimization to obtain the ideal values of \({h}_{f, } {h}_{g}\), and \({h}_{\theta }\).

$${\in }_{m}^{f}=\frac{1}{k+1}\sum_{j=0}^{k}{\left[{N}_{f}{(\sum_{i=0}^{m}\widehat{f}\left(\zeta \right),\sum_{i=0}^{m}\widehat{g}\left(\zeta \right))}_{\zeta =j\delta \zeta }\right]}^{2}$$
(28)
$${\in }_{m}^{g}=\frac{1}{k+1}\sum_{j=0}^{k}{\left[{N}_{g}{(\sum_{i=0}^{m}\widehat{f}\left(\zeta \right),\sum_{i=0}^{m}\widehat{g}\left(\zeta \right))}_{\zeta =j\delta \zeta }\right]}^{2}$$
(29)
$${\in }_{m}^{\theta }=\frac{1}{k+1}\sum_{j=0}^{k}{\left[{N}_{\theta }{(\sum_{i=0}^{m}\widehat{f}\left(\zeta \right),\sum_{i=0}^{m}\widehat{g}\left(\zeta \right), \sum_{i=0}^{m}\widehat{\theta }\left(\zeta \right))}_{\zeta =j\delta \zeta }\right]}^{2}$$
(30)

Afterwards [41],

$${\in }_{m}^{t}={\in }_{m}^{f}+{\in }_{m}^{g}+{\in }_{m}^{\theta }$$
(31)

However, \(m=28,\) \(\delta \zeta =0.5,\) and \({\in }_{m}^{t}\) stand for total squared residual error. The Mathematica bvph2.0 is used to reduce the total average squared residual error. The overall averaged squared residual error is equal to \({\in }_{m}^{t}=509.584\). The ideal values of the convergence-control parameters at the second level of estimations are \({h}_{f}=0.104516,\) \({h}_{g}=-0.0483796\), and \({h}_{\theta }=-0.116166.\) The distinct average squared residual error using the best convergence control parameter values is displayed in Table 4. The averaged squared residual error is shown to decrease with more precise approximations.

Table 4 Shapes of nanoparticles related with sizes
Full size table

4 Discussion

Different forms of nanoparticles in a perspective of copper and titanium dioxide hybrid nanoparticles are included in base fluid called water across a moving surface, resulting in a three-directional and 3-D thermal energy occurrence in Newtonian fluid. We use numerical approaches to study this phenomenon of thermal energy transport. A related review of this flow model is provided below. Graphs are used to describe the relationship between velocity, temperature, entropy generation, and numerous factors.

4.1 Comparison in the Context of the Velocity Field

\(\mathrm{Cu}+{\mathrm{TiO}}_{2}/{\mathrm{H}}_{2}\mathrm{O}\) Hybrid nanofluids are suspended in a flow phenomena that is dependent on magnetic field, stretching ratio number, and volume fraction. Figure 2a–e, Fig. 3, Fig. 4, Fig. 5, Fig. 6, and Fig. 7a–e simulate the effect of magnetic number \((M)\) on the flow of copper and titanium dioxide (TiO2) hybrid nanofluids in view of various forms. These graphs provide indication that the magnetic number that appears as a result of the Lorentz effect causes the flow of \(\mathrm{Cu}+{\mathrm{TiO}}_{2}/{\mathrm{H}}_{2}\mathrm{O}\) hybrid nanofluids to slow down. Additionally, the negative Lorentz force plays a crucial role in increasing friction in the movement of copper and titanium dioxide hybrid nanoparticles. It has been noted that the Lorentz force is the opposing force to flow phenomena. Nanoparticle flow is thought to be normal for the magnetic field’s direction. Thus, flow is diminished. As a result, the distribution of copper and titanium dioxide hybrid nanoparticles slow down in the presence of nanoparticles of different forms. The flowing behavior of the stretching ratio number (c), which incorporates the effects of different types of nanoparticles, is also seen in Fig. 2a–e, Fig. 3, and Fig. 4a–e. As a ratio of the stretching numbers in the x- and y-direction, the stretching ratio number (c) determines the flow of \(\mathrm{Cu}+{\mathrm{TiO}}_{2}/{\mathrm{H}}_{2}\mathrm{O}\) hybrid nanofluids. Therefore, the high numbers of \((c)\) represent the surface stretching more in both directions (horizontal), as well as the surface wall extending more in the direction (horizontal). By using different shapes of nanoparticles, this increased stretching ratio in the x-direction causes a reduction in the flow of (\(\mathrm{Cu}+{\mathrm{TiO}}_{2}/{\mathrm{H}}_{2}\mathrm{O}\)). According to aforementioned figures, the flow of copper and titanium dioxide hybrid nanoparticles employing different morphology nanoparticles is increased via a large value of \((c)\), since \((c)\) has an opposite relationship to stretching number when seen in the y-direction. Figure 5a–e, Fig. 6a–e, and Fig. 7a–e depict the graphical evaluations of volume fraction (\(\varphi\)) related to copper and titanium dioxide hybrid nanoparticles with the appearance of different shape nanoparticles. The representations from such figures show that flow of \(\mathrm{Cu}+{\mathrm{TiO}}_{2}/{\mathrm{H}}_{2}\mathrm{O}\) hybrid nanofluids using different shape nanoparticles maximizes through greater values of volume fraction number. The influence of (\(\varphi\)) on the flow of titanium dioxide nanoparticles higher than the velocity of copper nanoparticles when different forms nanoparticles are present is included as well.

Fig. 2
figure 2

a–e Influence of \(M\) and \(c\) on \(f{'}\)

Full size image
Fig. 3
figure 3

a–e Implication of \(M\) and \(c\) on \(g{'}\)

Full size image
Fig. 4
figure 4

a–e Bearing of \(M\) and \(c\) on \(g{'}\)

Full size image
Fig. 5
figure 5

a–e Involvement of \(M\) and \(\varphi\) on \(f{'}\)

Full size image
Fig. 6
figure 6

a–e Comportment of \(M\) and \(\varphi\) on \(g{'}\)

Full size image
Fig. 7
figure 7

a–e Variation of \(\varphi\) and M on \(g{'}\)

Full size image

4.2 Comparison in the Context of the Temperature Field

The efficiency of several Prandtl and Eckert numbers on the impact of thermal energy by employing different nanoparticle shapes including the two types of \(\mathrm{Cu}+{\mathrm{TiO}}_{2}/{\mathrm{H}}_{2}\mathrm{O}\) hybrid nanofluids refers to Fig. 8a–e, Fig. 9, Fig. 10, and Fig. 11a–e. The following figures show predictions of Prandtl number with different forms of nanoparticles in the presence of \(\mathrm{Cu}+{\mathrm{TiO}}_{2}/{\mathrm{H}}_{2}\mathrm{O}\) hybrid nanofluids. The Prandtl number impacts thermal efficiency by introducing various types of hybrid nanoparticles, like suspensions of \(\mathrm{Cu}+{\mathrm{TiO}}_{2}/{\mathrm{H}}_{2}\mathrm{O}\), and the results show that heat production is lowered as a result of raising the amount of the Prandtl number. Figure 8a–e, Fig. 9, Fig. 10, and Fig. 11a–e use nanoparticles in different forms to show how heat is transferred when \(\mathrm{Cu}+{\mathrm{TiO}}_{2}/{\mathrm{H}}_{2}\mathrm{O}\) hybrid nanoparticles are present. Eckert’s number is shown to minimize heat energy in the condition of nanoparticles with the different forms in these graphs. When compared to the case of copper hybrid nanoparticles, the effect of titanium dioxide hybrid nanoparticles under the action with the different shapes of nanoparticles has a greater reducing effect on the layers of thermal boundary. Additionally, it is shown that \(Ec\) has an inverse relationship to heat energy dissipation. Greater amounts of Ec thus produce less heat energy.

Fig. 8
figure 8

a–e Impact of \(Ec\) and \(Pr\) on \(\theta\)

Full size image
Fig. 9
figure 9

a–e Impact of \(Ec\) and \(Pr\) on \(\theta\)

Full size image
Fig. 10
figure 10

a–e Effect of \(Rd\) and \(\lambda\) on \(\theta\)

Full size image
Fig. 11
figure 11

a–e Effect of \(Rd\) and \(\lambda\) on \(\theta\)

Full size image

Figure 10a–e and Fig. 11a–e illustrate the effects of thermal radiation and heat generation. The larger temperature was caused by the greater radiation and heat generation. The substance collects larger amounts of energy as a result of increasing radiation and heat generation, which causes the temperature to rise.

4.3 Analysis of Entropy Generation

The fluctuation in \(NG\) by temperature difference parameter \(A\) can be observed in Fig. 12a. Here, a rising impact is shown. The consequence of \(Br\) on the entropy \(NG\) can be observed in Fig. 12b. The entropy rate increases in this situation, in contrast to greater Brinkman number estimates. Actually, \(Br\) is the source of heat generated within the fluid-moving area. Entropy is boosted by the heat produced and the heat transmitted through the wall. Because of the lower heat conductivity allowed by the greater Brinkman number, \(NG\) is enhanced. The relationship between \(Ec\) and \(NG\) is shown in Fig. 12c, which shows that when \(Ec\) rises, entropy formation accelerates. The impact of \(M\) on \(NG\) can be observed in Fig. 12d. Entropy production rates increase with increasing magnetic parameter \(M\) estimations. A higher magnetic parameter effect causes an increase in the Lorentz force, which in essence raises temperature by increasing the impedance of thin film fluid motion. As seen in Fig. 12d, this increases the wall’s thermal transfer efficiency. Figure 12e illustrates the evolution of entropy for \(Pr\), showing how increasing the \(Pr\) number causes the flow field’s entropy to increase. The influence of \(Rd\) on entropy is illustrated in Fig. 12f. The Reynolds number is utilized in Fig. 12g to show how the entropy profile fluctuates. \(NG\) increases when \(Re\) rises. Physically, a higher Reynolds number causes its inertial force to raise the viscous force, which increases the fluid’s movement disturbance and encourages the development of more entropy. Consequently, the influence of heat transfer causes entropy to grow.

Fig. 12
figure 12

a–g Evolution \(A, Br, Ec, M, Pr, Rd, Re\) on \(NG\)

Full size image

5 Conclusion

Under the influence of two distinct kinds of nanoparticles known as copper and titanium dioxide hybrid nanofluids, thermal energy transfer in a Newtonian fluid past a melting 3D surface and Cattaneo-Christov double diffusion with different forms of nanoparticles is addressed, and the formation of model is solved using OHAM. Here is an overview of the main points of the analysis that was shown:

  • When the Lorentz force is high, the momentum of the walls dissipates gradually.

  • Compared to an increase in the stretching ratio number \((c)\), wall momentum occurs less widely.

  • As volume friction increases (\(\varphi\)), weak velocity is produced.

  • Thermal layer thickness and temperature are on the decline, as shown by a rise in the Prandtl number \((Pr)\).

  • The highest level of heat energy is produced due to the elevated Eckert number \((Ec)\).

  • Thermal radiation \((Rd)\) and heat absorption \((\lambda )\) both affect how temperatures are distributed.

  • Entropy optimisation was strengthened by the greater Reynolds number value.

  • Higher levels of the magnetic parameter, the Brinkman number, thermal radiation, Eckert number, and the Reynolds number result in an increase in entropy generation.