Dynamics of shape factor with Joule heating and thermal stratification on magnetohydrodynamic ${\mathbf{A}\mathbf{l}}_{2}{\mathbf{O}}_{3}-\mathbf{C}\mathbf{u}-\mathbf{T}\mathbf{i}{\mathbf{O}}_{2}/{\mathbf{H}}_{2}\mathbf{O}$ nanofluid of stretching disk: an irreversibility analysis

Abstract

There is great potential for improving the efficiency and sustainability of many industrial processes, including advanced cooling systems and aerospace applications, by understanding the dynamics of shape factor in magnetohydrodynamic (MHD) ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ nanofluid on a stretching disk as a function of Joule heating and thermal stratification. Given the aforementioned applications, the primary aim of the present study is to examine the entropy analysis pertaining to the hydromagnetic radiative stagnation point flow of a ternary nanofluid. This flow is facilitated by a stretching disk that possesses various characteristics, including shape factor, variable viscosity, thermal stratification, viscous dissipation, mass suction, and joule heating. We used suitable transformations to turn a set of linked partial differential equations (PDEs) into a system of ordinary differential equations to simplify the computations. The bvp4c solver solved these altered equations numerically. Our results were almost identical to prior findings in particular circumstances, with a relative error of 0%. Visualizations showed velocity, temperature, entropy production, Bejan number, skin friction, and the Nusselt number. Velocity profile decreases and temperature profile increases for variable viscosity parameter. Higher Eckert number and radiation parameter values boost thermal profiles, according to our research. Temperature distribution decreased as magnetic and suction parameters increased. Both the Eckert number and the thermal stratification parameter have a negative correlation with the Nusselt number. Compared to conventional fluids, nanofluids enhance the Nusselt number of nanofluids by roughly 10.2%, hybrid nanofluids by around 19.8%, and ternary hybrid nanofluids by about 38.05% when the parameter $S$ is set from 2.0 to 2.4 with nanoparticles of 0.01. Nanoparticle volume fraction, Eckert number, and Brinkmann all contribute to an increase in entropy production and a drop in the Bejan number. Radiation also helps with Bejan and entropy.

Introduction

According to the idea that was put forward by Choi [1], the formation of a nanofluid is defined as the addition of nanoparticles, whether they are metallic or non-metallic, into a carrier or base fluid such as blood, motor oil, ethylene glycol, or water. Nanofluids have received a lot of attention in recent years due to the many ways in which they may be useful and their wide range of applications [2,3,4]. As a result, they are having an impact on a wide range of technical fields, such as industrial production, scientific research, and different engineering disciplines. In this context, a limited number of illustrations can be provided, encompassing advanced cryopreservation methods, fuel synthesis, contemporary approaches to pharmaceutical administration, a variety of sophisticated machinery and apparatus, the realm of nanofabrication, and the effective thermal regulation and energy optimization of various electronic circuits. After these notable findings, there has been a significant body of study undertaken globally about energy transportation and the features of its flow. Numerous endeavors have been undertaken by researchers to augment convective heat transfer in liquid mediums. This has been accomplished by the incorporation of nanomaterials, including ${\text{Cu}},\mathrm{ Ag},\mathrm{ Si}{{\text{O}}}_{2}, {{\text{Fe}}}_{3}{{\text{O}}}_{4}, {{\text{Al}}}_{2}{{\text{O}}}_{3},\mathrm{ Ti}{{\text{O}}}_{2},\mathrm{ CNTs},$ graphene, and several other solid substances, into routinely used base fluids such as kerosene oil, ${{\text{H}}}_{2}{\text{O}}$, ${{\text{CH}}}_{3}{\text{OH}}$, blood, ${{\text{C}}}_{2}{{\text{H}}}_{6}{{\text{O}}}_{2}$, and countless additional mediums [5, 6]. Various categories of nanofluids have been shown to augment the thermal conductivity of host fluids, thereby exerting a substantial influence on the efficiency of heat transfer [7, 8]. The investigation of nanofluid flow in many practical geometries has been extensively pursued by different researchers, owing to the extensive range of applications associated with this phenomenon [9]. The study conducted by Das et al. [10] focuses on the investigation of entropy formation in the boundary layer of a nanofluid consisting of water and different nanoparticles, including copper (${\text{Cu}}$), aluminum oxide (${{\text{Al}}}_{2}{{\text{O}}}_{3}$), and titanium dioxide (${{\text{TiO}}}_{2}$). The present study investigates the behavior of a nanofluid as it flows across a radially stretched disk located inside a porous medium. The analysis considers the convective boundary conditions. Tshivhi and Makinde [11] conducted a study to examine the impact of a magnetic field on the augmentation of heat transfer in nanofluid-based coolants, specifically focusing on ${\text{Cu}}-{{\text{H}}}_{2}{\text{O}}$ water, ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{{\text{H}}}_{2}{\text{O}}$, and ${{\text{Fe}}}_{3}{{\text{O}}}_{4}-{{\text{H}}}_{2}{\text{O}}$. The researchers undertake their investigation on surfaces that experience simultaneous shrinkage and expansion, coupled with convective heating and lubrication. The work conducted by Mahmood et al. [12] seeks to examine the production of entropy in a viscous nanofluid composed of ${{\text{TiO}}}_{2}$ and ${{\text{C}}}_{2}{{\text{H}}}_{6}{{\text{O}}}_{2}$ as it passes through a permeably exponentially extending surface situated in a porous medium. The objective of the research by Abdelsalam et al. [13] is to examine the characteristics of a non-Newtonian nanofluid induced by peristaltic waves in an asymmetrical channel. There has been a deluge of recent publications [14,15,16] detailing the experimental and computational enhancement of heat transport via the use of different nanofluids.

An additional aspect within the domain of nanofluids pertains to the development of hybrid nanofluids. A hybrid nanofluid is the name given to the situation in which two distinct kinds of nanoparticles are mixed together inside a single carrier fluid. Recent years have seen a rise in the amount of focus placed by researchers on the study of hybrid nanofluid flow. This may be attributed to the exceptional properties that this phenomenon has. By using hybrid nanofluid flows, which provide both advantages simultaneously, it is possible to enhance both the chemical and the physical features of the materials being worked with. When contrasted with binary nanofluids, the boost in heat transfer rates that was observed by hybrid nanofluids was much more efficient. This is principally attributable to their greater thermal conductivities as well as their flexibility to be customized in accordance with certain requirements. These fluids are useful in a wide variety of fields, including engineering and the medical sciences, among others. Using the bvp4c solver that is included in the MATLAB programmed, Waini and colleagues [17] investigated the flow of hybrid nano-liquids across a stretched surface. A computational examination of the dynamics of a hybrid nanofluid, namely ${\text{Cu}}-{{\text{Al}}}_{2}{{\text{O}}}_{3}/{{\text{H}}}_{2}{\text{O}}$, was carried out by Khan and associates [18] across a fascinating domain comprising a porous wedge that either extends or shrinks. The application of numerical simulation to the study of the flow and thermal properties of an ${\text{Cu}}-{{\text{Al}}}_{2}{{\text{O}}}_{3}/{{\text{H}}}_{2}{\text{O}}$ hybrid nanofluid caused by the convective heating of a disk surface is the primary purpose of the research carried out by Ali and his colleagues [19]. The shooting procedure was used by Sulochana and Prasanna Kumar [20] in order to obtain data about the motion of a hybrid nanofluid boundary layer over a stretched surface. The finite element approach was used for the purpose of analyzing Bouslimi and colleagues' [21] investigation of the motion of the Sutterby hybrid nanofluid. The findings that Bilal and his co-authors [22] achieved by using the shooting approach to study the flow of hybrid nanofluids inside circular cylindrical microchannels were reported. The mobility of a hybrid nanofluid over a flat plate was investigated by Alzahrani and colleagues [23] using the homotopy approach. Ramzan and colleagues [24] developed solutions for the transportation of hybrid nanofluids between two spinning disks by employing the bvp4c approach. The motion of hybrid nanofluids was the subject of an in-depth study that was carried out by Saleem and co-authors [25]. The fundamental purpose of the research that was carried out by Rafique and his colleagues [26] was to investigate the flow properties of a 3D hybrid nanofluid moving over a stretched surface while taking into consideration different levels of the fluid's viscosity. Research by Abdelsalam and Bhatti [27] tracks how nano-diamonds and silica nanoparticles behave in a hybrid model of a nanofluidic system. There are three different forms of catheterized tapered arteries that the nanofluid may go through: converging tapered, non-tapered, and diverging tapered. Hybrid nanofluid models with various geometries were investigated by researchers [28,29,30].

Recent research efforts in hybrid nanofluids have been concentrated on the development of further improvements. Researchers have developed a whole new kind of nanofluid by combining three distinct types of nanoparticles with the base fluid. This new form of nanofluid has been properly named ternary hybrid nanofluids. Researchers in the modern day are showing a significant amount of interest in these ternary hybrid nanofluids due to the increased thermophysical characteristics that they possess. Ternary hybrid nanofluids, in comparison to binary and hybrid nanofluids, offer improved heat transfer properties. Researchers have shown a significant interest in investigating the flow behavior of ternary hybrid nanofluids, and as a result, research has been initiated over an extremely broad spectrum of situations and settings. The movement of ternary nanofluids across a sliding surface was investigated in work carried out by Rafique and colleagues [31]. The Runge–Kutta–Fehlberg approach was used by Goud and his colleagues [32] in order to investigate the motion of ternary hybrid nanofluids contained inside a dovetail fin. Researchers led by Mahmood and his colleagues [33] investigated the effect of heat production and absorption as well as mass suction on the magnetohydrodynamic (MHD) stagnation point flow over a nonlinearly stretching and contracting sheet that was covered with a tri-hybrid nanofluid that included water. Using finite element analysis, Sohail and co-authors [34] developed a computer method to investigate the motion of a ternary hybrid nanofluid that was caused by a stretching sheet. The study undertaken by Mahmood et al. [35] examines the practical applications of a ternary hybrid nanofluid, namely ${\text{Cu}}-{{\text{Fe}}}_{3}{{\text{O}}}_{4}-{{\text{SiO}}}_{2}/{\text{SA}}$, in real-world scenarios. This research investigates the behavior of fluid flow inside a stagnation area on a curved surface that is subjected to either stretching or shrinking. The analysis considers the effects of suction and the Lorentz force. Therefore, Mishra et al. [36] conducted a comprehensive analysis, drawing inspiration from the intrinsic characteristics of the base fluid and the ternary nanoparticles (${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{CuO}}-{\text{Cu}}$). The present study entails a thorough examination of a cylindrical object characterized by a non-uniform radius, with particular emphasis placed on identifying and analyzing saddle and nodal points. The proposed model combines several important aspects, including dissipation, first-order thermal slip, surface convection, and stretching and shrinking effects.

Stagnation point flow can be used in several ways in aerodynamics and other fields. When fluid moves close to the area where a stiff surface has stopped moving, these kinds of flows tend to slow down. This is true whether the fluid is moving through the substance or is being stopped by the fluid's dynamic properties. Researchers have studied stagnation point for a long time because it has so many uses in engineering. For example, fans can be used to cool down electronics, nuclear reactors can be cooled, and many other engineering processes use hydrodynamics. The stagnation point flow is an important concept in the physical world because it can be used to calculate the velocity gradients and the rate of heat and mass transfer in the vicinity of the stagnation area of frames in high-speed flows [37]. It is also used to find out how to keep bearings from rusting and how to cool sweat. Recently, Borrelli et al. [38] recently talked about how buoyancy affects flow at a stagnation point in three dimensions (3D). They said that buoyancy tends to push water in a different direction. Islam et al. [39] have conducted a study on the properties of an unstable double-diffusive mixed convection flow of nanofluids in the boundary layer next to a vertical area at the stagnation point. The study undertaken by Tadesse et al. [40] focuses on the examination of a two-dimensional magnetohydrodynamic stagnation point flow of magnetite ferrofluid. The flow under consideration takes place in a Darcy–Forchheimer porous medium where a stretching or shrinking sheet is present. Various effects, including viscous dissipation, suction or injection, and convective heating, are considered in this analysis. The research conducted by Khan et al. [41] investigates the phenomenon of oblique hydromagnetic stagnation point flow. The present study investigates a flow configuration that encompasses a nanofluid exhibiting variable viscosity, possessing both electrical conductivity and optical density, and flowing over an incompressible viscous medium. The medium is subject to convective heating, and the study incorporates the impact of thermal radiation.

Nanofluids that demonstrate the effects of magnetohydrodynamics (MHD) have been acknowledged for their capacity to control fluid flow and improve the energy efficiency of electrically conductive liquids. Moreover, when confronted with very high temperatures, the influence of thermally nonlinear radiation outweighs that of thermally linear radiation, highlighting its crucial contribution to the thermal characteristics of the generated materials. In the manufacturing industries, it's important to have fluids that are heated by an electric current in presence of a strong magnetic field, like when crystals grow when they melt. The Lorentz forces move in different directions when an electric current and a magnetic field work together. This effect stops fluids from moving in a way called convection, which changes how heat moves. Ariel [42] numerically studied the flow near the point where it stops moving numerically when the magnetic field is small. The perturbation method was used when the magnetic field was strong. Raju and Sundeep [43] showed that as the magnetic number goes up, so does the rate of heat and mass transfer. They investigated the magnetohydrodynamic (MHD) flow of a non-Newtonian fluid through a rotating plate by using computational methods. Khan et al. [44] were the first to offer the innovative notion of activation energy of MHD convectional movement over a stretchy surface consisting of nonlinearly thermal radiations. They did this by employing numerical simulations to illustrate their findings. Narayana et al. [45] took into consideration influence of thermal radiations, in addition to the numerical findings of MHD pair stress Casson nanofluid over an extended sheet. Gangadhar et al. [46] use a novel spectral relaxation technique to investigate the characteristics of an axisymmetric, stable, and laminar boundary layer flow in their study. The present study investigates heat transmission processes across a heated disk using a viscous, incompressible, non-Newtonian Eyring-Powell fluid. The study considers many parameters, including thermal radiation and Newtonian heating. Elkoumy et al. [47] examine the effects of a continuous transverse magnetic field on the flow of an electrically conducting Maxwell fluid in a two-dimensional channel with porous walls.

A fluid's thickness, often known as its viscosity, is crucial when discussing its velocity and the transfer of heat through it. It has been assumed in several studies that this thickness remains constant. However, one thing that may truly change things is the temperature. When the temperature rises, the fluid's viscosity decreases as it is suspended in a momentum barrier layer. Heat is accelerated along the wall as a result of this switcheroo. When gases are heated, they indeed thicken, but liquids. On the other side, they lose mass. Thus, the relationship between a fluid's thickness and its expansion with heat is quite close. In their study, Seddeek and Salama [48] explored the effects of changing the viscosity as well as the thermal conductivity of an incompressible, viscous, and conductive fluid that was flowing in a two-dimensional unstable laminar flow. Soman et al. [49] examined heat transport, nanofluids, and ionic liquid viscosity. In this study, Gbadeyan and colleagues [50] investigated the effects of temperature convection and velocity slip on the nanofluid flow's thickness and heat-carrying capacity. Hussain and colleagues [51] investigated the mixed convection currents of nanofluids, with a special emphasis on the variation of their viscosity. The boundary layer flow, heat and mass transport in electrically conductive nanofluids, and the effects of various external factors such as magnetic fields, thermal radiation, and changing viscosity were studied by Makinde and colleagues [52]. The new focal point of this investigation is to study how a nanofluid acts when flowing across a surface subjected to convective heating and radial stretching.

Thermal stratification is one of the most important and natural process that can happen. This is because the different layers have different amounts of matter in them. Due to change in temperature, molecules with high densities may cluster at bottom of surface, whereas molecules with low densities may rise to the top. This can happen when the temperature of a material changes and the density of the material changes. Convective flow in a fluid with different layers of temperatures is a big problem. This kind of flow happens in many places, from business and industry to climate and weather and more. The fact that this kind of flow happens in such a wide variety of contexts is the key to understanding the relevance of this issue. When there is a difference in the densities of the different layers of water, a process known as stratification will take place. In this scenario, there are a lot of different things to consider. When it comes to determining whether one volume of water will float on top of another volume of water, the density of the water is one of the most important factors to take into account. All fluids that are confined by walls that are heated in different ways create a thermal stratification. Both theoretical and practical scientists have been devoting a growing portion of their time and energy over the course of the last several decades to the investigation of the thermodynamics of heat and mass transport in thermally stratified fluids. Thermal stratification in vertically stratified environments is usually induced by temperature variations or variable fluid densities, according to Moorthy and Senthil [53]. Takhar and Pop [54] looked at free convection from a vertical plate that was submerged in a porous medium with different layers of temperatures. In line with the idea of boundary layer, they used vertical plate that was submerged in medium. Tiwari and Singh [55] undertook research to explore the phenomenon of natural convection inside a thermally stratified fluid with the intention of acquiring better knowledge of the underlying processes that are at play in this phenomenon.

The dissipation of thermal energy during irreversible processes often links to the formation of entropy. This loss is caused by several factors, such as molecule collisions, molecular vibration, kinetic energy, and spin moments. These factors result in fluctuations in isolated, closed systems and the generation of entropy. The notion of entropy generation is of great importance in the domains of bioengineering and business. Mburu et al. [56] scrutinized the consequences of chemical reactions, entropy generation, and magnetic fields due to nanofluids' motion around an inclined cylinder. The Buongiorno model has been chosen for the analysis. There was research carried out by Acharya and colleagues [57] that demonstrated the performance of heat transfer and entropy formation in a regenerative cooling channel of a rocket engine. Mahmood et al. [58] presented a study to show the generation of entropy through a porous surface made with ${{\text{TiO}}}_{2}/{{\text{C}}}_{2}{{\text{H}}}_{6}{{\text{O}}}_{2}$ by a nanofluid. An examination of the entropy production of a ${\text{Cu}}-{{\text{Al}}}_{2}{{\text{O}}}_{3}/$ EG hybrid nanofluid in a rotating channel shows that heightened entropy generation is seen with the application of a greater magnetic field. The presence of a magnetic field leads to increased resistance, leading to higher levels of Joule heating inside the system Das et al. [59]. In a separate investigation centered on non-Newtonian Carreau hybrid nanofluid, the researchers noted that the use of a hybrid nanoparticle system resulted in a greater generation of entropy in comparison to a system using a single nanomaterial Naganthran et al. [60]. Ghali et al. [61] conducted more research on the investigation of entropy in hybrid nanofluids, therefore enhancing the comprehension of this intricate phenomenon.

An exhaustive analysis of the aforementioned literature is only feasible to a restricted degree. The scientific literature currently lacks an examination of the creation of entropy and heat transmission in magnetohydrodynamic (MHD) stagnation point flow in Al₂O₃–Cu-TiO₂/H₂O, as shown by the existing research. The objective of this study is to develop a computational model by conducting a numerical analysis of heat transfer, entropy generation, and the Bejan number of a magnetohydrodynamic (MHD) ternary hybrid nanofluid. The model will take into account various factors such as shape factor, variable viscosity, thermal radiation, viscous dissipation, joule heating, and thermal stratification over a stretching disk. This study examines the nanoparticles Al₂O₃, Cu, and TiO₂ in conjunction with a base fluid of water. The engineering applications of each nanoparticle, namely Al₂O₃, Cu, and TiO₂, exhibit distinct characteristics and benefits across many engineering domains. Al₂O₃ nanoparticles possess exceptional thermal conductivity and stability, rendering them well-suited for augmenting heat transfer in nanofluids. Copper nanoparticles possess exceptional thermal and electrical conductivity, making them very advantageous for applications in electronic and thermal control. The photocatalytic capabilities and stability of titanium dioxide (TiO₂) nanoparticles have been well recognized, making them suitable for many applications such as solar energy harvesting and self-cleaning surfaces. Furthermore, appropriate methods transform the governing partial differential equations (PDEs) to simplify them into a dimensionless system. The LNS methodology is used to get the solution to the changed system using the bvp4c method. Graphs and tables depict the results. This contribution has the potential to boost industrial productivity, especially in areas such as the industrial and process sectors. The major aim of this study is to get a deeper understanding of the flow properties of tri-hybrid nanofluids, which have potential applications in several industrial and medical fields. The findings of this study might potentially be used to enhance thermal processes by optimizing the utilization of material assets, such as heat pumps and refrigerants, in order to achieve maximum efficiency. The plan is to proceed as follows:

• Stimulate thermally stratified MHD stagnation point flow across a stretching disk.

• Find out how each factor affects the profiles in its own way.

• Find out how thermal stratification and thermal radiation affect the heat transfer.

• The impact of variable viscosity is studied to accurately predict the flow and heat transfer rate.

• The shape factor of nanoparticles for engineering parameters is considered for velocity, temperature, skin friction, Nusselt number, Bejan number, and entropy generation profiles.

• The impact of nanoparticles, Brinkmann, Eckert number, thermal radiation, Reynold number, and magnetic parameters on the entropy generation and Bejan number profiles is analyzed.

Problem formulation

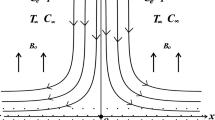
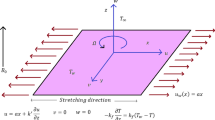
The research that is being presented here looks at steady flow of a ternary hybrid nanofluid in two dimensions while considering an incompressible MHD stagnation point flow. This nanofluid is made by mixing ${{\text{Al}}}_{2}{{\text{O}}}_{3},{\text{Cu}},$ and ${{\text{TiO}}}_{2}$ into a base fluid of water. Figure 1 is a diagram that shows what a flow situation looks like. Here, we use cylindrical polar coordinates $\left(z,r\right),$ where $z$ is axial length and $r$ is radial length synchronized along flow direction to calculate the mass suction velocity ${u}_{{\text{w}}}$, and the radius of a stretched permeable disk is denoted as $a$. Also, it is assumed that velocity of mass transfer is ${u}_{{\text{w}}}=-ar$, and ${B}_{0}$ is used to show how strong the magnetic field is. The flow is symmetric about the plane defined by $z=0$ and axisymmetric about $z-$ axis, with stagnation line at $z=0$ and $r=a.$ Also, velocity of mass flow is ${w}_{{\text{w}}}\left(r\right)$, where ${w}_{{\text{w}}}\left(r\right)>0$ for injection and ${w}_{{\text{w}}}\left(r\right)<0$ for suction. ${u}_{{\text{e}}}\left(r\right)=br$ shows the free stream's velocity. The constant wall surface temperature, ${T}_{{\text{w}}}={T}_{0}+B\left(r/L\right)$ and the constant air temperature, ${T}_{\infty }={T}_{0}+A\left(r/L\right), {T}_{0}$ is initial ambient temperature. In addition, there are several other assumptions linked to physical model that are examined and analyzed. Some of these other assumptions are as follows:

• The flow is laminar.

• This model does not consider other phenomena’s such as thermal radiation or the hall effect. Those are just a few examples.

• Both base fluid and nanoparticles have their temperatures controlled in such a way that they remain in a state of thermal equilibrium. This can be achieved by ensuring that the temperature of the base fluid is kept constant.

• Viscous dissipation, thermal radiation, and joule heating are also considered.

• The disk was designed to have a permeable surface on purpose so that it would be easier to perform the operation of fluid suction.

• Entropy generation and Bejan number are analyzed.

• Shape factor effect is considered.

Fig. 1

The physical model being examined in this investigation

This is how the equations can be used to describe flow of ternary hybrid nanofluid: ([31]).

Law of conservation of mass:

$$ \frac{{\partial \left( {ru} \right)}}{\partial r} + \frac{{\partial \left( {rw} \right)}}{\partial z} = 0, $$

(1)

Law of momentum conservation is as follows:

$$ u\frac{\partial u}{{\partial r}} + w\frac{\partial u}{{\partial z}} = u_{{\text{e}}} \frac{{{\text{d}}u_{{\text{e}}} }}{{{\text{d}}r}} + \frac{1}{{\rho_{{{\text{mnf}}}} }}\left[ {\frac{{\partial \mu_{{{\text{mnf}}}} \left( T \right)}}{\partial z}\frac{\partial u}{{\partial z}} + \mu_{{{\text{mnf}}}} \left( T \right)\left( {\frac{{\partial^{2} u}}{{\partial z^{2} }}} \right)} \right] - \frac{{\sigma_{{{\text{mnf}}}} }}{{\rho_{{{\text{mnf}}}} }}B_{0}^{2} \left( {u - u_{{\text{e}}} } \right), $$

(2)

The principle of the energy conservation:

$$ w\frac{\partial T}{{\partial z}} + u\frac{\partial T}{{\partial r}} = \frac{{k_{{{\text{mnf}}}} }}{{\left( {\rho C_{\text{p}} } \right)_{{{\text{mnf}}}} }}\left( {\frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) + \frac{{\mu_{{{\text{mnf}}}} \left( T \right)}}{{\left( {\rho C_{\text{p}} } \right)_{{{\text{mnf}}}} }}\left( {\frac{\partial u}{{\partial z}}} \right)^{2} + \frac{{\sigma_{{{\text{mnf}}}} }}{{\left( {\rho C_{\text{p}} } \right)_{{{\text{mnf}}}} }}B_{0}^{2} \left( {u - u_{{\text{e}}} } \right)^{2} - \frac{1}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{mnf}}}} }}\left( {\frac{{\partial q_{{\text{r}}} }}{\partial z}} \right). $$

(3)

$u$ and $w$ each represent component of velocity that is associated with $r$- and $z$-directions. After this, boundary conditions are as follows [31, 62]:

$$ \begin{gathered} u = u_{{\text{w}}} \left( r \right) = ar,w = w_{{\text{w}}} \left( r \right), T = T_{{\text{w}}} \;{\text{at}}\;z = 0, \hfill \\ u \to u_{{\text{e}}} \left( r \right) \to br, T \to T_{\infty } ,\;{\text{as}}\;z \to \infty \hfill \\ \end{gathered} $$

(4)

The symbols $T$, ${\mu }_{{\text{mnf}}},$ ${\rho }_{{\text{mnf}}}$, ${k}_{{\text{mnf}}}$ , and ${\left(\rho {C}_{{\text{p}}}\right)}_{{\text{mnf}}}$ represent temperatures, dynamic viscosities, densities, thermal conductivities, and heat capacities of ternary hybrid nanofluids, respectively.

Radiative heat flow, abbreviated as ${q}_{{\text{r}}}$, is determined by using the Roseland approximation to the following equation (see [63]):

$$ q_{{\text{r}}} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{4} }}{\partial z}, $$

(5)

The coefficient of mean absorption (${k}^{*}$) and the Stefan–Boltzmann constant (${\sigma }^{*}$) are denoted by these symbols, respectively. The fundamental assumption of our work is that the temperature variation inside the flow is negligible. The quantity ${T}^{4}$ arises from the expansion of the equation ($T-{T}_{\infty }$) using the Taylor series method, while neglecting higher-order terms.

$${T}^{4}\approx 4{{T}^{3}}_{\infty }T-3{{T}^{3}}_{\infty }.$$

The following equation presents an elaborated version of the energy equation.

$$ w\frac{\partial T}{{\partial z}} + u\frac{\partial T}{{\partial r}} = \frac{{k_{{{\text{mnf}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{mnf}}}} }}\left( {\frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) + \frac{{\mu_{{{\text{mnf}}}} \left( T \right)}}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{mnf}}}} }}\left( {\frac{\partial u}{{\partial z}}} \right)^{2} + \frac{{\sigma_{{{\text{mnf}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{mnf}}}} }}B_{0}^{2} \left( {u - u_{{\text{e}}} } \right)^{2} + \frac{1}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{hnf}}}} }}\frac{{16\sigma^{*} T^{3}_{\infty } }}{{3k^{*} }}\frac{{\partial^{2} T}}{{\partial z^{2} }}. $$

(6)

Table 1 displays the characteristics of alumina ${{\text{Al}}}_{2}{{\text{O}}}_{3}$, titanium dioxide ${{\text{TiO}}}_{2}$, copper ${\text{Cu}}$, and water ${{\text{H}}}_{2}{\text{O}}$ as a base fluid, along with several additional thermophysical parameters. The correlation characteristics of a ternary hybrid nanofluid consisting of ${{\text{Al}}}_{2}{{\text{O}}}_{3},\mathrm{ Cu},\mathrm{ Ti}{{\text{O}}}_{2},{{\text{H}}}_{2}{\text{O}}$ are shown in Table 2. The empirical shape factor, denoted as $m$, is calculated as $m=3/\psi$, where $\psi$ represents the sphericity. The values of $\psi$ for nanoparticles of various shapes may be found in Table 3. In Table 2, $\phi ={\phi }_{1}+{\phi }_{2}+{\phi }_{3}.$ Table 4 also shows the effective viscosity relation values for non-spherical nanoparticles, which are ${A}_{1}$ and ${A}_{2}$.

Table 1 The quantitative properties of ternary hybrid nanoparticles in combination with water (see [31])

Table 2 The ternary hybrid nanofluid's temperature-related properties (see [31, 33])

Table 3 Form factors with sphericity of distinct nanoparticles [44, 45]

Table 4 Effective viscosity values for non-spherical nanoparticles, with respect to ${A}_{1}$ and ${A}_{2}$ [44, 45]

When doing these computations, it is crucial to consider many factors. One of the variables under consideration is denoted as ${\mu }_{{\text{f}}}(T)$, representing the viscosity coefficient. It is established that this coefficient exhibits an inverse relationship with temperature, as follows (see [63]):

$$ \frac{1}{{\mu_{{\text{f}}} \left( T \right)}} = \frac{1}{{\mu_{{{\text{f}}_{\infty } }} }}\left[ {\varepsilon \left( {T - T_{\infty } } \right) + 1} \right]\;{\text{i.e.}},\;\frac{1}{{\mu_{{\text{f}}} }} = \left( {T - T_{r} } \right)a, $$

(7)

here,

$$ a = \frac{\varepsilon }{{\mu_{{{\text{f}}_{\infty } }} }},T_{{\text{r}}} = - \frac{1}{\varepsilon } + T_{\infty } $$

Choosing appropriate reference temperatures for correlations may be helpful in a number of real-world contexts. In the present context, the variables ' $a$' and '${T}_{\text{r}}$' are considered constants, with their specific values determined by the thermal characteristics of the fluid and the reference location, indicated as '$\epsilon$,' which is likewise a constant. In the case of liquids, the value of ' $a$' is positive, whereas for gases, the value of '$a$' is negative. The variable '$T$' is used to signify the temperature, while the constants ${T}_{\infty }$ and ${\mu }_{{f}_{\infty }}$ represent the viscosity coefficient and temperature, respectively, at locations that are far from the surface.

Non-similarity analysis

By using the non-similarity variables, a non-similar solution for a ternary hybrid nanofluid flow system may be found (see ref [31, 62]):

$$ u = brf^{\prime}\left( {\xi ,\eta } \right),\;w = - 2\sqrt {b\nu_{{\text{f}}} } f\left( {\xi ,\eta } \right), \;\theta \left( {\xi ,\eta } \right) = \frac{{T - T_{\infty } }}{{T_{{\text{w}}} - T_{\infty } }},\;\eta = \sqrt {\frac{b}{{\nu_{{\text{f}}} }}} z,\;\xi = \frac{x}{l} $$

(8)

Using (8), we obtained the following:

$$ \frac{{\mu_{{{\text{mnf}}}} /\mu_{{\text{f}}} }}{{\rho_{{{\text{mnf}}}} /\rho_{{\text{f}}} }}\frac{1}{{\left( {1 - \frac{\theta }{{\theta_{{\text{r}}} }}} \right)}}\frac{{\partial^{3} f}}{{\partial \eta^{3} }} + \frac{1}{{\theta_{{\text{r}}} \left( {1 - \frac{\theta }{{\theta_{{\text{r}}} }}} \right)^{2} }}\left( {\frac{\partial \theta }{{\partial \eta }}\frac{{\partial^{2} f}}{{\partial \eta^{2} }}} \right) + 2f\frac{{\partial^{2} f}}{{\partial \eta^{2} }} + 1 - \left( {\frac{\partial f}{{\partial \eta }}} \right)^{2} - \frac{{\sigma_{{{\text{mnf}}}} /\sigma_{{\text{f}}} }}{{\rho_{{{\text{mnf}}}} /\rho_{{\text{f}}} }}M\left( {\frac{\partial f}{{\partial \eta }} - 1} \right) = \xi \left( {\frac{\partial f}{{\partial \eta }}\frac{{\partial^{2} f}}{\partial \eta \partial \xi }} \right), $$

(9)

$$ \begin{aligned} & \frac{1}{{Pr_{{\text{f}}} \left( T \right)}}\left[ {\left\{ {\frac{{k_{{{\text{mnf}}}} }}{{k_{{\text{f}}} }} + \frac{4}{3}Rd} \right\}\frac{{\partial^{2} \theta }}{{\partial \eta^{2} }}} \right] + \frac{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{mnf}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}\left[ {f\frac{\partial \theta }{{\partial \eta }} - \theta \frac{\partial f}{{\partial \eta }} + \frac{{\mu_{{{\text{mnf}}}} }}{{\mu_{{\text{f}}} }}\frac{1}{{\left( {1 - \frac{\theta }{{\theta_{{\text{r}}} }}} \right)}}Ec\xi^{2} \left( {\frac{{\partial^{2} f}}{{\partial \eta^{2} }}} \right)^{2} + } \right. \\ \left. {\;\;\;\;2MEc\xi \frac{{\sigma_{{{\text{mnf}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{mnf}}}} }}\left( {f^{\prime} - 1} \right)^{2} } \right] = \frac{{\left( {\rho C_{p} } \right)_{{{\text{mnf}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}Pr_{{\text{f}}} \left( T \right)\left( {1 - \frac{\theta }{{\theta_{{\text{r}}} }}} \right)\frac{{k_{{\text{f}}} }}{{\mu_{{{\text{mnf}}}} \left( T \right)C_{{\text{p}}} }}\xi \left( {\frac{\partial f}{{\partial \eta }}\frac{\partial \theta }{{\partial \xi }}} \right) \\ \end{aligned} $$

(10)

Changes made to the boundary conditions (4) to become.

$$ \begin{gathered} f\left( {\xi ,0} \right) = S, \frac{\partial f}{{\partial \eta }}\left( {\xi ,0} \right) = \lambda , \theta \left( {\xi ,0} \right) = 1 - \delta , \hfill \\ \frac{\partial f}{{\partial \eta }}\left( {\xi ,\eta } \right) \to 1, \theta \left( {\xi ,\eta } \right) \to 0, as \eta \to \infty . \hfill \\ \end{gathered} $$

(11)

In the preceding equations, variable Prandtl number: The variable Prandtl number is defined as a result of the variations in viscosity throughout the boundary layer. ${Pr}_{{\text{f}}}\left(T\right)=\frac{{\mu }_{{\text{mnf}}}(T){C}_{{\text{p}}}}{{k}_{{\text{f}}}}=\frac{\left(\frac{{\theta }_{{\text{r}}}-\theta }{{\theta }_{{\text{r}}}}\right){\mu }_{{\text{mnf}}}(T){C}_{{\text{p}}}}{{k}_{{\text{f}}}},$ so we get, ${Pr}_{{\text{f}}}={Pr}_{{\text{f}}}\left(T\right)\left(1-\frac{\theta }{{\theta }_{{\text{r}}}}\right)\frac{{k}_{f}}{{\mu }_{{\text{mnf}}}(T){C}_{{\text{p}}}}.$ So applying this in Eq. (10), we get,

$$\left[\left\{\frac{{k}_{{\text{mnf}}}}{{k}_{{\text{f}}}}+\frac{4}{3}Rd\right\}\frac{{\partial }^{2}\theta }{\partial {\eta }^{2}}\right]+\frac{{\left(\rho {C}_{{\text{p}}}\right)}_{{\text{mnf}}}}{{\left(\rho {C}_{{\text{p}}}\right)}_{{\text{f}}}}{{\text{Pr}}}_{{\text{f}}}\left(T\right)\left(1-\frac{\theta }{{\theta }_{{\text{r}}}}\right)\frac{{k}_{{\text{f}}}}{{\mu }_{{\text{mnf}}}(T){C}_{{\text{p}}}}\left[2f\frac{\partial \theta }{\partial \eta }-\theta \frac{\partial f}{\partial \eta }+\frac{{\mu }_{{\text{mnf}}}}{{\mu }_{{\text{f}}}}\frac{1}{\left(1-\frac{\theta }{{\theta }_{{\text{r}}}}\right)}Ec{\xi }^{2}{\left(\frac{{\partial }^{2}f}{\partial {\eta }^{2}}\right)}^{2}+{\text{MEc}}\xi \frac{{\sigma }_{{\text{mnf}}}}{{\left(\rho {C}_{p}\right)}_{{\text{mnf}}}}{\left({f}^{\mathrm{^{\prime}}}-1\right)}^{2}\right]=\frac{{\left(\rho {C}_{{\text{p}}}\right)}_{{\text{mnf}}}}{{\left(\rho {C}_{{\text{p}}}\right)}_{{\text{f}}}}{{\text{Pr}}}_{{\text{f}}}\left(T\right)\left(1-\frac{\theta }{{\theta }_{r}}\right)\frac{{k}_{{\text{f}}}}{{\mu }_{{\text{mnf}}}(T){C}_{{\text{p}}}}\xi \left(\frac{\partial f}{\partial \eta }\frac{\partial \theta }{\partial \xi }\right),$$

(12)

The stretching parameter, denoted as ${\lambda={a/b}}$, shows that a positive $\lambda$ value suggests the occurrence of stretching in the sheet. $M=\frac{{\sigma }_{{\text{f}}}{B}_{0}^{2}{b}^{2}}{{2\rho }_{{\text{f}}}}$ signifies magnetic parameter. Eckert number is ${\text{Ec}}=\frac{{b}^{2}}{\left({T}_{{\text{w}}}-{T}_{\infty }\right){\left({C}_{{\text{p}}}\right)}_{{\text{f}}}}$. ${\theta }_{{\text{r}}}=\frac{1}{\epsilon \left({T}_{{\text{w}}}-{T}_{\infty }\right)}$ is viscosity variation parameter. The symbol $\delta =\frac{A}{B}$ is used to denote the parameter associated with thermal stratification. Radiation parameter is ${\text{Rd}}=\frac{4{\sigma }^{*}{T}_{\infty }^{3}}{{k}^{*}{k}_{f}}$.

This inquiry demonstrates a strong interest in the friction coefficients (${C}_{{\text{f}}}$) and the local Nusselt number (${{\text{Nu}}}_{{\text{r}}}$), with a specific emphasis on the investigation's concentration on.

$$ C_{{\text{f}}} = \frac{2}{{\rho_{{\text{f}}} w_{{\text{e}}}^{2} }}\mu_{{{\text{mnf}}}} \left( T \right)\left( {\frac{\partial u}{{\partial z}}} \right)_{z = 0} ,{\text{Nu}}_{{\text{r}}} = - \frac{a}{{k_{{\text{f}}} \left( {T_{{\text{w}}} - T_{\infty } } \right)}}k_{{{\text{mnf}}}} \left( {\frac{\partial T}{{\partial r}}} \right)_{z = 0} + \left( {q_{r} } \right)_{z = 0} . $$

(13)

By using Eqs. (8) and (13), it is feasible to derive the following conclusions:

$$ \frac{1}{2}{\text{Re}}_{{\text{r}}}^{1/2} C_{{\text{f}}} = \frac{{\left( {1 - \phi_{3} } \right)^{ - 2.5} \left( {1 - \phi_{2} } \right)^{ - 2.5} \left( {1 - \phi_{1} } \right)^{ - 2.5} }}{{\left( {1 - \frac{\theta }{{\theta_{r} }}} \right)}}\frac{{\partial^{2} f}}{{\partial \eta^{2} }}\left( {\xi ,0} \right), {\text{Re}}_{{\text{r}}}^{ - 1/2} {\text{Nu}}_{{\text{r}}} = - 2\left\{ {\frac{{k_{{{\text{mnf}}}} }}{{k_{{\text{f}}} }} + \frac{4}{3}Rd} \right\}\frac{\partial \theta }{{\partial \eta }}\left( {\xi ,0} \right), $$

(14)

Local non-similar methods

For solving non-similarity boundary layers, local similarity is a common strategy. Based on my analysis, the $\xi \partial \left(.\right)/\partial \xi$ term in Eqs. (9), (11), and (12) is small enough to be estimated to zero. Assuming the structure of ODE's, the computational assignment is explained in (15)–(16). While the local similarity solution or initial extent of truncation may seem desirable from a computational standpoint, the accuracy of the results obtained by numerical analysis is questionable. This occurs when the right edge of the equation is unclear or undefined. Sparrow and Yu [64] used the local non-similarity approach to solve non-similar boundary layer equations and get the results, which helped them overcome these problems.

First level truncation

When $\xi \ll 1$, the terms included in the equation $\xi \partial \left(.\right)/\partial \xi$ may be disregarded. As a result, we get by removing the terms from the right side of Eqs. (9) and (12).

$$ \frac{{\mu _{{{\text{mnf}}}} /\mu _{{\text{f}}} }}{{\rho _{{{\text{mnf}}}} /\rho _{{\text{f}}} }}\frac{1}{{\left( {1 - \frac{\theta }{{\theta _{{\text{r}}} }}} \right)}}f^{{\prime \prime \prime }} + \frac{1}{{\theta _{{\text{r}}} \left( {1 - \frac{\theta }{{\theta _{{\text{r}}} }}} \right)^{2} }}\theta ^{\prime } f^{{\prime \prime }} + 2ff^{{\prime \prime }} + 1 - \frac{{\sigma _{{{\text{mnf}}}} /\sigma _{{\text{f}}} }}{{\rho _{{{\text{mnf}}}} /\rho _{{\text{f}}} }}M\left( {f^{\prime } - 1} \right) - f^{{\prime 2}} = 0, $$

(15)

$$ \left[ {\left\{ {\frac{{k_{{{\text{mnf}}}} }}{{k_{{\text{f}}} }} + \frac{4}{3}{\text{Rd}}} \right\}\theta ^{{\prime \prime }} } \right] + \frac{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{mnf}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}{\text{Pr}}_{{\text{f}}} \left( T \right)\left( {1 - \frac{\theta }{{\theta _{r} }}} \right)\frac{{k_{{\text{f}}} }}{{\mu _{{{\text{mnf}}}} (T)C_{{\text{p}}} }}\left[ {2f\theta ^{\prime } - \theta f^{\prime } + \frac{{\mu _{{{\text{mnf}}}} }}{{\mu _{{\text{f}}} }}\frac{1}{{\left( {1 - \frac{\theta }{{\theta _{{\text{r}}} }}} \right)}}{\text{Ec}}\xi ^{2} \left( {f^{{\prime \prime }} } \right)^{2} + {\text{MEc}}\xi \frac{{\sigma _{{{\text{mnf}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{mnf}}}} }}\left( {f^{\prime } - 1} \right)^{2} } \right] = 0 $$

(16)

Second-order truncation

In order to perform truncation at a more advanced level, the following additional functions are introduced:

$$I\left(\xi ,\eta \right)= \frac{\partial f}{\partial \xi }, K\left(\xi ,\eta \right)=\frac{\partial \theta }{\partial \xi }.$$

(17)

During the initial stage, the Eqs. (9) and (12) for the functions $f$ and $\theta$, respectively, stay the same.

$$\frac{{\mu }_{{\text{mnf}}}/{\mu }_{{\text{f}}}}{{\rho }_{{\text{mnf}}}/{\rho }_{{\text{f}}}}\frac{1}{\left(1-\frac{\theta }{{\theta }_{{\text{r}}}}\right)}{f}^{{\prime}{\prime}{\prime}}+\frac{1}{{{\theta }_{{\text{r}}}\left(1-\frac{\theta }{{\theta }_{{\text{r}}}}\right)}^{2}}{\theta }{\prime}{f}^{{\prime}{\prime}}+2f{f}^{{\prime}{\prime}}+1-\frac{{\sigma }_{{\text{mnf}}}/{\sigma }_{{\text{f}}}}{{\rho }_{{\text{mnf}}}/{\rho }_{{\text{f}}}}M\left({f}{\prime}-\lambda 1\right)-{f}^{{\prime}2}=\xi {f}{\prime}I{\prime},$$

(18)

$$\frac{1}{{\text{Pr}}}\left[\left\{\frac{{k}_{{\text{mnf}}}}{{k}_{{\text{f}}}}+\frac{4}{3}{\text{Rd}}\right\}{\theta }^{{\prime}{\prime}}\right]+\frac{{\left(\rho {C}_{{\text{p}}}\right)}_{{\text{mnf}}}}{{\left(\rho {C}_{{\text{p}}}\right)}_{{\text{f}}}}{{\text{Pr}}}_{{\text{f}}}\left(T\right)\left(1-\frac{\theta }{{\theta }_{{\text{r}}}}\right)\frac{{k}_{{\text{f}}}}{{\mu }_{{\text{mnf}}}(T){C}_{{\text{p}}}}\left[2f{\theta }{\prime}-\theta {f}{\prime}+\frac{{\mu }_{{\text{mnf}}}}{{\mu }_{{\text{f}}}}\frac{1}{\left(1-\frac{\theta }{{\theta }_{{\text{r}}}}\right)}{\text{Ec}}{\xi }^{2}{\left({f}^{{\prime}{\prime}}\right)}^{2}+{\text{MEc}}\xi \frac{{\sigma }_{{\text{mnf}}}}{{\left(\rho {C}_{p}\right)}_{{\text{mnf}}}}{\left({f}{\prime}-1\right)}^{2}\right]=\frac{{\left(\rho {C}_{{\text{p}}}\right)}_{{\text{mnf}}}}{{\left(\rho {C}_{{\text{p}}}\right)}_{{\text{f}}}}{{\text{Pr}}}_{{\text{f}}}\left(T\right)\left(1-\frac{\theta }{{\theta }_{r}}\right)\frac{{k}_{{\text{f}}}}{{\mu }_{{\text{mnf}}}(T){C}_{{\text{p}}}}\xi K.$$

(19)

With transformed boundary conditions:

$$ \begin{gathered} f\left( {\xi ,\eta } \right) = S, \frac{\partial f}{{\partial \eta }}\left( {\xi ,\eta } \right) = \lambda , \theta \left( {\xi ,\eta } \right) \to 1,\;{\text{as}}\; \eta \to 0, \hfill \\ \frac{\partial f}{{\partial \eta }}\left( {\xi ,\eta } \right) \to 1, \theta \left( {\xi ,\eta } \right) \to 0, \;{\text{as}} \;\eta \to \infty . \hfill \\ \end{gathered} $$

(20)

Regarding the variable $\xi ,$ the Eqs. (18, 19) are differentiated to provide additional Eqs. (21, 22) for $I$ and $K,$ along with their respective boundary conditions (22), which are as follows:

$$ \frac{{\mu_{mnf} /\mu_{\text{f}} }}{{\rho_{mnf} /\rho_{\text{f}} }}\frac{1}{{\left( {1 - \frac{\theta }{{\theta_{\text{r}} }}} \right)}}f^{\prime\prime\prime} + \frac{1}{{\theta_{\text{r}} \left( {1 - \frac{\theta }{{\theta_{\text{r}} }}} \right)^{2} }}\theta^{\prime}f^{\prime\prime} + 2ff^{\prime\prime} + 1 - \frac{{\sigma_{mnf} /\sigma_{\text{f}} }}{{\rho_{mnf} /\rho_{\text{f}} }}M\left( {f^{\prime} - 1} \right) - f^{^{\prime}2} - \xi I^{\prime} = 0, $$

(21)

$$ \begin{gathered} \frac{1}{\Pr }\left[ {\left\{ {\frac{{k_{{{\text{mnf}}}} }}{{k_{{\text{f}}} }} + \frac{4}{3}{\text{Rd}}} \right\}\theta^{\prime\prime}} \right] + \frac{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{mnf}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}\Pr_{{\text{f}}} \left( T \right)\left( {1 - \frac{\theta }{{\theta_{{\text{r}}} }}} \right)\frac{{k_{{\text{f}}} }}{{\mu_{{{\text{mnf}}}} \left( T \right)C_{{\text{p}}} }}\left[ {2f\theta^{\prime} - \theta f^{\prime} + \frac{{\mu_{{{\text{mnf}}}} }}{{\mu_{{\text{f}}} }}\frac{1}{{\left( {1 - \frac{\theta }{{\theta_{{\text{r}}} }}} \right)}}{\text{Ec}}\xi^{2} \left( {f^{\prime\prime}} \right)^{2} + {\text{MEc}}\xi \frac{{\sigma_{{{\text{mnf}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{mnf}}}} }}\left( {f^{\prime} - 1} \right)^{2} } \right] \hfill \\ \;\;\;\;\;\;\;\; - \frac{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{mnf}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}\Pr_{{\text{f}}} \left( T \right)\left( {1 - \frac{\theta }{{\theta_{{\text{r}}} }}} \right)\frac{{k_{{\text{f}}} }}{{\mu_{{{\text{mnf}}}} \left( T \right)C_{{\text{p}}} }}\xi K. \hfill \\ \end{gathered} $$

(22)

As such, the model must adhere to the matching boundary conditions.

$$ \begin{gathered} I\left( {\xi ,0} \right) = S, I^{\prime}\left( {\xi ,0} \right) = \lambda , K\left( {\xi ,0} \right) \to 1,\; \hfill \\ I^{\prime}\left( {\xi ,\infty } \right) \to 1, K\left( {\xi ,\infty } \right) \to 0. \hfill \\ \end{gathered} $$

(23)

At this level of truncation, the variables $\partial I/\partial \xi , \partial I/\partial \xi$ and $\partial K/\partial \xi$, together with their derivatives, were ignored with respect to $\eta$ to achieve precise findings.

Entropy generation and Bejan number

This section will concentrate on techniques for quantifying entropy to assess the extent of irreversibility inside a system. The following is an expression that may be used to describe it using mathematical language (see ref. [65]):

$$ E_{{\text{G}}} \left( {\xi ,\eta } \right) = \frac{{k_{{{\text{mnf}}}} }}{{\left( {T_{\infty } } \right)^{2} }}\left[ {\left( {\frac{\partial T}{{\partial z}}} \right)^{2} + \frac{{16\sigma^{*} T^{3}_{\infty } }}{{3k^{*} }}\frac{{\partial^{2} T}}{{\partial z^{2} }}} \right] + \frac{{\mu_{{{\text{mnf}}}} \left( T \right)}}{{T_{\infty } }}\left( {\frac{\partial u}{{\partial z}}} \right)^{2} + \frac{{\sigma_{{{\text{mnf}}}} B_{0}^{2} \left( {u - u_{{\text{e}}} } \right)^{2} }}{{T_{\infty } }}, $$

(24)

or

$$ N_{{\text{s}}} \left( {\xi ,\eta } \right) = {\text{Re}} \left[ {\frac{{k_{{{\text{mnf}}}} }}{{k_{{\text{f}}} }}\left( {1 + \frac{4}{3}{\text{Rd}}} \right)} \right]\left( {\frac{\partial \theta }{{\partial \eta }}} \right)^{2} + {\text{Br}}{\text{Re}} \xi^{2} \mu_{{{\text{mnf}}}} \frac{1}{\alpha }\frac{1}{{\left( {1 - \frac{\theta }{{\theta_{r} }}} \right)}}\left( {\frac{{\partial^{2} f}}{{\partial \eta^{2} }}} \right)^{2} + \frac{{\sigma_{{{\text{mnf}}}} }}{{\sigma_{f} }}{\text{MBr}}{\text{Re}} \xi \left( {\frac{\partial f}{{\partial \eta }}} \right)^{2} , $$

(25)

The heat transfer irreversibility-to-total irreversibility ratio is the Bejan Number. It may be expressed mathematically as (see [65]).

$$ {\text{Be}}\left( {\xi ,\eta } \right) = \frac{{{\text{Re}} \left[ {\frac{{k_{{{\text{mnf}}}} }}{{k_{{\text{f}}} }}\left( {1 + \frac{4}{3}{\text{Rd}}} \right)} \right]\left( {\frac{\partial \theta }{{\partial \eta }}} \right)^{2} }}{{N_{{\text{s}}} \left( {\xi ,\eta } \right)}}. $$

(26)

${\text{Br}}=\frac{{b}^{2}}{\left({T}_{{\text{w}}}-{T}_{\infty }\right){k}_{{\text{f}}}}$ is Brinkman number, $\alpha =\frac{{T}_{{\text{w}}}-{T}_{\infty }}{{T}_{\infty }}$ is temperature difference parameter, and $Re$ is Reynold number.

Code validation

The best way to figure out if model is correct to (I) compare numbers from current and already published studies and (II) make sure that boundary condition (10) in equation is met. As consequence of this, correctness of this model may be demonstrated by connecting values of ${f}^{{\prime}{\prime}}(0)$ reported in Tables 5 and 6 with those discovered in Kashia et al. [66] and Alqahtani et al. [62] for a particular case of viscous fluid. This will indicate that the model is an accurate representation of reality. The precision of the present result is evaluated by calculating the estimated percentage of relative error $\left({\epsilon }_{A}=\left|\frac{\mathrm{Present solution}-\mathrm{Previous Solution}}{\mathrm{Present Solution}}\right|\times 100\%\right).$ The variation, represented as ${\epsilon }_{A}$, between the current data and the prior inputs is seen to be quite modest, as shown by the data presented in Tables 5 and 6. This proves that present model and code are precise. The tables that are presented here demonstrate that the accuracy of currently used code and model is sufficient to be considered acceptable.

Table 5 ${f}^{{\prime}{\prime}}(0)$ for $\lambda$ and $M$ when $S={\text{Ec}}={\text{Rd}}=\delta ={\theta }_{{\text{r}}}=0$ for conventional fluid is tabulated and compared

Table 6 ${f}^{{\prime}{\prime}}(0)$ when $={\text{Ec}}=\delta ={\theta }_{\text{r}}=0$ for regular fluid is presented and assessed

Results and discussion

Equations (9) and (10), along with the boundary conditions described in Eq. (11), constitute a system of dimensionless, nonlinear partial differential equations (PDEs) that lack direct analytical solutions. By using MATLAB's built-in bvp4c algorithm and integrating the LNS approach up to its second truncation level, we have successfully produced valuable outcomes for our specific case. The bvp4c package in MATLAB, which is based on finite difference approaches and employs a three-stage Lobatto IIIA formula, plays a crucial role in this procedure. The error assessment functionality in bvp4c aids in estimating the numerical simulation error, guaranteeing that our graphical simulations adhere to the tolerance thresholds specified by bvp4c. The Bvp4c method is utilized in this study, to investigate different values for governing parameters. The volume fraction of ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ ternary hybrid nanofluid is chosen within range of (see [31]) $0.00\le {\phi }_{3}\le 0.025$ when ${\phi }_{1}+{\phi }_{2}=0.02$. Other parameters are chosen based on their consistency with solutions in a stretched flow situation and on references to another research. This means that $0.0\le {\text{Ec}}\le 1.0$ (Eckert number), $0.0\le M\le 0.5$ (magnetic parameter), $2.0\le S\le 2.4$ (suction), $0.0\le \delta \le 0.3$ (thermal stratification parameter), $-2.5\le {\theta }_{{\text{r}}}\le -0.5$ (viscosity parameter), $0.0\le {\text{Rd}}\le 1.0$ (radiation parameter) $0.0\le \lambda \le 1.0$ (stretching parameter), $0.0\le {\text{Re}}\le 5$ (Reynold number), and $0.0\le {\text{Br}}\le 1.0$ (Brinkmann number). The values of the control parameters are shown in the tables and graphs. These figures are based on the extent to which the far-field boundary conditions (11) are satisfied. The current condition is shown in Figs. 2–17, which also show the impacts of skin friction, Nusselt number, temperature, velocity, and entropy production. This study focuses on the investigation of the flow features of a ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ nanofluid with nanoparticles shape factor effect across a stretched disk. In this study, we also considered the comparative analysis of the distinct shapes (Bricks, Platelets, Disk, and Cylinder).

Fig. 2

a, b Influence of ${\phi }_{3}=0.005, 0.01, 0.015, 0.02$ on velocity $f{\prime}(\xi ,\eta )$ and temperature $\theta (\xi ,\eta )$ profiles

Velocity ${\varvec{f}}{\prime}({\varvec{\eta}})$ and Temperature ${\varvec{\theta}}({\varvec{\eta}})$ profiles

In this part, an analysis was performed on the results by manipulating several factors, including volume fraction $\left({\phi }_{3}\right)$, magnetic field strength ($M$), suction effect ($S$), thermal stratification parameter ($\delta$), Eckert number (${\text{Ec}}$), and viscosity parameter (${\theta }_{r}$). The major purpose of this research was to evaluate the influence of a number of different parameters on the plots of axial velocity $f{\prime}(\xi ,\eta )$ and temperature $\theta (\xi ,\eta )$ for the ternary hybrid nanofluid.

Changing the volume fraction of ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ ternary hybrid nanoparticles from ${\phi }_{3}=\mathrm{0.005,0.01,0.015,0.02}$ resulted in the examination of different velocity $f{\prime}(\xi ,\eta )$ and temperature $\theta (\xi ,\eta )$ profiles in Fig. 2a and b, respectively. As can be observed in Fig. 2a, the volume percentage of ternary hybrid nanoparticles has an effect on the velocity profile, which is denoted by the symbol ${f}{\prime}(\xi ,\eta ).$ Based on the findings, an augmentation in the proportion of ternary hybrid nanoparticles leads to an elevation in the viscosity of the fluid, hence facilitating a higher rate of fluid movement. Furthermore, while seeing Fig. 2a, it becomes apparent that the thickness of the momentum barrier layer diminishes as the volume of ternary hybrid nanoparticles rises. Consequently, there is an increase in the speed of the fluid and a more prominent change in its gradient. The impact of the ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ ternary hybrid nanoparticle volume fraction (${\phi }_{3}$) on the temperature $\theta (\xi ,\eta )$ profile is seen in Fig. 2b. An increase in parameter ${\phi }_{3}$ results in an elevated $\theta (\xi ,\eta )$ distribution, causing an expansion of the thermal boundary layer. One possible explanation for the observed phenomena is the positive link between the fluid's thermal conductivity and the ${\phi }_{3}$ of ternary hybrid nanoparticles. Nanofluids characterized by elevated nanoparticle volume fractions provide an increased number of routes, thereby facilitating enhanced heat conduction. This results in an increase in temperature for the whole ternary hybrid nanofluid, as shown in Fig. 2b. This implies the gadget can absorb more heat, which means it will remain at the ideal temperature for a longer period of time. An important factor in the enhanced stability of ternary hybrid nanofluids is their chemical inertness. Disk-shaped ternary hybrid nanoparticles have a higher temperature profile than brick-, disk-, and platelet-shaped ternary hybrid nanoparticles.

The velocity $f{\prime}(\xi ,\eta )$ and temperature $\theta (\xi ,\eta )$ profiles are shown in Fig. 3a and b, respectively, to demonstrate the encouragement of the magnetic parameter ($M$) on the system. Figure 3a shows how the parameter M affects the velocity profile, $f{\prime}(\xi ,\eta )$. The effect of the magnetic parameter on the temperature profile is seen in Fig. 3b. As the magnetic parameter increases, the velocity profile becomes steeper, and the temperature becomes flatter. In theory, magnetic parameters could make the Lorentz force slow things down, but in this case, it speeds things up. When a magnetic field is present, a force is known as the Lorentz force opposes the flow of a fluid. The magnitude of this force is precisely proportional to $M$. As a result, the Lorentz force increases as $M$ goes up. When $M$, gets stronger, the resistance to the flow of fluid goes up, which makes the flow slow down. This effect is common in magnetohydrodynamics. Fluids can do it in several scenarios. $M$ appearance greatly affects fluid temperature. This force transfers fluid temperature from surface to flow. Figure 3b clearly depicts the dispersion of temperature. Drag forces present in the fluid flow cause a reduction in both the temperature field and the thickness of the boundary layer. The current investigation has shown that the inclusion of the magnetic parameter has a beneficial effect on heat conduction, as corroborated by prior research findings. The authors recognize that the manipulation of control settings has the potential to provide diverse results. Figure 3a shows that bricks-shaped nanoparticles show a better velocity profile compared to other shapes (disk, platelets, and cylinders).

Fig. 3

a, b Impression of $M=0.1, 0.2, 0.3, 0.4, 0.5$ on ${f}{\prime}\left(\eta \right),$ $\theta \left(\eta \right)$

Figure 4a and b shows the effects of mass suction $S$ on velocity $f{\prime}(\xi ,\eta )$ and temperature $\theta (\xi ,\eta )$ profile for stretching disk. The velocity profile, $f{\prime}(\xi ,\eta )$, can be observed to be affected by the suction parameter in Fig. 4a. Meanwhile, Fig. 4b illustrates the influence of the suction parameter on the temperature profile $\theta (\xi ,\eta )$. The velocity profile increases while the temperature profile decreases as the suction parameter increases. The increase in density is attributed to the addition of additional particles. Suction reduces the momentum barrier layer, hence improving the flow of the stretched and shrunken surface. Figure 4b illustrates the relationship between temperature and the suction parameter $S$. As parameter $S$ increases, there is a simultaneous decrease in temperature. As the suction is applied, it reduces the temperature of the boundary layer flow. It is used in nuclear power plants as well as magnetohydrodynamic (MHD) power plants, along with several other industrial applications. The cause of the weakening flow has been identified as the constrained vorticity inside a boundary layer. Figure 4a shows that bricks-shaped nanoparticles show a better velocity profile of mass suction parameter compared to other shapes (disk, platelets, and cylinders).

Fig. 4

a, b Consequence of $S=2.1, 2.2, 2.3, 2.4$ on ${f}{\prime}\left(\eta \right)$ and $\theta \left(\eta \right)$

The velocity $f{\prime}(\xi ,\eta )$ and temperature $\theta (\xi ,\eta )$ profiles for the stretching disk are examined in Fig. 5a and b by altering the viscosity parameter (${\theta }_{{\text{r}}}$) within the range of ${\theta }_{{\text{r}}}=-0.5, -1.0, -1.5, -2.0$. Figure 5a depicts the impact of the viscosity parameter on the velocity profile $f{\prime}(\xi ,\eta )$. Figure 5b illustrates how the viscosity parameter affects the temperature $\theta (\xi ,\eta )$ curve. The velocity profile is diminishing, but the temperature profile is rising as the viscosity parameter decreases. It is obvious that the presence of viscosity entails the existence of viscous forces. The presence of viscous forces will cause a drop in the velocity profile, resulting in a slower flow. When the ${\theta }_{{\text{r}}}$ is decreased, the fluid temperature increases because this drop in viscosity leads to greater heat energy generated by lower resistive forces. This increase in heat energy causes the temperature to rise. Increased fluid flow will result in a greater amount of kinetic energy being generated. Figure 5a shows that the velocity profile against variable viscosity for disk-shaped nanoparticles reduces quickly compared to other (bricks-, platelets-, and cylinder-shaped) nanoparticles while Fig. 5b shows that the temperature profile increases better for disk-shaped nanoparticles.

Fig. 5

a, b Consequence of ${\theta }_{{\text{r}}}=-0.5, -1.0, -1.5, -2.0$ on ${f}{\prime}\left(\eta \right)$ and $\theta \left(\eta \right)$

Figure 6a, b depicts the impact of ${\text{Ec}}$ on the temperature $\theta (\xi ,\eta )$ distribution for a stretched disk. Figure 6a shows how the Eckert number affects the temperature profile $\theta (\xi ,\eta )$, whereas Fig. 6b illustrates the effect of the thermal stratification parameter $\delta$ on the temperature profile $\theta (\xi ,\eta )$. The presence of friction between fluid layers results in an increase in temperature, as shown in the ${\text{Ec}}$ number. The increase in temperature occurs when the kinetic energy of particles transforms into internal energy. From a physical standpoint, a rise in the Eckert number ${\text{Ec}}$ leads to a higher magnitude of energy release, facilitating the expansion of thermal energy and augmenting the thermal boundary layer. Conversely, an augmentation in temperature results in the generation of supplementary thermal energy, causing an elevation in the temperature distribution of the fluid. The relationship between the thermal stratification parameter $\delta$ and the temperature $\theta (\xi ,\eta )$ profile is shown in Fig. 6b, indicating that an increase in δ leads to a corresponding increase in $\theta (\xi ,\eta )$. The phenomenon of thermal stratification results in an elevation of the fluid's temperature, posing challenges in controlling its velocity. This is mostly attributed to the rise in temperature caused by decreased heat transfer at the surface region.

Fig. 6

a, b Consequence of ${\text{Ec}}=0.12, 0.4, 0.6, 0.8$ and $\delta =0.05, 0.1, 0.15, 0.2$ on $\theta (\eta )$ and c Impact of ${\text{Rd}}=0.2, 0.4, 0.6, 0.8$ on $\theta \left(\eta \right)$

Figure 6c illustrates the influence of various values of the thermal radiation parameter (${\text{Rd}}$) on the temperature profile of a ternary hybrid nanofluid with varied forms of nanoparticles. As the radiation parameter rises, the $\theta (\xi ,\eta )$ profile of a ternary hybrid nanofluid also increases. As the significance of radiation in the process of heat transfer intensifies (owing to higher temperatures or other variables that amplify radiation), the temperature of the nanofluid experiences a more pronounced rise. This phenomenon may occur due to the enhanced radiation absorption and emission capabilities of the nanoparticles compared to the base fluid. The heightened absorption and release of radiation result in a rise in the fluid's total temperature. Ternary hybrid nanofluids, through their optimized amalgamation of nanoparticles, are expected to exhibit enhanced efficacy in interacting with radiation, perhaps elucidating the observed rise in temperature corresponding to higher radiation parameters. Among the many shapes (bricks, platelets, disk, and cylinder) of nanoparticles in Fig. 6a, b and c, the disk shape has the greatest values for the temperature profiles.

Impacts of governing parameters on entropy generation and Bejan number

This part examines the impact of several parameters on the entropy generation and Bejan number profiles of ternary hybrid nanofluid, taking into account various form (brick, cylinder, platelets, and disk) aspects. Figure 7a and b demonstrates the impact of different volume fractions (${\upphi }_{3}$) of ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ ternary hybrid nanofluid, including nanoparticles of varying shapes (brick, cylinder, platelets, and disk), on the profile of entropy production and Bejan number. As the volume percentage of nanoparticles increases, the rise in entropy profile of a ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ ternary hybrid nanofluid can be attributed to the following factors: Viscosity Alterations: The addition of more nanoparticles may modify the viscosity of the fluid. Increased viscosity often leads to greater resistance to fluid movement, resulting in increased loss of energy as heat and hence higher entropy. Effects of the boundary layer: Higher nanoparticle concentrations may influence the parameters of the fluid's boundary layer, possibly resulting in a thicker boundary layer and altered flow characteristics. This modification may lead to a rise in entropy production, particularly in situations involving convective heat transfer. As ${\phi }_{3}$ increases, Fig. 7b shows the Bejan number profile decreases. As the Bejan number profile decreases, convective heat transfer, rather than primarily conductive heat transfer, becomes more prevalent. With higher volume fractions of nanoparticles, the convective heat transfer becomes more noticeable due to improved thermal conductivity and the disruption of boundary layers. This causes the Bejan number to drop as the system shifts to favor convective heat transfer.

Fig. 7

a, b Impact of ${\phi }_{3}=0.005, 0.01, 0.015, 0.02$ on entropy generation and Bejan number profile

Figure 8a and b shows how different Brinkmann number values (${\text{Br}}$) affect the entropy generation and Bejan number profile of a ternary hybrid nanofluid with nanoparticles having different shapes. The entropy profile of a ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ ternary hybrid nanofluid goes up as the Brinkmann number (${\text{Br}}$) goes up, as shown in Fig. 8a. This is because of the way the Brinkmann number itself works and how it affects the properties of the fluid. A greater ${\text{Br}}$ number implies an increasing importance of viscous dissipation relative to conductive heat transfer. Increasing viscous dissipation results in a greater development of entropy, mainly caused by the transformation of kinetic energy into heat. Additionally, a greater Brinkmann number leads to an increase in the internal friction inside the nanofluid. This heightened friction transforms a greater amount of mechanical energy derived from fluid movement into thermal energy. The process of conversion is intrinsically less efficient and produces a greater amount of entropy. On the other hand, as can be shown in Fig. 8b, the Bejan number profile decreases with increasing Brinkmann number. A thinner thermal boundary layer is seen close to the heated surface as the Brinkmann number rises. Increased heat transmission from the surface to the bulk fluid makes convective heat transfer simpler because the boundary layer is thinner.

Fig. 8

a, b Impact of ${\text{Br}}=0.2, 0.4, 0.6, 0.8$ on entropy generation and Bejan number profile

The picture in Fig. 9a and b shows how different Eckert number values (${\text{Ec}}$) affect the entropy generation and Bejan number profiles of a ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ ternary hybrid nanofluid that has nanoparticles of different shapes. Understanding the physical implications of the Eckert number in thermofluidic can help explain the increase in the entropy profile of a ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ ternary hybrid nanofluid as the Eckert number (${\text{Ec}}$) increases as shown in Fig. 9a. A higher Eckert number signifies a more significant transformation of kinetic energy into thermal energy. The conversion process inevitably leads to a rise in entropy, since it often includes dissipative processes that convert ordered kinetic energy into random thermal energy. An increase in the Eckert number indicates a greater conversion of kinetic energy from the fluid into heat. As a result, the temperature of the fluid increases. Elevated temperatures often correlate with increased molecular agitation and disorder, hence leading to an elevation in entropy. The transformation of kinetic energy into thermal energy may generate substantial temperature gradients inside the nanofluid. The presence of these gradients indicates a condition of non-equilibrium, which directly contributes to the development of entropy. The system inherently moves toward a state of balance, and this progression entails the production of entropy. However, Fig. 9b shows that the Bejan number profile of the ternary hybrid nanofluid falls as Eckert number (${\text{Ec}}$) grows for different nanoparticle forms. As ${\text{Ec}}$ rises, Bejan number profile decreases. Physically, kinetic energy dominates thermal energy as Eckert number increases. In ternary hybrid nanofluids, convective heat transport from fluid motion is more essential than thermal diffusion.

Fig. 9

a, b Impact of ${\text{Ec}}=0.1, 0.2, 0.3, 0.4$ on entropy generation and Bejan number profile

Figure 10a and b illustrates the impact of different magnetic parameter $M$ on the formation of entropy and Bejan number profiles in ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ ternary hybrid nanofluids. Considering the effects of magnetic fields on the characteristics and behavior of the fluid, this explains the rise in the entropy profile in Fig. 10a of a ternary hybrid nanofluid with increasing values of the magnetic parameter ($M$). The rationale behind this is: The magnetic parameter ($M$) indicates the presence of magnetohydrodynamic (MHD) processes in the fluid. As the magnetic field strength rises, the impact on the fluid flow becomes more significant. Magnetic fields can modify the flow properties, resulting in the formation of intricate flow patterns. The intricate nature of this phenomenon often results in amplified energy dissipation and, as a result, elevated entropy production. Additionally, a greater $M$ value, indicating a strong magnetic field, might result in more viscous dissipation in the fluid. The interaction between the magnetic field and the electrically conducting particles in the nanofluid results in resistance to the flow. The resistance transforms the energy of motion into thermal energy, increasing the level of disorder in the system, known as entropy. In contrast, the physical rationale explains, as shown in Fig. 10b, why the Bejan number profile of ternary hybrid nanofluid decreases as the magnetic parameter ($M$) increases for nanoparticles of various shapes: The applied magnetic field strength in relation to the fluid flow is represented by the magnetic parameter. Because of the Lorentz force acting on the conducting fluid, higher magnetic parameters have the tendency to reduce fluid motion and turbulence. A lower Bejan number is the result of this suppression, which lessens the nanofluid's convective heat transmission.

Fig.10

a, b Impact of $M=0.1, 0.2, 0.3, 0.4$ on entropy generation and Bejan number profile

Figure 11a and b demonstrates the impact of different thermal radiation parameters (${\text{Rd}}$) on the formation of entropy and Bejan number in ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ ternary hybrid nanofluids. Increasing values of the thermal radiation parameter ($Rd$) explain the rise in the entropy profile of a ternary hybrid nanofluid in Fig. 11a, using the principles of heat transfer and fluid dynamics. The thermal radiation parameter (${\text{Rd}}$) measures the relative importance of radiative heat transfer compared to conduction. Increasing ${\text{Rd}}$ signifies an intensified impact of thermal radiation on the heat transfer mechanism. Radiative heat transmission has a broader spatial distribution compared to conduction and often entails more significant variations in temperature. The presence of these gradients might result in a higher level of entropy as the system attempts to achieve thermal equilibrium. Additionally, greater values of ${\text{Rd}}$ often indicate the presence of substantial temperature variations within the fluid. Significant variations in temperature are a key factor in the creation of entropy since they indicate a higher level of thermal imbalance. As seen in Fig. 11b, using physical logic, we can understand why the Bejan number profile of ternary hybrid nanofluid increases as the radiation parameter (${\text{Rd}}$) increases for various shaped nanoparticles: An increase in the radiation parameter (${\text{Rd}}$) indicates that radiative heat transmission is more important than convective and conductive heat transfer processes. The role of radiative heat transfer may grow in ternary hybrid nanofluids, especially those with strong radiative characteristics, when surface-to-fluid temperature gradients and other such phenomena are present.

Fig.11

a, b Impact of ${\text{Rd}}=0.1, 0.3, 0.5, 0.7$ on entropy generation and Bejan number profile

Altering the Reynolds number (${\text{Re}}$) has an influence on the entropy production and Bejan number in ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ ternary hybrid nanofluids, as shown in Fig. 12a, b. By analyzing the flow and heat transfer dynamics, one can physically explain why the entropy profile of a ternary hybrid nanofluid increases as the Reynolds number (${\text{Re}}$) parameter rises: The Reynolds number quantifies the relative importance of viscous and inertial forces in a fluid. Typically, a laminar (smooth and regular) flow will become a turbulent (chaotic and irregular) one as $Re$ rises. Increased energy dissipation and, by extension, entropy creation are hallmarks of turbulent flow, which is defined by fast fluctuations and mixing. In addition, more efficient transmission of heat is possible with higher Reynolds numbers due to the increased mixing of the fluid. The flip side of this is that nanoparticles and fluid particles collide and interact more often, which increases the entropy owing to the greater rates of mixing and energy dissipation and creates more complicated flow patterns. In addition, layer effects at boundaries: The boundary layer, or the fluid immediately around the surface, undergoes changes in thickness and properties as ${\text{Re}}$ rises. Especially in cases of convective heat transfer, these modifications might affect the momentum and heat transmission within the fluid, which in turn can increase the development of entropy. The rise in the Bejan number profile seen in Fig. 12b of the ternary hybrid nanofluid as the Reynolds number (${\text{Re}}$) increases for nanoparticles of various shapes may be elucidated using physical reasoning: As Reynolds numbers increase, there is a reduction in the thickness of the thermal boundary layer in the vicinity of the heated surface. The reduced thickness of the boundary layer enhances the efficiency of heat transmission from the surface to the bulk fluid, hence promoting convective heat transfer.

Fig.12

a, b Impact of ${\text{Re}}=1, 2, 3, 4$ on entropy generation and Bejan number profile

Out of the various forms of nanoparticles shown in Figs. 7–12 (bricks, platelets, disk, and cylinder), the disk shape exhibits the highest values for the Bejan number profiles.

Governing parameters impacts on Nusselt number and skin friction

This section delves into the examination of several factors and their impact on physical measures, notably the measurement of skin friction $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and the rate of heat transfer ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$ at a given place. The evaluation of local heat transfer rate ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$ and skin friction $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ has significant importance in the industrial context. The aforementioned values possess considerable significance due to their practical use within the industrial domain. Changes in parameters change skin friction coefficient $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and local heat transfer rate ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$.

Figure 13a and b shows impact of ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ nanoparticle volume fraction $\left({\phi }_{3}\right)$ sideways with $\lambda$ on $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. The findings pertaining to $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ are shown in Fig. 13a, showcasing the relationship between the stretching parameter and the volume fraction. Fig. 13b shows impact on ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. It has been found that size of the skin friction goes up as the value of ${\phi }_{3}$ goes up. The viscosity of a base fluid is accelerated as a consequence of the collisions that take place between nanoparticles and the fluid. This process results in a decrease in the thickness of the momentum boundary barrier, thereby leading to an increase in surface skin friction. Moreover, it can be noted that there is an inverse relationship between the ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$ and the volume fraction ${\phi }_{3}$ as it grows.

Fig. 13

a, b Impression of ${\phi }_{3}=0.005, 0.01, 0.015, 0.02, 0.025$ with $\lambda$ on $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$

Figure 14a and b depicts the impact of the magnetic parameter $\left(M\right)$ in combination with the stretching parameter $\lambda$ on $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. Figure 14a illustrates the relationship between the $M$ and $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ when it is paired with the stretching parameter. On the other hand, Fig. 14b depicts the effect of the magnetic parameter on the ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. These data demonstrate a clear relationship between increasing $M$ and a corresponding increase in $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$. Consequently, the boundary layer experiences a greater influx of energy as the Lorentz force intensifies. As the magnetic control becomes stronger in the ternary hybrid nanofluid regime, the boundary layer increases in thickness, resulting in a decrease in heat transfer rate. The conduction of heat over the walls and the elongation of the disk contribute to the decrease in the Nusselt number.

Fig. 14

a, b Consequence of $M=0.1, 0.2, 0.3, 0.4, 0.5$ with $\lambda$ on $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$

Figure 15a and b shows how the effect of several estimates of mass suction $\left(S=2.0, 2.1, 2.2, 2.3, 2.4\right)$ with $\lambda$ on $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. Figure 15a and b shows outcome of suction parameter $\mathrm{with stretched parameter} \lambda$ on $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and Nusselt number. When suction is used to create fluid flow, the boundary layer separation stays unchanged, although there is an upsurge in the ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. As the parameter $S$ goes up, the $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and local heat transfer rate ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$ go up. Suction is needed to improve $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. On other hand, suction can be used to improve both $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$ near the wall. Enhanced heat transfer takes place when fluid particles experience acceleration when they are drawn toward a surface.

Fig. 15

a, b Consequence of $S=2.0, 2.1, 2.2, 2.3, 2.4$ with $\lambda$ on $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$

Figure 16a, b shows how influence of different estimated of viscosity parameter $\left({\theta }_{{\text{r}}}\right)$ along with stretched parameter on $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. The $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ data are displayed in Fig. 16a in relation to the viscosity parameter and the $\lambda$. Figure 16b depicts the influence of the variable in question on the ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. The fluid experiences motion due to the application of stretching, resulting in a reduction in the force of skin friction between the fluid and the surface as the viscosity parameter drops. As a result, there is a reduction in $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$. It is noteworthy that an upsurge in the variable viscosity parameter enhances both heat transfer and fluid flow, while a drop in this parameter has the opposite effect.

Fig. 16

a, b Consequence of ${\theta }_{r}=-\mathrm{2,5}, -2.0, -1.5, -1.0, -0.5$ with $\lambda$ on $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$

The interaction between the Eckert number (${\text{Ec}}$) and the thermal stratification parameter ($\delta$) on the ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$ is investigated in Fig. 17a, b. The Eckert number is varied at values of ${\text{Ec}}=0.2, 0.4, 0.6, 0.8, 1.0$, while the thermal stratification parameter is varied at values of $\delta =0.05, 0.1, 0.15, 0.2, \mathrm{0.25,0.3}$. These variations are seen to influence the stretching parameter and subsequently affect the local heat transfer. In Fig. 17a, the relationship between the Eckert number and the stretching parameter $\lambda$ is shown, specifically in relation to the ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. Figure 17(b) presents the influence of the thermal stratification parameter, in concurrence with the $\lambda$ on the ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. An increase in the ${\text{Ec}}$ is followed by sequential increases in temperature as well as an increase in the thickness of the boundary layer. As a consequence of this, the temperature of the wall rises as the Eckert number rises, which ultimately leads to a reduction in the rate at which heat is transmitted. The temperature fluctuations seen at various levels inside the boundary layer are sometimes referred to as "thermally stratified." Due to the phenomenon of temperature stratification, the process of freezing liquid leads to the condensation of the liquid at the lowermost part of the structure. This condensation results in a reduction in the kinetic energy, ultimately leading to a fall in the ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2}$.

Fig. 17

a, b Consequence of ${\text{Ec}}=0.1, 0.2, 0.3, 0.4, 0.5$ and $\delta =\mathrm{0.01,0.02}, 0.03, 0.04, 0.05$ with $\lambda$ on ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. c Consequence of ${\text{Rd}}=0.1, 0.2, 0.3, \mathrm{0.4,0.5}$ with $\lambda$ on ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$

Figure 17c displays the impact of varying amounts of heat radiation on the Nusselt number ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$ profile. The figure shows the behavior of a ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ ternary hybrid nanofluid, including nanoparticles of varied shapes. A grasp of principles in heat transfer and nanofluid dynamics is necessary to see that the ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$ profile of a ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ ternary hybrid nanofluid diminishes as the radiation parameter increases. The statement implies that with an increase in the radiation parameter (which signifies a stronger influence of thermal radiation in the heat transfer mechanism), there is a corresponding drop in the ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. This suggests that the efficiency of convective heat transfer decreases compared to conductive heat transfer when there is a higher level of thermal radiation. This scenario is plausible if the rise in radiation results in a more homogeneous dispersion of temperature throughout the fluid. Under such circumstances, the temperature gradient, which is responsible for driving convection, may diminish, resulting in a drop in the efficiency of convective heat transfer. Alternatively, it is plausible that the nanoparticles, known for their efficient heat conduction, may not exhibit the same level of effectiveness in heat transfer by radiation. With increasing radiation, the heat transmission mechanism switches from convection and conduction to radiation, with nanoparticles playing a more significant role.

The nanoparticles shown in Fig. 13–17 exhibit various forms, including bricks, platelets, disks, and cylinders. Notably, the platelet shape demonstrates the highest values in terms of skin friction and Nusselt number profiles.

Conclusions

This study examines the effects of thermal radiation, external magnetic field, shape factor effects, Joule heating, thermal stratification, and viscous dissipation on the entropy generation of a ternary hybrid nanofluid composed of titanium oxide (TiO₂), copper (Cu), and titanium oxide (Al₂O₃) nanoparticles, with water serving as the base fluid. The investigation is conducted over a stretching disk. The graphical representation of the ternary hybrid nanofluid is examined, providing appropriate explanations for the velocity, temperature, entropy production, Bejan number, skin friction, and Nusselt number profiles. The dimensionless system has been addressed by using the local non-similarity technique via bvp4c. The study results may be succinctly described as follows:

• Nanoparticles with a platelet form exhibit greater skin friction and Nusselt number profiles in comparison to nanoparticles with brick, disk, and cylinder shapes.

• The temperature profiles of disk-shaped nanoparticles are greater than those of brick-, platelet-, and cylinder-shaped nanoparticles.

• The rate of change of velocity, $f{\prime}(\xi ,\eta )$, drops, and the temperature profiles, θ $(\xi ,\eta )$, shows an increasing pattern when the ${\phi }_{3}$ value of ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ nanoparticles increase for various nanoparticle shapes.

• Among the many shapes of nanoparticles, the cylinder form has the greatest values for the velocity and entropy generation profiles and disk shapes for temperature profiles.

• A rise in the values of suction and magnetic components leads to an increase in the velocity $f{\prime}(\xi ,\eta )$ profile, while the temperature θ $(\xi ,\eta )$ profile exhibits a decrease.

• The velocity profile decreases as the viscosity parameter decreases, but the temperature profile increases.

• The temperature profile shows a positive correlation with increases in both the Eckert number (${\text{Ec}}$), radiation (${\text{Rd}}$), and thermal stratification ($\delta$) parameters.

• The Nusselt number goes down as the levels of the ternary hybrid nanoparticle volume fraction ${\phi }_{3}$, the magnetic parameter $M$, and the stretching parameter $\lambda$ go up. In contrast, skin friction has a positive correlation with these metrics.

• The decrease in the viscosity parameter is linked to a simultaneous reduction in both skin friction and ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. In contrast, an elevation in the suction parameter results in a simultaneous augmentation of both the $(0.5{C}_{{\text{f}}} {{({\text{Re}}}_{{\text{r}}})}^\frac{1}{2})$ and the ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$.

• An upward trend in both the Eckert number (${\text{Ec}}$) and the thermal stratification parameter ($\delta$) results in a decline in the ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$.

• Increasing the mass suction $S$ from 2.0 to 2.4 leads to significant improvements in the ${{\text{Nu}}}_{{\text{r}}}{{({\text{Re}}}_{{\text{r}}})}^{-\frac{1}{2}}$. Nanofluids show a boost of about 10.2%, whereas hybrid nanofluids result in a 19.8% rise, and ternary hybrid nanofluids exhibit a significant augmentation of 38.05% compared to regular fluids.

• The Nusselt number for ${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$ nanoparticles shaped like bricks rises by around 0.9823% when ${\text{Rd}}$ goes from 0.1 to 0.5 and mass suction is 2.0.

• The Nusselt number for cylinder-shaped ternary hybrid nanoparticles reduces by roughly 1.223% when the variable viscosity ${\theta }_{{\text{r}}}$ varies from −1.0 to −2.0, while maintaining a nanoparticles volume fraction of 1%.

• The profiles of entropy generation and Bejan numbers exhibit an upward trend as the radiation and Reynolds number parameters rise.

• The entropy generation profile exhibits an upward trend as the volume percentage of nanoparticles, Eckert number, and Brinkmann number rise. Conversely, the Bejan number profiles show a downward trend in relation to these parameters.

Practical applications

The aim of our work is to examine how the shape factor is affected by joule heating and thermal stratification in magnetohydrodynamic ternary hybrid nanofluids. The knowledge acquired from this study may be used to enhance the efficiency of cooling apparatuses, such as heat sinks, thermal spreaders, and heat exchangers. Engineers may improve the efficiency of cooling systems by utilizing the processes revealed in our investigation, allowing for better heat dissipation.

Potential limitations

• A possible constraint of our work is the reduction of the physical system to enable mathematical analysis. While our model does capture fundamental characteristics of the phenomena being studied, it may not completely depict the intricacies of real-world situations.

• Further, our research is limited to a certain system architecture (stretched disk) and ternary hybrid nanofluid composition (${{\text{Al}}}_{2}{{\text{O}}}_{3}-{\text{Cu}}-{{\text{TiO}}}_{2}/{{\text{H}}}_{2}{\text{O}}$). Our results may not be applicable to different geometries or nanofluid compositions, but they do allow for a thorough examination of a well-defined situation.

Future scope

• The investigation of the turbulent flow of a ternary hybrid nanofluid may be conducted inside porous media.

• A non-Newtonian ternary hybrid nanofluid flow may be used to evaluate the model.

• Velocity slip circumstances with melting heat transfer and thermal jump are feasible choices for boundary circumstances.