1 Introduction

While industrial companies consume about one-third of energy around the world, today’s high-tech processors are one of the main culprit to energy consumption [25]. Wisely use of energy has been proven as a chief solution to deal with scarcity of energy for sustainable development in future [10, 28]. Cost-saving modes and environment related attitudes have been the main motivation of industries to reduce their energy consumption [1]. Furthermore, increases in energy tariffs in recent years have given rise to environmentally conscious policies [35]. It is estimated that numerous modern technologies will be emerged in the future to solve energy-saving problems [12, 32]. Bhowmik et al. [3] studied a green energy planning problem for sustainable development considering various decision-making strategies, integrated approaches and combined methods. Mohammadi et al. [29] provided an all-encompassing survey on the different applications of energy hubs in various energy consumption sectors.

In order to manage energy consumption, a broad range of solutions can be found in the literature. Lu et al. [26] introduced a mixed-integer nonlinear programming under dynamic electricity pricing for optimizing the operation schedule of building with energy generation and energy storage. Khoshnevisan et al. [20] proposed an evolutionary algorithm for optimal consumption of energy in an agriculture system. de Queiroz [8] formulated and solved the hydro-thermal electrical power system scheduling optimization problem, in which power generators were arranged over a finite time horizon to supply system demand. Motalleb et al. [31] proposed an algorithm to optimize demand response schedule for using distributed energy storage systems as a source of ancillary services. Recently, Barak et al. [2] used a multi-objective particle swarm optimization algorithm to manage energy and greenhouse gas emissions in an agricultural production system. Khushairi et al. [21] studied the installation problem of a thermal energy storage system in buildings to transfer energy demands from peak hours to off-peak times in order to reduce peak energy load.

In general, there are several works in the literature addressing energy oriented scheduling problems in different applications. Fang et al. [11] introduced a novel scheduling approach to decrease both peak power load and carbon footprints where tasks could be processed at different speeds with various energy consumptions. Jin et al. [18] proposed an exact day-ahead scheduling approach to integrate an urban energy system. Le and Wright [24] addressed scheduling of workloads in a network of datacenters to decrease energy cost and carbon footprint. Radhakrishnan et al. [34] investigated a token based scheduling approach as a new energy efficient policy for commercial buildings’ HVAC systems. Zhang et al. [44] presented a new bi-objective genetic algorithm for workflow scheduling to reduce energy consumption and to heighten system reliability. Tang et al. [40] proposed a dynamic model for a flexible flow shop scheduling problem to reduce both energy consumption and makespan. They developed an improved version of the particle swarm optimization algorithm to solve their problem. Golari et al. [13] studied a multi‐period, production‐inventory planning model in a multi‐plant manufacturing system powered with onsite and grid renewable energy.

High fluctuations in energy demand have been a crucial problem for energy supply systems to effectively fulfillment of the demand. To cope with this issue, energy supply systems try to manage the demand by contriving time-of-use energy tariffs under which the energy price varies from hour to hour depending on the demand. This strategy changes the demand behavior so as to decrease the peak-hours load. Although a study by Jacopo [17] reveals that the average energy consumption may occasionally increase under time-of-use energy tariffs, this approach has been among the most common strategies to reshape the demand rate. A limited number of research works can be found regarding the time-of-use energy tariffs. Shrouf et al. [37] studied the production scheduling problem in order to minimize the total energy consumption cost. Zhang et al. [44] proposed an integer programming formulation for scheduled manufacturing to minimize both electricity cost and carbon footprint under time-dependent tariffs. Gong et al. [14] formulated the single machine scheduling problem with power-down mechanism under time-of-use tariffs and utilized a genetic algorithm to solve their problem. Sharma et al. [36] proposed a scheduling model which combines the economic and ecological features of a multi-machine setup operating with a time-of-use tariff. They estimated the peak load and energy consumption by applying discrete event simulation. Che et al. [7] developed a continuous-time mixed-integer programming formulation for the energy-conscious single machine scheduling problem with time-dependent electricity tariffs. Dhakouani et al. [9] studied approaches for better integration of renewable energies. For a recent survey on challenges for the integration of renewables we refer to Sinsel et al. [38].

Although the above mentioned works have investigated problems addressing energy-conscious issues in machine scheduling context, the literature is scarce in works within project scheduling field. In the sole found work, Okubo et al. [33] presented an integer programming model and a constraint programming model for resource constrained project scheduling problem (RCPSP) with realistic energy constraints. They used a heuristic-mode restriction approach called mask calculation to solve the problem. In addition, only renewable resources are taken into account in typical RCPSPs to provide the base schedule, while nonrenewable resources such as electricity are considered unlimitedly available without any contribution in scheduling process. Furthermore, multi-skilled project scheduling problem (MSPSP) is a version of RCPSP in which renewable workforce have several skills. This gives flexibility to project managers to schedule project activities.

The MSPSP is vastly studied in the literature over the past years [15, 19, 27, [42]. The main motivation of this paper is to extend MSPSP considering allowance for preempting activities and time-of-use tariffs for energy consumption. Indeed, the flexible structure of multi-skilled workforce under a time-of-use tariff for energy price would be beneficial in deriving an energy-efficient solution. Based on the best of the authors’ knowledge, this paper is the first work in the field of project scheduling which involves time-of-use tariffs for energy price to schedule preemptable activities within a multi-skilled environment. In this regard, an integer programming formulation is proposed for a preemptive multi-skilled project scheduling problem under time-of-use tariffs for energy prices. By analyzing the solution space of the proposed model, two intelligent meta-heuristic algorithms based on electromagnetic like algorithm (EMA) and genetic algorithm (GA) are utilized to solve the sophisticated problem at hand. The performances of the algorithms are compared with each other based on a set of problem instances.

The remainder on this paper is structured in the following sections. The problem description and the mathematical presentation of the preemptive multi-skilled project scheduling problem under time-of-use tariff, called PMSPSP-TOU thereafter, are given in the next section. Section 3 focuses on two utilized solution algorithms to tackle large instances of PMSPSP-TOU. Sections 4 provides computational results, while Sect. 5 describes the managerial insights regarding energy efficiency obtained by the proposed formulation. Finally, Sect. 6 concludes the paper with several suggestions for future research.

2 Problem description

PMSPSP-TOU can be represented as an activity-on-node (\( AON \)) graph,\( G = \left( {N,A} \right) \), where \( N \) denotes the set of the project’s activities and \( A \) denotes the set of finish-to-start precedence relations between the activities with zero time-lags. The activities are numbered from a dummy start activity 0 to a dummy end activity \( n + 1 \). Processing of the activities can be preempted at discrete time instants and restarted at a later time with a time-dependent restarting cost of energy. The objective is to find the optimal assignment of the staff members to the required skills and the optimal schedule of activities such that the total energy cost is minimized.

The assumptions involved to formulate PMSPSP-TOU are as follows:

  • Renewable resources are multi-skilled workforce.

  • Non-renewable resource is electrical energy under time-of-use tariff.

  • Non-renewable resource is electrical energy which is considered continuously available.

  • All parameters are known with certainty.

  • Setup times of all activities are considered in their processing times.

  • Resuming the preempted activities requires no additional setup times.

  • Processing times of all activities are positive integers.

  • Each staff member can be devoted to at most one skill of one activity at an hour.

  • All the assigned staff members are available at the start of an activity.

  • All the assigned staff members to an activity have to start their work concurrently.

  • Each activity may need one or more skill(s) to be performed.

As a pure mathematical integer programming formulation is intended to be developed for the PMSPSP-TOU, the following notation is used:

Set of staff members

\( R = \left\{ {1, \ldots ,M} \right\} \)

Set of skills

\( V = \left\{ {1, \ldots ,S} \right\} \)

Set of working days

\( W = \left\{ {1, \ldots ,D} \right\} \)

Set of time instants

\( F = \left\{ {0,1, \ldots ,T} \right\} \)

Set of parts of activity i

\( K_{i} = \left\{ {0,1, \ldots ,P_{i} } \right\} \)

\( P_{i} \)

Processing time of activity \( i \)

\( pc_{it} \)

Cost of energy consumption for activity \( i \) at time instant \( t \)

\( \alpha_{it} \)

Cost of restarting activity \( i \) at time instant \( t \)

\( b_{is} \)

Required number of staff members to perform skill \( s \) of activity \( i \)

M

A positive big number

\( r_{ms} \)

1 If staff member \( m \) has skill \( s \);

0 otherwise

\( Z_{iktd} \) (decision variable)

1 If part \( k \) of activity \( i \) is done at time instant \( t \) of day \( d; \)

0 otherwise

\( X_{imktd} \) (decision variable)

1 If part \( k \) of activity \( i \) is done by staff \( m \) at time instant \( t \) of day \( d; \)

0 otherwise

\( Y_{imks} \) (decision variable)

1 if skill \( s \) of part \( k \) of activity \( i \) is done by staff \( m \);

0 otherwise

\( \gamma_{iktd} \) (decision variable)

1 if part \( k \) of activity \( i \) is restarted at time instant \( t \) of day \( d \);

0 otherwise

\( W_{ik} \) (decision variable)

1 if part \( k \) of activity \( i \) is preempted;

0 otherwise

Inspired by the formulation developed by Montaya et al. [30], PMSPSP-TOU can be formulated as follows:

$$ Min f = \mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{t = 0}^{T} \mathop \sum \limits_{k = 1}^{{P_{i} }} \left( {pc_{it} \times Z_{iktd} + \alpha_{it} \times \gamma_{iktd} } \right) $$
(1)

The objective function in Eq. (1) minimizes the total cost of energy consumed to process project activities and the restarted preempted activities. In minimizing Eq. (1), the following constraints have to be considered. Violation from these constraints will culminate in solutions which cannot be implemented in practice.

$$ \mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{t = 0}^{T} Z_{iktd} = 1\quad \forall i \in N,k \in K_{i} $$
(2)

Constraint set (2) guarantees that each part of any activity should be performed only once during the project horizon.

$$ \left[ {\mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{t = 0}^{T - 1} \left( {\left( {\left( {d - 1} \right) \times T} \right) + t} \right) \times Z_{iktd} } \right] + 1 \le \left[ {\mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{t = 0}^{T} \left( {\left( {\left( {d - 1} \right) \times T} \right) + t} \right) \times Z_{{i\left( {k + 1} \right)td}} } \right]\quad \forall i \in N,k \in K_{i} |P $$
(3)

Constraint set (3) preserves precedence relations between successive parts of each activity.

$$ \left[ {\mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{t = 0}^{T - 1} \left( {\left( {\left( {d - 1} \right) \times T} \right) + t} \right) \times Z_{iktd} } \right] + 1 \le \left[ {\mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{t = 0}^{T} \left( {\left( {\left( {d - 1} \right) \times T} \right) + t} \right) \times Z_{j1td} } \right]\quad \forall \left( {i,j} \right)\epsilon A,k \in K_{i} $$
(4)

Constraint set (4) maintains finish-to-start precedence relations between the activities with zero time-lags.

$$ \mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{k = 1}^{{P_{i} }} X_{imktd} \le v_{md} \quad \forall m \in R,t \in F,d \in W $$
(5)

Constraint set (5) describes that each staff member should be devoted to at most one part of one activity at any time instant.

$$ Y_{imsk} \le r_{ms} \quad \forall i \in N, m \in R, s \in V,k \in K_{i} $$
(6)

Constraint set (6) declares that the assigned staff members to an activity should have the required skills to process the activity.

$$ X_{imktd} \le Z_{iktd} \quad \forall i \in N, m \in R, t \in F,d \in W,k \in K_{i} $$
(7)
$$ X_{imktd} + 1 \le Z_{iktd} + \mathop \sum \limits_{s = 1}^{S} Y_{imsk} \quad \forall i \in N, m \in R, t \in F,d \in W,k \in K_{i} $$
(8)

Constraint sets (7) and (8) enforce all the assigned staff members to start their work on the related part of the activity, concurrently.

$$ \mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{m = 1}^{M} \mathop \sum \limits_{t = 0}^{T} X_{imktd} \le \mathop \sum \limits_{s = 1}^{S} b_{is} \quad \forall i \in N, k \in K_{i} $$
(9)

Constraint set (9) assures that the total number of assigned staff members to a part of an activity should not violate the given required number of staffs to perform that activity.

$$ \mathop \sum \limits_{m = 1}^{M} Y_{imks} = b_{is} \quad \forall i \in N, s \in V,k \in K_{i} $$
(10)

Constraint set (10) guarantees that the total assigned staff members to perform a skill for a part of an activity should be equal to the required number of staff members for performing that skill.

$$ \mathop \sum \limits_{d = 1}^{D} \mathop \sum \limits_{t = 0}^{T} X_{imktd} = \mathop \sum \limits_{s = 1}^{S} Y_{imks} \quad i \in N, m \in R,k \in K_{i} $$
(11)

Constraint set (11) declares that each part of any activity is implemented by the assigned staff members to it.

$$ \left[ {\mathop \sum \limits_{{t^{\prime} = 0}}^{T} d^{\prime} \times Z_{{i\left( {k + 1} \right)t^{\prime}d^{\prime}}} } \right] - \left[ {\mathop \sum \limits_{t = 0}^{T} d \times Z_{iktd} } \right] - \left( {Z_{{i\left( {k + 1} \right)1\left( {d + 1} \right)}} + Z_{ikTd} - 1} \right) \le M \times \left( {1 - \mathop \sum \limits_{t = 0}^{T} Z_{iktd} + W_{{i\left( {k + 1} \right)}} } \right)\quad \forall i \in N,d \in W,d^{{\prime }} \ge d,k \in K_{i} |P_{i} $$
(12)

Constraint set (12) preserves the logical relations between \( Z_{iktd} \) and \( W_{ik} \) in different days.

$$ t^{{\prime }} \times Z_{{i\left( {k + 1} \right)t^{\prime}d}} - t^{{\prime }} \times Z_{iktd} \le 1 + \left( {M \times \left( {1 - Z_{iktd} } \right) + W_{{i\left( {k + 1} \right)}} } \right)\quad \forall i \in N,d \in W, t \in F\left| {1,t^{{\prime }} \ge t, k \in K_{i} } \right|P $$
(13)

Constraint set (13) preserves these relations within any single day. More specifically, constraint sets (12) and (13) impel \( W_{ik} \) to be 1, when \( k \) th and (\( k + 1 \))th part of activity \( i \) are done at nonconsecutive time frames (hours).

$$ W_{ik} + Z_{iktd} \le 1 + \gamma_{iktd} \quad \forall i \in N, t \in F,d \in W,k \in K $$
(14)

Constraint set (14) maintains the logical relation between \( Z_{iktd} \), \( W_{ik} \) and \( \gamma_{iktd} \) by impelling \( \gamma_{iktd} \) to be 1, when \( k \) th part of activity \( i \) is preempted to be performed later at time instant \( t \) of day \( d \).

$$ Z_{iktd} ,X_{imktd} ,Y_{imks} ,\gamma_{iktd} ,W_{ik} \in \left\{ {0,1} \right\}\quad \forall i \in N, \forall m \in R, s \in V, t \in F,d \in W,k \in K_{i} $$
(15)

Finally, constraint set (15) describes that all decision variables are binary.

3 The algorithms

Although the developed formulation in Sect. 2 can be applied to solve small-scale instances of PMSPSP-TOU on commercial solvers, achieving the optimal solution of large-scale instances within a reasonable time is impossible due to computational complexity of the problem. In this section, an intelligent meta-heuristic based on electromagnetic-like algorithm (EMA) is proposed to solve PMSPSP-TOU. Furthermore, a genetic algorithm (GA) is developed as a competitive approach to evaluate performance of the proposed EMA.

3.1 Ciphering and deciphering schemes

A ciphering scheme based on random-key is applied in the proposed meta-heuristics. In random-key scheme which guarantees satisfaction of all the constraints, each solution is represented as a vector that assigns a real number between 0 and 1 to each activity in the project [22]. In this structure, a specific solution is represented by numbers between 0 and 1 in B + 1 rows where B is the maximum number of workforce required to perform the activities. This number plays the role of the priority of that activity. Moreover, the number of elements in these rows is equal to the sum of the processing times of the corresponding activities. Since all the numbers used in generating a solution structure are meaningless, a deciphering mechanism is needed to give special meaning to these numbers. Based on the assumptions of the proposed model, the following restrictions have been considered in ciphering process:

  • Precedence relation between the activities are satisfied.

  • All the required skills are assigned to each activity.

  • The assigned workforce has the ability to executing the required skill.

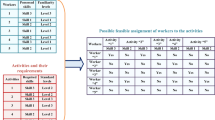
With illustrative propose, let consider a small example with 4 workforce, 3 skills, 3 activities and detailed information shown in Tables 1 and 2.

Table 1 Precedence relations and skill requirements in the illustrative example
Full size table
Table 2 The skills of the staff in the illustrative example
Full size table

A solution representation in five rows (Activity 3 has the maximum required number of workforce of 4, i.e., B = 4) and 7 columns (sum of the processing times of the activities is 7) is depicted in Fig. 1 for this illustrative example.

Fig. 1
figure 1

Schematic representation of a solution structure (ciphering scheme)

Full size image

The first phase in the deciphering mechanism is related to identifying feasible sequence of performing the activities. The input of this phase are the project network and solution structure as depicted in Fig. 1. To this end, each activity \( j \) with processing time of \( d_{j} \) is replaced by \( d_{j} \) parts and each assignment of the part is considered as a distinctive stage. At the beginning of each stage, a part counter for each activity and an activity set is defined. Part counter is an index which denotes each part of the current activity \( j \) with initial value of \( d_{j} \). In each iteration, the parts of non-dummy activities for which their predecessors are finished are placed in the activity set. Then, the following procedure is applied to assign the parts of the activities to the sequence. At each stage \( i \), a ceil integer number obtained by multiplying the number of members in the activity set (\( n_{i} \)) by the \( i \)th number in the first row in Fig. 1 is called \( m_{i} \). Then, \( m_{i}^{th} \) member of the activity set is assigned to stage \( i \). Consequently, one unit is subtracted from the assigned activity part counter value. After each assignment, activities which their part counter value reaches to zero means that they are completed, so these are discarded and the activity set will be updated. In addition, the completed activities will be removed from predecessors of the remaining activities. This process continues until the part counter of all the activities becomes zero. The procedure of assigning activities to the sequence is schematically presented in Fig. 2. Moreover, Table 3 describes details of the assignment process.

Fig. 2
figure 2

Schematic representation of sequencing the activities (deciphering scheme for the first row)

Full size image
Table 3 Detailed calculation of assigning parts of the activities to the sequence
Full size table

The second phase of deciphering mechanism relates to the assignment of the workforce to the activities according to Fig. 2. In this phase, the \( \left( {i + 1} \right){\text{th}} \) row of the solution structure for the \( i{\text{th}} \) workforce, i.e., the second row for the first workforce, the third row for the second workforce and so on, will be considered. To do this, a skill set containing workforce which can perform the current skill is defined and an ascending order is used to allocate workforce to different skills of each activity. At the beginning of each step, a set S including workforce which has the required skill is organized according to Table 2. After that, the following procedure is used to assign workforce to different skills of each activity. At the \( j{\text{th}} \) step of the \( i{\text{th}} \) stage, a ceil integer number resulted by multiplying the number of members (\( n_{ij} \)) in the skill set S by the \( i{\text{th}} \) element of \( \left( {j + 1} \right){\text{th}} \) row is computed and called \( m_{ij} \). Then, \( m_{ij}^{th} \) member of the skill set S is allocated to the \( k{\text{th}} \) skill. Then, the assigned workforce is discarded from all the skill sets S. Iteratively, another workforce is assigned to the \( k{\text{th}} \) skill if needed.

This procedure is repeated until the assigning process of all needed workforce to different skills of each activity ends. The mechanism involved in the second phase of the proposed deciphering process is depicted in Fig. 3 with detailed computations in Table 4 for the illustrative example at hand.

Fig. 3
figure 3

Schematic representation of workforce assignment (second phase of deciphering scheme)

Full size image
Table 4 Detailed calculation of workforce assignment to the required skills of activities
Full size table

3.2 Priority based schedule generation scheme

Because of the special structure of PMSPSP-TOU, a compatible scheme is developed in this section to generate a schedule for a given sequence of activities and workforce assignment. In the proposed scheme, the time frames (hours) within a day are sorted in an ascending order according to their energy consumption cost. Then, the following procedure is performed to identify the position of the \( i{\text{th}} \) section of activity \( j \). Firstly, the first ranked time frame, \( S_{ij} , \) which is eligible based on precedence relations, is identified. Then, for a given project deadline an upper bound for starting the \( i{\text{th}} \) section of activity \( j \), \( LS_{ij} \), is calculated,. Next, the first time frame after, \( min\left( {S_{ij} ,LS_{ij} } \right), \) in which all the required resources are available is selected as the start time of the \( i{\text{th}} \) section of activity \( j \). This procedure continues until the start times of all activities are assigned.

To demonstrate the above generation scheme, consider the cost of energy consumption for a 24 h period of the illustrative example at hand reported in Table 5. Moreover, it is assumed that all the three activities have to be completed in two working days. We further assume that all workforces are available except Staff 4 that is in vacation in the first day.

Table 5 Price of energy consumed by each activity during different hours of a day
Full size table

For the sequence of activities in Fig. 2 and the workforce assignment in Fig. 3, the resulting schedule is presented in Fig. 4. As it can be observed, all the activities are arranged within time frames 3–8 (hours) during 2 days which have the minimal cost of energy consumption. Note that while the cost of energy to execute all activities is 80, considering the cost of restarting preempted activities (25 for all activities), the total cost of energy will be 155.

Fig. 4
figure 4

The schedule for the illustrative example using the priority based schedule generation scheme

Full size image

3.3 Preemption elimination local search

Upon the generation of a schedule, a novel local search algorithm is implemented in this section to eliminate non-beneficial preemptions. This would be a tradeoff between performing the activities at high rate energy periods and the restarting cost of preempted activities. As mentioned before, each activity \( j \) with processing time of \( d_{j} \) is replaced by \( d_{j} \) parts and each part is scheduled as a distinctive sub-activity which may give rise to preemptions. In the proposed compatible schedule generation scheme, a main iterative loop is considered to find appropriate balanced schedules. To do this, the algorithm iteratively scans time frames \( t \) in order to find the \( i{\text{th}} \) section of the activity \( j \) which is preempted at \( t \) while \( i \) is not the last section of the activity \( j \). In case where there is such a preemption, the local search seeks the time frames after \( t \) to find the first two successive time frames called \( \mathop t\limits^{{\prime }} \) and \( \mathop t\limits^{{\prime }} + 1 \), where the \( i{\text{th}} \) and \( (i + 1){\text{th}} \) sections of activity \( j \) can be scheduled without preemption. Then, the priority based schedule generation scheme is employed to schedule the remaining sections of the activities after time frame \( \mathop t\limits^{{\prime }} + 1 \). The resulted schedule is replaced by the current schedule if its total cost becomes lower than the current cost of the schedule. Otherwise, the current schedule is held. This procedure continues until no improvement is observed.

The application of the preemption elimination local search on the schedule reported in Fig. 4 is shown in Fig. 5. It is clear that all the activities are scheduled within a day without any preemption. Note that using this procedure the cost of energy to execute all the activities is 80, while there is no extra cost to restart preempted activities. The steps involved in the preemption elimination local search applied on the illustrative example are reported in Table 6.

Fig. 5
figure 5

Schedule for the illustrative example after applying the preemption elimination local search

Full size image
Table 6 Steps of the activity preemption elimination algorithm
Full size table

3.4 The utilized EMA

In this section, the population-based electromagnetic like algorithm (EMA) is used to find a satisfying solution for PMSPSP-TOU. EMA was firstly introduced by [Birbil & Fang [4]], where its several successful applications can be found in the literature [6, 23, 41, 43]. In this algorithm, a solution is considered as a charged particle, based on which an evaluation function is used to identify its fitness. EMA exploits the fact that charged particles in a population put force on each other and calculates the resultant forces inserted to each particle using the vector sum method. The main mechanism in this algorithm begins with generating initial feasible solutions containing particles with charges. Then, the force inserted to each particle is calculated based on the charges. After that, the fitness of the particles is obtained using the evaluation function in order to assess the performance of the new particles created in their new positions. These particles will be replaced with previously generated particles if the fitness value becomes remarkably better than the fitness value of the particles generated in previous generations. This process is pursued until the best possible solution is obtained.

The main procedure of EMA involves four different phases including generating initial solutions, local search, calculating resultant vector of the forces inserted to each particle and particles’ movement in direction of their resultant vector. These phases are discussed in details in the next sub-sections.

3.4.1 Initial solutions

Initial solutions of EMA are first generated based on the ciphering and deciphering schemes presented in Sect. 3.1. Then, a priority-based schedule generation scheme is used to specify the start times of all activities. At the end of this phase the novel heuristic preemption elimination local search algorithm discussed in Sect. 3.3 is employed to improve the quality of the schedules.

3.4.2 Resultant forces inserted to each particle

As mentioned before, all the particles in the current population insert force to each other and that the particle with the highest value of fitness function is selected as a near-optimum solution. This solution attracts other solutions while the worst solution repels the other solutions. The force that two solutions insert to each other has a reverse relation with their squared distance. In addition, this force has a direct relation with the charge of both particles. In other words, the following equation is used to compute the force that two particles insert to each other.

$$ q^{i} = e^{{\left[ {\frac{{ - n\left( {f_{i} - f_{best} } \right)}}{{\mathop \sum \nolimits_{k = 1}^{m} \left( {f_{k} - f_{best} } \right)}}} \right]}} ;\quad i = 1,2, \ldots ,m $$
(16)

In Eq. (16), \( n \) denotes dimension of the problem,\( q^{i} \) denotes the charge of the \( i{\text{th}} \) particle,\( f_{i} \) and \( f_{best} \) denote the fitness value of the \( i{\text{th}} \) charged particle and the fitness value of the best particle, respectively. In addition, while all the initial generated particles are neutral, for each pair of particles, the particle with the higher fitness value has an attractive role and the other particle has a repelling role. The particle with the highest fitness value attracts all other particles. Equation (17) is used to calculate the force that the \( i{\text{th}} \) particle inserts to \( j{\text{th}} \) particle.

$$ F_{ij} = \left\{ {\begin{array}{*{20}c} {\left( {x_{i} - x_{j} } \right)\frac{{q^{i} .q^{j} }}{{x_{i} - x_{j}^{2} }}, {\text{if f}}_{j} < {\text{f}}_{i} ; \quad i = 1, \ldots ,m} \\ {\left( {x_{j} - x_{i} } \right)\frac{{q^{i} .q^{j} }}{{x_{i} - x_{j}^{2} }}, {\text{if f}}_{j} > {\text{f}}_{i} ;\quad j = 1, \ldots ,m} \\ \end{array} } \right. $$
(17)

In Eq. (17), \( {\text{F}}_{ij} \) is the force that the \( i{\text{th}} \) particle inserts to the \( j{\text{th}} \) particle and the positions of both the \( i{\text{th}} \) and the \( j{\text{th}} \) particles are respectively denoted by \( x_{i} \) and \( x_{j} \). Moreover, the resultant force inserted to each particle can be computed as follows:

$$ F_{i} = \mathop \sum \limits_{j = 1}^{m} F_{ij} ;\quad i = 1,2, \ldots ,m. $$
(18)

To avoid trapping into local optima, the algorithm proposed by Birbil et al. [5] is used in which the particle with the highest distance from the best solution has the most possibility of being attracted by other particles. This particle can be found using:

$$ x_{p} = {\text{argmax}}\left\{ {x_{best} - x_{i} ,i = 1,2, \ldots ,m} \right\} $$
(19)

where, \( x_{p} \) and \( x_{best} \) denote the position of the furthest and the best particles, respectively. In addition, the force that the furthest particle inserts to other particles is calculated by

$$ F_{pj} = \left\{ {\begin{array}{*{20}c} {\left( {x_{j} - x_{p} } \right)\frac{{\lambda \times q^{i} \times q^{j} }}{{x_{p} - x_{j}^{2} }}, {\text{if f}}_{j} < {\text{f}}_{p} } \\ {\left( {x_{p} - x_{i} } \right)\frac{{\lambda \times q^{i} \times q^{j} }}{{x_{p} - x_{j}^{2} }}, {\text{if f}}_{j} > {\text{f}}_{p} } \\ \end{array} } \right.;\quad j = 1,2, \ldots ,m $$
(20)

where, \( \lambda \) is a random number generated between 0 and 1 and \( {\text{F}}_{pj} \) denotes the force that the furthest particle inserts to the other particles.

3.4.3 Particle’s movement

As each particle moves in the solution space based on its force, the quantity of the particles’ movements is obtained using

$$ x_{i} = x_{i} + \alpha \times \left( {RNG} \right) \times \frac{{F_{i} }}{{F_{i} }};\quad i = 1,2, \ldots ,m $$
(21)
$$ RNG_{k} = \left\{ {\begin{array}{*{20}c} {U_{k} - x_{ik} , x < 0} \\ { - \left( {x_{ik} - l_{k} } \right), x \ge 0} \\ \end{array} } \right.;\quad k = 1, \ldots ,n, $$
(22)

where, the upper and the lower bounds of the \( k{\text{th}} \) dimension and particles’ movement radius are respectively shown by \( U_{k} \), \( l_{k} \) and \( \alpha \), respectively. This movement will lead all the particles towards the best solution.

3.4.4 Local search

A simple local search mechanism presented by Birbil and Fang [4] is used in this paper to explore space around each particle. This method uses the lower and the upper bounds of the dimension to search space around each solution to find better solutions. The new solutions discovered by this mechanism are replaced with the current ones if their fitness value becomes better than the fitness value of the existing solutions. Otherwise, the existing solution is conveyed to the next iteration.

3.4.5 Stopping conditions

Several criteria such as a limited CPU time, a pre-specified number of iterations and so on can be considered as a stopping condition. In this paper, the utilized EMA stops when the best value of the fitness function in a predefined number of iterations is not changed significantly.

3.5 The proposed GA

A genetic algorithm (GA) is developed in this section as a competitive algorithm to validate the results obtained and to evaluate the performance of the utilized EMA in solving large-scale instances of the PMSPSP-TOU. GA which was firstly introduced by Holland [16], has been used successfully in many project scheduling problems [14, 44]. The most significant advantage of this algorithm is its multidirectional capability on seeking solution space to keep best solutions obtained in previous iterations and to convey them to the next generations. In this algorithm, the ciphering and deciphering schemes presented in Sect. 3.1 is first used here to generate an initial population. Then, the fitness of the solutions in the initial population is evaluated, based on which a roulette wheel mechanism is employed to identify parent solutions to be used in a uniform crossover operator to generate offspring solutions. Moreover, three different mutation operators, i.e., swap, insertion and reversion, are used randomly to avoid premature convergence and trapping into local optima. The current solutions and the offspring solutions are next combined together. After that, all the solutions are evaluated to transfer a predefined percent of the solutions with higher quality to the next generations. This process continues until the specified stopping condition is met.

3.6 Parameter tuning

All the parameters used in the utilized EMA and GA should be set precisely to enhance the performance of the algorithms. This calibration process is performed using some test problems generated as follows.

  • The processing time of an activity,\( P_{i} \), follows a uniform distribution in the interval [2,4], i.e., \( P_{i} \sim {\text{uniform}} \left[ {2, 4} \right] \).

  • An element of the capability matrix of performing skills by workforces,\( r_{ms} , \) is either zero or one, i.e., \( r_{ms} \sim {\text{integer}} \left\{ {0,1} \right\} \).

  • The consumption price of energy \( \left( {pc_{it} } \right) \) is considered different within time intervals 3–10, 11–18 and 2–19 with random values following a uniform distribution in [1000,15,000], [2000,3000], [1500,2000], respectively.

  • The cost of restarting preempted activities \( \left( {a_{it} } \right) \) within time intervals 3–10, 11–18, and 2–19 is considered a uniform random value in [3000,4000], [2000,2500], [4000,5000], respectively.

  • The workforce availability follows \( v_{md} \sim {\text{integer}} \left\{ {0,1} \right\} \).

  • The number of required workforces to perform different activities follows \( b_{is} \sim {\text{integer}} \left\{ {1,3} \right\} \).

As there is no benchmark available in the literature regarding the PMSPSP-TOU, 50 different test problems are generated in this paper to evaluate the performance of the utilized algorithms in order to calibrate their parameters. These problems are divided into small and large scale problems. In addition, they are classified based on the number of activities (N), the number of skills (S), the number of workforces (M) and the number of work days (D), as reported in Table 7. The solutions of these problems are used to evaluate the performances of the two solution algorithms.

Table 7 The general data of the test problems
Full size table

The Taguchi method, as an alternative to full factorial experimental design, is applied in this paper to tune the main parameters of the meta-heuristics. Taguchi method can remarkably decrease the number of experiments required for identifying the optimal levels of the parameters [39]. All the factors used in this method can be divided in two main groups including noise and controllable factors. This method is mainly designed to identify the optimal level of the parameters so that the effect of noise factors is minimized while the effect of the controllable factors is maximized. Hence, a signal to noise ratio is used in this method to measure the deviations involved in the response variable as follows.

$$ \left( {S/N} \right) = - 10\log \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{nr} \left( {Y_{i}^{2} } \right)}}{nr}} \right) $$
(23)

In Eq. (23), the response variable and the number of orthogonal arrays are denoted by \( Y \) and \( nr \), respectively.

All the parameters are assumed to have three levels as low (Level 1), medium (Level 2) and high (Level 3) shown in Table 8. Based on these levels and the response obtained for a specific problem, the Minitab software that uses the Taguchi L9 design is then used to tune the parameters of EMA and GA. Each design is implemented three times on MATLAB software, based on which their mean is presented in Tables 9 and 10. In addition, the corresponding values of the \( S/N \) ratio for each algorithm are shown in Fig. 6 in order to indicate the best levels of the parameters shown in the last column of Table 8.

Table 8 Algorithm parameter ranges along with their levels
Full size table
Table 9 Computational results to tune parameters of EMA
Full size table
Table 10 Computational results to tune parameters of GA
Full size table
Fig. 6
figure 6

S/N ratio plots of the proposed EMA and GA

Full size image

4 Computational results

In this section, the 50 generated test problems are used to evaluate the performance of the utilized solution algorithms. Problems 1–10 which can be solved optimally using the GAMS software in a reasonable computational time are considered as small scale problems while the other problems are classified as large scale problems.

Both the algorithms are coded in MATLAB software and all the problems are solved on a PC with Core I 5 CPU and 4 GB RAM. The result of solving small size problems by the meta-heuristics is compared to the global optimal solutions of GAMS. In additions, the result of solving large scale problems is compared to the upper bound solutions obtained by the GAMS software within 1 h computational time. These results are shown in Table 11. In addition, the convergence trend of the best solution and the mean of the solutions obtained by GA and EMA for Problem 27 (as a representative for all test problems) are presented in Fig. 7.

Table 11 The result of solving all the test problems
Full size table
Fig. 7
figure 7

Problem 27’s convergence trend of the best and the mean solutions in different iterations

Full size image

A measure called relative percentage deviation (RPD) is used to eliminate the effect of the size of the problem on the quality of the solution obtained using the solution algorithms. This measure is defined as:

$$ RPD_{ij} = \frac{{\left( {Sol_{ij} - BestSol_{j} } \right)}}{{BestSol_{j} }} \times 100;\quad \forall j = 1, \ldots ,50,i = EMA,GA $$
(24)

where the best solution reported for \( j{\text{th}} \) test problem, the best solution of the \( j{\text{th}} \) test problem reported by \( i{\text{th}} \) algorithm and the distance of the solution obtained by the \( i{\text{th}} \) algorithm from the best solution of the \( j{\text{th}} \) test problem are respectively denoted by \( BestSol_{j} \), \( Sol_{ij} \) and \( RPD_{ij} \).

A simple investigation of the results presented in Table 11 reveals that the deviance between solutions of ten small size problems obtained by the developed meta-heuristics and the corresponding optimal results of the GAMS software is negligible measured by relative deviance percentage of Dev %GA vs GAMS and Dev %EMA vs GAMS. More specifically, EMA gained optimal solutions for 6 out of 10 small scale problems while GA solved 4 out of 10 problems to optimality. Also, EMA and GA have resulted on average 8.54% and 6.26% better solutions than GAMS solver. In addition, the result of solving large scale problems by the means of the algorithms is approximately better than the local solutions resulted by implementation of the GAMS software in 1 h CPU-time. Moreover, the average RPD of 0.75 and 3.28 for EMA and GA, respectively, confirms satisfying performance of the utilized algorithms to tackle PMSPSP-TOU. Finally, a paired t test is implemented on the Minitab software to compare the performance of the solution algorithms in solving all 50 test problems. The statistical results reported in Table 12 show that the solutions obtained by EMA are remarkably better than the ones obtained by GA at a significance level of 0.05.

Table 12 The results of paired t-test for comparing performance of the algorithms
Full size table

5 Managerial insights

This section is devoted to highlight the energy efficiency aspects of the developed project scheduling model. To this end, a case project with ten activities, three skills and four workforces is considered to illustrate the way the schedule resulted from the proposed model saves energy costs. In this example, it is assumed that all the workforces are available and the project should be performed in 2 days. Besides, we assume that all the workforces are able to perform all the skills. The energy price and the cost of starting preempted activities are assumed the same for all the activities. Other required information related the example is given in Table 13.

Table 13 Predecessor relations, execution time, required skills and workforces of the problem
Full size table

In order to have a meaningful interpretation, two scenarios are considered regarding energy consumption tariff. In the first scenario, a time-dependent scheme is assumed for energy consumption tariff, while the second scenario has a fixed energy consumption cost throughout the project’s horizon. The required data regarding the energy consumption tariffs for both scenarios are given in Table 14.

Table 14 Energy consumption costs and preempted activities’ restarting costs
Full size table

This problem instance is solved using the developed EMA of this paper. The resulting Gant chart for the first and the second scenarios are shown in Figs. 8 and 9, respectively. As it can be observed from Fig. 8, all the activities are scheduled to be implemented within the low cost hours, i.e., 2:00–10:00 a.m. during 2 days. This schedule will cost 20,500 for energy consumption. On the other hand, in the schedule obtained for the second scenario represented in Fig. 9, all the activities are arranged consecutively in the first day within 00:00–17:00 p.m. The total cost of energy consumption for the schedule obtained in the second scenario equals to 30,000 which is 46.3% more than the one in the first scenario. By comparison of the above two scenarios, it can be concluded that the first scenario which involves time-of-use energy tariff, respects to social responsibility along with minimizing cost of energy which is requisite of sustainable development. This mastery of the first scenario would be expected because of the compatible schedule generation scheme described in Sect. 3.2 followed by a preemption eliminative local search described in Sect. 3.3.

Fig. 8
figure 8

Gant chart for the first scenario (with time-of-use energy tariff)

Full size image
Fig. 9
figure 9

Gant chart for the second scenario (with fixed energy tariff)

Full size image

6 Conclusion

Although energy efficient decisions have been a struggle by organizations to cut down their energy related costs, nowadays it is identified as a core function of sustainable management to be ready to endure in competitive global market. This paper focused on a sustainable framework to derive an energy efficient schedule for a preemptive multi-skilled resource constrained project under a time-of-use policy for energy tariff. The problem was formulated as a pure integer programming model named PMSPSP-TOU. Then, two meta-heuristic algorithms based on genetic and electromagnetic was developed to overcome computational complexity of the PMSPSP-TOU. Special ciphering scheme and deciphering mechanism, intelligent local search heuristics and calibrated parameters were the noticeable features of the proposed EMA and GA. In addition, a compatible schedule generation scheme was developed to respect the time-of-use characteristics of the problem. The performance of the solution algorithms were evaluated based on 50 random test instances with up to 30 activities. The results showed that both the algorithms give solutions with far ignorable deviance from the optimum solution resulted by GAMS. Moreover, for the instances with more than ten activities for which the optimum solution cannot be achieved, the proposed EMA and GA obtained far better solutions than the upper bounds provided by GAMS. While the proposed EMA gives more robust solutions than GA measured by the average relative percentage deviation (RPD), a statistical test showed that the quality of the solutions obtained by EMA is better than the one using GA. Finally, the proposed model was implemented to solve an example with 10 activities under two scenarios for energy tariff; with time-of-use and fixed tariff. The solutions obtained for both scenarios showed that the scenario under time-of-use energy tariff gives a base schedule which takes into account social responsibility while the scenario under fixed energy tariff only tries to optimize project’s makespan with high cost of energy consumption.

Findings of this paper can help decision makers in project-oriented organizations that have concerns about scheduling their projects under time-of-use energy tariffs. Several extensions are possible for interested reader. One can extend the current work when there is a dynamic policy for time-of-use energy tariffs. Another extension can be considering multiple modes for activities with different levels of energy requirements.