Identification of Constitutive Model Parameters for Nimonic 80A Superalloy

Abstract

Nimonic 80A is a nickel-chrome superalloy, commonly used due to its high resistance against creep, oxidation, and temperature corrosion. This paper presents the material constitutive models of Nimonic 80A superalloy. Johnson–Cook (JC) and modified JC model is preferred among the different material constitutive equations (Zerill Armstrong, Bodner Partom, Arrhenius type) due to its accuracy in the literature. Three different types of compression tests were applied to determine the equation parameters. Firstly, quasi-static tests were performed at room temperature. These tests were conducted at 10⁻³, 10⁻², and 10⁻¹ s⁻¹ strain rates. Secondly, compression tests were performed at room temperature at high strain rates (370–954 s⁻¹) using the Split-Hopkinson pressure bar. Finally, compression tests were performed at a temperature level from 24 to 200 °C at the reference strain rate (10⁻³ s⁻¹). Johnson–Cook and modified JC model parameters of Nimonic 80A were determined with the data obtained from these tests, and they were finally verified statistically.

1 Introduction

Superalloys are chemically complex alloys based on iron, cobalt, or nickel. Nimonic 80A alloy belongs to nickel-based superalloys and are referred to as materials suitable for use at high temperatures. These materials show high creep and rupture strength at elevated temperature by the precipitation hardening of aluminum and titanium elements, and materials also have high corrosion resistance [1], because they contain 20% chromium and comparatively small content of aluminum [2]. Nimonic 80A alloy is widely used in jet engines and gas turbines due to its superior resistance against creep, oxidation, and temperature corrosion [3].

On the other hand, nickel-based superalloys are among the most difficult to process due to their high thermal–mechanical properties. In particular, numerical modeling of the cutting process is being applied as an alternative solution [4], since the researches on machining are expensive and time consuming. Among the numerical methods used in the modeling of the cutting process, the most preferred technique is the finite element method. During chip formation process, huge improvements in the machining mechanics is provided [5,6,7] by means of finite element softwares (ANSYS, ABAQUS, DEFORM, ADVANTEDGE, etc.) which help to forecast the cutting forces, temperature, and stress values. Thus, the cutting conditions can be optimized in the machining operations, and it is possible to make significant contributions to lower production cost by decreasing the tool cost [8]. In this sense, finite element method has become an indispensable tool in the analysis of manufacturing processes and engineering designs.

Based on the finite elements, the experimental results (force, temperature, etc.) of manufacturing processes should be compatible with the simulation results obtained from the computer softwares. In this context, it is very important to model the materials correctly in the simulation packages. Many constitutive material models are proposed that can represent high strain behaviors at wide range of strain rates and temperatures [9]. These models are Zerilli–Armstrong, Bodner–Partom, and Johnson–Cook material models, and it is emphasized that the Johnson–Cook material model is commonly used for many finite element packages [9]. It is necessary to perform dynamic tests as well as quasi-static experiments and high-temperature experiments in order to determine the Johnson–Cook material model. This requires a Split-Hopkinson pressure bar, which is a very onerous process. There are several studies related to the installation of Split-Hopkinson bar in the literature [10,11,12,13,14]. Through these devices, several studies related to the determination of the Johnson–Cook parameters in the literature have been made. In this context, Gupta and colleagues used Johnson–Cook material parameters for three different cast aluminum alloys using high strain rate range (10⁻³–5000 s⁻¹) and high temperature ranges (235 °C and 435 °C) [15]. Dorogoy and Rittel determined Johnson–Cook parameters of Ti6Al4V material with quasi-static, dynamic, and high-temperature tests using shear-compression specimen (SCS) sample [9]. Shrot and Baker determined the Johnson–Cook material parameters of the AISI 52100 steel using machining simulations using the inverse identification method [16]. Banerjee et al. [17] identified the Johnson–Cook material model for the armor steel with quasi-static, dynamic, and high-temperature tests. The common characteristic to all these studies is to determine the JC material model of any material, and these authors emphasized that JC model has higher accurate results than other constitutive models. They also specified that tensile or compression tests can be applied depending on their usage area. In the light of this information, it can be clearly understood that there is not any constitutive model of Nimonic 80A in the literature, and thus, there is no finite element simulation for any plastic deformation process related to this material. In this context, it is aimed to determine the Johnson–Cook material parameters of the Nimonic 80A superalloy using standard compression samples. Finally, modified JC parameters have also been determined, and the high accuracy of JC model has been verified statistically.

2 Experimental and Constitutive Model

The experimental procedures consist of three steps to determine the Johnson–Cook model parameters of the Nimonic 80A alloy.

2.1 Dynamic Experiments

In the first stage, dynamic experiments were carried out with 370–954 s⁻¹ strain rates on the Split-Hopkinson pressure bar (SHPB) apparatus belonging to the Material Laboratory of Ghent University. The images of undeformed and deformed samples which are used for dynamic experiments are shown in Fig. 1. The sample had 4 mm diameter and 3.74 mm length.

Fig. 1

Compression test sample

2.2 Quasi-Static Experiments

In the second stage, quasi-static experiments at strain rates of 10⁻³, 10⁻² and 10⁻¹ s⁻¹ were performed by using Instron Universal Testing Machine having 50 kN maximum capacity in Ghent University. The machine was stopped manually near 50 kN load since the material was very ductile and did not crack spontaneously. The quasi-static sample had the same dimension as the sample used in dynamic experiments.

2.3 High-Temperature Experiments

In the third stage, the high-temperature tests between 24 and 200 °C were carried out by Zwick/Roell Z600 Universal Testing Machine in Iron and Steel Institute of Karabük University. The high-temperature sample was also similar to other test samples as shown in Fig. 1. All experimental procedures are shown in Fig. 2.

Fig. 2

Experimental methodology

The mechanical/physical properties and chemical composition of the Nimonic 80A alloy used in this study are given in Tables 1 and 2, respectively, in the light of material certification from the purchased company. The properties in Table 1 were needed for plastic deformation simulations in software packages.

Table 1 Mechanical and physical properties of Nimonic 80A

Table 2 Chemical composition of Nimonic 80A

3 JC Model and Determination of Parameters

The plastic deformation behavior of Nimonic 80A alloy has been taken into account in the Johnson–Cook model [18]. This material model is particularly suitable for modeling the high deformation rate of metal. It is usually used in adiabatic transient dynamic analyses. In the Johnson–Cook model, it is assumed that the yield stress (σ⁰) is in the following form:

$$\sigma^{0} = \left( {A + B\left( {\varepsilon^{p} } \right)^{n} } \right)\left( {1 + C \ln \left( {\frac{{\dot{\varepsilon }^{p} }}{{\dot{\varepsilon }_{0} }}} \right)} \right)\left( {1 - \left( {\hat{T}} \right)^{m} } \right)$$

(1)

and

$$\hat{T} = \left\{ {\begin{array}{*{20}l} {0 } \hfill & {{\text{for}}\quad T < T_{\text{r}} } \hfill \\ {\frac{{T - T_{\text{r}} }}{{T_{\text{m}} - T_{\text{r}} }} } \hfill & {{\text{for}}\quad T_{\text{r}} \le T \le T_{\text{m}} } \hfill \\ 1 \hfill & {{\text{for}}\quad T > T_{\text{m}} } \hfill \\ \end{array} } \right.$$

(2)

In Eq. (1), parameters obtained from mechanical tests that are A, B, C, n and m are yield stress below room temperature, strain hardening, strain rate constant, strain hardening constant, and thermal softening constant, respectively. The other parameters ɛ^p, $\dot{\varepsilon }^{p}$, $\dot{\varepsilon }_{0}$, T_r, T_m, and T are equivalent plastic strain, plastic strain rate, reference strain rate, room temperature, melting temperature, and reference temperature, respectively. Also, $\dot{\varepsilon }_{0}$ and C are usually measured at the reference temperature or below it.

4 Determination of “A, B and n”

In the Johnson–Cook material model, A indicates the yield stress at the reference strain rate (10⁻³ s⁻¹). Constant A has been determined as 487 MPa according to the curve shown in Fig. 3 which is created with average of three stress–strain diagram at room temperature and reference strain rate.

Fig. 3

Compression test in reference strain rate and room temperature

According to the test at the reference strain rate, the part where the yield stress starts is assumed as zero strain, and the constants B and n are determined according to the linear increase in stress values at each elongation amount. This assumption is between the yield stress and the maximum stress. According to Fig. 3, compressive yield stress values at 10, 20, and 30% strains are found to be about 748, 1003 and 1254 MPa. Based on these average stress–strain values and Eq. 3, the constants B and n have been calculated as 2511 MPa and 0.983, respectively.

$$\sigma^{0} = \left( {A + B\left( {\varepsilon^{p} } \right)^{n} } \right)$$

(3)

5 Determination of “C”

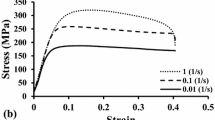
In the Johnson–Cook material model, C indicates the strain rate constant. It is observed that the compressive stress increases with the increase in strain rate in the compression tests carried out at room temperature. This is consistent with the literature [9]. The change in stress values depending on increase in the strain rate is shown in Fig. 4.

Fig. 4

Stress–strain graph for dynamic tests

It is observed that the yield stresses are measured as 487, 500, and 513 MPa at 10⁻³, 10⁻², and 10⁻¹ s⁻¹ strain rate values in the light of experimental data (Fig. 5). At dynamic strain rate values that are 370, 720, and 954 s⁻¹, yield stresses increases to 562, 566, and 568 MPa, respectively, as expected. σ⁰ and $\dot{\varepsilon }_{0}$ are constants with values of 487 MPa and 10⁻³ s⁻¹, respectively. When other five values (10⁻², 10⁻¹, 370, 720, and 954 s⁻¹) are inserted in Eq. 4, σ values are 500, 513, 562, 566, and 568 MPa, respectively. There are five equations with one unknown. Thus, the average value of constant C can be calculated as 0.0116 according to this average stress–strain rate values and Eq. 4.

Fig. 5

Stress–strain graph for high temperature tests

$$\sigma = \sigma^{0} \left( {1 + C \ln \left( {\frac{{\dot{\varepsilon }^{p} }}{{\dot{\varepsilon }_{0} }}} \right)} \right)$$

(4)

6 Determination of “m”

In the Johnson–Cook material model, the symbol m indicates the temperature constant. In the compression tests carried out at the reference strain rate (10⁻³ s⁻¹), the yield stress values generally decreases with increase in test temperature, as mentioned by some researchers [19,20,21]. The change in the compressive stress by increasing the test temperature is shown in Fig. 5.

The yield stresses have been measured as 487, 465, and 450 MPa at 24, 100, and 200 °C, respectively, as shown in Fig. 5 created by experimental data from high-temperature tests. σ⁰, T_r and T_m are constants and 487 MPa, 24 °C, and 1365 °C, respectively. When other two values (100 and 200 °C) are inserted to Eq. 5, σ values are 465 and 450 MPa, respectively. There are two equations with one unknown. The average value of the constant m value has been calculated as 1.162 according to the stress–temperature graph and Eq. 5.

$$\sigma = \sigma^{0} \left( {1 - \left( {\frac{{T - T_{r} }}{{T_{m} - T_{r} }}} \right)^{m} } \right)$$

(5)

The Johnson–Cook material parameters of the Nimonic 80A alloy are given in Table 3 in the light of quasi-static, dynamic, and high-temperature experiments.

Table 3 JC parameters of Nimonic 80A

7 Modified JC Model and Determination of Parameters

The plastic deformation behavior of Nimonic 80A alloy has also been considered by the modified JC model. In the modified JC model, it is assumed that the yield stress (σ⁰) is in the following form:

$$\sigma^{0} = \left( {A_{1} + B_{1} \varepsilon + B_{2} \varepsilon^{2} } \right)\left( {1 + C_{1} \ln \left( {\frac{{\dot{\varepsilon }^{p} }}{{\dot{\varepsilon }_{0} }}} \right)} \right)\exp \left[ {\left( {\lambda_{1} + \lambda_{2} \ln \left( {\frac{{\dot{\varepsilon }^{p} }}{{\dot{\varepsilon }_{0} }}} \right)} \right)\left( {T - T_{\text{ref}} } \right)} \right]$$

(6)

A₁, B₁, B₂, C₁, λ₁, and λ₂ are the material constants, and their meanings are the same as the Johnson–Cook model parameters.

8 Determination of “A ₁ , B ₁ and B ₂”

In the modified JC material model, A₁ indicates the yield stress at the reference strain rate (10⁻³ s⁻¹) and temperature (24 °C). A₁ constant is determined as 487 MPa according to the curve shown in Fig. 3 which is created with an average of three stress–strain diagram at room temperature and reference strain rate. According to the test at the reference strain rate, the yield stress point is assumed as zero strain, and the constants of B and n were determined according to the linear increase in stress values at each strain. This assumption is between the yield stress and the maximum stress. When three strain values (10, 20 and 30%) are inserted to Eq. 6, σ values are 748, 1003 and 1254 MPa, respectively. There are three equations with two unknown. Based on these average stress–strain values and Eq. 6, the average of the constants B₁ and B₂ are calculated as 2640 MPa and − 300 MPa, respectively.

9 Determination of “C ₁”

In the modified JC material model, C₁ indicates the strain rate constant. It is observed that the compressive stress increases with the increase in strain rate in the compression tests carried out at room temperature. When the tests are performed at reference temperature and reference strain, the equation converts to Eq. 4.

$$\sigma^{0} = \left( {1 + C_{1} \ln \left( {\frac{{\dot{\varepsilon }^{p} }}{{\dot{\varepsilon }_{0} }}} \right)} \right) = \left( {1 + C \ln \left( {\frac{{\dot{\varepsilon }^{p} }}{{\dot{\varepsilon }_{0} }}} \right)} \right)$$

where C₁ = C = 0.0116.

10 Determination of “λ ₁ and λ ₂”

In the modified JC material model, λ₁ and λ₂ indicate the temperature constants. When the tests are conducted at reference strain and strain rate, the equation converts to Eq. 7.

$$\sigma = \sigma^{0} \cdot \exp \left[ {\left( {\lambda_{1} } \right)\left( {T - T_{\text{ref}} } \right)} \right]$$

(7)

σ⁰ is already 487 MPa. Thus, when the two temperature values (100 and 200 °C) are inserted to Eq. 7, σ values are 465 and 450 MPa, respectively. There are two equations with one unknown. The average value of constant λ₁ can be calculated as − 0.00053 according to the stress–temperature graph and Eq. 7.

When the tests are performed at reference strain, 10⁻² and 10⁻¹ s⁻¹ strain rates and at 100 °C, σ values are 480 and 493 MPa, respectively. There are two equations with one unknown. Hence the average value of the constant λ₂ can be calculated as − 0.0000032 according to Eq. 8.

$$\sigma = 487\left( {1 + C_{1} \ln \left( {\frac{{\dot{\varepsilon }^{p} }}{{\dot{\varepsilon }_{0} }}} \right)} \right)\exp \left[ {\left( {\lambda_{1} + \lambda_{2} \ln \left( {\frac{{\dot{\varepsilon }^{p} }}{{\dot{\varepsilon }_{0} }}} \right)} \right)\left( {T - T_{\text{ref}} } \right)} \right]$$

(8)

The modified JC material parameters of the Nimonic 80A alloy are given in Table 4 in the light of quasi-static, dynamic, and high-temperature experiments.

Table 4 Modified JC parameters of Nimonic 80A

11 Verification of Constitutive Models

In the next stage of the study, the reliability of the models has been evaluated with various error control methods to show the suitability of the constitutive models developed with the experimental studies.

Since the constitutive models are developed with a certain error (the difference between the value obtained from the experimental and predicted results, e), the average of the sum of these error values must be minimized. This means that the mean-squared error (MSE) is a criterion that also determines the model performance. When the model results fit the actual test results; root mean square error (RMSE), coefficient of determination (R²) and mean absolute percentage error (MAPE) are determined. In addition, percent error (% error) values of all the values found in the finite element modeling result analysis are set:

$${\text{MSE}} = \frac{1}{p}\mathop \sum \limits_{i} e_{i}^{2} = \frac{1}{p}\mathop \sum \limits_{i} \left( {t_{i} - o_{i} } \right)^{2}$$

(9)

$${\text{RMSE}} = \sqrt {\text{MSE}} = \sqrt {\frac{1}{p}\mathop \sum \limits_{i} e_{i}^{2} } = \sqrt {\frac{1}{p}\mathop \sum \limits_{i} \left( {t_{i} - o_{i} } \right)^{2} }$$

(10)

$$R^{2} = 1 - \left( {\frac{{\mathop \sum \nolimits_{i} \left( {t_{i} - o_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i} o_{i}^{2} }}} \right)$$

(11)

$$\% {\text{Error}} = \frac{{\left| {t_{i} - o_{i} } \right|}}{{t_{i} }}\, \times \,100$$

(12)

$${\text{MAPE}} = \frac{1}{p}\mathop \sum \limits_{i} \frac{{\left| {t_{i} - o_{i} } \right|}}{{t_{i} }}\, \times \,100$$

(13)

p, t_i, o_i and e_i are the number of sample experiments, the value of the output variable obtained from the end result of the experiment, the value of the output layer found after the end element analysis, and the error value, respectively in Eqs. 9–13. The % error is calculated for all samples and the highest of them give the maximum percentage error (Eq. 11). Mean absolute percent error (MAPE) values are found by dividing the percent error totals by the sample number. In Eq. 10, the closeness of RMSE to 0 is used as a criterion indicating the success rate of the developed model. In Eq. 11, R² is a coefficient that indicates the correspondence between the actual experimental results and the model results. The closer to R² value to 1, the higher the success rate of the developed model. Equation 13 shows the applicability of the smallest MAPE value model in the equation.

Table 5 gives the root mean square error (RMSE), the coefficient of determination (R²), and the mean absolute percent error (±% MAPE) values of the constitutive models based on Johnson–Cook and modified JC.

Table 5 Error control table for constitutive models

The comparison of experimental and predicted values by the Johnson–Cook and modified JC model under the strain rate of 10⁻³ s⁻¹ is shown in Figs. 6 and 7, respectively.

Fig. 6

Comparison of experimental and predicted values by the Johnson–Cook model

Fig. 7

Comparison of experimental and predicted values by the modified JC model

According Table 5, Figs. 6 and 7, the Johnson–Cook and modified JC models have been developed with high accuracy. However, the Johnson–Cook model is more accurate (%4.74 deviation) than modified JC model (%5.51 deviation). This situation proves that these two models are applicable and can be used in future research.

12 Microstructural Evolution

Microstructural analysis is important for determination of the flow behavior changes based on internal structure properties of the material. Thus, microstructural evolution has been evaluated in the last stage of the study. In this context, the samples have been cut perpendicular to compression direction before being mechanically ground and polished for microstructural evolution at different strain rates. The specimens have been electrolytically etched prior to examination in 10 pct HC1 in methanol at room temperature, and these samples are examined under optical microscope. The micrographs of the samples which are original and obtained with compression tests are presented in Fig. 6. The material structure is composed of equiaxed grains as shown in Fig. 8. While there is more elongation of the grains in a direction perpendicular to the direction of compression at low strain rate (Fig. 8b), at the same time, grain boundary orientation (banding) appears clearly. At high strain rate, the elongation of the grains is lower than that of low strain rates (Fig. 8c). This situation has been referred to dislocation locking. Moreover, the dynamic samples could not be compressed as quasi-static samples, since yield stress increases with increasing strain rate in high-speed compression (seen Fig. 4).

Fig. 8

Microstructure, SEM, and EDS of samples, a original, b low speed (10⁻³ s⁻¹), c) high speed (954 s⁻¹)

Additionally, energy-dispersive X-ray spectroscopy (EDS) analysis has also been conducted by scanning electron microscope (SEM) in order to evaluate the compositional variation of as-received material and the samples after compression tests. From Fig. 8, SEM images of the samples demonstrate that Nimonic 80A alloys are the precipitation-hardening nickel-based superalloys. This hardening phenomenon is provided by Ni₃Ti precipitates as shown in EDS analysis, as mentioned in Ref. [22].

13 Conclusion

This study has focused on determination of Johnson–Cook and modified JC parameters of a new material that will be important in aerospace and engineering areas requiring high-temperature characteristics. For this reason, Johnson–Cook and modified JC material parameters of Nimonic 80A nickel-based superalloy have been determined. The conclusions from this study are summarized below.

• The strain rate of 10⁻³ s⁻¹ was used in this study as the reference strain rate while 1 s⁻¹ was usually used in the literature. The use of very small strain rates might have caused the experiments to take a very long time. However, the use of the small strain rate (10⁻³ s⁻¹) meant the larger strain rate scale (ranging from 10⁻³ to 10³ s⁻¹). This large scale was found to be more appropriate in terms of giving accurate results for strain rate constant, because “C” constant was determined by taking average of “10⁻³–10³ s⁻¹” instead of “1–10³ s⁻¹”. At high strain rate, the elongation of the grains was lower than that of low strain rates since yield stress increased with increase in strain rate in high-speed compression.

• The Johnson–Cook model was more accurate (%4.74 deviation) than modified JC model (%5.51 deviation). This situation proved that the two models were applicable and could be used in future research.

• It was possible to simulate a finite element model of any plastic deformation process, especially forging, rolling, and deep drawing that generated compressive stress by using JC parameters of Nimonic 80A material determined by using the compression tests.

• The availability of the Johnson–Cook parameters of the material could be investigated by comparing the experimental and FEA analysis results.