Rock slope stability charts based on limit equilibrium method incorporating Generalized Hoek–Brown strength criterion for static and seismic conditions

Abstract

Stability charts present a graphical approach for the estimation of factor of safety (FOS) of a finite slope with uniform soil properties which are routinely used by geotechnical engineers. They provide a way for quick and efficient determination of stability of slopes sidestepping the need for carrying out actual analysis. In the present work, authors have developed stability charts of rock mass to determine global minimum FOS for rock slope stability problems. The rock mass is modelled by incorporating generalized Hoek–Brown strength criterion proposed by Hoek et al. (Hoek–Brown criterion—2002 edition, 2002). Limit equilibrium technique based Morgenstern and Price (Géotechnique 15:79–93, 1965) method is used to determine the value of factor of safety of the rock slope against failure. An evolutionary optimization method i.e. Particle swarm optimization (PSO) is used to search for the minimum FOS values and the associated critical failure surface out of all possible slip surfaces. A MATLAB code has been developed for this purpose. The charts have been developed for the entire range of Geological Strength Index (GSI) values ranging from 0 to 100 for intact rock mass characterized by the disturbance factor D = 0 for both static and seismic loading conditions. The seismic slope analysis is performed by an equivalent static method using a horizontal seismic coefficient (k_h) with values ranging from 0.10 to 0.30. Stability charts contain stability numbers which are inversely proportional to FOS value of the slope. In the present work, stability numbers are plotted for different inclination angles ($\beta$) equal to 15°, 30°,45°, 60° and 75^+°, respectively, for both static and seismic conditions considering the variations of other material parameters such as $m_{i}$ and ${\text{GSI}}$. Stability numbers are observed to increase with an increase in angle of inclination ($\beta$) of the slope and correspondingly FOS values follow a decreasing trend. However, stability numbers follow a decreasing pattern with increasing values of material parameters $m_{i}$ and ${\text{GSI}}$ designating improved rock quality with corresponding increase in FOS values of the rock slope.

Introduction

In previous decades, different strength criteria were suggested by various researchers to calculate the shear strength of the rock mass based on Hoek–Brown strength criterion (Hoek 1983; Londe 1988; Hoek and Brown 1997; Kumar 1998; Hoek et al. 2002; Carranza-Torres 2004; Priest 2005; Shen et al. 2012b, a). The nonlinear generalized Hoek–Brown failure criterion (Hoek et al. 2002) is famous among the scientist for determining the strength of rock mass. This criterion became widely popular among the researchers for estimating the shear strength of various types of intact and fractured rock mass (Priest 2005). Amongst other popular strength criterion for expressing soil/rock mass behavior such as Mohr–Coulomb criterion, more than one input parameters i.e. cohesion, angle of internal friction, dilation angles are needed. On the other hand, Hoek–Brown criterion uses uniaxial compressive strength ($\sigma_{{{\text{c}}i}}$), $m_{i}$ and ${\text{GSI}}$ as input parameters. Also, the initial condition and damage state of the material can be simulated in the criterion. When rock samples are tested in triaxial set up, their normal stress vs shear stress behavior shows a nonlinear pattern (Hoek 1983). Mohr–Coulomb failure criteria states that the relationship between normal and shear stress is linear. Hoek–Brown (1983) failure criteria and Generalized Hoek–Brown failure criteria (Hoek et al. 2002) are able to represent the nonlinear nature of the normal stress vs shear stress pattern of rock material. Because of nonlinear nature of normal stress vs shear stress behavior, it is necessary to determine instantaneous cohesion and instantaneous angle of internal friction while dealing with rocks. For linear Mohr–Coulomb criteria, cohesion and angle of internal friction will always remain constant over the entire range of failure envelop. Therefore, if Mohr–Coulomb failure criteria is used for representing rock material, the nonlinear normal stress vs shear stress pattern will not be properly modelled. The changing nature of both cohesion and angle of internal friction can be better evaluated from Hoek–Brown (1983) and generalized Hoek–Brown (Hoek et al. 2002) yield criteria over the entire range of failure envelop. Also, Mohr–Coulomb failure criteria gives a larger value of tensile strength compared to the tensile strength predicted by Hoek–Brown criteria (1983). Triaxial test results reveal that the tensile strength of rock predicted by Hoek–Brown criteria is nearer to the actual values. Furthermore, generalized Hoek–Brown (Hoek et al. 2002) introduced a disturbance factor $D$ which could be used to represent the initial damage state of the rock material in a very simple manner by considering the values of disturbance factor ranging from 0 to 1. This ability of considering initial damage state of the material is not available with Mohr–Coulomb failure criteria. Shi et al. (2016) developed modified form of Hoek–Brown failure criterion for anisotropic rock mass. Such flexibility obviously puts Hoek–Brown criterion in an advantageous position for expressing properties of rock materials. Ismael et al. (2014) suggested a simplified approach to directly consider intact rock anisotropy in Hoek–Brown failure criterion. Zuo et al. (2015) developed a different approach for theoretical derivation of the Hoek–Brown failure criterion for rock materials. In recent time, Hoek and Brown (2019) have demonstrated the practical application of the failure criterion using the parameter Geological Strength Index (GSI).

Recently, many researchers have performed the stability analysis of rock mass based on Hoek–Brown strength criterion. In geotechnical engineering, the stability analysis of the rock slope is an important problem and plays a major role when designs of tunnel, dam, road and other civil engineering structure are carried out. Sari (2019) analyzed the stability of cut slopes using empirical, kinematical, numerical and limit equilibrium methods.The problem of rock slope stability is a challenging task and engineers have concentrated on assessing the slope stability of rock mass (Hoek and Bray 1981; Goodman 1989; Wyllie and Mah 2004; Basahel and Mitri 2017). Analysis of rock slopes requires evaluation of factor of safety (FOS) for the sliding mass. Limit equilibrium techniques (Fellenius 1936; Janbu 1954; Bishop 1955; Lowe and Karafiath 1960; Morgenstern and Price 1965; Spencer 1967) are most famous among researchers for determination of FOS of any slopes against failure. In this context, stability charts have become a convenient way of determining the stability of any slope problem without carrying out extensive calculations. Taylor (1937) had developed first stability charts for soil slope based on limit equilibrium technique. Afterwards, many investigators have tried to develop stability chart for rock slope based on rock mass strength criteria, but it has proven very demanding task due to the difficulty involved in assessing the strength of rock mass. Many researchers have given idea to overcome the problem of estimating rock slope strength and analysis of rock slope stability such (Jaeger, 1971; Goodman and Kieffer 2000). For rock masses, the stability charts developed by Hoek and Bray (1981) serve the purpose of quick estimation of factor of safety of rock slopes for different slope geometries. Zanbak (1983) had developed stability charts for rock slopes susceptible to toppling. Lyamin and Sloan (2002) and Krabbenhoft et al. (2005) have developed finite element upper and lower bound technique for true stability solutions for geotechnical problem. Furthermore, stability charts were presented by Siad (2003) based on the upper bound approach which is useful for estimating FOS of rock slopes under seismic excitations.

Later, Li et al. (2008) developed stability chart-based solution based on Hoek–Brown criteria using numerical limit analysis. Li et al. (2009) also suggested stability chart solution based on limit analysis methods considering seismic effects on rock mass. In their work, pseudo-static method for determining the rock slope stability was adopted. More recently, Belghali et al. (2017) performed the pseudo-static stability analysis of rock slopes reinforced by passive bolts using the generalized Hoek–Brown criterion. Sun et al. (2019) performed experimental and numerical investigations of the seismic response of a rock–soil mixture deposit slope.

Furthermore, most of the earlier works on rock slope stability charts were based on limit analysis methods (Lyamin and Sloan 2002; Krabbenhoft et al. 2005; Li et al. 2008, 2009). It is a well-known fact that the upper bound limit analysis of slope will overestimate the factor of safety (FOS) of the slope; whereas, the lower bound limit analysis usually underestimates the FOS value unless the solutions are not exact. True or exact value of FOS will only be obtained if both upper and lower bound analysis show true convergence (Huang et al. 2013). That is why, traditional limit equilibrium approach with an appropriate optimization algorithm to find out the lowest FOS value and associated critical failure surface is deemed more reliable. Little efforts have been made to develop rock slope stability charts based on limit equilibrium techniques involving a proper optimization approach to arrive at the minimum FOS value and the corresponding critical failure surface incorporating GHB strength criteria. It is further observed that limit equilibrium-based approaches of rock slope analyses had used the concept of circular failure surfaces during slope analysis (Deng et al. 2017). The consideration of circular shape of failure surface may not represent the actual shape of failure surface. In this regard, a failure surface composed of piecewise linear segments is deemed more suitable for representing the actual shape failure surface as it has the ability to represent any general shape of failure surface. Recently, Kumar et al. (2019a, b) carried out rock slope analysis based on limit equilibrium method where failure surface was assumed to be composed of piecewise linear segments.

In this paper, authors have developed stability charts of rock mass to determine the global minimum FOS for rock slope stability problems. An appropriate nonlinear strength criterion is used in the form of generalized Hoek–Brown (GHB) criteria proposed by Hoek et al. (2002). Limit Equilibrium technique based Morgenstern and Price (1965) method is utilized to determine the value of factor of safety of the rock slope against failure. The method was developed specifically for any general shape of failure surface, including circular as well as non-circular shape, and it satisfies both force and moment equilibrium of all slices inside the failure mass. In the present work, trial failure surfaces are generated using piecewise linear segments which is considered suitable for representing any general shape of the failure surface. An evolutionary optimization method i.e. Particle Swarm Optimization (PSO) is used to search for the minimum FOS values and the associated critical failure surface out of all possible slip surfaces (Kumar et al. 2019a; Himanshu et al. 2020). Stability charts have been developed for both static and seismic loading conditions of intact rock slopes with different angle of inclinations ($\beta$) = 15°, 30°, 45°, 60° and 75°. A MATLAB code has been developed for this purpose. The charts have been developed for entire range of Geological Strength Index (GSI) values ranging from 0 to 100 for intact rock mass characterized by the disturbance factor D = 0. Both static and seismic analyses have been carried out while developing the stability charts for intact rock mass. Different values of horizontal seismic coefficients have been used while developing the charts considering seismic loading.

Methodology and modelling

Generalized Hoek–Brown failure criterion

To model the failure characteristics of different types intact and fractured rock mass, Hoek and Brown (1980, 1997) proposed the nonlinear failure criterion which gained popularity amongst researchers all over the world. Recently, a Generalized Hoek–Brown failure criterion (GHB) was proposed by Hoek et al. (2002) after modifying the originally proposed yield criterion. The GHB criterion is expressed as follows:

$$ \sigma_{1} = \sigma_{3} + \sigma_{ci} \left\{ {\left( {\frac{{m_{b} \sigma_{3} }}{{\sigma_{{{\text{ci}}}} }}} \right) + s} \right\}^{a} , $$

(1)

where $\sigma_{1}$ = major effective principal stress at failure.

$\sigma_{3}$ = minor effective principal stress at failure.

$\sigma_{ci}$ = uniaxial compressive strength of the intact rock material.

Here, $s$, $m_{b}$ and $a$ are Hoek–Brown material parameters. The parameter $m_{b}$ depends on its initial value $m_{i}$. The parameters $s$ and $a$ depend on the characteristics of the rock mass. These parameters are further expressed as functions of Geological Strength Index (GSI) of the rock mass and a disturbance D. The GSI values usually range from 0 to 100. A GSI value of 0 represents a rock mass of very poor quality; whereas, a value equal to 100 signifies intact rock with very good strength. The degree of interlocking of constituent blocks inside any rock mass is expressed using the term GSI. Hoek et al.(2002) introduced a disturbance factor D to express the presence of initial disturbance in the rock mass caused by stress relaxation and damage. The expressions of $s$, $m_{b}$ and $a$ are as follows:

$$ m_{b} = m_{i} \exp \left( {\frac{{{\text{GSI}} - 100}}{28 - 14D}} \right), $$

(2)

$$ s = \exp \left( {\frac{{{\text{GSI}} - 100}}{9 - 3D}} \right), $$

(3)

$$ a = 0.5 + \frac{{{\text{e}}^{{\left( {\frac{{ - {\text{GSI}}}}{15}} \right)}} - {\text{e}}^{{\left( {\frac{ - 20}{3}} \right)}} }}{6}, $$

(4)

where,$m_{i}$ is the Hoek–Brown constant for intact rock. Thus, Eqs. (3)–(4) cover the whole range of GSI values (0–100) in a very effective way. The generalized expression of the Hoek–Brown failure criterion in Eq. (1) can be represented as follows:

$$ \sigma_{1} = \sigma_{3} + \sigma_{{{\text{ci}}}} \left( {m_{{\text{f}}} } \right)^{a} , $$

(5)

where

$$ m_{{\text{f}}} = \left( {\frac{{m_{b} \sigma_{3} }}{{\sigma_{{{\text{ci}}}} }}} \right) + s. $$

(6)

In the Hoek and Brown (1997) failure criterion, the parameter $s$ was considered equal to zero for GSI less than 25. In GHB criterion proposed by Hoek et al.(2002), the parameter $s$ is modified to assume a very low positive value for low values of GSI. The GHB criterion with non-zero s is adopted in the present work to model the rock mass.

Equation (5) expresses the relationship between major and minor principal stresses of any rock mass as per GHB criterion (Hoek et al. 2002). A relationship proposed by Balmer (1952) may be utilized to express Eq. (5) in terms of normal and shear stresses. The procedure is as follows:

$$ \tau = \left( {\sigma_{n} - \sigma_{3} } \right)\sqrt {\frac{{\partial \sigma_{1} }}{{\partial \sigma_{3} }}} , $$

(7)

$$ \sigma_{n} = \sigma_{3} + \frac{{\sigma_{1} - \sigma_{3} }}{{\frac{{\partial \sigma_{1} }}{{\partial \sigma_{3} }} + 1}}. $$

(8)

Differentiating Eq. (1) with the respect of $\sigma_{3}$, we get

$$ \frac{{\partial \sigma_{1} }}{{\partial \sigma_{3} }} = 1 + am_{b} \left( {\frac{{m_{b} \sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{a - 1} . $$

(9)

After substituting Eq. (9) into Eqs. (7) and (8), respectively, the GHB criterion can be modified as follows:

$$ \tau = \left( {\sigma_{n} - \sigma_{3} } \right)\sqrt {1 + am_{b} \left( {\frac{{m_{b} }}{{\sigma_{ci} }}\sigma_{3} + s} \right)^{a - 1} } , $$

(10)

$$ \sigma_{n} = \sigma_{{3}} \, + \frac{{\sigma_{{{\text{ci}}}} \left( {\frac{{m_{b} \sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{a} }}{{2 + am_{b} \left( {\frac{{m_{b} \sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{a - 1} }} \, {.} $$

(11)

From the nonlinear shear stress $\left( \tau \right)$ vs. normal stress $\left( {\sigma_{n} } \right)$ failure envelop, the instantaneous angle of internal friction $\varphi_{i}$ can be expressed using general formula suggested by Balmer (1952):

$$ \tan \phi_{i} = \frac{\partial \tau }{{\partial \sigma_{n} }}. $$

(12)

Finally, to calculate an instantaneous angle of internal friction $\varphi_{i}$, the following expression can be used (Shen et al. 2012a):

$$ \varphi_{i} = \arcsin \left( {1 - \frac{2}{{2 + am_{b} \left( {\frac{{\sigma_{3} }}{{\sigma_{ci} }}m_{b} + s} \right)^{a - 1} }}} \right). $$

(13)

The instantaneous cohesion can be calculated by solving the Mohr–Coulomb strength equation:

$$ c_{i} = \tau - \sigma_{n} \tan \phi_{i} . $$

(14)

The instantaneous Mohr–Coulomb strength parameters (i.e. $c_{i}$ and $\phi_{i}$) are determined using Eqs. (7)–(14). Solving Eq. (11) is a challenging task since it is a nonlinear expression involving the term $\sigma_{{3}}$ which itself is initially unknown.

Solution of 2D Hoek–Brown yield criterion

Numerous triaxial tests on intact rocks of different types have revealed that the normal stress vs. shear stress behaviur is nonlinear (Hoek 1983). Therefore, it would be inappropriate to consider constant values of cohesion and angle of internal friction along the range of failure envelop as is done in case of linear Mohr–Coulomb failure criteria. Hoek (1983) stated that it would be more logical to estimate instantaneous effective cohesion $\left( {c^{\prime}} \right)$ and instantaneous effective angle of internal friction $\left( {\phi^{\prime}} \right)$ for rock materials under any applied normal stress $\left( {\sigma_{n} } \right)$. Equation (11) shows the GHB criteria as a function of normal stress $\left( {\sigma_{n} } \right)$, minor principal stress $\left( {\sigma_{3} } \right)$ and known GHB material parameters $s$,$m_{b}$ and $a$. While solving the generalized Hoek–Brown (GHB) strength criterion, the minor principal stress $\left( {\sigma_{3} } \right)$ is determined from Eq. (11) for any known value of applied normal stress $\left( {\sigma_{n} } \right)$. After obtaining the value of minor principal stress $\left( {\sigma_{3} } \right)$, Eqs. (13) and (14) are used to calculate the instantaneous values of Mohr–Coulomb shear strength parameters (i.e. $\varphi_{i}$ and $c_{i}$). Many researchers (Kumar 1998; Priest 2005; Shen et al. 2012a, b) proposed their own expressions to obtain the value of minor principal stress $\left( {\sigma_{3} } \right)$ from Eq. (11) and subsequently calculate the instantaneous Mohr–Coulomb shear strength parameters (i.e. $\varphi_{i}$ and $c_{i}$). Recently, Kumar et al. (2019b) developed a numerical procedure using Newton–Raphson method to solve Eq. (11) for minor principal stress $\left( {\sigma_{3} } \right)$ which is used in the present work for slope analysis and development of stability charts.

Generation of trial failure surface

Slope analysis using limit equilibrium technique starts with an assumption of any failure surface with a predetermined shape. It may be circular, logarithmic spiral or any other general shape. Different methods of trial failure surface generation and their performances have been reported earlier. Various researchers (Malkawi et al. 2001; McCombie and Wilkinson 2002; Cheng et al. 2007a, b; Kumar et al. 2019a) have discussed about different methods of generating trial failure surface and their performance in slope analysis. The trial failure surface must satisfy the condition of kinematic admissibility and should be concave upward. These requirements are fulfilled by satisfying the following equation:

$$ \alpha_{1} < \alpha_{2} < \cdots < \alpha_{{{\text{nsls}} - 1}} < \alpha_{{{\text{nsls}}}} , $$

(15)

where $\alpha_{i} \, =$ angle of inclination of the base of the ith slice.

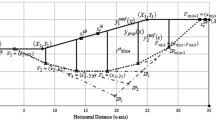
A simple technique for generating failure surface composed of piecewise linear segments is discussed in detail by Kumar et al. (2019a) and Himanshu et al. (2019). This method is used in the current work. The non-circular failure surface with discrete number of slices is characterized by three control variables $\left( {x_{{\text{l}}} , \, x_{{\text{r}}} , \, \alpha_{{\text{l}}} , \, \alpha_{{\text{r}}} } \right)$. The variables $(x_{{\text{l}}} , \, y_{{\text{l}}} )$ and $(x_{{\text{r}}} , \, y_{{\text{r}}} {)}$ describe the coordinates of initial and final intersection points of the slip surface with the ground surface. The angles $\alpha_{{\text{l}}}$ and $\alpha_{{\text{r}}}$ represent the vertical inclination angles of the base of initial and final slices, respectively. The procedure is depicted in Fig. 1 for any general slope and a trial failure surface composed of piecewise linear segments. The ordinates of two end points $y_{{\text{l}}}$ and $y_{{\text{r}}}$ are actually obtained using the equation of top surface of the slope $y_{1}^{{{\text{surf}}}} \left( x \right)$ for known values of $\left( {x_{{\text{l}}} ,x_{{\text{r}}} } \right)$ and therefore are treated as dependent variables. That is why, $\left( {x_{{\text{l}}} , \, x_{{\text{r}}} , \, \alpha_{{\text{l}}} , \, \alpha_{{\text{r}}} } \right)$ are treated as the controlling variable while generating the trial failure surface. Readers are requested to refer to the works of Kumar et al. (2019a) and Himanshu et al. (2019) where more details of the generation process of the non-circular trial failure surface can be found.

Fig. 1

(Source: Kumar et al. 2019a)

Trial non-circular failure surface.

The objective function of PSO

Analysis of any slope, as per limit equilibrium method, depends on the mobilized downward force aiding the movement and the resisting shear force acting against it. The factor of safety (FOS) is defined as the ratio of the resisting force and the mobilizing force

$$ f = {\text{FOS }} = \frac{{\sum {{\text{Sr}}_{i} } }}{{\sum {{\text{Sm}}_{i} } }}. $$

(16)

Here, $\sum {{\text{Sr}}_{i} }$ is the summation of the shear resistance and $\sum {{\text{Sm}}_{i} }$ is the summation of the mobilized shear. Zhu et al. (2005) presented an algorithm implementing Morgenstern and Price (1965) method for calculating FOS of any slope. A Matlab code was developed by Kumar et al. (2019a) implementing the algorithm presented by Zhu et al. (2005). In the present work, same code has been used for calculating the FOS of the rock slope implementing Morgenstern and Price (1965) method. A brief description of the algorithm is presented below:

$$ {\text{Shear strength }}\left( {{\text{resistance}}} \right){\text{ of}}\;{\text{slice:}}\;{\text{Sr}}_{i} = c^{\prime}_{i} l_{i} + N^{\prime}_{i} \tan \varphi^{\prime}_{i} , $$

(17)

$$ {\text{Shear stress }}\left( {{\text{mobilized}}} \right){\text{ of}} {\text{slice:}}\;{\text{Sm}}_{i} \, = (c^{\prime}_{i} l_{i} + N^{\prime}_{i} \tan \varphi^{\prime}_{i} )/F. $$

(18)

Here, $c^{\prime}_{i}$ and $\phi^{\prime}_{i}$ are effective cohesion and effective angle of internal friction applicable for the $i{\text{th}}$ slice. Also, $l_{i}$ and $N^{\prime}_{i}$ are the length of the base of the $i{\text{th}}$ slice and the effective normal force on it, respectively. Also, $F$ is the factor of safety applied to obtain developed or mobilized shear strength.

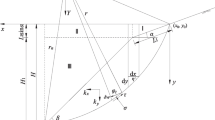
Morgenstern and Price (1965) method considers both inter-slice normal force $({\text{En}})$ and inter-slice shear force $({\text{Es}} = f^{n} \lambda {\text{ En}})$ with variable force function $f^{n}$ along the slice as shown in Fig. 2. Here, $\lambda$ is defined as scaling factor. In the present work, author uses a half-sine force function for $f^{n}$ while evaluating FOS.

Fig. 2

Forces acting on $i{\text{th}}$ slice

Figure 2 shows a typical slice $\left( i \right)$ having width $w_{i}$, height $h_{i}$ and base angle $\alpha_{i}$. The base–normal $N^{\prime}_{i}$ is obtained by observing the equilibrium of all vertical forces acting on the slice as follows:

$$ N^{\prime}_{i} = (W_{i} + {\text{Es}}_{i + 1} - {\text{Es}}_{i} )\cos \alpha_{i} + ( - k_{h} \, W_{i} - {\text{En}}_{i + 1} + {\text{En}}_{i} )\sin \alpha_{i} - U_{i} . $$

(19)

In Eq. (19), $W_{i}$, $U_{i}$ and $k_{h}$ are the weight, pore pressure and horizontal seismic coefficient for the $i{\text{th}}$ slice. From the consideration of equilibrium of all horizontal forces on $i{\text{th}}$ slice, the expression of mobilized shear force ${\text{Sm}}_{i}$ can be obtained as follows:

$$ {\text{Sm}}_{i} \, = (c^{\prime}_{i} l_{i} + N^{\prime}_{i} \tan \varphi^{\prime}_{i} )/F_{i} = (W_{i} + {\text{Es}}_{i + 1} - {\text{Es}}_{i} )\sin \alpha_{i} - ( - k_{h} \, W_{i} - {\text{En}}_{i + 1} + {\text{En}}_{i} )\cos \alpha_{i} . $$

(20)

Using the relationship ${\text{Es}} = f^{n} \lambda {\text{ En}}$ and substituting Eq. (19) into Eq. (20), following expression can be obtained:

$$ \begin{gathered} {\text{En}}_{i + 1} [(\sin \alpha_{i} - f_{i + 1}^{n} \, \lambda \cos \alpha_{i} ){\text{tan}}\varphi_{i}^{{\prime }} + (\cos \alpha_{i} + f_{i + 1}^{n} \, \lambda \sin \alpha_{i} )F] \, - {\text{Sr}}_{i}^{{\prime }} \hfill \\ \, = {\text{En}}_{i} [(\sin \alpha_{i} - f_{i}^{n} \, \lambda \cos \alpha_{i} ){\text{tan}}\varphi_{i}^{{\prime }} + (\cos \alpha_{i} + f_{i}^{n} \, \lambda \sin \alpha_{i} )F] \, - {\text{Sm}}_{i}^{{\prime }} . \hfill \\ \end{gathered} $$

(21)

The forces ${\text{Sr}}_{i}^{{\prime }} {\text{ and Sm}}_{i}^{{\prime }}$ represent the total shear resistance and mobilized shear for any particular $i{\text{th}}$ slice. The expressions of ${\text{Sr}}_{i}^{{\prime }} {\text{ and Sm}}_{i}^{{\prime }}$ are as follows:

$$ {\text{Sr}}_{i}^{{\prime }} = (W_{i} {\text{ cos}}\alpha_{i} - k_{h} \, W_{i \, } {\text{sin}}\alpha_{i} - U_{i} ){\text{tan}}\varphi_{i}^{{\prime }} + c_{i}^{{\prime }} l_{i} , $$

(22)

$$ {\text{Sm}}_{i}^{{\prime }} = W_{i} {\text{ sin}}\alpha_{i} + k_{h} \, W_{i} {\text{ cos}}\alpha_{i} . $$

(23)

Equation (21) is rearranged in a modified form as follows:

$$ {\text{En}}_{i + 1} \, \chi_{i + 1} \, \eta_{{{\text{i}} + {1}}} = {\text{En}}_{i} \, \chi_{i} - F{\text{ Sm}}_{i}^{{\prime }} + {\text{Sr}}_{i}^{{\prime }} , $$

(24a)

$$ \chi_{i} = (\sin \alpha_{i} - f_{i}^{n} \, \lambda \cos \alpha_{i} ){\text{tan}}\varphi^{\prime}_{i} + (\cos \alpha_{i} + f_{i}^{n} \, \lambda \sin \alpha_{i} )F, $$

(24b)

$$ \chi_{i + 1} = (\sin \alpha_{i + 1} - f_{i + 1}^{n} \, \lambda \cos \alpha_{i + 1} ){\text{tan}}\varphi^{\prime}_{i + 1} + (\cos \alpha_{i + 1} + f_{i + 1}^{n} \, \lambda \sin \alpha_{i + 1} )F, $$

(24c)

$$ \eta_{i + 1} = {{[(\sin \alpha_{i} - f_{i + 1}^{n} \, \lambda \cos \alpha_{i} ){\text{tan}}\varphi_{i}^{{\prime }} + (\cos \alpha_{i} + f_{i + 1}^{n} \, \lambda \sin \alpha_{i} )F]} \mathord{\left/ {\vphantom {{[(\sin \alpha_{i} - f_{i + 1}^{n} \, \lambda \cos \alpha_{i} ){\text{tan}}\varphi_{i}^{{\prime }} + (\cos \alpha_{i} + f_{i + 1}^{n} \, \lambda \sin \alpha_{i} )F]} {\chi_{i + 1} }}} \right. \kern-\nulldelimiterspace} {\chi_{i + 1} }}. $$

(24d)

In Eq. (24a), the inter-slice normal forces should meet the boundary conditions i.e. boundary values for two end slices at left and right of the failure surface. The boundary values are: ${\text{En}}_{1} = {\text{En}}_{{{\text{nsls}} + 1}} = 0$. Using the conditions of force equilibrium, the factor of safety (FOS) can be obtained as:

$$ {\text{FOS}} = F = \frac{{{\text{Sr}}_{1}^{{\prime }} + \sum\nolimits_{i = 2}^{{i = {\text{nsls}}}} {\left( {{\text{Sr}}_{i}^{{\prime }} \prod\nolimits_{j = 2}^{j = i} {\eta_{j} } } \right)} }}{{{\text{Sm}}_{1}^{{\prime }} + \sum\nolimits_{i = 2}^{{i = {\text{nsls}}}} {\left( {{\text{Sm}}_{i}^{{\prime }} \prod\nolimits_{j = 2}^{j = i} {\eta_{j} } } \right)} }}. $$

(25)

The readers are requested to refer to the work of Zhu et al. (2005) for more detailed description for solving Eq. (25).

Particle Swarm Optimization method to search for the critical failure surface

It is important to find out the critical failure surface with minimum FOS out of all possible failure surfaces. For this purpose, Particle Swarm Optimization (PSO) is used in the present work. While generating a segmented piecewise linear failure surface in the present work, four control variables are involved. The left most coordinate $(x_{{\text{l}}} )$ and rightmost x-coordinate $(x_{{\text{r}}} )$ of the trial failure surface constitute first two variables/particles. The angles made by the leftmost slice ($\alpha_{{\text{l}}}$) and the rightmost slice ($\alpha_{{\text{r}}}$) with the horizontal form the next two variables/particles. Any particle in the swarm is defined as:

$$ P_{i} = { (}x_{{i{\text{l}}}} {, }x_{{i{\text{r}}}} {, }\alpha_{{i{\text{l}}}} {, }\alpha_{{i{\text{r}}}} {)}^{T} \, \in {\text{ A; }}i = \, 1, 2, 3, \, 4, \ldots ,N. $$

(26)

The position ($X_{i}^{k}$) and velocity ($V_{i}^{k}$) are constantly updated as the particles move inside the search space A. Here $k$ represents the number of iteration steps in PSO algorithm. Therefore,

$$ X_{i}^{k} \, = \, \left( {x_{i1}^{k} {, }x_{i2}^{k} , \, x_{i3}^{k} , \, x_{i4}^{k} } \right) \, \in {\text{ A, }}i = \, 1, 2, 3,{ 4,} \ldots ,N, $$

(27)

$$ V_{i}^{k} \, = ( \, v_{i1}^{k} {, }v_{i2}^{k} , \, v_{i3}^{k} { , }v_{i4}^{k} {)}^{T} \quad i = \, 1, 2, 3,{ 4,} \ldots ,N. $$

(28)

In the early form of PSO, each particle employs Eq. (29) to update their velocity (Eberhart and Kennedy 1995; Kennedy and Eberhart 1995; Eberhart et al. 1996)

$$\begin{aligned}V_{i}^{k + 1} &= \, V_{i}^{k} \, + \, c_{1} \, \times {\text{rand}}_{1} \, \times { (}X_{{{\text{pbest}}}}^{k} - X_{i}^{k} {) } \\& \quad+ \, c_{2} \, \times {\text{ rand}}_{2} \, \times { (}X_{{{\text{sbest}}}}^{k} \, - \, X_{i}^{k} {)}{\text{.}}\end{aligned}$$

(29)

The early PSO variants (Shi and Eberhart 2008) are plagued by the problem of premature convergence and thus were unable to find the optimized solution. To alleviate this problem, another parameter ($\omega$), the inertia weight coefficient is introduced to original equation resulting into new velocity Eq. (30) of PSO (Eberhart and Shi 1998; Shi and Eberhart 1998)

$$\begin{aligned}V_{i}^{k + 1} & = \, \omega^{{\text{k}}} \, \times \, V_{i}^{k} \, + \, c_{1} \, \times {\text{rand}}_{1} \, \times { (}X_{{{\text{pbest}}}}^{k} - \, X_{i}^{k} {) } \\& \quad + \, c_{2} \, \times {\text{ rand}}_{2} \, \times { (}X_{{{\text{sbest}}}}^{k} \, - X_{i}^{k} {)}{\text{.}}\end{aligned}$$

(30)

The inertia weight ($\omega$) can be assumed to follow a linearly decreasing pattern between maximum ($\omega_{{{\text{max}}}}$) and minimum ($\omega_{{{\text{min}}}}$) values as follows:

$$ \omega^{k} \, = \, \omega_{{{\text{max}}}} - { (}\omega_{\max } \, - \, \omega_{{{\text{min}}}} ) \, \frac{k}{{k_{{{\text{max}}}} }}. $$

(31)

Later, contemporary standard PSO (CS-PSO) version was developed by Clerc and Kennedy (2002) in which velocity of the particles is updated as follows:

$$\begin{aligned}V_{i}^{k + 1} & = \, \eta \, \times \, V_{i}^{k} \, + \, c_{1} \, \times {\text{rand}}_{1} \, \times { (}X_{{{\text{pbest}}}}^{k} - \, X_{i}^{k} {) } \\& \quad + \, c_{2} \, \times {\text{ rand}}_{2} \, \times { (}X_{{{\text{sbest}}}}^{k} \, - \, X_{i}^{k} {)}{\text{.}}\end{aligned}$$

(32)

For all the above cases-mentioned, particle’s positions are updated as follows:

$$ X_{i}^{k + 1} \, = \, X_{i}^{k} \, + \, V_{i}^{k + 1} . $$

(33)

The constriction coefficient $(\eta )$ is determined as suggested by Clerc and Kennedy (2002):

$$ \eta = \frac{2}{{\left| {2 - \phi - \sqrt {\phi^{2} - 4\phi } } \right|}}, $$

(34)

where $\phi = c_{1} + c_{2}$.

The cognitive $(c_{1} )$ and social $(c_{2} )$ parameters in Eq. (34) in CS-PSO variant are considered equal to 2.05. In this present work, contemporary standard PSO with velocity clamping is used. This is required so that the modified velocity does not make the particle jump out from the domain of interest. A bound is applied as follows:

$$ \left| {V_{i}^{k + 1} } \right| \le V_{\max } \quad i = \, 1, 2, 3,{ 4,} \ldots ,N. $$

(35)

Restriction is also applied on the updated value of particle’s position so that it will also not move beyond the search space A. A bound is applied as follows:

$$ \left| {X_{i}^{k + 1} } \right| \le X_{\max } \quad i = \, 1, 2, 3,{ 4,} \ldots ,N. $$

(36)

The upper and lower bound of particle position are expressed as $X_{\max } = \left( {x_{{\text{l}}}^{{{\text{ub}}}} , \, x_{{\text{r}}}^{{{\text{ub}}}} , \, \alpha_{{\text{l}}}^{{{\text{ub}}}} , \, \alpha_{{\text{r}}}^{{{\text{ub}}}} } \right)$ and $X_{\min } = \left( {x_{{\text{l}}}^{{{\text{lb}}}} , \, x_{{\text{r}}}^{{{\text{lb}}}} , \, \alpha_{{\text{l}}}^{{{\text{lb}}}} , \, \alpha_{{\text{r}}}^{{{\text{lb}}}} } \right)$, respectively.

Formulation of stability chart

Stability charts present a series of graphs which are useful for estimation of the factor of safety (FOS) of any slope with known geometry and material properties. These graphs eliminate the need for carrying out actual stability analysis of the slope and provide an alternative way for quick and efficient analysis of any slope. Ever since Taylor (1937) introduced stability charts for clayey slopes, many researchers embraced the idea to develop stability charts for rock slopes (Michalowski 2002, 2010; Gao et al. 2013; Eid 2014; Sun et al. 2017). The effects of the seismic loadings (Yang et al. 2004; Yang 2007) and pore pressure (Yang and Zou 2006) on the rock slope stability were considered. Li et al. (2008) suggested stability chart-based solution based on Hoek–Brown criteria using numerical limit analysis. Li et al. (2009) also proposed stability chart solution based on limit analysis methods consider with seismic effect for rock mass. In this analysis, Li et al. (2009) had adopted Pseudo-static method for determining the rock slope stability.

It is desirable to build such charts for rock slopes based on generalized Hoek–Brown strength criterion of rock mass (Hoek et al. 2002). In the present study, stability charts for rock slopes have been developed incorporating generalized Hoek–Brown material parameters. The FOS of the slope is determined using limit equilibrium method based Morgenstern and Price (1965) formulation. Particle Swarm Optimization (PSO) technique is used to determine the critical failure surface with global minimum FOS for rock slope stability problems. The associated material properties of rock mass are: uniaxial compressive strength ($\sigma_{ci}$), Geological Strength Index (GSI), intact rock mass parameter m_i, unit weight of rock mass ($\gamma$), height of slope (H) and slope angle ($\beta$). In this article, stability charts have been prepared for slope angles ($\beta$) = 15°, 30°, 45°, 60° and 75°. Considering a FOS F for any slope, the stability number is defined as:

$$ N = \frac{{\sigma_{ci} }}{{\gamma {\text{HF}}}}. $$

(37)

Results and discussion

In this paper, authors have strived to develop stability charts of rock slopes incorporating GHB criterion proposed by Hoek et al. (2002). Morgenstern and Price (1965) method based on limit equilibrium technique is adopted to determine the value of factor of safety of the rock slope against failure. An evolutionary optimization method i.e. Particle Swarm Optimization (PSO) is used to search for the minimum FOS values and the associated critical failure surface out of all possible slip surfaces. A MATLAB code has been developed for this purpose. The charts have been developed for entire range of Geological Strength Index (GSI) values ranging from 0 to 100 for intact rock mass characterized by the disturbance factor D = 0. The associated material properties of rock mass have been taken from the works of Li et al. (2008). The corresponding values of minimum FOS are presented in Table 1. The results presented in Table 1 show that minimum factor of safety (FOS) values decrease with increasing slope angle $\left( \beta \right)$. It can also be observed that calculated stability numbers obtained from Eq. (37) decrease with increasing GSI and m_i.

Table 1 Analysis of rock slope stability and develop the stability chart based on limit equilibrium M–P method (material properties as per Li et al. 2008)

Figure 3a–e present the rock stability charts for the rock slope angles $\beta$ = 15°, 30°, 45°, 60° and 75° for range of GSI values and $m_{i}$ mentioned in Table 1. The figures reveal that the stability numbers increase with increasing inclination angles of rock slope for given GSI and $m_{i}$. Correspondingly, factor of safety (FOS) will tend to decrease with increasing slope angle $\beta$. However, if any individual stability chart for any given slope angle is studied, it can be seen that the stability number N follows a decreasing pattern if the parameters GSI or $m_{i}$ increase.

Fig. 3

Stability number from limit equilibrium M–P method at different GSI values for different slope angles a $\beta = 15{^\circ }$, b $\beta = 30{^\circ }$, c $\beta = 45{^\circ }$, d $\beta = 60{^\circ }$, e $\beta = 75{^\circ }$

It is desirable to check the type of slope failure (i.e. base failure, face failure or toe failure) which will take place for the stability charts developed and presented in Fig. 3a–e. Figure 4a presents the critical failure surface (CFS) for the parameters GSI = 50, $m_{i}$ = 25 and slope angle $\beta$ = 15⁰. It is seen that the induced slope failure corresponds to deep-seated base failure. For other values of material properties (i.e. GSI and $m_{i}$), base failures have been observed at the same slope angle (i.e. $\beta$ = 15°). Figure 4b shows the CFS for the chosen rock parameters GSI = 50, $m_{i}$ = 25 and $\beta$ = 30°. However, in this case, toe failure is found to take place. Similarly, for $\beta$ = 45°, 60° and 75°, toe failures happen as observed in Fig. 4c–e, respectively. Furthermore, if the material parameters are altered for any give slope angle $\beta$ (i.e. for either of 30°, 45°, 60° and 75°), the observed failure mode only corresponds to toe failure. Therefore, it may be inferred that base failure is the most likely mode failure for low value of slope angle $\beta$. If the slope angle increases (i.e. $\beta \ge 30{^\circ }$), the mode of failure gradually shifts from base to toe failure. From this study, it is also observed that the value of factor of safety increases with decreasing slope angle of rock mass. For all the charts presented in Fig. 3a–e and CFS shown in Fig. 4a–e, Particle Swarm Optimization (PSO) method has been used to search the CFS. In the present study, the calculated values of stability numbers are very close to those obtained by Li et al. (2008, 2009) where limit analysis technique was used to perform slope analysis.

Fig. 4

Critical failure surface (CFS) for GSI = 50 and m_{i =} 25 at different slope angles a $\beta = 15{^\circ }$, b $\beta = 30{^\circ }$, c $\beta = 45{^\circ }$, d $\beta = 60{^\circ }$, e $\beta = 75{^\circ }$

Stability charts for seismic loading conditions

Next, the stability charts have been developed for the rock slope considering the effect of seismic loading. During rock slope stability analysis, the intact rock mass has an uniaxial compressive strength $\left( {\sigma_{ci} } \right)$, intact rock yield parameter $\left( {m_{i} } \right)$, unit weight $\left( \gamma \right)$ and geological strength index $\left( {{\text{GSI}}} \right)$. These values are usually considered constant throughout the slope. The effect of seismic excitation is incorporated by considering the presence of an equivalent pseudo-static horizontal force equal to $k_{{\text{h}}} W$ acting on the slope mass. Here, $k_{{\text{h}}}$ is the horizontal seismic coefficient and $W$ is the weight of any slice. The limit equilibrium-based Morgenstern–Price method has been utilized to calculate the value of FOS of the rock slope. PSO is used to search for the CFS out of all considered failure surfaces along with the corresponding minimum FOS value of the slope.

In this study, the stability charts are developed considering for horizontal seismic coefficient $k_{h}$ = 0.1, 0.15, 0.20, 0.25 and 0.30 with different slope angles $\beta$ = 15°, 30°, 45°, 60° and 75°, respectively. The stability charts shown in Fig. 5a–e correspond to the case $k_{{\text{h}}}$ = 0.1 for different values of slope angle. If the stability charts are compared with those presented in Fig. 3a–e for non-seismic case, it is observed that the stability number N increases. Correspondingly, the FOS values for seismic case decrease compared to the non-seismic case. The stability charts presented in Fig. 5a–e follow similar trends with those presented for non-seismic case with respect to change in material parameters (i.e. GSI and $m_{i}$) and slope angle $\beta$. The stability number $N$ follows a decreasing pattern with increasing values of GSI and $m_{i}$. On the other hand, if the slope angle $\beta$ increases, the stability number $N$ is found to increase with corresponding decrease in FOS value of the slope.

Fig. 5

Stability number from limit equilibrium M–P method at different GSI values with $k_{{\text{h}}}$ = 0.10 for different slope angles a $\beta = 15{^\circ }$, b $\beta = 30{^\circ }$, c $\beta = 45{^\circ }$, d $\beta = 60{^\circ }$, e $\beta = 75{^\circ }$

The stability charts shown in Fig. 6a–e correspond to the case when $k_{{\text{h}}}$ = 0.15 for different values of slope angles. If the stability charts are compared with those presented in Fig. 3a–e for non-seismic case and Fig. 5a–e for seismic case with $k_{{\text{h}}}$ = 0.10, it is observed that the stability number N increases. Correspondingly, the FOS values for seismic case $k_{{\text{h}}}$ = 0.15 decrease compared to the non-seismic case and for seismic case with $k_{{\text{h}}}$ = 0.10.

Fig. 6

Stability number from limit equilibrium M–P method at different GSI values with $k_{{\text{h}}}$ = 0.15 for different slope angles a $\beta = 15{^\circ }$, b $\beta = 30{^\circ }$, c $\beta = 45{^\circ }$, d $\beta = 60{^\circ }$, e $\beta = 75{^\circ }$

The stability charts presented in Fig. 6a–e follow similar trends as those presented for non-seismic case and seismic case for $k_{h}$ = 0.1 with respect to change in material parameters (i.e. GSI and $m_{i}$) and slope angle $\beta$. The stability number $N$ follows a decreasing trend with increasing values of GSI and $m_{i}$. On the other hand, if the slope angle $\beta$ increases, the stability number $N$ increases with corresponding decrease in FOS value of the slope.

Figure 7a–e show the stability charts with $k_{{\text{h}}}$ = 0.20 for different values of slope angles $\beta$ = 15°, 30°, 45°, 60° and 75°, respectively. In all these cases, the stability number N is found to increase with corresponding decrease in FOS values as the slope angle $\beta$ and the horizontal seismic coefficient $k_{{\text{h}}}$ increase. The nature of the stability charts is found to follow similar pattern with respect to change in material parameters i.e. GSI and $m_{i}$. If the values GSI and $m_{i}$ increase signifying better-quality rocks, the stability number $N$ decreases with corresponding increase in FOS values.

Fig. 7

Stability number from limit equilibrium M–P method at different GSI values with $k_{{\text{h}}}$ = 0.20 for different slope angles a $\beta = 15{^\circ }$, b $\beta = 30{^\circ }$, c $\beta = 45{^\circ }$, d $\beta = 60{^\circ }$, e $\beta = 75{^\circ }$

In a similar manner, stability charts have been developed considering the value of horizontal seismic coefficient $k_{{\text{h}}}$ = 0.25 which have been presented in Fig. 8a–e. If the stability charts for $k_{{\text{h}}}$ = 0.25 are compared with previous cases, it can be seen that the stability number shifts upwards indicating corresponding fall in the value of factor of safety of the slope. However, the trends of Fig. 8a–e resemble the charts developed for lower values of $k_{{\text{h}}}$.

Fig. 8

Stability number from limit equilibrium M–P method at different GSI values with $k_{{\text{h}}}$ = 0.25 for different slope angles (a) $\beta = 15^{0}$, (b) $\beta = 30^{0}$, (c) $\beta = 45^{0}$, (d) $\beta = 60^{0}$, (e) $\beta = 75^{0}$

Also, stability charts have been developed for $k_{{\text{h}}}$ = 0.30 for slope geometries with varying slope angles. These charts are presented in Fig. 9a–e. The nature of the stability charts again follows similar trend as previously discussed up to angle $\beta$ = 15°, 30°, 45° and 60° in Fig. 9a–d. But the nature of the stability chart for angle $\beta$ = 75° and $k_{h}$ = 0.30 has been found to be different in Fig. 9e. It is found that for $m_{i} \ge 15$ and ${\text{GSI}} \le 50$, the trend of variation of stability number becomes flatter with increase in $m_{i}$. Similar trends were reported by Li et al. (2009) for slope angle $\beta$ = 75° and $k_{{\text{h}}}$ = 0.30. Generally, it is expected that FOS values should increase with corresponding improvement of material parameter $m_{i}$ signifying better rock quality, a trend that did not emerge from Fig. 9e. Therefore, the results shown in Fig. 9e (for $\beta$ = 75° and $k_{{\text{h}}}$ = 0.30) should be considered with caution. Hence, further investigations are necessary when rock slopes are analyzed for high slope angles and high lateral seismic coefficients considering Hoek–Brown strength criterion.

Fig. 9

Stability number from limit equilibrium M–P method at different GSI values with $k_{h}$ = 0.30 for different slope angles a $\beta = 15{^\circ }$, b $\beta = 30{^\circ }$, c $\beta = 45{^\circ }$, d $\beta = 60{^\circ }$, e $\beta = 75{^\circ }$

It would be interesting to investigate the nature of variation of stability number N with material parameter m_i with changing values of horizontal seismic coefficients $k_{{\text{h}}}$. The other material parameter (i.e. GSI) is considered to be constant while developing the plots shown in Fig. 10a–e for different slope angles $\beta$ = 15°, 30°, 45°, 60° and 75°, respectively. From Fig. 10a–e, it is observed that the stability number (N) of rock mass increases as the $k_{{\text{h}}}$ value increases. Therefore, the FOS values of the slope will decrease correspondingly.

Fig. 10

Stability number for different horizontal seismic coefficient ($k_{{\text{h}}}$) at different slope angles a $\beta = 15{^\circ }$, b $\beta = 30{^\circ }$, c $\beta = 45{^\circ }$, d $\beta = 60{^\circ }$, e $\beta = 75{^\circ }$

The variation between normalized major principal stresses $\left( {\frac{{\sigma_{3} }}{{\sigma_{ci} }}} \right)$ and minor principal stresses $\left( {\frac{{\sigma_{1} }}{{\sigma_{ci} }}} \right)$ has been calculated using Eq. (1) and presented in Fig. 11 for seismic loading case with (k_h = 0.10 and 0.30) for the entire extent of the failure surface. The material parameters considered are Geological strength index (GSI) = 100, $m_{i}$ = 15 and 35 and slope angle ($\beta$) = 60⁰. It is observed that the range of principal stress values of intact rock mass at GSI = 100, $m_{i}$ = 35 and k_h = 0.10 fall more in compression zone compared to GSI = 100, $m_{i}$ = 35 and k_h = 0.30. Similar behavior is observed for intact rock mass with GSI = 100, $m_{i}$ = 15 with k_h = 0.10 and 0.30. But the portion of principal stress is found to extend more towards tensile region when k_h is increased from 0.10 to 0.30. It is also found that the range of principal stress in the tension region is more for rock mass with GSI = 100 and $m_{i}$ = 15 than GSI = 100 and $m_{i}$ = 35.

Fig. 11

The Hoek–Brown failure envelop for variable m_i and horizontal seismic coefficient ($k_{{\text{h}}}$) with $\beta$ = 60⁰

Conclusions

In the present work, rock slope stability charts have been developed after incorporating the generalized Hoek–Brown strength criterion suggested by Hoek et al.(2002). Morgenstern and Price (1965) method has been used to determine the FOS of the rock slopes with failure surfaces assumed to be composed of piecewise linear segments. An evolutionary optimization method i.e. Contemporary Standard Particle swarm optimization (CS-PSO) has been used to search for the minimum FOS values and the associated critical failure surface. The charts have been developed for entire range of Geological Strength Index (GSI) values ranging from 0 to 100 for intact rock mass characterized by the disturbance factor D = 0. It is observed that the stability numbers follow an increasing pattern as the slope inclination increases. Also, the stability numbers follow a decreasing trend as the Hoek–Brown material parameter $m_{i}$ and GSI increase.

Both static and seismic analyses have been carried out while developing the stability charts for intact rock mass. The charts have been developed for slopes with inclination angles $\beta$ = 15°, 30°, 45°, 60° and 75°, respectively. When the slope angle is less (i.e. $\beta \le 15{^\circ }$), the mode of failure is identified as base failure. The mode of failure gradually shifts towards toe failure as the slope angle increases. Five values of horizontal seismic coefficient i.e. 0.10, 0.15, 0.20, 0.25 and 0.30 have been used while developing the stability charts for seismic loading condition. As the slope inclination increase, the stability numbers increase with corresponding reduction in associated factor of safety for both static and seismic case. Furthermore, it is also observed that the stability of the slope is adversely affected when higher seismic loading is applied. These results into increase in stability numbers compared to non-seismic case. It is observed that the nature of stability charts become flattish for high angle of inclination ($\beta \ge 75{^\circ }$) and horizontal seismic coefficient $k_{{\text{h}}} \ge 0.30$ with increasing $m_{i}$ values, a trend which does not quite fit with general notion. A decreasing trend of stability number $N$ with improving $m_{i}$ values would have more in the line with expectation. Therefore, this particular aspect deserves further attention from the researchers.

If the nature of principal stresses along the failure surface is observed, it can be found that the stresses increasingly shift towards tensile region as the magnitude of seismic loading and the slope inclination are increased. On the other hand, if the Hoek–Brown material constants i.e. GSI and m_i values are increased, the pattern of principal stresses along the failure surface shift towards compression region.