Introduction

One of the most important factors in wise management of water resources is a proper attitude and a vision of future events which may happen. This has not been exempted in water resources management. Awareness of the status of water resources in a region, especially in arid and semiarid regions, where groundwater is scarce and vital plays an important role in the planning process for different sectors such as domestic, industry and agriculture. Due to the stochastic nature of hydrologic parameters such as groundwater level, its status in the future can be predicted using statistical analysis, mathematical models, etc. Evaluation and forecast of groundwater level through specific models help in groundwater resources management. Hence, we can use time series modeling to predict groundwater level fluctuations during the following months for optimal and proper management of groundwater resources.

Since groundwater resources are mostly related to many factors and have complex fluctuations, it is necessary to decompose the complexity and their variations by mathematical methods (Lu et al. 2013). Among the different available robust tools, the artificial neural networks (ANNs) and ARIMA models are commonly used to hydro-climatological variables forecasting (Choubin et al. 2014; Sigaroodi et al. 2014; Choubin et al. 2016a, b, 2017a).

ARIMA models are a mathematical approach capable to simulating the both stationary and non-stationary time series. However, these models are lesser studied in the field of groundwater resources. In recent years, ARIMA model has been used for predicting hydro-meteorological parameters (e.g., Boochabun et al. 2004; Abghari et al. 2010; Chattopadhyay and Chattopadhyay 2010; Chattopadhyay et al. 2011; Zakaria et al. 2012). Also, Lee et al. (2009) used ARIMA model according to the Box–Jenkins method to groundwater level forecasting in Changwon, Korea.

The intelligence knowledge methods such as neural networks as have been applied for groundwater level forecasting (Coulibaly et al. 2001; Lin and Chen 2005; Daliakopoulos et al. 2005; Bidwell 2005; Nayak et al. 2006; Tsanis et al. 2008; Trichakis et al. 2009; Banerjee et al. 2009; Sethi et al. 2010; Dash et al. 2010; Behzad et al. 2010; Nourani et al. 2008; 2011; Shirmohammadi et al. 2013). However, in the previous studies, determining the optimal input variables for nonlinear models (such as ANN) in groundwater modeling is less considered. In this regard, Rashidi et al. (2016) mentioned that determination of optimal parameters in nonlinear modeling is important. They used gamma test to selecting the best input to simulate the suspended sediment. Also, Jajarmizadeh et al. (2015) applied gamma test to identifying the best combination of the input variables for support vector machines (SVM) to predict the stream flow in a semiarid basin in Iran.

Therefore, the objectives of this research are (1) determining the optimal input combination for ANN modeling approach; (2) selecting the best length of data during training and testing periods in the ANN model; and (3) comparing the performance of linear (ARIMA) and nonlinear (ANN) mathematical models in monthly groundwater level forecasting at a semiarid region of Iran. Besides the time series model considered for groundwater level forecasting, another advantage of this study is determining the optimal input combination and best length of training and testing data in the ANN model based on the gamma and M-tests.

Materials and methods

Study area and data

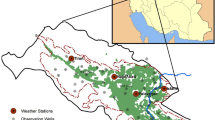
The study area is located in Shiraz basin, Fars province, southwestern Iran. Shiraz basin extends between 52°12′ and 52°45′ E longitude and 29° 25′ to 29° 58′ N latitude and 1450 km2. Location of Shiraz aquifer and piezometric monitoring wells, hydrometric and meteorological stations is shown in Fig. 1. The long-term average annual precipitation of Shiraz plain is 350 mm. The time period considered in this study is 18 years (1993–2010), and the data used are including monthly total precipitation, monthly average stream flow, temperature, evaporation and groundwater level.

Fig. 1
figure 1

Location of Shiraz basin, Iran

Full size image

ARIMA models

Box and Jenkins (1970) introduced autoregressive integrated moving average (ARIMA) models which are a class of linear models representing stationary and non-stationary time series. If non-stationarity (d) is combined to a mixed ARMA (p, q) model, then the general ARIMA (p, d, q) is obtained. Equation for non-seasonal ARIMA model of order (p, d, q) for a standard normal variable (Z t ) is as follows (Box and Jenkins, 1970):

$$ \varphi \left( B \right)\left( {1 - B} \right)^{d} Z_{t} = \theta \left( B \right)\,\varepsilon_{t} $$
(1)

In Eq. 1, ϕ(B) and θ(B) polynomial of degree p and q, respectively, are:

$$ \varphi (B) = 1 - \varphi_{1} B - \varphi_{2} B^{2} - \cdots - \varphi_{p} B^{p} $$
(2)
$$ \theta (B) = 1 - \theta_{1} B - \theta_{2} B^{2} - \cdots - \theta_{q} B^{q} $$
(3)

where p is the number of autoregressive terms, d is the number of differences and q is the number of moving average terms.

The time series modeling with Box–Jenkins approach is consisting three steps namely identification, estimation and diagnostic check (Box and Jenkins 1970). In this study, the time series were tested for normality and then Augmented Dickey–Fuller (ADF) and Phillips–Perron (PP) tests were used to analyze groundwater level time series stationarity. Non-stationary series converted to stationary ones through the method of differencing (Yurekli et al. 2007) that number of differencing determined the value of d. ADF or unit root test by Dickey and Fuller (1979) and PP method by Phillip and Perron (1988) were conducted. Then, the graphical properties of the autocorrelation function and the partial autocorrelation function were used in the estimation step, to determine the value of p and q. To select the best fitted model, we used the minimum amount of Akaike Information Criterion (AIC) and Schwarz Bayesian Criterion (SBC). In the general case, the AIC is (Akaike 1974):

$$ {\text{AIC}} = - 2\log (L) + 2m $$
(4)

where m is the number of parameters in the statistical model and L is the maximized value of the likelihood function for the estimated model. SBC criterion (Schwarz 1978) is similar in use to Akaike’s index which is defined as:

$$ {\text{SBC}} = - 2\log (L) + m\ln (n) $$
(5)

where n is denotes the number of observations.

In the diagnostic checking step, the models must be checked for adequacy. In this study, we used Kolmogorov–Smirnov (K–S) test and P–P plot to check the normality of residuals, while Portmanteau test was considered as the criterion to determine the independence of the residuals.

Artificial neural networks

An artificial neural network retrieved from natural nerve cells in order to transform the inputs into meaningful outputs. In this study, we used a feedforward artificial neural network called multilayer perceptron (MLP) for groundwater level forecasting. According to Kim and Valdés (2003), MLP is able to simulate 90% of the processes related with the climate. The Levenberg–Marquardt algorithm is one of the fastest methods implemented with high performance for neural network training (Huang et al. 2006). So, we have used it as the training algorithm in the MLP, also the Logsig and Purelin transfer function in the hidden and output layers. The time lags of t−1, t−2, t−3 and t−4 for input layers were chosen to forecasting of the monthly groundwater level from one to 4 months ahead (t + 1, t + 2, t + 3, t + 4), while hidden neurons was determined by trial-and-error process.

Gamma test

Koncar (1997) and Agalbjörn et al. (1997) reported the gamma statistic (Γ) which can provide the best mean square error in any nonlinear smooth models (Han et al. 2010). The gamma test is based on N [k,i], which are the kth (1 ≤ k ≤ p) nearest neighbors x N [k,i] for each vector x i(1 ≤ k ≤ p). Particularly, the gamma test is taken from the Delta function of the input vectors (Moghaddamnia 2009c),

$$ \delta_{m} \left( k \right) = 1/M\mathop \sum \limits_{i = 1}^{M} |x_{{N \left[ {k,i} \right]}} - x_{i} |^{2} \ldots \left( {1 \le \, k \, \le \, p} \right) $$
(6)

where|…| gives the meaning Euclidean distance, and the corresponding gamma function of the output values,

$$ \gamma_{m} \left( k \right) = 1/2M\mathop \sum \limits_{i = 1}^{M} \left| {y_{{N \left[ {k,i} \right]}} - y_{i} } \right|^{2} \ldots \left( {1 \le \, k \, \le \, p} \right) $$
(7)

where y N [k, i] is the corresponding y value for the kth nearest neighbor of xi in Eq. 6. In order to calculate Γ, a least squares regression line is constructed for the p points (δ m (k), γ m (k)).

$$ \gamma = \, A\delta + \, \varGamma $$
(8)

The intercept on the y axis (δ = 0) is the Γ value, as can be shown, γ m(k) → Var(r) in probability as δ m(k) → 0.

The graphical output of Eq. 7 provides valuable information. First, the intercept (Γ) on the y axis (or gamma) represents an estimate of the best MSE attainable utilizing a modeling method for unclear smooth functions of continuous variables (Evans and Jones 2002). Second, the gradient gives the complexity of model (whatever slope be steeper indicates that model have greater complexity), (Moghaddamnia 2009c). V-ratio returns a scale invariant noise estimate between 0 and 1. A V-ratio close to zero shows a high degree of predictability (by a smooth model) of the specific output. The V-ratio is obtained by dividing the gamma to the output data variance, (Durrant 2001). Smaller values of the gamma and V-ratio indicate the optimal combination of the used input data (Agalbjörn et al. 1997; Končar 1997).

M-test

Determining the proper length for the training data is important to improve the prediction (Choubin et al. 2014). Wingamma M-test curve is a method for determining the number of data required to produce a stable asymptote. Here, we used M-test based on the V-ratio and gamma value to select the best length of training and testing data in the neural networks method similar to some other works (e.g., Evans and Jones 2002; Remesan et al. 2008; Moghaddamnia et al. 2008; 2009a, b; Piri et al. 2009; Tsui et al. 2002; Piri et al. 2009; Singh 2005; Stefansson et al. 1997; Noori et al. 2010; Han et al. 2010). The values of V-ratio and gamma statistics are determined with increasing number of data points. Data length is determined based on M-test curve stabilized for a specific value of V-ratio and gamma statistics. This test reduces overfitting in the nonlinear modeling (Shamim et al. 2016).

Data normalization

Data normalization is the best way to ensuring data integrity and eliminating redundancy (Choubin et al. 2017b). Thus, the hydrologic data must be normalized, and the best range recommended for normalization is between 0.05 and 0.95 (Hsu et al. 1955). Thus, the series was normalized to the range [0.05, 0.95] as follows:

$$ X_{\text{norm}} = \, 0.05 + 0.95 \frac{{X - X_{\hbox{min} } }}{{X_{\hbox{max} } - X_{\hbox{min} } }} $$
(9)

where X norm and X r are the normalized and the original inputs, and X min and X max are the minimum and maximum of input ranges, respectively.

Performance criteria

The performance criteria used in the current research are RMSE, MAE and R (Eqs. 10, 11 and 12). Also, Violin plot (Hintze and Nelson 1998) was used to visual diagnostic analysis.

$$ {\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {(O_{i} - P_{i} )}^{2} } $$
(10)
$$ {\text{MAE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| ( \right.O_{i} - P_{i} \left. ) \right|} $$
(11)
$$ R = \frac{{\sum\limits_{i = 1}^{N} {(O_{i} - \overline{O} )(P_{i} - \overline{P} )} }}{{\sqrt {\sum\limits_{i = 1}^{N} {(O_{i} - \overline{O} )^{2} \sum\limits_{i = 1}^{N} {} (P_{i} - \overline{P} )^{2} } } }} $$
(12)

where N is the number of data points, O i and P i are the observed and predicted value, \( {\bar{\text{O}}} \) and \( {\bar{\text{P}}} \) are the mean of the observed and predicted values, respectively.

Results

Selection of the ARIMA model structure

At this step, the stationary and normality status of the GL time series were investigated. Table 1 shows the result of ADF and PP test before and after differencing. The null hypothesis of the ADF and PP test is H 0: θ = 0 (i.e., the data are non-stationary and need to be differenced to make it stationary). When the opposite hypothesis is true that P value is lower than confidence level (α = 0.01). Table 1 indicates unit root test for assessing the stationary status of the GL time series. First, unit root test was conducted for groundwater level time series (i.e., the observed data without any differencing). According to Table 1 and the significance level of ADF and PP test statistic (P value > 0.01), GL data are non-stationary and need to be converted to stationary ones for time series modeling. Then, stationarity of data was evaluated through first differencing of the time series. The results indicate that the GL time series is stationary after the first differencing (P value < 0.01; Table 1). Afterward, using the Box–Jenkins method in the estimation step, the orders of p and q (p ≤ 2 and q ≤ 4) were determined through the graphical properties of the autocorrelation function and the partial autocorrelation function. The best fitted model among the different models was identified based on the orders of p and q and evaluation of AIC and SBC criteria through trial-and-error method. The best model was ARIMA (2, 1, 2) with lowest AIC and SBC than other candidate models (114.2 and 129.9, respectively).

Table 1 ADF and P–P test for evaluation of stationary status of the GL time series
Full size table

The result of Portmanteau test showed that the residuals are independent, since Ljung–Box–Pierce statistic, i.e., Q statistic is less than χ 2 value (Q = 32.399 < χ 2 = 33.4) with degrees of freedom equal to 17 in the one percent confidence level. The normality of the residuals was confirmed through probability–probability (P–P) plot and Kolmogorov–Smirnov Test (Z value of K–S test is equal to 0.45 with the P value of 0.98 which is greater than 0.05, so the residuals distribution is normal). The result of Portmanteau test and K–S test showed that ARIMA (2, 1, 2) can be adequately used for prediction purposes. Table 2 shows the coefficients for the ARIMA (2, 1, 2) model. As regards to ϕ 1 + ϕ 2 < 1 and θ 1 + θ 2 < 1, the values obtained are allowable. Finally, the forecast of ARIMA (2, 1, 2) is generated by the following equation for the next month (t + 1).

$$ Y_{t + 1} = Y_{t} + \varphi_{1} Y_{t} - \varphi_{1} Y_{t - 1} + \varphi_{2} Y_{t - 1} - \varphi_{2} Y_{t - 2} - \theta_{1} e_{t} - \theta_{2} e_{t - 1} + c $$
(13)
$$ Y_{t + 1} = Y_{t} + 1. 7 2 8 1 { }Y_{t} - 1. 7 2 8 1 { }Y_{t - 1} - 0. 9 9 8 8 { }Y_{t - 1} + 0. 9 9 8 8 { }Y_{t - 2} - 1. 7 0 7 3 { }e_{t} + 0. 9 5 8 { }e_{t - 1} - 0. 0 0 6 $$
(14)

where Y is the groundwater level and e is the white noise (the difference between observed and predicted groundwater level).

Table 2 Coefficients of the ARIMA (2, 1, 2) model
Full size table

Model input selection and training data length

Mostly, the limiting factor on the predictive accuracy of the model will be measurement noise or insufficient data. Wingamma software package estimates the least mean squared error that any smooth data model can achieve on the given data without over-training. In this study, we have determined the best combination of input data, length of training and testing data with gamma test and M-test, respectively. To determine the best combination of input data, the different combinations were applied to assess their influence on the groundwater level modeling. We used genetic algorithms (GA) for finding the best combinations that the optimal combination has minimum of gamma (Г). The goal of model identification for a particular output is to choose a selection of inputs that minimizes the asymptotic value of the modulus of the gamma statistic. At each time step ahead (up to 4 ahead steps), we choose the suitable combination of the inputs including precipitation (P), stream flow (SF), temperature (T), evaporation (E) and groundwater level (GL). Table 3 shows the different combination for 1 month ahead. The optimal combination was selected on the basis of the least amount of V-ratio and gamma statistic. Table 3 clearly shows that V-ratio and gamma statistic in the 10111 mask are less than others. Therefore, the combination of precipitation (P), temperature (T), evaporation (E) and groundwater level (GL) can make a good model compared to the other inputs combination (for 1 month ahead).

Table 3 Determining the best combination for GL forecasting in 1 month ahead
Full size table

After achieving the optimal input combination, M-test was used to determine the proper length of training and testing data (Fig. 2) for the best combination of 10111 model (i.e., with P, T, E, GL) in the 1 time step ahead. M-test curve stabilized around 180 data points with the gamma statistic equal to 0.00083. The value of V-ratio is close to zero in the 180 data points which indicate a high degree of predictability of the output data by a smooth model. Therefore, the best length of training data is about 180 data (i.e., 83% of the total data). The result of gamma and M-test in the model input selection and training and testing data length for 1–4 time steps ahead is shown in Table 4.

Fig. 2
figure 2

M-test curve: the variation of gamma statistic and V-ratio with unique data points to determining the proper length for training data

Full size image
Table 4 Optimal input combination and data length obtained through gamma and M-test
Full size table

Results of forecasting groundwater level by ARIMA and MLP network

The multilayer perceptron (MLP) neural network and ARIMA modeling were done for forecasting groundwater level. We used the results of gamma test (the optimal input combination) and M-test (training and testing data length) to forecasting of groundwater level by MLP neural network (Table 4). The root-mean-square error (RMSE), mean absolute error (MAE) and correlation coefficient (R) were calculated to check the accuracy of the models performance (Table 5). The results indicate that ARIMA (2, 1, 2) has a better performance than the MLP. So that in the ARIMA model, RMSE and MAE values are less whiles the value of R is more than the MLP. It is noticeable that ARIMA model predicts based on the historical data, so the model performance is not different in the months ahead. The result of MLP (4, 14, 1) neural network shows that model has better performance in the 1 month ahead forecasting. MLP (4, 14, 1), i.e., multilayer perceptron network with 4 input neurons (obtained by the gamma test), 14 neurons in the hidden layer (obtained by trial and error) and has one output neuron. Figure 3 shows the scatter plot of testing data sets between the observed and forecasted by MLP (4, 14, 1) and ARIMA (2, 1, 2) for 1 month ahead. As shown, ARIMA have better fit with the observation (R 2 = 0.96) than MLP model (R 2 = 0.85). Figure 3 confirms higher accuracy of the results obtained from ANN and ARIMA in the forecasting GL and the observed versus forecasted data results by MLP and ARIMA in 1 month ahead are presented in Fig. 4.

Table 5 Performance of MLP and ARIMA models for GL forecasting
Full size table
Fig. 3
figure 3

Scatter plots between observed and forecasted data by MLP and ARIMA in 1 month ahead for testing data sets

Full size image
Fig. 4
figure 4

Observed versus forecasted data by MLP and ARIMA in 1 month ahead

Full size image

In addition to the performance criteria (Table 5) and scatter plot (Fig. 3), we applied the Violin plot (Hintze and Nelson 1998) to evaluate the model performance. This plot is a boxplot combined with kernel density plots, to show the probability distribution of the data (Choubin et al. 2017a). The Violin plot (Fig. 5) indicates the visual performance of models in forecasting the GL in 1 month ahead, where the ARIMA model has better fit with the observation compared with the MLP model. As, the median of the observed data is well predicted by ARIMA (white points in the graphs), also the 25th and 75th percentiles (thick lines in plots) in ARIMA have better fit than the MLP model. Although, ARIMA overestimated the 5th percentile (thin lower line in violin plots) of GL data than MLP but have closer fit with the observation in 95th percentile (thin upper line in the violin plots).

Fig. 5
figure 5

Violin plots for comparison of the models performance in 1 month ahead

Full size image

Discussions

One of the most important stages in sustainable utilization of groundwater resources is understand of groundwater level fluctuations. Exploitation and utilization of groundwater resources in the Shiraz aquifer and persistently drought periods in recent years are caused a dramatic reduction in groundwater table. As a result, forecasting the groundwater level as a tool for better and proper management is very crucial and important issue in this the plains.

In this study, we tried to forecast the groundwater level (GL) from one to four months ahead in Shiraz plain, Iran. The result of the ANN indicated that the model has better performance in the 1 months ahead forecasting. Similarly, Shirmohammadi et al. (2013) reported that prediction of groundwater level for 1 and 2 months ahead is better than 3 months ahead.

We also evaluated various performance criteria to examine the abilities of ANN and ARIMA models in forecasting the GL. Although the result of ANN model was satisfactory in the one month ahead forecasting (RMSE = 0.537, MAE = 0.446 and R = 0.874), the evaluation results showed that the ARIMA model performs better than the ANN (RMSE = 0.209, MAE = 0.171 and R = 0.980). Lee et al. (2009) have obtained satisfactory results for groundwater level forecasting by ARIMA model according to the Box–Jenkins method. Also, some other studies (Voudouris 2002; Aflatooni and Mardaneh 2011; Adhikary et al. 2012; Lu et al. 2013) have successfully demonstrated the performance of ARIMA model in the groundwater level forecasting. Lu et al. (2013) suggested that ARIMA model has less accuracy in groundwater level forecasting compared with the decomposition method in China. The scatter and violin plots of current study reveal that the predicted values have suitable fit with the observed data, both in ANN and in ARIMA models, although the ARIMA model performance is better than MLP neural network. Narayanan et al. (2013) suggested that ARIMA modeling is capable to forecast of premonsoon rainfall over the northwest part of India. Yang et al. (2009) indicated that the backpropagation ANN (BPANN) model is superior to the integrated time series (ITS) in forecasting the groundwater level time series.

Selection of the proper input variables and the training data length in the neural network method using gamma and M-test is one of the advantages of this study. Jajarmizadeh et al. (2015) and Rashidi et al. (2016) suggested that preprocessing the input variables in forecasting process by nonlinear models is important as confirmed by the current study results. Also, Kakaei Lafdani et al. (2013) indicated that ANN models based on gamma test can estimate accurately during training and testing periods.

According to the Moghaddamnia et al. (2009c), gamma test reduces huge workload of the trial-and-error process prior to the actual model development. One reason for efficiency of the gamma test is that it can immediately tell us directly from the data whether or not we have sufficient data form a smooth nonlinear model and how a model can present good results.

Conclusions

The results show that both of ANN and ARIMA have good forecasting accuracy, and they are suitable for the forecasting the groundwater level in semiarid regions. This study presented how the gamma test and M-test can be applied together to reduce the huge workload of the trial and error in nonlinear modeling process. In general, the potential of identifying the input parameters and best length of training data may turn gamma test and M-test as an efficient technique for preprocessing the data to predict the groundwater level. It might be helpful for future researches to use these methods as a time-consuming approach for swiftly attaining the appropriate results. We, in this study, indicated that both performance of MLP (4, 14, 1) and ARIMA (2, 1, 2) are satisfactory in the groundwater level forecasting for 1 month ahead. Some works have suggested that ANNs can be a promising alternative to the traditional ARMA structure; however, this study demonstrates that ARIMA model can be useful to predict the groundwater level.